Climate during the Last Glacial Maximum in the Northern Sawatch Range, Colorado, USA
Abstract
1. Introduction
2. Regional Setting
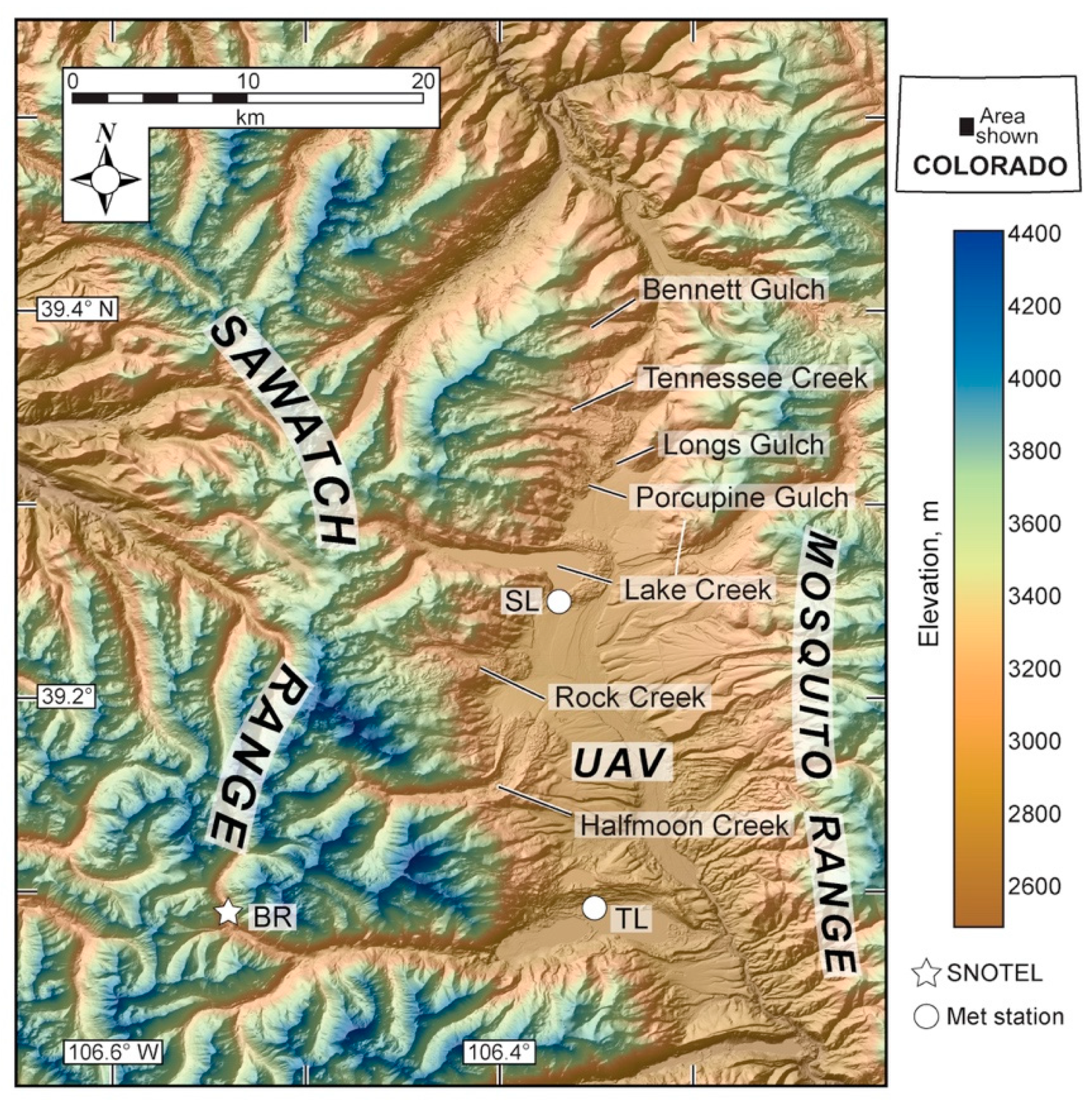
2.1. Geologic and Geomorphic Setting
2.2. Modern Climate
3. Materials and Methods
3.1. Cosmogenic Exposure Dating of LGM Moraines
3.2. Glacier Reconstruction
3.3. Temperature-Index Modeling and Simulation of Glacier Mass Balance
- (1)
- (2)
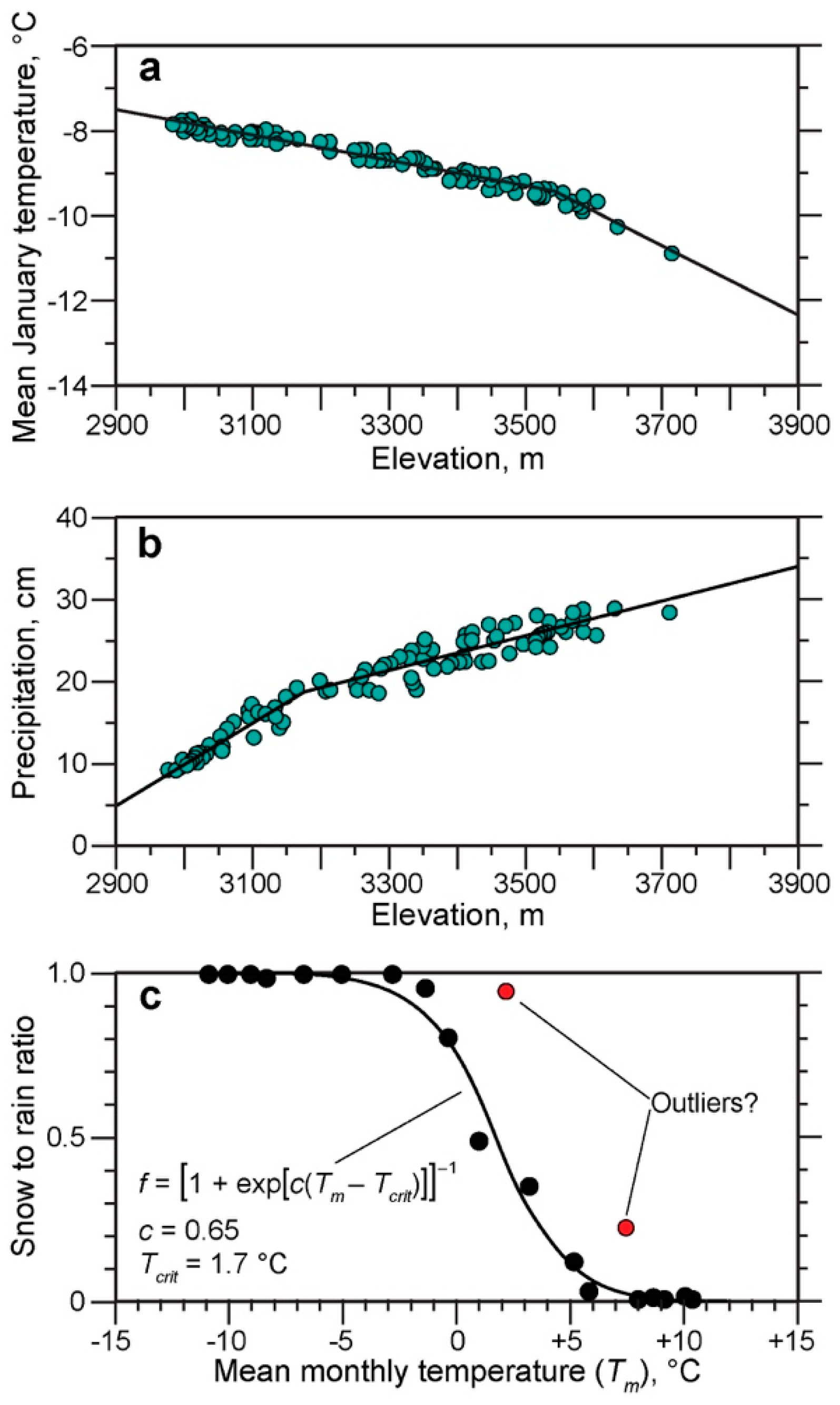
- Lacking a sufficient number of meteorological stations—especially at higher elevations—Tjan(z) is determined using the modern lapse rate for January obtained from PRISM climate data (Table 1) sampled over the extent of glacier surfaces in conjunction with a value of Tjan(z) at some reference elevation. PRISM data suggest two different lapse rates should be used in each valley according to the elevation interval under consideration, therefore data were fit using piecewise linear splines (Figure 3). The fitting routine [53] yields a continuous function that optimizes the elevation of the breakpoints (or knots) in the linear fits. Use of the spline fits resulted in slightly better agreement between the modeled and PRISM temperatures than did simple linear regressions.
- (3)
- Equation (4) also implies a uniform perturbation of temperature ∆T over the year, hence no temperature seasonality is examined in the present study.
- (4)
- Values of k in the valleys studied varied between 1.18 and 1.20 and were chosen to minimize the difference between simulated mean monthly temperatures and those obtained from the PRISM data and any relevant meteorological station(s) during the ablation season (May through September). Priority is given to the ablation season because of the temperature dependence of melting in the TM.
4. Results
4.1. 10Be Cosmogenic Exposure Ages
4.2. Glacier Reconstructions
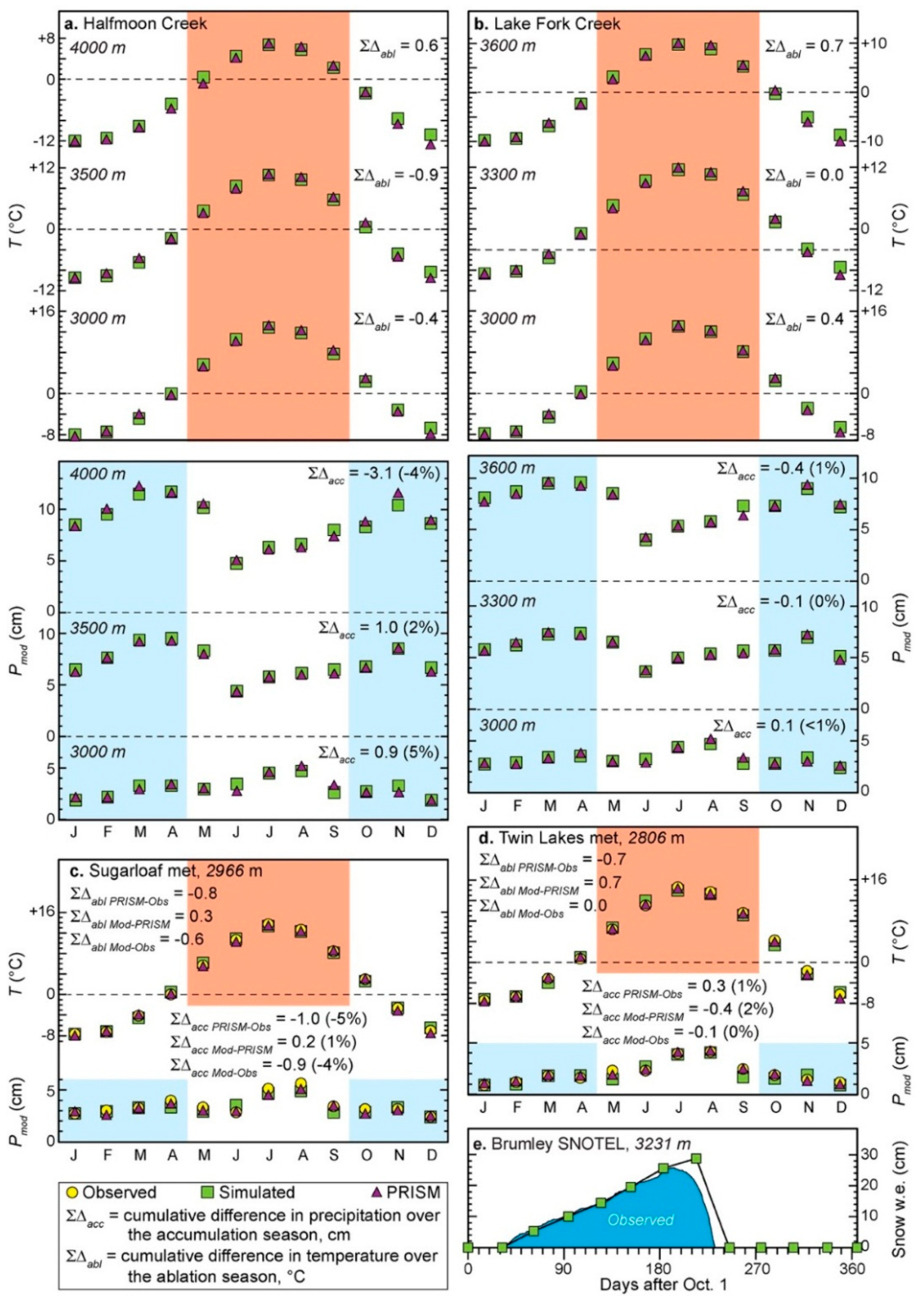
4.3. Temperature-Index Modeling: Model Skill
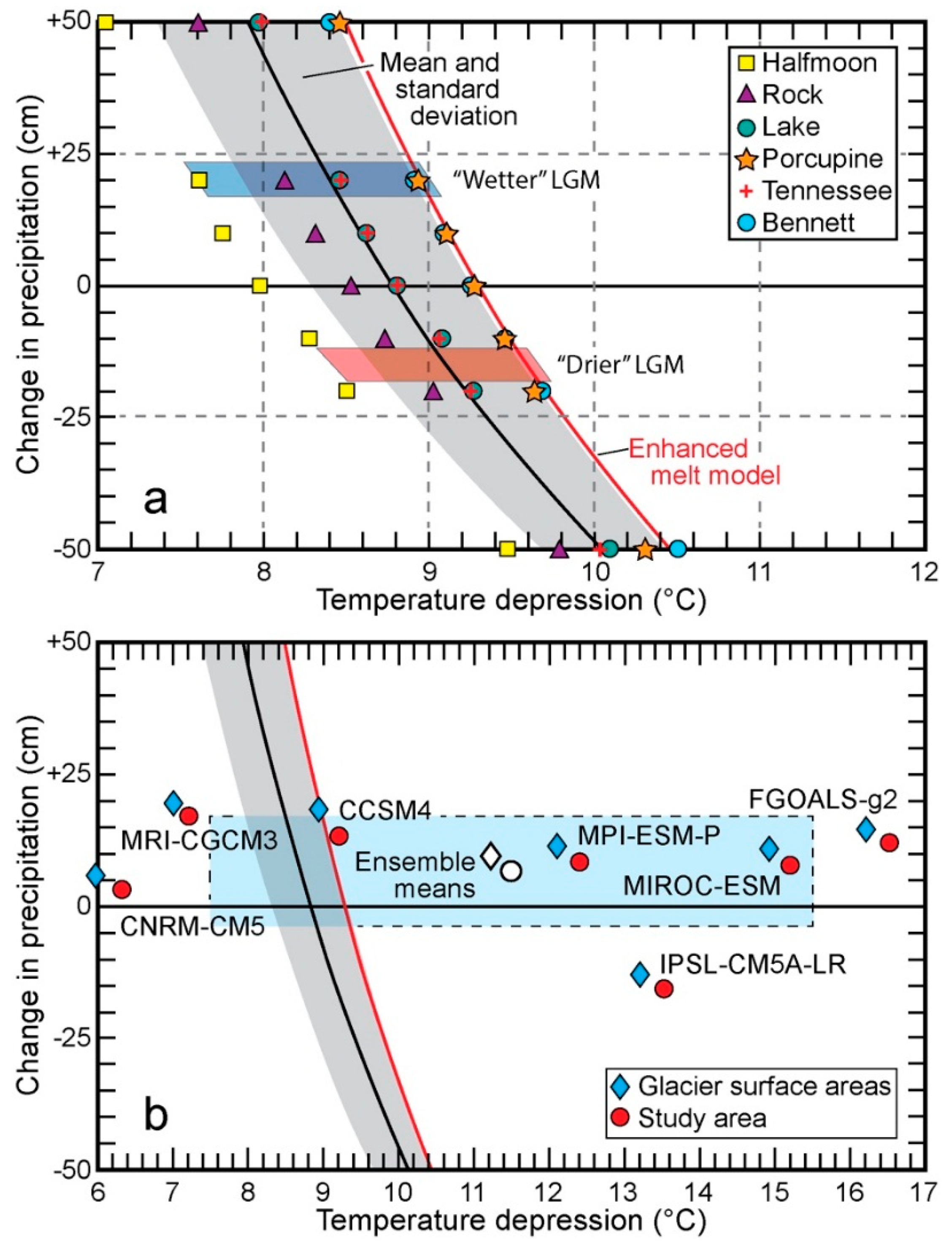
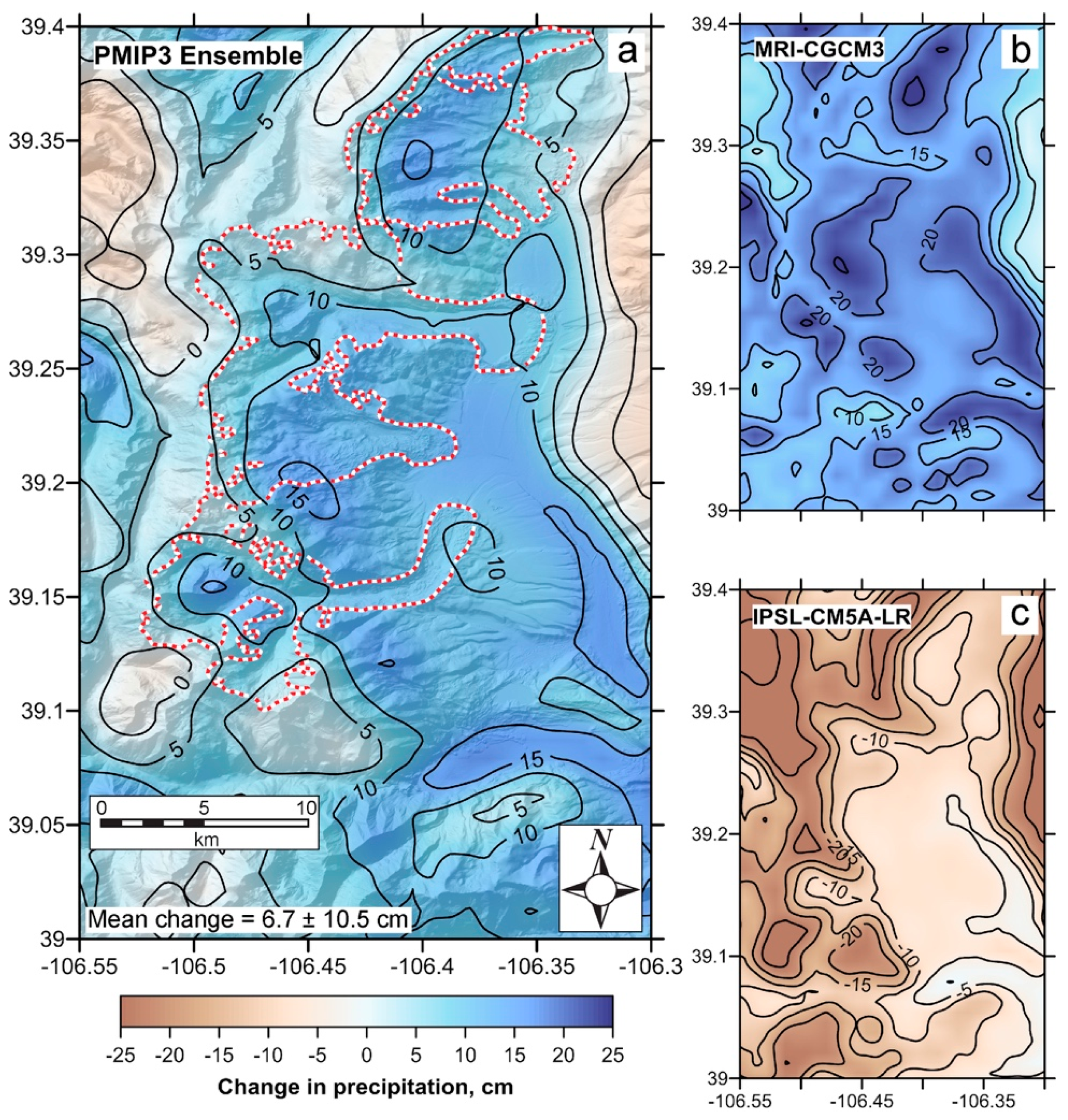
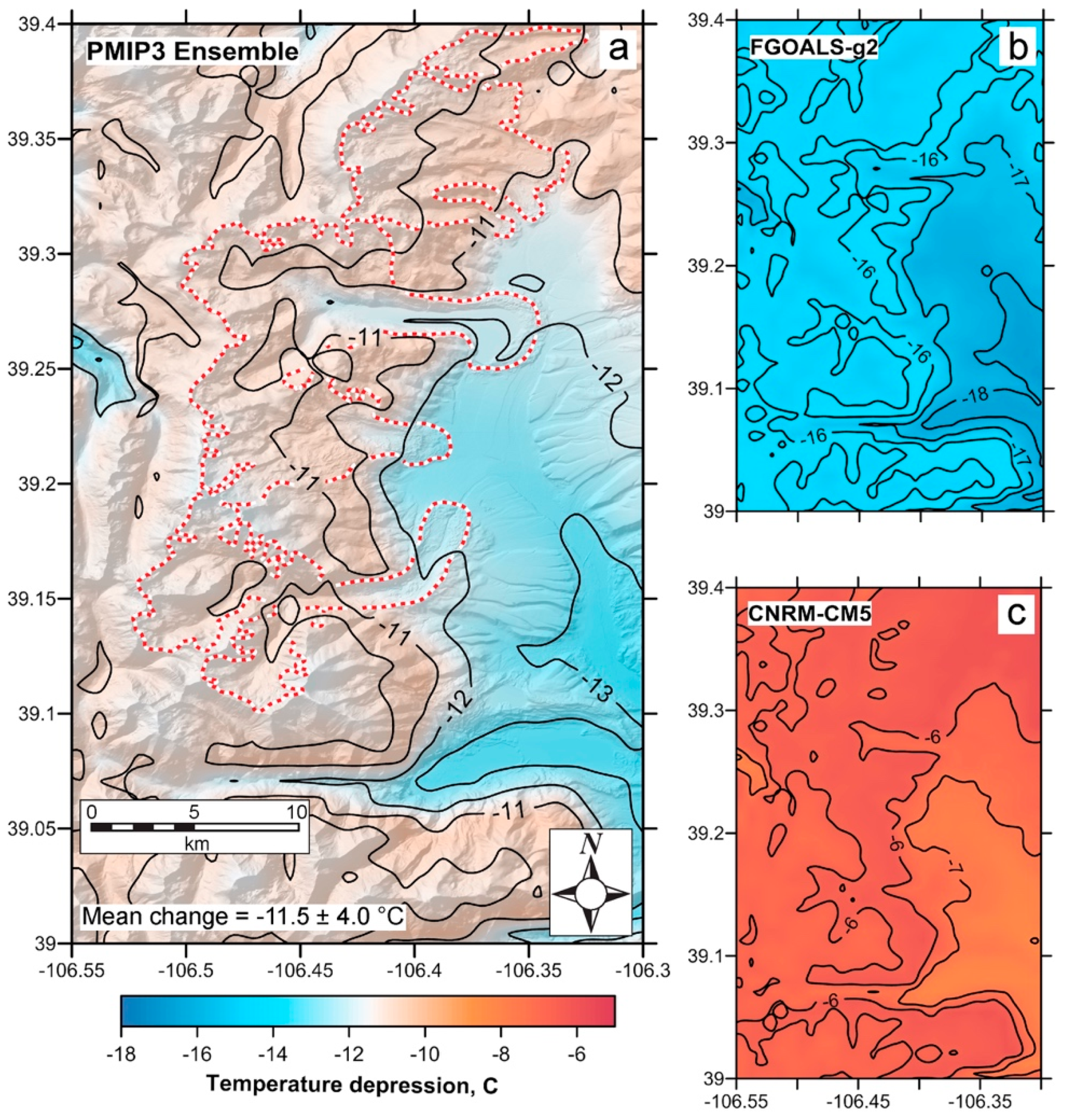
4.4. Temperature-Index Modeling: Inferring Late Pleistocene Glacial Climate
5. Discussion
5.1. Chronology of the Local LGM
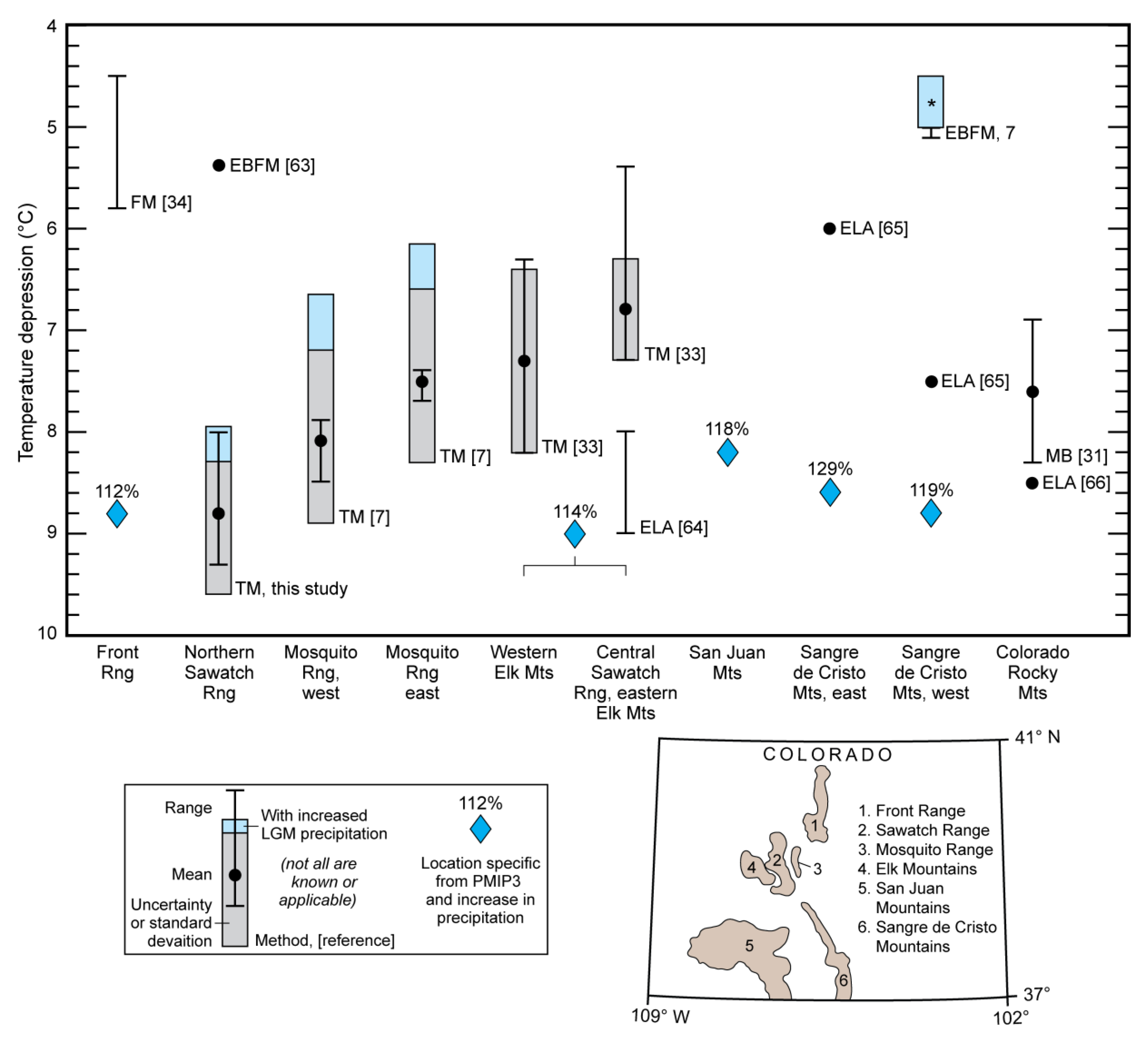
5.2. Regional LGM Temperature Depression and Constraints on Precipitation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Licciardi, J.M.; Clark, P.U.; Brook, E.J.; Elmore, D.; Sharma, P. Variable responses of western U.S. glaciers during the last deglaciation. Geology 2004, 32, 81–84. [Google Scholar] [CrossRef]
- Thackray, G.D. Varied climatic and topographic influences on late Pleistocene mountain glaciation in the western United States. J. Quat. Sci. 2008, 23, 671–681. [Google Scholar] [CrossRef]
- Laabs, B.J.C.; Refsnider, K.A.; Munroe, J.S.; Mickelson, D.M.; Applegate, P.J.; Singer, B.S.; Caffee, M.W. Latest Pleistocene glacial chronology of the Uinta Mountains: Support for moisture-driven asynchrony of the last deglaciation. Quat Sci. Rev. 2009, 28, 1171–1187. [Google Scholar] [CrossRef]
- Young, N.E.; Briner, J.P.; Leonard, E.M.; Licciardi, J.M.; Lee, K. Assessing climatic and non-climatic forcing of Pinedale glaciation and deglaciation in the western U.S. Geology 2011, 39, 171–174. [Google Scholar] [CrossRef]
- Leonard, E.M.; Laabs, B.J.C.; Plummer, M.A.; Kroner, R.K.; Brugger, K.A.; Spiess, V.M.; Refsnider, K.A.; Xia, Y.; Caffee, M.W. Late Pleistocene glaciation and deglaciation in the Crestone Peaks area, Sangre de Cristo Mountains, USA-chronology and paleoclimate. Quat. Sci. Rev. 2017, 158, 127–144. [Google Scholar] [CrossRef]
- Quirk, B.J.; Moore, J.R.; Laabs, B.J.C.; Caffee, M.W.; Plummer, M.A. Termination II, last glacial maximum, and late glacial chronologies and paleoclimate from Big Cottonwood Canyon, Wasatch Mountains, Utah. Geol. Soc. Am. Bull. 2018, 30, 1889–1902. [Google Scholar] [CrossRef]
- Brugger, K.A.; Laabs, B.; Reimers, A.; Bensen, N. Late Pleistocene glaciation in the Mosquito Range, Colorado, USA: Chronology and climate. J. Quat. Sci. 2019, 34, 187–202. [Google Scholar] [CrossRef]
- Shakun, J.D.; Clark, P.U.; He, F.; Lifton, N.A.; Liu, Z.; Otto-Bliesner, B.L. Regional and global forcing of glacier retreat during the last deglaciation. Nat. Comm. 2015, 6, 8059. [Google Scholar] [CrossRef]
- Laabs, B.J.; Leonard, E.M.; Licciardi, J.M.; Munroe, J.S. Cosmogenic chronologies of late Pleistocene glacial maxima along the crest of the Rocky Mountains, USA. AGU Fall Meet. Abstr. 2018. Available online: http://adsabs.harvard.edu/abs/2018AGUFMPP13D1353L (accessed on 8 July 2019).
- Leonard, E.M.; Laabs, B.J.C.; Schweinsberg, A.D.; Russell, C.M.; Briner, J.P.; Young, N.E. Deglaciation of the Colorado Rocky Mountains following the Last Glacial Maximum. Cuad. Investig. Geogr. 2017, 43, 497–526. [Google Scholar] [CrossRef]
- Schaefer, J.M.; Denton, G.H.; Barrell, D.J.; Ivy-Ochs, S.; Kubik, P.W.; Andersen, B.G.; Phillips, F.M.; Lowell, T.V.; Schlüchter, C. Near-synchronous interhemispheric termination of the last glacial maximum in mid-latitudes. Science 2006, 312, 1510–1513. [Google Scholar] [CrossRef] [PubMed]
- Shakun, J.D.; Clark, P.U.; He, F.; Marcott, S.A.; Liu, Z.; Otto-Bliesner, B.L.; Schmittner, A.; Bard, E. Global warming preceded by increasing carbon dioxide concentrations during the last deglaciation. Nature 2012, 484, 49. [Google Scholar] [CrossRef] [PubMed]
- Hostetler, S.W.; Clark, P.U. Climatic controls of western U.S. glaciers at the last glacial maximum. Quat. Sci. Rev. 1997, 16, 505–511. [Google Scholar] [CrossRef]
- Licciardi, J.M.; Pierce, K.L. History and dynamics of the Greater Yellowstone Glacial System during the last two glaciations. Quat. Sci. Rev. 2018, 200, 1–33. [Google Scholar] [CrossRef]
- Wagner, J.D.; Cole, J.E.; Beck, J.W.; Patchett, P.J.; Henderson, G.M.; Barnett, H.R. Moisture variability in the southwestern United States linked to abrupt glacial climate change. Nat. Geosci. 2010, 3, 110–113. [Google Scholar] [CrossRef]
- Asmerom, Y.; Polyak, V.J.; Burns, S.J. Variable winter moisture in the southwestern United States linked to rapid glacial climate shifts. Nat. Geosci. 2010, 3, 114–117. [Google Scholar] [CrossRef]
- Bartlein, P.J.; Harrison, S.P.; Brewer, S.; Connor, S.; Davis, B.A.S.; Gajewski, K.; Guiot, G.; Harrison-Prentice, T.I.; Henderson, A.; Peyron, O.; et al. Pollen-based continental climate reconstructions at 6 and 21 ka: A global synthesis. Clim. Dyn. 2011, 37, 775–802. [Google Scholar] [CrossRef]
- Lyle, M.; Heusser, L.; Ravelo, C.; Yamamoto, M.; Barron, J.; Diffenbaugh, N.S.; Herbert, T.; Andreasen, D. Out of the Tropics: The Pacific, Great Basin Lakes, and the late Pleistocene water cycle in the western United States. Science 2012, 337, 1629–1633. [Google Scholar] [CrossRef]
- Munroe, J.S.; Laabs, B.J.C. Temporal correspondence between pluvial lake highstands in the southwestern US and Heinrich Event 1. J. Quat. Sci. 2013, 28, 49–58. [Google Scholar] [CrossRef]
- Ibarra, D.E.; Egger, A.E.; Weaver, K.L.; Harris, C.R.; Maher, K. Rise and fall of late Pleistocene pluvial lakes in response to reduced evaporation and precipitation: Evidence from Lake Surprise, California. Geol. Soc. Am. Bull. 2014, 126, 1387–1415. [Google Scholar] [CrossRef]
- Ibarra, D.E.; Oster, J.L.; Winnick, M.J.; Caves Rugenstein, J.K.; Byrne, M.; Chamberlain, C.P. Warm and cold wet states in the western United States during the Pliocene-Pleistocene. Geology 2018, 46, 355–358. [Google Scholar] [CrossRef]
- Moseley, G.E.; Edwards, R.L.; Wendt, K.A.; Cheng, H.; Dublyansky, Y.; Lu, Y.; Boch, R.; Spötl, C. Reconciliation of the Devils Hole climate record with orbital forcing. Science 2016, 351, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Hudson, A.M.; Hatchett, B.J.; Quade, J.; Boyle, D.P.; Bassett, S.D.; Ali, G.; De los Santos, M.G. North-south dipole in winter hydroclimate in the western United States during the last glaciation. Sci. Rep. 2019, 9, 4826. [Google Scholar] [CrossRef]
- Kutzbach, J.E.; Wright, H.E., Jr. Simulation of the climate of 18,000 years BP: Results for the North American/North Atlantic/European sector and comparison with the geologic record of North America. Quat. Sci. Rev. 1985, 4, 147–187. [Google Scholar] [CrossRef]
- Kim, S.-J.; Crowley, T.J.; Erickson, D.J.; Govindasamy, B.; Duffy, P.B.; Lee, B.Y. High-resolution climate simulation of the last glacial maximum. Clim. Dyn. 2008, 31, 1–16. [Google Scholar] [CrossRef]
- Oster, J.L.; Ibarra, D.E.; Winnick, M.J.; Maher, K. Steering of westerly storms over western North America at the Last Glacial Maximum. Nat. Geosci. 2015, 8, 201–205. [Google Scholar] [CrossRef]
- Lora, J.M.; Mitchell, J.L.; Tripati, A.E. Abrupt reorganization of North Pacific and western North American climate during the last glaciation. Geophys. Res. Lett. 2016, 43, 11796–11804. [Google Scholar] [CrossRef]
- Lora, J.M.; Mitchell, J.L.; Risi, C.; Tripati, A.E. North Pacific atmospheric rivers and their influence on western North America at the Last Glacial Maximum. Geophys. Res. Lett. 2017, 44, 1051–1059. [Google Scholar] [CrossRef]
- Morrill, C.; Lowry, D.P.; Hoell, A. Thermodynamic and dynamic causes of pluvial conditions during the last glacial maximum. Geophys. Res. Lett. 2018, 45, 335–345. [Google Scholar] [CrossRef]
- Laabs, B.J.; Plummer, M.A.; Mickelson, D.M. Climate during the last glacial maximum in the Wasatch and southern Uinta Mountains inferred from glacier modeling. Geomorphology 2006, 75, 300–317. [Google Scholar] [CrossRef]
- Leonard, E.M. Modeled patterns of late Pleistocene glacier inception and growth in the Southern and Central Rocky Mountains, USA: Sensitivity to climate change and paleoclimatic implications. Quat. Sci. Rev. 2007, 26, 2152–2166. [Google Scholar] [CrossRef]
- Ward, D.W.; Anderson, R.S.; Guido, Z.S.; Briner, J.P. Numerical modeling of cosmogenic deglaciation records, Front Range and San Juan Mountains, Colorado. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef]
- Brugger, K.A. Climate in the southern Sawatch Range and Elk Mountains, Colorado, USA, during the Last Glacial Maximum: Inferences using a simple degree-day model. Arct. Antarct. Alp. Res. 2010, 42, 164–178. [Google Scholar] [CrossRef][Green Version]
- Dühnforth, M.; Anderson, R.S. Reconstructing the glacial history of green lakes valley, North Boulder Creek, Colorado Front Range. Arct. Antarct. Alp. Res. 2011, 43, 527–542. [Google Scholar] [CrossRef]
- Birkel, S.D.; Putnam, A.E.; Denton, G.H.; Koons, P.O.; Fastook, J.L.; Putnam, D.E.; Maasch, K.A. Climate inferences from a glaciological resconstruction of the late Pleistocene Wind River ice cap, Wind River Range, Wyoming. Arct. Antarct. Alp. Res. 2012, 44, 265–276. [Google Scholar] [CrossRef]
- Kellogg, K.S.; Shroba, R.R.; Ruleman, C.A.; Bohannon, R.G.; McIntosh, W.C.; Premo, W.R.; Cosca, M.A.; Moscati, R.J.; Brandt, T.R. Geologic map of the Upper Arkansas River Valley region, north-central Colorado. U.S. Geological Survey Sci. Investig. Map 2017, 3382. [Google Scholar] [CrossRef]
- Gosse, J.C.; Phillips, F.M. Terrestrial in situ cosmogenic nuclides: Theory and application. Quat. Sci. Rev. 2001, 20, 1475–1560. [Google Scholar] [CrossRef]
- Lifton, N.; Sato, T.; Dunai, T.J. Scaling in situ cosmogenic nuclide production rates using analytical approximations to atmospheric cosmic-ray fluxes. Earth Planet. Sci. Lett. 2014, 386, 149–160. [Google Scholar] [CrossRef]
- Lifton, N.; Caffee, M.; Finkel, R.; Marrero, S.; Nishiizumi, K.; Phillips, F.M.; Goehring, B.; Gosse, J.; Stone, J.; Schaefer, J.; et al. In situ cosmogenic nuclide production rate calibration for the CRONUS Earth project from Lake Bonneville, Utah, shoreline features. Quat. Geochronol. 2015, 26, 56–69. [Google Scholar] [CrossRef]
- Balco, G.; Stone, J.; Lifton, N.; Dunai, T. A complete and easily accessible means of calculating surface exposure ages or erosion rates from 10Be and 26Al measurements. Quat. Geochronol. 2008, 3, 174–195. [Google Scholar] [CrossRef]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers, 4th ed.; Elsevier: Boston, MA, USA, 2010. [Google Scholar]
- Nye, J.F. The flow of a glacier in a channel of rectangular, elliptic or parabolic cross-section. J. Glaciol. 1965, 5, 661–690. [Google Scholar] [CrossRef]
- Bindschadler, R.; Harrison, W.D.; Raymond, C.F.; Crossen, R. Geometry and dynamics of a surge-type glacier. J. Glaciol. 1977, 18, 181–194. [Google Scholar] [CrossRef]
- Yang, W.; Guo, X.; Yao, T.; Yang, K.; Zhoa, L.; Li, S.; Zhu, M. Summertime surface energy budget and ablation modeling in the ablation zone of a maritime Tibetan glacier. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Vincent, C.; Six, D. Relative contribution of solar radiation and temperature in enhanced temperature-index melt models from a case study at Glacier de Saint-Sorlin, France. Ann. Glaciol. 2013, 54, 11–17. [Google Scholar] [CrossRef]
- Réveillet, M.; Vincent, C.; Six, D.; Rabatel, A. Which empirical model is best suited to simulate glacier mass balances? J. Glaciol. 2017, 63, 39–54. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Brock, B.; Strasser, U.; Burlando, P.; Funk, M.; Corripio, J. An enhanced temperature-index glacier melt model including a shortwave radiation balance: Development and testing for Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2005, 175, 573–587. [Google Scholar] [CrossRef]
- Gabbi, J.; Carenzo, M.; Pellicciotto, F.; Bauder, A.; Funk, M. A comparison of empirical and physically based glacier surface melt models for long-term simulation of glacier response. J. Glaciol. 2014, 60, 1140–1154. [Google Scholar] [CrossRef]
- Matthews, T.; Hodgkins, R.; Wilby, R.L.; Gudmundsson, S.; Pálsson, F.; Björnsson, H.; Carr, S. Conditioning temperature-index model parameters on synoptic weather types for glacier melt simulations. Hydrol. Process. 2015, 29, 1027–1045. [Google Scholar] [CrossRef]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Braithwaite, R.J. Temperature and precipitation climate at the equilibrium-line altitude of glaciers expressed by the degree-day factor for melting snow. J. Glaciol. 2008, 54, 437–444. [Google Scholar] [CrossRef]
- Hodgkins, R.; Carr, S.; Pálsson, F.; Gudmundsson, S.; Björnsson, H. Sensitivity analysis of temperature-index melt simulations to near-surface lapse rates and degree-day factors at Vestari-Hagafellsjökull, Langjökull, Iceland. Hydrol. Process. 2012, 26, 3736–3748. [Google Scholar] [CrossRef]
- Muggeo, V.M.R. Segmented: An R package to fit regression models with broken-line relationships. R News 2008, 8, 20–25. [Google Scholar]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the coterminous United States. Int. J. Climatol. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Lowry, D.P.; Morrill, C. Is the Last Glacial Maximum a reverse analog for future hydroclimate changes in the America? Clim. Dyn. 2019, 52, 4407–4427. [Google Scholar] [CrossRef]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Climatologies at high resolution for the Earth’s land surface areas. Sci. Data 2017, 4, 170122. [Google Scholar] [CrossRef] [PubMed]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Data from: Climatologies at high resolution for the Earth’s land surface areas. Datadryad 2017. [Google Scholar] [CrossRef]
- Flato, G.; Marotzke, J.; Abiodun, B.; Braconnot, P.; Chou, S.C.; Collins, W.; Cox, P.; Driouech, F.; Emori, S.; Eyring, V.; et al. Evaluation of climate models. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M.M.B., Allen, S.K., Bosschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 741–866. [Google Scholar]
- Beyer, R.; Krapp, M.; Manica, A. A systematic comparison of bias correction methods for paleoclimate simulations. Clim. Past Discuss. 2019. in review. [Google Scholar] [CrossRef]
- Hawkins, E.; Ortega, P.; Suckling, E.; Schurer, A.; Hegerl, G.; Jones, P.; Joshi, M.; Osborn, T.J.; Masson-Delmotte, V.; Mignot, J.; et al. Estimating changes in global temperature since the preindustrial period. Bull. Am. Meteorol. Soc. 2017, 98, 1841–1856. [Google Scholar] [CrossRef]
- Annan, J.D.; Hargreaves, J.C. A perspective on model-data surface temperature comparisons at the Last Glacial Maximum. Quat. Sci. Rev. 2015, 107, 1–10. [Google Scholar] [CrossRef]
- Lorenz, D.J.; Nieto-Lugilde, D.; Blois, J.L.; Fitzpatrick, M.C.; Williams, J.W. Downscaled and debiased climate simulations for North America from 21,000 years ago to 2100 AD. Sci. Data 2016, 3, 160048. [Google Scholar] [CrossRef]
- Schweinsberg, A.D.; Briner, J.P.; Shroba, R.R.; Licciardi, J.M.; Leonard, E.M.; Brugger, K.A.; Russell, C.M. Pinedale glacial history of the upper Arkansas River valley: New moraine chronologies, modeling results, and geologic mapping. In Unfolding the Geology of the West, Proceedings of the Geological Society of America Field Guide; Keller, S.M., Morgan, M.L., Eds.; Geological Society of America: Boulder, CO, USA, 2016; Volume 44, pp. 335–353. [Google Scholar]
- Brugger, K.A.; Goldstein, B.S. Paleoglacier reconstruction and late Pleistocene equilibrium-line altitudes, southern Sawatch Range, Colorado. In Glacial Processes Past and Present; GSA Special Paper, 337; Mickelson, D.M., Attig, J.W., Eds.; Geological Society of America: Boulder, CO, USA, 1999; pp. 103–112. [Google Scholar]
- Refsnider, K.A.; Brugger, K.A.; Leonard, E.M.; McCalpin, J.P.; Armstrong, P.P. Last glacial maximum equilibrium-line altitude trends and precipitation patterns in the Sangre de Cristo Mountains, southern Colorado, USA. Boreas 2009, 38, 663–678. [Google Scholar] [CrossRef]
- Leonard, E.M. Climatic change in the Colorado Rocky Mountains: Estimates based on modern climate at late Pleistocene equilibrium lines. Arct. Alp. Res. 1989, 21, 245–255. [Google Scholar] [CrossRef]

| Valley | dTjan/dz (°C m−1) | dPWinter/dz (cm m−1) | dPSpring/dz (cm m−1) | dPSummer/dz (cm m−1) | dPFall/dz (cm m−1) |
|---|---|---|---|---|---|
| Halfmoon | +0.0005 (<3156 m) | 0.0312 (<3449 m) | 0.0400 (<3418 m) | 0.0108 (<3292m) | 0.0296 (<3417 m) |
| −0.0048 (>3156 m) | 0.0128 (>3449 m) | 0.0124 (>3418 m) | 0.0027 (>3292 m) | 0.0098 (>3417 m) | |
| Rock | −0.0026 (<3469 m) | 0.0244 (<3999 m) | 0.0297 (<3760 m) | 0.0071 (<3182m) | 0.0246 (<3770 m) |
| −0.0058 (>3469 m) | 0.0004 (>3999 m) | 0.0138 (>3760 m) | 0.0053 (>3182 m) | 0.0100 (>3770 m) | |
| Lake Fork | −0.0030 (<3539 m) | 0.0363 (<3171 m) | 0.0514 (<3168 m) | 0.0168 (<3060m) | 0.0425 (<3167 m) |
| −0.0080 (>3539 m) | 0.0228 (>3171 m) | 0.0210 (>3168 m) | 0.0034 (>3060 m) | 0.0174 (>3167 m) | |
| Porcupine | −0.0042 (<3307 m) | 0.0197 (<3244 m) | 0.0256 (<3257 m) | 0.0116 (<3229m) | 0.0176 (<3267 m) |
| −0.0019 (>3307 m) | 0.0268 (>3244 m) | 0.0321 (>3257 m) | 0.0215 (>3229 m) | 0.0236 (>3267 m) | |
| Tennessee | −0.0035 (<3482 m) | 0.0246 (<3567 m) | 0.0301 (<3565 m) | 0.0146 (<3160m) | 0.0199 (<3560 m) |
| −0.0058 (>3482 m) | 0.0073 (>3567 m) | 0.0090 (>3565 m) | 0.0028 (>3160 m) | 0.0057 (>3560 m) | |
| Bennett | −0.0016 (<3423 m) | 0.0152 | 0.0198 | 0.0039 | 0.0114 |
| −0.0075 (>3423 m) | - | - | - | - |
| Glacier | Area, km2 | Length, km* | Average Thickness, m† | Maximum Thickness, m† | Average Slope, Degrees | Average Driving Stress, kPa | AAR-Derived ELA† |
|---|---|---|---|---|---|---|---|
| Halfmoon Creek | 44.3 | 16.7 | 120 | 240 | 4.8 | 87 | 3475 |
| Rock Creek | 29.0 | 10.9 | 80 | 150 | 7.6 | 100 | 3385 |
| Lake Fork Creek | 63.6 | 15.0 | 140 | 260 | 4.2 | 100 | 3365 |
| Porcupine Gulch | 5.8 | 7.0 | 75 | 125 | 5.7 | 77 | 3310 |
| Tennessee complex | 38.2 | 9.7 | 80 | 150 | 6.0 | 84 | 3360 |
| Bennett Gulch | 8.3 | 6.9 | 75 | 115 | 5.6 | 79 | 3345 |
| Climate Parameters and Differences | Values | ||||
|---|---|---|---|---|---|
| Rock Creek | |||||
| Elevation, m (number of PRISM locations averaged) | 3000 (n = 5) | 3250 (n = 6) | 3500 (n = 6) | 3750 (n = 6) | 4000 (n = 4) |
| Modeled mean annual temperature, °C | 1.8 | 0.9 | 0.0 | −1.7 | −3.3 |
| PRISM mean annual temperature, °C | 1.8 ± 0.0 | 1.0 ± 0.0 | −0.1 ± 0.1 | −1.9 ± 0.1 | −3.7 ± 0.0 |
| Difference, °C | 0.0 | −0.1 | 0.1 | 0.2 | 0.4 |
| Mean ± standard deviation of monthly differences, °C | 0.0 ± 0.5 | −0.5 ± 0.6 | 0.1 ± 0.7 | 0.2 ± 0.7 | 0.3 ± 0.7 |
| Cumulative difference temperatures during ablation season, °C | −0.2 | −0.2 | <−0.1 | <0.1 | 0.5 |
| Modeled mean annual precipitation, cm | 41.1 | 62.4 | 83.4 | 103.9 | 118.3 |
| PRISM mean annual precipitation, cm | 40.4 ± 1.1 | 62.5 ± 3.8 | 83.2 ± 5.1 | 105.8 ± 3.2 | 117.7 ± 3.3 |
| Difference, cm (%) | 0.6 (1%) | −0.1 (<1%) | 0.2 (<1%) | −1.9 (2%) | 0.6 (1%) |
| Mean ± standard deviation of monthly differences, cm | 0.1 ± 0.4 | 0.0 ± 0.2 | 0.0 ± 0.2 | −0.2 ± 0.5 | 0.1 ± 0.7 |
| Cumulative difference in precipitation during accumulation season, cm (%) | 1.1 (5%) | 0.3 (<1%) | −0.2 (<1%) | −2.0 (3%) | −2.0 (<1%) |
| Halfmoon Creek | |||||
| Elevation, m (number of PRISM locations averaged) | 3000 (n = 4) | 3250 (n = 7) | 3500 (n = 11) | 3750 (n = 16) | 4000 (n = 9) |
| Modeled mean annual temperature, °C | 1.7 | 1.1 | −0.3 | −1.8 | −3.2 |
| PRISM mean annual temperature, °C | 1.8 ± 0.0 | 0.9 ± 0.1 | −0.2 ±0.1 | −1.8 ± 0.1 | −3.6 ± 0.1 |
| Difference, °C | −0.1 | 0.2 | −0.1 | 0.0 | 0.4 |
| Mean ± standard deviation of monthly differences, °C | 0.0 ± 0.6 | 0.2 ± 0.6 | −0.1 ± 0.7 | 0.0 ± 0.7 | 0.4 ± 0.8 |
| Cumulative difference temperatures during ablation season, °C | −0.4 | 1.2 | −0.9 | −0.9 | 0.6 |
| Modeled mean annual precipitation, cm | 36.6 | 64.5 | 85.9 | 95.3 | 104.7 |
| PRISM mean annual precipitation, cm | 36.5 ± 1.9 | 68.7 ± 7.1 | 84.1 ± 7.5 | 96.4 ± 5.6 | 107.5 ± 10 |
| Difference, cm (%) | 0.1 (<1%) | −4.2 (6%) | 1.7 (2%) | −1.1 (1%) | −2.8 (3%) |
| Mean ± standard deviation of monthly differences, cm | 0.0 ± 0.4 | −0.4 ± 0.3 | 0.1 ± 0.2 | −0.1 ± 0.3 | −0.2 ± 0.5 |
| Cumulative difference in precipitation during accumulation season, cm (%) | 0.9 (5%) | −3.0 (7%) | 1.0 (2%) | −1.7 (3%) | −3.1 (4%) |
| Lake Fork Creek | |||||
| Elevation, m (number of PRISM locations averaged) | 3000 (n = 5) | 3150 (n = 8) | 3300 (n = 9) | 3450 (n = 15) | 3600 (n = 10) |
| Modeled mean annual temperature, °C | 2.0 | 1.4 | 0.8 | 0.2 | −0.7 |
| PRISM mean and stand deviation of annual temperature, °C | 1.9 ± 0.0 | 1.3 ± 0.0 | 0.7 ± 0.1 | 0.1 ± 0.1 | −0.7 ± 0.1 |
| Difference, °C | 0.1 | 0.1 | 0.1 | 0.1 | 0.0 |
| Mean ± standard deviation of monthly differences, °C | 0.1 ± 0.5 | 0.1 ± 0.6 | 0.0 ± 0.7 | 0.1 ± 0.7 | 0.0 ± 0.7 |
| Cumulative difference temperatures during ablation season, °C | 0.4 | 0.4 | 0.0 | −0.2 | −0.7 |
| Modeled mean annual precipitation, cm | 39.3 | 59.0 | 71.0 | 80.7 | 90.4 |
| PRISM mean and standard deviation of annual precipitation, cm | 39.8 ± 1.4 | 57.8 ± 4.0 | 70.9 ± 5.4 | 81.6 ± 5.9 | 89.2 ± 2.9 |
| Difference, cm (%) | −0.5 (1%) | 1.2 (2%) | 0.1 (<1%) | −0.9 (1%) | 1.1 (1%) |
| Mean ± standard deviation of monthly differences, cm | 0.0 ± 0.3 | 0.1 ± 0.1 | 0.0 ± 0.2 | 0.0 ± 0.3 | 0.1 ± 0.4 |
| Cumulative difference in precipitation during accumulation season, cm (%) | 0.1 (<1%) | 1.0 (3%) | −0.1 (<1%) | −0.7 (1%) | 0.4 (1%) |
| Tennessee Creek/Longs Gulch | |||||
| Elevation, m (number of PRISM locations averaged) | 3100 (n = 5) | 3300 (n = 8) | 3500 (n = 8) | 3700 (n = 8) | |
| Modeled mean annual temperature, °C | 1.5 | 0.7 | −0.2 | −1.4 | |
| PRISM mean and stand deviation of annual temperature, °C | 1.4 ± 0.0 | 0.7 ± 0.1 | 0.0 ±0.1 | −1.5 ± 0.1 | |
| Difference, °C | 0.1 | 0.0 | −0.2 | 0.1 | |
| Mean ± standard deviation of monthly differences, °C | 0.1 ± 0.6 | 0.0 ± 0.7 | −0.1 ± 0.7 | 0.0 ± 0.6 | |
| Cumulative difference temperatures during ablation season, °C | −0.6 | −0.4 | −0.6 | 0.4 | |
| Modeled mean annual precipitation, cm | 53.1 | 69.4 | 84.9 | 93.2 | |
| PRISM mean and standard deviation of annual precipitation, cm | 53.0 ± 0.7 | 69.6 ± 1.3 | 84.8 ± 5.9 | 94.1 ± 3.0 | |
| Difference, cm (%) | −0.5 (1%) | −0.6 (1%) | −0.7 (1%) | −0.8 (1%) | |
| Mean ± standard deviation of monthly differences, cm | 0.0 ± 0.3 | 0.0 ±0.1 | 0.0 ± 0.2 | -0.1 ± 0.4 | |
| Cumulative difference in precipitation during accumulation season, cm (%) | 0.6 (2%) | −0.3 (1%) | −0.2 (<1%) | −1.2 (2%) | |
| Bennett Gulch | |||||
| Elevation, m (number of PRISM locations averaged) | 3200 (n = 4) | 3350 (n = 5) | 3500 (n = 5) | 3650 (n = 1) | |
| Modeled mean annual temperature, °C | 1.1 | 0.8 | 0.0 | −1.3 | |
| PRISM mean and stand deviation of annual temperature, °C | 1.0 ± 0.1 | 0.8 ± 0.1 | 0.0 ± 0.0 | −1.2 | |
| Difference, °C | 0.1 | 0.0 | 0.0 | −0.1 | |
| Mean ± standard deviation of monthly differences, °C | 0.1 ± 0.7 | −0.1 ± 0.7 | −0.1 ± 0.7 | 0.0 ± 0.7 | |
| Cumulative difference temperatures during ablation season, °C | 0.3 | 0.0 | 0.0 | −0.3 | |
| Modeled mean annual precipitation, cm | 62.7 | 70.2 | 77.8 | 85.3 | |
| PRISM mean and standard deviation of annual precipitation, cm | 61.9 ± 1.2 | 71.5 ± 2.0 | 77.2 ± 1.8 | 85.0 | |
| Difference, cm (%) | 0.6 (1%) | -1.3 (2%) | 0.6 (1%) | 0.3 (<1%) | |
| Mean ± standard deviation of monthly differences, cm | 0.1 ± 0.1 | -0.1 ± 0.1 | 0.1 ± 0.2 | 0.0 ± 0.3 | |
| Cumulative difference in precipitation during accumulation season, cm (%) | 0.8 (2%) | −1.1 (2%) | 0.2 (<1%) | −0.3 (1%) | |
| Porcupine Gulch | |||||
| Elevation, m (number of PRISM locations averaged) | 3100 (n = 3) | 3250 (n = 3) | 3400 (n = 4) | 3550 (n = 3) | |
| Modeled mean annual temperature, °C | 1.5 | 0.8 | 0.3 | 0 | |
| PRISM mean annual temperature, °C | 1.4 ±0.0 | 0.8 ± 0.0 | 0.4 ± 0.1 | −0.2 ± 0.0 | |
| Difference, °C | 0.1 | 0 | −0.1 | 0.2 | |
| Mean ± standard deviation of monthly differences, °C | 0.1 ± 0.6 | 0.0 ± 0.7 | 0.0 ± 0.7 | 0.1 ± 0.7 | |
| Cumulative difference temperatures during ablation season, °C | 0.4 | −0.4 | −0.7 | 0.7 | |
| Modeled mean annual precipitation, cm | 52 | 62.4 | 75.7 | 88.4 | |
| PRISM mean annual precipitation, cm | 52.5 ± 0.4 | 63.8 ± 2.5 | 75.4 ± 3.3 | 87.2 ± 3.2 | |
| Difference, cm (%) | −0.5 (1%) | −0.4 (1%) | 0.3 (< 1%) | 1.1 (1%) | |
| Mean ± standard deviation of monthly differences, cm | 0.0 ± 0.2 | 0.0 ± 0.1 | 0.0 ± 0.2 | 0.1 ± 0.4 | |
| Cumulative difference in precipitation during accumulation season, cm (%) | 0.0 (<1 %) | −0.5 (1%) | −0.1 (<0%) | 0.3 (1%) | |
| Model Parameter | Temperature Depression, °C | Steady-State ELA, m* | ||||
|---|---|---|---|---|---|---|
| Precipitation change (F), cm | 0 | 10 | –10 | |||
| Melt factors (mf), snow/ice, m w.e. °C−1 d−1 | 0.0045/0.008 | 0.006/0.010 | 0.0025/0.006 | 0.0045/0.008 | ||
| Glacier | ||||||
| Halfmoon Creek (southernmost) | 8.0 | 8.4 | 7.2 | 7.8 | 8.2 | 3500 |
| Rock Creek | 8.5 | 8.9 | 7.8 | 8.3 | 8.7 | 3470 |
| Lake Creek | 8.8 | 9.2 | 8.1 | 8.6 | 9.0 | 3410 |
| Porcupine Gulch | 9.3 | 9.6 | 8.6 | 9.1 | 9.4 | 3345 |
| Tennessee complex | 8.8 | 9.2 | 8.1 | 8.6 | 9.0 | 3435 |
| Bennett Gulch (northernmost) | 9.2 | 9.7 | 8.6 | 9.1 | 9.5 | 3435 |
| Means | 8.8 ± 0.5 | 9.2 ± 0.5 | 8.1 ± 0.5 | 8.6 ± 0.5 | 9.0 ± 0.5 | 3435 ± 55 |
| Parameter | |||||
|---|---|---|---|---|---|
| Potential Change in LGM Precipitation, (F) cm | Melt Threshold Temperature, °C | Melt Factors (mf), cm w.e. d−1 °C−1 | Effect of Glacier Hypsometry Error, °C | Total* | |
| Initial value | 0.0 | +1.0 | ice 0.0080 snow 0.0045 | - | |
| Variation | ±10 | 0.0 | ±0.002 | ±0.2 | |
| Effects, °C | +0.2 | 0.0 | +0.7 | +0.2 | +0.8 |
| −0.2 | 0.0 | −0.4 | −0.2 | −0.5 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brugger, K.A.; Ruleman, C.A.; Caffee, M.W.; Mason, C.C. Climate during the Last Glacial Maximum in the Northern Sawatch Range, Colorado, USA. Quaternary 2019, 2, 36. https://doi.org/10.3390/quat2040036
Brugger KA, Ruleman CA, Caffee MW, Mason CC. Climate during the Last Glacial Maximum in the Northern Sawatch Range, Colorado, USA. Quaternary. 2019; 2(4):36. https://doi.org/10.3390/quat2040036
Chicago/Turabian StyleBrugger, Keith A., Chester A. Ruleman, Marc W. Caffee, and Cody C. Mason. 2019. "Climate during the Last Glacial Maximum in the Northern Sawatch Range, Colorado, USA" Quaternary 2, no. 4: 36. https://doi.org/10.3390/quat2040036
APA StyleBrugger, K. A., Ruleman, C. A., Caffee, M. W., & Mason, C. C. (2019). Climate during the Last Glacial Maximum in the Northern Sawatch Range, Colorado, USA. Quaternary, 2(4), 36. https://doi.org/10.3390/quat2040036





