Static Analysis of a Composite Box Plate with Functionally Graded Foam Core
Abstract
1. Introduction
2. Materials and Methods
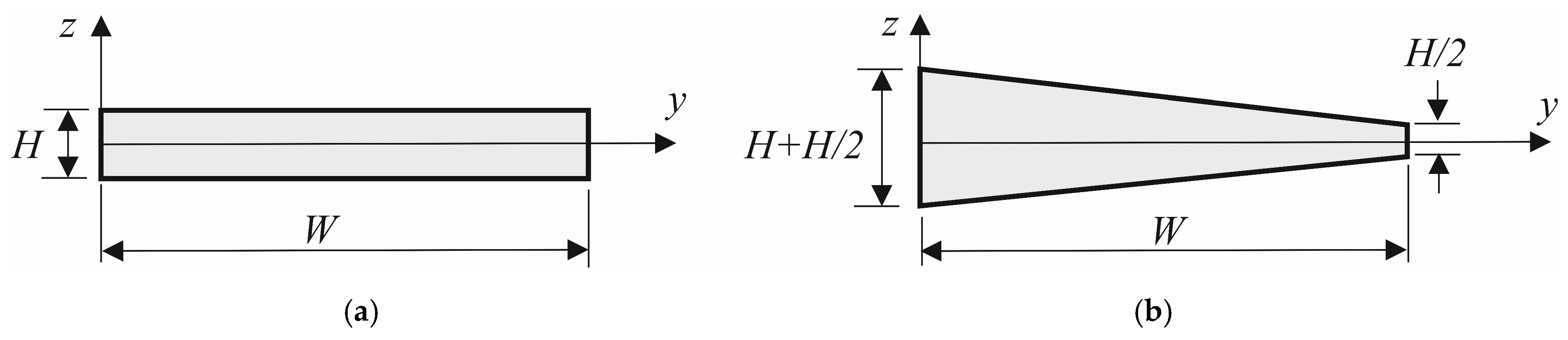
2.1. Configuration of Composite Box Plate
2.2. Material Properties
2.2.1. Material Properties of Foam and GFRP
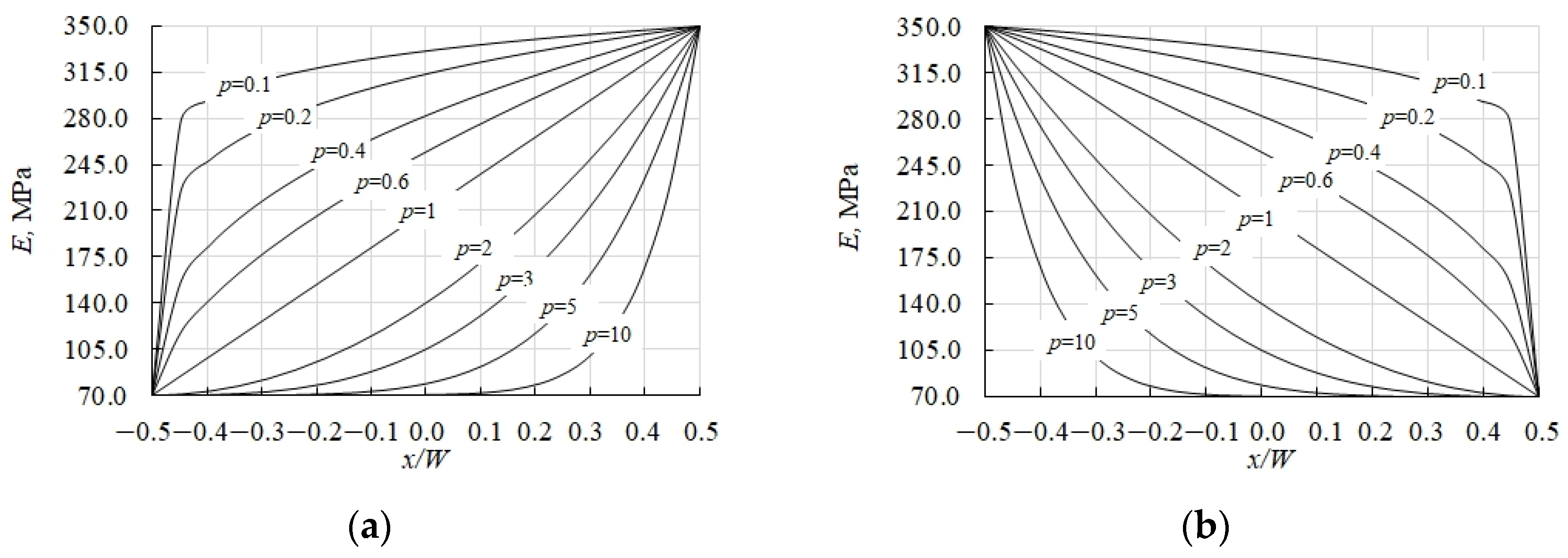
2.2.2. Formulation of FGM Model
2.3. Static Behaviuor of FG Composite Box Plate
2.4. Static Deflection Analysis
2.5. Numerical Accuracy and Modelling
2.5.1. Comparison Studies
2.5.2. Convergence and Validation of Finite Element Model of Composite Box Plate with FG Foam Filled
3. Results
3.1. Results for Type 1 Model with Constant Thickness
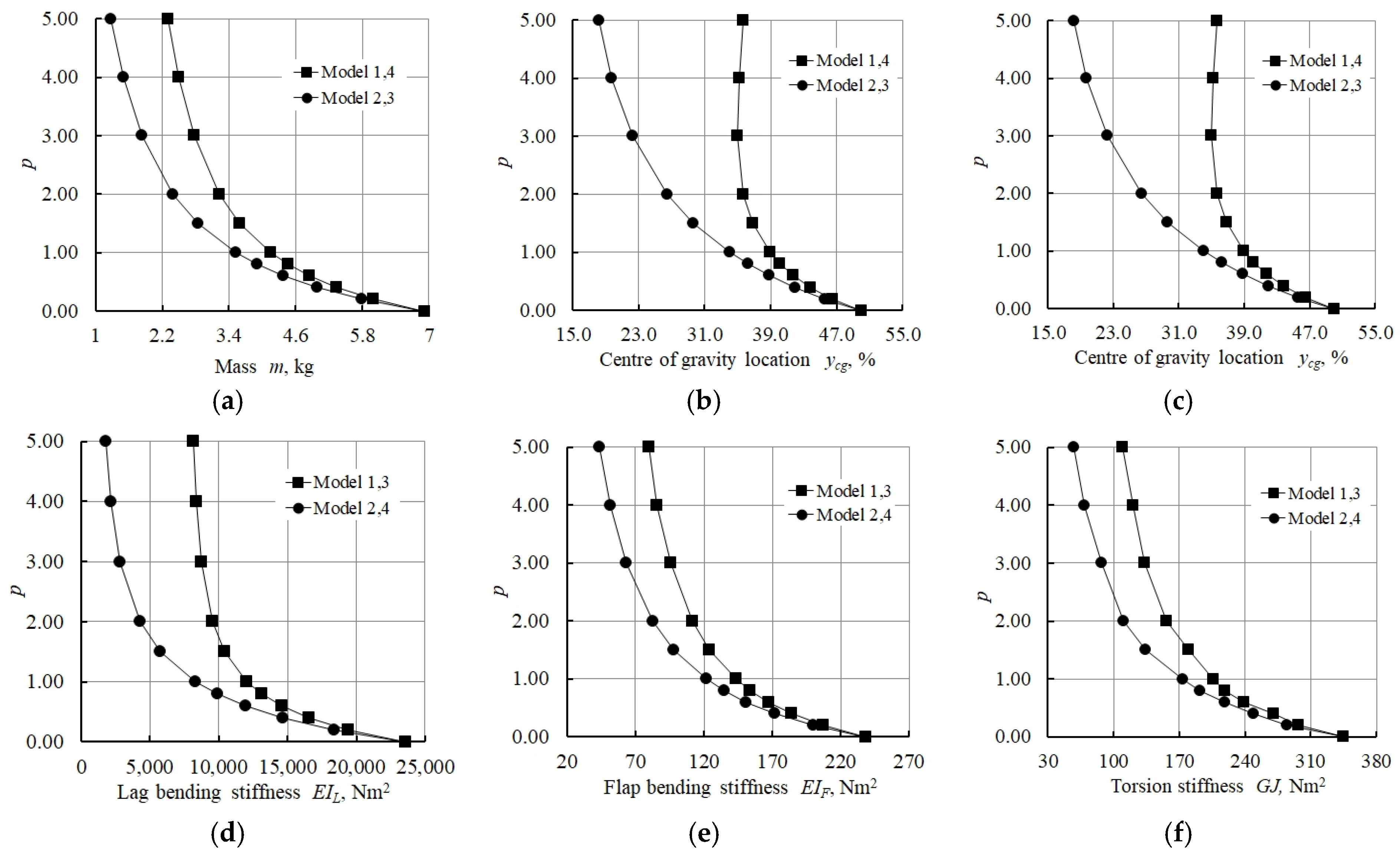
3.1.1. Numerical Modelling of Box Plate with FG Foam
3.1.2. Numerical Modelling of Composite Box Plate with FG Foam
3.2. Results for Type 2 Model with Variable Thickness
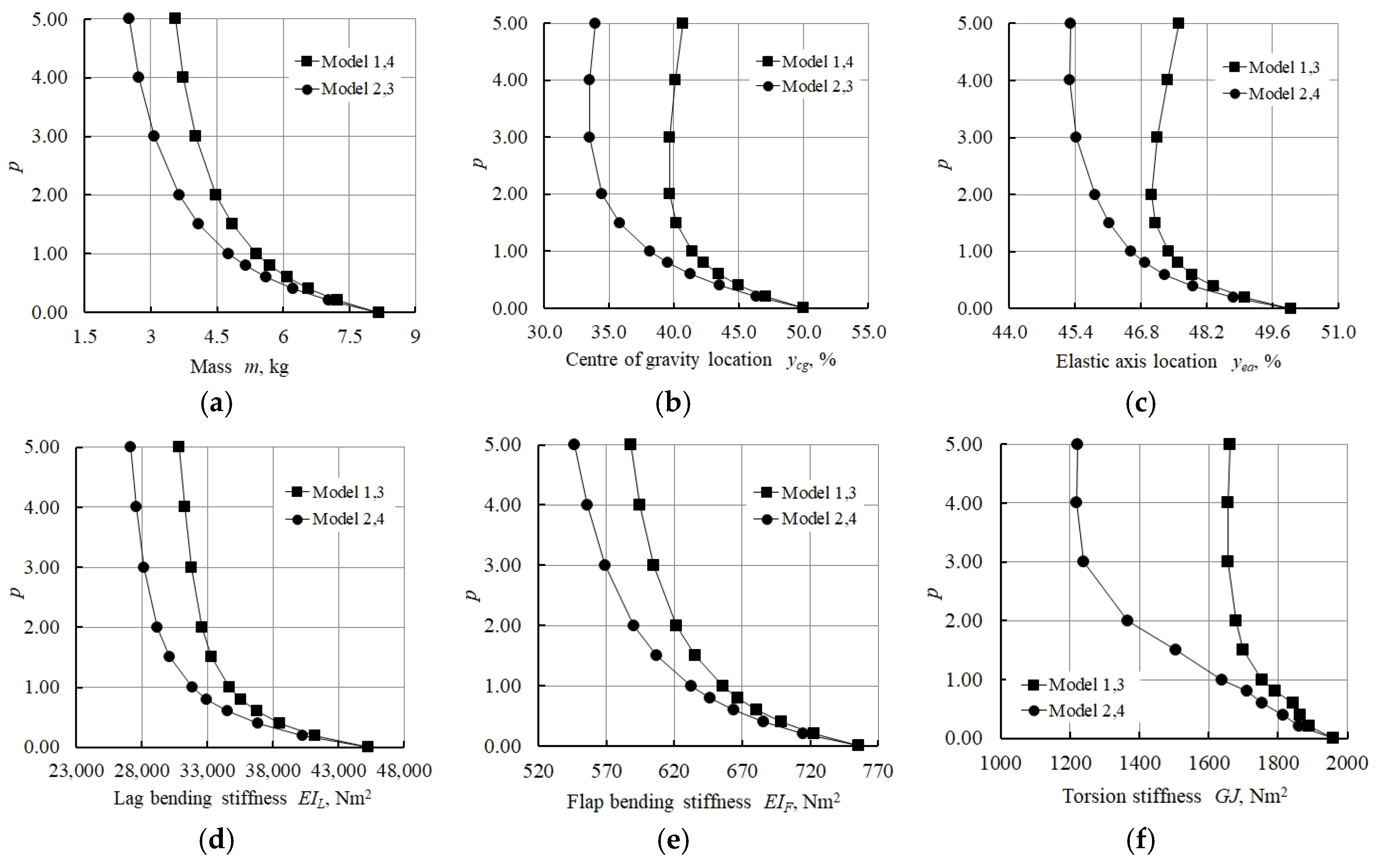
3.2.1. Numerical Modelling of a Variable Thickness Box Plate with FG Foam
3.2.2. Numerical Modelling of a Variable Thickness Composite Box Plate with FG Foam
4. Conclusions
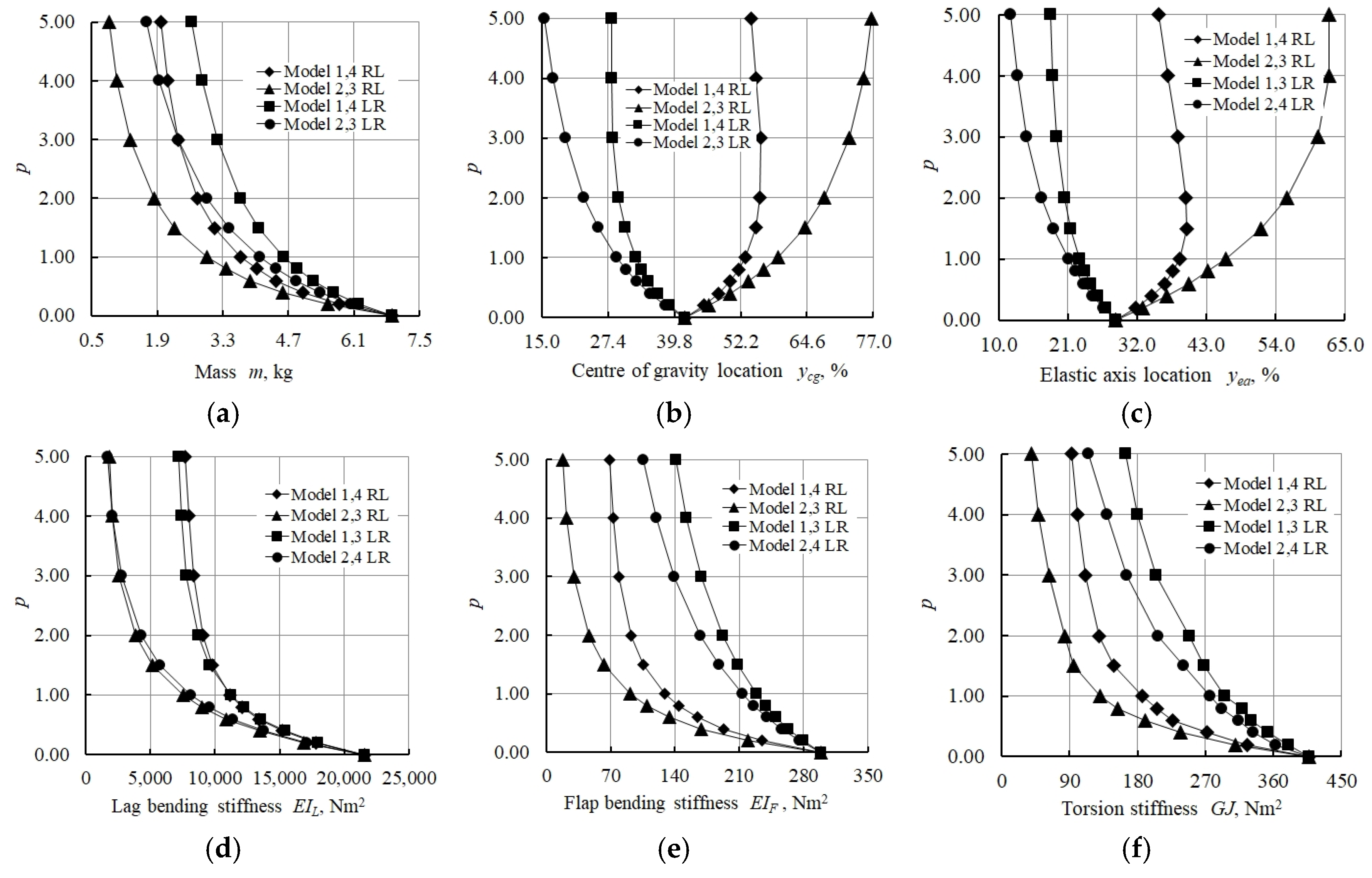
- The lowest values of the distance between the locations of the centre of gravity and elastic axis in the study of the numerical model of a graded foam with constant thickness, without considering the composite shell, were obtained for Models 1 and 2 (see Table 4).
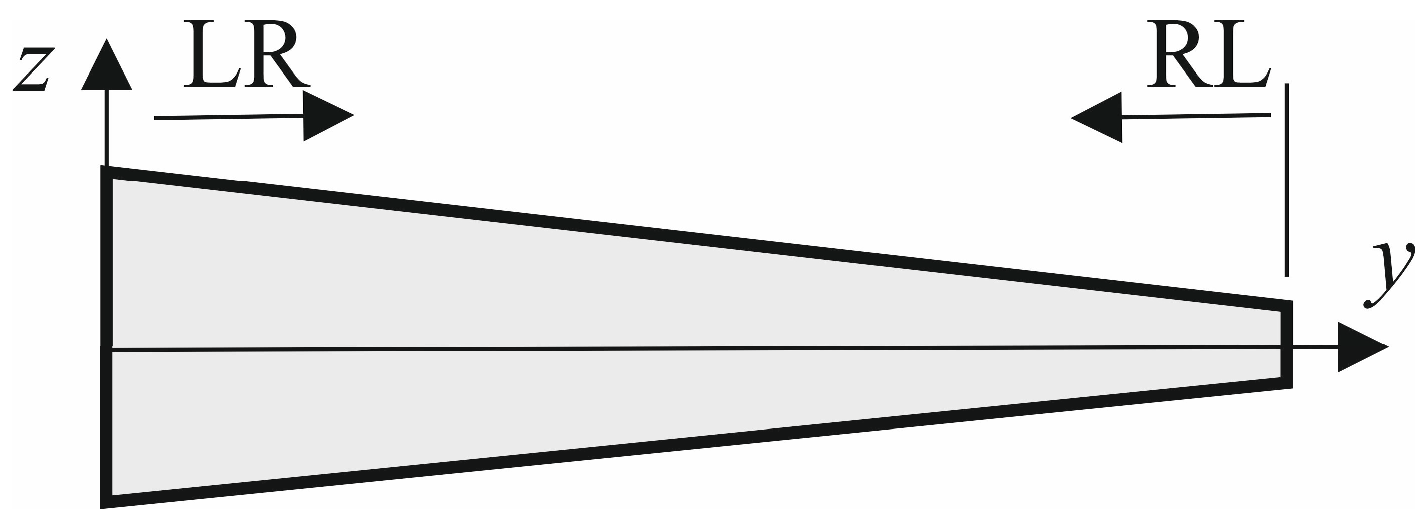
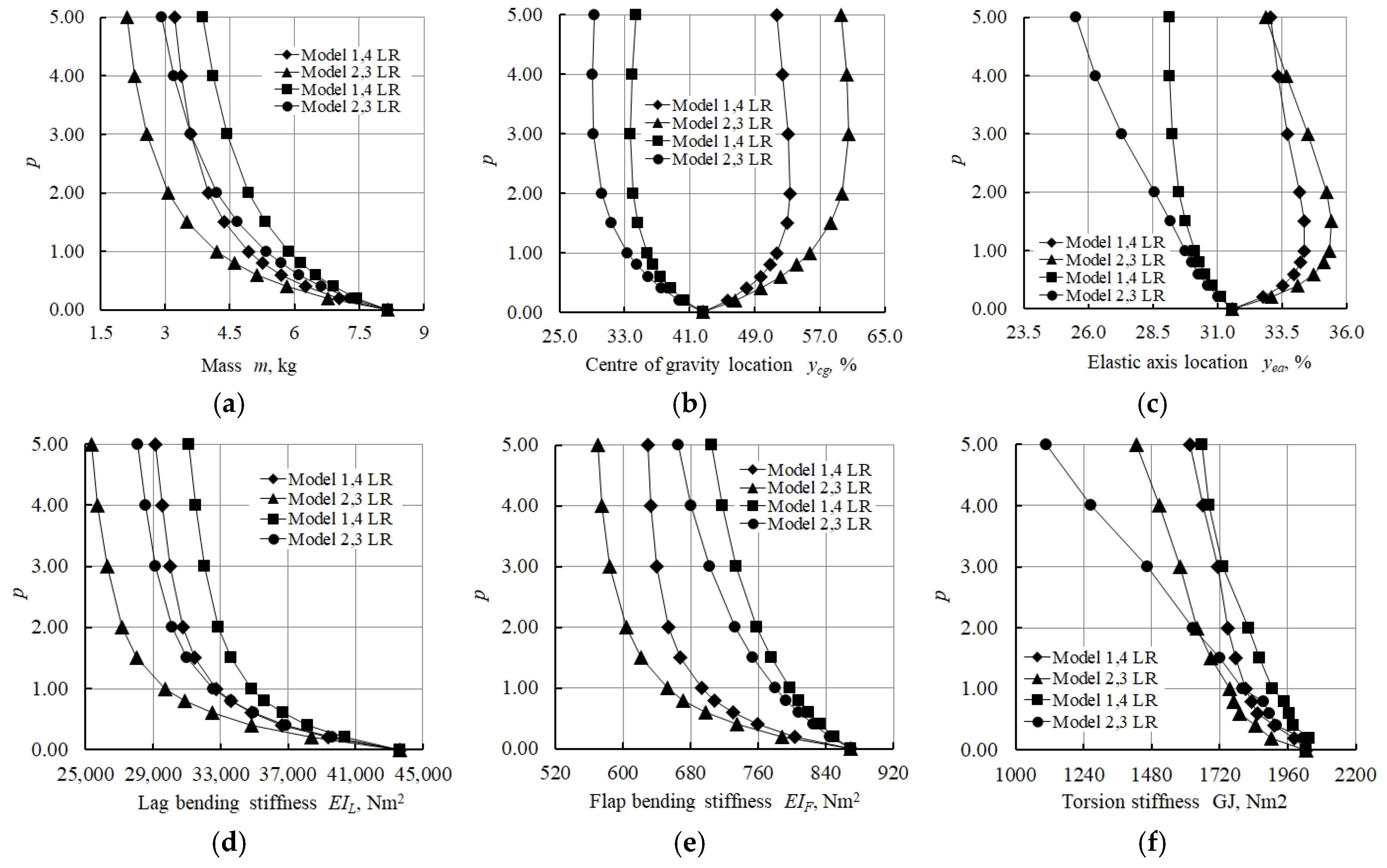
- The lowest values of the distance between the locations of the centre of gravity and elastic axis in the study of the numerical model of a graded foam of variable thickness, without considering the composite shell, were obtained for Models 2 LR and 3 LR (see Table 6).
- The addition of a composite shell limited the shifting of the centre of gravity and elastic axis locations along the width of the structure and increased the overall rigidity of all structures considered.
- The distance between centre of gravity and elastic axis locations decreased with the increasing power law index p for Models 1 LR to 4 LR. The lowest value, equal to 0.05, was displayed by Model 3 LR.
- RL models with the direction of the gradient change of foam material properties from right to left, on the contrary, showed an increasing distance between the centre of gravity and elastic axis, with growing power law index p.
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FG | Functionally graded |
| FGM | Functionally gradient materials |
| FE | Finite element |
| FEM | Finite element method |
| LR | Left to right |
| RL | Right to left |
References
- Suresh, S.; Mortensen, A. Fundamental of Functionally Graded Materials; CRC Press: London, UK, 1998; 176p. [Google Scholar]
- Niino, M.; Hirai, T.; Watanabe, R. The functionally gradient materials. J. Jpn. Soc. Compos. Mater. 1987, 13, 257–264. [Google Scholar] [CrossRef]
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A review of theories for the modelling and analysis of functionally graded plates and shells. Compos. Struct. 2015, 128, 70–86. [Google Scholar] [CrossRef]
- Van, T.D.; Van, V.P.; Hoang, N.N. On the development of refined plate theory for static bending behaviuor of functionally graded plates. Math. Probl. Eng. 2020, 2836763. [Google Scholar] [CrossRef]
- Reddy, J.N. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Sayyad, A.S.; Ghugal, Y.M. Modelling and analysis of functionally graded sandwich beams: A review. Mech. Adv. Mater. Struct. 2009, 26, 1776–1795. [Google Scholar] [CrossRef]
- Srikarun, B.; Songsuwan, W.; Wattanasakulpong, N. Linear and nonlinear static bending of sandwich beams with functionally graded porous core under different distributed loads. Compos. Struct. 2021, 276, 114538. [Google Scholar] [CrossRef]
- Pandey, S.; Pradyumna, S. Analysis of functionally graded sandwich plates using a higher-order layerwise theory. Compos. Part B Eng. 2018, 153, 325–336. [Google Scholar] [CrossRef]
- Van Vinh, P. Static bending analysis of functionally graded sandwich beams using a novel mixed beam element based on first-order shear deformation theory. Forces Mech. 2021, 4, 100039. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, Y.; Wang, X.; Chu, F. Bending Analysis of Symmetrical Porous Functionally Graded Sandwich Panels. Symmetry 2025, 17, 327. [Google Scholar] [CrossRef]
- Suethao, S.; Shah, D.U.; Smitthipong, W. Recent Progress in Processing Functionally Graded Polymer Foams. Materials 2020, 13, 4060. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Song, L.; Chen, F.; Fan, P.; Sun, L.; Zhong, M.; Yang, J. Preparation of polymer foams with a gradient of cell size: Further exploring the nucleation efect of porous inorganic materials in polymer foaming. Mater. Today Commun. 2016, 9, 1–6. [Google Scholar] [CrossRef]
- Timothy, J.J.; Meschke, G. A cascade continuum micromechanics model for the effective elastic properties of porous materials. Int. J. Solids Struct. 2016, 83, 1–12. [Google Scholar] [CrossRef]
- Bashir, A.S.; Munusamy, Y.; Chew, T.L.; Ismail, H.; Ramasamy, S. Mechanical, thermal, and morphological properties of (eggshell powder)–filled natural rubber latex foam. J. Vinyl Addit. Technol. 2015, 23, 3–12. [Google Scholar] [CrossRef]
- Tan, X.M.; Rodrigue, D. Density graded polymer composite foams. Cellular Polymers 2023, 42, 25–51. [Google Scholar] [CrossRef]
- Pinto, J.; Escudero, J.; Solórzano, E.; Rodriguez-Perez, M.A. A novel route to produce structural polymer foams with a controlled solid skin–porous core structure based on gas diffusion mechanisms. J. Sandw. Struct. Mater. 2020, 22, 822–832. [Google Scholar] [CrossRef]
- Llewelyn, G.; Rees, A.; Griths, C.A.; Jacobi, M. A novel hybrid foaming method for low–pressure microcellular foam production of unfilled and talc–filled copolymer polypropylenes. Polymers 2019, 11, 1896. [Google Scholar] [CrossRef]
- Onder, O.C.; Yilgor, E.; Yilgor, I. Preparation of monolithic polycaprolactone foams with controlled morphology. Polymer 2018, 136, 166–178. [Google Scholar] [CrossRef]
- Song, W.; Barber, K.; Lee, K.Y. Heat–induced bubble expansion as a route to increase the porosity of foam–templated bio–based macroporous polymers. Polymer 2017, 118, 97–106. [Google Scholar] [CrossRef]
- Kieback, B.; Neubrand, A.; Riedel, H. Processing techniques for functionally graded materials. Mater. Sci. Eng. A 2003, 362, 81–106. [Google Scholar] [CrossRef]
- Lee, N.J.; Jang, J.; Park, M.; Choe, C.R. Characterization of functionally gradient epoxy/carbon fibre composite prepared under centrifugal force. J. Mater. Sci. 1997, 32, 2013–2020. [Google Scholar] [CrossRef]
- Klingshirn, C.; Koizumi, M.; Haupert, F.; Giertzsch, H.; Friedrich, K. Structure and wear of centrifuged epoxy-resin/carbon fiber functionally graded materials. J. Mater. Sci. Lett. 2000, 19, 263–266. [Google Scholar] [CrossRef]
- Stellbrink, K.; Hausser, G.; Steegmuller, R. One-component composites as functionally gradient materials. J. Thermoplast. Compos. Mater. 1999, 12, 188–200. [Google Scholar] [CrossRef]
- Chen, Z.; Yan, Q.; Huang, Z.; Shen, Q.; Zhang, L. Preparation and characterization of novel functional gradient syntactic foam. Adv. Mater. Res. 2009, 66, 284–287. [Google Scholar] [CrossRef]
- Zhang, W.; Deodhar, S.; Yao, D. Geometrical confining effects in compression molding of co-continuous polymer blends. Ann. Biomed. Eng. 2010, 38, 1954–1964. [Google Scholar] [CrossRef]
- Yao, D.; Zhang, W.; Zhou, J.G. Controllable growth of gradient porous structures. Biomacromolecules 2009, 10, 1282–1286. [Google Scholar] [CrossRef]
- Torres-Sanchez, C.; Corney, J.R. Toward functionally graded cellular microstructures. J. Mech. Des. 2009, 131, 8. [Google Scholar] [CrossRef]
- Elsing, J.; Quell, A.; Stubenrauch, C. Toward functionally graded polymer foams using microfluidics. Adv. Eng. Mater. 2017, 19, 1700195. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, P.; Li, W. Fabrication of functionally graded porous polymer via supercritical CO2 foaming. Compos. Part B Eng. 2011, 42, 318–325. [Google Scholar] [CrossRef]
- Reichert, G. Helicopter vibration control—A survey. Vertica 1981, 5, 1–29. [Google Scholar] [CrossRef]
- Friedmann, P.P.; Millott, T.A. Vibration reduction in rotorcraft using active control—A comparison of various approaches. J. Guid. Control Dyn. 1981, 18, 664–673. [Google Scholar] [CrossRef]
- Grohmann, B.A.; Maucher, C.; Prunhuber, T.; Jänker, P.; Dieterich, O.; Enenkl, B.; Bauer, M.; Ahci, E.; Altmikus, A.; Baier, H. Multidisciplinary Design and Optimization of Active Trailing Edge for Smart Helicopter Rotor Blade. Mech. Adv. Mater. Struct. 2008, 15, 307–324. [Google Scholar] [CrossRef]
- Wierach, P.; Opitz, S.; Kalow, S. Experimental investigation of an active twist model rotor blade with a low voltage actuation system. Aeronaut. J. 2015, 119, 1499–1512. [Google Scholar] [CrossRef]
- Kovalovs, A.; Barkanov, E.; Ruchevskis, S.; Wesolowski, M. Modelling and Design of a Full-Scale Rotor Blade with Embedded Piezocomposite Actuators. Mech. Compos. Mater. 2017, 53, 179–192. [Google Scholar] [CrossRef]
- Mohamed, I.; Şimşek, S.; Kahya, V.; Lanc, D. Computational modelling of functionally graded sandwich beams with porous core using an Ansys APDL-based approach. Mech. Based Des. Struct. Mach. 2024, 53, 4337–4358. [Google Scholar] [CrossRef]
- Al-Itbi, S.K.A.; Noori, A.R. Finite Element Analysis for the Static Response of Functionally Graded Porous Sandwich Beams. Int. J. Eng. Technol. 2023, 8, 13–20. [Google Scholar] [CrossRef]
- Ozmen, U.; Ozhan, B.B. Computational Modelling of Functionally Graded Beams: A Novel Approach. J. Vib. Eng. Technol. 2022, 10, 2693–2701. [Google Scholar] [CrossRef]
- Zainab, A.M.; Luay, A. Calculating the fundamental frequency of power law functionally graded beam using ANSYS software. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1090, 012014. [Google Scholar] [CrossRef]
- Yildirim, S. Free Vibration Analysis of Sandwich Beams with Functionally-Graded-Cores by Complementary Functions Method. AIAA J. 2020, 58, 5431–5439. [Google Scholar] [CrossRef]
- EVONIK Homepage. Available online: https://performance-foams.evonik.com/en/downloads/product-information (accessed on 31 May 2025).
- Zheng, J.; Xiang, J.; Luo, Z.; Ren, Y. Crashworthiness design of transport aircraft subfloor using polymer foams. Int. J. Crashworthiness 2011, 16, 375–383. [Google Scholar] [CrossRef]
- Zhang, D.G.; Zhou, Y.H. A theoretical analysis of FGM thin plates based on physical neutral surface. Comp. Mater. Sci. 2008, 44, 716–720. [Google Scholar] [CrossRef]
- Ruan, M.; Wang, Z.M. Transverse vibrations of moving skew plates made of functionally graded material. J. Vib. Control. 2016, 22, 3504–3517. [Google Scholar] [CrossRef]
- Nayak, P.; Armani, A. Optimal Design of Functionally Graded Parts. Metals 2022, 12, 1335. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent developments in modelling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Ferreira, A.J.M.; Batra, R.C.; Rouque, C.M.C.; Qian, L.F.; Martins, P.A.L.S. Static analysis of functionally graded plates using third-order shear deformation theory and a meshless method. Compos. Struct. 2005, 69, 449–457. [Google Scholar] [CrossRef]
- Srividhya, S.; Basant, K.; Gupta, R.K.; Rajagopal, A.; Reddy, J.N. Influence of the homogenization scheme on the bending response of functionally graded plates. Acta Mech. 2018, 229, 4071–4089. [Google Scholar] [CrossRef]
- Kadoli, R.; Akhtar, K.; Ganesan, N. Static analysis of functionally graded beams using higher order shear deformation theory. Appl. Math. Modell. 2008, 32, 2509–2525. [Google Scholar] [CrossRef]
- Li, X.F.; Wang, B.L.; Han, J.C. A higher-order theory for static and dynamic analyses of functionally graded beams. Arch. Appl. Mech. 2010, 80, 1197–1212. [Google Scholar] [CrossRef]
- Wright, J.R.; Cooper, J.E. Introduction to Aircraft Aeroelasticity and Loads, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Cui, L.; Kiernan, S.; Gilchrist, M.D. Designing the energy absorption capacity of functionally graded foam materials. Mater. Sci. Eng. A 2009, 507, 215–225. [Google Scholar] [CrossRef]
- Sun, G.; Li, G.; Hou, S.; Zhou, S.; Li, W.; Li, Q. Crashworthiness design for functionally graded foam-filled thin-walled structures. Mater. Sci. Eng. A. 2010, 527, 1911–1919. [Google Scholar] [CrossRef]
- Koohbor, B.; Kidane, A. Design optimization of continuously and discretely graded foam materials for efficient energy absorption. Mater. Des. 2016, 102, 151–161. [Google Scholar] [CrossRef]
- Li, S.; Li, Q.M.; Tse, K.M.; Pang, T. Functionally graded foam materials for head impact protection. Thin-Walled Struct. 2024, 203, 112193. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X.; Liu, S.; Chen, T.; Hu, Z. Crashworthiness design for bi-graded composite circular structures. Constr. Build. Mater. 2008, 168, 633–649. [Google Scholar] [CrossRef]
- Riemenschneider, J.; Keye, S.; Wierach, P.; Mercier Des Rochettes, H. Overview of the common DLR/ONERA project active twist blade (ATB). In Proceedings of the 30th European Rotorcraft Forum, Marseille, France, 14–16 September 2004; pp. 273–281. [Google Scholar]
- Shojaeefard, M.H.; Googarchin, H.S.; Mahinzare, M.; Ghadiri, M. Free Vibration and Critical Angular Velocity of a Rotating Variable Thickness Two-Directional FG Circular Microplate. Microsyst. Technol. 2018, 24, 1525–1543. [Google Scholar] [CrossRef]
- Mahinzare, M.; Barooti, M.M.; Ghadiri, M. Vibrational Investigation of the Spinning Bi-Dimensional Functionally Graded (2-FGM) Micro Plate Subjected to Thermal Load in Thermal Environment. Microsyst. Technol. 2018, 24, 1695–1711. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Hong, T.T.; Vinh, P.V.; Thom, D.V. An Efficient Beam Element Based on Quasi-3D Theory for Static Bending Analysis of Functionally Graded Beams. Materials 2019, 12, 2198. [Google Scholar] [CrossRef]





| Foam | Young’s Modulus, MPa | Density, kg/m3 | Poisson’s Ratio |
|---|---|---|---|
| ROHACELL®51 WF | 75 | 52 | 0.3 |
| ROHACELL®71 WF | 105 | 75 | 0.3 |
| ROHACELL®110 WF | 180 | 110 | 0.3 |
| ROHACELL®200 WF | 350 | 205 | 0.3 |
| Model | Value | Young’s Modulus, MPa | Density, kg/m3 | Poisson’s Ratio |
|---|---|---|---|---|
| Model 1 | Minimum | 70.0 | 41.0 | 0.3 |
| Maximum | 350.0 | 205.0 | 0.3 | |
| Model 2 | Minimum | 7.0 | 4.10 | 0.3 |
| Maximum | 350 | 205 | 0.3 | |
| Model 3 | Minimum | 70.0 | 4.10 | 0.3 |
| Maximum | 350.0 | 205 | 0.3 | |
| Model 4 | Minimum | 7.0 | 41.0 | 0.3 |
| Maximum | 350 | 205.0 | 0.3 |
| l/h | Source | Power Law Index p | ||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 5 | 10 | ||
| 5 | [60] | 54.29 | 86.36 | 98.29 | 109.48 | 118.75 |
| Present-ANSYS | 53.90 | 86.09 | 98.30 | 109.44 | 118.72 | |
| Δ% | 0.71 | 0.31 | 0.01 | 0.04 | 0.02 | |
| 10 | [60] | 52.83 | 84.19 | 95.59 | 105.93 | 114.84 |
| Present-ANSYS | 52.60 | 84.30 | 96.03 | 106.34 | 115.24 | |
| Δ% | 0.44 | 0.13 | 0.46 | 0.39 | 0.34 | |
| 20 | [60] | 52.46 | 83.64 | 94.90 | 105.02 | 113.84 |
| Present-ANSYS | 52.39 | 84.05 | 95.68 | 105.80 | 114.62 | |
| Δ% | 0.12 | 0.49 | 0.82 | 0.74 | 0.68 | |
| 100 | [60] | 52.32 | 83.44 | 94.65 | 104.70 | 113.49 |
| Present-ANSYS | 52.44 | 84.16 | 95.78 | 105.86 | 114.66 | |
| Δ% | 0.23 | 0.86 | 1.20 | 1.11 | 1.04 | |
| Number of Layers | Size of Finite Element | Centre of Gravity | Elastic Axis | Mass of Model | Flap Bending Stiffness | Lag Bending Stiffness | Torsion Stiffness |
|---|---|---|---|---|---|---|---|
| mm | , % | , % | , kg | ||||
| 20 | 15.0 | 38.92 | 38.41 | 4.151 | 144 | 12,056 | 214 |
| 40 | 7.5 | 38.90 | 38.39 | 4.151 | 144 | 12,036 | 203 |
| 60 | 5.0 | 38.89 | 38.37 | 4.151 | 143 | 12,027 | 207 |
| 80 | 3.75 | 38.89 | 38.37 | 4.151 | 143 | 12,019 | 208 |
| 100 | 3.0 | 38.89 | 38.37 | 4.151 | 143 | 12,011 | 206 |
| Power Law Index | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| 0.0 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.2 | 0.13 | 0.16 | 0.81 | 1.09 |
| 0.4 | 0.24 | 0.30 | 1.68 | 2.22 |
| 0.6 | 0.34 | 0.42 | 2.58 | 3.35 |
| 0.8 | 0.44 | 0.54 | 3.49 | 4.46 |
| 1.0 | 0.52 | 0.64 | 4.38 | 5.54 |
| 1.5 | 0.67 | 0.85 | 6.53 | 8.05 |
| 2.0 | 0.77 | 1.02 | 8.50 | 10.29 |
| 3.0 | 0.82 | 1.19 | 11.91 | 13.92 |
| 4.0 | 0.78 | 1.20 | 14.65 | 16.63 |
| 5.0 | 0.70 | 1.16 | 16.83 | 18.68 |
| Power Law Index | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| 0.0 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.2 | 1.89 | 2.40 | 2.64 | 1.64 |
| 0.4 | 3.34 | 4.38 | 4.82 | 2.91 |
| 0.6 | 4.45 | 6.01 | 6.59 | 3.87 |
| 0.8 | 5.29 | 7.34 | 8.04 | 4.60 |
| 1.0 | 5.93 | 8.43 | 9.22 | 5.14 |
| 1.5 | 6.90 | 10.32 | 11.30 | 5.93 |
| 2.0 | 7.34 | 11.33 | 12.55 | 6.13 |
| 3.0 | 7.49 | 11.95 | 13.67 | 5.77 |
| 4.0 | 7.25 | 11.79 | 13.87 | 5.16 |
| 5.0 | 6.88 | 11.37 | 13.66 | 4.58 |
| Power Law Index | Mode 1 LR | Model 2 LR | Model 3 LR | Model 4 LR | Mode 1 RL | Model 2 RL | Model 3 RL | Model 4 RL |
|---|---|---|---|---|---|---|---|---|
| 0.0 | 13.07 | 13.07 | 13.07 | 13.07 | 13.07 | 13.07 | 13.07 | 13.07 |
| 0.2 | 11.86 | 11.53 | 11.14 | 12.25 | 13.44 | 13.47 | 14.45 | 12.45 |
| 0.4 | 10.99 | 10.31 | 9.55 | 11.75 | 13.69 | 13.57 | 15.86 | 11.40 |
| 0.6 | 10.36 | 9.35 | 8.22 | 11.49 | 13.91 | 13.50 | 17.34 | 10.07 |
| 0.8 | 9.91 | 8.57 | 7.08 | 11.40 | 14.15 | 13.32 | 18.87 | 8.60 |
| 1.0 | 9.58 | 7.94 | 6.09 | 11.43 | 14.42 | 13.09 | 20.44 | 7.07 |
| 1.5 | 9.12 | 6.82 | 4.08 | 11.86 | 15.21 | 12.46 | 24.38 | 3.30 |
| 2.0 | 8.97 | 6.06 | 2.52 | 12.51 | 16.05 | 11.99 | 28.08 | 0.04 |
| 3.0 | 9.11 | 4.97 | 0.20 | 13.88 | 17.45 | 11.84 | 34.15 | 4.85 |
| 4.0 | 9.47 | 4.16 | 1.46 | 15.09 | 18.28 | 12.69 | 38.37 | 7.40 |
| 5.0 | 9.89 | 3.60 | 2.71 | 16.21 | 18.67 | 14.14 | 41.17 | 8.35 |
| Power Law Index | Model 1 LR | Model 2 LR | Model 3 LR | Model 4 LR | Model 1 RL | Model 2 RL | Model 3 RL | Model 4 RL |
|---|---|---|---|---|---|---|---|---|
| 0.0 | 11.04 | 11.04 | 11.04 | 11.04 | 11.04 | 11.04 | 11.04 | 11.04 |
| 0.2 | 9.22 | 8.75 | 8.65 | 9.32 | 12.94 | 13.47 | 13.78 | 12.62 |
| 0.4 | 7.88 | 6.98 | 6.80 | 8.07 | 14.48 | 15.62 | 16.19 | 13.91 |
| 0.6 | 6.90 | 5.59 | 5.34 | 7.15 | 15.71 | 17.48 | 18.25 | 14.95 |
| 0.8 | 6.16 | 4.49 | 4.18 | 6.47 | 16.68 | 19.08 | 19.98 | 15.77 |
| 1.0 | 5.62 | 3.63 | 3.26 | 5.99 | 17.42 | 20.44 | 21.43 | 16.44 |
| 1.5 | 4.81 | 2.25 | 1.67 | 5.40 | 18.60 | 22.95 | 24.02 | 17.53 |
| 2.0 | 4.49 | 1.71 | 0.74 | 5.45 | 19.15 | 24.51 | 25.56 | 18.11 |
| 3.0 | 4.49 | 1.91 | 0.05 | 6.44 | 19.35 | 26.04 | 26.84 | 18.56 |
| 4.0 | 4.83 | 2.76 | 0.12 | 7.71 | 19.06 | 26.59 | 26.93 | 18.72 |
| 5.0 | 5.26 | 3.77 | 0.11 | 8.92 | 18.63 | 26.71 | 26.54 | 18.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovalovs, A. Static Analysis of a Composite Box Plate with Functionally Graded Foam Core. J. Manuf. Mater. Process. 2025, 9, 209. https://doi.org/10.3390/jmmp9070209
Kovalovs A. Static Analysis of a Composite Box Plate with Functionally Graded Foam Core. Journal of Manufacturing and Materials Processing. 2025; 9(7):209. https://doi.org/10.3390/jmmp9070209
Chicago/Turabian StyleKovalovs, Andrejs. 2025. "Static Analysis of a Composite Box Plate with Functionally Graded Foam Core" Journal of Manufacturing and Materials Processing 9, no. 7: 209. https://doi.org/10.3390/jmmp9070209
APA StyleKovalovs, A. (2025). Static Analysis of a Composite Box Plate with Functionally Graded Foam Core. Journal of Manufacturing and Materials Processing, 9(7), 209. https://doi.org/10.3390/jmmp9070209





