Quasi-Static Compressive Behavior and Energy Absorption Performance of Polyether Imide Auxetic Structures Made by Fused Deposition Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometries
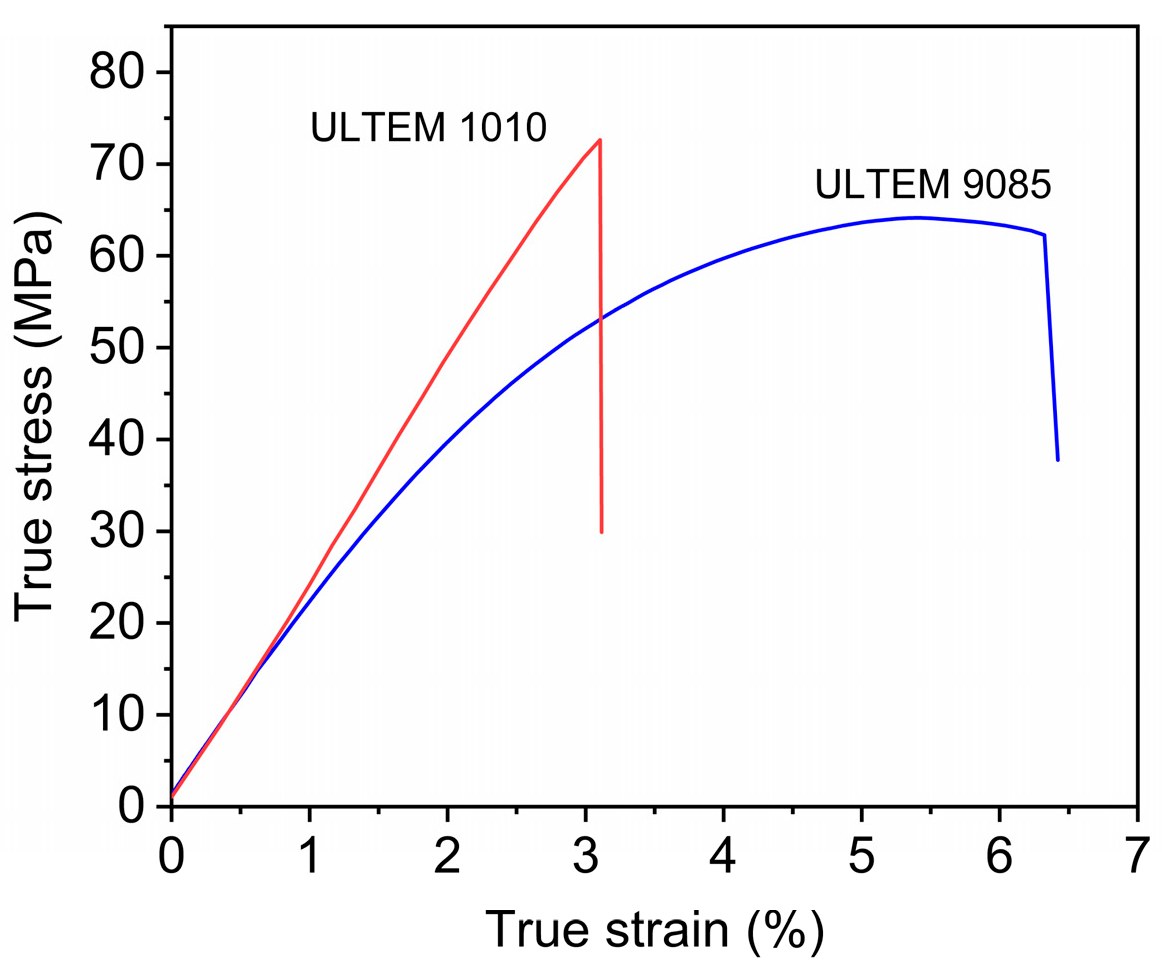
2.2. Raw Materials and FDM Process
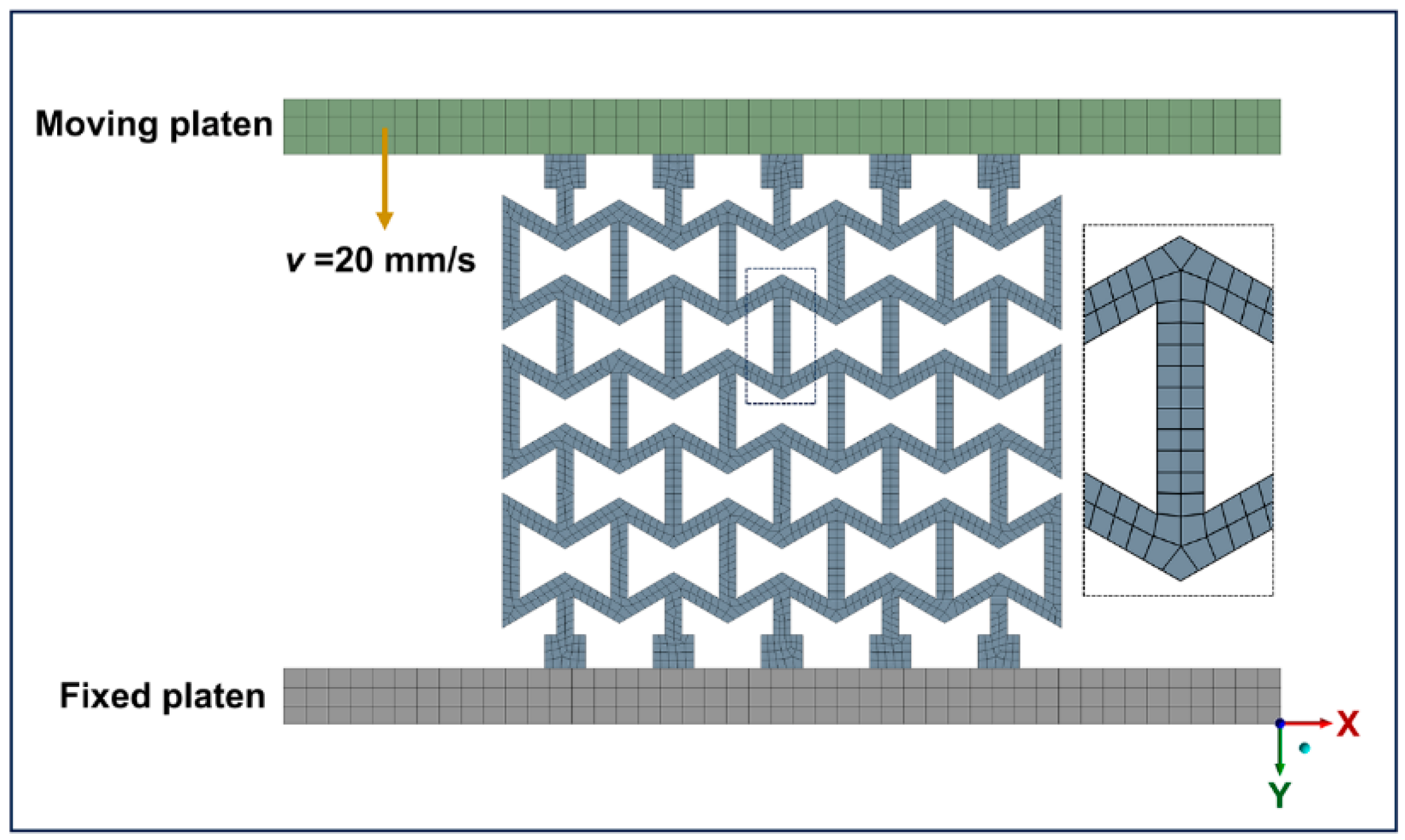
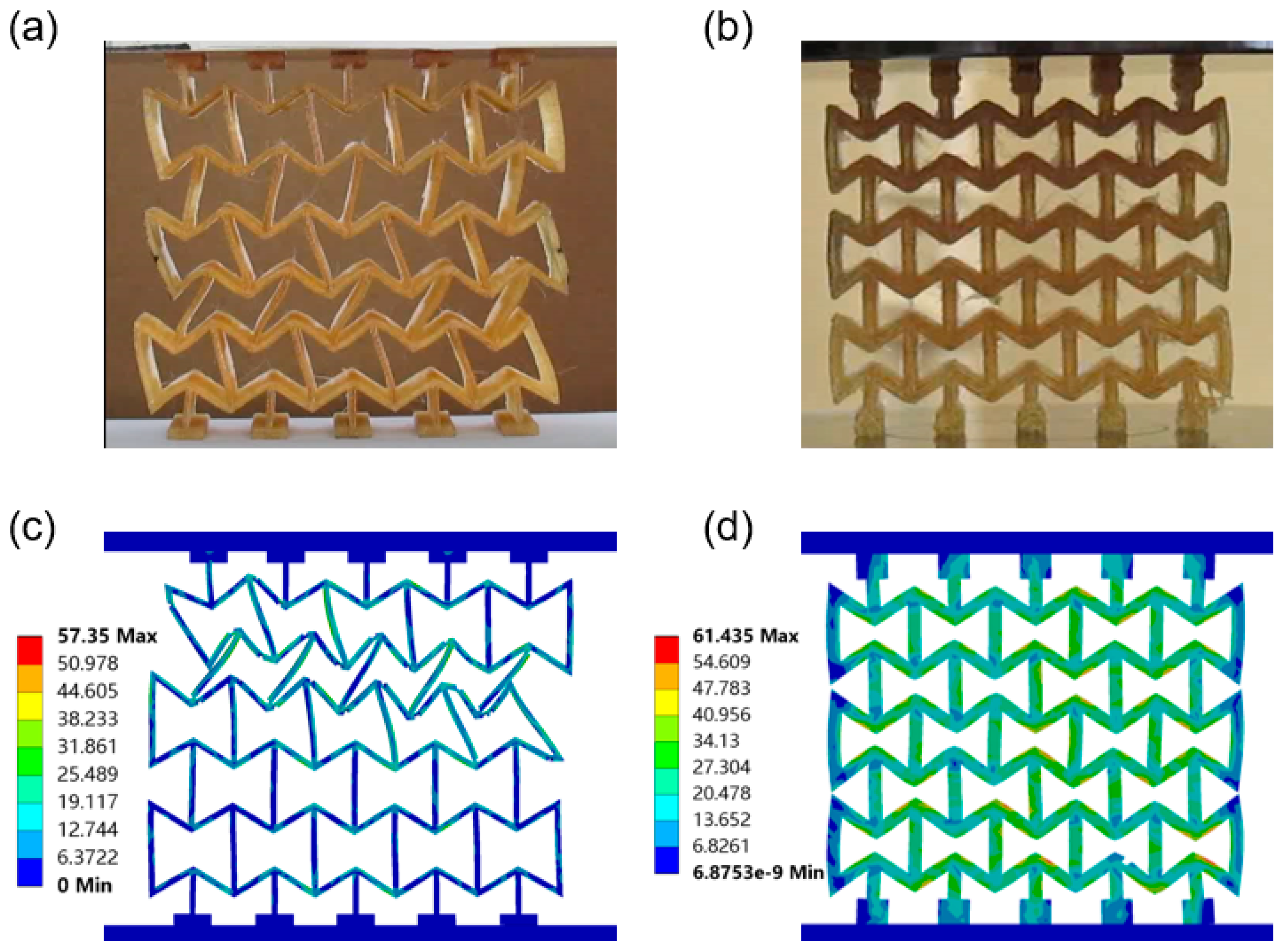
2.3. FE Simulation
2.4. Quasi-Static Compression Experiments
3. Results
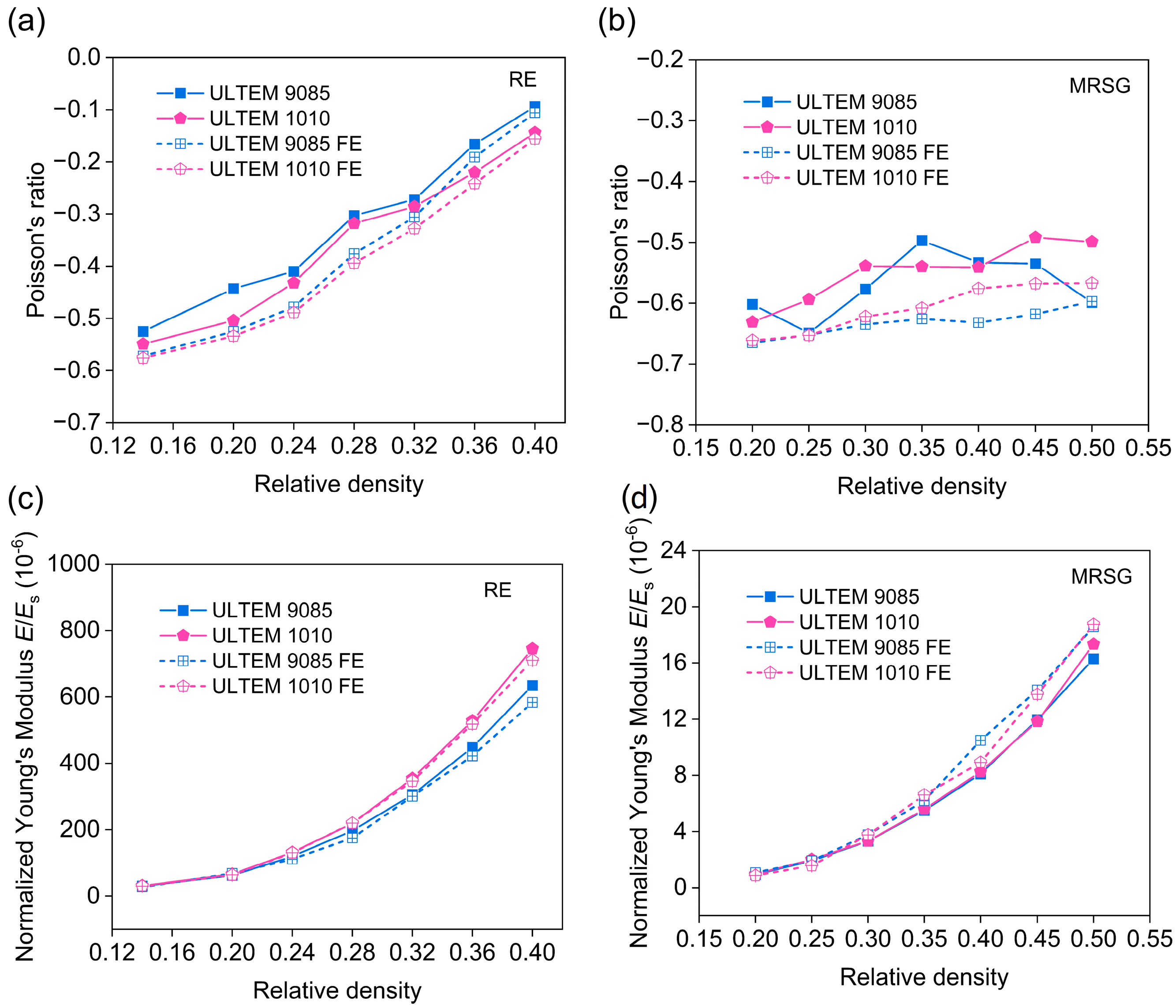
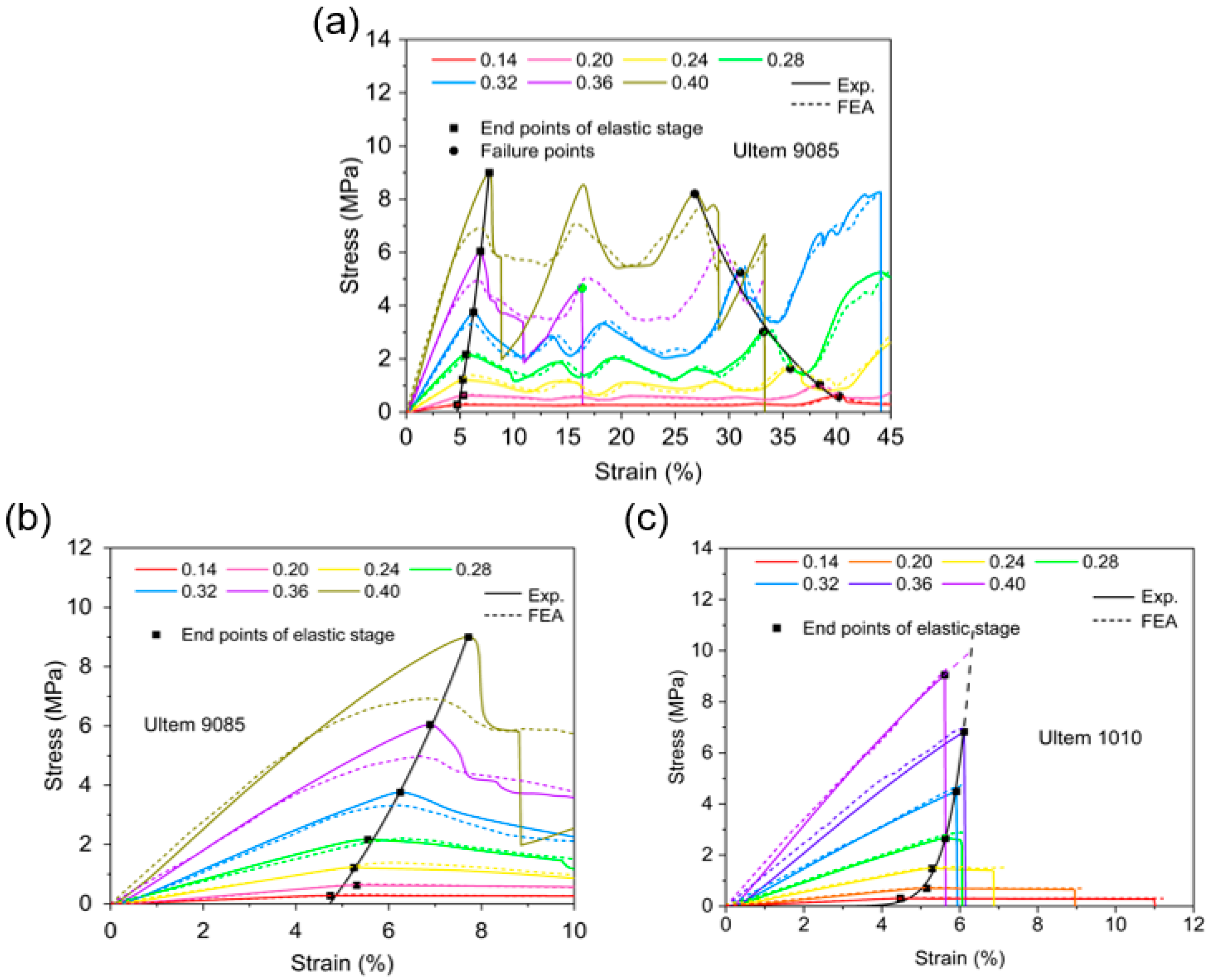
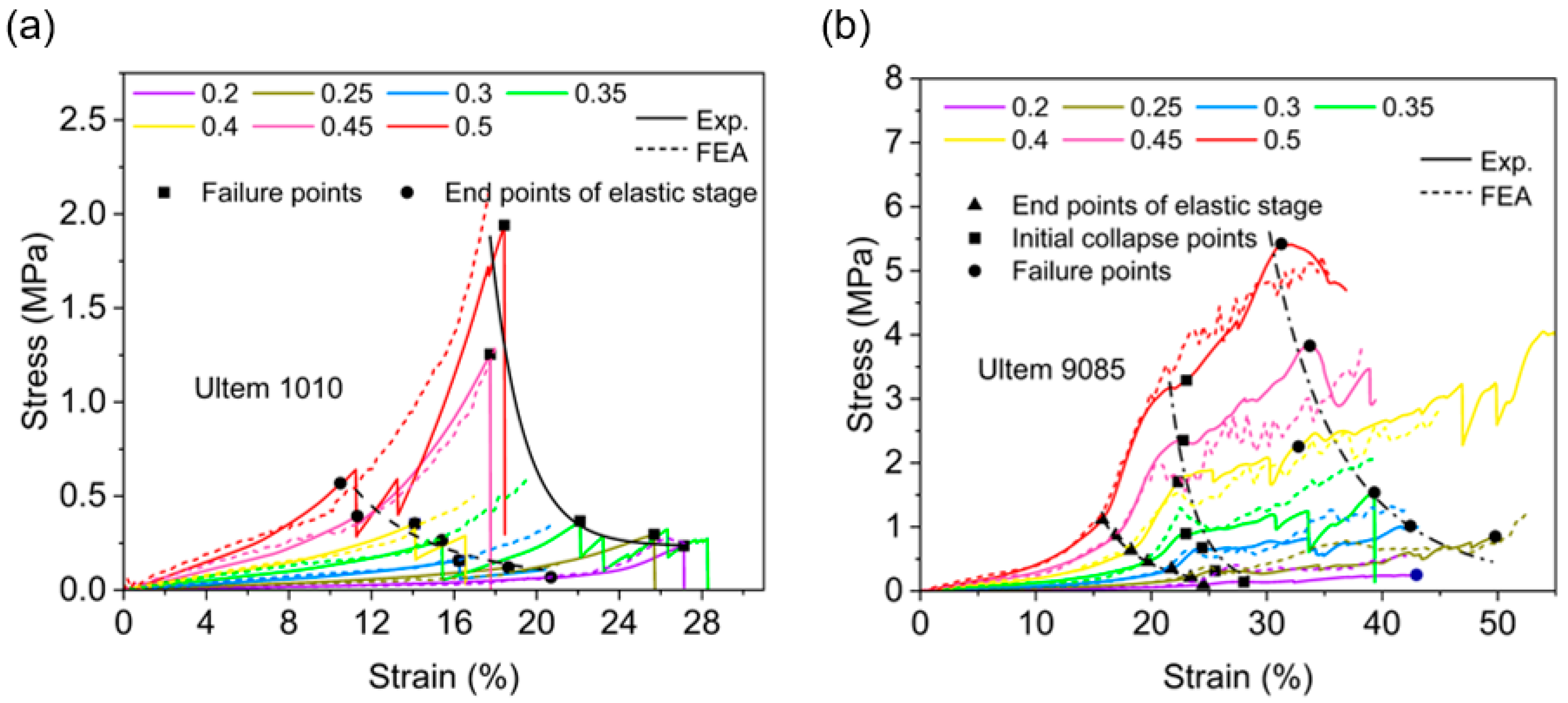
3.1. Poisson’s Ratio and Equivalent Young’s Modulus
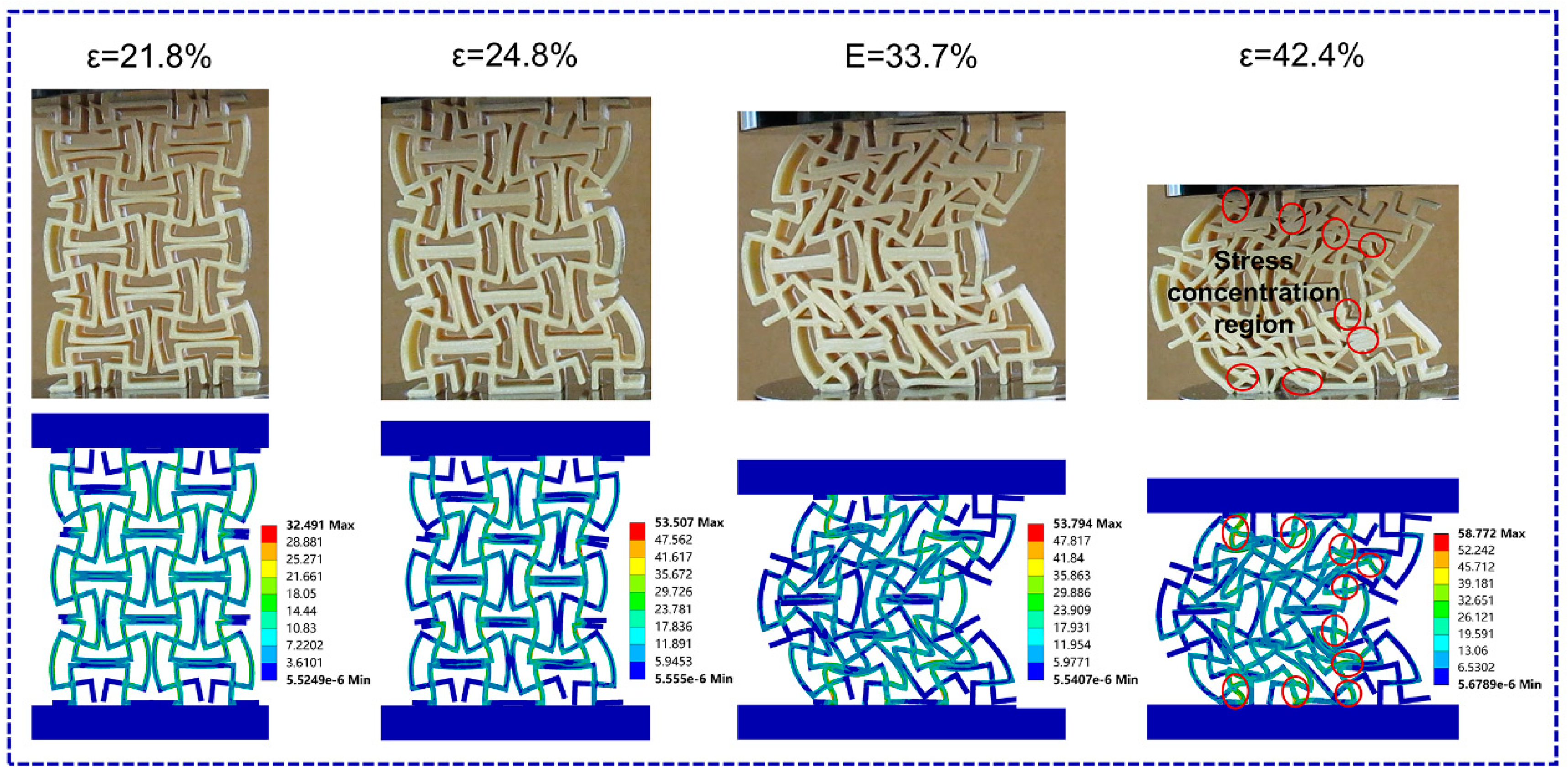
3.2. Deformation Behavior
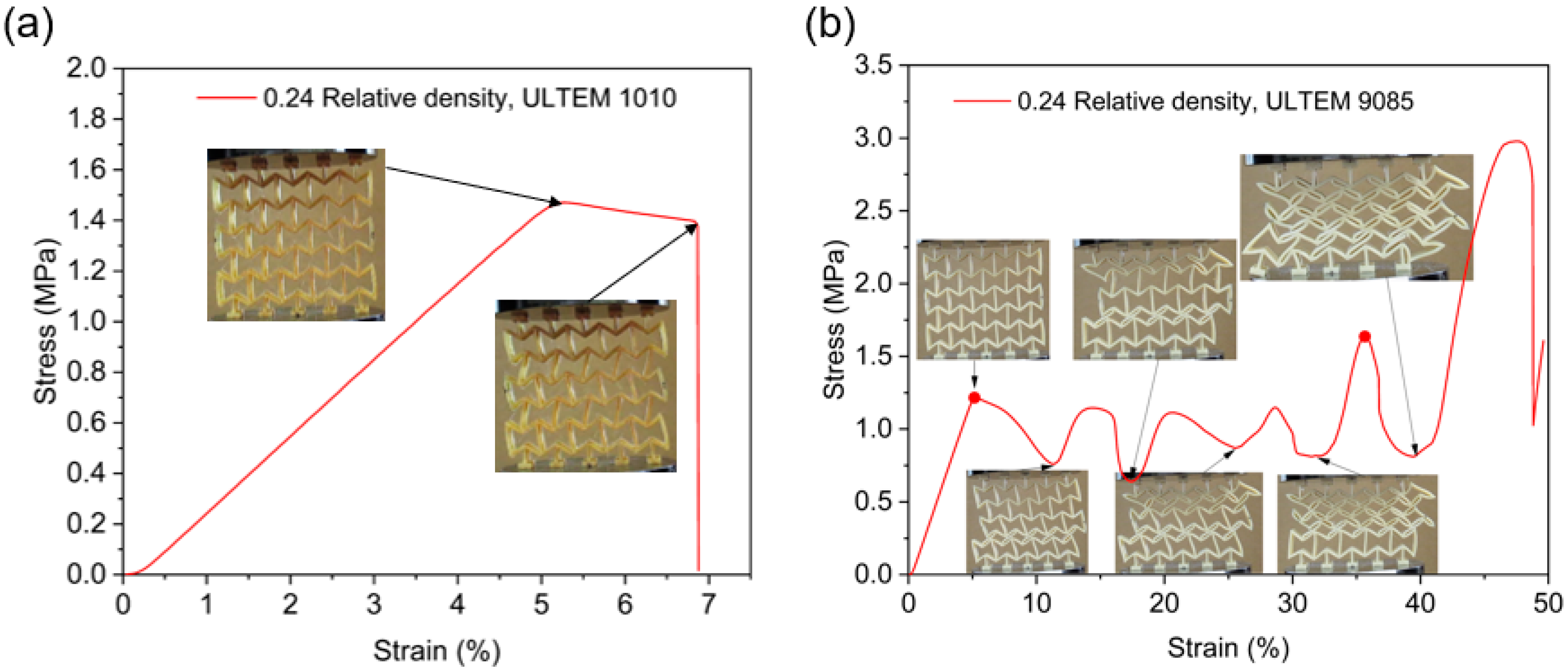
3.2.1. RE Structures
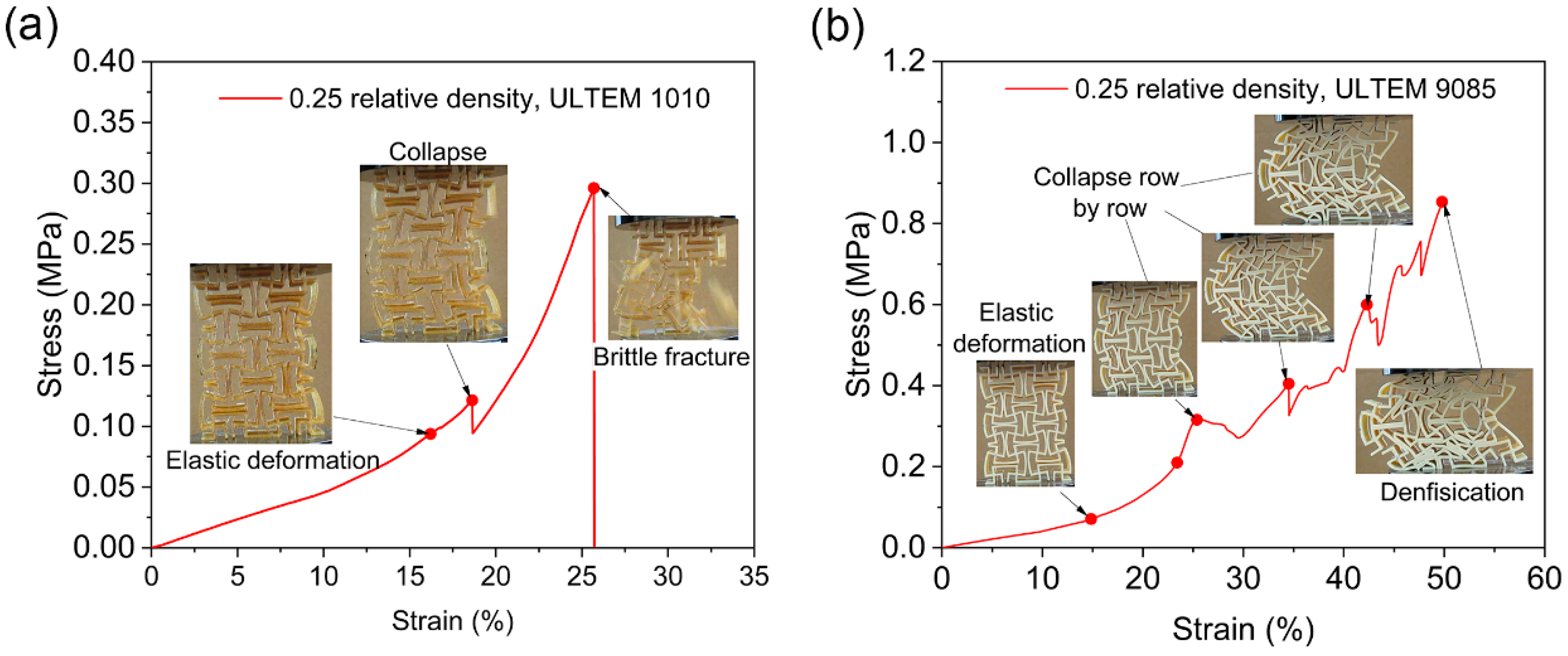
3.2.2. MRSG Structures
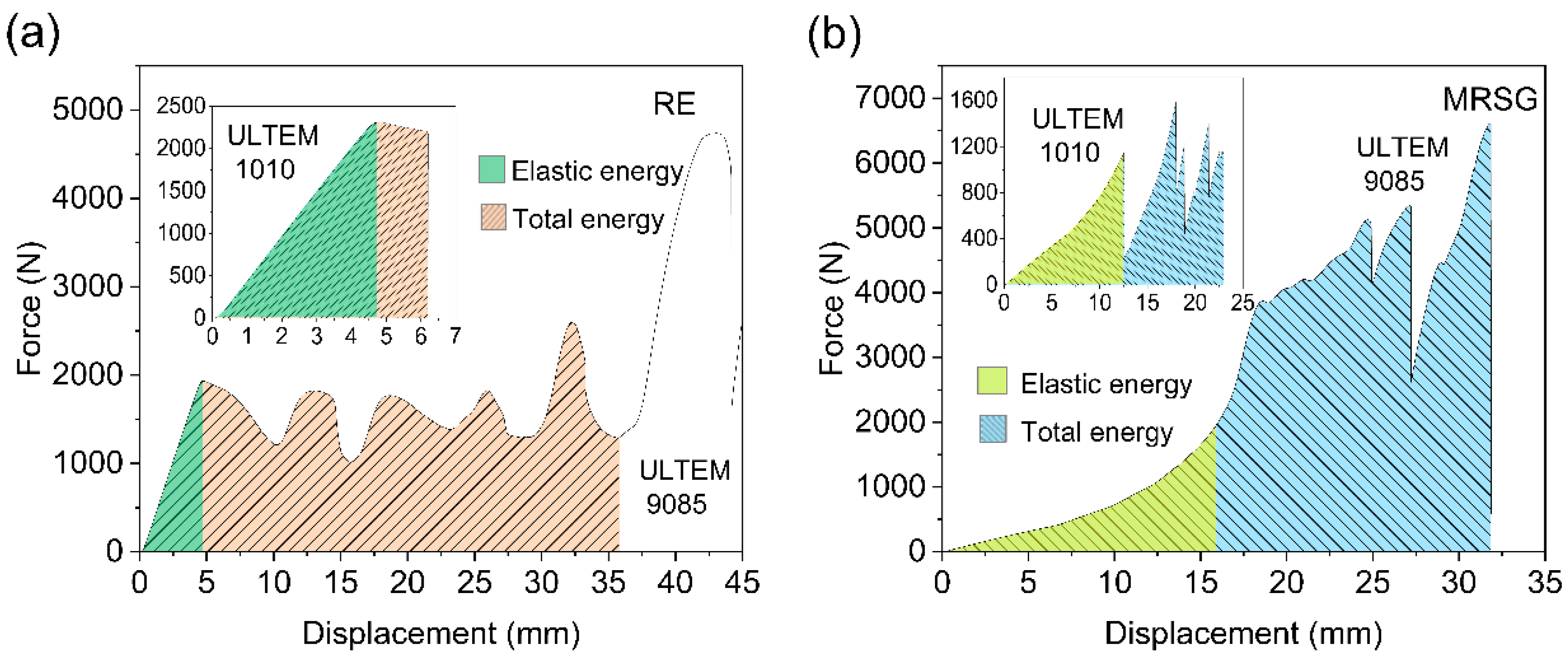
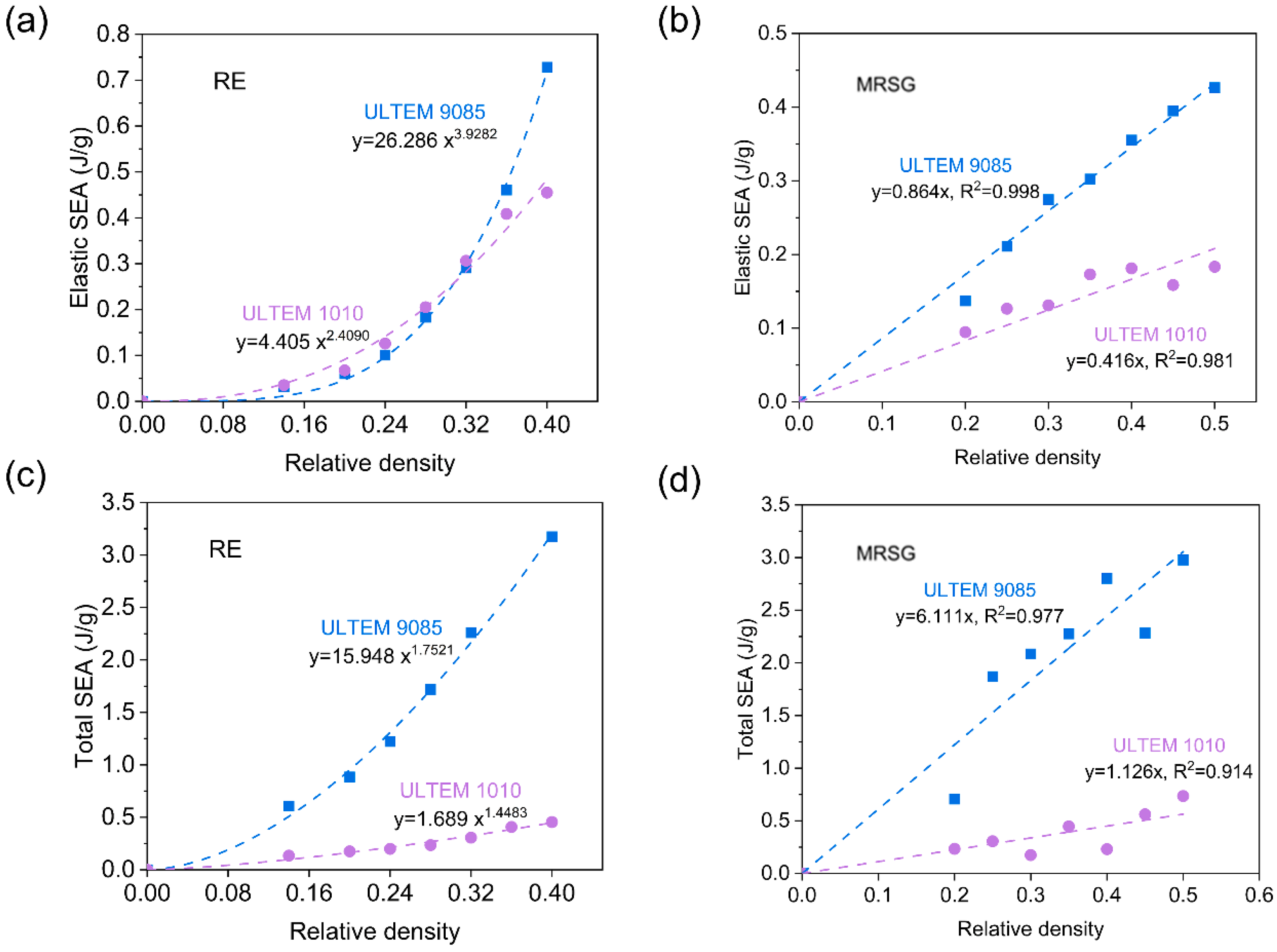
3.3. Energy Absorption
4. Discussion
4.1. Poisson’s Ratio and Equivalent Young’s Modulus
4.2. Deformation Behavior
4.2.1. RE Structures
4.2.2. MRSG Structures
4.3. Energy Absorption
5. Conclusions
- In the elastic deformation stage, the Poisson’s ratio and equivalent Young’s modulus of the RE and MRSG auxetic structures are not significantly related to the properties of the parent material but are closely related to the structural configuration parameters.
- The deformation behavior of the ULTEM 9085 auxetic structures exhibited three stages: elastic stage, plateau stage, and densification stage, while the ULTEM 1010 structures only underwent the elastic stage or the elastic and early buckling stages. The damage mode of the ULTEM 9085 structures was elastoplastic yielding failure, which was different from the brittle fracture mode of the ULTEM 1010 structures.
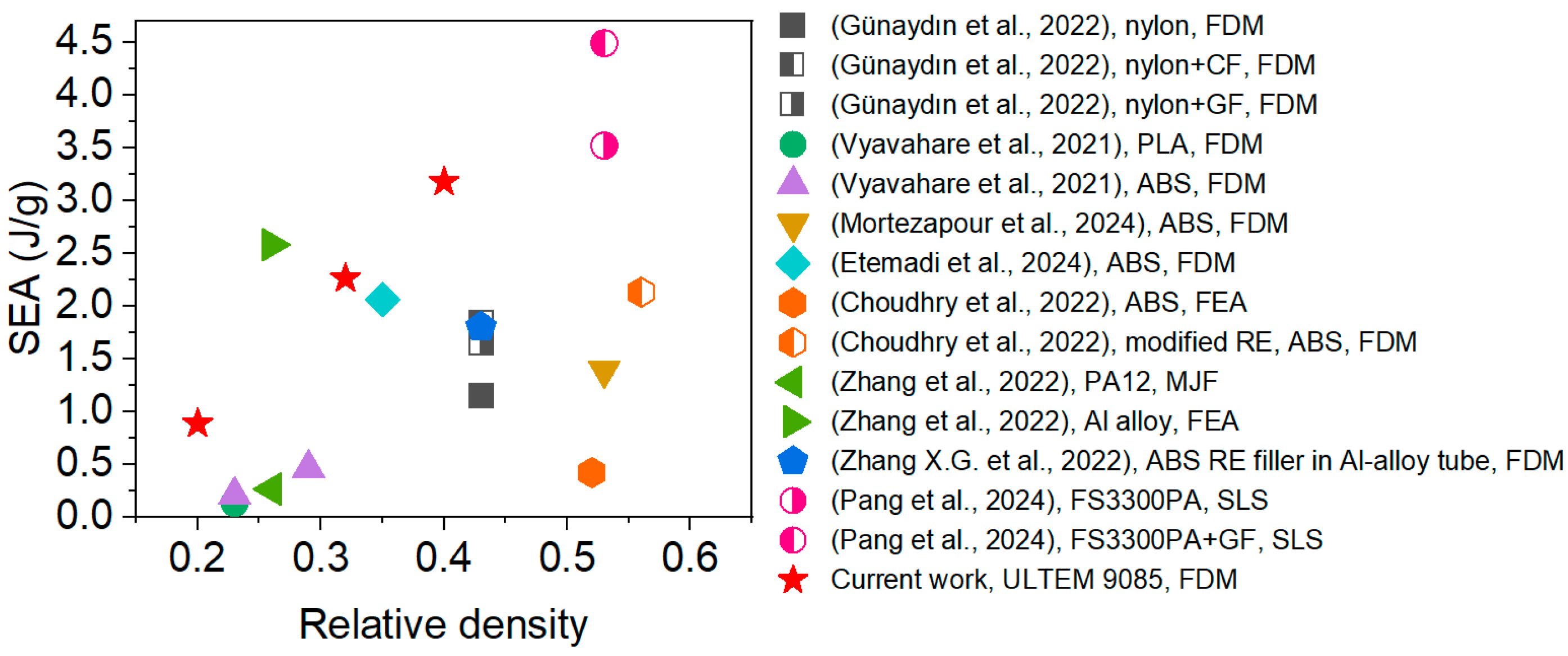
- The energy absorption of the ductile ULTEM 9085 structures was significantly higher than that of the brittle ULTEM 1010 structures. A linear correlation exists between the relative density and SEA of MRSG structures in the studied relative density range, whereas the RE structures follow a power function relationship.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NPR | Negative Poisson’s ratio |
| AM | Additive manufacturing |
| FDM | Fused deposition modeling |
| PEI | Polyetherimide |
| RE | Re-entrant |
| MRSG | Missing rib square grid |
| FE | Finite element |
| FST | Flame smoke toxicity |
| SEA | Specific energy absorption |
References
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Gao, Q.; Liao, W.H. Energy absorption of thin walled tube filled with gradient auxetic structures-theory and simulation. Int. J. Mech. Sci. 2021, 201, 106475. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, X.; Zhang, J.; Lu, G.; Tse, K.M. A review on energy absorption performance of auxetic composites with fillings. Thin-Walled Struct. 2024, 205, 112348. [Google Scholar] [CrossRef]
- Yang, S.; Chalivendra, V.B.; Kim, Y.K. Fracture and impact characterization of novel auxetic Kevlar®/Epoxy laminated composites. Compos. Struct. 2017, 168, 120–129. [Google Scholar] [CrossRef]
- Wagih, A.; Mahmoud, H.A.; Lubineau, G. 3D printed auxetic metal stiffener for lightweight metal-composite T-joints with high strength and toughness. Mater. Des. 2024, 241, 112963. [Google Scholar] [CrossRef]
- Hu, L.L.; Zhou, M.Z.; Deng, H. Dynamic indentation of auxetic and non-auxetic honeycombs under large deformation. Compos. Struct. 2019, 207, 323–330. [Google Scholar] [CrossRef]
- Li, T.T.; Liu, F.; Wang, L.F. Enhancing indentation and impact resistance in auxetic composite materials. Compos. Part B-Eng. 2020, 198, 108229. [Google Scholar] [CrossRef]
- Cheng, H.C.; Scarpa, F.; Panzera, T.H.; Farrow, I.; Peng, H.X. Shear Stiffness and Energy Absorption of Auxetic Open Cell Foams as Sandwich Cores. Phys. Status Solidi B-Basic Solid State Phys. 2019, 256, 1800411. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, L.; Ren, X.; Zhang, X.Y.; Tao, Z.; Xie, Y.M. Design and analysis of an auxetic metamaterial with tuneable stiffness. Compos. Struct. 2022, 281, 114997. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L. Auxetic materials. Proc. Inst. Mech. Eng. Part G-J. Aerosp. Eng. 2007, 221, 565–575. [Google Scholar] [CrossRef]
- Balan, P.M.; Mertens, A.J.; Bahubalendruni, M. Auxetic mechanical metamaterials and their futuristic developments: A state-of-art review. Mater. Today Commun. 2023, 34, 105285. [Google Scholar] [CrossRef]
- Nguyen, H.; Fangueiro, R.; Ferreira, F.; Nguyen, Q. Auxetic materials and structures for potential defense applications: An overview and recent developments. Text. Res. J. 2023, 93, 5268–5306. [Google Scholar] [CrossRef]
- Wei, L.L.; Zhao, X.; Yu, Q.; Zhu, G.H. A novel star auxetic honeycomb with enhanced in-plane crushing strength. Thin-Walled Struct. 2020, 149, 106623. [Google Scholar] [CrossRef]
- Foster, L.; Peketi, P.; Allen, T.; Senior, T.; Duncan, O.; Alderson, A. Application of Auxetic Foam in Sports Helmets. Appl. Sci.-Basel 2018, 8, 354. [Google Scholar] [CrossRef]
- Günaydin, K.; Gülcan, O.; Türkmen, H.S. Experimental and numerical crushing performance of crash boxes filled with re-entrant and anti-tetrachiral auxetic structures. Int. J. Crashworthiness 2023, 28, 649–663. [Google Scholar] [CrossRef]
- Luo, F.; Zhang, S.L.; Yang, D.Q. Anti-Explosion Performance of Composite Blast Wall with an Auxetic Re-Entrant Honeycomb Core for Offshore Platforms. J. Mar. Sci. Eng. 2020, 8, 182. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Z.X.; Yang, Z.Y.; Li, X. A novel re-entrant auxetic honeycomb with enhanced in-plane impact resistance. Compos. Struct. 2019, 208, 758–770. [Google Scholar] [CrossRef]
- Yang, C.; Vora, H.D.; Chang, Y. Behavior of auxetic structures under compression and impact forces. Smart Mater. Struct. 2018, 27, 025012. [Google Scholar] [CrossRef]
- Imbalzano, G.; Linforth, S.; Ngo, T.D.; Lee, P.V.S.; Tran, P. Blast resistance of auxetic and honeycomb sandwich panels: Comparisons and parametric designs. Compos. Struct. 2018, 183, 242–261. [Google Scholar] [CrossRef]
- Qi, C.; Remennikov, A.; Pei, L.Z.; Yang, S.; Yu, Z.H.; Ngo, T.D. Impact and close-in blast response of auxetic honeycomb-cored sandwich panels: Experimental tests and numerical simulations. Compos. Struct. 2017, 180, 161–178. [Google Scholar] [CrossRef]
- Kalubadanage, D.; Remennikov, A.; Ngo, T.; Qi, C. Close-in blast resistance of large-scale auxetic re-entrant honeycomb sandwich panels. J. Sandw. Struct. Mater. 2021, 23, 4016–4053. [Google Scholar] [CrossRef]
- Li, D.; Yin, J.H.; Dong, L.; Lakes, R.S. Strong re-entrant cellular structures with negative Poisson’s ratio. J. Mater. Sci. 2018, 53, 3493–3499. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Wang, Z.; Zhou, S.W.; Shao, J.W.; Wu, X. Novel Negative Poisson’s Ratio Lattice Structures with Enhanced Stiffness and Energy Absorption Capacity. Materials 2018, 11, 1095. [Google Scholar] [CrossRef]
- Fu, M.H.; Chen, Y.; Hu, L.L. Bilinear elastic characteristic of enhanced auxetic honeycombs. Compos. Struct. 2017, 175, 101–110. [Google Scholar] [CrossRef]
- Wang, G.X.; Deng, X.L. In-plane mechanical behavior design of novel re-entrant and hexagonal combined honeycombs. Mater. Today Commun. 2024, 40, 109729. [Google Scholar] [CrossRef]
- Li, D.; Yin, J.H.; Dong, L.; Lakes, R.S. Numerical analysis on mechanical behaviors of hierarchical cellular structures with negative Poisson’s ratio. Smart Mater. Struct. 2017, 26, 025014. [Google Scholar] [CrossRef]
- Hou, J.H.; Li, D.; Dong, L. Mechanical behaviors of hierarchical cellular structures with negative Poisson’s ratio. J. Mater. Sci. 2018, 53, 10209–10216. [Google Scholar] [CrossRef]
- Smith, C.W.; Grima, J.N.; Evans, K.E. A novel mechanism for generating auxetic behaviour in reticulated foams: Missing rib foam model. Acta Mater. 2000, 48, 4349–4356. [Google Scholar] [CrossRef]
- Gaspar, N.; Ren, X.; Smith, C.; Grima, J.; Evans, K. Novel honeycombs with auxetic behaviour. Acta Mater. 2005, 53, 2439–2445. [Google Scholar] [CrossRef]
- Lim, T.C. Analogies across auxetic models based on deformation mechanism. Phys. Status Solidi-Rapid Res. Lett. 2017, 11, 1600440. [Google Scholar] [CrossRef]
- Farrugia, P.S.; Gatt, R.; Lonardelli, E.Z.; Grima, J.N.; Evans, K.E. Different Deformation Mechanisms Leading to Auxetic Behavior Exhibited by Missing Rib Square Grid Structures. Phys. Status Solidi B-Basic Solid State Phys. 2019, 256, 1800186. [Google Scholar] [CrossRef]
- Xu, Y.; Šavija, B. Auxetic cementitious composites (ACCs) with excellent compressive ductility: Experiments and modeling. Mater. Des. 2024, 237, 112572. [Google Scholar] [CrossRef]
- Fíla, T.; Zlámal, P.; Jiroušek, O.; Falta, J.; Koudelka, P.; Kytýř, D.; Doktor, T.; Valach, J. Impact Testing of Polymer-filled Auxetics Using Split Hopkinson Pressure Bar. Adv. Eng. Mater. 2017, 19, 1700076. [Google Scholar] [CrossRef]
- Mahesh, V.; Maladkar, P.G.; Sadaram, G.S.; Joseph, A.; Mahesh, V.; Harursampath, D. Experimental investigation of the in-plane quasi-static mechanical behaviour of additively-manufactured polyethylene terephthalate/organically modified montmorillonite nanoclay composite auxetic structures. J. Thermoplast. Compos. Mater. 2022, 36, 4021–4041. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, L.-H.; Xu, H.-Q.; Zhou, W. A novel anti-missing-rib lozenge lattice metamaterial with enhanced mechanical properties. Mater. Today Commun. 2024, 38, 108151. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Jiang, S.H.; Li, J.; Pokkalla, D.K.; Wang, Q.Y.; Zhang, C.Z. Novel Isotropic Anti-Tri-Missing Rib Auxetics with Prescribed In-Plane Mechanical Properties Over Large Deformations. Int. J. Appl. Mech. 2021, 13, 2150115. [Google Scholar] [CrossRef]
- Jiang, D.R.; Thissen, H.; Hughes, T.C.; Yang, K.; Wilson, R.; Murphy, A.B.; Nguyen, V. Advances in additive manufacturing of auxetic structures for biomedical applications. Mater. Today Commun. 2024, 40, 110045. [Google Scholar] [CrossRef]
- Gromat, T.; Gardan, J.; Saifouni, O.; Makke, A.; Recho, N. Generative design for additive manufacturing of polymeric auxetic materials produced by fused filament fabrication. Int. J. Interact. Des. Manuf.-Ijidem 2023, 17, 2943–2955. [Google Scholar] [CrossRef]
- Dziewit, P.; Platek, P.; Janiszewski, J.; Sarzynski, M.; Grazka, M.; Paszkowski, R. Mechanical Response of Additive Manufactured Regular Cellular Structures in Quasi-Static Loading Conditions-Part I Experimental Investigations. In Proceedings of the 7th International Conference on Mechanics and Materials in Design (M2D), Albufeira, Portugal, 11–15 June 2017; pp. 1061–1074. [Google Scholar]
- Farrokhabadi, A.; Veisi, H.; Gharehbaghi, H.; Montesano, J.; Behravesh, A.H.; Hedayati, S.K. Investigation of the energy absorption capacity of foam-filled 3D-printed glass fiber reinforced thermoplastic auxetic honeycomb structures. Mech. Adv. Mater. Struct. 2023, 30, 758–769. [Google Scholar] [CrossRef]
- Ding, S.L.; Zou, B.; Wang, P.; Ding, H.J. Effects of nozzle temperature and building orientation on mechanical properties and microstructure of PEEK and PEI printed by 3D-FDM. Polym. Test. 2019, 78, 105948. [Google Scholar] [CrossRef]
- Retolaza, J.; Gondra, K.; Ansola, R.; Allue, A. Mechanical research to optimize parameter selection for PPS material processed by FDM. Mater. Manuf. Process. 2022, 37, 1332–1338. [Google Scholar] [CrossRef]
- Appalsamy, T.; Hamilton, S.L.; Kgaphola, M.J. Tensile Test Analysis of 3D Printed Specimens with Varying Print Orientation and Infill Density. J. Compos. Sci. 2024, 8, 121. [Google Scholar] [CrossRef]
- Michelis, P.; Spitas, V. Numerical and experimental analysis of a triangular auxetic core made of CFR-PEEK using the Directionally Reinforced Integrated Single-yarn (DIRIS) architecture. Compos. Sci. Technol. 2010, 70, 1064–1071. [Google Scholar] [CrossRef]
- Ren, L.; Wu, W.; Ren, L.; Song, Z.; Liu, Q.; Li, B.; Wu, Q.; Zhou, X. 3D Printing of Auxetic Metamaterials with High-Temperature and Programmable Mechanical Properties. Adv. Mater. Technol. 2022, 7, 2101546. [Google Scholar] [CrossRef]
- He, P.; Wang, S.; Zhang, M.; Sang, L.; Tong, L.; Hou, W. Compression performance of 3D-printed thermoplastic auxetic structures. Thin-Walled Struct. 2024, 197, 111558. [Google Scholar] [CrossRef]
- Andrew, J.J.; Alhashmi, H.; Schiffer, A.; Kumar, S.; Deshpande, V.S. Energy absorption and self-sensing performance of 3D printed CF/PEEK cellular composites. Mater. Des. 2021, 208, 109863. [Google Scholar] [CrossRef]
- Günaydın, K.; Rea, C.; Kazancı, Z. Energy absorption enhancement of additively manufactured hexagonal and re-entrant (auxetic) lattice structures by using multi-material reinforcements. Addit. Manuf. 2022, 59, 103076. [Google Scholar] [CrossRef]
- Vyavahare, S.; Kumar, S. Numerical and experimental investigation of FDM fabricated re-entrant auxetic structures of ABS and PLA materials under compressive loading. Rapid Prototyp. J. 2021, 27, 223–244. [Google Scholar] [CrossRef]
- Mortezapour, A.R.; Monazzah, A.H.; Sarfaraz, R.; Sameezadeh, M. Energy absorption of multi-scale hierarchically graded auxetic structures: Experimental and simulation methods. Prog. Addit. Manuf. 2024, 10, 291–308. [Google Scholar] [CrossRef]
- Etemadi, E.; Hosseinabadi, M.; Taghizadeh, M.; Scarpa, F.; Hu, H. Enhancing the energy absorption capability of auxetic metamaterials through auxetic cells within re-entrant circular units. Eng. Struct. 2024, 315, 118379. [Google Scholar] [CrossRef]
- Choudhry, N.K.; Panda, B.; Kumar, S. In-plane energy absorption characteristics of a modified re-entrant auxetic structure fabricated via 3D printing. Compos. Part B Eng. 2022, 228, 109437. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H.; Tian, R.; Xue, Q.; Guan, H.; Yang, X. Quasi-static compression and dynamic crushing behaviors of novel hybrid re-entrant auxetic metamaterials with enhanced energy-absorption. Compos. Struct. 2022, 288, 115399. [Google Scholar] [CrossRef]
- Zhang, X.G.; Jiang, W.; Zhang, Y.; Luo, C.; Zhang, X.Y.; Han, D.; Hao, J.; Teng, X.C.; Xie, Y.M.; Ren, X. Energy absorption properties of composite tubes with hexagonal and re-entrant honeycomb fillers. Constr. Build. Mater. 2022, 356, 129298. [Google Scholar] [CrossRef]
- Pang, L.; Ma, Y.; Song, X.; Wang, H.; Wang, L.; Peng, W.; Wan, Y.; Feng, R. Experimental and simulation study on effects of material and loading direction on the quasi-static compression behavior of re-entrant honeycomb structure. Mater. Today Commun. 2024, 39, 109005. [Google Scholar] [CrossRef]
- Gatt, R.; Attard, D.; Farrugia, P.S.; Azzopardi, K.M.; Mizzi, L.; Brincat, J.P.; Grima, J.N. A realistic generic model for anti-tetrachiral systems. Phys. Status Solidi B-Basic Solid State Phys. 2013, 250, 2012–2019. [Google Scholar] [CrossRef]
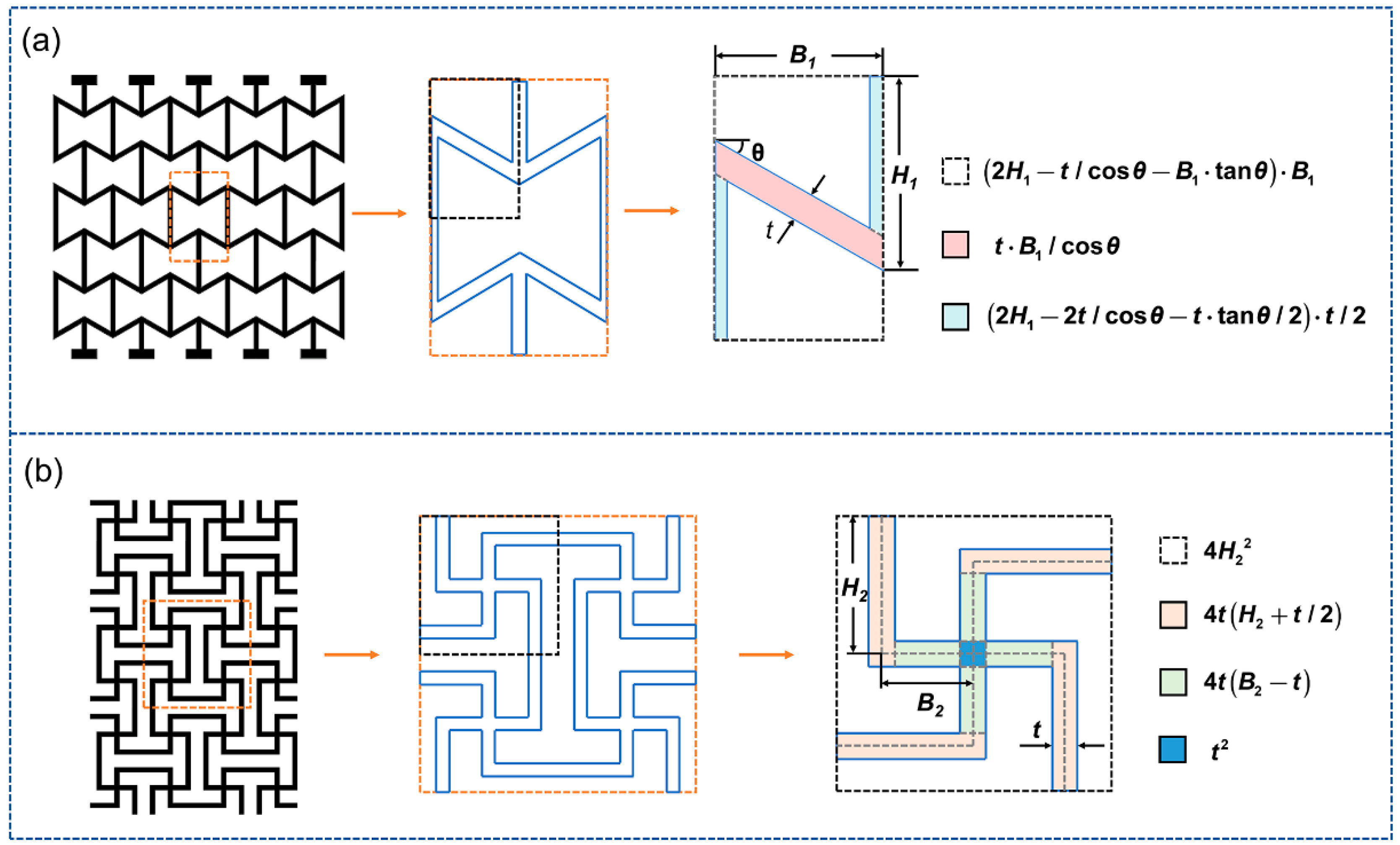




| Relative Density (RE) | H1 (mm) | B1 (mm) | Relative Density (MRSG) | H2 (mm) | B2 (mm) |
|---|---|---|---|---|---|
| 0.14 | 16.79 | 14.54 | 0.20 | 12.47 | 8.31 |
| 0.20 | 11.78 | 10.20 | 0.25 | 9.93 | 6.62 |
| 0.24 | 9.83 | 8.51 | 0.30 | 8.23 | 5.49 |
| 0.28 | 8.44 | 7.31 | 0.35 | 7.02 | 4.68 |
| 0.32 | 7.40 | 6.41 | 0.40 | 6.11 | 4.08 |
| 0.36 | 6.59 | 5.71 | 0.45 | 5.41 | 3.60 |
| 0.40 | 5.94 | 5.14 | 0.50 | 4.84 | 3.23 |
| Materials | Density (g/cm3) | Young’s Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|
| ULTEM 9085 | 1.34 | 2147 | 0.40 |
| ULTEM 1010 | 1.27 | 2289 | 0.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Aliaksandr, L.; Narkevich, H.; Hao, S.; Chen, Y.; He, Y.; Tian, J.; Dai, S.; Yang, C. Quasi-Static Compressive Behavior and Energy Absorption Performance of Polyether Imide Auxetic Structures Made by Fused Deposition Modeling. J. Manuf. Mater. Process. 2025, 9, 155. https://doi.org/10.3390/jmmp9050155
Xu J, Aliaksandr L, Narkevich H, Hao S, Chen Y, He Y, Tian J, Dai S, Yang C. Quasi-Static Compressive Behavior and Energy Absorption Performance of Polyether Imide Auxetic Structures Made by Fused Deposition Modeling. Journal of Manufacturing and Materials Processing. 2025; 9(5):155. https://doi.org/10.3390/jmmp9050155
Chicago/Turabian StyleXu, Jing, Liubimau Aliaksandr, Hanna Narkevich, Sijia Hao, Yubin Chen, Yuguang He, Junpeng Tian, Shenglong Dai, and Cheng Yang. 2025. "Quasi-Static Compressive Behavior and Energy Absorption Performance of Polyether Imide Auxetic Structures Made by Fused Deposition Modeling" Journal of Manufacturing and Materials Processing 9, no. 5: 155. https://doi.org/10.3390/jmmp9050155
APA StyleXu, J., Aliaksandr, L., Narkevich, H., Hao, S., Chen, Y., He, Y., Tian, J., Dai, S., & Yang, C. (2025). Quasi-Static Compressive Behavior and Energy Absorption Performance of Polyether Imide Auxetic Structures Made by Fused Deposition Modeling. Journal of Manufacturing and Materials Processing, 9(5), 155. https://doi.org/10.3390/jmmp9050155






