Leveraging Intelligent Machines for Sustainable and Intelligent Manufacturing Systems

Abstract

This study presents an intelligent machine developed for real-time quality monitoring during CNC turning, aimed at improving cutting efficiency and reducing production energy. A dynamometer integrated into the CNC machine captures decomposed cutting forces using the Daubechies wavelet transform. These force ratios are correlated with key workpiece dimensions: surface roughness, average roughness, straightness, and roundness. Two predictive models—nonlinear regression and a feed-forward neural network with Levenberg–Marquardt backpropagation—are employed to estimate these parameters under varying cutting conditions. Experimental results indicate that nonlinear regression models outperform neural networks in predictive accuracy. The proposed system offers effective in-process control of machining quality, contributing to shorter cycle times, lower defect rates, and more sustainable manufacturing practices.

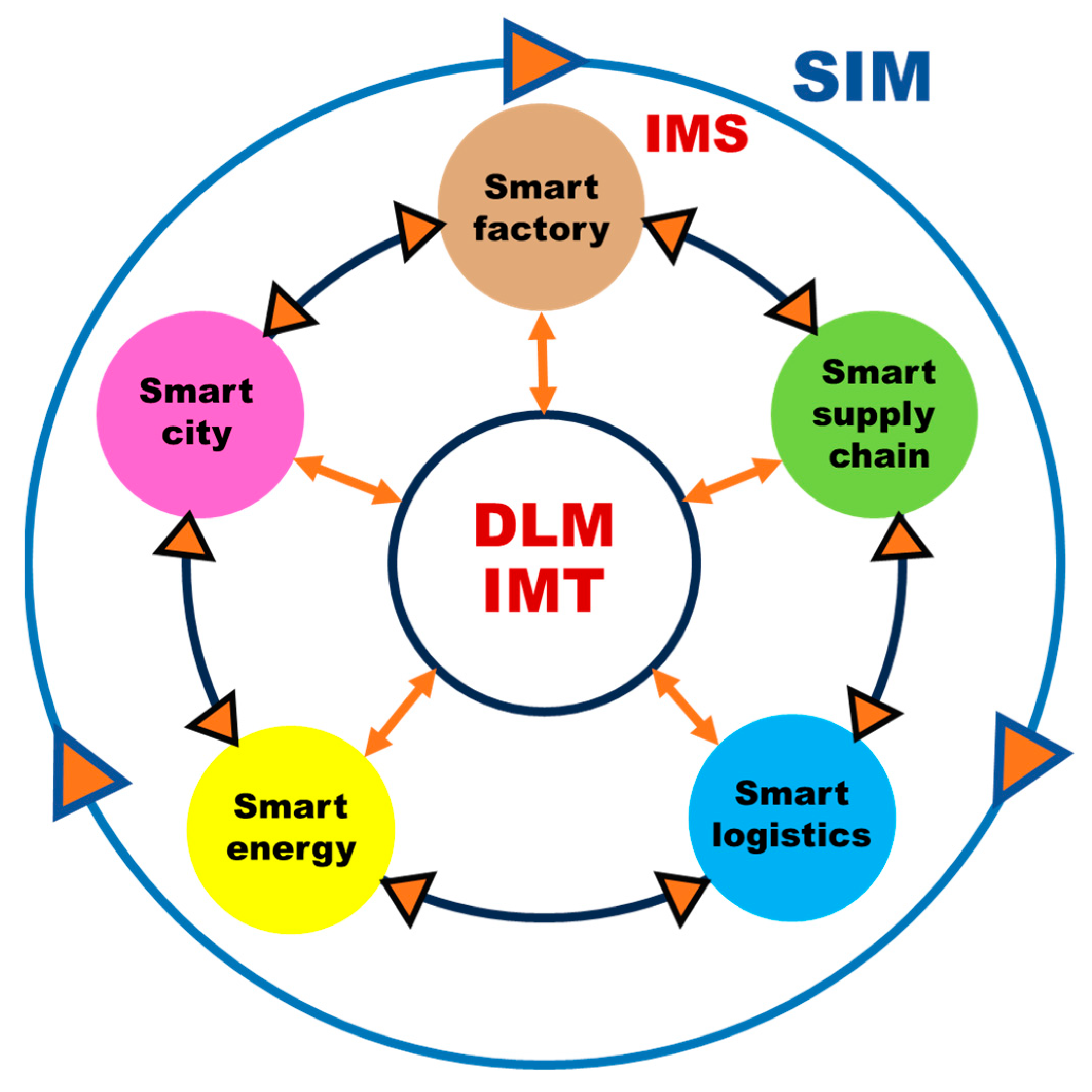
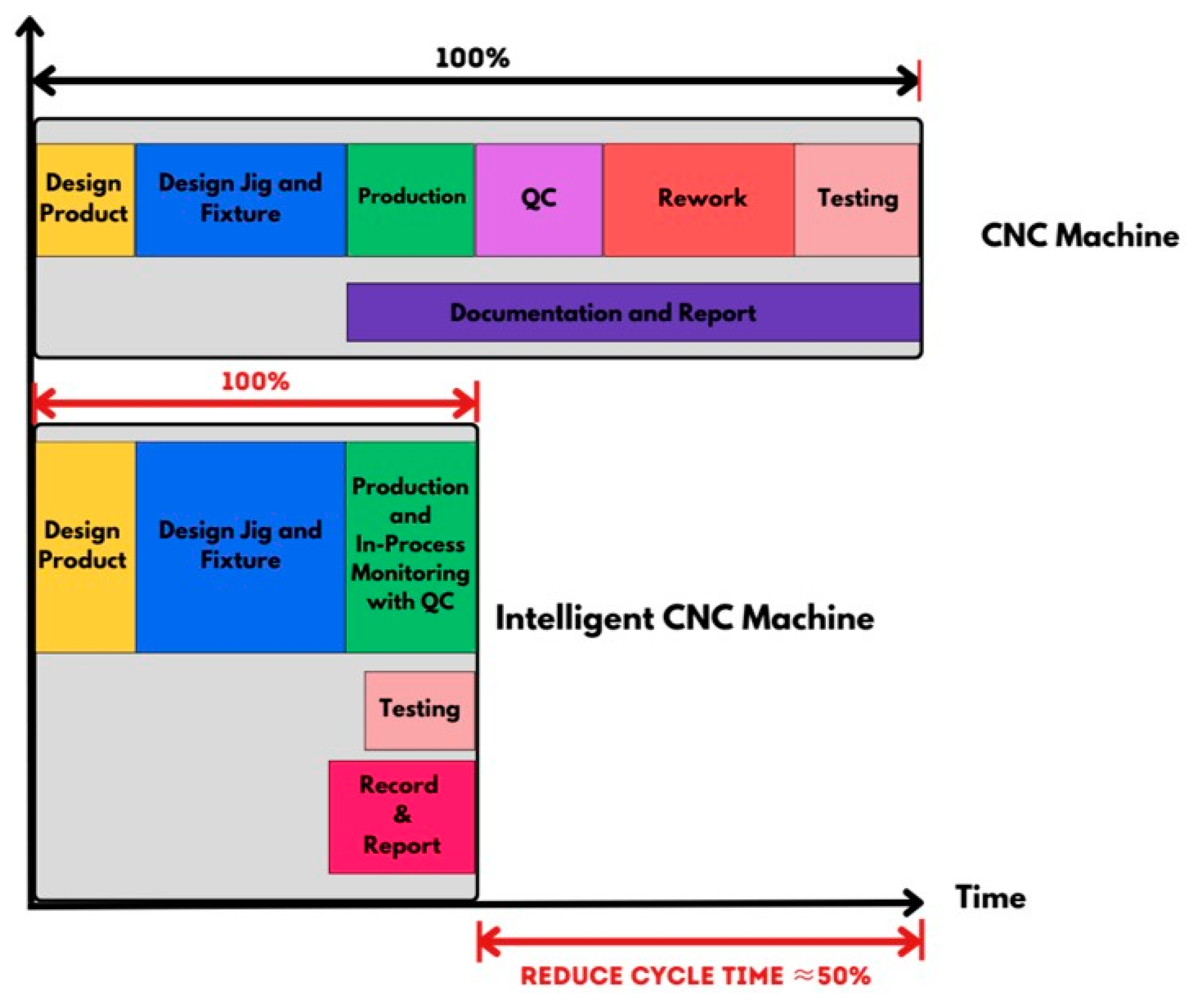
1. Introduction

Presently, digital lean manufacturing (DLM) and the intelligent machine tool (IMT) have become more important at the core of the intelligent manufacturing system (IMS) to promote and drive sustainable and intelligent manufacturing (SIM) in the near future, in which in-process monitoring and quality control are normally applied to achieve the SIM system, as shown in Figure 1. Since intelligent machines can help eliminate waste and carbon dioxide, especially from rework processes, this reflects the digital lean and leads to the smart factory [1,2]. Consequently, the smart supply chain can be optimised and planned with smart logistics for smart energy, which can be finally developed into the smart city to reduce the CO₂ emissions for calculating the carbon footprint of products. Hence, this paper presents the advanced works [3,4] of the author to continue and propose an intelligent CNC turning method to monitor the average surface roughness, the surface roughness, the straightness, and the roundness of the workpieces concurrently, which are the critical dimensions of precision parts.

However, those dimensions, which depend on the combinations of cutting conditions, cannot be measured and estimated directly during in-process turning. Therefore, it is necessary to examine the cutting conditions to predict all dimensions, which are the desired parameters of the final workpiece, in order to reduce rejection, rework and production energy for sustainable and intelligent manufacturing systems [5,6].

The in-process prediction of surface roughness, straightness, and roundness in the CNC turning process has been proposed by an artificial neural network using a decomposed cutting force ratio [4,5,6]. However, the proposed system has never been compared with the nonlinear regression models [7,8]. Moreover, the nonlinear models have not been utilised to generate the in-process prediction models of those parameters at the same time as the combination of cutting conditions [9,10,11]. Many researchers have investigated the critical dimensions [12,13], the cutting parameters [14,15], the cutting forces [16], and the workpiece quality [17]. The Daubechies wavelet transform has been adopted recently to decompose the dynamic cutting forces to monitor the signals which correspond with the surface roughness, straightness, and roundness, respectively, in time and frequency domains [18,19].

Therefore, this paper presents the continued work of the author to compare the in-process monitoring and prediction of surface roughness, straightness, and roundness simultaneously between nonlinear regression models and an approach using an artificial neural network, as shown in Figure 2.

Referring to the literature reviews [20,21,22,23], the decomposed cutting forces (Fx, Fy, Fz) can filter out the desired signals to specific levels of the wavelet transform, such as the signals of surface roughness, straightness, and roundness [24,25]. As a consequence, the roughness of the surface, the straightness, and the roundness can be estimated based on those decomposed cutting forces [26,27,28,29]. However, they have not been monitored and calculated simultaneously in the CNC turning process in the past [30,31].

In order to realise an intelligent CNC turning machine for a sustainable and intelligent manufacturing system, the in-process monitoring system is proposed to forecast the average surface roughness, the surface roughness, the straightness, and the roundness concurrently [32,33,34,35,36]. The nonlinear regression models are employed to represent the relations of the tool wear, the average surface roughness, the surface roughness, the roundness, the cutting conditions, and the ratios of decomposed cutting forces by utilising regression analysis [37,38,39]. Finally, the experimentally obtained models will be compared to the artificial neural network to compute all critical dimensions during in-process CNC turning, as shown in Figure 2. The new in-process monitoring system is illustrated to predict the average surface roughness, the surface roughness, the straightness, and the roundness simultaneously by utilising the decomposed cutting forces, as shown in Figure 3.

Unlike previous studies [40,41], this study uniquely compares nonlinear regression and neural networks for in-process prediction of all critical geometrical parameters (Ra, Rz, St, Ro) simultaneously, based on cutting force decomposition under varying cutting conditions. Prior works addressed one or two parameters independently and did not integrate predictive performance across all four.

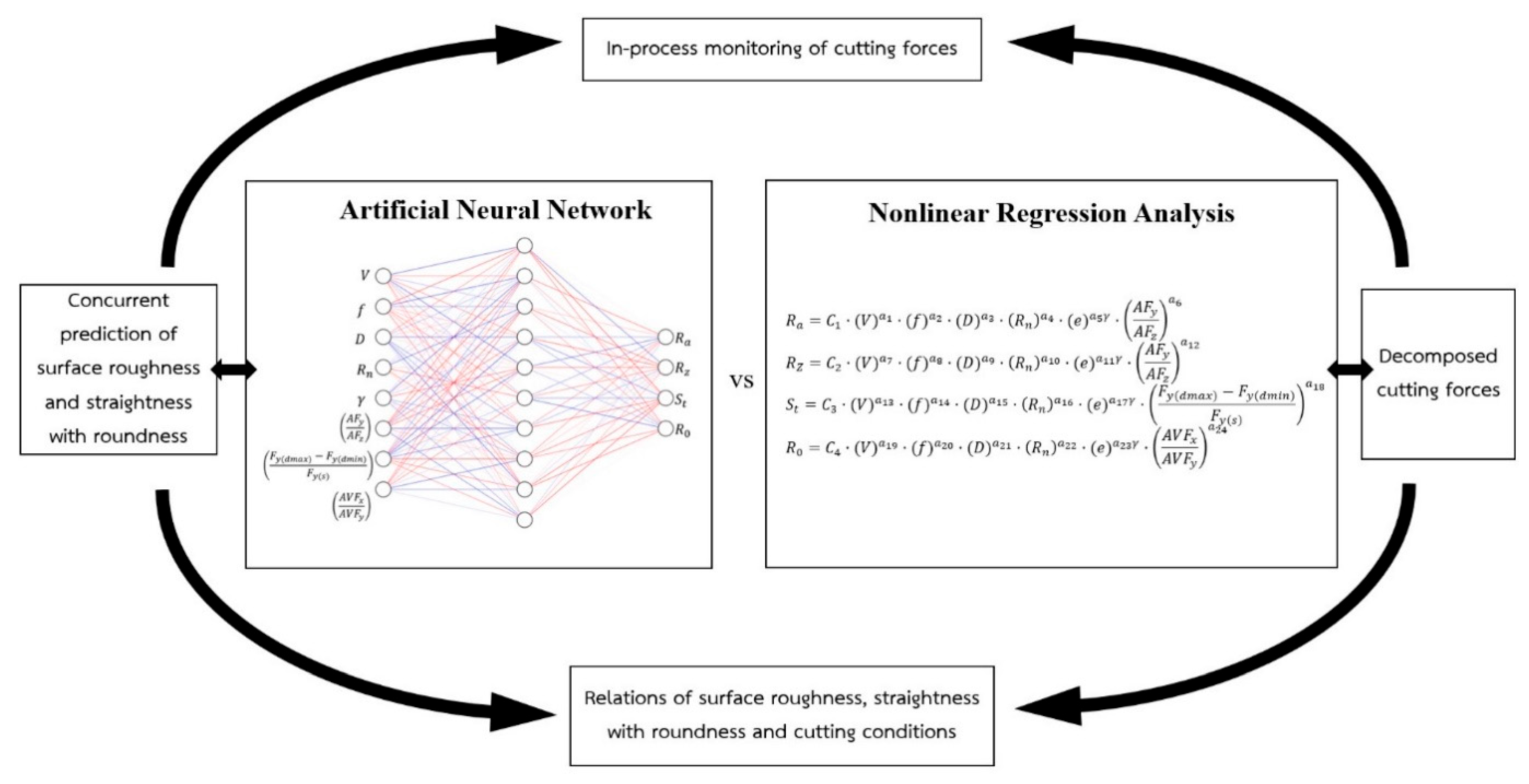
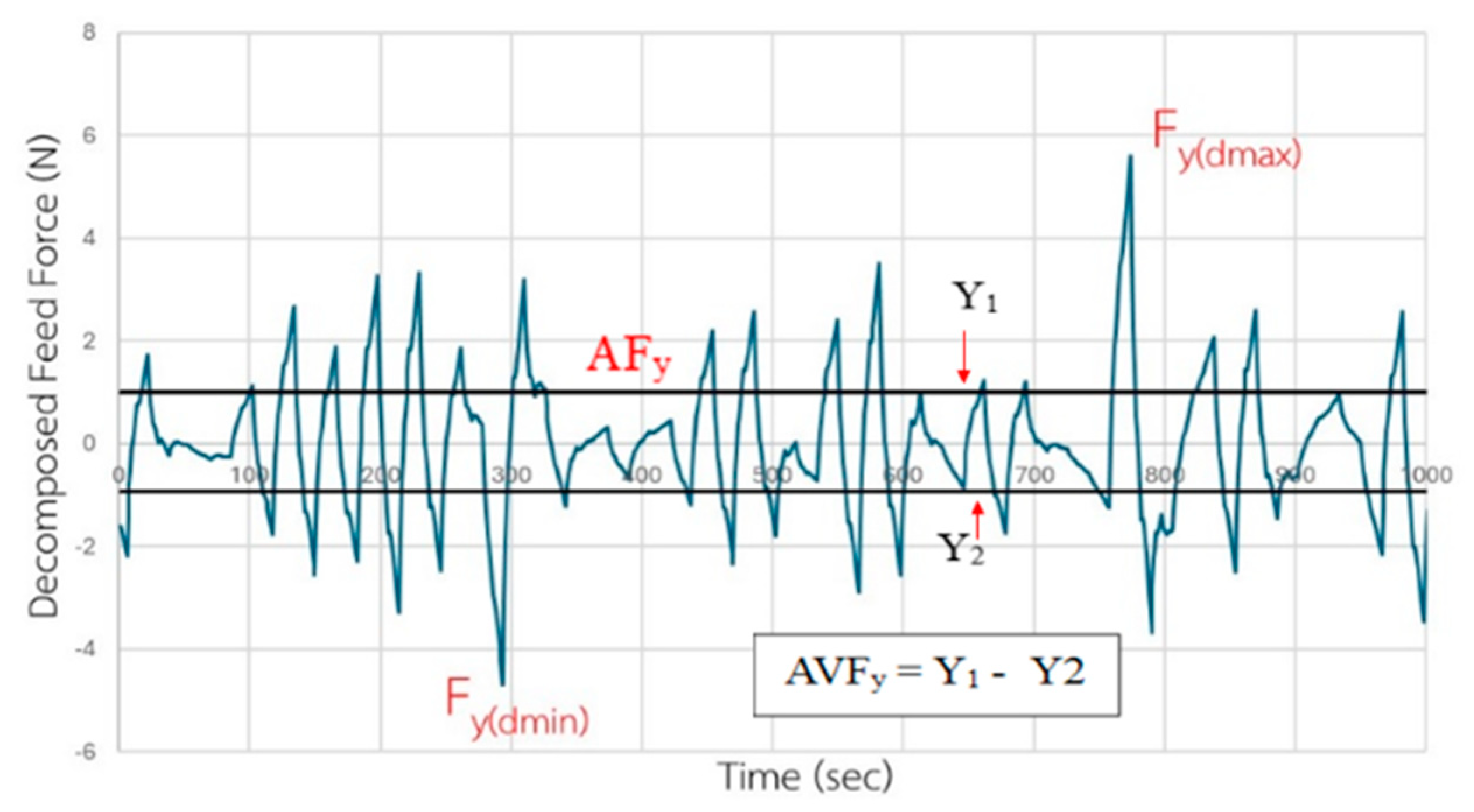
2. Relations of Decomposed Cutting Forces Versus Surface Roughness with Straightness and Roundness

According to the theoretical surface roughness, the decomposed feed force is most sensitive to the surface roughness and straightness profiles, which are the same as the feed rate direction [42,43]. The feed rate and the tool nose radius generally create the feed marks on the machined surface [44,45,46,47]. The profile of surface roughness can be represented by the straightness profile, which is the same. Their profiles can be obtained at the same frequency during measuring. However, the roundness profile corresponds with the decomposed radial force (Fx) [48], and the roundness error is normal for the decomposed feed force (Fy) [49].

Preliminary experiments are conducted to monitor the relations of decomposed feed force, decomposed radial force, surface roughness, straightness, and roundness profiles simultaneously [50,51], which are measured off-line using the roundness tester, the straightness and surface roughness tester, as shown in Figure 3. An example of an experimentally obtained profile of surface roughness and straightness versus the decomposed feed force on the 8th level separated from the chip breaking and noise signals is illustrated in Figure 4 with the use of a cutting speed of 200 m/min, feed rate of 0.15 mm/rev, depth of cut of 0.4 mm, tool nose radius of 0.4 mm and rake angle of 11°. The profile of surface roughness and straightness occurs at the frequency of 33 Hz, which is consistent with the amplitude of decomposed feed force, which happens at the same frequency in the frequency domain, as shown in Figure 4. Consequently, the experimentally decomposed radial force and the corresponding roundness profile are illustrated in Figure 5.

The Daubechies wavelet transform can decompose the cutting forces and identify the frequency of specific parameters such as surface roughness, straightness, and roundness, respectively [52,53]. However, the cutting conditions may affect the decomposed cutting forces in predicting those parameters. It is, therefore, necessary to eliminate those combinations of cutting conditions from the decomposed cutting forces. Hence, the distance of maximum peak F_y(dmax) to minimum valley F_y(dmin) of the decomposed feed force is considered to calculate the straightness error, as shown in Figure 6. However, the distance of the maximum peak to the minimum valley is dimensionless by taking its ratio to its static feed force (F_y(dmax) − F_y(dmin))/F_y(s). The ratio of the area of that decomposed feed force AF_y to that of decomposed main force AF_z is generalised and adopted to estimate the surface roughness. The trapezoidal rule is applied to compute the areas of that ratio (AF_y/AF_z). The roundness error can be forecasted by normalising and taking the ratio of the average variance of decomposed radial force to that of decomposed feed force (AVF_x/AVF_y) [49].

3. In-Process Prediction of Surface Roughness and Straightness with Roundness

To estimate the surface roughness, straightness and roundness during the CNC turning process concurrently, the in-process prediction models of those parameters have been newly proposed and developed in terms of exponential forms which have been employed to generate those models with the ratio of decomposed feed force to decomposed main force (AFy/AFz), ratio of the peak-to-valley amplitude of decomposed feed force to its static feed force (Fy(dmax) − Fy(dmin))/Fy(s), and the ratio of the average variance of decomposed radial force to that of the decomposed feed force (AVFx/AVFy). Statistical testing, both a normality test and independent test with variance stability test, will be introduced to validate the experimentally obtained data and models as reliable at the 95% confidence level.

The effects of combinations of cutting conditions, which are the cutting speed, the depth of cut, the feed rate, the nose radius, and the rake angle, are considered in order to compare the effectiveness and prediction accuracy of the experimentally obtained models with the results of the neural network approach. Hence, the relations of the average surface roughness, the surface roughness, the straightness, the roundness, the cutting conditions, and the ratio of decomposed cutting forces are expressed below:

$$R_a=C_1\cdot {\left(V\right)}^{a_1}\cdot {\left(f\right)}^{a_2}\cdot {\left(D\right)}^{a_3}\cdot {\left(R_n\right)}^{a_4}\cdot {\left(e\right)}^{a_5\gamma }\cdot {\left({\displaystyle \frac{A{F}_y}{A{F}_z}}\right)}^{a_6}$$

(1)

$$R_Z=C_2\cdot {(V)}^{a_7}\cdot {(f)}^{a_8}\cdot {(D)}^{a_9}\cdot {\left(R_n\right)}^{a_{10}}\cdot {(e)}^{a_{11}\gamma }\cdot {\left({\displaystyle \frac{A{F}_y}{A{F}_z}}\right)}^{a_{12}}$$

(2)

$$S_t=C_3\cdot {(V)}^{a_{13}}\cdot {(f)}^{a_{14}}\cdot {(D)}^{a_{15}}\cdot {\left(R_n\right)}^{a_{16}}\cdot {(e)}^{a_{17}\gamma }\cdot {\left({\displaystyle \frac{F_{y\left(dmax\right)}-F_{y\left(dmin\right)}}{F_{y\left(s\right)}}}\right)}^{a_{18}}$$

(3)

$$R_o=C_4\cdot {(V)}^{a_{19}}\cdot {(f)}^{a_{20}}\cdot {(D)}^{a_{21}}\cdot {\left(R_n\right)}^{a_{22}}\cdot {(e)}^{a_{23}\gamma }\cdot {\left({\displaystyle \frac{AV{F}_x}{AV{F}_y}}\right)}^{a_{24}}$$

(4)

where R_a is the average surface roughness in µm, R_z is the surface roughness in µm, S_t is the straightness error in µm, R_o is the roundness error in µm, V is the cutting speed in m/min, f is the feed rate in mm/rev, R_n is the tool nose radius in mm, D is the depth of cut in mm, and $\gamma$ is the rake angle in degree.

Meanwhile, a1 to a24 and C1 to C4 are the powers and coefficients of the models, respectively, which are obtained based on the experimentally obtained data by applying the nonlinear regression analysis and the least square method at a 95% confidence level. It is supposed that the proposed in-process models can predict all dimensions effectively during the CNC turning process simultaneously, which has never been compared with the neural network approach before.

On the other hand, the Levenberg–Marquardt neural network and feed-forward backpropagation algorithm with eight inputs [54,55,56] are utilised to train with those required dimensions to investigate the prediction accuracy compared with the above models, as shown in Figure 2. The major cutting conditions, which are the cutting speed, the depth of cut, the feed rate, the tool nose radius, and the rake angle, are important inputs to predict those parameters simultaneously. The in-process monitoring system between the neural network approach and nonlinear regression analysis has never been performed before to calculate those dimensions concurrently. It is understood that the proposed system can predict all critical parameters well during in-process CNC turning to achieve sustainable and intelligent manufacturing in the future.

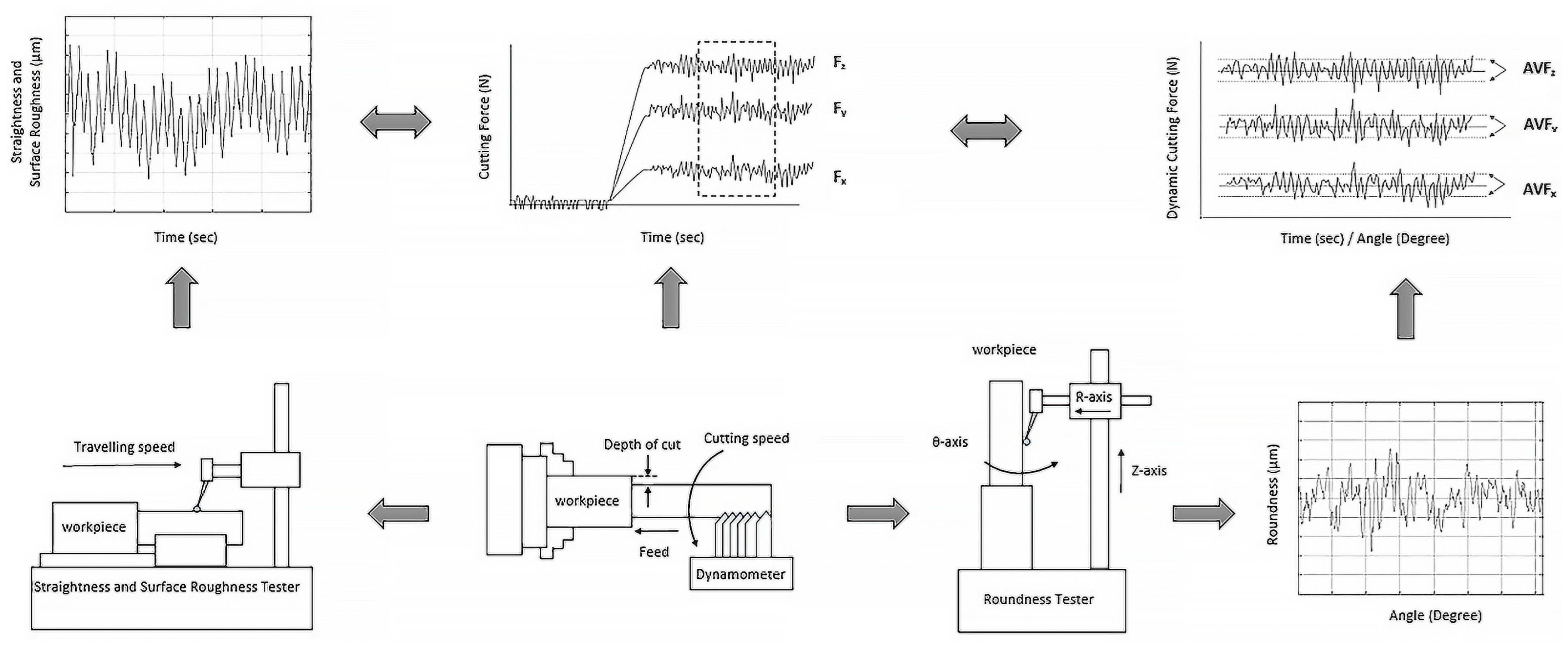
4. Experimental Setup and Cutting Conditions

The cutting experiments for nonlinear regression analysis are executed on the MAZAK CNC turning (4-axis NEXUS 200MY/MSY). Plain carbon steel (S45C) and coated carbide tools are adopted to prove the proposed method by using the different tool nose radiuses and rake angles. The major cutting conditions of 214 runs are presented in

Table 1. Major cutting conditions.

Parameter	Value
Cutting Tool	Coated Carbide
Workpiece	S45C
Cutting Speed (m/min)	100, 150, 180, 200, 260
Feed Rate (mm/rev)	0.1, 0.15, 0.2, 0.25, 0.3
Depth of Cut (mm)	0.2, 0.4, 0.5, 0.6, 0.8
Nose Radius (mm)	0.4, 0.8
Rake Angle (degree)	–6, +11

. The neural network system will be optimised, referring to the minimum prediction error or the maximum correlation coefficient (R), and after that, the ratio of experiments for the neural network approach will be set as training, testing, and validation, respectively. Consequently, the experimentally obtained results are executed and evaluated at the same time.

Figure 7 shows the MAZAK 4-axis CNC turning centre, where the Y-axis allows off-centre machining and the live tooling on the turret facilitates complex profiles. Specifications include a max spindle speed of 5000 rpm and a tool turret with 12 stations.

The dynamometer (Kistler model: 9121 - The Kistler Model 9121, a quartz 3-component toolholder dynamometer, manufactured by Kistler Instrumente AG, headquartered in Winterthur, Switzerland) is attached to the turret of the CNC turning machine with a sampling rate of 10 kHz and a low-pass filtered frequency of 5 kHz before applying the Daubechies wavelet transform to obtain the decomposed cutting forces, as shown in Figure 7. The dynamometer is calibrated, and hence, the decomposed cutting forces are promising in computing the average surface roughness, surface roughness, straightness, and roundness. The straightness and surface roughness tester (Mitutoyo SJ-400) and the roundness tester (TSK, model: Rondcom43c) are adopted to measure the machined surface roughness, straightness, and roundness error, respectively. The cutting tests start with new cutting conditions for each coated carbide tool.

The following procedures are introduced to fit Equations (1)–(4) and train the neural network system to obtain the weights in the hidden layers, which are finally set to 10 for better processing time and accuracy.

(1)

Record the decomposed cutting forces under the major cutting conditions.

(2)

Monitor the corresponding time records of the surface roughness, straightness, and roundness profile with the decomposed cutting forces in the time and frequency domains.

(3)

Measure the surface roughness, straightness, and roundness profiles for each cutting condition.

(4)

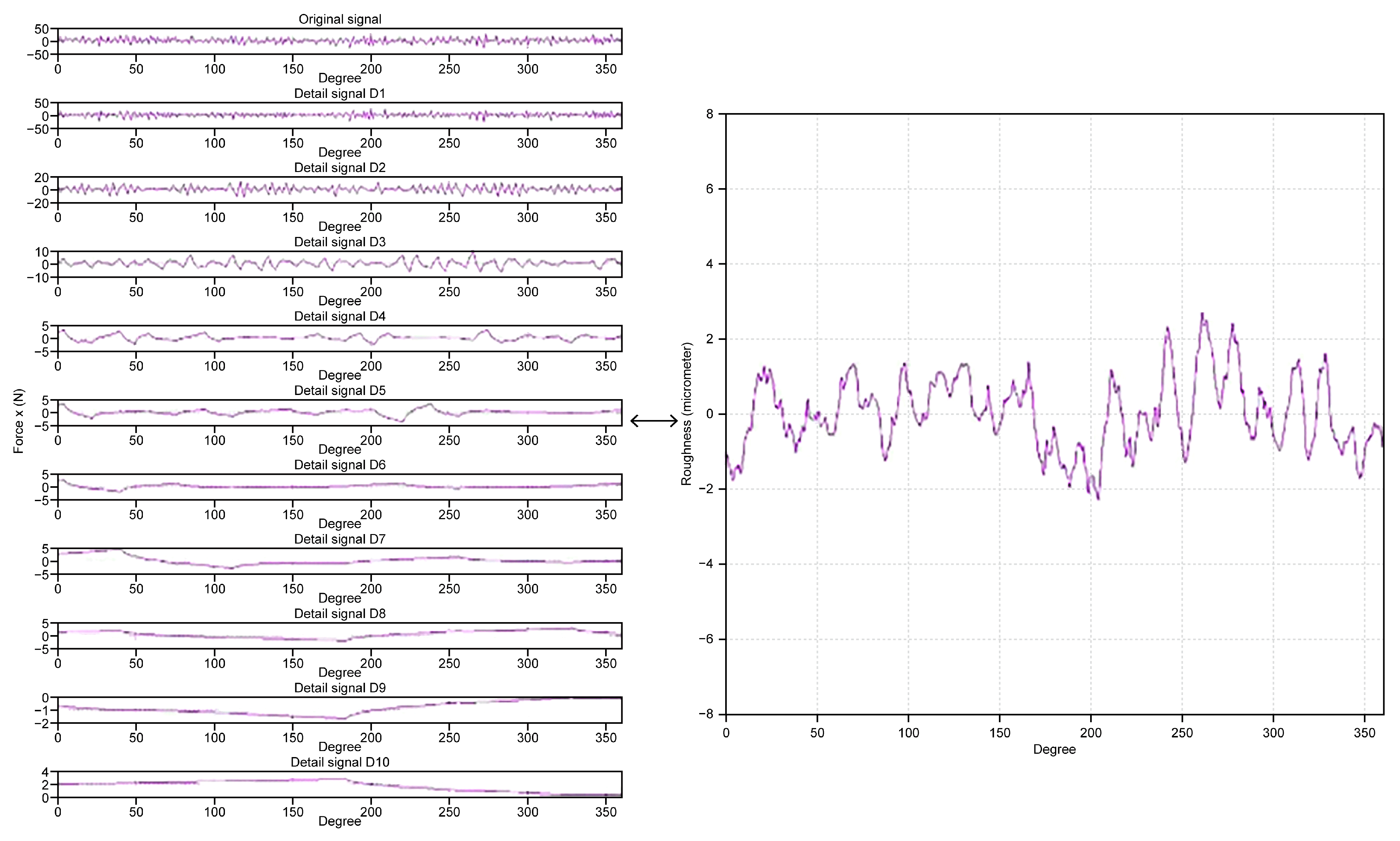
Compute the ratios of decomposed cutting forces of ${\displaystyle \frac{{\mathrm{A}\mathrm{F}}_{\mathrm{y}}}{{\mathrm{A}\mathrm{F}}_{\mathrm{z}}}}$, ${\displaystyle \frac{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}\right)}-{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{i}\mathrm{n}\right)}}{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{s}\right)}}}$, and ${\displaystyle \frac{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{x}}}{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{y}}}}$ on the 8th level of the wavelet transform, respectively.

(5)

Analyse the experimental data from steps (1) to (4) before optimising models (1) to (4) by utilising statistical analyses.

(6)

Determine the feed-forward backpropagation neural network system for the average surface roughness (Ra), the surface roughness (Rz), the straightness (St), and the roundness (Ro) with the ratios of decomposed cutting forces under major cutting conditions to obtain the highest prediction accuracy or correlation coefficient (R).

(7)

Verify and compare the experimentally obtained equations from the above step (5) with the neural network system from step (6).

The neural network consisted of a feed-forward architecture with 1 hidden layer of 10 neurons, trained using the Levenberg–Marquardt backpropagation algorithm. Inputs include V, f, D, Rn, rake angle, and decomposed force ratios. The data were split as 80% training, 10% validation, and 10% test.

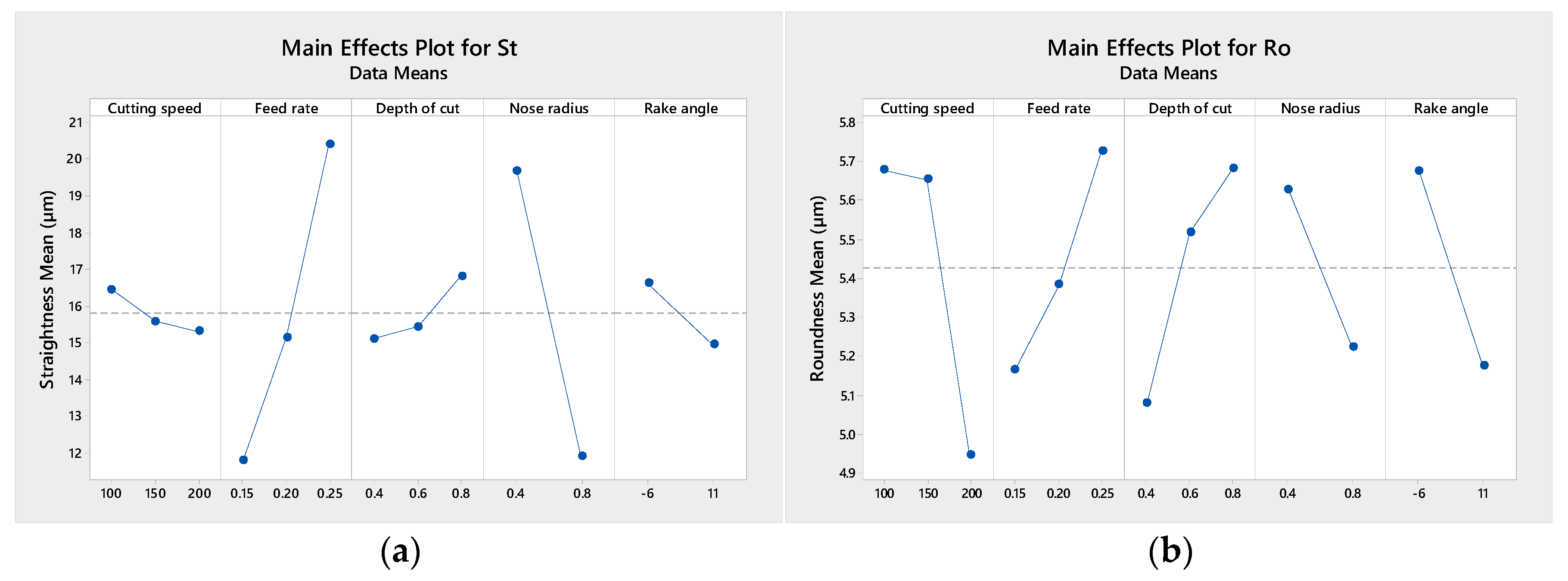
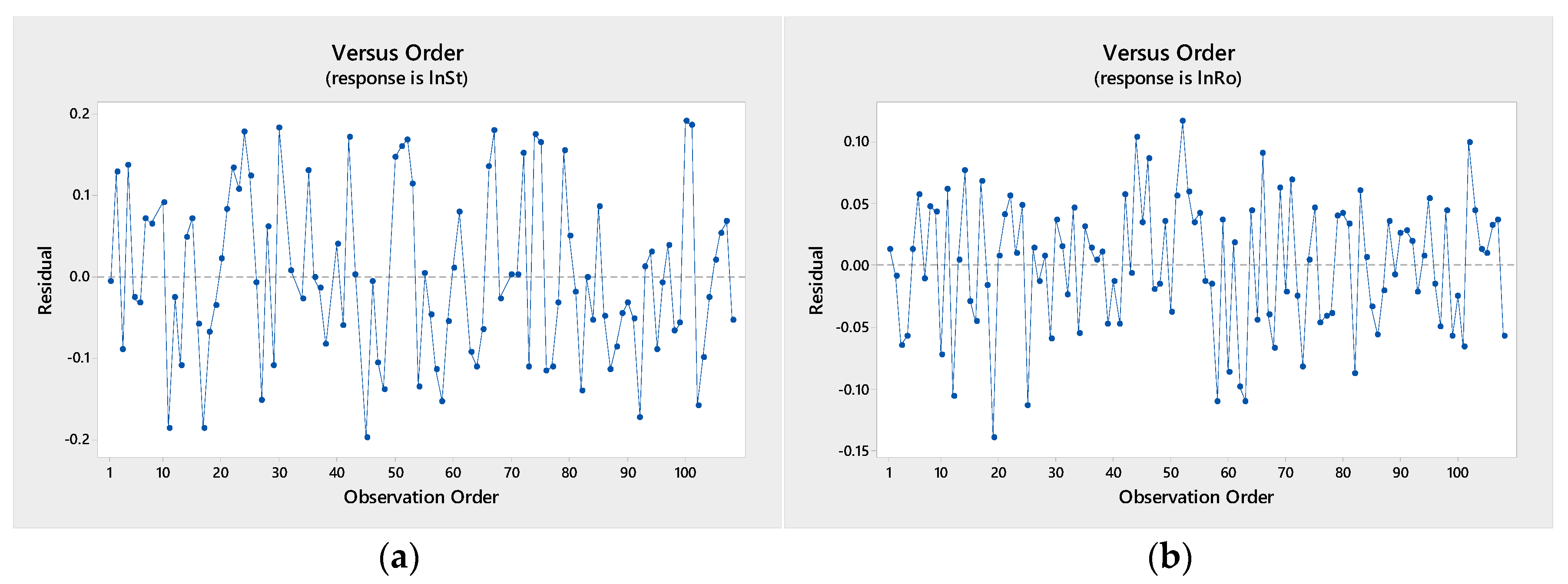
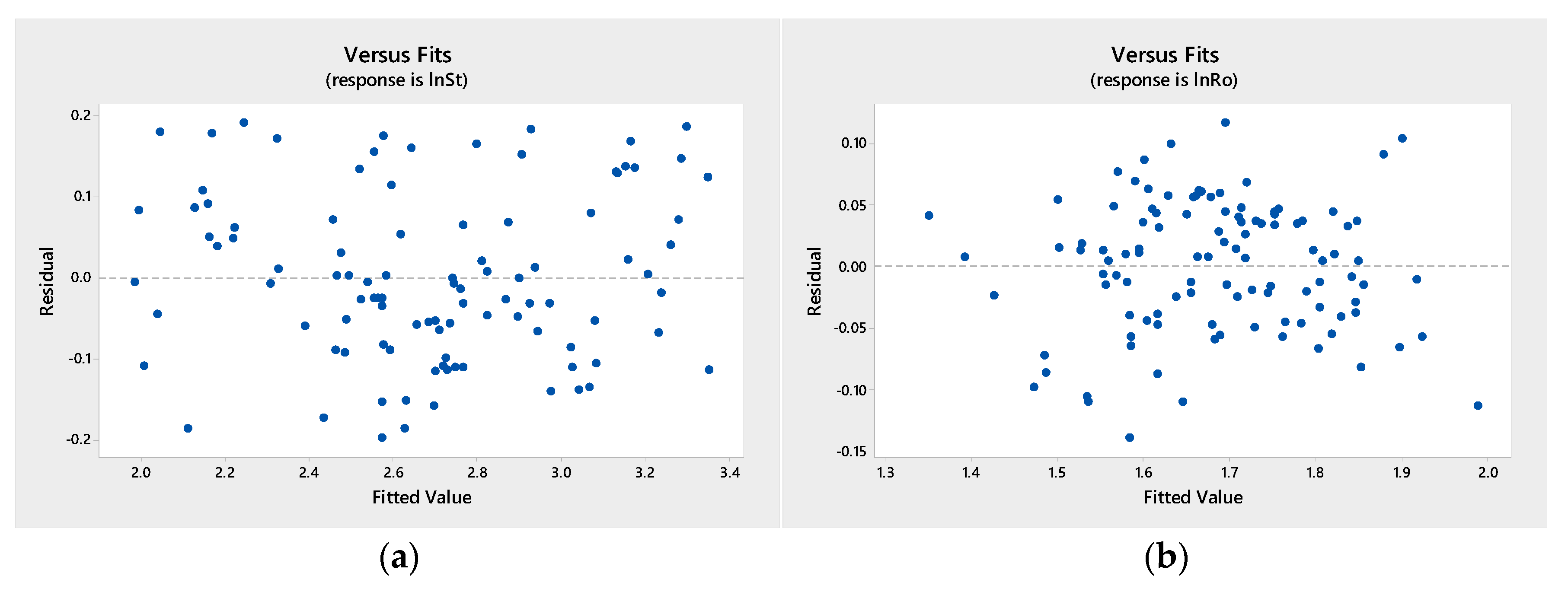
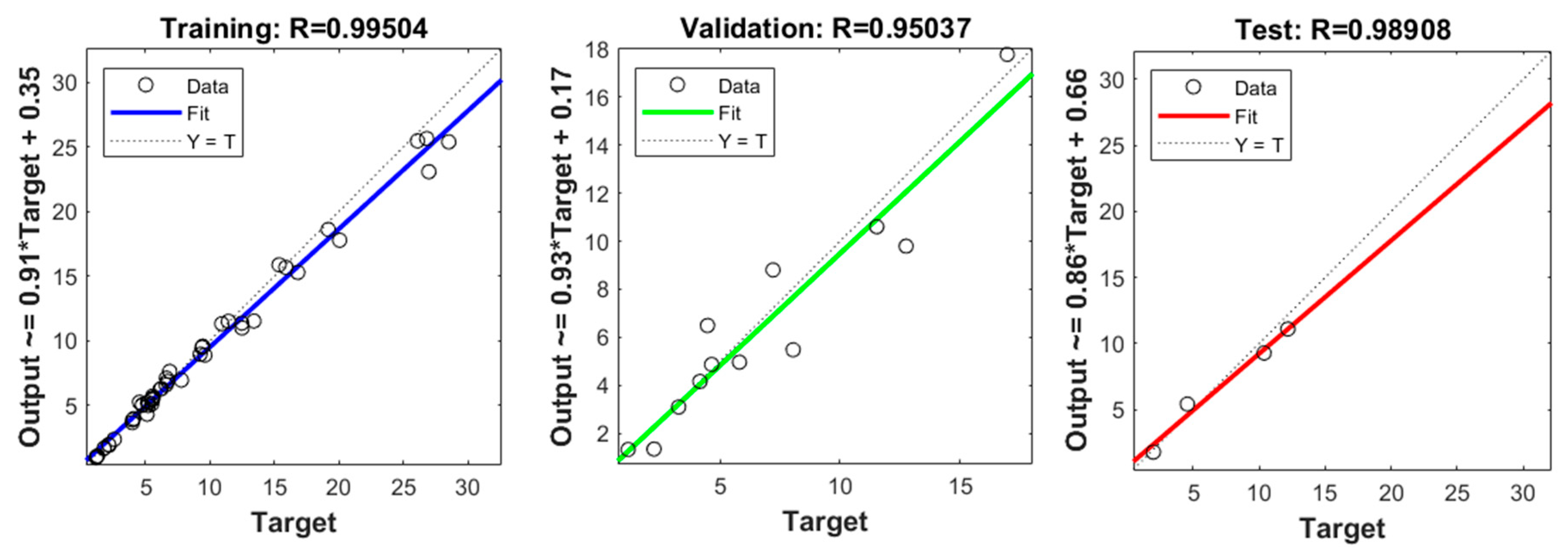
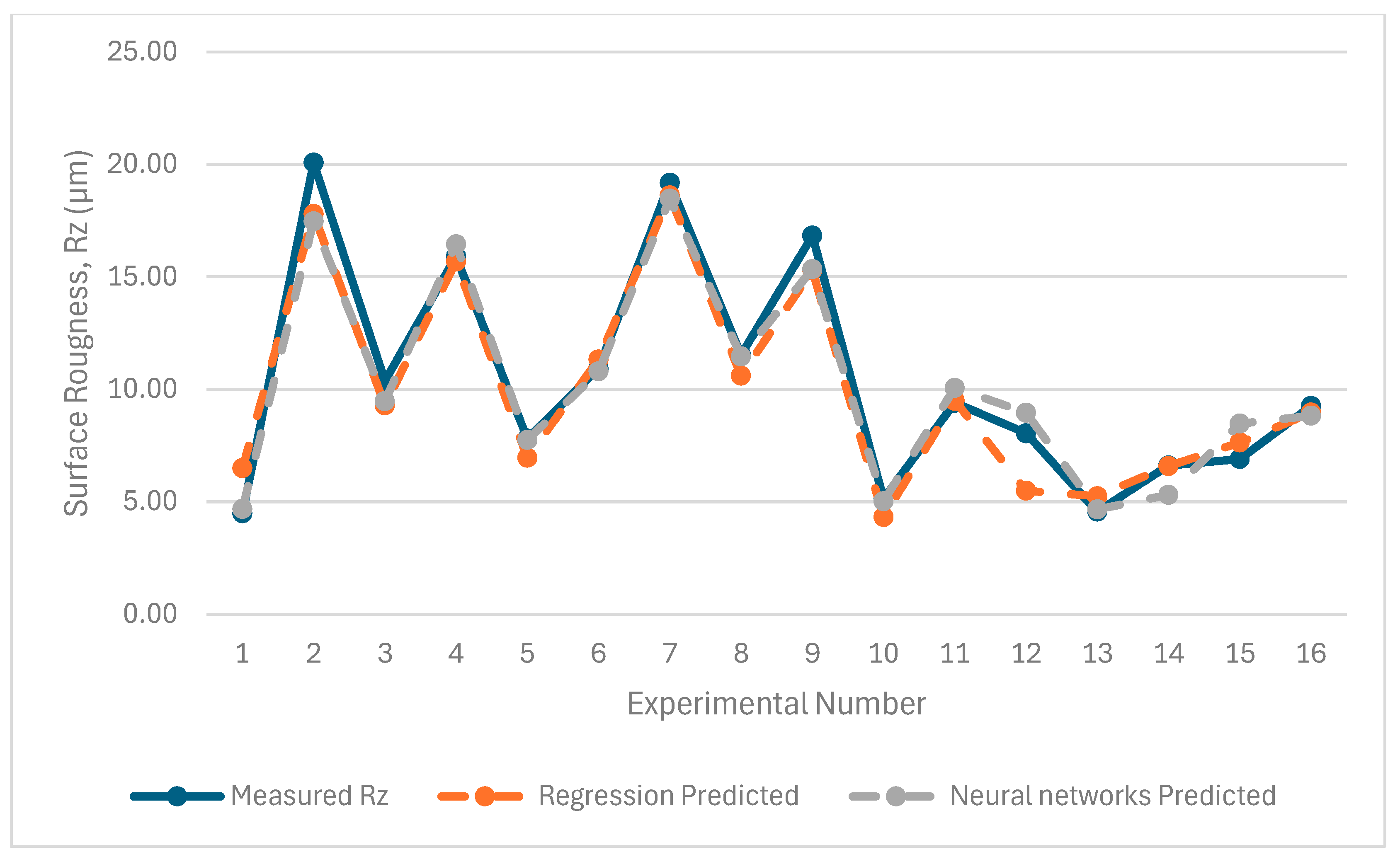
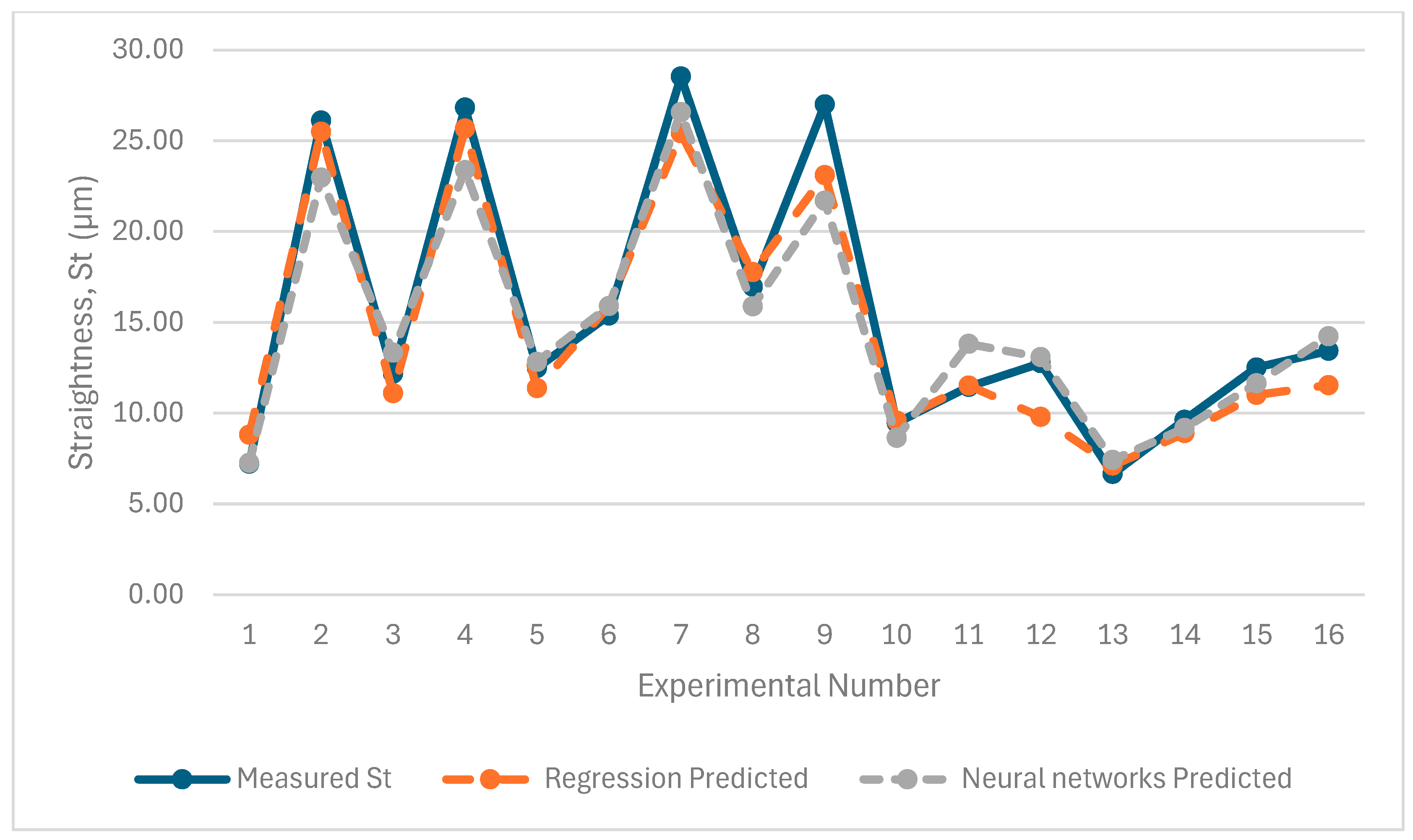
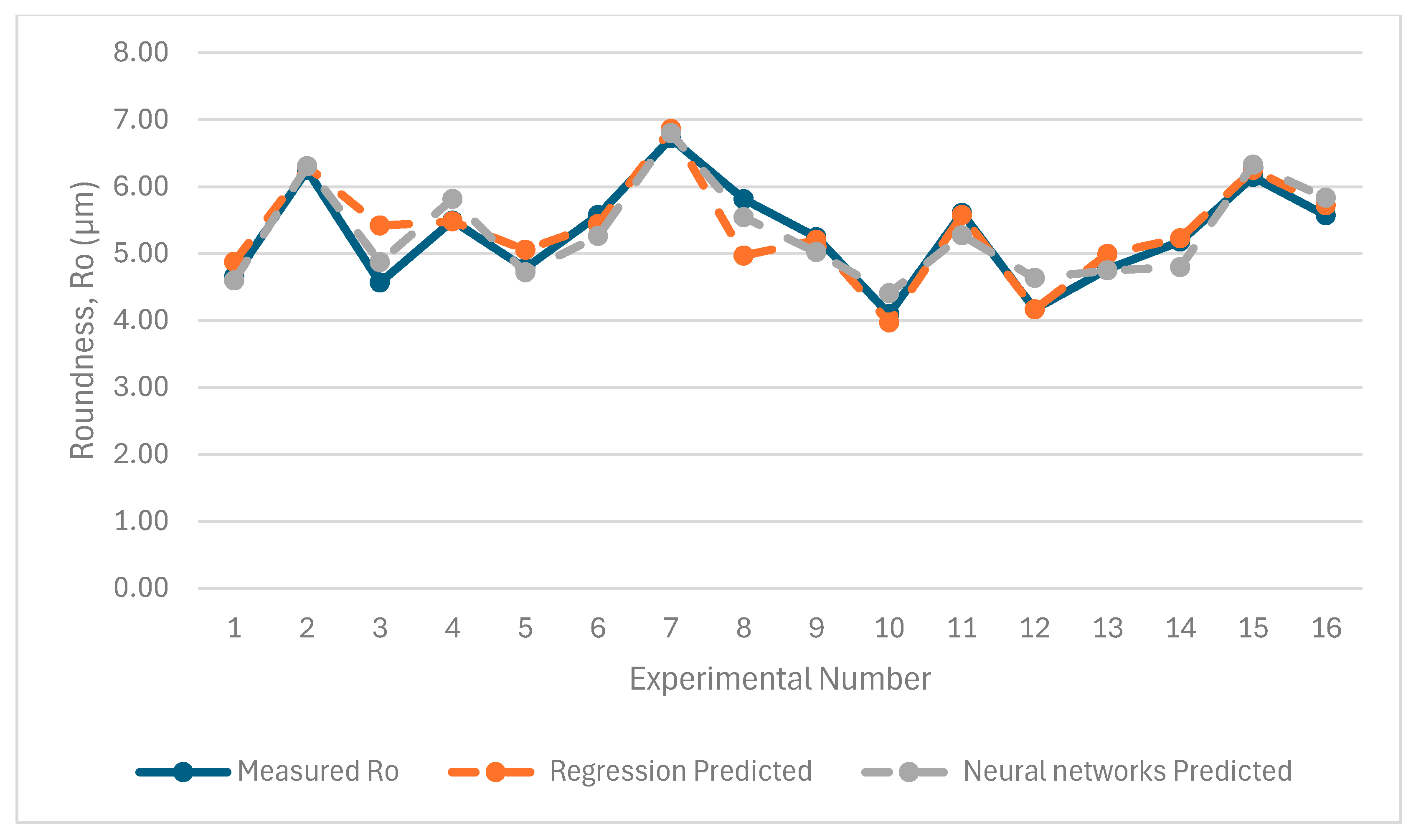
5. Experimental Results and Discussions

The experimentally obtained results of average surface roughness, surface roughness, straightness and roundness show the same trend when the cutting conditions are changed. Therefore, an example of experimentally obtained straightness and roundness versus the cutting conditions is illustrated in Figure 8. It is understood that as the cutting speed increases, the straightness and roundness errors decrease because the work material becomes softer due to the higher cutting temperature, which leads to lower cutting forces. As a result, the straightness and roundness errors might be less at the higher cutting speed. The above reasons can also help explain an improvement in surface roughness when cutting at a higher speed. Each experimental condition was repeated three times, and average values were taken. The standard deviation was <5% across all measurements, confirming high repeatability.

An increase in feed rate and depth of cut causes high straightness and roundness errors due to the larger cutting forces, as a result of the increase in straightness and roundness errors. It is concluded that the larger tool nose radius can improve the straightness and roundness errors because the areas of feed marks, which have remained on the surface finish, are eliminated by the contacting area between the tool nose radius and the machined surface, which can also explain the better surface roughness. The higher rake angle results in better chip flowability as a consequence of the lower cutting force. Therefore, the straightness and roundness errors are also reduced.

Firstly, the experimentally obtained data need to be validated by statistical analyses before generating the in-process prediction models and training the neural network system [8,14,48], as shown in Figure 2. These analyses include the normal test, the independent test, and the variance test, respectively.

The example of experimentally obtained normal distributions of average surface roughness and surface roughness shows that the experimentally obtained data lie on the linear line, as shown in Figure 9. Their p-values are 0.568 and 0.206, which are more than 0.05 at a significance level of 0.05 (α = 0.05). Therefore, it is understood that the experimentally obtained data of average surface roughness and surface roughness are normally distributed. The experimentally obtained normal distributions of straightness and roundness have the same trends and p-values of 0.056 and 0. 112, which are higher than 0.05, respectively. It can be concluded that the residuals have a normal distribution.

The experimentally obtained independent test is a test to measure the data distribution. The example of experimentally obtained data of straightness and roundness is illustrated by the residual versus the observation order, as shown in Figure 10. The deviations of the experimentally obtained data are independent and not certain patterns. The experimentally obtained data are uniformly distributed on the zero line. In summary, the experimentally obtained independent tests of straightness and roundness have good data independence. Furthermore, the experimentally obtained data of average surface roughness and surface roughness are also independent, respectively.

Figure 11 illustrates an example of experimentally obtained variance tests, which present the relation between residual and fitted values of straightness and roundness. The experimentally obtained data appear as a random scatter around the zero-center line; as a result, the experimentally obtained data are independent. Hence, the assumption of equal variance becomes valid because the common variance and mean value are zero. Moreover, the residual is independent not only of straightness and roundness but also of average surface roughness and surface roughness.

When referring to the above statistical analyses, it is understood that the experimentally obtained data can be used to develop reliable models, and there are no outliers in the experimentally collected data. The nonlinear forms of Equations (1)–(4) are converted and computed firstly by taking the logarithmic transformation, as shown in Equations (5)–(8). The regression coefficients are obtained based on the actual cutting results by utilising the nonlinear regression analysis with the least square method.

$${lnR}_a=3.718-0.19lnV+1.3961lnf+0.0796lnD-0.6401ln{R}_n-0.01391\gamma -0.289ln\left({\displaystyle \frac{A{F}_y}{A{F}_z}}\right)$$

(5)

$${lnR}_z=5.207-0.2012lnV+1.2917lnf+0.1357lnD-0.6514ln{R}_n-0.00807\gamma -0.295ln\left({\displaystyle \frac{A{F}_y}{A{F}_z}}\right)$$

(6)

$${lnS}_t=4.531-0.0910lnV+1.1638lnf+0.0841lnD-0.7127ln{R}_n-0.00679\gamma -0.079ln\left({\displaystyle \frac{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}\right)}-{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{i}\mathrm{n}\right)}}{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{s}\right)}}}\right)$$

(7)

$${lnR}_o=2.138-0.0819lnV+0.0888lnf+0.0571lnD-0.0609ln{R}_n-0.004671\gamma +0.3048ln\left({\displaystyle \frac{AV{F}_x}{AV{F}_y}}\right)$$

(8)

The above Equations (5)–(8) are substituted by the natural logarithm and transformed to the original exponential form, as shown in Equations (9)–(12). We can be confident that the experimentally obtained models of in-process prediction of average surface roughness, surface roughness, straightness, and roundness are practicable and valid at a high significance (p-value = 0.000) at a 95% confidence level. Therefore, the proposed nonlinear models are believable and useful to predict the in-process average surface roughness, surface roughness, straightness and roundness, respectively, by utilising the cutting conditions and in-process monitoring of decomposed cutting forces as the predictors.

$$R_a=e^{3.718}\cdot V^{-0.19}\cdot f^{1.3961}\cdot D^{0.0796}\cdot {R_n}^{-0.6401}\cdot e^{-0.01391\gamma }\cdot {\left({\displaystyle \frac{A{F}_y}{A{F}_z}}\right)}^{-0.289}$$

(9)

$$R_Z=e^{5.207}\cdot V^{-0.2012}\cdot f^{1.2917}\cdot D^{0.1357}\cdot {R_n}^{-0.6541}\cdot e^{-0.0807\gamma }\cdot {\left({\displaystyle \frac{A{F}_y}{A{F}_z}}\right)}^{-0.295}$$

(10)

$$S_t=e^{4.531}\cdot V^{-0.0910}\cdot f^{1.1638}\cdot D^{0.0841}\cdot {R_n}^{-0.7127}\cdot e^{-0.00679\gamma }\cdot {\left({\displaystyle \frac{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}\right)}-{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{i}\mathrm{n}\right)}}{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{s}\right)}}}\right)}^{-0.079}$$

(11)

$$R_o=e^{2.138}\cdot V^{-0.0819}\cdot f^{0.0888}\cdot D^{0.0571}\cdot {R_n}^{-0.0609}\cdot e^{-0.00467\gamma }\cdot {\left({\displaystyle \frac{AV{F}_x}{AV{F}_y}}\right)}^{0.3048}$$

(12)

The signs and amplitudes of the powers in Equations (9)–(12) present the direction and effect of cutting conditions and ratios of ${\displaystyle \frac{{\mathrm{A}\mathrm{F}}_{\mathrm{y}}}{{\mathrm{A}\mathrm{F}}_{\mathrm{z}}}}$, $\left({\displaystyle \frac{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}\right)}-{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{i}\mathrm{n}\right)}}{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{s}\right)}}}\right)$, and ${\displaystyle \frac{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{x}}}{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{y}}}}$ on the average surface roughness, the surface roughness, the straightness, and the roundness, respectively. It is noticed that the average surface roughness, surface roughness, and straightness will be improved when the ratios of ${\displaystyle \frac{{\mathrm{A}\mathrm{F}}_{\mathrm{y}}}{{\mathrm{A}\mathrm{F}}_{\mathrm{z}}}}$ and $\left({\displaystyle \frac{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}\right)}-{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{i}\mathrm{n}\right)}}{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{s}\right)}}}\right)$ increase due to the negative power, as shown in Equations (9)–(11). Vice versa, the roundness becomes worse while the ratio of ${\displaystyle \frac{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{x}}}{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{y}}}}$ progresses as its power is positive, as shown in Equation (12).

The in-process monitoring and quality control of average surface roughness, surface roughness, straightness, and roundness are simultaneously compared between nonlinear regression models and artificial neural networks in Figure 2. The artificial neural network is required to train and optimise the system. After optimising the neural network system to obtain the closest prediction values or the highest correlation coefficient (R), the ratio of experiments for the neural network approach is decided as training of 80%, validation of 10%, and test of 10%, respectively, as shown in Figure 12. The experimentally obtained correlation coefficients (R) of training, validation, and test of the neural network system are 0.995, 0.95, and 0.989, respectively. It is interpreted that all parameters of average roughness, roughness, straightness, and roundness can be predicted simultaneously with the ratios of ${\displaystyle \frac{{\mathrm{A}\mathrm{F}}_{\mathrm{y}}}{{\mathrm{A}\mathrm{F}}_{\mathrm{z}}}}$, $\left({\displaystyle \frac{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}\right)}-{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{i}\mathrm{n}\right)}}{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{s}\right)}}}\right)$, and ${\displaystyle \frac{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{x}}}{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{y}}}}$ during the in-process CNC turning. Hence, the experimentally obtained results from the trained neural network system will be compared and checked at the same time as the experimentally obtained results from in-process prediction models.

The confirmation tests are introduced to validate and verify the prediction accuracy of the in-process prediction models and the trained neural network, as shown in

Table 2. Confirmation tests.

Cutting Tool	Coated Carbide
Cutting condition	Dry cutting
Workpiece	S45C
Cutting speed (m/min)	100, 150, 200
Feed rate (mm/rev)	0.15, 0.2, 0.25
Depth of cut (mm)	0.4, 0.6, 0.8
Nose radius (mm)	0.4, 0.8
Rake angle (degree)	−6, +11

. Figure 13, Figure 14, Figure 15 and Figure 16 illustrate the experimentally measured average roughness, surface roughness, straightness, and roundness versus the experimentally predicted ones from the trained neural network and nonlinear regression models, respectively. It is understood that the average roughness, surface roughness, straightness, and roundness can be well estimated by in-process prediction models, which are closer to the measured ones than the ones from trained neural networks. A comparison of prediction accuracy between trained neural networks and nonlinear regression models is summarised in

Table 3. Summarised prediction accuracy of nonlinear regression models and neural network system.

In-Process Prediction System	Prediction Accuracy
	Average Surface Roughness (Ra)	Surface Roughness (Rz)	Straightness (St)	Roundness (Ro)
Nonlinear regression models	92.10%	92.82%	91.55%	95.52%
Trained neural network	88.08%	88.70%	90.89%	96.02%

. It is implied that the nonlinear regression models can forecast the average roughness, the surface roughness, the straightness, and the roundness simultaneously during in-process CNC turning, which has a higher prediction accuracy of over 90% than the ones from the trained neural network by utilising the ratios of ${\displaystyle \frac{{\mathrm{A}\mathrm{F}}_{\mathrm{y}}}{{\mathrm{A}\mathrm{F}}_{\mathrm{z}}}}$, $\left({\displaystyle \frac{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}\right)}-{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{i}\mathrm{n}\right)}}{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{s}\right)}}}\right)$, and ${\displaystyle \frac{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{x}}}{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{y}}}}$.

Although Figure 13, Figure 14, Figure 15 and Figure 16 demonstrate the close alignment between measured and predicted values using both the nonlinear regression model and trained neural network, there is a visible tendency suggesting potential overfitting in the neural network predictions. It is particularly evident in the higher experimental numbers, where the neural network curves follow the fluctuations of the measured values more closely than the regression model. While this may reflect high sensitivity, it could also indicate that the network has adapted too closely to the training data, potentially reducing generalisability to unseen data. Despite the high correlation coefficients observed during the validation and testing phases (R > 0.95), this behaviour highlights the importance of further optimisation through techniques such as cross-validation or regularisation. Moreover, the robustness of the nonlinear regression models is confirmed by their more consistent alignment with the measured values across all experimental runs, supporting their higher reliability and predictive accuracy, as reported in Table 3.

The nonlinear model outperformed in Ra, Rz, and St due to its stability and lower variance across all experimental ranges, whereas the neural network showed higher R only for Ro, suggesting possible sensitivity to noise in radial forces.

It is noticed that the nonlinear regression models have higher prediction accuracy than the trained neural network based on the experimental data in Table 2 and Table 3. The highest advantage of the in-process prediction system is that all critical parameters of the average roughness, surface roughness, straightness, and roundness can be monitored, and the quality of the workpiece can be controlled during the in-process CNC turning, which can assist in reducing the production cycle time by approximately 50%, as shown in Figure 17, since the quality control is monitored simultaneously during in-process CNC turning, which compares the CNC turning machine with the intelligent one [16,37,46,56].

Figure 17 illustrates the production cycle time obtained from the CNC machine and the intelligent CNC machine. Quality control can be checked during production during in-process CNC turning by using an intelligent CNC machine, which can also record and generate the production report concurrently [4,30,39]. In-process monitoring and quality control have never been proposed before to achieve a sustainable and intelligent manufacturing system, which can be developed and implemented well by utilising the ratios of ${\displaystyle \frac{{\mathrm{A}\mathrm{F}}_{\mathrm{y}}}{{\mathrm{A}\mathrm{F}}_{\mathrm{z}}}}$, $\left({\displaystyle \frac{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{x}\right)}-{\mathrm{F}}_{\mathrm{y}\left(\mathrm{d}\mathrm{m}\mathrm{i}\mathrm{n}\right)}}{{\mathrm{F}}_{\mathrm{y}\left(\mathrm{s}\right)}}}\right)$, and ${\displaystyle \frac{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{x}}}{{\mathrm{A}\mathrm{V}\mathrm{F}}_{\mathrm{y}}}}$. It can be concluded that all dimensions can be well identified and controlled at the same time during in-process turning with higher accuracy by applying the nonlinear regression models.

Hence, it is understood that the intelligent CNC turning machine can eliminate rejects, reworks, times and costs from a reproduction of the new parts, which can reduce greenhouse gas and energy, leading to a sustainable and intelligent manufacturing system in the near future [57,58,59,60], as shown in Figure 1. It is implied that digital transformation (DX) in terms of intelligent CNC machines is necessary to help improve green transformation (GX) and reduce time and energy consumption for sustainable and intelligent manufacturing systems, as shown in Figure 17.

6. Conclusions

To realise a sustainable and intelligent manufacturing system, the proposed intelligent machine can monitor and control the quality of the workpiece in terms of the average roughness, the surface roughness, the straightness, and the roundness simultaneously during in-process CNC turning by utilising the ratio of decomposed feed force to decomposed main force (AFy/AFz), the ratio of the peak-to-valley amplitude of decomposed feed force to its static feed force (Fy(dmax) – Fy(dmin))/Fy(s), and the ratio of the average variance of decomposed radial force to that of the decomposed feed force (AVFx/AVFy), which are obtained by adopting Daubechies wavelet transform. The nonlinear regression analyses and artificial neural network as the feed-forward neural network with back propagation algorithm are applied to predict the in-process average roughness, surface roughness, straightness, and roundness simultaneously.

Statistical analyses have validated the experimentally obtained data before modelling the in-process prediction and training the neural network system, which are the normal test, the independent test, and the variance test, respectively. The effects of cutting conditions on those parameters, which correspond with the in-process prediction models, are explained. The experimentally obtained results showed that the average roughness, surface roughness, straightness, and roundness could be predicted well and with higher accuracy by nonlinear regression analyses compared to trained neural networks. The largest benefit of the in-process prediction system is that all critical parameters of the average roughness, surface roughness, straightness, and roundness can be monitored, and the quality of the workpiece can be controlled during the in-process CNC turning, which can aid in reducing the production cycle time and control the quality of workpiece simultaneously during in-process CNC turning.

The comparison between the CNC turning machine and an intelligent CNC turning machine has been described as beneficial, as it can monitor and control the quality of the workpiece and record and generate the production report concurrently during in-process CNC turning. It is concluded that the proposed and developed intelligent CNC turning machine can leverage intelligent machines and lead to a sustainable and intelligent manufacturing system in the near future.