Design of the Dual-Path Cold Spray Nozzle to Improve Deposition Efficiency

Abstract

This paper designs a Dual path cold spray nozzle and studies its performance during the cold spray process through numerical simulations and optimization experiments. The gas flow field inside the nozzle and the particle acceleration process were simulated using Fluent software2020R1. The orthogonal experimental method was used to analyze the effects of five geometric parameters on the nozzle performance, determining the optimal design parameter combination. Modeling and simulation calculations based on the optimal parameter combination showed that the average particle impact velocity increased by nearly 17 m/s, the number of particles exceeding the theoretical critical velocity increased by nearly 100, and the theoretical deposition efficiency improved by 10%. Experimental results indicated that compared to the single-channel nozzle, the deposition efficiency increased from 20.22% to 28.26%, the porosity improved from 10.51% to 9.12%, and the deposition microhardness also increased. The experimental test data were in good agreement with the previous numerical simulation results, validating the accuracy of the simulation model and providing an important theoretical reference for the optimization and improvement of subsequent process parameters.

1. Introduction

Cold spraying is a new solid-state material surface deposition process [1]. During the spraying process, high-temperature compressed gas (typically nitrogen, air, or helium) is used as the propellant gas to accelerate metal particle powders to a high velocity, causing plastic deformation upon impact with the substrate (usually metal), resulting in adhesion to the substrate [2,3,4,5,6]. Cold spraying can be categorized into two types: high-pressure cold spraying and low-pressure cold spraying. In low-pressure cold spraying systems, the gas pressure used is typically less than 1 MPa [7]. Compared to high-pressure cold spraying equipment, low-pressure cold spraying equipment offers advantages such as portability and low consumption, making it widely used in industrial fields such as corrosion mitigation and protection, dimensional restoration, and repair and remanufacturing of castings and molds [8,9,10]. Additionally, it is particularly beneficial for on-site maintenance of equipment in certain areas, such as outdoor military equipment repairs. With the rise of additive manufacturing, cold spraying technology has gained significant attention. Despite the high deposition efficiency of high-pressure cold spraying [11], it is challenging to precisely control the growth of deposits, and excessive deposition growth can easily lead to collisions with the spray gun [12,13,14]. Moreover, the high cost, significant resource consumption, and limited mobility of high-pressure systems present issues that need to be addressed. As a crucial branch of cold spraying, low-pressure cold spraying, with its simple equipment and low cost, holds significant engineering importance in enhancing its performance.

Despite its advantages in certain aspects, low-pressure cold spraying exhibits inferior deposition performance compared to high-pressure cold spraying. Particularly when applying low-pressure cold spraying technology in the field of additive manufacturing, the low powder deposition efficiency can increase production costs and limit the application of this technology. In the cold spraying process, deposition efficiency is one of the key indicators for measuring process performance, as it directly impacts the quality of the deposition, production costs, and the application scope of the process. Therefore, improving the deposition efficiency of cold spraying has become a focal point of research in this field. To this end, deposition efficiencies can be improved through auxiliary enhancement techniques, including additional assistive technologies and improved nozzle design.

In terms of additional assistive technologies: The laser-assisted cold spraying (LACS) technique proposed by Bray et al. [15] uses laser heating of the powder and substrate to reduce the critical velocity of the powder particles, thereby enhancing deposition efficiency; The magnetic field-assisted cold spraying (MACS) studied by Astarita et al. [3] employs an external magnetic field to accelerate ferromagnetic powder particles, leading to improved deposition efficiency; Furthermore, Wang et al. [16] uses plasma-assisted low pressure cold spraying (PALCS) technique to heat the powder only at the outlet to prevent oxidation during the heating process, which can effectively improve deposition efficiency. The application of assistive technologies has achieved some success in improving the deposition efficiency of cold spraying, but these technologies still face several challenges and limitations. For instance, while LACS enhances deposition efficiency by using laser heating to lower the critical velocity of powder particles, it involves high equipment costs, complex processes, and a propensity for defects. MACS increases deposition efficiency by accelerating ferromagnetic powder particles through an external magnetic field. However, this technology is limited to magnetic powders and cannot be used for non-magnetic materials. Moreover, although PALCS improves deposition efficiency by preventing powder oxidation, its processing cost is high, it has stringent requirements for the working environment, and the process parameters are complex and difficult to control.

Some of the research results in improving nozzle design are listed below. Jodoin et al. [17] propose a new cold spraying method, i.e., pulsed gas dynamic spray(PGDS), which is different from the traditional cold spraying method in that it utilizes high-pressure pulsed gas flow to intermittently propel the powder particles, which can be heated to higher temperatures while ensuring the impact velocity, reducing the critical deposition velocity and improving the deposition efficiency. However, the two high-frequency shut-off valves controlling the high-pressure pulsed gas flow and the powder need to be opened/closed asynchronously, which requires high control accuracy. Luo et al. [18] combine the shock tunnel and cold spraying technology to develop a shock tunnel produced cold spray, which accelerates the powder particles through the high-speed gas flow generated by the shock tunnel, allowing the powder particles to reach a high impact velocity, and the deposition efficiency is subsequently increased. But, the temperature field and particle velocity distribution generated by the shock tunnel produced cold spray are difficult to control, and the process complexity is high. A pressure relief channel nozzle designed by Bierschenk et al. [19] adds a pressure relief channel to the traditional Laval nozzle, which can effectively reduce the pressure in the stagnation zone downstream of the bow shock and improve the powder impact velocity, and although some of powder particles may escape from the pressure relief channel, the deposition efficiency is still improved. Whereas, this new nozzle is only suitable for micro-cold spraying with small powder particle size for the time being.

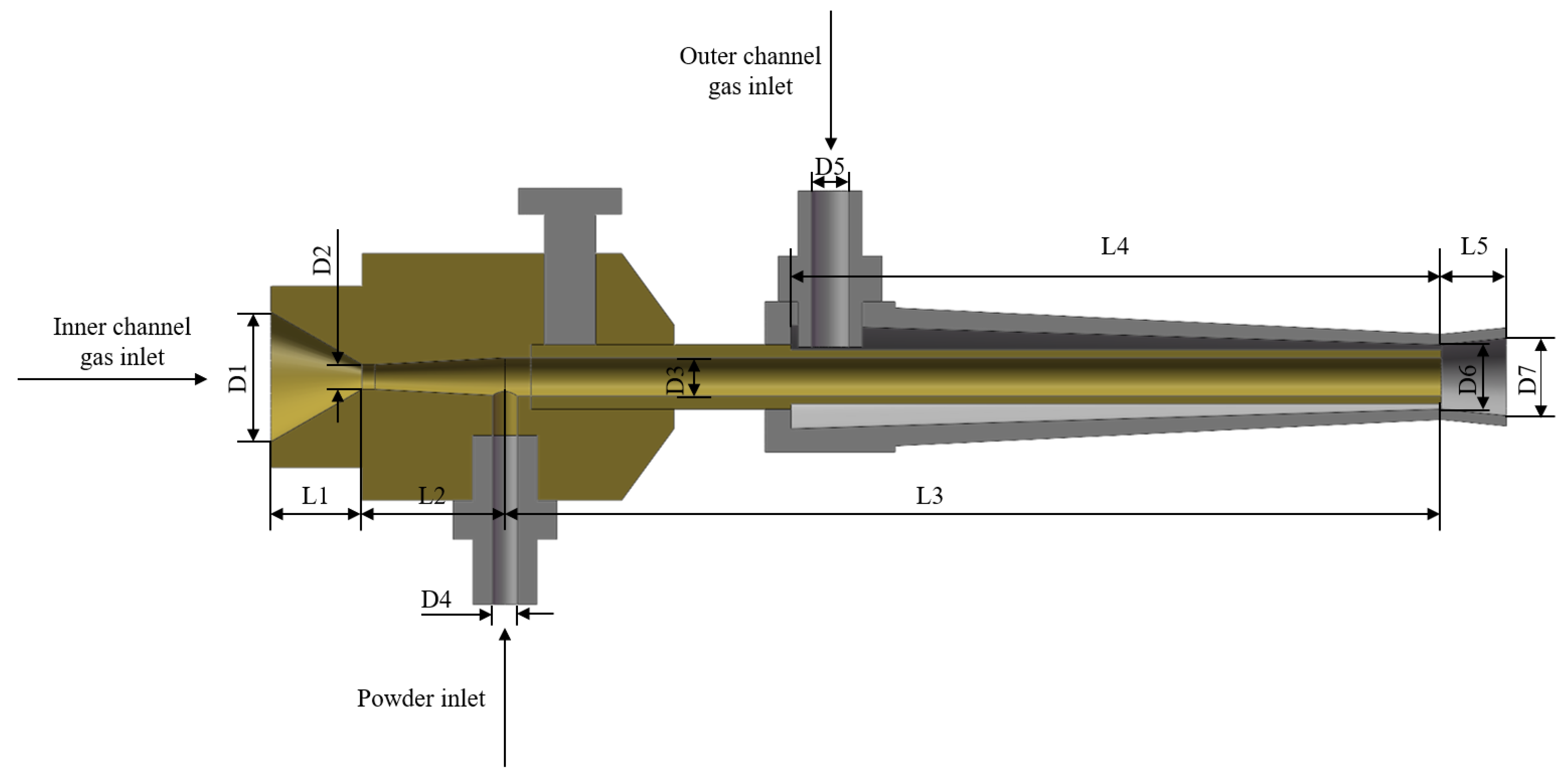
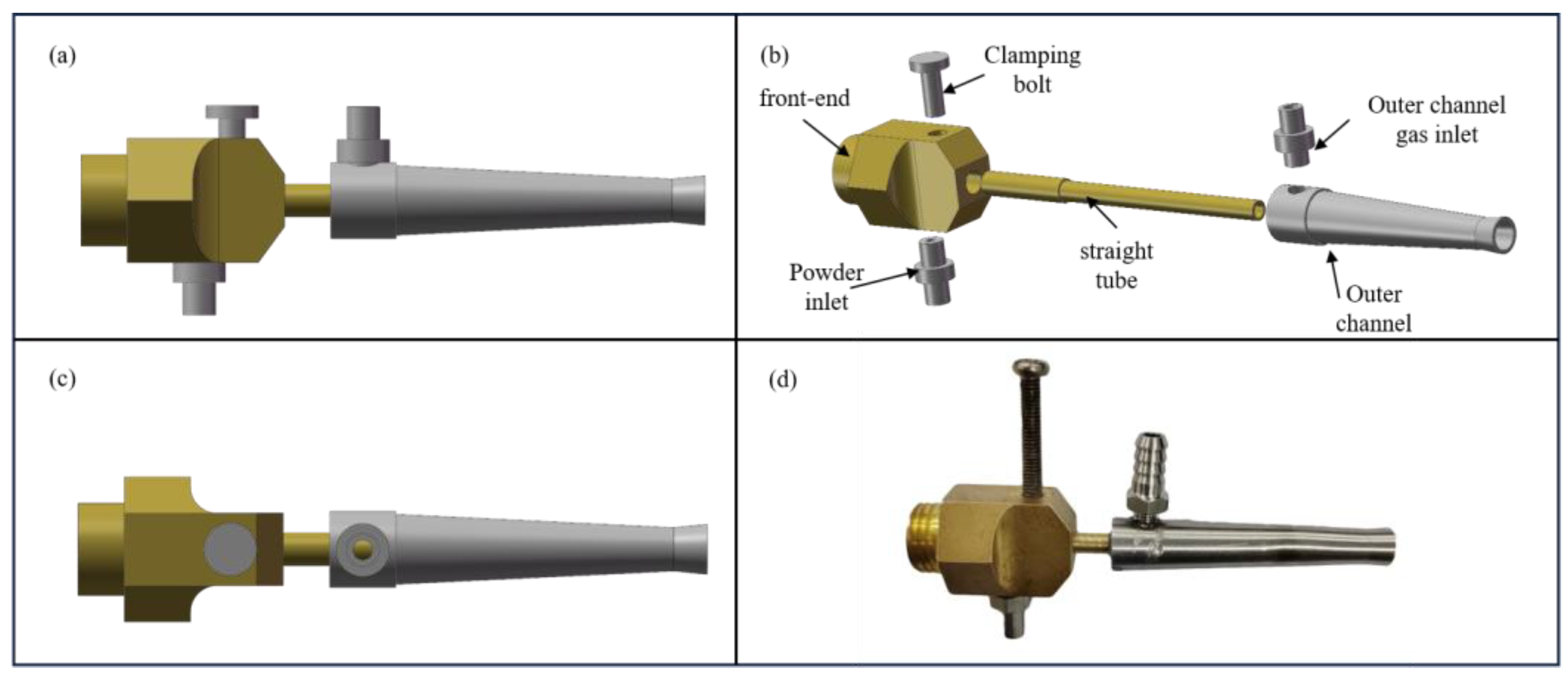
The limitations of these auxiliary enhancement techniques indicate a need to explore more universal and cost-effective methods for improving the deposition efficiency of cold spraying. Therefore, this study proposes a novel Dual path nozzle design aimed at enhancing spraying efficiency by optimizing the internal airflow structure of the nozzle, without relying on external auxiliary equipment or complex process conditions. Through the synergistic effect of the inner and outer channels, this study aims to achieve dual improvements in particle impact velocity and spraying uniformity without incurring additional costs and complexity, thereby effectively increasing deposition efficiency and reducing production costs. In the proposed design, the inner layer still employs a supersonic nozzle to ensure the normal progress of the spraying process, while the outer layer adopts a convergent-divergent outer channel structure.

2. Research Method

2.1. Geometry

Through preliminary exploratory research, it was found that adopting a convergent-divergent outer channel structure can enhance the particle impact velocity, thereby improving the particle deposition efficiency. Therefore, the cross-section of the Dual path nozzle structure is shown in Figure 1. The inner channel structure remains the Convergent Divergent Barrel (CDB) supersonic nozzle, with geometric parameter values optimized through previous numerical simulations of the CDB nozzle [20], as shown in

Table 1. Geometric parameters of the inner layer CDB nozzle.

CDB Nozzle Parameter	Value (mm)
Inlet diameter (D1)	10
Throat diameter (D2)	2
Outlet diameter (D3)	3
Powder injection diameter (D4)	2
Convergent length (L1)	7
Divergent length (L2)	11
Barrel length (L3)	70
Injection angle ($°$)	90

. The outer channel structure is a convergent-divergent structure, with initial geometric parameter values as listed in

Table 2. Parameters of the outer channel structure.

Name	Value (mm)
Inlet diameter (D5)	8
Throat diameter (D6)	5
Outlet diameter (D7)	6
Convergent length (L4)	50
Divergent length (L5)	5

.

2.2. Materials

The spraying particles used in the experiment were pure aluminum powder with a spherical morphology. The powder was purchased from Beijing Techny New Materials and Technology Co., Ltd. (Beijing, China) Figure 2a shows the microscopic image of the aluminum particles, and Figure 2b displays the particle size distribution, ranging from 10 to 50 μm. The particle size distribution was analyzed by ImageJ.

Table 3. Properties of aluminum powder particles.

Material	Thermal Conductivity (W/m K)	Density (kg/m3)	Specific Heat Capacity (J/kg K)	Thermal Diffusivity (m2/s)
Aluminum	202.4	2719	871	8.55 × 10−5

lists the material properties of the aluminum particles [21]. For the substrate material in this spraying experiment, 316 L steel was used. The substrate samples were obtained using wire cutting methods, with dimensions of 15 × 15 × 5.5 mm, and were polished using 300 and 600 grit sandpaper.

2.3. Experimental Setup

As shown in Figure 3, the design of the dual-path cold spraying nozzle consists of three main parts. In Figure 3b, part 1 is the front-end that includes the converging and diverging portions of the inner channel, part 2 is the straight tube that mates with part 1, and part 3 constitutes the outer channel structure that mates with part 2. The straight tube and the front-end are mounted together by means of a bore and shaft fit and secured by clamping bolt, the outer channel is connected to the straight tube by means of pipe threads, and both the powder inlet and the outer channel gas inlet are connected to the front-end and the outer channel, respectively, by means of pipe threads. Figure 3d shows the actual dual-path nozzle. The inner channel is made of brass while the outer channel is made of stainless steel.

The type of cold spray equipment is LP-TCY-III manufactured by Beijing Techny New Materials and Technology Co., Ltd. The schematic diagram illustrating the setup of the dual path nozzle experimental environment is shown in Figure 4. An air compressor depicted in the figure serves the purpose of supplying compressed air to the entire cold spraying system. Due to the differing gas pressures at the entrances of the inner and outer channels, an external piping system is necessary, with pressure control at the outer channel entrance managed by a pressure regulator. The inner channel is connected to a supersonic cold spray machine, which provides the spray powder. Powder delivery through the inner channel is facilitated by the Venturi effect generated within the inner supersonic nozzle structure, accelerating deposition onto the substrate to complete the entire cold spraying process.

In the experimental process, compressed air is used as the accelerating gas. The inlet pressure is 0.8 MPa with a temperature of 500 °C, and the powder feeding rate is approximately 0.524 g/s. The standoff is 20 mm, a parameter previously identified in earlier studies as optimal for low-pressure cold spraying [22].

After preparing the depositions, it is necessary to observe them using metallographic techniques to evaluate their properties. Samples should be cut to standard dimensions using a wire cutting tool. Subsequently, metallographic samples are prepared by embedding them in epoxy resin. Next, the surfaces are polished using a CT-MPT-IZ metallographic polishing machine. Once the samples are polished, they undergo immersion corrosion testing. Following this, examination is conducted using a 4XC (4XB-C) inverted metallographic microscope to observe the interface for material diffusion and grain distribution. Additionally, the microstructure of the cross-section of the prepared depositions is further observed using a GeminiSEM500 field emission scanning electron microscope (SEM).

Porosity is a crucial indicator for evaluating deposition quality as it directly influences material strength and thermal/electrical conductivity. In this study, porosity within the deposition is calculated. The cross-sectional image of the deposition is observed and magnified 200 times under an optical microscope. Image-J V1.8.0 software is then used to adjust the grayscale values and color thresholds of the image to facilitate identification of the image to differentiate between pores and materials in the deposition, which in turn lead to the calculation of the porosity, i.e., the ratio of pore area to total area.

Hardness typically refers to a material’s resistance to localized deformation and is an important indicator of deposition performance, partly reflecting wear resistance and mechanical properties. In the study, HVS-1000Z microhardness tester is used for microhardness measurement. During the measurement process, 5 points are randomly selected for microhardness measurement on the surface of the polished pretreated specimen with a load of 30 gf and a loading time of 10 s. Finally, the average value of the 5 measurement points is taken as the microhardness value of the specimen.

2.4. Dual-Path Nozzle Geometric Optimization Method

Due to the convergence-divergence external channel structure having five geometric parameters, their specific impacts on the internal gas flow field, particle acceleration behavior, and particle distribution are currently unclear, as well as the rules governing these impacts and their relative importance. Furthermore, there is limited existing research on this topic in previous literature. However, individually studying these five geometric parameters would require extensive simulation time and significant computational resources. To reduce the number of simulations while optimizing the external channel geometry, a scientific experimental method known as orthogonal experimental design is employed. It is capable of studying multiple factors at different levels simultaneously, and the general process is shown in Figure 5.

3. Numerical Modeling

3.1. Computational Domain

The nozzle model mesh consists of a hexahedral-hexagonal grid, as shown in Figure 6. The maximum mesh size is set to 0.3 mm, and the minimum mesh size is set to 0.05 mm. Boundary layer meshing is accomplished using inflation layers, and mesh refinement is applied at the nozzle outlet. The total number of mesh elements exceeds 880,000, ensuring computational results independent of mesh density. A comparison of results with mesh grids of approximately 440,000, 1,000,000, and 15,000,000 revealed that convergence was not achieved with 440,000 grids due to poor mesh quality. There were no significant differences in results between the cases of 880,000 meshes and the higher counts of 1,000,000 and 15,000,000 meshes. The distance from the outlet of the inner CDB nozzle to the substrate is set at 20 mm.

3.2. Gas Phase

In this simulation experiment, compressed air is used as the driving gas, treated as ideal and compressible with a specific heat capacity ratio of 1.4, its equation of state is Equation (1). The molecular mass of air is 28.966. Based on these assumptions, the Reynolds-averaged Navier-Stokes equations in their general conservation form for continuity, momentum, and energy are employed to include and explain the effects of turbulence in the flow field, expressed by Equations (2)–(4).Clearly, the standard $k$-$\epsilon$ model is not suitable for this 3D problem involving the suction airflow from the powder feed point. The Realizable $k$-$\epsilon$ model does not account for low Reynolds number viscosity effects, such as those near the wall. The accuracy of turbulence eddies is a crucial factor throughout the simulation process. Therefore, for the gas flow inside the nozzle, the RNG $k$-$\epsilon$ model proposed by Yakhot et al. [23] and further developed by Ounis et al. [24] is used for predictive calculations, as shown in Equations (5) and (6). This turbulence model accurately simulates both high-speed and low-speed flow regions within the flow field.

Ideal gas equation of state:

$$p/\rho =RT$$

(1)

Mass:

$$\partial (\rho {\mu }_i)/\partial x_i=0$$

(2)

Momentum:

$$\partial (\rho {\mu }_i{\mu }_j)/\partial x_j=\partial \left[{\mu }_{eff}\left(\partial {\mu }_i/\partial x_j+\partial {\mu }_i/\partial x_i\right)-(2{\mu }_{eff}/3)(\partial {\mu }_k/\partial x_k)\right]/\partial x_j-\partial p/\partial x_i$$

(3)

Energy:

$$\partial (\rho {\mu }_i{\mu }_j)/\partial x_j+\partial p/\partial x_i=\partial \left[{\mu }_{eff}\left(\partial {\mu }_i/\partial x_j+\partial {\mu }_i/\partial x_i\right)-(2{\mu }_{eff}/3)(\partial {\mu }_k/\partial x_k)\right]/\partial x_j$$

(4)

Turbulence energy:

$$\partial \left(\rho {\mu }_{i}k\right)/\partial x_j=\partial \left[{\alpha }_k{\mu }_{eff}\left(\partial k/\partial x_i\right)\right]/\partial x_i+{\mu }_i{S}^2-\rho \epsilon$$

(5)

Turbulence energy dissipation:

$$\partial \left(\rho {\mu }_i\epsilon \right)/\partial x_j=\partial \left[{\alpha }_{\epsilon }{\mu }_{eff}\left(\partial \epsilon /\partial x_i\right)\right]/\partial x_i+C_{1\epsilon }{\mu }_i{S}^2\epsilon /k-C_{2\epsilon }\rho {\epsilon }^2/k-R$$

(6)

where, $p$ is the gas pressure, $\rho$ is the gas density, R is the ideal gas constant, T is the gas temperature, $\mu$ is the viscosity of gas, ${\mu }_{eff}$ is the effective viscosity coefficient, k is the k equation coefficient, $\epsilon$ is the turbulence energy dissipation, ${\alpha }_k$ and ${\alpha }_k$ are the reciprocals of the effective Prandtl number of the k and $\epsilon$ equations, S is the mean-velocity strain-rate tensor coefficient, constants $C_{\mu }$, $C_{1\epsilon }$ and $C_{2\epsilon }$ have the value of 0.085, 1.42, 1.68.

3.3. Particle-Fluid Interaction

In this simulation, pure aluminum particles with diameters ranging from 20–50 μm are used. The Discrete Phase Model (DPM) in Fluent is employed to calculate the particles’ acceleration process and distribution. In the DPM model, particles are treated as discrete phases dispersed within a continuous phase, and their motion in the flow field is computed using Lagrangian equations. Gravity is neglected, expressed in Equation (7). To address the acceleration of particles by compressed air, Mors and Alexander’s model [25] is utilized, the relevant formulas are shown in Equations (8)–(10). Thermal conduction within particles is assumed negligible, treating particles as isothermal. The force $F_x$, which includes terms like effective mass force, pressure gradient-induced force, and thermophoretic force, is considered negligible in this study. The values of $a_1$, $a_2$, and $a_3$ can be referenced in

Table 4. Drag coefficients of spherical particles.

$\mathbf{Re}$	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$
$\mathrm{Re}$ < 0.1	0	24.0	0
0.1 < $\mathrm{Re}$ < 1.0	3.69	22.73	0.0903
1.0 < $\mathrm{Re}$ < 10.0	1.222	29.1667	−3.8889
10.0 < $\mathrm{Re}$ < 100.0	0.6167	46.5	−116.67
100.0 < $\mathrm{Re}$ < 1000.0	0.3644	98.33	−2778
1000.0 < $\mathrm{Re}$ < 5000.0	0.357	148.62	−4.75 $\times$ 105
5000.0 < $\mathrm{Re}$ < 10,000.0	0.46	−490.456	57.87 $\times$ 104
10,000.0 < $\mathrm{Re}$ < 50,000.0	0.5191	−1662.5	5.4167 $\times$ 105

[26]. Mehmood et al. [27], Gabor et al. [28] and Wan et al. [29] use Mors and Alexander’s model to calculate the effect of compressed air on particles velocity, and the simulation results match the experimental results closely. To account for particle dispersion due to turbulent effects, a stochastic tracking model is employed. Specifically, the Discrete Random Walk (DRW) model is used in this case to predict the fluctuating components of particle velocities [30].

$$d{u}_p/dt=F_D+F_x$$

(7)

$$F_D=\left(18\mu /{\rho }_p{d}_p^2\right)\left(C_D {\mathrm{Re}}_p/24\right)(u_g-u_p)$$

(8)

$${\mathrm{Re}}_p=\left(\rho d_p\left|u_g-u_p\right|\right)/\mu$$

(9)

$$C_D=a_1+\left(a_2/\mathrm{Re}\right)+\left(a_3/{\mathrm{Re}}^2\right)$$

(10)

where, $u_p$ is the velocity of the particles, $F_D$ is the drag force, ${\rho }_p$ is the particles density, $d_p$ is the diameter of particle, $C_D$ is the drag force coefficient, ${\mathrm{Re}}_p$ is the particle Reynold’s number, $u_g$ is the velocity of the gas, $\mathrm{Re}$ is the gas Reynold’s number.

3.4. Boundary Conditions

In order to accurately simulate the interaction between the fluid and the boundary of the calculation domain, boundary conditions need to be set up, as shown in Figure 7. The simulation setup involved setting the preheating chamber for gas flow as a pressure inlet with a pressure value of 0.8 MPa and a temperature of 773 K. Additionally, the inlet of the external channel was set as a pressure inlet with a pressure of 0.35 MPa and a temperature of 300 K. The boundaries at the outlet of the powder injection tube at the upper end and the region of free jet were set as pressure outlets with a pressure of 0.1 MPa and a temperature of ambient room temperature. The nozzle exit was configured as the internal flow field, while all other relevant surfaces were set as standard wall surfaces for the simulation calculations. Powder particles were injected into the nozzle through outlet 1 of the pressure outlet with an initial velocity set to 0 m/s. In real experiments, due to constraints in the external channel structure and size, the pressure gas enters vertically; however, for simplification in the simulation, it was modeled as entering radially into the internal part of the external channel. The wall conditions were set as immovable and adiabatic, utilizing standard wall functions for near-wall treatment, which are effective for a wide range of wall boundary flows [31].

The simulation was conducted using a density-based solver under steady-state conditions. Mass flow rates were monitored at the inlet, outlet 1, and outlet 2 in each iteration. The Courant number was set to 2, and relaxation factors were adjusted as necessary. The simulation continued until convergence criteria were met, typically when the mass flow rates at the two monitoring points were equal, indicating a steady state.

3.5. Modeling Validation

Using a CDB nozzle, cold spray experiments were conducted with multiple spray sessions to measure the diameter of spray points and calculate deposition efficiency (DE). The specific steps to calculate the DE are as follows: Before conducting the cold spraying experiment, the weight of the substrate plate was measured by the digital electronic scale, denoted as $m_0$. After the spraying is completed, the weight of deposition and substrate plate was measured, denoted as $m_1$. The weight of particles not deposited on the substrate plate was measured as $m_2$. Therefore, the equation for the DE is:

$$DE=\left[\left(m_1-m_0\right)/\left(m_1-m_0+m_2\right)\right]\times 100\%$$

(11)

By measurement, the diameter of the spray point was approximately 5.7 mm. Deposition efficiency of the depositions was calculated across multiple sessions to determine the average value, reducing experimental error, yielding an actual average deposition efficiency of approximately 20.22%.

The premise for calculating the theoretical deposition efficiency of particles is to determine their theoretical critical velocity. The critical velocity is defined as the minimum velocity at which particles can effectively deposit during the cold spray process. However, the critical velocity depends on factors such as particle size, temperature, and substrate material. According to an empirical formula proposed by Schmidt et al. [32], the calculation of the critical velocity is approximately as follows:

$$V_{cr}=0.64\sqrt{\left(\left(16{\sigma }_{Ts}/\left({\rho }_P\left(T_m-293\right)\right)\right)+C_p\right)\left(T_m-T_{pi}\right)}$$

(12)

where, ${\sigma }_{Ts}$ is the ultimate tensile strength, $T_m$ is the melting point of particles, $C_p$ is the specific heat capacity of particles, and $T_{pi}$ is the impact temperature of particles (based on simulation results).

The optimized geometric parameters of the CDB nozzle used in simulations are shown in Table 1. After conducting simulation calculations and obtaining results as presented in

Table 5. Simulation results data for CDB nozzle.

Name	Average Impact Velocity of Particles (m/s)	Average Particle Temperature (K)	Spray Spot Diameter (mm)	Number of Particles Exceeding the Critical Velocity
CDB nozzle	346	400	5.36	243

, the critical velocity of particles is approximately 400 m/s under simulation conditions with an inlet pressure of 0.8 MPa and a temperature of 773 K. A total of 1050 particles were released during the simulation, out of which 243 particles exceeded the critical velocity and are considered to effectively deposit. Therefore, the deposition efficiency is 23%. Experimentally, the average deposition efficiency of aluminum particles was measured at 20.22%. Additionally, particles exceeding the theoretical critical velocity are assumed to effectively deposit, allowing calculation of the simulated spray point diameter, which is approximately 5.36 mm. In contrast, the experimental spray point diameter was approximately 5.7 mm. Comparison of the simulated and experimental spray point diameters indicates close agreement in data, validating the correctness of the numerical simulation model.

4. Results

4.1. Geometric Optimization of Dual-Path Nozzle

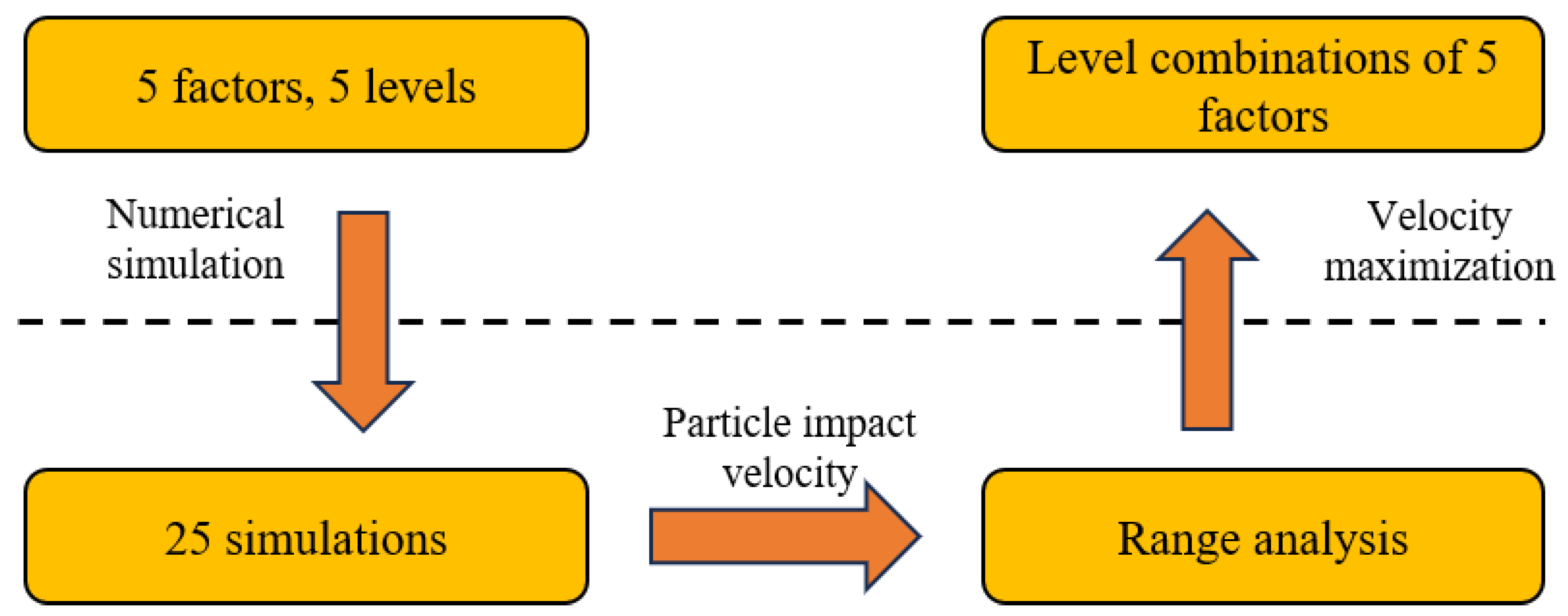
As shown in

Table 6. Five factors and five levels of the outer channel.

Levels	Factors
	Inlet Diameter/mm	Throat Diameter/mm	Outlet Diameter/mm	Convergent Length/mm	Divergent Length/mm
1	6	4.8	5.6	10	3
2	7	5.0	5.8	20	5
3	8	5.2	6.0	30	7
4	9	5.4	6.2	40	9
5	10	5.6	6.4	50	11

, this orthogonal experiment employs a 5-factor, 5-level design, necessitating a total of 25 simulations. Using CATIA.composer.2024 software, 25 sets of three-dimensional nozzle models were created. The modeling process strictly followed the parameters specified in orthogonal experimental

Table 7. Orthogonal experimental design table.

Numbers	Inlet Diameter/mm	Throat Diameter/mm	Outlet Diameter/mm	Convergent Length/mm	Divergent Length/mm
1	6	4.8	5.6	10	3
2	6	5.0	5.8	20	5
3	6	5.2	6.0	30	7
4	6	5.4	6.2	40	9
5	6	5.6	6.4	50	11
6	7	4.8	5.8	30	9
7	7	5.0	6.0	40	11
8	7	5.2	6.2	50	3
9	7	5.4	6.4	10	5
10	7	5.6	5.6	20	7
11	8	4.8	6.0	50	5
12	8	5.0	6.2	10	7
13	8	5.2	6.4	20	9
14	8	5.4	5.6	30	11
15	8	5.6	5.8	40	3
16	9	4.8	6.2	20	11
17	9	5.0	6.4	30	3
18	9	5.2	5.6	40	5
19	9	5.4	5.8	50	7
20	9	5.6	6.0	10	9
21	10	4.8	6.4	40	7
22	10	5.0	5.6	50	9
23	10	5.2	5.8	10	11
24	10	5.4	6.0	20	3
25	10	5.6	6.2	30	5

to ensure the accuracy of the experiments. Subsequently, Fluent 2020R1 software was used to compute each model group, analyzing internal gas flow dynamics and particle acceleration processes.

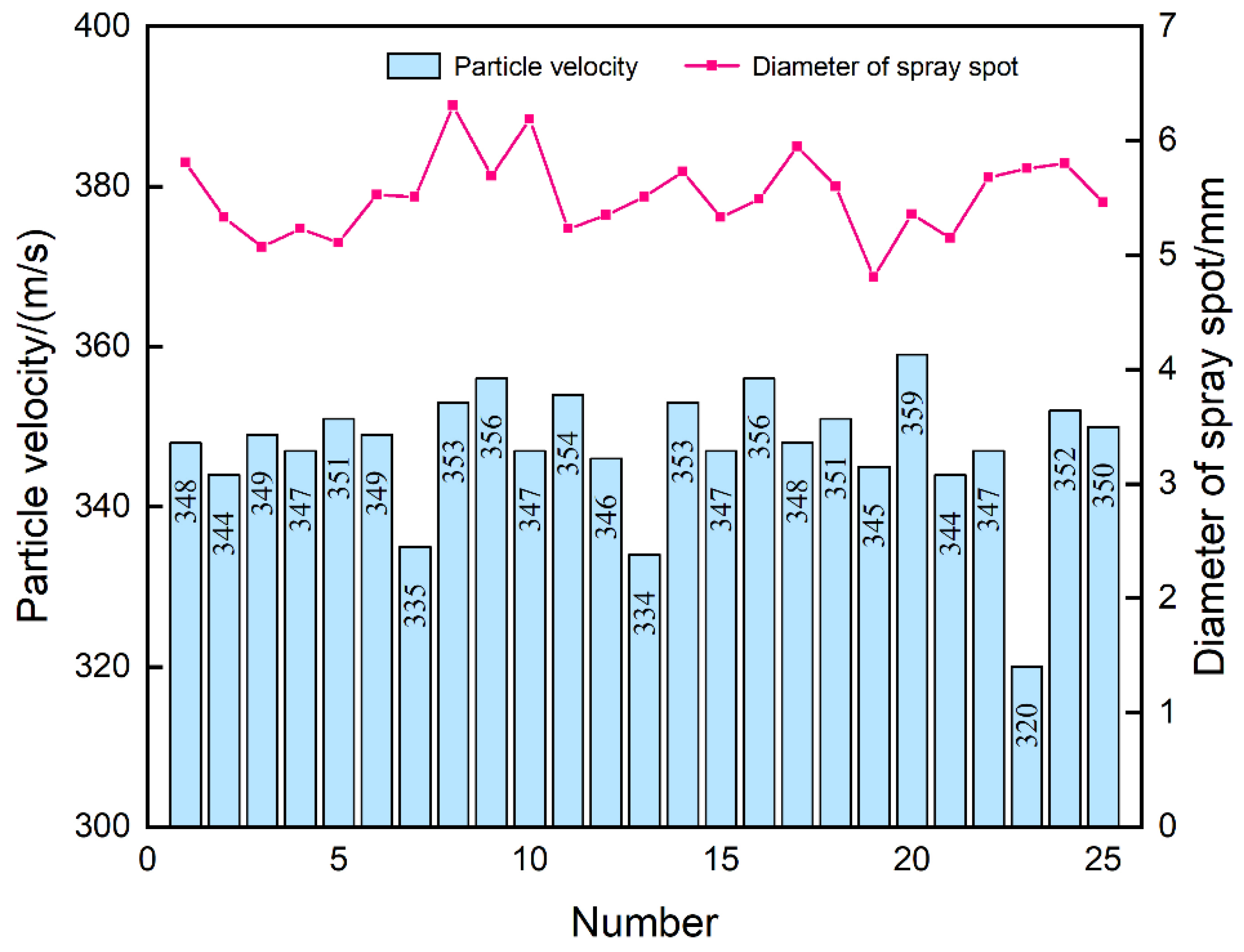
The results obtained from the simulation experiments are shown in Figure 8. Using Minitab v21.2.0 software, the range analysis was conducted on the data obtained from the simulations specified in the orthogonal experimental table. In range analysis

Table 8. Range analysis table.

	Inlet Diameter/mm	Throat Diameter/mm	Outlet Diameter/mm	Convergent Length/mm	Divergent Length/mm
$K_{i1}$	1739.0	1751.0	1746.0	1729.0	1748.0
$K_{i2}$	1740.0	1720.0	1705.0	1733.0	1755.0
$K_{i3}$	1734.0	1707.0	1749.0	1749.0	1731.0
$K_{i4}$	1759.0	1753.0	1752.0	1724.0	1736.0
$K_{i5}$	1713.0	1754.0	1733.0	1750.0	1715.0
$k_{i1}$	347.8	350.2	349.2	345.8	349.6
$k_{i2}$	348.0	344.0	341.0	346.6	351.0
$k_{i3}$	346.8	341.4	349.8	349.8	346.2
$k_{i4}$	351.8	350.6	350.4	344.8	347.2
$k_{i5}$	342.6	350.8	346.6	350.0	343.0
$R_i$	9.2	9.4	9.4	5.2	8.0

, i denotes the factor, j denotes the level, and $K_{ij}$ represents the sum of all simulations corresponding to factor i and level j in all simulations, while $k_{ij}$ is the arithmetic mean. $R_i$ represents the range, i.e., the difference between the maximum and minimum values of $k_{ij}$.

The optimal experimental design within the tested range comprises combinations of levels for each factor that maximize particle impact velocity. Among the tested combinations, A₄B₅C₄D₅E₂ (Inlet diameter 9 mm, throat diameter 5.6 mm, outlet diameter 6.2 mm, convergent length 50 mm, divergent length 5 mm) is identified as the optimal combination for maximizing particle impact velocity. Meanwhile, A larger range R_i indicates a greater influence of that factor on particle impact velocity. So, the order of influence on particle impact velocity is as follows: throat diameter > outlet diameter > inlet diameter > convergent length > divergent length. Finally, the range analysis was performed again based on the spray spot diameter, yielding R_i of less than 0.6 for all factors, indicating that the effect of the outer channel geometry on the spray spot diameter is small.

4.2. Effect of Air Pressure on Particle Velocity and Diameter of Spray Spot

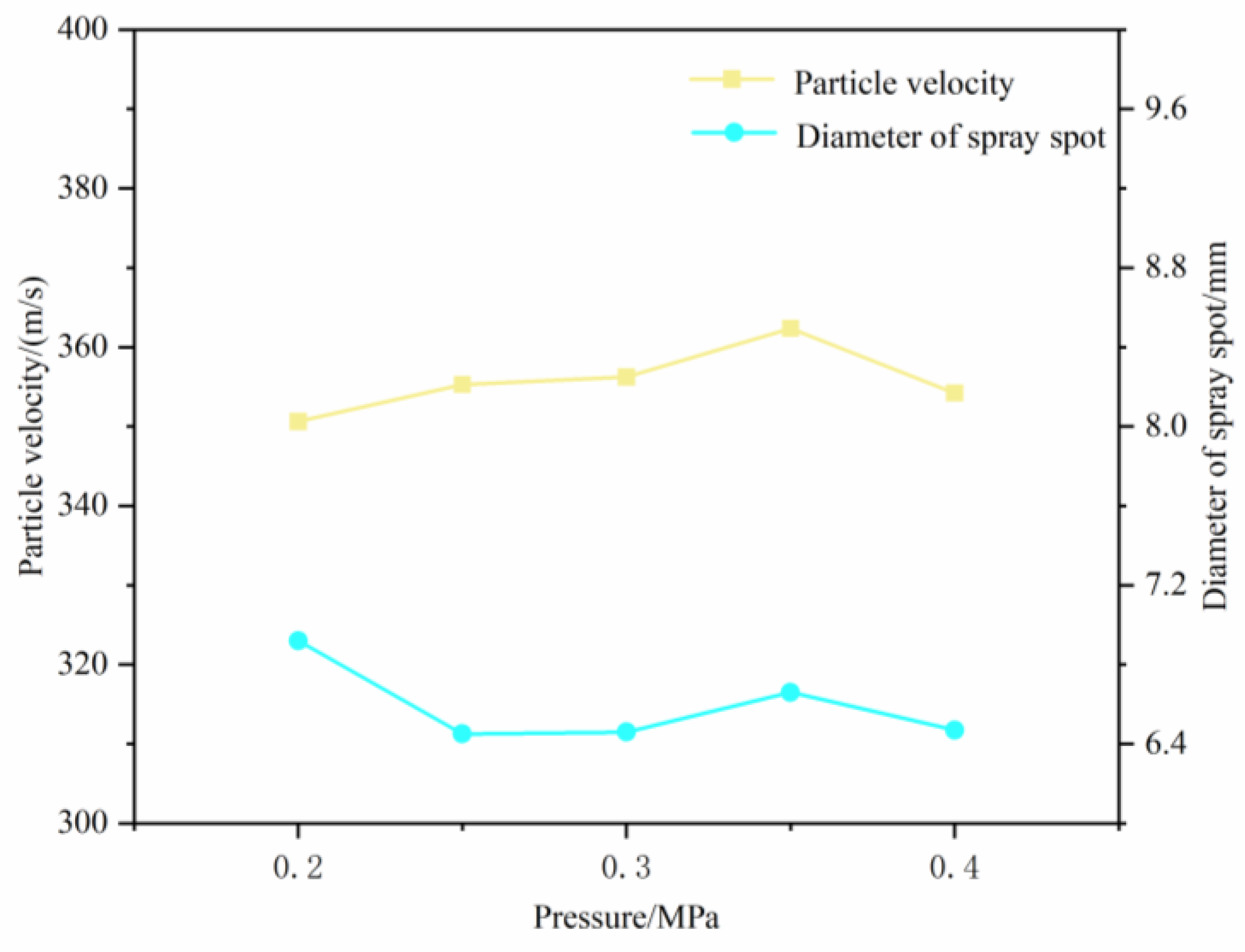
Using orthogonal experimental design, the optimal parameter combination was determined through mathematical analysis. Based on this, the entrance pressure of the external channel was varied to investigate its effect on particle impact velocity and spray area diameter, as shown in

Table 9. Experimental parameters of gas pressure.

Number	Pressure (MPa)
1	0.2
2	0.25
3	0.3
4	0.35
5	0.4

.

As shown in Figure 9, while keeping other simulation conditions constant, varying the entrance pressure of the external channel results in changes in particle impact velocity and spray area diameter. From the graph, it is found that between 0.2 MPa and 0.35 MPa, there is an increasing trend of particle impact velocity with the increase of gas pressure. This indicates that increasing the gas pressure at the entrance of the external channel constrains the particles accelerated through the internal channel nozzle, thereby enhancing particle impact velocity, consequently improving deposition performance. However, this constraint has limited effect on particle divergence, and the particle impact velocity starts to decrease when the gas pressure exceeds 0.35 MPa. Furthermore, it is observed that when the gas pressure exceeds 0.4 MPa and reaches 0.45 MPa, there is a sharp decrease in particle impact velocity, with almost no particles exceeding the theoretical critical velocity. This suggests that beyond a certain pressure threshold at the external channel entrance, not only does particle impact velocity not increase, but it also affects the flow of gas within the internal channel, leading to spray failure. For the spray spot diameter, the gas pressure has little effect and the size is around 6.5 mm.

4.3. Comparison of CDB and Dual-Path Nozzle

According to the previous subsection, the optimized dual-path nozzle has the best spraying effect when the inlet pressure of the outer channel is 0.35 MPa. Therefore, the CDB nozzle and the optimized dual-path nozzle were compared under this spraying condition.

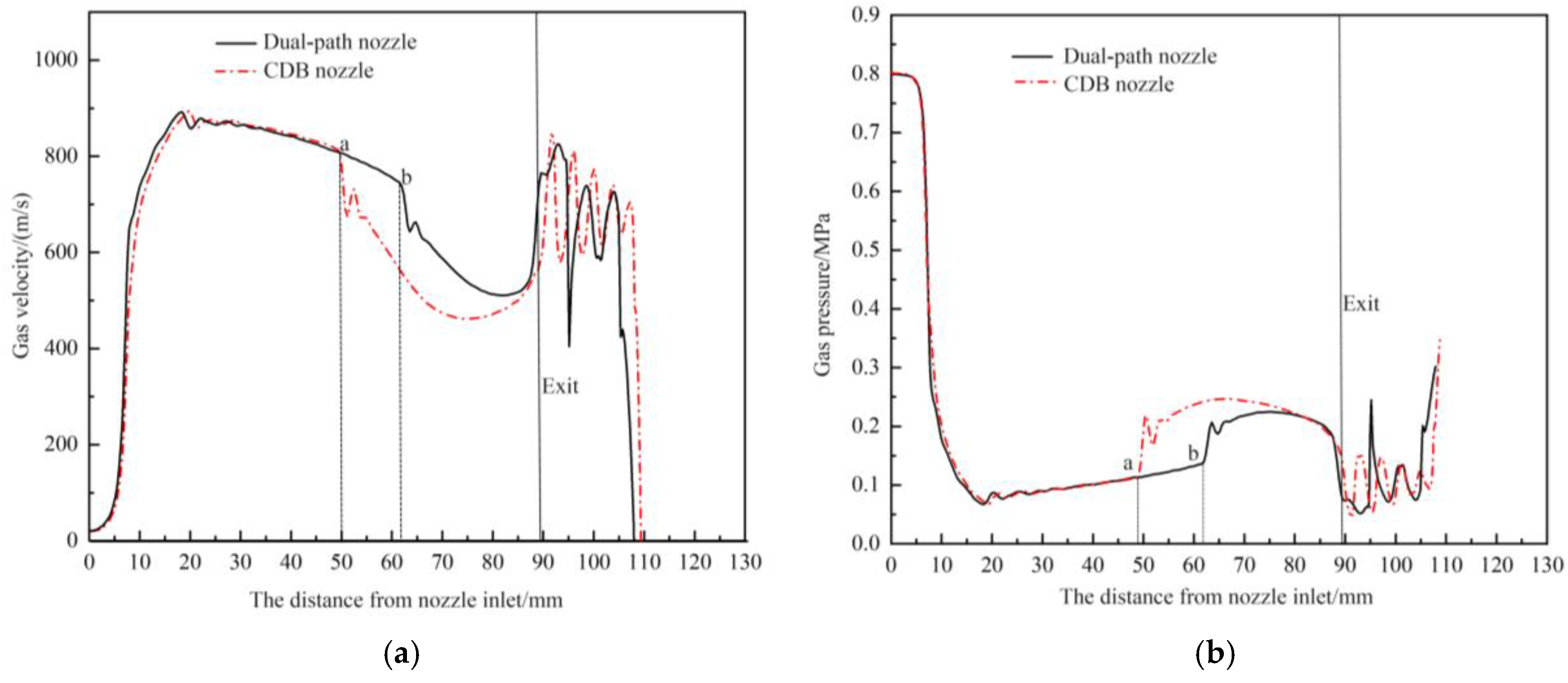
Figure 10 depicts the variation of gas pressure and velocity along the centerline of the CDB nozzle and the optimized dual-path nozzle. The solid black line represents the gas velocity and pressure variation inside the dual-path nozzle, while the dashed red line represents the variation within the inner channel. It can be observed from the figure that the trends of gas velocity and pressure along the centerline are generally similar for both nozzles. However, in the nozzle without an outer channel structure, gas velocity sharply decreases starting at point ‘a’ approximately 50 mm downstream from the nozzle inlet. This characteristic is typical of convergent-divergent-straight (CDS) supersonic nozzles, where gas, after the divergent section, enters a straight section with an unchanged cross-sectional area, leading to incomplete expansion due to friction with the nozzle walls, thereby causing a decrease in gas velocity. In contrast, in the dual-path nozzle, the sharp decrease in gas velocity occurs at point ‘b’ approximately 62 mm downstream from the nozzle inlet. Regarding the pressure variation, the gas pressure inside the nozzle without an outer channel structure increases earlier compared to the dual-path nozzle. This earlier pressure rise indicates a decrease in gas velocity as the gas undergoes pressure reduction and acceleration processes. This observation is consistent with the changes in gas velocity. It indicates that the outer channel structure can prolong the gas expansion distance, extend the pressure reduction and acceleration processes in the straight section, thereby enhancing the acceleration of particles within the straight section and increasing their impact velocity. 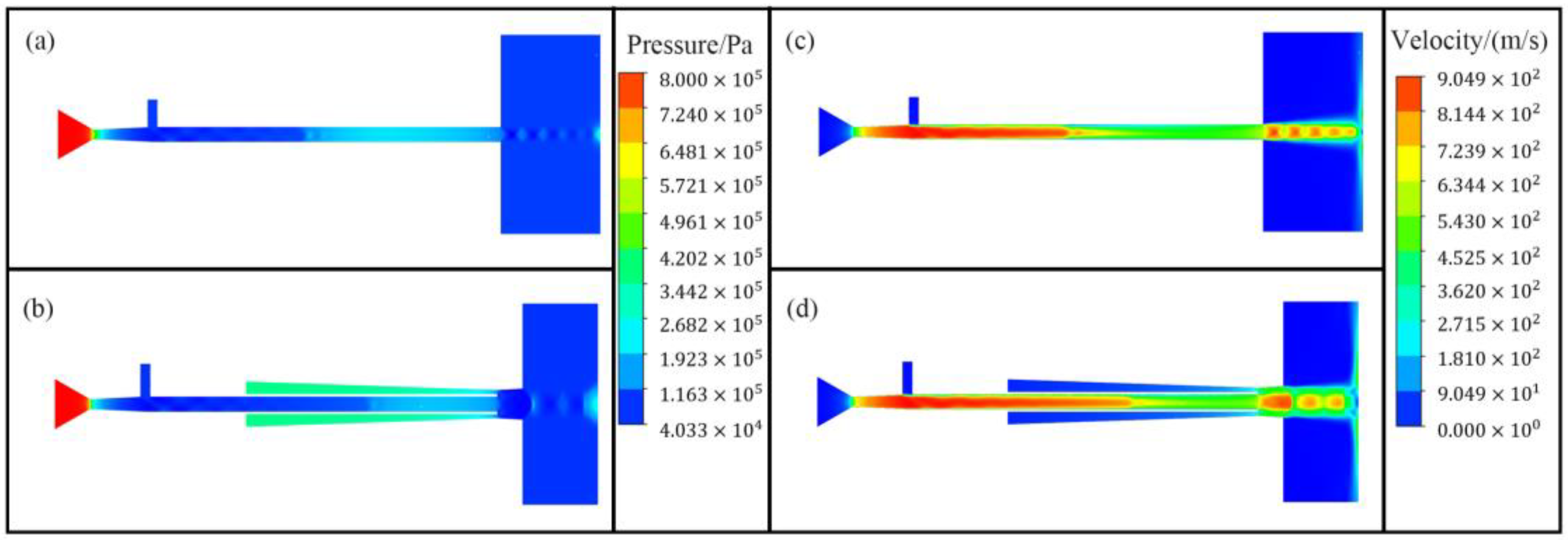Figure 11 presents contour plots of gas velocity and pressure within both types of nozzles.

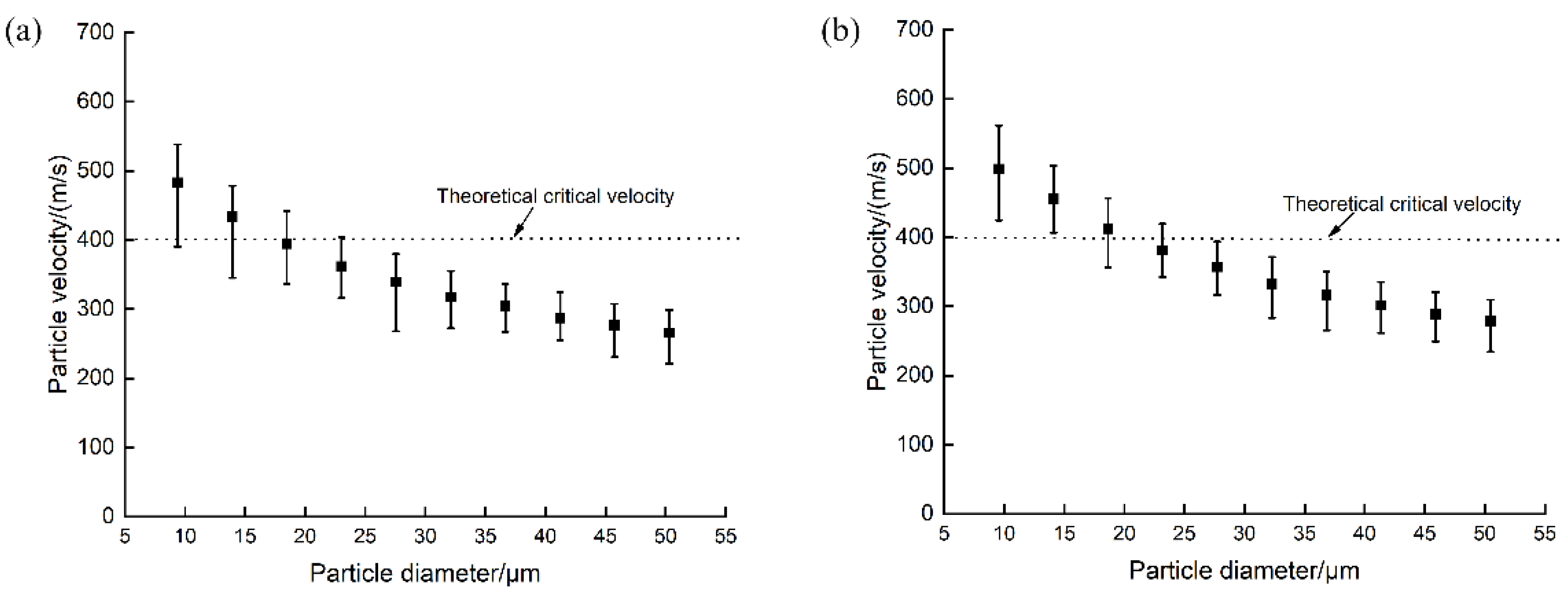
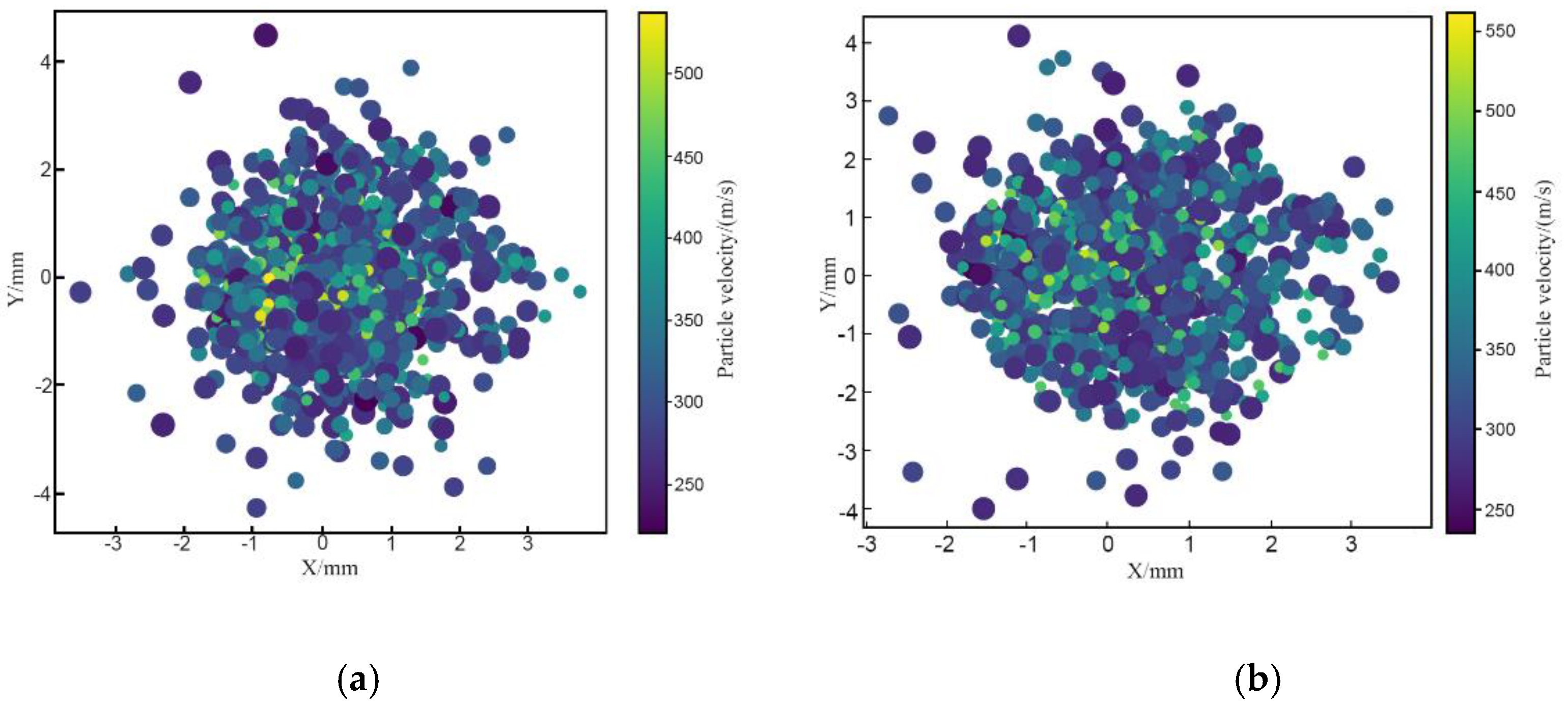
The theoretical critical velocity of aluminum particles under simulated conditions of 0.8 MPa and 773 K is approximately 400 m/s. The temperature is the particle temperature at impact. Figure 12 displays the footprint distribution of all aluminum particles using CDB and dual-path nozzles under these conditions. Figure 13 presents the distribution of impact velocities of all simulated particles from both nozzles, with particle diameters ranging from 10–50 μm. The total number of injected particles and the number of particles per diameter are consistent between simulations. From the figures, it is evident that particles accelerated by the dual-path nozzle exceed 400 m/s in greater numbers compared to those accelerated by the CDB nozzle. Particularly, aluminum particles with diameters less than 15 μm exceed the critical velocity. Additionally, for particles with a diameter of 25 μm, a significant majority accelerated by the dual-path nozzle have impact velocities below the theoretical critical velocity. In contrast, all particles accelerated by the CDB nozzle have impact velocities below the critical velocity, illustrating why the deposition efficiency of low-pressure cold spray is relatively low. Calculation of all particle data yields that the average impact velocity of particles using the dual-path nozzle is 363 m/s, which is 23 m/s higher than that achieved using the CDB nozzle without an outer channel structure. Furthermore, the number of particles exceeding the critical velocity increases by nearly 100, equating to an approximate 10% improvement in deposition efficiency. Considering particles exceeding the theoretical critical velocity as effectively deposition, the simulated spray diameter using the dual-path nozzle measures 6.69 mm, whereas that using the CDB nozzle measures 5.36 mm. In summary, a comparison of the simulation results of the CDB nozzle and the dual-path nozzle is shown in

Table 10. Comparison of simulation results between CDB nozzle and dual−path nozzle.

Name	Average Impact Velocity of Particles (m/s)	Spray Spot Diameter (mm)	Number of Particles Exceeding the Critical Velocity
Dual-path nozzle	369	6.69	343
CDB nozzle	346	5.36	243

, which indicates that using the dual-path nozzle enhances particle impact velocities and consequently improves deposition efficiency.

Figure 14 respectively show different deposits and their cross-sectional profiles obtained through cold spray experiments. Among them, Sample 1 uses a CDB nozzle, while Sample 2 uses a dual-path nozzle. It can be clearly seen from the figure that the deposition diameter obtained solely using the inner channel nozzle is approximately 5.7 mm, with a height of about 5.5 mm. In contrast, the deposition produced using the dual-path nozzle has a diameter of 7 mm and a height of 6.5 mm. These results indicate that using a nozzle with an outer channel structure enhances particle deposition efficiency, enabling more particles to reach critical velocity and deposit onto the substrate. Consequently, this results in depositions with larger diameters and greater heights.

As shown in

Table 11. Spray spot diameter for CDB nozzle and dual−path nozzle.

Name	Spray Spot Diameter/mm
CDB nozzle	5.7 (Experiment)
	5.4 (Simulation)
Dual-path nozzle	7.0 (Experiment)
	6.7 (Simulation)

, the difference between the actual spray spot diameter obtained by using the dual-path nozzle and that obtained by numerical simulation is about 0.3 mm, which is a very small difference, further verifying the accuracy of the simulation model. At the same time, the spray spot diameter of the dual-path nozzle is larger than that of the CDB nozzle, which may be due to the increase in the kinetic energy of the impact of the particle beam, the particle inertia increases, and it is difficult for the airflow in the outer channel to effectively constrain the particle flow, which results in an increase in the spray spot diameter. However, the difference between the two is only about 1.3 mm, which can be explained to some extent that the main role of the outer channel is to increase the impact velocity of the particles, which has little effect on the spray spot diameter.

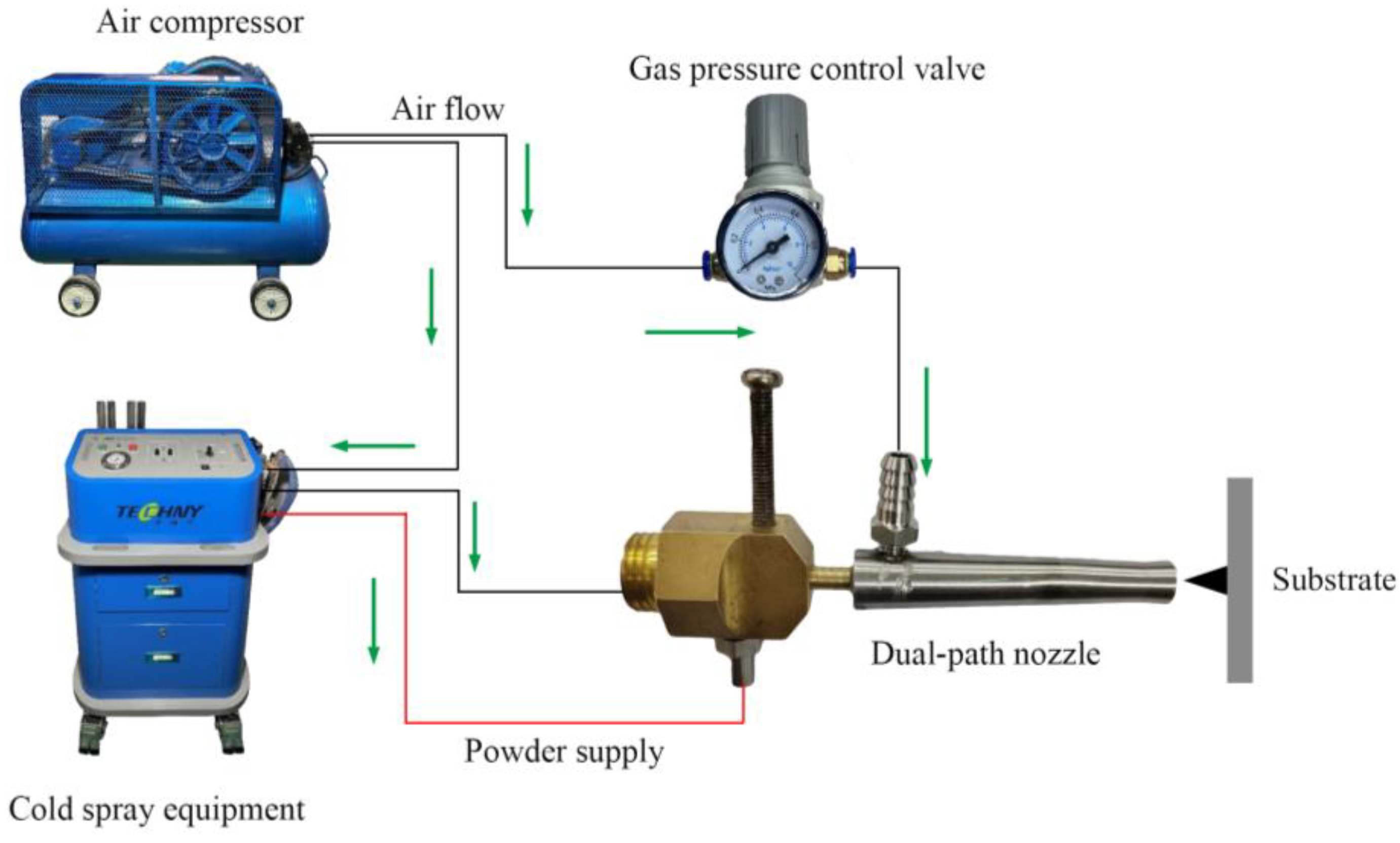
Three sets of replicated experiments were designed to reduce randomness. Each cold spray experiment was evaluated for particle deposition efficiency, and the results were recorded. Based on the collected data, deposition efficiencies for each group were calculated and are detailed in Figure 15. Subsequently, the average deposition efficiencies of depositions produced using the two different nozzles were determined. By comparing the particle deposition efficiencies for the two nozzles, it can be observed that the average deposition efficiency using only the inner channel nozzle is approximately 20%, aligning with the characteristic low deposition efficiency of low-pressure cold spray and closely matching the simulated results, thereby validating the accuracy of the numerical simulation model. On the other hand, the actual average deposition efficiency of particles using the dual-path nozzle is approximately 28%, representing an improvement of about 8% over the nozzle without an outer channel structure. Correspondingly, the simulated deposition efficiency is 10%, indicating a close agreement between the actual and simulated results. This further confirms that the use of an outer channel structure enhances particle impact velocities, thereby improving particle deposition efficiency.

4.4. Evaluation of the Depositions

To investigate the influence of the optimized dual-path nozzle on the microstructure and mechanical properties of aluminum deposition, three groups of repeated experiments were designed under the condition that the inlet pressure of the outer pressure of the outer channel was 0.35 MPa to compare the optimized dual-path nozzle with the CDB nozzle.

Based on the data measured using Image-J V1.8.0 software, porosity values for three groups of depositions were determined, as detailed in Figure 16. Comparing the data from the figure reveals that the porosity of depositions prepared using the inner channel nozzle is approximately 10.51%, whereas depositions prepared using the dual-path nozzle structure exhibit a porosity of about 9.12%. These results indicate that the dual-path nozzle enhances particle impact velocities. Higher impact velocities promote tighter particle bonding, thereby reducing deposition porosity. The study findings underscore that the porosity can be reduced by choosing an appropriate nozzle structure to a certain extent.

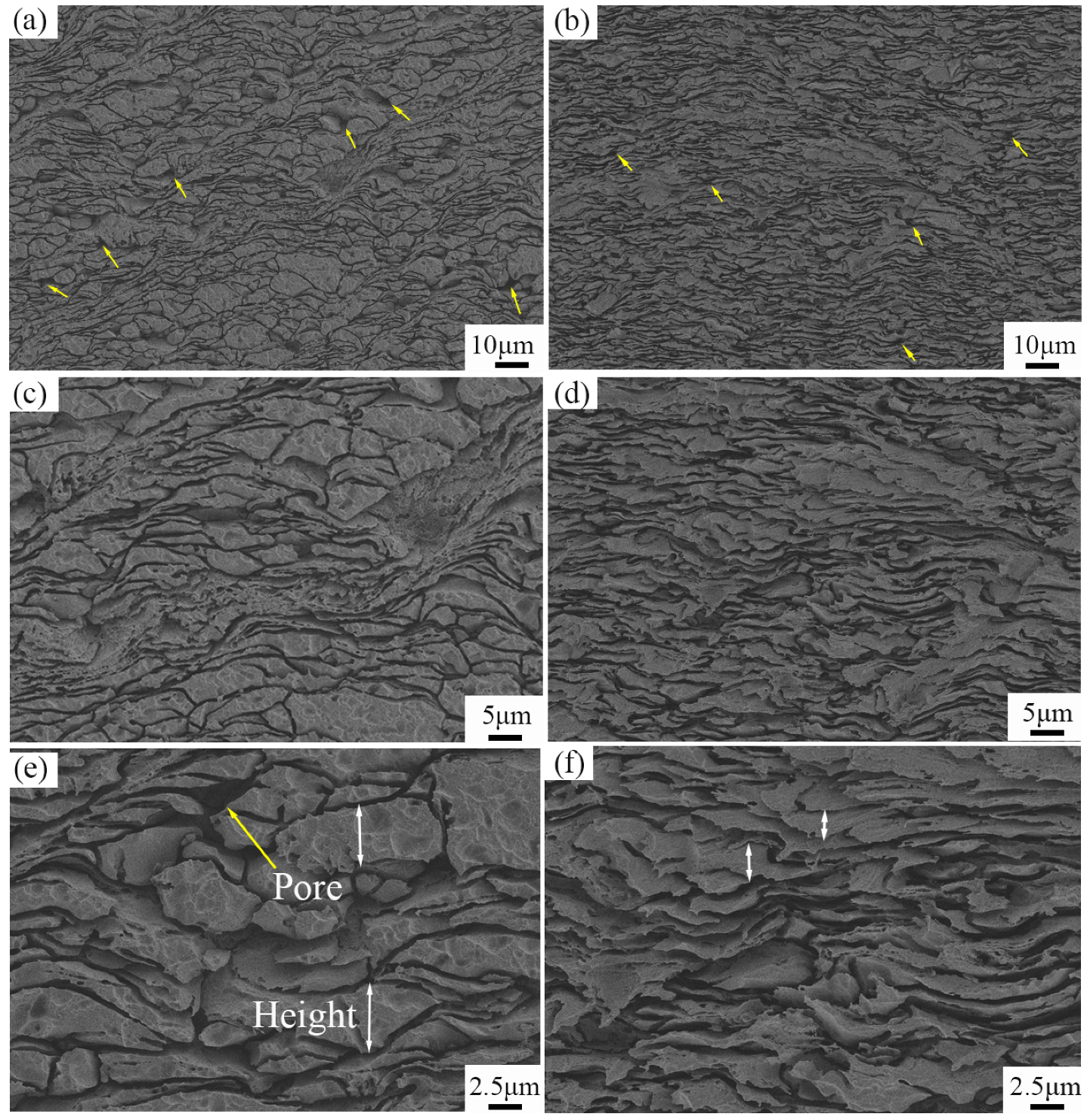
Figure 17 presents cross-sectional morphologies of depositions obtained via SEM. Panels (a), (c), and (e) depict microstructures of depositions produced using the inner channel nozzle at magnifications of 250×, 500×, and 1000× respectively, while panels (b), (d), and (f) depict microstructures of depositions produced using the dual-path nozzle at the same magnifications. In these images, yellow arrows indicate larger pores within the depositions, while white double arrows denote the height of aluminum particles deformed upon deposition onto the substrate. Observing Figure 18, compared to high-pressure cold spraying, depositions produced by low-pressure cold spraying exhibit higher porosity with a greater number of larger pores, indicating poorer densification. Comparing the microstructures of depositions produced using the two different nozzle structures reveals that depositions from the dual-path nozzle exhibit fewer large pores on their cross-sections and tighter particle bonding. This observation stems from the higher flight velocities attained by particles within the dual-path nozzle, resulting in more effective particle compaction upon impact. Furthermore, increased particle impact velocities lead to greater particle deformation and increased particle-to-particle collisions, as evidenced by the significantly higher deformation height indicated by the white arrows in panel (f) compared to panel (e) of Figure 17. Therefore, these results reaffirm that using a dual-path nozzle structure during cold spraying enhances particle impact velocities, thereby improving deposition performance. This improvement not only reduces deposition porosity but also enhances deposition densification.

Figure 18 presents SEM micrographs at a magnification of 250, where panel (a) represents a deposition produced using the inner channel nozzle, and panel (b) represents a deposition produced using the dual-path nozzle. The micrographs reveal indentations at the interface between the deposition and the substrate, with depositions produced using the dual-path nozzle showing more pronounced indentations. This observation underscores the ability of the dual-path nozzle to impart higher particle impact velocities. However, it is important to note that these phenomena are influenced by thermal softening effects. At spraying temperatures reaching 500 °C, the substrate surface experiences preheating, which is a significant heat transfer mechanism. Moreover, the flight velocity of powder particles increases with spraying temperature, and upon impact with the substrate, the higher kinetic energy of particles is converted into thermal energy. As a result, thermal softening occurs on the substrate surface, facilitating cooperative deformation between powder particles and the substrate. This transformation from physical bonding to mechanical interlocking enhances the bond strength between powder particles and the substrate, further improving deposition adhesion.

The microhardness of three groups of depositions was measured; experimental results showed that the average microhardness of depositions produced using the inner channel nozzle is 33.4 ± 0.2 Hv, while those produced using the dual-path nozzle are 34.2 ± 0.2 Hv. The microhardness of depositions is primarily influenced by the deposition porosity and the extent of work hardening experienced after particle plastic deformation. Despite the slight difference in deposition hardness, there is still a discernible improvement. This is attributed to the higher velocity particles achieve within the dual-path nozzle, increasing the degree of deformation caused by particle-to-particle impacts and thereby reducing porosity. Significant plastic deformation increases the density of dislocations, leading to a slight increase in microhardness.

5. Conclusions

This study proposes a novel dual-path structured cold spray nozzle design aimed at enhancing the deposition efficiency of low-pressure cold spray. Through numerical simulations and experimental research, several key conclusions have been drawn:

• Using orthogonal experimental design methods, the geometric parameters of the external channels of the dual-path nozzle were optimized. The optimal parameter combination obtained includes an entrance diameter of 9 mm, throat diameter of 5.6 mm, exit diameter of 6.2 mm, converging section length of 50 mm, and diverging section length of 5 mm.
• Numerical simulation results indicate that an appropriate inlet pressure for the external channels (0.35 MPa) can increase particle impact velocity and thereby enhance deposition efficiency. Compared to a single internal channel nozzle, the dual-path structure increases the average particle impact velocity by 23 m/s, leading to a theoretical deposition efficiency improvement of approximately 10%.
• Experimental results validate the conclusions drawn from numerical simulations. Aluminum depositions produced with the dual-path nozzle exhibit larger diameters and heights compared to those produced with a single internal channel nozzle, resulting in an actual deposition efficiency increase of approximately 8% and a reduction in porosity by about 1.4%. Scanning electron microscope analysis reveals that the dual-path structure effectively increases particle deformation, thereby reducing porosity and enhancing deposition density and microhardness.
• The dual-path nozzle design proposed in this study enhances deposition efficiency in low-pressure cold spray without requiring additional complex equipment or processes, which is significant for expanding the application of cold spray in additive manufacturing and other fields.

In conclusion, the dual-path nozzle provides a new and effective approach to improving the deposition efficiency of low-pressure cold spray, offering important theoretical implications and practical applications. Future research could focus on investigating the impact of dual-path structures on cold spray behavior with different materials and establishing quantitative relationships between structural parameters and deposition efficiency to further optimize nozzle design.