Knowledge-Based Adaptive Design of Experiments (KADoE) for Grinding Process Optimization Using an Expert System in the Context of Industry 4.0

Abstract

The integration of human–cyber–physical systems (HCPSs), IoT, digital twins, and big data analytics underpins Industry 4.0, transforming traditional manufacturing into smart manufacturing with capabilities for real-time monitoring, quality assessment, and anomaly detection. A key advancement is the transition from static to adaptive design of experiments (DoE), using real-time analytics for iterative refinement. This paper introduces an innovative adaptive DoE embedded in an expert system for grinding, combining data-driven and knowledge-based methodologies. The KSF Grinding Expert™ system recommends optimized grinding control variables, guided by a multi-objective optimization framework using Non-dominated Sorting Genetic Algorithm II (NSGA-II) and Gray Relational Analysis (GRA). The rule-based adaptive DoE iteratively refines recommendations through feedback and historical insights, reducing the number of trials by excluding suboptimal parameters. A case study validates the approach, demonstrating significant enhancements in process efficiency and precision. This knowledge-based adaptive strategy reduces experimental trials, adapts DoE according to different grinding processes, and can prevent critical defects such as surface cracks. In the case study, optimized results which are offered by the expert system and validated with over 90% accuracy are incorporated into the system’s knowledge base, enabling continuous improvement and reduced experimentation in future iterations.

1. Introduction

The concept of Industry 4.0, which originated in Germany [1], represents the fourth industrial revolution aimed at achieving smart autonomous production through the integration of information and communication technologies with manufacturing activities [2,3]. Industry 4.0, often referred to as smart manufacturing, brings together human–cyber–physical systems (HCPSs) [4,5] using IoT-driven technologies, digital twins, and big data analytics. 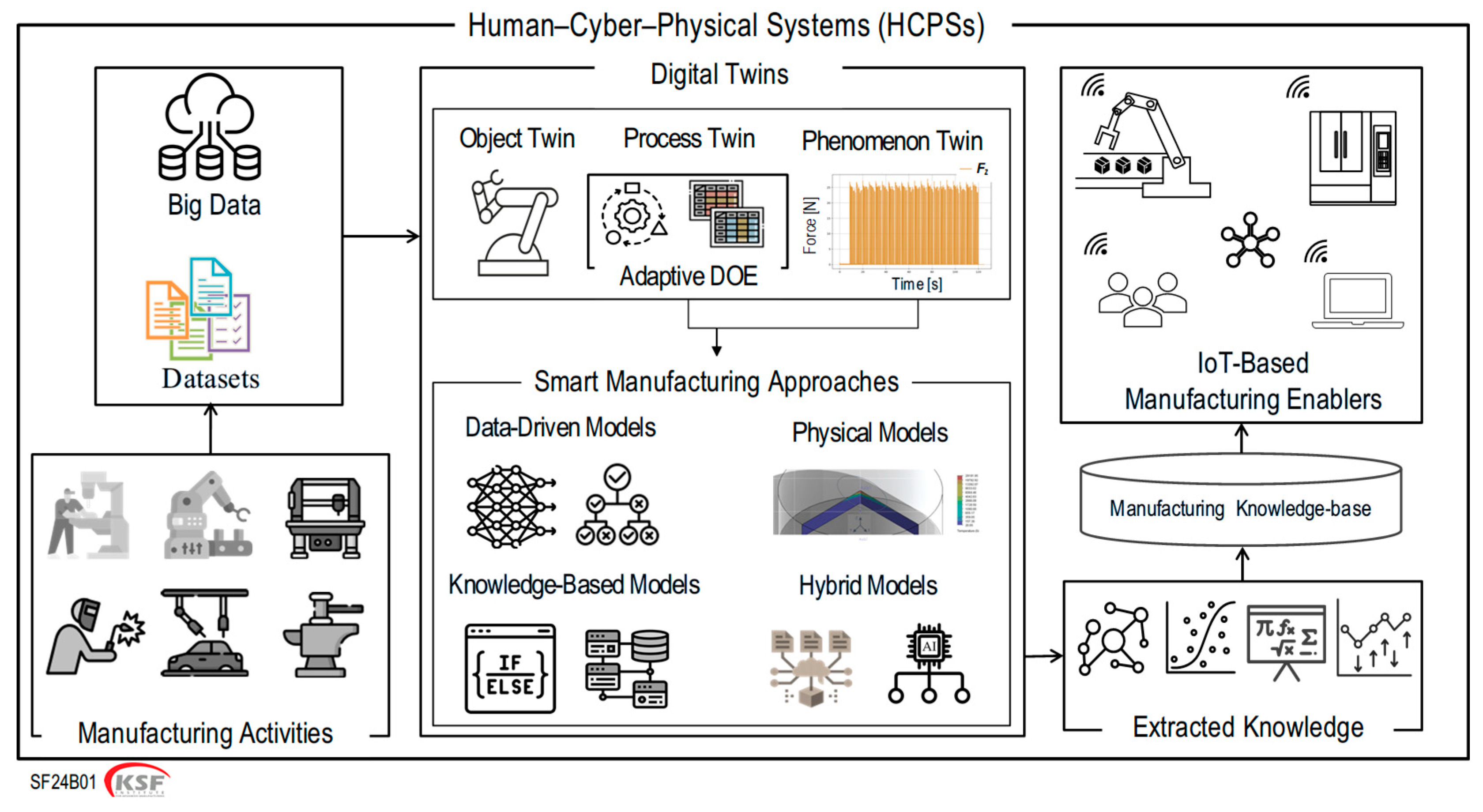It seamlessly links conventional manufacturing tools like CAD/CAM systems, CNC machines, and robotics into a unified IoT network, creating a more interconnected and intelligent production environment [6,7]. Digital twins, key components of Industry 4.0, are categorized into three main types: object twins, representing physical entities like tools or workpieces; process twins, simulating manufacturing processes in real time; and phenomenon twins, modeling underlying physical behaviors such as force dynamics or thermal effects [8]. These categories are essential for facilitating real-time monitoring and enhancing the optimization of machining processes [9,10], such as grinding—a critical stage in high-precision manufacturing [11]. The application of smart manufacturing systems in machining [12] introduces advanced capabilities such as real-time data analysis and quality assessment [13,14], optimization, and anomaly detection, enhancing both efficiency and product quality [9]. Online monitoring modules detect and assess the specific working conditions of the machine tool, tool, and workpiece in real-time [15].

Grinding, a widely employed machining process, benefits greatly from such advancements. As a critical step in producing high-quality products, grinding involves complex dynamics that make monitoring and parameter optimization particularly challenging [16]. Within these smart manufacturing systems, quality prediction and process monitoring are essential for optimizing grinding performance. This includes surface roughness monitoring and prediction [17,18], as well as process parameter optimization to achieve the best combination of evaluation variables such as surface roughness, material removal rate (MRR), and force [16,19,20]. In addition, online process monitoring for excessive heat generation during grinding can play a crucial role in anomaly detection, as it helps identify potential process deviations that could lead to surface burns, thermal damage, or residual stresses. Such monitoring systems have been shown to be highly effective in mitigating these issues, as highlighted in recent studies on thermal modeling and real-time temperature monitoring in grinding processes [21]. Design of experiments (DoE), like response surface methodology and Taguchi methods, are extensively utilized in grinding and are regarded as the benchmark for optimization in industrial experiments [22,23]. However, these traditional DoE techniques perform well when relationships between process parameters and outcomes are simple [24]. However, these methods face limitations in complex grinding processes due to nonlinear dynamics between parameters and desired results. Adaptive design of experiments (ADoE) dynamically adjusts experimental parameters based on outcomes from earlier trials, significantly reducing the number of tests required [25,26,27]. This approach contrasts with traditional DoE, which relies on a predetermined and unchanging set of conditions throughout the process [28]. Incorporating ADoE into process twins allows the systematic experimentation to be enhanced by real-time adjustments, enabling smart manufacturing systems to respond dynamically to process variations. In the concept of ADoE, the systematic experimentation will be enhanced by allowing for real-time adjustments based on process feedback, thus improving the adaptability and responsiveness of manufacturing systems [29]. Since autonomy and adaptability are important in smart manufacturing systems, the transition from static traditional DoE methods to adaptive DoE is crucial for enabling dynamic, real-time optimization and improved responsiveness to process variations.

Within the context of smart manufacturing systems, AI-based approaches have shown strong performance in tasks like anomaly detection, classification, and quality prediction. As a result, these approaches can be integrated into adaptive DoE. These approaches are categorized into four groups: data-driven, physical, knowledge-based, and hybrid models. Proper method selection is crucial for effective implementation in Industry 4.0 [30]. Figure 1 illustrates how HCPSs connect with various smart manufacturing approaches. It highlights the role of digital twins, the use of real-time datasets, and the interplay between different modeling strategies in guiding adaptive experimentation. By situating adaptive DoE within this holistic ecosystem, the figure provides a conceptual roadmap for understanding the subsequent sections of this research.

Data-driven models, including deep learning and machine learning, are particularly well suited for smart manufacturing systems because of their flexibility, scalability, and ability to perform sophisticated analytics [31,32,33]. These models excel at identifying intricate patterns within large datasets and can continuously enhance their performance as additional data are introduced. They are adept at managing the massive volumes of data generated by multiple sensors and IoT devices, supporting real-time decision-making, predictive maintenance, quality assurance, and process refinement. However, these models come with challenges, such as the need for high-quality, labeled data, significant computational power, and specialized technical knowledge. On the other hand, rule-based systems are simpler and more straightforward, relying on predefined rules based on expert knowledge. This makes them easier and faster to deploy, as they do not require extensive datasets or advanced computational infrastructure [34]. The importance of the use of these systems will be more significant when we want to address the "black-box" nature of algorithmic systems in data-driven approaches [35,36]. There is a growing emphasis on developing fair, transparent, and accountable algorithmic decision-making processes. Knowledge-based methods, which utilize expert systems and ontologies to encode manufacturing knowledge, are inherently aligned with rule-based systems. These methods have the potential to mitigate data inequality and the black-box problem in sophisticated machine learning and AI-driven decision-making approaches. Knowledge-based and rule-based systems play a crucial role here by providing a structured approach to data analysis and decision-making, ensuring consistency and reliability in the interpretation of data streams [37]. These systems facilitate the extraction and formalization of manufacturing rules from unstructured text, enabling early manufacturability feedback and enhancing the reliability of knowledge representation [38].

The following literature review summarizes scholarly works in the areas of decision-making systems in smart manufacturing, design of experiments (DoE) and its application in manufacturing systems, knowledge-based and rule-based systems in smart manufacturing, adaptive systems in smart manufacturing, and adaptive DoE systems.

In the domain of decision-making systems in smart manufacturing, various approaches have been explored to optimize manufacturing performance. Kim et al. [16] developed a data-driven system using machine learning and metaheuristic algorithms to optimize grinding parameters, achieving a 77.83% reduction in fault rates and a 17.64% decrease in cycle time. Similarly, Helu et al. [34] utilized IIoT-based real-time data analysis and control-feedback loops, resulting in a 20% reduction in downtime and a 15% increase in resource utilization. These studies highlight the effectiveness of integrating data-driven approaches with real-time monitoring to enhance decision-making in smart manufacturing. Ghosh et al. [6] developed a big data analytics system for machining decision-making in smart manufacturing, optimizing dry EDM processes by identifying key variables such as current and voltage, which improved material removal rates and reduced tool wear. These studies highlight the effectiveness of integrating data-driven and advanced modeling approaches with real-time monitoring to enhance decision-making in smart manufacturing. Fattahi et al. [39] proposed a novel decision-making framework that uses two-dimensional plots from big data as decision-relevant information. This approach effectively addresses scenarios where traditional numerical decision-making methods fall short, offering a graphical approach to evaluating alternatives based on multi-criteria objectives.

Another crucial methodology in smart manufacturing is the design of experiments (DoE), which plays a pivotal role in optimizing experimental efficiency. Tanco et al. [40] identified a gap in industrial applications of DoE, noting that while 95% of industries conduct experiments, only 20% employ formal DoE methods. Jankovic et al. [22] demonstrated that definitive screening designs can achieve similar accuracy to full factorial designs with 30% fewer experimental runs, showcasing the potential for more efficient DoE applications in complex manufacturing processes.

In addition to data-driven decision-making and experimental optimization, knowledge-based and rule-based systems offer structured frameworks for enhancing reliability and interpretability in manufacturing. Cao et al. [30] introduced a hybrid system combining statistical AI and symbolic AI for predictive maintenance, significantly improving anomaly detection and failure prediction accuracy. Grosan and Abraham [35] emphasized the adaptability of rule-based systems through IF-THEN logic, which ensures consistent and interpretable decisions. Pérez et al. [41] proposed an adaptive neuro-fuzzy inference system (ANFIS) for modeling experimental data in manufacturing engineering, outperforming conventional methods in handling nonlinearities. These systems address the “black-box” limitations of purely data-driven models, promoting fairness and accountability in manufacturing decision-making [36,37,38].

The increasing complexity of manufacturing environments has led to the development of adaptive systems that dynamically respond to changing conditions. Jin et al. [42] developed an adaptive process planning approach for rapid prototyping, reducing build time and improving geometrical accuracy. Pellicciari et al. [43] designed adaptive manufacturing lines with mechatronic integration and virtual commissioning tools, resulting in improved system adaptability. Moreno et al. [44] focused on uncertainty reduction in self-adaptive systems, enhancing reliable decision-making in dynamic environments.

Building upon adaptive methodologies, adaptive DoE systems have emerged as a powerful tool for improving experimental design robustness. Kaneko [28] utilized Gaussian mixture regression for high-dimensional adaptive experiments, while Da Ronch et al. [45] applied adaptive DoE to aerodynamic load estimations, balancing exploration and accuracy. Caparini et al. [46] introduced a gradient-based adaptive DoE methodology resistant to noise, enhancing robustness in unreplicated experiments. Picheny et al. [47] developed methods for accurately approximating target regions, improving reliability in constrained optimization. Fiez et al. [48] addressed challenges in industrial adaptive experimental design under non-stationarity, creating a framework for counterfactual inference to enhance A/B/N testing efficiency. Foster et al. [49] introduced Deep Adaptive Design (DAD) to reduce the computational cost of Bayesian experimental design, facilitating rapid real-time decision-making. Despite these advancements, integrating rule-based logic into adaptive DoE remains underexplored, presenting an opportunity for enhancing transparency and fairness in complex machining processes like grinding.

While substantial research exists on DoE and data-driven decision-making in smart manufacturing, most studies focus on static DoE frameworks that do not dynamically refine experimental conditions based on real-time feedback. Additionally, purely data-driven approaches often function as black-box models, limiting interpretability and adaptability in industrial applications. There is a notable gap in integrating rule-based and knowledge-based systems within adaptive frameworks, which would enable a transparent and expert-driven decision-making process. This study addresses these limitations by developing a rule-based adaptive DoE methodology tailored for grinding process optimization, ensuring real-time responsiveness and systematic knowledge integration. By incorporating expert-driven rules, AI-based predictions, and iterative experimental refinement, the proposed approach enhances efficiency, precision, and adaptability compared to traditional static DoE methods. Moreover, this framework improves explainability in AI-driven decision-making, making it more applicable to real-world industrial environments. These advancements align with Industry 4.0 objectives, supporting smart, autonomous, and knowledge-driven manufacturing systems.

The subsequent section introduces the structure of the “KSF Grinding Expert™ system”, detailing its components and capabilities in integrating real-time data feedback. Following this, the adaptive DoE structure is described in the context of the expert system, with an emphasis on the integration of rule-based and data-driven approaches. Finally, a case study is presented that demonstrates the application of this adaptive DoE framework to a flat grinding process, highlighting its practical implementation and outcomes.

2. KSF Grinding Expert™ System: A Comprehensive Overview

While there are established solutions for process planning and cutting parameter recommendations in other machining processes such as milling [50,51] and turning [52,53], the complex nature of grinding processes has prevented the development of comprehensive solutions for this purpose [54,55]. Since errors in grinding can lead to significant financial losses, these processes are typically performed by experienced machine operators [56].

In many cases, grinding parameters are determined either through the expert’s experience or by trial and error, and often do not represent the optimal processing conditions [57]. Additionally, the selection of grinding and dressing tools, process fluid, workpiece clamping systems, and appropriate dressing and grinding parameters plays a crucial role in achieving optimal results [58]. Machine operators without sufficient experience in grinding technology often find these decisions overwhelming. Consequently, they tend to rely on grinding and dressing tools, process parameters and methods that have been traditionally used for similar workpieces or recommended by tool manufacturers [59]. Evaluating grinding errors on workpieces is also a significant challenge for most operators. To address these challenges, an expert system for grinding processes was developed at KSF Institute for Advanced Manufacturing. This system provides optimal support for the design and execution of grinding processes, achieving excellent results by recommending suitable grinding wheels, grinding parameters, dressing tools, and dressing parameters. Additionally, it includes a troubleshooting module for correcting errors in faulty grinding processes.

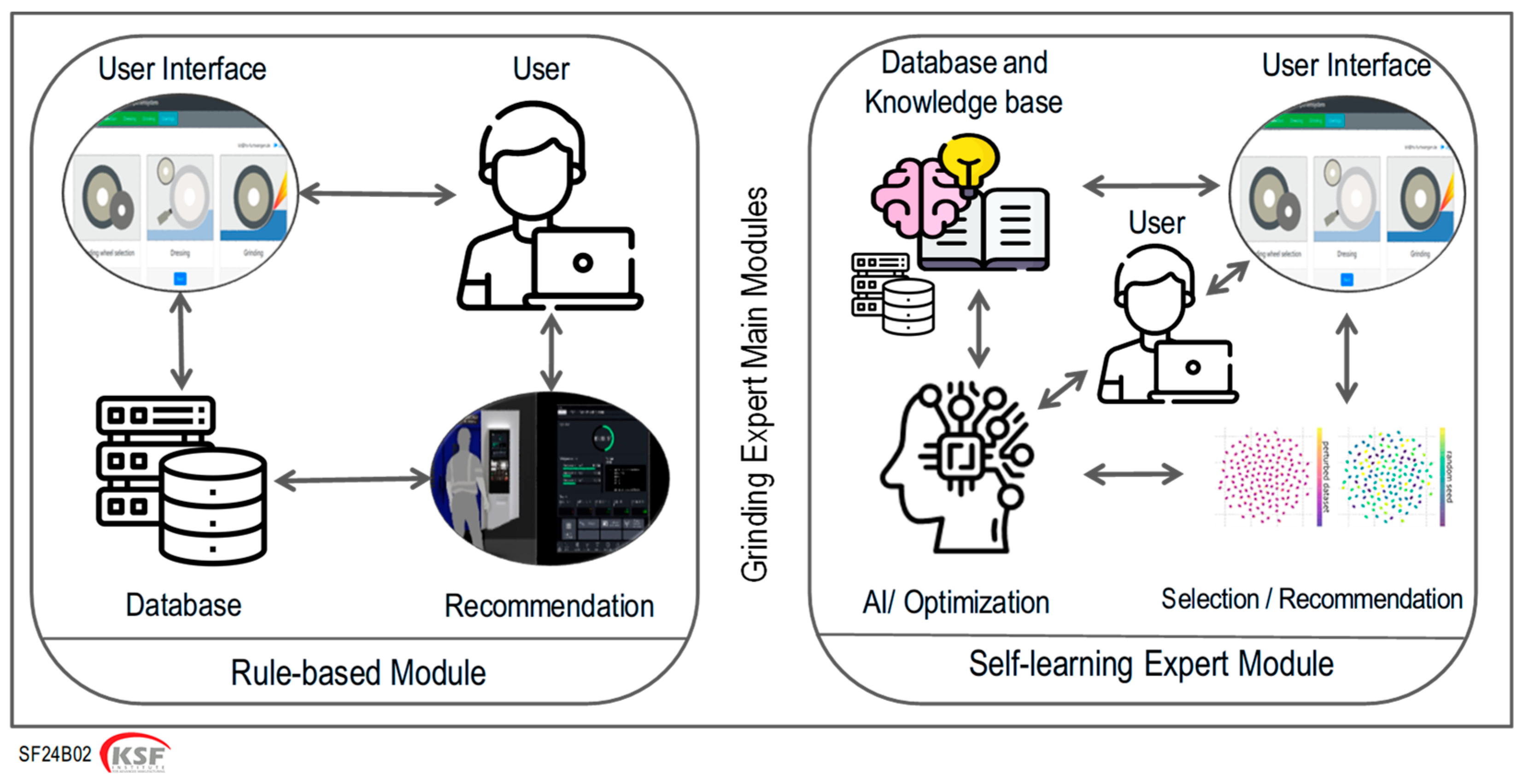
The KSF Grinding Expert™ system [55,60], designed primarily for grinding process planning and parameter recommendations, consists of two primary modules: the rule-based module and the self-learning expert module, as illustrated in Figure 2. These modules based on a hybrid model approach enhance decision-making, enable adaptive experimentation, and optimize grinding processes in smart manufacturing environments. By integrating human expertise, data-driven insights, and real-time adaptability, the system achieves exceptional results.

2.1. Rule-Based Module

The rule-based module serves as the foundational decision-support layer of the KSF Grinding Expert™ system. This module uses a structured database and expert knowledge encoded into IF-THEN rules (a knowledge base) to provide reliable recommendations for grinding parameters.

2.1.1. Key Features of Rule-Based Module

The module offers several essential functionalities to enhance the grinding process. It suggests optimal dressing and grinding tools and parameters to achieve the desired process outcomes, ensuring efficient and high-quality performance. Additionally, a user-friendly interface allows users to input process requirements, review system recommendations, and refine parameter selections as needed, making the system interactive and adaptable. To further improve decision-making, the module utilizes historical data to validate and refine rule-based recommendations, ensuring consistent and reliable performance over time.

2.1.2. Example of Application

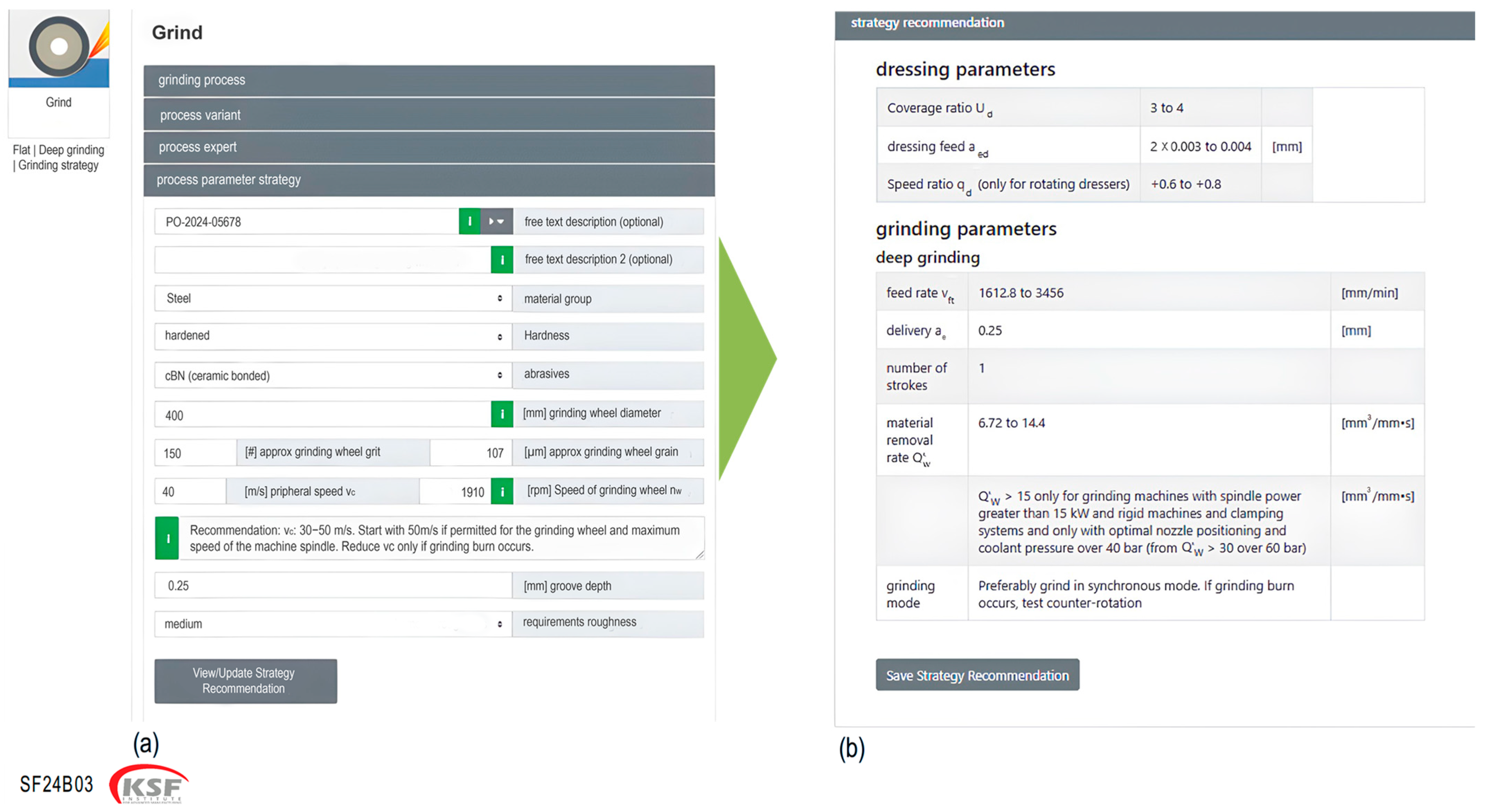
Figure 3 illustrates an example of the practical application of the rule-based module within the KSF Grinding Expert™ system. The system features a user input interface (Figure 3a), where parameters for a flat (deep) grinding operation on hardened steel are specified. The grinding wheel selection module within the software generates a suitable wheel specification based on the process requirements. In this case, the workpiece material is hardened steel, and the selected grinding wheel is a cBN vitrified-bonded type with a 400 mm diameter and a grain size of 107 µm (#150). The wheel peripheral speed is set to 40 m/s, ensuring optimal cutting conditions. The process is designed to achieve a medium surface roughness, with a groove depth of 0.25 mm, meeting the defined quality standards.

Upon receiving these inputs, the system’s knowledge base generates process strategies and recommendations for both grinding and dressing processes (Figure 3b). Notably, the rule-based module also incorporates definitional knowledge [61] regarding material removal rate (Q′_w) and grinding mode limits. The key dressing parameters include an overlap ratio (U_d) of 3–4, a dressing depth of cut (a_ed) of 0.003–0.004 mm, and a dressing speed ratio (q_d) of +0.6 to +0.8 for rotating dressers. Recommended grinding parameters entail a workpiece feed rate (v_ft) of 1612–3456 mm/min, a single-pass depth of cut (a_e) of 0.25 mm, and a material removal rate (Q′_w) ranging from 6.7 to 14.4 mm³/mm/s, which requires spindle power above 15 kW and coolant pressure exceeding 40 bar. The module’s detailed notes on spindle power and coolant pressure further ensure safe and efficient operation, helping to reduce process-related risks and enhance productivity.

2.2. Self-Learning Expert Module

The self-learning expert module forms the advanced layer of the KSF Grinding Expert™ system, designed to complement the rule-based module by incorporating data-driven methods and adaptive optimization strategies. Unlike the rule-based approach, the self-learning expert module leverages machine learning and multi-objective optimization to analyze process-specific data, enabling the customization of parameters for different machine types, clamping systems, and process fluids. This module ensures continuous improvement and adaptability through iterative feedback mechanisms, allowing for a precise definition of surface quality and material removal rates tailored to each unique grinding process. By utilizing advanced analytics and real-time data integration, the self-learning expert module overcomes the limitations of the rule-based system, providing a more flexible, scalable, and accurate solution for optimizing grinding operations. This hybrid approach combines the simplicity and consistency of rule-based systems with the adaptability and deep analytical capabilities of data-driven models, resulting in enhanced efficiency, improved product quality, and optimized process times in smart manufacturing environments.

2.2.1. Key Features of Self-Learning Expert Module

Figure 4 illustrates the structure and functionality of the self-learning expert module, which is designed to enhance process optimization through adaptive experimentation, predictive modeling, multi-objective optimization, and continuous learning. The system begins by employing an adaptive design of experiments (DoE) to systematically explore the parameter space. By defining the range of control variables (CVs) relevant to the dressing and grinding process—such as cutting speed, feed rate, and depth of cut—the system ensures comprehensive experimentation. This structured approach facilitates data collection while capturing the influence of varying process conditions.

2.2.2. Process Workflow

Once the experimental data are gathered, predictive models are developed to estimate evaluation variables (EVs), including surface roughness, material removal rate, and tool wear. In this part, various machine learning techniques, such as linear regression and random forest regression, could be employed to capture the relationships between control variables and evaluation outcomes. This modeling step enhances the system’s ability to predict process performance accurately. The system applies Non-Dominated Sorting Genetic Algorithm II (NSGA-II) to identify optimal trade-offs between conflicting objectives, such as maximizing material removal rate while minimizing surface roughness. A recommended dataset is generated, showcasing pareto-optimal solutions for users to evaluate and implement. For systematic decision-making, the recommended solutions are ranked using Gray Relational Analysis (GRA). This ranking aids in selecting the most suitable parameter combinations, offering a structured approach for decision-making. A key feature of the expert module is its feedback adaptation capability. The module incorporates user feedback and real-world validation data to refine its models and recommendations iteratively. This adaptive mechanism ensures that the system evolves with new data, maintaining its relevance and accuracy in dynamic manufacturing environments.

Figure 5 shows an example how feedback adaptation enhances the self-learning expert system by using real-time test outcomes—such as surface cracks and burns—to update its rule-based logic. Whenever critical conditions occur, they are detected and integrated into the knowledge base, enabling the system to refine its decision-making as new data are validated.

This iterative process ensures that the rule-based system remains responsive to changing conditions, continuously improving its accuracy and relevance. By tracking unsafe parameter combinations (e.g., excessive cutting speeds or material removal rates) and adding them as constraints or refining parametric models, the system proactively mitigates future failures. This approach enables ongoing optimizations in manufacturing efficiency, product quality, and process safety.

3. Knowledge-Based Adaptive Design of Experiments (KADoE)

The knowledge-based adaptive design of experiments (DoE) is a systematic methodology embedded within the KSF Grinding Expert™ system, integrating simple, but effective rule-based logics with dynamic experimental design. As illustrated in Figure 6, the process starts with the selection of the grinding process and wheel. This is followed by consulting a comprehensive knowledge base comprising historical data, best practices, and predefined DoE matrices. The methodology dynamically adjusts the number of control variables (e.g., grinding and dressing parameters) based on the selected grinding process. The system then generates a tailored initial DoE matrix. For example, if the process has been defined with three control variables, a four-row DoE matrix is deployed, while for four to seven control variables, an eight-row matrix is used. These matrices are designed to minimize the number of trials required for effective, data-driven learning. After generating the initial DoE matrix and removing any redundant or repetitive experiments, the user conducts the prescribed experiments to gather evaluation variables such as surface roughness and spindle power. During this phase, any critical conditions, such as cracks or burns, are flagged by the system, triggering immediate refinement of the DoE matrix or removal of problematic runs from future experiments. If the total number of experiments—considering flagged tests and those already included in the knowledge base—falls below the predefined minimum, the system prompts the user to adjust the control variable ranges (minimum and maximum) to generate a new DoE matrix. This process operates iteratively through a rule-based feedback mechanism. The iterative refinement continues until a stable and reliable set of experiments is achieved. Subsequently, advanced machine learning and optimization techniques validate the results. Once confirmed, the newly discovered parameter boundaries, process rules, and insights are added to the knowledge base. This ensures that future DoE iterations remain accurate, efficient, and relevant in guiding high-quality grinding outcomes.

Hence, the adaptive DoE ensures the reduction in redundant or unsafe experiments, continuous improvement of the knowledge base, and reliable, efficient process optimization by leveraging feedback-driven, data-driven insights. By emphasizing iterative learning and dynamic adaptation, this methodology offers precise control over dressing and grinding parameters and fosters robust decision-making in industrial environments, ultimately enhancing product quality and operational efficiency.

Figure 7 illustrates an example of how the adaptive DoE system dynamically refines experimental designs based on user objectives and knowledge-based feedback within the KSF Grinding Expert™ system after receiving the optimized levels within the self-learning expert system. Users begin by choosing an optimization goal, e.g., balanced, best roughness, highest material removal rate, or lowest force. In response, the self-learning expert system generates optimized parameter suggestions that are either tested or excluded if they already exist in the knowledge base. As new experiments are completed, their data—such as material removal rate (Qʹ_W) or surface roughness (R_a)—are continuously integrated into the knowledge base, preventing redundant tests and leveraging historical insights. The feedback loop then refines the DoE matrix; if fewer than five experiments remain after filtering, users are prompted to redefine or add variables to maintain robust testing coverage. Subsequently, a revised DoE matrix is produced, combining both system knowledge and user preferences. Optimized outcomes—validated through the expert system—are finally presented to the user with precise, goal-specific recommendations.

In practice, this rule-based adaptation delivers three significant benefits. Dynamic refinement is achieved as iterative feedback ensures that parameters evolve over time, continuously improving quality and efficiency. Additionally, knowledge utilization plays a crucial role by combining historical data with current results, effectively eliminating unnecessary experiments and accelerating the optimization process. Finally, the system offers user-centric flexibility, seamlessly adapting to varied objectives while balancing surface quality, productivity, and resource utilization.

4. Case Study: Performing Flat Grinding Tests Within KSF Grinding Expert™ System

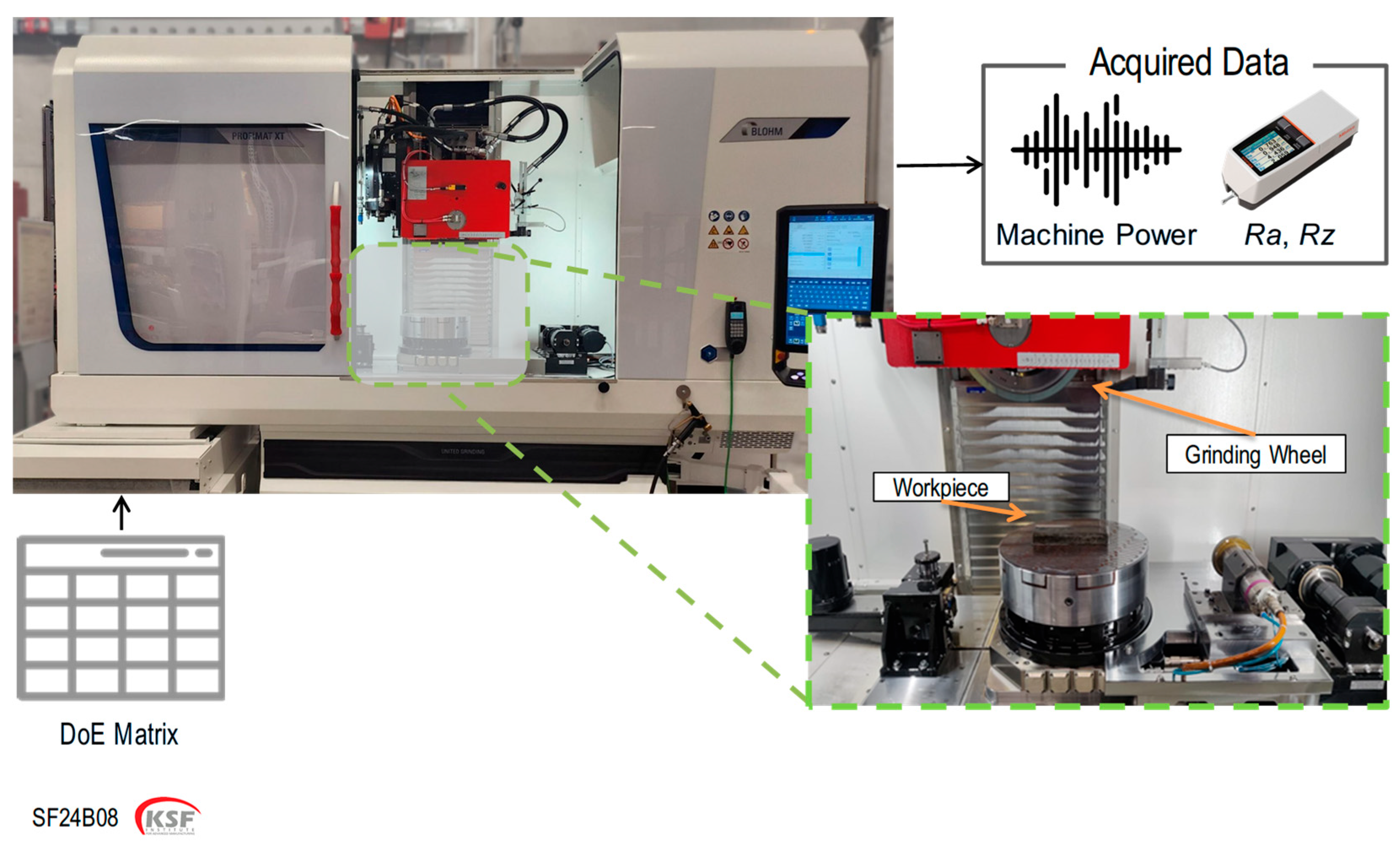
To evaluate the practical application of the KADoE methodology integrated into the KSF Grinding Expert™ system, a series of flat grinding tests was planned and conducted using a CNC high-speed high-power Blohm flat grinding machine according to the initial DoE matrix obtained from KSF Grinding Expert™. The experimental setup is shown in Figure 8. The primary goal was to validate how the system’s iterative, rule-based, and hybrid approaches adapt process parameters in DoE. After performing tests, machine power and surface roughness values were measured, and according to the procedure mentioned in Figure 6, the critical areas (if any) could be included in the knowledge base in order to refine the next DoE. These values will also be included in the self-learning expert system for offering optimized values.

Table 1. Machine and grinding wheel specifications for performing the case study.

Machine Parameter	Specification
Grinding Machine	Blohm PROFIMAT XT
Grinding wheel	Vitrified cBN-B91C100
Workpiece	42CrMo4b–(60 HRC)-100 × 50 × 20
Dresser	Rotary Diamond Dresser (D426 G)
Coolant	Grinding Oil
Control variables	Depth of Cut (ae) [mm], Grinding Wheel Speed (vc) [m/s], Workpiece Feed Rate (vw) [mm/min], Overlap Ratio (Ud), Dressing Speed Ratio (qd)
Evaluation variables	Spindle Power (P) [W], Surface Roughness Ra [µm], Rz [µm]

summarizes the machine setup and parameters used to perform this case study. Blohm PROFIMAT XT served as the grinding machine, paired with a vitrified bonded cBN grinding wheel (B91C100) and a rotary diamond dresser (D426 G). The workpiece material was 42CrMo4b with 60 HRC, with dimensions of 100 × 50 × 20 mm, and grinding oil was used as the process fluid to manage heat and friction. The workpiece was pre-ground, and during the grinding process for each experiment, pre-grinding was repeated under the same conditions to ensure consistency.

For each type of grinding process, the system’s knowledge base already includes the most significant control variables, ensuring that the optimization process focuses on the most impactful parameters. In this study, the key control variables include depth of cut (a_e), grinding wheel speed (v_c), workpiece feed rate (v_w), dressing overlap ratio (U_d), and dressing speed ratio (q_d). These variables were adjusted to explore their impact on key evaluation variables such as spindle power (P) and surface roughness (Ra, Rz).

Figure 9 presents the self-learning expert module within the KSF Grinding Expert system, structured into four key domains: grinding parameter domain, control variable domain, doe and test result domain, and optimization domain. Each domain communicates bi-directionally with the system’s knowledge base, which stores and updates the rule sets. This knowledge base subsequently delivers adaptive guidance and feedback through the user interface. By using this cyclical flow of information, the system continually refines its recommendations based on real-time data, user inputs, and validated test outcomes.

4.1. Domain 1: Grinding Parameter Domain

Within this domain, the user first defines high-level objectives and constraints. For the presented case study, the target surface roughness (Ra) was set to 0.2 µm, and the process selected was flat grinding, and reciprocating grinding was the sub-process. The user also specifies a superabrasive (cBN) wheel with a vitrified bond and a diamond rotary dresser (form roller) under a high removal rate (roughing) condition. Once these parameters are entered, the system’s rule-based logic automatically activates the corresponding datasets in the knowledge base. It can be defined as the following logic rules:

• If the process is flat grinding;
• If the sub-process is reciprocating grinding;
• If the wheel is superabrasive cBN with a vitrified bond;
• If the dresser is a diamond rotary dresser.
  Then, the knowledge-based system retrieves and displays the most relevant control variables for the next phases of the workflow.

4.2. Domain 2: Control Variable Domain

This domain presents the control variables relevant to the specific configuration selected in Domain 1. Once the user has identified flat grinding, reciprocating grinding, superabrasive cBN wheel with vitrified bond, and rotary dresser, the system’s rule-based engine automatically displays the associated control variables—namely depth of cut (a_e), grinding wheel speed (v_c), workpiece feed rate (v_w), overlap ratio (U_d), and dressing speed ratio (q_d). At this stage, the user is prompted to define minimum, current, and maximum levels for each variable, which can directly influence the DoE matrix. For instance, in this case study, the user enters v_c = 50 m/s (current), 80 m/s (max); v_w = 10,000 mm/min (min), 17,000 mm/min (current), 25,000 mm/min (max); and a_e = 0.005 mm (min), 0.017 mm (current), and 0.025 mm (max).

Once these values are entered, the system checks its knowledge base to calculate the expected material removal rate and other performance indicators. If the inferred risk of grinding burn or part damage is high (based on if–then rules), it issues an alert, allowing the user to either proceed at their own risk or adjust the control variables. This interactive feedback loop constitutes a second layer of rule-based adaptation, where the user can refine input parameters in real time. After acknowledging or resolving any warnings, the user also entered the current used dressing overlap ratio (U_d) = 2.4 and the dressing speed ratio (q_d) = 0.7. All these inputs collectively shape the subsequent DoE and guide the system toward an optimized, safe operating window.

4.3. Domain 3: DoE and Test Result Domain

This domain involves generating experimental plans based on the two rule-based adaptations described in Domains 1 and 2. Once the system confirms the high-level objectives and accepts or modifies the chosen control variables, it selects the most suitable DoE template from its knowledge base. The experiments could then be carried out, and the corresponding evaluation variables—in this case, surface roughness and force—could be recorded.

In this particular case study, Test #4 (v_c = 50 m/s; v_w = 25,000 mm/min; a_e = 0.025 mm, U_d = 2 and q_d = 0.8) identified a critical zone with surface cracks, meaning the desired roughness values could not be measured or validated. Consequently, these parameters were not logged by the user, prompting the system’s self-learning mechanism to adapt future DoE templates. By actively avoiding or adjusting parameters known to induce cracks, the next set of experiments focuses on safer operating windows. This iterative process also helps to optimize the grinding process, reducing the total number of subsequent experiments while improving the system’s ability to meet the user’s surface-quality goals.

4.4. Domain 4: Optimization Domain

This domain focuses on refining process parameters based on user-selected objectives and the insights gained from previous domains. In the self-learning module of the grinding expert system, once a critical zone is identified (e.g., high risk of surface cracks), the optimization logic can adapt itself by a fewer number of experiments. In this step, users are presented with four optimization scenarios—balanced, best roughness (we selected this scenario in this case study), highest material removal rate, and lowest force—and can choose the one that best meets their goals. Accordingly, the system computes a set of recommended optimized points and predicts the expected evaluation variables for each scenario. It has to be mentioned that if the system determines that the target value cannot be achieved within the given desired Ra, the system issues an alert to the user, recommending a modification of input constrain.

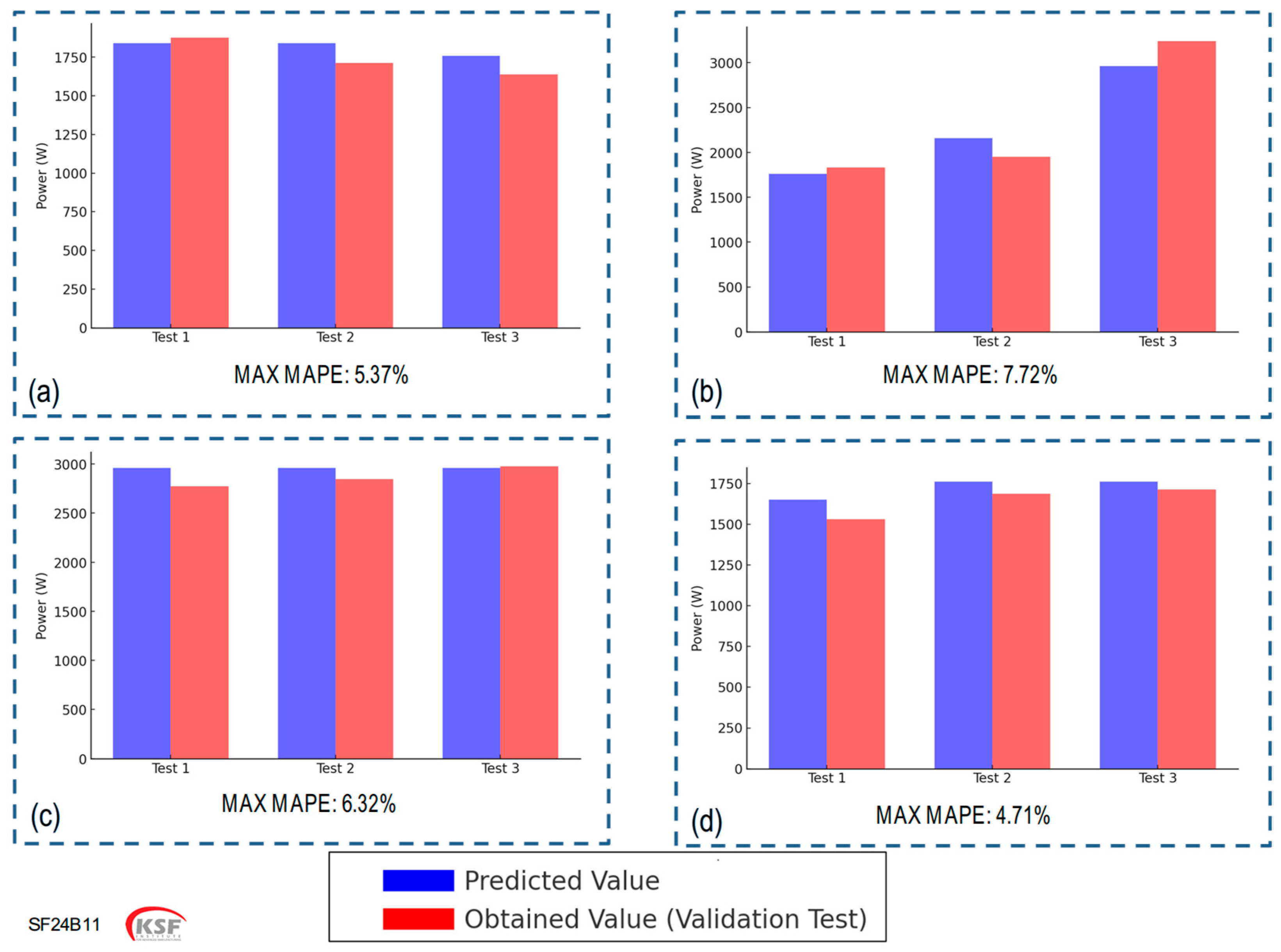
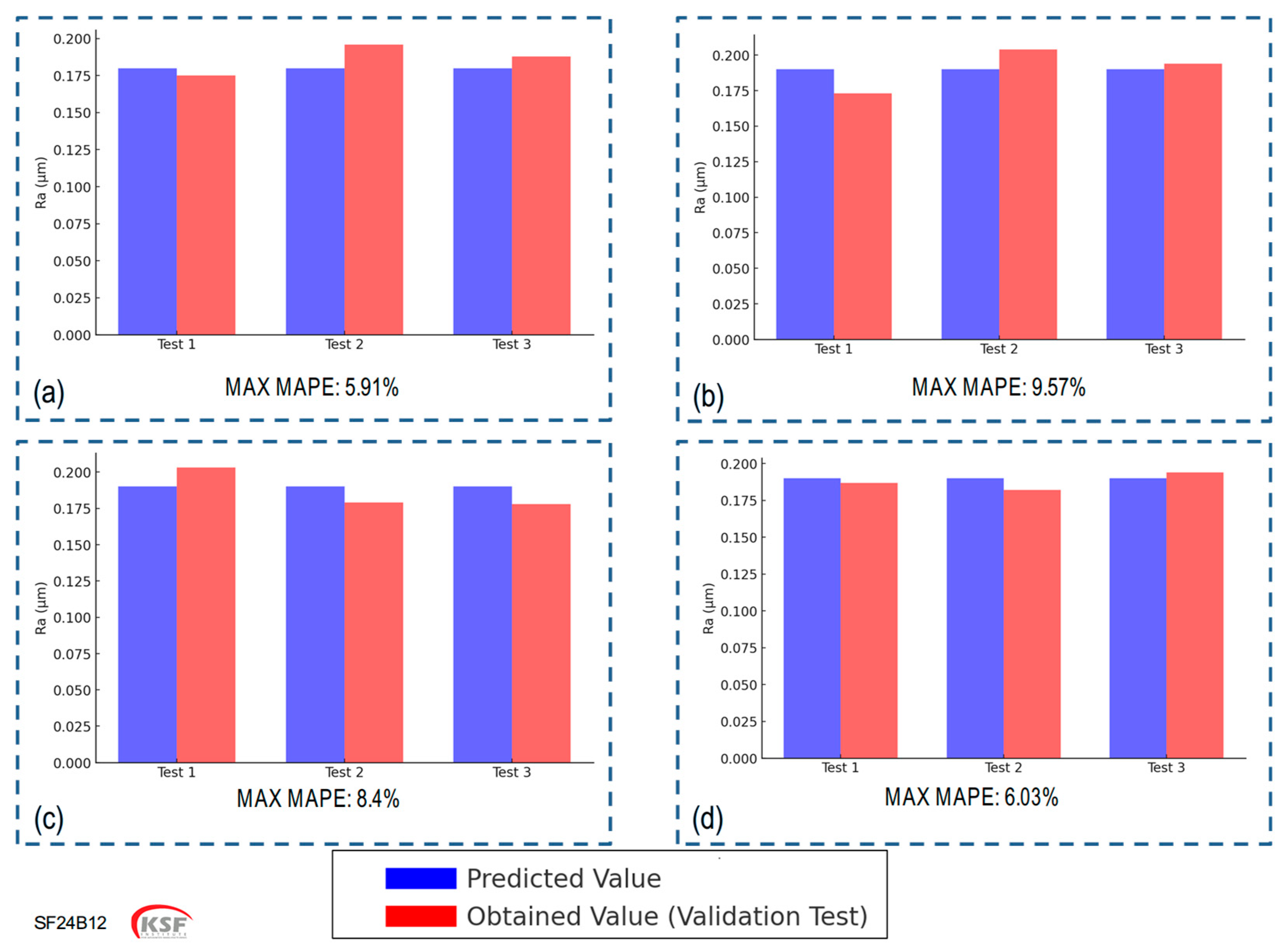
If subsequent validation tests confirm the recommended settings with acceptable accuracy (in this case study, at least 90% agreement with predicted results), the user “approves” the new parameters by clicking a confirmation button. These confirmed results then become a part of the knowledge base, reducing the number of experiments needed in future.

5. Results and Discussion

In the previous section, we comprehensively discussed the performed case study and demonstrated how the knowledge-based DoE methodology successfully contributed to several key aspects. Tailoring the control variable domain was achieved as the system dynamically adjusted the range of control variables based on the selected process, ensuring consistency between user-defined objectives and experimental planning. Furthermore, the adaptive modification of the DoE matrix allowed the system to iteratively refine the experimental setup by optimizing process parameters based on relevant control variables. Another critical aspect was the inclusion of critical conditions, where identified risk zones—such as surface cracks or grinding burns—were integrated into the knowledge base to prevent similar issues in future experiments. Additionally, validated test results were incorporated into the system’s knowledge base, enhancing future DoE adaptations and continuously improving process efficiency. This iterative and adaptive process underscores the core functionality of the KSF Grinding Expert™ system in ensuring both process reliability and optimization.

5.1. Focus on the Optimization Domain

As shown in Figure 10, the optimization domain within the KSF Grinding Expert™ system enables AI-driven decision-making to recommend optimized process parameters across four distinct scenarios. It has to be mentioned that these scenarios are defined for final ranking and selection to select between the datapoints out of multi-objective optimization solutions. Considering defined scenarios, in the balanced optimization approach, equal priority is assigned to surface roughness, material removal rate (MRR), and force, providing a comprehensive strategy that ensures a balance between quality and productivity. Alternatively, the best roughness optimization scenario focuses on minimizing surface roughness, making it particularly suitable for processes where achieving superior surface quality is critical. In contrast, the highest material removal rate optimization prioritizes MRR to maximize efficiency and throughput, which is especially beneficial for roughing operations. Lastly, the lowest force optimization aims to minimize force, thereby reducing tool wear and enhancing process stability.

For each of these scenarios, the system suggests an optimized combination of control variables (e.g., v_c, a_e, v_w, U_d, q_d) tailored to achieve the user-defined goal. These recommendations are presented alongside predicted evaluation variables such as surface roughness (Ra) and spindle power (P), ensuring an informed and data-driven decision-making process.

5.2. Validation and Knowledge-Based Updates

In this case study, the primary goal was not to explore the AI-driven decision-making approach in detail but rather to validate the system’s ability to provide accurate predictions and adapt the knowledge base. The results demonstrated the following:

A threshold of 10% Mean Absolute Percentage Error (MAPE) was defined for the validation tests to be confirmed (corresponding to an accuracy of 90%). The validation process enabled the user to confirm or reject the test results through the system interface, ensuring reliability in the adaptive DoE approach. Figure 11 and Figure 12 illustrate the prediction accuracy for grinding power and surface roughness across the four optimization scenarios, comparing predicted values with the obtained validation test results. As shown in these figures, all 12 validation tests met the predefined accuracy threshold (90% accuracy, MAPE ≤ 10%), with the maximum MAPE values for both power and surface roughness staying below 10%. So, all of these results have been confirmed and the predicted results have been included in the system knowledge base. These results validate the robustness of the adaptive DoE methodology, reinforcing its applicability in real-time manufacturing optimization.

6. Conclusions

This work presented a knowledge-based adaptive DoE (KADoE) methodology for grinding process optimization within the KSF Grinding Expert™ system, demonstrating how domain expertise can be effectively merged with data-driven strategies in an Industry 4.0 environment. By tailoring experimental matrices to the number and range of control variables—and dynamically refining them based on newly acquired data—the proposed approach moves beyond traditional static DoE methods. The rule-based adaptation mechanism ensures that unsafe or redundant parameters, such as those causing surface cracks or other defects, are immediately flagged and omitted from subsequent tests, thereby minimizing resource expenditure while enhancing process reliability.

Through a practical flat grinding case study, the adaptive procedure validated its efficacy in real manufacturing settings: (1) fewer overall trials were required to arrive at stable process windows, (2) previously documented “critical zones” in grinding were systematically avoided, and (3) the system could respond to changing objectives, such as prioritizing surface quality, maximizing material removal rate, or reducing force. The seamless integration of optimization approaches (via NSGA-II and GRA) within a rule-based expert system further underscores the flexibility and robustness of this framework. Also, the validated predicted results (in this case, with the accuracy of more than 90%) became a part of knowledge base and can reduce the number of next DoE trials.

These findings support broader implications for smart manufacturing, illustrating how continuous feedback loops—informed by both historical knowledge and real-time sensor data—can iteratively optimize machining processes. Future work could extend this adaptive DoE methodology to other complex manufacturing scenarios, integrate more sophisticated digital twin models, and incorporate additional evaluation metrics (e.g., thermal effects, power consumption) for truly holistic process optimization in Industry 4.0 contexts.

This study demonstrated the effectiveness of knowledge-based adaptive design of experiments (KADoE) by integrating rule-based decision-making and adaptive DoE principles. Beyond the immediate findings, the integration of adaptive DoE with knowledge-based systems presents broader opportunities for industrial applications. Future research can explore expanding this approach to other machining and manufacturing processes, such as milling, turning, and additive manufacturing, to validate its scalability across different production environments. Additionally, integrating advanced machine learning techniques, including deep learning, Bayesian optimization, and reinforcement learning, could enhance the system’s ability to dynamically adjust experimental conditions while reducing the number of required trials. Finally, to ensure seamless adoption in industrial settings, future work should focus on improving user interaction and decision support systems. The development of explainable AI (XAI) techniques and interactive feedback mechanisms would allow manufacturing engineers to better interpret and trust AI-driven optimization recommendations. By addressing these areas, future research can extend the impact of adaptive DoE in industrial applications, ensuring more reliable, scalable, and efficient process optimization strategies across various manufacturing domains.