Flange Buckling Mechanism in Incremental Shape Rolling of an Automotive-Type Variable Width Component
Abstract
1. Introduction
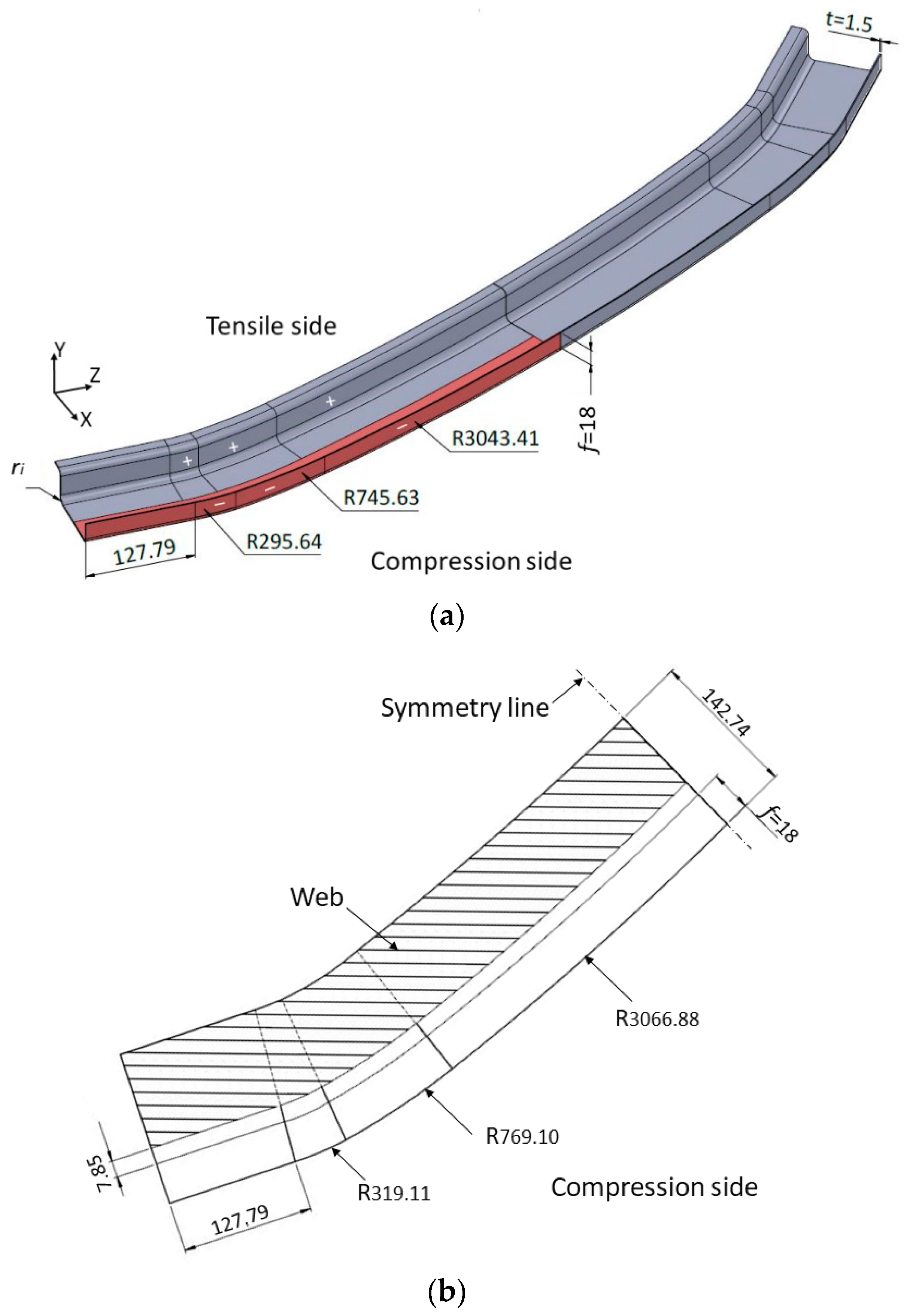
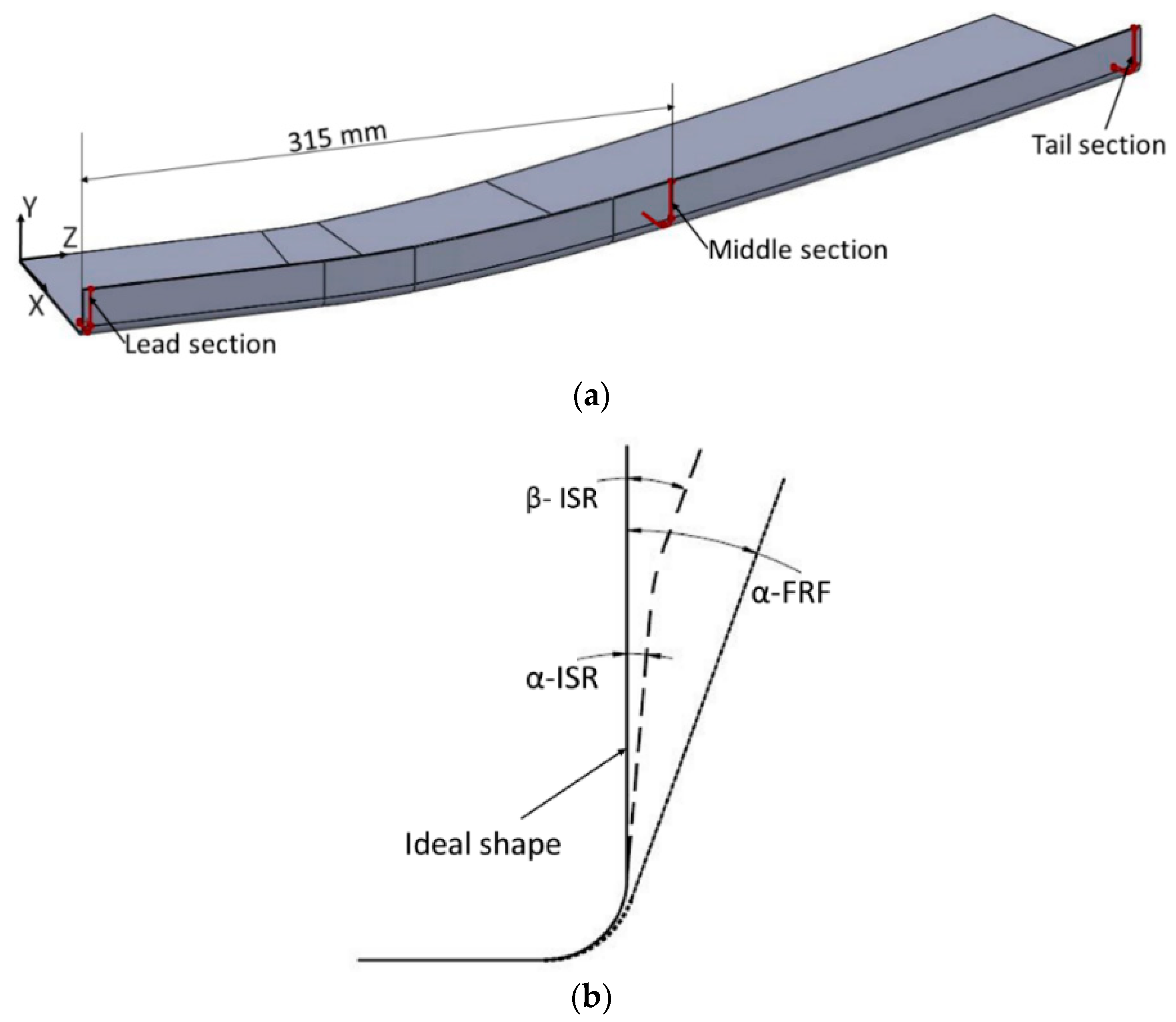
2. Profile Geometry Materials
3. The Experimental Setup
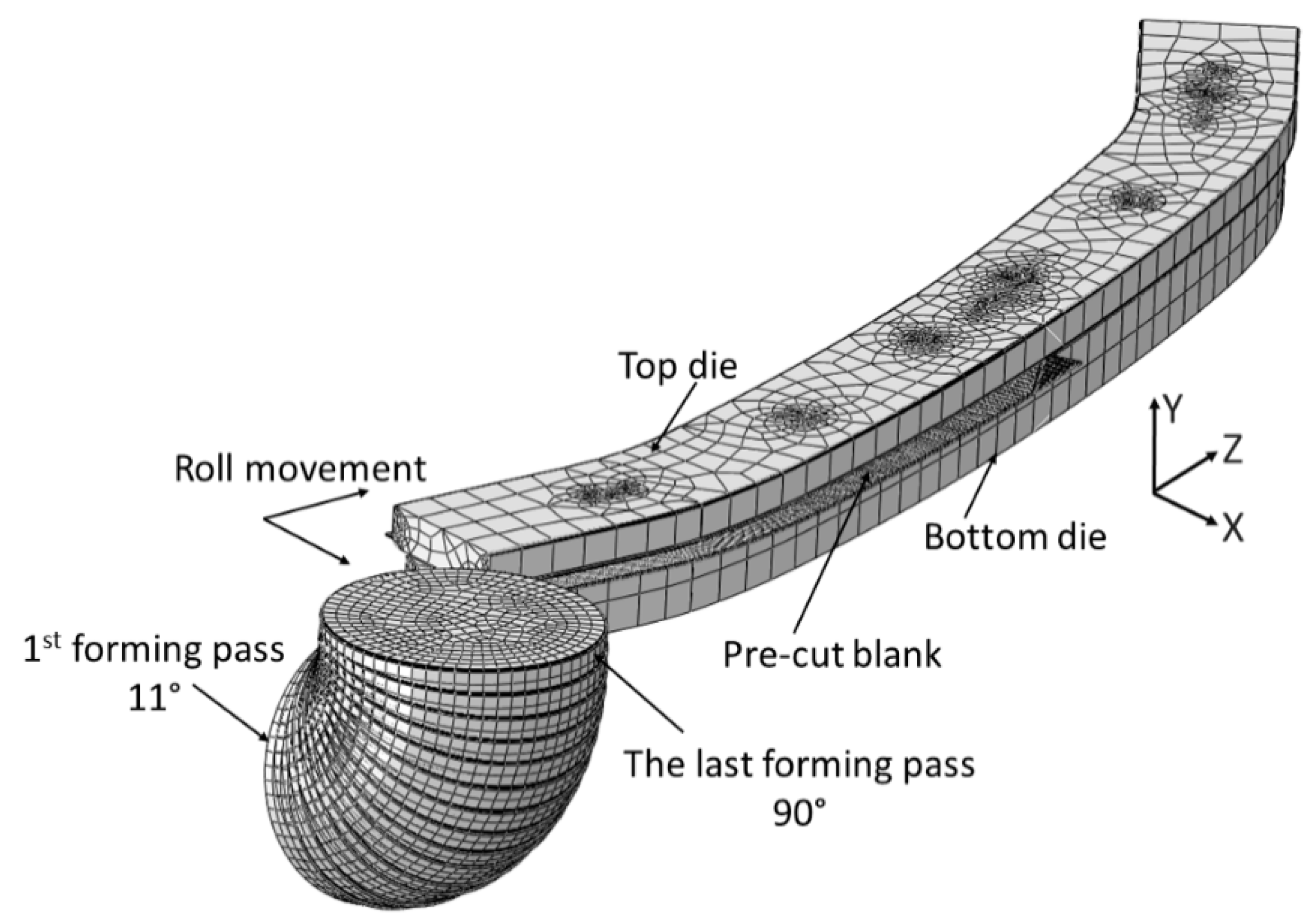
3.1. Incremental Shape Rolling
3.2. Flexible Roll Forming
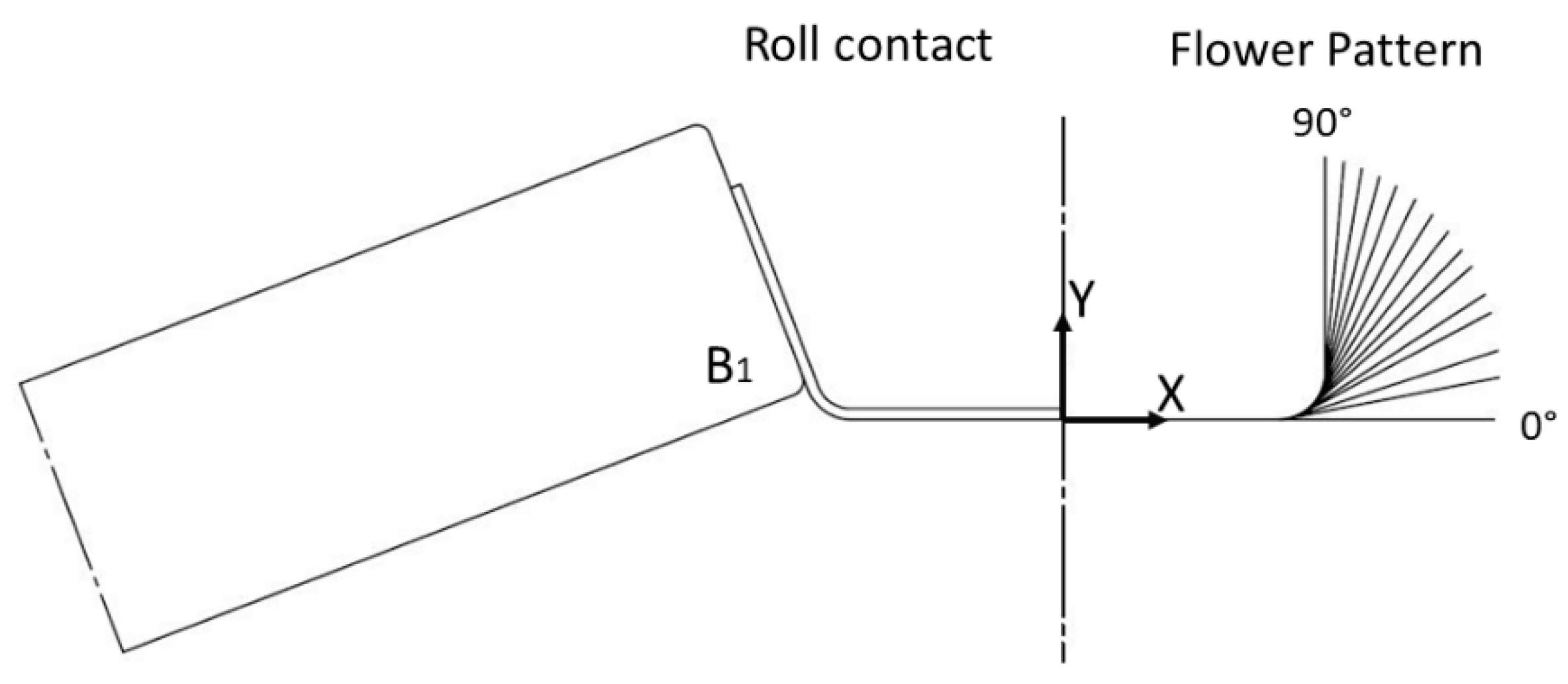
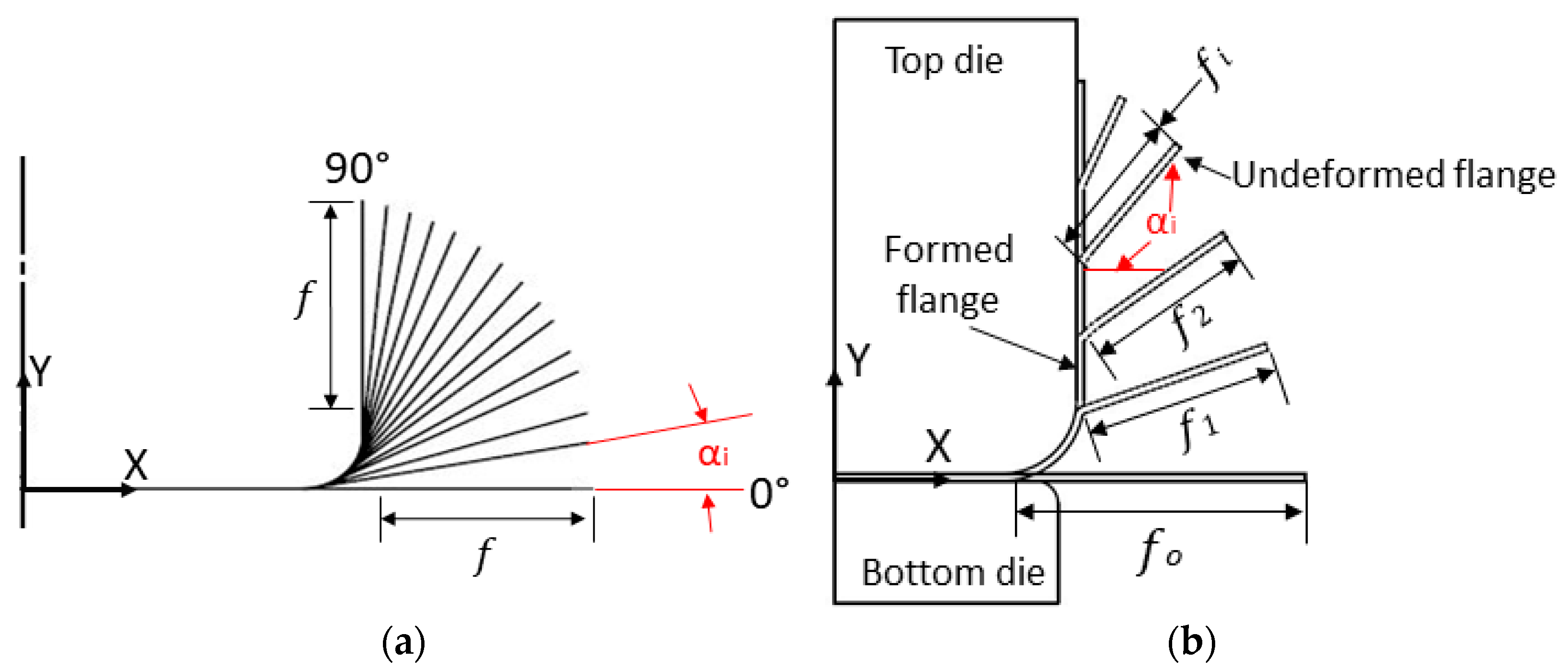
3.3. Shape Analysis
4. The Finite Element Analysis
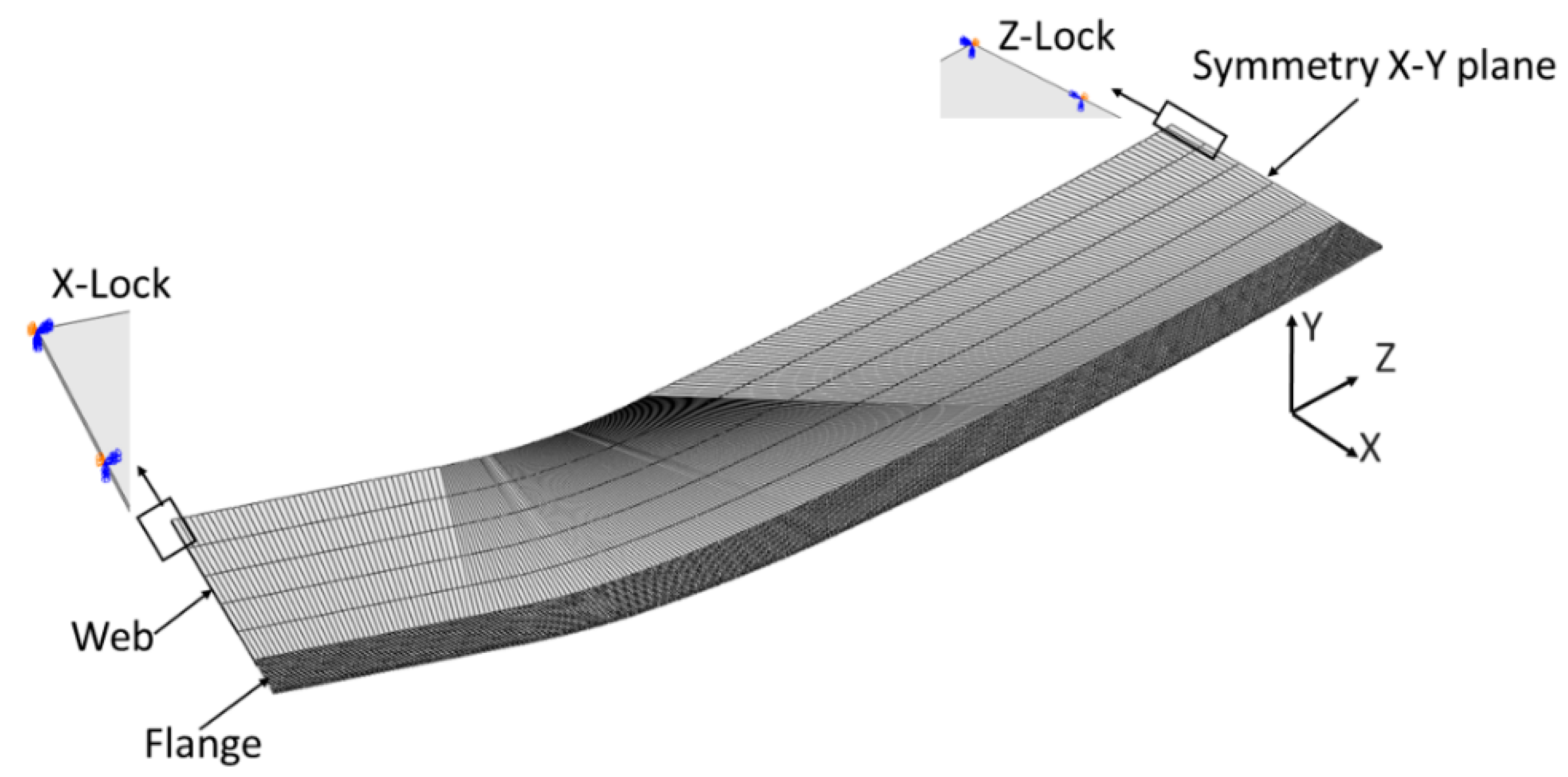
4.1. The ISR Process
4.2. The FRF Process
5. Results
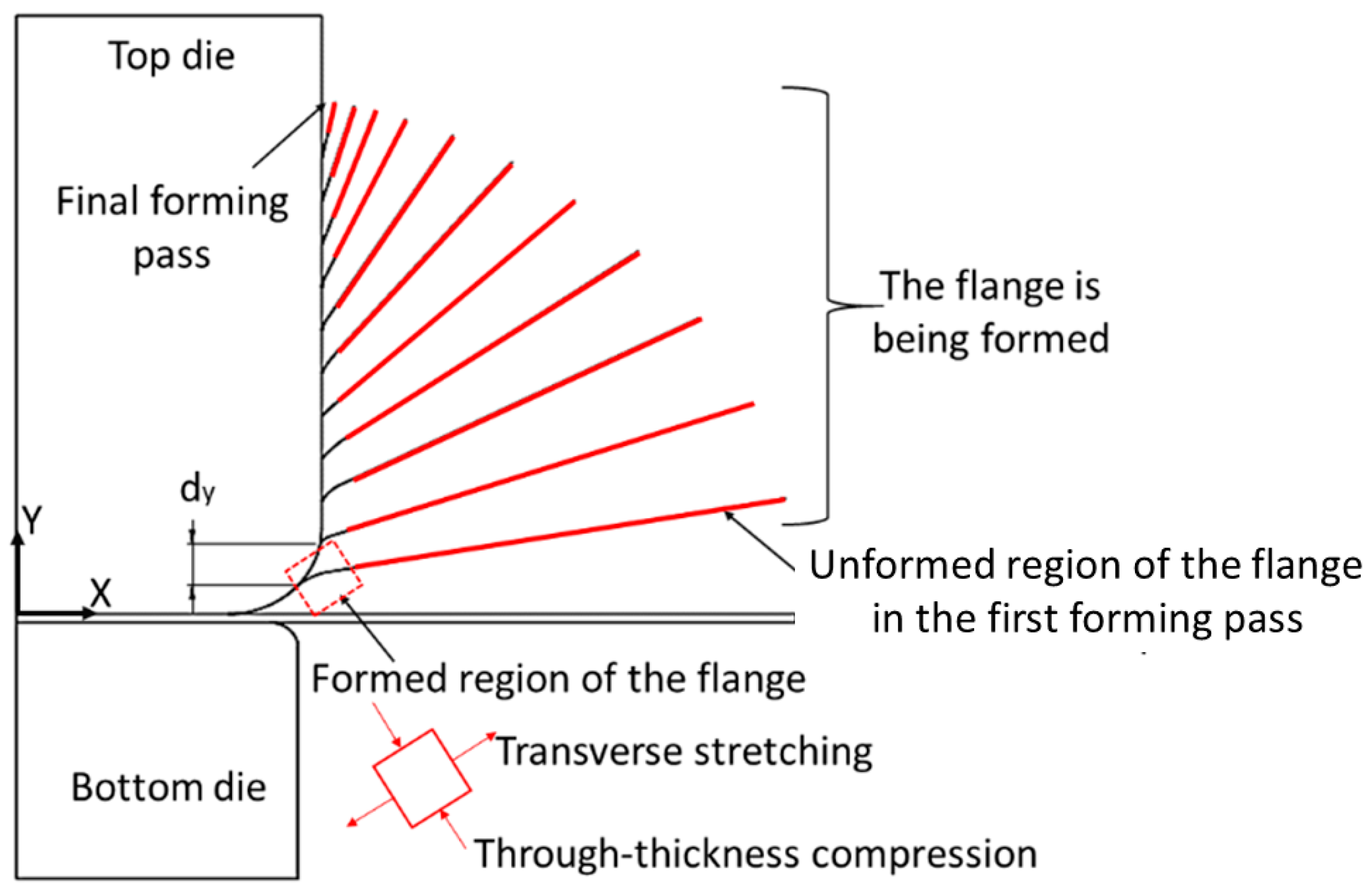
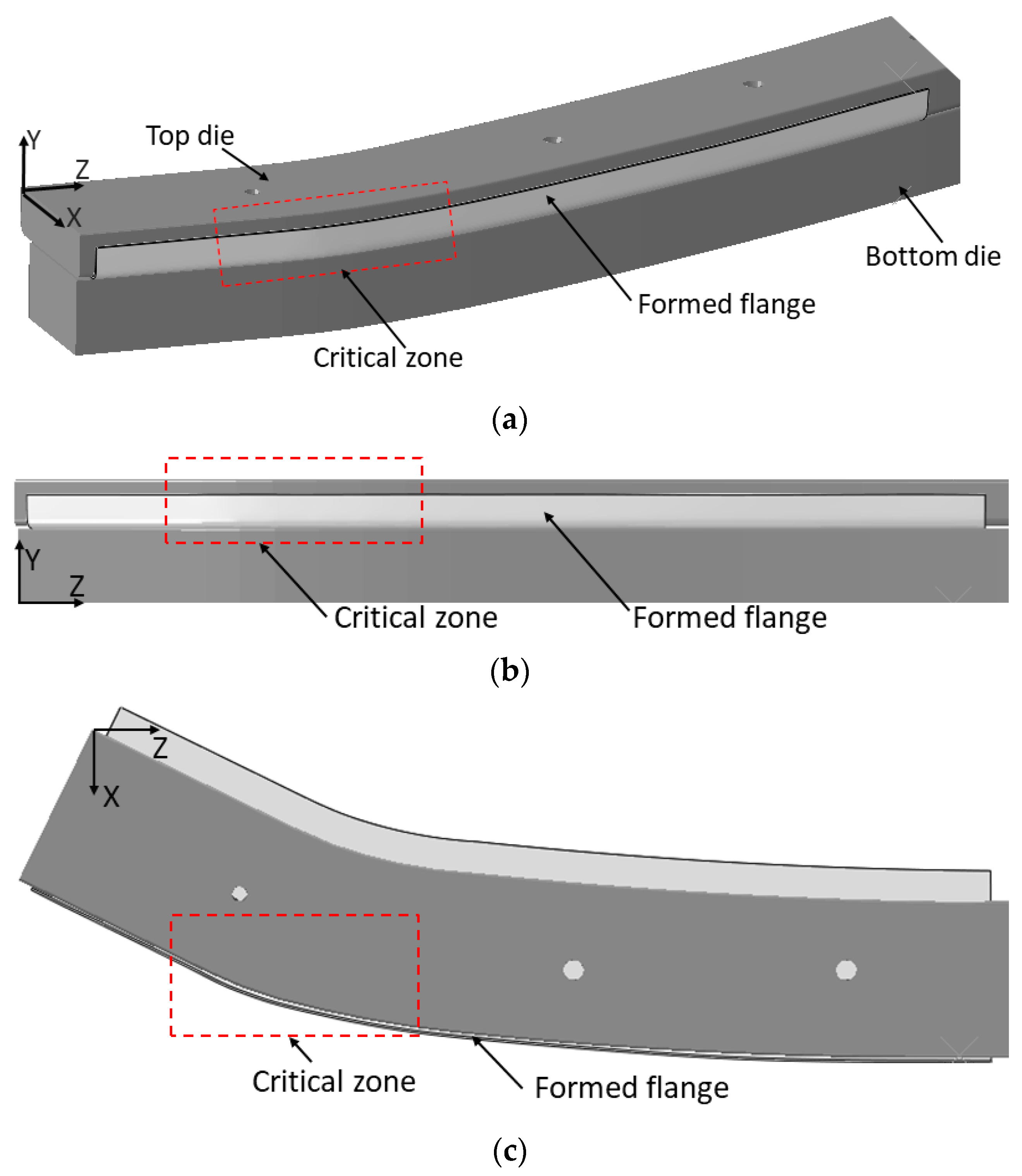
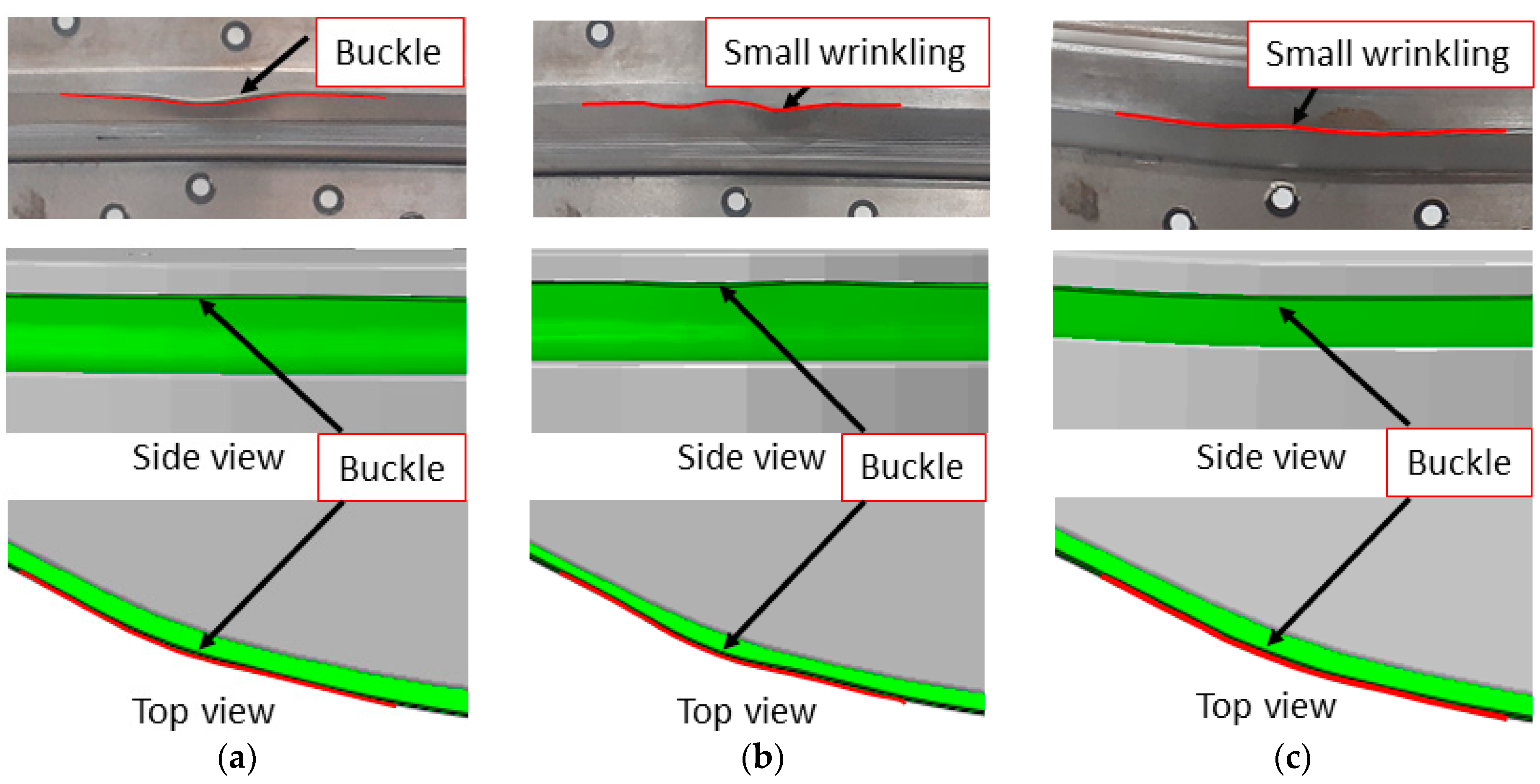
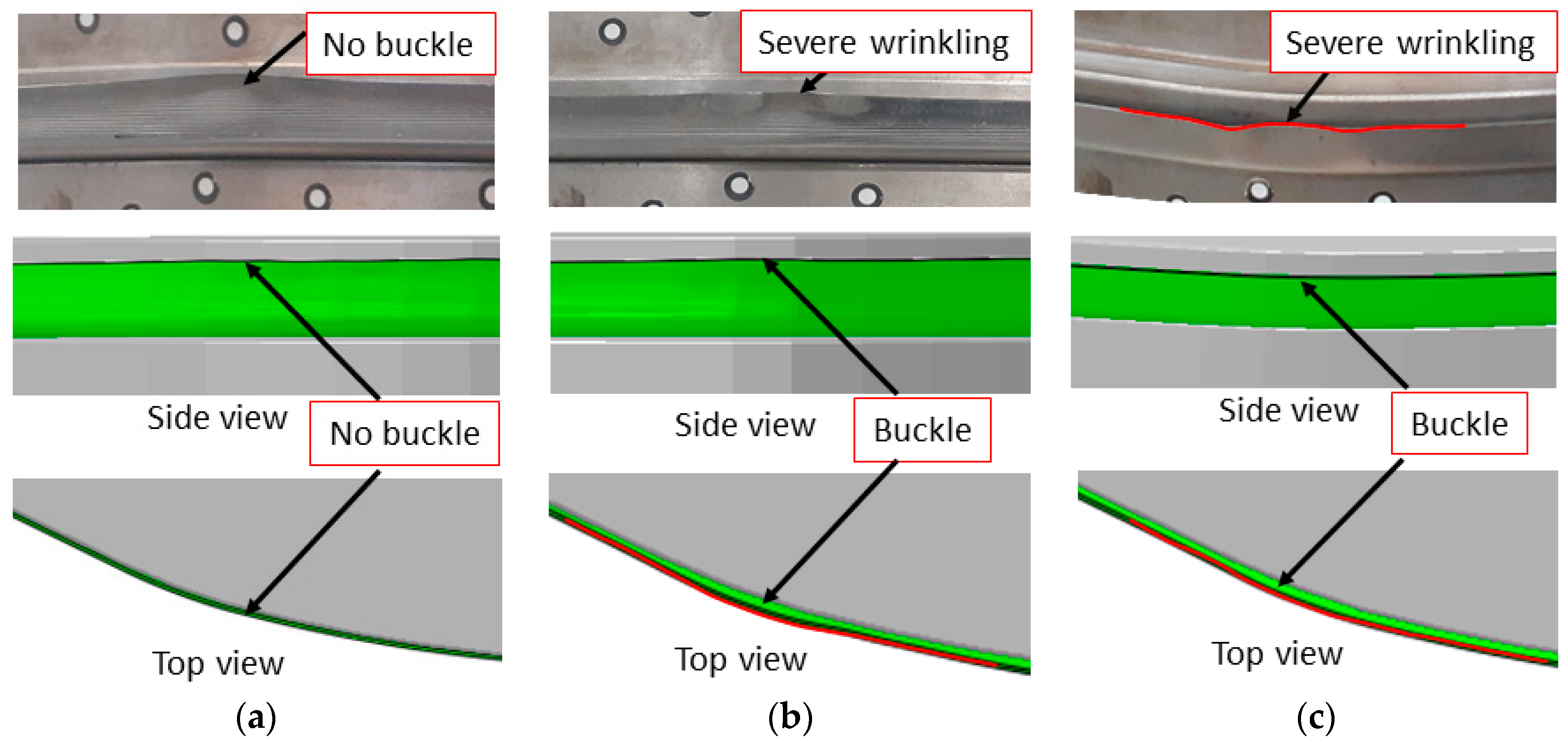
5.1. Flange Wrinkling
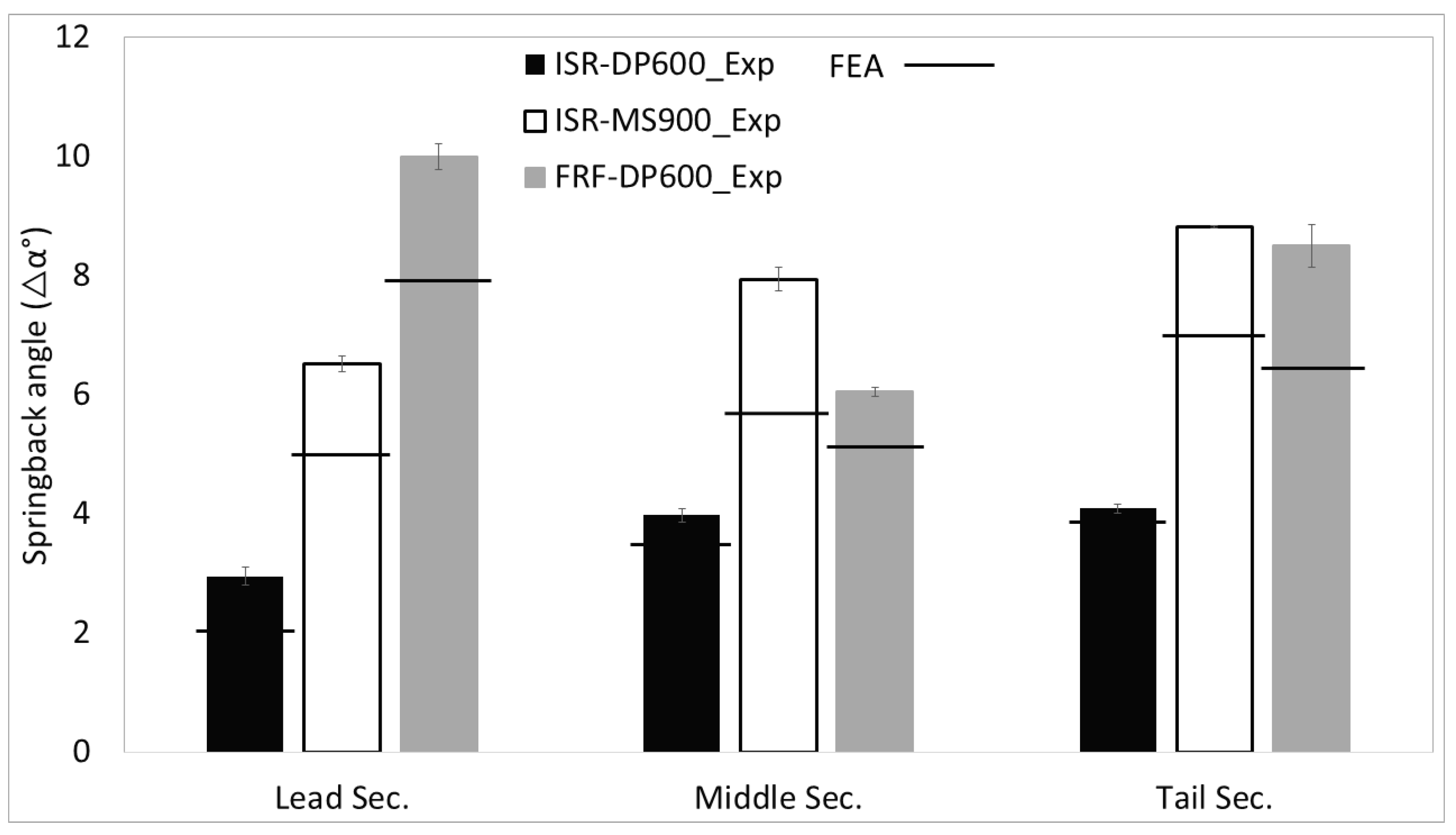
5.2. Springback
6. Discussion
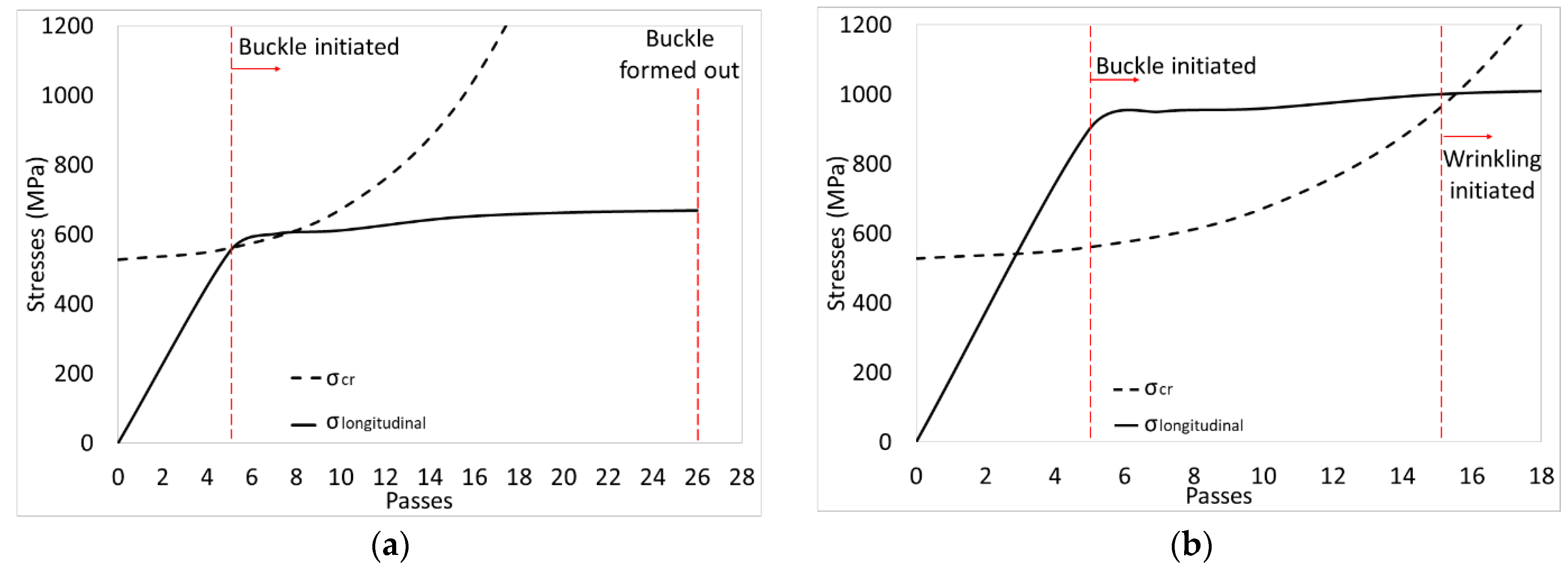
- Why does a flange buckle form out in ISR while it turns into a wrinkle in the FRF process?
- Why is the flange buckle not formed out when ISR MS900?
6.1. Buckling Limit in FRF
6.2. Buckling Limit in ISR
6.3. Proposed Mechanism for Buckles Forming out in ISR the DP600
6.4. Proposed Mechanism for the MS900 Showing Wrinkling in the Flange
7. Conclusions
- In both the ISR and the FRF process the critical buckling stress in the flange is exceeded, and this leads to flange buckling in the early stages of forming in all investigated forming cases and material conditions.
- In FRF the critical buckling stress and the flange length are constant while the forming angle increases. This results in the stress condition in the flange favoring buckling growth and wrinkle initiation with further progression of forming.
- In contrast to FRF, in ISR the critical flange length reduces with increasing the number of forming passes. This increases the critical buckling stresses towards the end of forming and leads to the buckle being formed out when applying ISR to the DP600 steel.
- When ISR MS900 the initial flange buckle transitions into a wrinkle. This is related to the higher material strength, which results in a higher initial longitudinal stress in the flange and causes the buckle to grow into a wrinkle before the stress condition favors a buckling reduction. The developed wrinkle cannot be formed out and therefore continues to grow in severity in the subsequent passes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Australian Government. The Department of Infrastructure, Transport, Regional Development and Communications. Available online: https://www.infrastructure.gov.au/infrastructure-transport-vehicles/vehicles/vehicle-safety-environment (accessed on 22 November 2022).
- Baluch, N.; Udin, Z.M.; Abdullah, C.S. Advanced High Strength Steel in Auto Industry: An Overview. Eng. Appl. Sci. Res. 2014, 4, 686–689. [Google Scholar] [CrossRef]
- Sun, G.; Deng, M.; Zheng, G.; Li, Q. Design for cost performance of crashworthy structures made of high strength steel. Thin-Walled Struct. 2019, 138, 458–472. [Google Scholar] [CrossRef]
- Lim, Y.; Venugopal, R.; Ulsoy, A.G. Process Control for Sheet-Metal Stamping; Springer: London, UK, 2014. [Google Scholar]
- Mori, K.; Bariani, P.F.; Behrens, B.A.; Brosius, A.; Bruschi, S.; Maeno, T.; Merklein, M.; Yanagimoto, J. Hot stamping of ultra-high strength steel parts. CIRP Ann. Manuf. Technol. 2017, 66, 755–777. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Y.; Daniel, W.J.T.; Meehan, P.A.; Liu, Z.; Ding, S. Longitudinal strain development in Chain-die forming AHSS products: Analytical modelling, finite element analysis and experimental verification. J. Mater. Process. Technol. 2017, 243, 322–334. [Google Scholar] [CrossRef]
- Safdarian, R.; Naeini, H.M. The effects of forming parameters on the cold roll forming of channel section. Thin-Walled Struct. 2015, 92, 130–136. [Google Scholar] [CrossRef]
- Bui, Q.V.; Ponthot, J.P. Numerical simulation of cold roll-forming processes. J. Mater. Process. Technol. 2008, 202, 275–282. [Google Scholar] [CrossRef]
- Cheng, J.-J.; Cao, J.-G.; Zhao, Q.-F.; Liu, J.; Yu, N.; Zhao, R.-G. A novel approach to springback control of high-strength steel in cold roll forming. Int. J. Adv. Manuf. Technol. 2020, 107, 1793–1804. [Google Scholar] [CrossRef]
- Groche, P.S.R. Umformtechnik für die Produkte von morgen. Mater. Und Werkst. Mater. Sci. Eng. Technol. 2000, 31, 958–963. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, H.; Li, Q.; Qian, B.; Mpofu, K. Simulation and experimental verification of flexible roll forming of steel sheets. Int. J. Adv. Manuf. Technol. 2014, 72, 209–220. [Google Scholar] [CrossRef]
- Groche, P.; Güngör, B.; Kilz, J. Straight roll formed profiles through partial rolling. CIRP Ann. 2023, 72, 229–232. [Google Scholar] [CrossRef]
- Badparva, H.; Naeini, H.M.; Kasaei, M.M.; Asl, Y.D.; Abbaszadeh, B.; da Silva, L.F.M. Deformation length in flexible roll forming. Int. J. Adv. Manuf. Technol. 2023, 125, 1229–1238. [Google Scholar] [CrossRef]
- Rezaei, R.; Moslemi Naeini, H.; Tafti, R.A.; Kasaei, M.M.; Mohammadi, M.; Abbaszadeh, B. Effect of bend curve on web warping in flexible roll formed profiles. Int. J. Adv. Manuf. Technol. 2017, 93, 3625–3636. [Google Scholar] [CrossRef]
- Woo, Y.Y.; Oh, I.Y.; Hwang, T.W.; Moon, Y.H. Analysis of shape defects during flexible roll forming of steel/aluminum double-layered blanks. Int. J. Mater. Form. 2019, 13, 861–872. [Google Scholar] [CrossRef]
- Stamp. 3D Roll Forming. The Technology of the Future: Roll Forming with Variable Section. Available online: https://www.stam.it/en/roll-forming-lines/3d-roll-forming/ (accessed on 10 December 2024).
- Abeyrathna, B.; Rolfe, B.; Harrasser, J.; Sedlmaier, A.; Rui, G.; Pan, L.; Weiss, M. Prototyping of automotive components with variable width and depth. In Proceedings of the 36th IDDRG Conference, Munich, Germany, 2–6 July 2017. [Google Scholar]
- Groche, P.; Zettler, A.; Berner, S.; Schneider, G. Development and verification of a one-step-model for the design of flexible roll formed parts. Int. J. Mater. Form. 2010, 4, 371–377. [Google Scholar] [CrossRef]
- Kasaei, M.M.; Naeini, H.M.; Abbaszadeh, B.; Mohammadi, M.; Ghodsi, M.; Kiuchi, M.; Zolghadr, R.; Liaghat, G.; Tafti, R.A.; Tehrani, M.S. Flange wrinkling in flexible roll forming Process. Procedia Eng. 2014, 81, 245–250. [Google Scholar] [CrossRef]
- Abeyrathna, B.; Ghanei, S.; Rolfe, B.; Taube, R.; Weiss, M. Optimising part quality in the flexible roll forming of an automotive component. Int. J. Adv. Manuf. Technol. 2021, 118, 3361–3373. [Google Scholar] [CrossRef]
- Essa, A.; Abeyrathna, B.; Rolfe, B.; Weiss, M. Incremental shape rolling of a variable depth profile. J. Mater. Process. Technol. 2023, 316, 117964. [Google Scholar] [CrossRef]
- Wang, L.; Long, H. Investigation of material deformation in multi-pass conventional metal spinning. Mater. Des. 2011, 32, 2891–2899. [Google Scholar] [CrossRef]
- Music, O.; Allwood, J.M.; Kawai, K. A review of the mechanics of metal spinning. J. Mater. Process. Technol. 2010, 210, 3–23. [Google Scholar] [CrossRef]
- Jia, Z.; Li, L.; Han, Z.R.; Fan, Z.J.; Liu, B.M. Experimental study on wrinkle suppressing in multi-pass drawing spinning of 304 stainless steel cylinder. Int. J. Adv. Manuf. Technol. 2018, 100, 111–116. [Google Scholar] [CrossRef]
- Essa, A.; Abeyrathna, B.; Rolfe, B.; Weiss, M. Incremental shape rolling of top-hat shaped automotive structural and crash components. J. Mater. Process. Technol. 2023, 321, 118162. [Google Scholar] [CrossRef]
- ASTM E8/E8M-22; Standard Test Methods for Tension Testing of Metallic Materials. ASTM: West Conshohocken, PA, USA, 2016.
- Essa, A.; Abeyrathna, B.; Rolfe, B.; Weiss, M. Prototyping of straight section components using incremental shape rolling. Int. J. Adv. Manuf. Technol. 2022, 121, 3883–3901. [Google Scholar] [CrossRef]
- HandyScan3D. n.d. Available online: https://www.creaform3d.com/en (accessed on 10 November 2022).
- Geomagic. n.d. Available online: http://www.geomagic.com/en/ (accessed on 10 November 2022).
- Abaqus_Documentation. n.d. Available online: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/index.html (accessed on 8 December 2022).
- Woo, Y.Y.; Han, S.W.; Oh, I.Y.; Moon, Y.H. Shape defects in the flexible roll forming of automotive parts. Int. J. Automot. Technol. 2019, 20, 227–236. [Google Scholar] [CrossRef]
- Sreenivas, A.; Abeyrathna, B.; Rolfe, B.; Weiss, M. Development of a reversible top-hat forming approach for reducing flange wrinkling in flexible roll forming. Int. J. Mech. Sci. 2023, 252, 108359. [Google Scholar] [CrossRef]
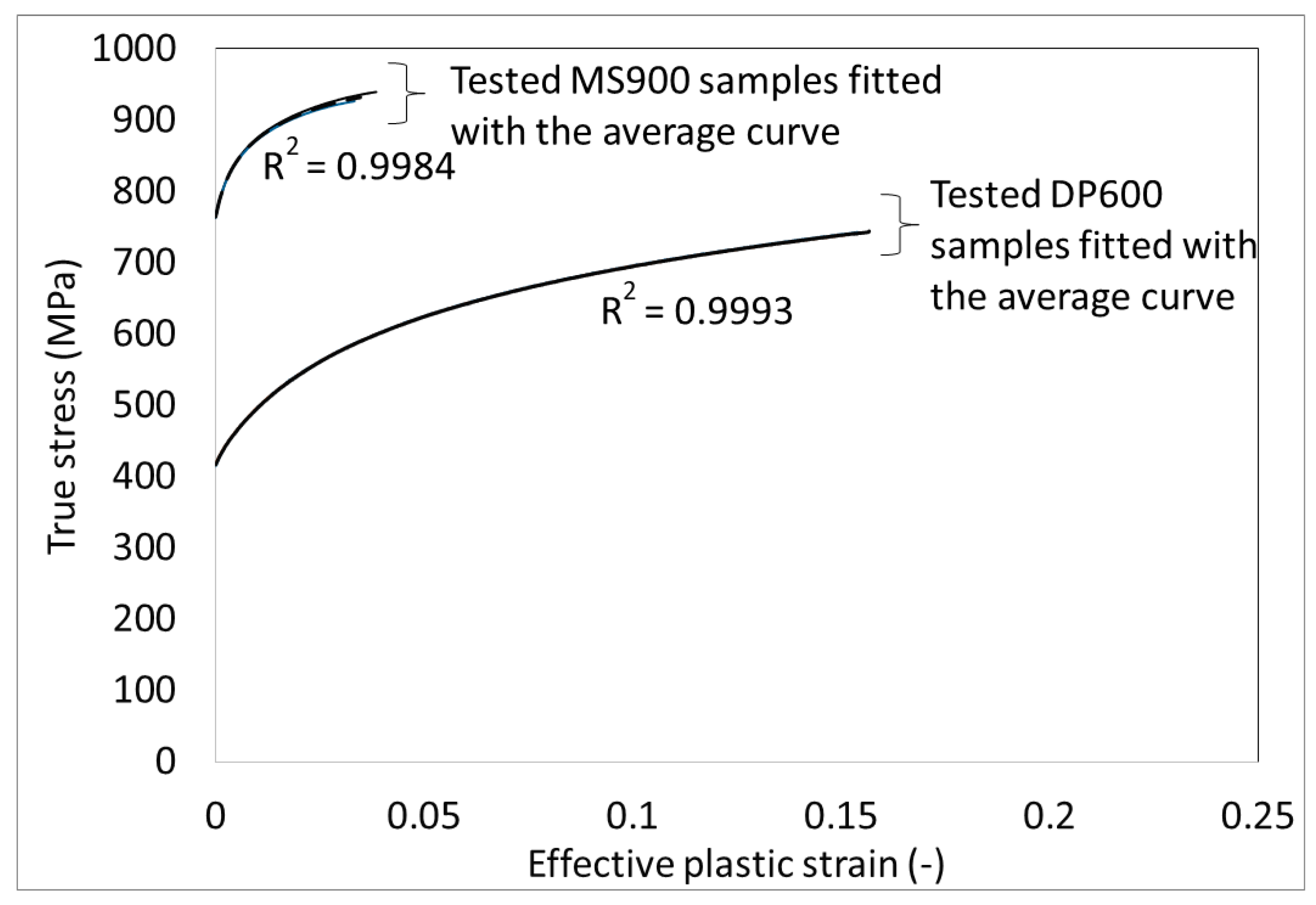






| Material | 0.2% Yield Strength (MPa) | Strain Hardening Exponent (n) | Strength Coefficient, K (MPa) |
|---|---|---|---|
| DP 600 | 414.5 | 0.11 | 897 |
| MS 900 | 763.2 | 0.08 | 1250 |
| Experiment Set | Material | Increment Size dy (mm) | Corresponding Forming Passes | Flange Length f (mm) | Forming Angle (α°) |
|---|---|---|---|---|---|
| ISR | DP 600 and MS 900 | 1 | 26 | 18 | |
| FRF | DP 600 | 14 | 18 | 11, 7, 10, 5, 8, 5, 6, 6, 6, 6, 5, 5, 5, 5 |
| Flange Length fi | Bend Angle (αi°) | ||
|---|---|---|---|
| Pass | DP600 | MS900 | |
| 5 | 20 | 43.77 | 47.07 |
| 10 | 15 | 65.2 | 71.56 |
| 15 | 10 | 82.25 | 86.52 |
| 20 | 5 | 87.69 | 87.69 |
| 24 | 1 | 90 | 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Essa, A.; Abeyrathna, B.; Rolfe, B.; Weiss, M. Flange Buckling Mechanism in Incremental Shape Rolling of an Automotive-Type Variable Width Component. J. Manuf. Mater. Process. 2024, 8, 290. https://doi.org/10.3390/jmmp8060290
Essa A, Abeyrathna B, Rolfe B, Weiss M. Flange Buckling Mechanism in Incremental Shape Rolling of an Automotive-Type Variable Width Component. Journal of Manufacturing and Materials Processing. 2024; 8(6):290. https://doi.org/10.3390/jmmp8060290
Chicago/Turabian StyleEssa, Abdelrahman, Buddhika Abeyrathna, Bernard Rolfe, and Matthias Weiss. 2024. "Flange Buckling Mechanism in Incremental Shape Rolling of an Automotive-Type Variable Width Component" Journal of Manufacturing and Materials Processing 8, no. 6: 290. https://doi.org/10.3390/jmmp8060290
APA StyleEssa, A., Abeyrathna, B., Rolfe, B., & Weiss, M. (2024). Flange Buckling Mechanism in Incremental Shape Rolling of an Automotive-Type Variable Width Component. Journal of Manufacturing and Materials Processing, 8(6), 290. https://doi.org/10.3390/jmmp8060290







