Modeling of Tensile Stress Distribution Considering Anisotropy of Mechanical Properties of Thin-Walled AlSi10Mg Samples Obtained by Selective Laser Melting
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials

2.2. Experimental Methods
2.3. Theoretical Methods
- Normal:
- 2.
- Logarithmically normal:
- 3.
- Logistical:
- 4.
- Cauchy:
- 5.
- Weibull:
- 6.
- Poisson:
- 7.
- Exponential:
- 8.
- Gumbel:
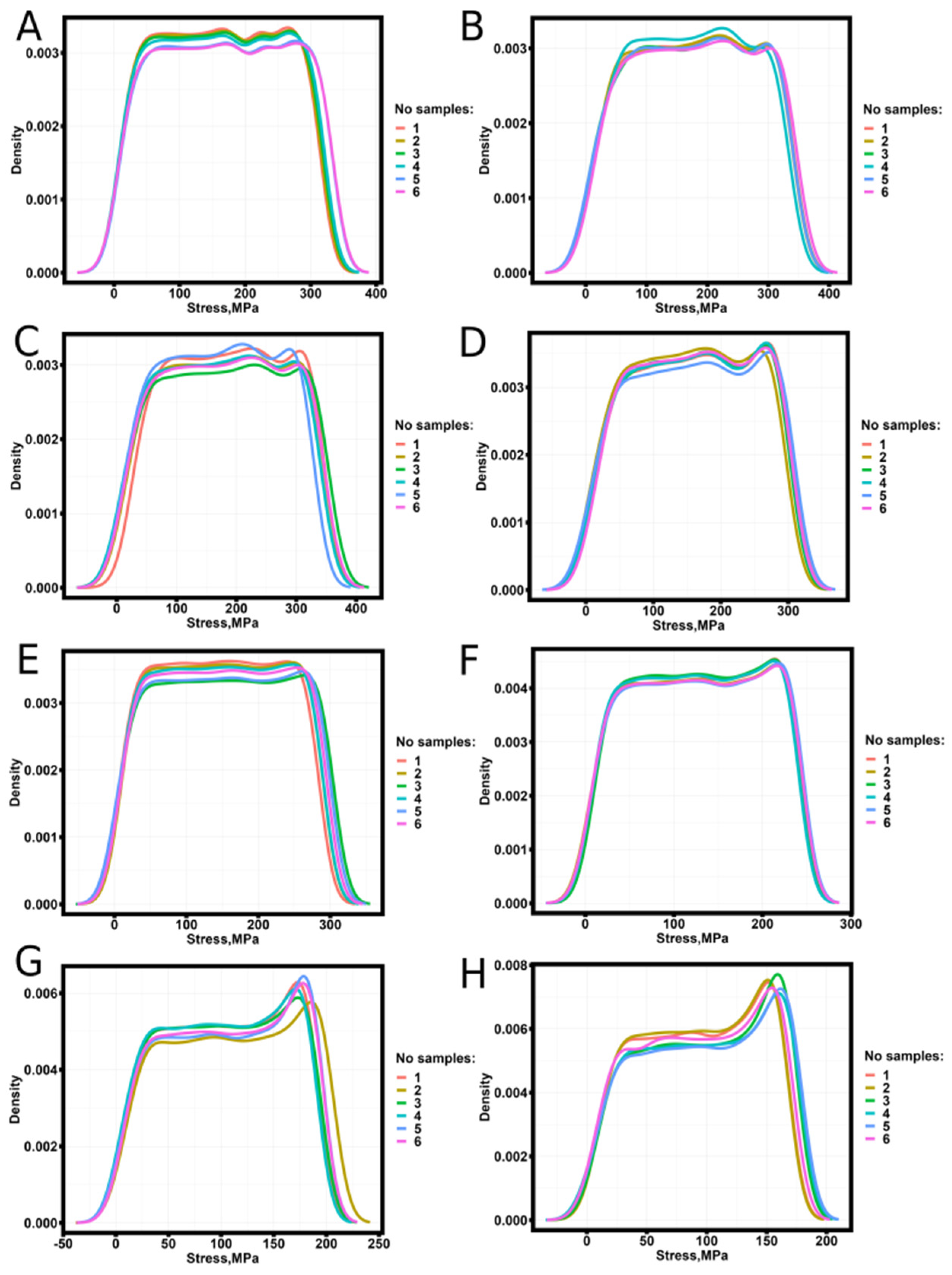
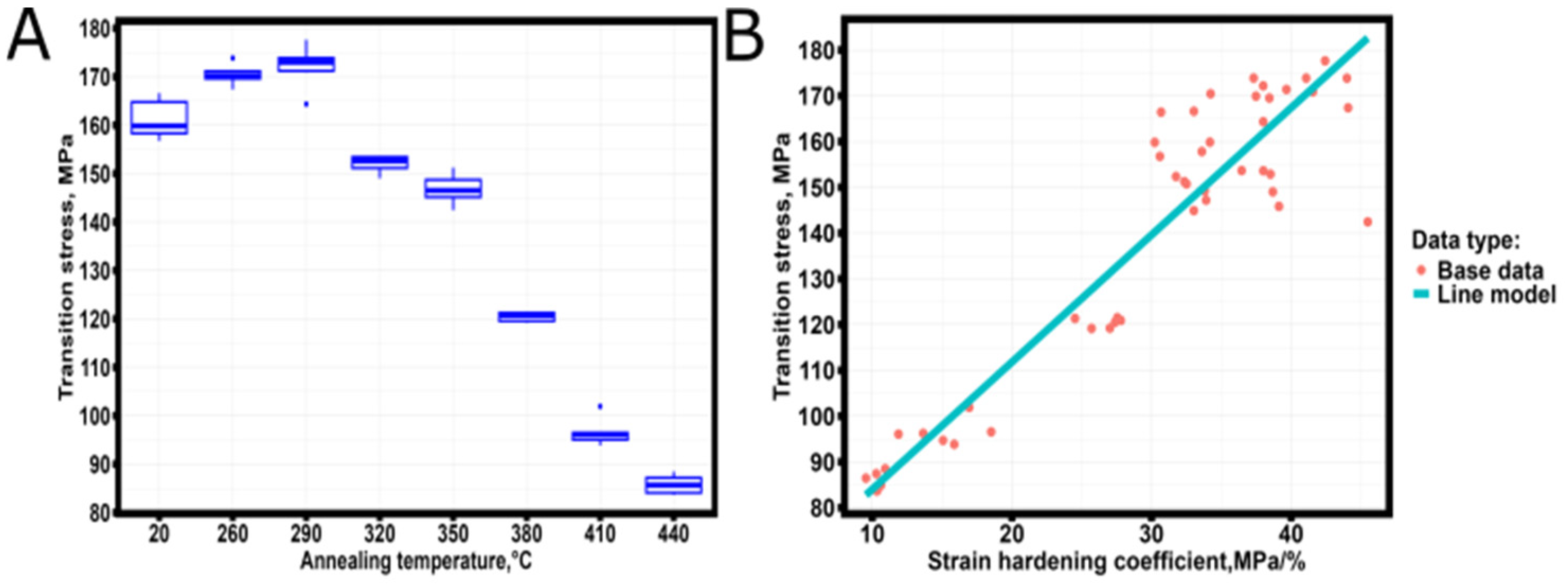
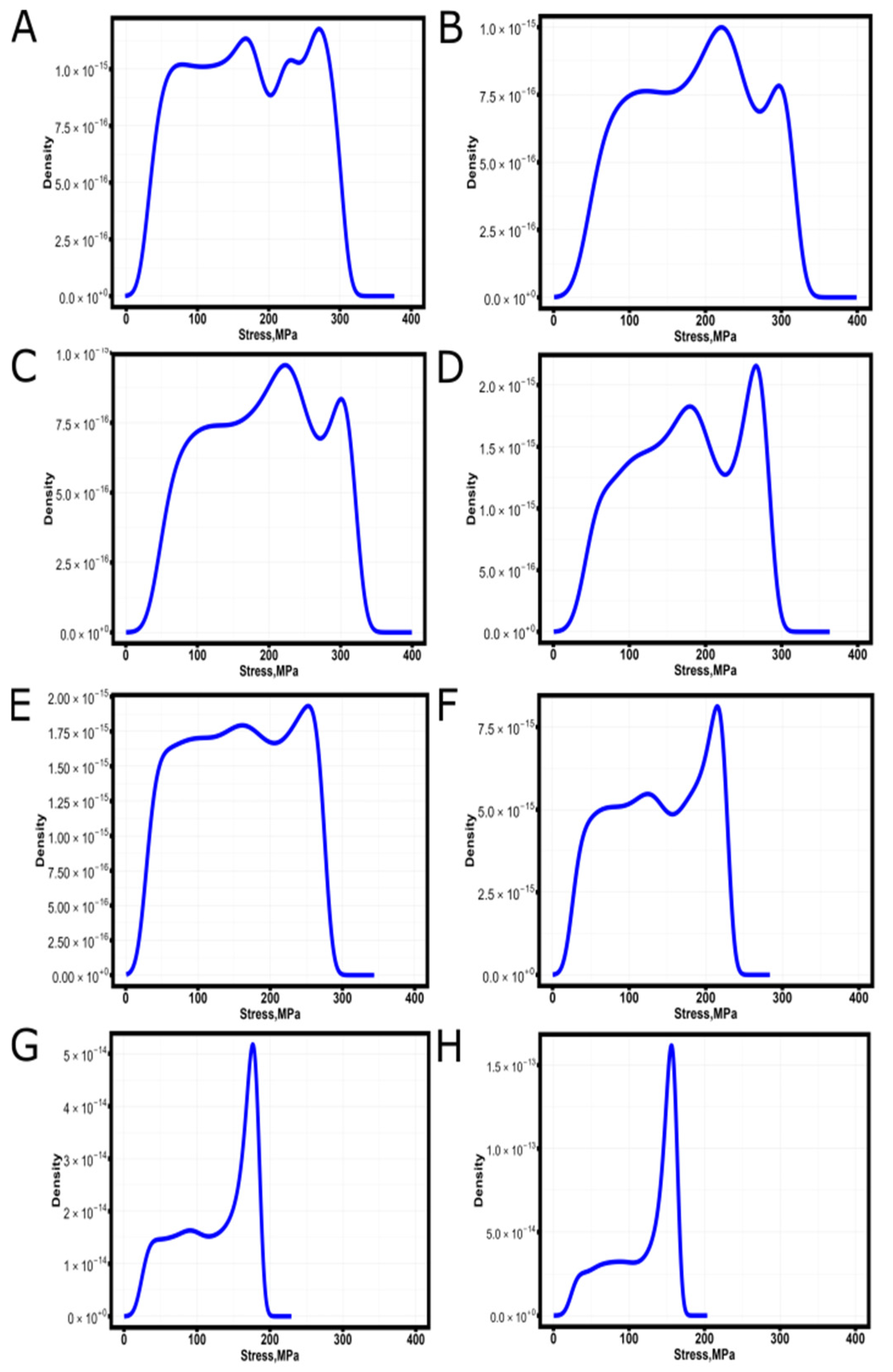
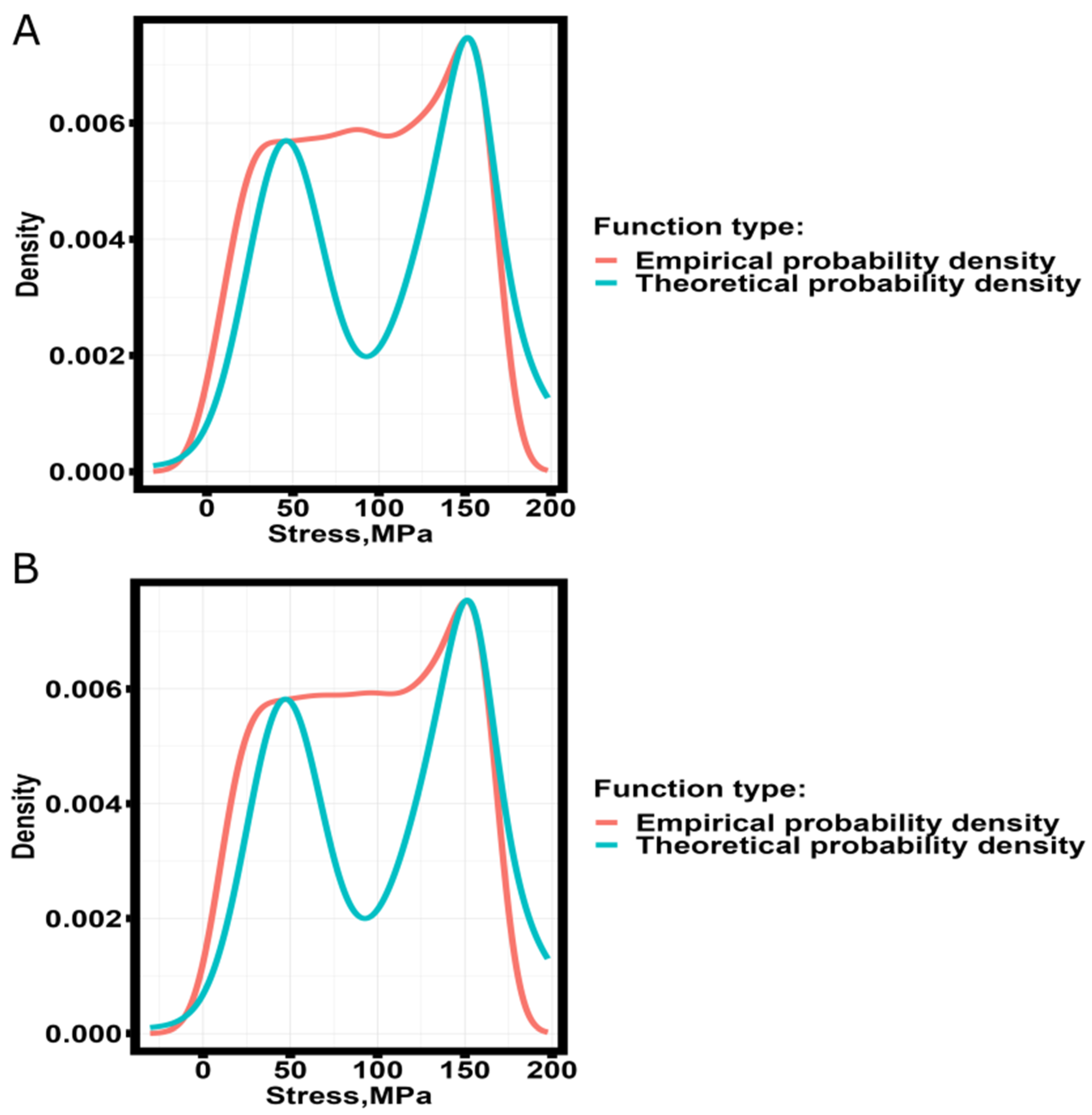
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huebner, K.H.; Dewhirst, D.L.; Smith, D.E.; Byrom, T.G. The Finite Element Method for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2001; ISBN 978-0-471-37078-9. [Google Scholar]
- Eymard, R. The finite volume method Handbook of Numerical Analysis. Handb. Numer. Anal. 2000, 7, 713–1020. [Google Scholar]
- Atanackovic, T.M.; Guran, A. Theory of Elasticity for Scientists and Engineers; Dover Books on Physics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 16 June 2000; ISBN 978-0-8176-4072-9. [Google Scholar]
- Rodríguez, J.F.; Thomas, J.P.; Renaud, J.E. Mechanical behaviour of acrylonitrile butadiene styrene (ABS) fused deposition materials. Experimental investigation. Rapid Prototyp. J. 2001, 7, 148–158. [Google Scholar] [CrossRef]
- Grigoriev, S.; Peretyagin, N.; Apelfeld, A.; Smirnov, A.; Morozov, A.; Torskaya, E.; Volosova, M.; Yanushevich, O.; Yarygin, N.; Krikheli, N.; et al. Investigation of Tribological Characteristics of PEO Coatings Formed on Ti6Al4V Titanium Alloy in Electrolytes with Graphene Oxide Additives. Materials 2023, 16, 3928. [Google Scholar] [CrossRef]
- Zak, G.; Haberer, M.; Park, C.B.; Benhabib, B. Mechanical properties of short fiber layered composites. Rapid Prototyp. J. 2000, 6, 107–118. [Google Scholar] [CrossRef]
- Contuzzi, N.; Campanelli, S.L.; Ludovico, A.D. 3D finite element analysis in the selective laser melting process. Int. J. Simul. Model. 2011, 10, 113–121. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, A.; Moghaddam, N.S.; Elahinia, M.; Karaca, H.E.; Mirzaeifar, R. Finite element modeling of selective laser melting 316L stainless steel parts for evaluating the mechanical properties. In Proceedings of the ASME 2016 11th International Manufacturing Science and Engineering Conference, Blacksburg, VA, USA, 27 June–1 July 2016; American Society of Mechanical Engineers: Richmond, VA, USA, 2016; Volume 49903. [Google Scholar]
- Păcurar, R.; Păcurar, A.; Petrilak, A.; Bâlc, N. Finite element analysis to predict the mechanical behavior of lattice structures made by selective laser melting technology. Appl. Mech. Mater. 2014, 657, 231–235. [Google Scholar] [CrossRef]
- Lawn, B.R. Fracture of Brittle Solids, 2nd ed.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Konov, S.; Frolov, A.; Shapovalov, P.; Peretyagin, P.; Grigoriev, S. Segmented Four-Element Photodiodes in a Three-Dimensional Laser Beam Angle Measurement. Photonics 2023, 10, 704. [Google Scholar] [CrossRef]
- Herrmann, H.J.; Roux, S. (Eds.) Statistical Models for the Fracture of Disordered Media; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Grigoriev, S.; Peretyagin, N.; Apelfeld, A.; Smirnov, A.; Yanushevich, O.; Krikheli, N.; Kramar, O.; Kramar, S.; Peretyagin, P. Investigation of MAO Coatings Characteristics on Titanium Products Obtained by EBM Method Using Additive Manufacturing. Materials 2022, 15, 4535. [Google Scholar] [CrossRef] [PubMed]
- Curtin, W.A. Size scaling of strength in heterogeneous materials. Phys. Rev. Lett. 1998, 80, 1445. [Google Scholar] [CrossRef]
- Smirnov, A.; Kuznetsova, E.; Pristinskiy, Y.; Podrabinnik, P.; Mironov, A.; Gershman, I.; Peretyagin, P. Effect of Milling Conditions on the Microstructural Design in Aluminum Based Alloy Fabricated by SPS. Metals 2019, 9, 1164. [Google Scholar] [CrossRef]
- Kurmysheva, A.Y.; Yanushevich, O.; Krikheli, N.; Kramar, O.; Vedenyapina, M.D.; Podrabinnik, P.; Solís Pinargote, N.W.; Smirnov, A.; Kuznetsova, E.; Malyavin, V.V.; et al. Adsorption Ability of Graphene Aerogel and Reduced Graphene Aerogel toward 2,4-D Herbicide and Salicylic Acid. Gels 2023, 9, 680. [Google Scholar] [CrossRef] [PubMed]
- Grigoriev, S.; Peretyagin, N.; Apelfeld, A.; Smirnov, A.; Rybkina, A.; Kameneva, E.; Zheltukhin, A.; Gerasimov, M.; Volosova, M.; Yanushevich, O.; et al. Investigation of the Characteristics of MAO Coatings Formed on Ti6Al4V Titanium Alloy in Electrolytes with Graphene Oxide Additives. J. Compos. Sci. 2023, 7, 142. [Google Scholar] [CrossRef]
- Skorodumov, S.V.; Neganov, D.A.; Studenov, E.P.; Poshibaev, P.V.; Nikitin, N.Y. Statistical analysis of mechanical test results for samples of pipes from trunk oil pipelines after long-term operation. Industr. Lab. Diagn. Mater. 2022, 88, 82–91. [Google Scholar] [CrossRef]
- Bolotin, V.V. Statistical Methods in Construction Mechanics; Publishing House of Literature on Construction: Moscow, Russia, 1965; p. 267. (In Russian) [Google Scholar]
- Weibull, W. Fatigue Testing and Analysis of Results; Pergamon Press: New York, NY, USA, 1961; p. 236. [Google Scholar]
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. 1951, 18, 290–293. [Google Scholar]
- Abdullin, M.R.; Berezin, A.V. Prediction of basic strength values of metallic materials by distribution of microdefects formed in the process of plastic deformation. Probl. Mech. Eng. Autom. 2006, 3, 40–44. (In Russian) [Google Scholar]
- Akaike, H. Applications of Statistics; Krishnaiah, P.R., Ed.; Elsevier: Amsterdam, The Netherlands, 1977; p. 27. [Google Scholar]
- Lu, C.; Danzer, R.; Fischer, F.D. Fracture statistics of brittle materials: Weibull or normal distribution. Phys. Rev. E 2002, 65, 067102. [Google Scholar] [CrossRef]
- Grigoriev, S.N.; Nikitin, N.; Yanushevich, O.; Kriheli, N.; Kramar, O.; Khmyrov, R.; Idarmachev, I.; Peretyagin, P. Experimental and Statistical Analysis of the Effect of Heat Treatment on Surface Roughness and Mechanical Properties of Thin-Walled Samples Obtained by Selective Laser Melting from the Material AlSi10Mg. Materials 2023, 16, 7326. [Google Scholar] [CrossRef]
- Smirnov, A.; Peretyagin, P.; Nikitin, N. Assessment Effect of Nanometer-Sized Al2O3 Fillers in Polylactide on Fracture Probability of Filament and 3D Printed Samples by FDM. Materials 2023, 16, 1671. [Google Scholar] [CrossRef]
- Mertens, A.; Delahaye, J.; Dedry, O.; Vertruyen, B.; Tchuindjang, J.T.; Habraken, A.M. Microstructure and Properties of SLM AlSi10Mg: Understanding the Influence of the Local Thermal History. Procedia Manuf. 2020, 47, 1089–1095. [Google Scholar] [CrossRef]
- Kempen, K.; Thijs, L.; Van Humbeeck, J.; Kruth, J.-P. Mechanical Properties of AlSi10Mg Produced by Selective Laser Melting. Phys. Procedia 2012, 39, 439–446. [Google Scholar] [CrossRef]
- Chen, J.; Hou, W.; Wang, X.; Chu, S.; Yang, Z. Microstructure, porosity and mechanical properties of selective laser melted AlSi10Mg. Chin. J. Aeronaut. 2020, 33, 2043–2054. [Google Scholar] [CrossRef]
- Rakesh, C.S.; Priyanka, N.; Jayaganthan, R.; Vasa, N.J. Effect of build atmosphere on the mechanical properties of AlSi10Mg produced by selective laser melting. Mater. Today Proc. 2018, 5, 17231–17238. [Google Scholar] [CrossRef]
- Yang, C.; Huang, Z.; Chen, T.; Ma, H.; Li, H.; Yan, A.; Li, P.; Hosoda, H.; Cai, W. Large recoverable strains with high recovery rates via cooperative regulation of texture and precipitation in additive manufactured NiTi alloy. Scr. Mater. 2024, 248, 116122. [Google Scholar] [CrossRef]
- Lu, H.; Liu, L.; Yang, C.; Luo, X.; Song, C.; Wang, Z.; Wang, J.; Su, Y.; Ding, Y.; Zhang, L.; et al. Simultaneous enhancement of mechanical and shape memory properties by heat-treatment homogenization of Ti2Ni precipitates in TiNi shape memory alloy fabricated by selective laser melting. J. Mater. Sci. Technol. 2021, 101, 205–216. [Google Scholar] [CrossRef]
- Lu, H.Z.; Ma, H.W.; Cai, W.S.; Luo, X.; Wang, Z.; Song, C.H.; Yin, S.; Yang, C. Stable tensile recovery strain induced by a Ni4Ti3 nanoprecipitate in a Ni50.4Ti49. 6 shape memory alloy fabricated via selective laser melting. Acta Mater. 2021, 219, 117261. [Google Scholar] [CrossRef]
- Li, W.; Li, S.; Liu, J.; Zhang, A.; Zhou, Y.; Wei, Q.; Yan, C.; Shi, Y. Effect of heat treatment on AlSi10Mg alloy fabricated by selective laser melting: Microstructure evolution, mechanical properties and fracture mechanism. Mater. Sci. Eng. A 2016, 663, 116–125. [Google Scholar] [CrossRef]
- Takata, N.; Kodaira, H.; Sekizawa, K.; Suzuki, A.; Kobashi, M. Change in microstructure of selectively laser melted AlSi10Mg alloy with heat treatments. Mater. Sci. Eng. A 2017, 704, 218–228. [Google Scholar] [CrossRef]
- Oakley, J.E.; O’Hagan, A. Probabilistic sensitivity analysis of complex models: A Bayesian approach. J. R. Stat. Soc. Ser. B Stat. Methodol. 2004, 66, 751–769. [Google Scholar] [CrossRef]
- El-Awady, A.; Ponnambalam, K. Integration of simulation and Markov Chains to support Bayesian Networks for probabilistic failure analysis of complex systems. Reliab. Eng. Syst. Saf. 2021, 211, 107511. [Google Scholar] [CrossRef]
- McLachlan, G.; Sharon, X.L.; Rathnayake, S.I. Finite mixture models. Annu. Rev. Stat. Appl. 2019, 6, 355–378. [Google Scholar] [CrossRef]
- Nikitin, N.Y. Calculation of Fracture Probability; Oding, I.A., Ed.; Scientific readings by them; Mechanical Properties of Structural Materials; Russian Academy of Sciences: Moscow, Russia, 2020. [Google Scholar]
- Smirnov, A.; Peretyagin, P.; Nikitin, N. Modeling of Stress Distribution and Fracture in ABS, PLA, and Alumina-Filled PLA Filaments and FDM-Printed Specimens. J. Compos. Sci. 2023, 7, 265. [Google Scholar] [CrossRef]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice and Visualization; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Sheather, S.J.; Jones, M.C. A reliable data-based bandwidth selection method for kernel density estimation. J. R. Stat. Soc. Ser. B 1991, 53, 683–690. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S; Springer: New York, NY, USA, 2002; pp. 435–446. [Google Scholar]
- Sinay, Y.G. Theory of Phase Transitions: Rigorous Results; Nauka, Main Editorial Office of Physical and Mathematical Literature: Moscow, Russia, 1980; 208 c. [Google Scholar]
- Delignette-Muller, M.L.; Dutang, C. fitdistrplus: An R package for fitting distributions. J. Stat. Softw. 2015, 64, 1–34. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theoretical Physics; Statistical Physics; Nauka: Moscow, Russia, 1964; Volume 5, p. 568. [Google Scholar]
- Patakham, U.; Palasay, A.; Wila, P.; Tongsri, R. MPB characteristics and Si morphologies on mechanical properties and fracture behavior of SLM AlSi10Mg. Mater. Sci. Eng. A 2021, 821, 141602. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; John Wiley & Sons: Hoboken, NJ, USA, 1981. [Google Scholar]
- Sena, L.A. Units of Physical Quantities and Their Dimensions. 1977. ISBN 5-02-013848-7. Available online: http://www.vixri.ru/?p=5242 (accessed on 19 August 2024). (In Russian).
- Rossi, R.J. Mathematical Statistics: An Introduction to Likelihood Based Inference; John Wiley & Sons: New York, NY, USA, 2018; p. 227. [Google Scholar]
- Cramér, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1946; p. 282. [Google Scholar]
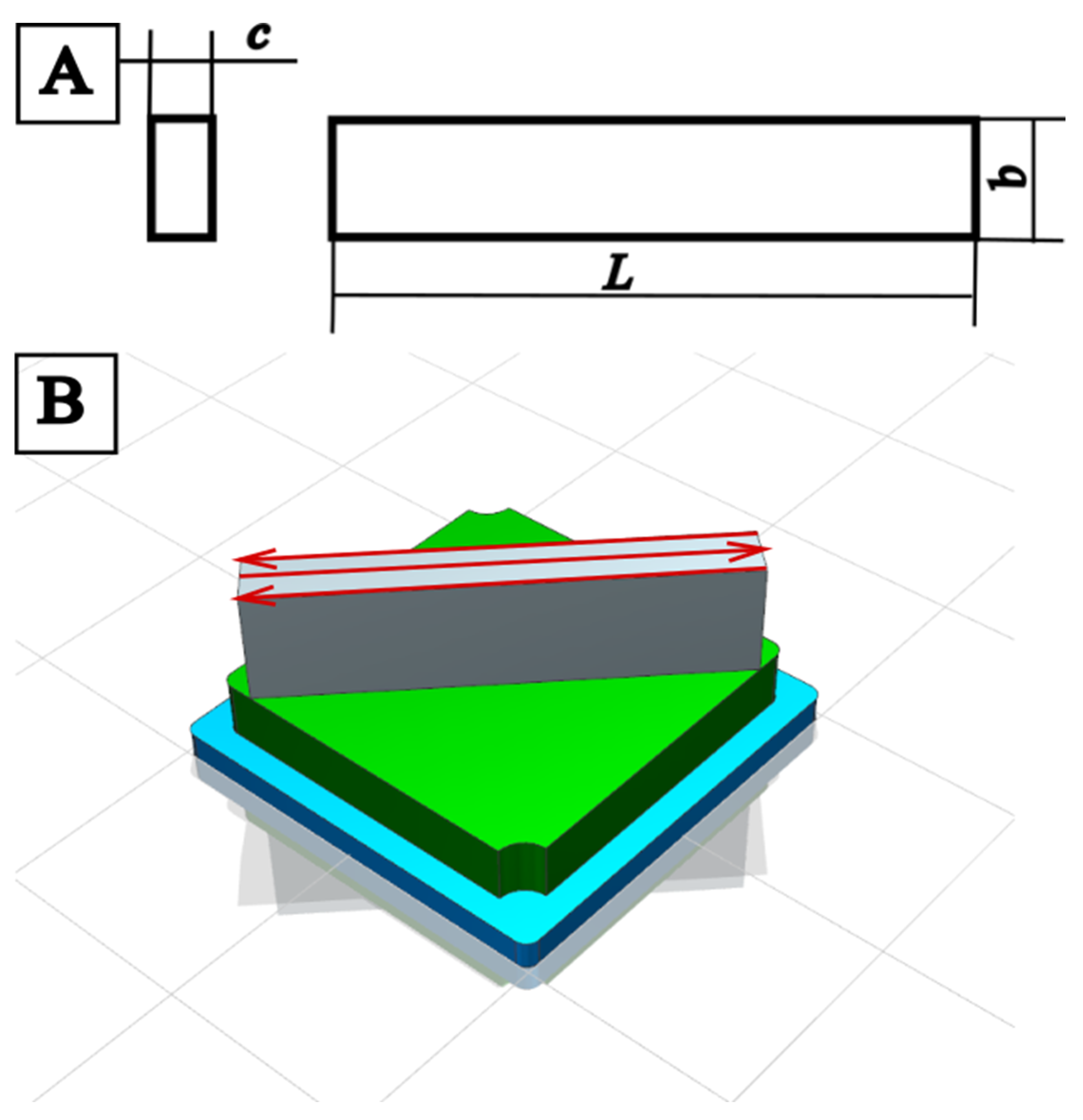


| Elements | Al | Si | Mg | O |
|---|---|---|---|---|
| Composition (wt. %) | 88.1850 | 9.9550 | 0.3275 | 1.5325 |
| No of Samples | Heat Treatment Temperature, °C | Distribution to the Left of σT | Distribution to the Right of σT | b by Weibull, to σT | a by Weibull, to σT | b by Weibull, from σT | a by Weibull, from σT |
|---|---|---|---|---|---|---|---|
| 1 | 20 | Weibull | Weibull | 92.261 | 1.906 | 254.575 | 5.944 |
| 2 | Weibull | Weibull | 92.051 | 1.890 | 255.687 | 6.027 | |
| 3 | Weibull | Weibull | 93.839 | 1.937 | 258.170 | 5.924 | |
| 4 | Weibull | Weibull | 94.371 | 1.898 | 260.610 | 5.984 | |
| 5 | Weibull | Weibull | 99.071 | 1.963 | 270.391 | 5.999 | |
| 6 | Weibull | Weibull | 97.306 | 1.911 | 270.089 | 5.898 | |
| 1 | 260 | Weibull | Weibull | 104.033 | 2.024 | 277.544 | 6.016 |
| 2 | Weibull | Weibull | 103.111 | 2.043 | 276.052 | 6.005 | |
| 3 | Normal * | Weibull | 90.063 | 47.118 | 276.595 | 5.984 | |
| 4 | Normal * | Weibull | 90.044 | 45.315 | 269.865 | 5.947 | |
| 5 | Normal * | Weibull | 89.980 | 47.091 | 276.279 | 5.965 | |
| 6 | Weibull | Weibull | 105.544 | 2.064 | 281.872 | 5.981 | |
| 1 | 290 | Weibull | Weibull | 112.842 | 2.604 | 281.012 | 5.944 |
| 2 | Weibull | Weibull | 107.185 | 2.128 | 281.507 | 6.025 | |
| 3 | Normal * | Weibull | 95.202 | 48.901 | 288.487 | 6.049 | |
| 4 | Normal * | Weibull | 90.954 | 47.085 | 277.021 | 5.998 | |
| 5 | Normal * | Weibull | 88.593 | 44.323 | 267.245 | 5.977 | |
| 6 | Weibull | Weibull | 105.544 | 2.064 | 281.872 | 5.981 | |
| 1 | 320 | Weibull | Weibull | 94.792 | 2.120 | 250.451 | 6.081 |
| 2 | Normal * | Weibull | 79.534 | 41.247 | 241.867 | 5.968 | |
| 3 | Normal * | Weibull | 81.495 | 41.480 | 246.803 | 6.024 | |
| 4 | Normal * | Weibull | 82.488 | 41.084 | 248.462 | 6.003 | |
| 5 | Normal * | Weibull | 81.527 | 43.051 | 252.825 | 5.993 | |
| 6 | Weibull | Weibull | 95.588 | 2.182 | 249.368 | 6.065 | |
| 1 | 350 | Normal * | Weibull | 74.503 | 39.728 | 230.789 | 5.976 |
| 2 | Weibull | Weibull | 87.562 | 2.004 | 236.017 | 6.054 | |
| 3 | Normal * | Weibull | 78.117 | 42.308 | 247.135 | 5.906 | |
| 4 | Normal * | Weibull | 75.439 | 39.915 | 235.329 | 5.911 | |
| 5 | Normal * | Weibull | 76.278 | 41.969 | 243.520 | 5.901 | |
| 6 | Weibull | Weibull | 86.505 | 1.907 | 239.640 | 5.934 | |
| 1 | 380 | Weibull | Weibull | 71.480 | 1.987 | 196.789 | 5.975 |
| 2 | Normal * | Weibull | 63.222 | 33.497 | 198.781 | 5.940 | |
| 3 | Weibull | Weibull | 73.144 | 2.108 | 197.160 | 5.988 | |
| 4 | Normal * | Weibull | 63.038 | 32.635 | 196.254 | 5.943 | |
| 5 | Normal * | Weibull | 64.704 | 33.599 | 201.026 | 6.009 | |
| 6 | Normal * | Weibull | 63.738 | 33.586 | 199.672 | 5.962 | |
| 1 | 410 | Normal * | Weibull | 51.430 | 25.870 | 158.854 | 6.148 |
| 2 | Weibull | Weibull | 62.150 | 2.066 | 170.462 | 6.092 | |
| 3 | Normal * | Weibull | 54.697 | 26.289 | 159.983 | 6.096 | |
| 4 | Normal * | Weibull | 49.755 | 25.972 | 157.128 | 6.027 | |
| 5 | Normal * | Weibull | 51.010 | 26.393 | 163.011 | 6.079 | |
| 6 | Normal * | Weibull | 51.879 | 25.945 | 162.573 | 6.043 | |
| 1 | 440 | Normal * | Weibull | 45.482 | 22.385 | 139.755 | 6.158 |
| 2 | Weibull | Weibull | 52.573 | 2.283 | 139.483 | 6.218 | |
| 3 | Weibull | Weibull | 53.685 | 2.204 | 146.332 | 6.230 | |
| 4 | Normal * | Weibull | 47.310 | 23.696 | 147.395 | 6.139 | |
| 5 | Normal * | Weibull | 48.066 | 23.824 | 148.953 | 6.226 | |
| 6 | Normal * | Weibull | 45.956 | 22.924 | 142.593 | 6.141 |
| Correlating Pairs | Spearman’s Correlation Coefficient | Estimated Value of Statistical Significance Level |
|---|---|---|
| b_left—σ0.2 | 0.865 | 2.343 × 10−15 |
| b_left—σU | 0.933 | <2.2 × 10−16 |
| b_left—ε0.2 | 0.841 | 7.314 × 10−14 |
| b_left—εU | −0.627 | 1.822 × 10−06 |
| a_left—σ0.2 | 0.193 | 0.189 |
| a_left—σU | 0.002 | 0.991 |
| a_left—ε0.2 | −0.095 | 0.520 |
| a_left—εU | −0.333 | 0.021 |
| b_right—σ0.2 | 0.934 | <2.2 × 10−16 |
| b_right—σU | 0.989 | <2.2 × 10−16 |
| b_right—ε0.2 | 0.859 | 6.015 × 10−15 |
| b_right—εU | −0.703 | 2.59 × 10−8 |
| a_right—σ0.2 | −0.437 | 0.002 |
| a_right—σU | −0.467 | 0.001 |
| a_right—ε0.2 | −0.479 | 0.001 |
| a_right—εU | 0.440 | 0.002 |
| Equation | SD | No Eq. |
|---|---|---|
| 5.657 | (19) | |
| 27.220 | (20) | |
| 1.485 | (21) | |
| 0.056 | (22) |
| No of Samples | Heat Treatment Temperature, °C | Deviation of Theory from Empirics (15), % |
|---|---|---|
| 1 | 20 | 3.986 × 10−3 |
| 2 | 3.925 × 10−3 | |
| 3 | 3.840 × 10−3 | |
| 4 | 3.745 × 10−3 | |
| 5 | 3.414 × 10−3 | |
| 6 | 3.408 × 10−3 | |
| 1 | 260 | 4.007 × 10−3 |
| 2 | 4.072 × 10−3 | |
| 3 | 3.940 × 10−3 | |
| 4 | 4.019 × 10−3 | |
| 5 | 3.710 × 10−3 | |
| 6 | 3.725 × 10−3 | |
| 1 | 290 | 4.163 × 10−3 |
| 2 | 3.876 × 10−3 | |
| 3 | 3.579 × 10−3 | |
| 4 | 4.039 × 10−3 | |
| 5 | 4.095 × 10−3 | |
| 6 | 3.861 × 10−3 | |
| 1 | 320 | 4.351 × 10−3 |
| 2 | 4.735 × 10−3 | |
| 3 | 4.458 × 10−3 | |
| 4 | 4.371 × 10−3 | |
| 5 | 4.086 × 10−3 | |
| 6 | 4.388 × 10−3 | |
| 1 | 350 | 4.398 × 10−3 |
| 2 | 4.197 × 10−3 | |
| 3 | 3.655 × 10−3 | |
| 4 | 4.164 × 10−3 | |
| 5 | 3.776 × 10−3 | |
| 6 | 3.974 × 10−3 | |
| 1 | 380 | 5.635 × 10−3 |
| 2 | 5.422 × 10−3 | |
| 3 | 5.657 × 10−3 | |
| 4 | 5.668 × 10−3 | |
| 5 | 5.272 × 10−3 | |
| 6 | 5.367 × 10−3 | |
| 1 | 410 | 7.045 × 10−3 |
| 2 | 6.551 × 10−3 | |
| 3 | 6.899 × 10−3 | |
| 4 | 6.952 × 10−3 | |
| 5 | 6.784 × 10−3 | |
| 6 | 6.917 × 10−3 | |
| 1 | 440 | 7.962 × 10−3 |
| 2 | 8.117 × 10−3 | |
| 3 | 7.009 × 10−3 | |
| 4 | 6.927 × 10−3 | |
| 5 | 6.755 × 10−3 | |
| 6 | 7.467 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigoriev, S.N.; Nikitin, N.Y.; Frolov, A.; Shapovalov, P.; Medeltsev, A.; Voronov, M.; Khmyrov, R.; Idarmachev, I.; Peretyagin, P. Modeling of Tensile Stress Distribution Considering Anisotropy of Mechanical Properties of Thin-Walled AlSi10Mg Samples Obtained by Selective Laser Melting. J. Manuf. Mater. Process. 2024, 8, 235. https://doi.org/10.3390/jmmp8050235
Grigoriev SN, Nikitin NY, Frolov A, Shapovalov P, Medeltsev A, Voronov M, Khmyrov R, Idarmachev I, Peretyagin P. Modeling of Tensile Stress Distribution Considering Anisotropy of Mechanical Properties of Thin-Walled AlSi10Mg Samples Obtained by Selective Laser Melting. Journal of Manufacturing and Materials Processing. 2024; 8(5):235. https://doi.org/10.3390/jmmp8050235
Chicago/Turabian StyleGrigoriev, Sergey N., Nikita Yu. Nikitin, Aleksander Frolov, Petr Shapovalov, Anton Medeltsev, Mikhail Voronov, Roman Khmyrov, Idarmach Idarmachev, and Pavel Peretyagin. 2024. "Modeling of Tensile Stress Distribution Considering Anisotropy of Mechanical Properties of Thin-Walled AlSi10Mg Samples Obtained by Selective Laser Melting" Journal of Manufacturing and Materials Processing 8, no. 5: 235. https://doi.org/10.3390/jmmp8050235
APA StyleGrigoriev, S. N., Nikitin, N. Y., Frolov, A., Shapovalov, P., Medeltsev, A., Voronov, M., Khmyrov, R., Idarmachev, I., & Peretyagin, P. (2024). Modeling of Tensile Stress Distribution Considering Anisotropy of Mechanical Properties of Thin-Walled AlSi10Mg Samples Obtained by Selective Laser Melting. Journal of Manufacturing and Materials Processing, 8(5), 235. https://doi.org/10.3390/jmmp8050235









