Abstract
Chip morphology is an intrinsic characteristic of the machining process that determines the quality of the process. When machining low machinability materials, the chips formed are usually long, continuous, and difficult to break. Due to the negative effect of the accumulation of the chip along the process, chip breakage and the correct extraction out of the machining area have become indispensable requirements. Although numerous chip-breaking methodologies have been proposed, modulation-assisted machining (MAM) is one of the most promising approaches, due to its independence from the workpiece material, tool geometry, and cutting conditions. In this work, a comparison of different modulation-assisted machining strategies, based on the modulation of the feed (F-MAM) or the depth of cut (D-MAM), were experimentally evaluated and compared to conventional turning in terms of chip morphology, surface roughness, and tool wear. Results showed that both MAM strategies enabled chip breakage and improved chip evacuation in comparison to conventional turning; however, D-MAM showed a better performance in terms of tool wear and surface roughness.
1. Introduction
In continuous machining processes, especially in turning operations, there are many factors that have an influence on the efficiency of the process and product quality. In addition, factors such as cutting parameters, tool wear, or chip morphology need to be controlled along the machining process to meet the established tolerances and to optimize production time. Nevertheless, one of the major challenges in the continuous machining process is chip formation. Unlike milling, where the tool constantly engages and disengages the workpiece, conventional turning, boring, and threading operations typically exhibit continuous cutting, creating long and continuous chips. This chip formation is usual when machining austenitic low machinability materials commonly used by the aeronautical industry, such as nickel-based superalloys or precipitation-hardened austenitic stainless steels. This issue is related to the material properties, as the high hardness of the material demands low cutting speeds to avoid high tool wear rates, and the austenitic nature of the metallic matrix makes it difficult to take the material to the breaking point and generate discontinuous chips, even with the use of advanced chip-breaker geometries. The excess chip length leads to the entanglement of the chip with the tool or with the workpiece, making chip evacuation a great challenge. Especially during the vertical turning of big parts, the need to remove the chips from the machine can generate the highest process inefficiencies in a machining installation. Also, the chip entanglement can generate damages on the tools and parts, which can lead to even greater time losses and, in the case of high added value parts, significantly higher costs [1].
However, there are some techniques that enable chip discontinuity and, therefore, improved chip evacuation:
- Cutting tool inserts with the chip breaker included in their geometry.
- Systems capable of breaking the continuous chip after it is generated [2,3].
- High-pressure cutting fluid to deform the chip and help in its breakage [4,5].
- Modulation-assisted machining (MAM).
In the present work, modulation-assisted machining is proposed as a chip control technique. This is based on nullifying the undeformed chip thickness in the cutting process, adding a harmonic oscillation on top of the standard movement of the tool. Such harmonic oscillation can be added both in the feed (F-MAM) or the depth of cut directions (D-MAM). This way, the insert periodically disengages the workpiece, producing discontinuous chips.
Concerning the development of this technique, the pioneering works in this chip-breaking approach were initiated by Satel et al. in 1961 [6], who described the kinematic conditions for sinusoidal tool oscillations in the direction of the feed (F-MAM). Ostwald [7] mathematically defined the required amplitude for the breakage of the chips, showing that the minimum amplitude to break the chip is obtained for ratios between a workpiece rotation frequency and an oscillation frequency (/) of 0.5, with this being the amplitude of half of the feed per revolution.
Regarding the practical achievement of the tool motion, Ostwald designed a mechanical apparatus composed of a flexible tool in the feed direction, which reached an oscillation frequency of 50 Hz and an amplitude of 1.12 mm. Due to the limited applicability, Skelton [8] presented a hydraulically actuated device capable of reaching 125 Hz of actuation and enabling the frequency of the oscillation and the amplitude to be set independently. In order to obtain higher actuator frequencies, fast tool servos (FTS) were used, which were able to produce oscillations of over 1 kHz in bandwidth in the feed direction [9]. Mechanical devices were also used for MAM chip breaking, as used by the MITIS company for drilling operations [10].
Apart from the beforementioned MAM applications, some works used the ordinary drives of the machines to perform required oscillations for the chip breakage. Chhabra et al. [11] designed a 400 Hz bandwidth linear drive capable of generating a linear motion with superimposed modulation in the feed direction, enabling chip breaking in drilling operations. Woody et al. [12] proposed a CNC toolpath-based approach to break the chips in turning operations. Although chip breakage was achieved, the modulation was programmed by means of trajectory generation in the CNC program, which is valid for its implementation at a workshop-level. According to the process parameters, Astarloa et al. [13] analyzed MAM parameters, oscillation frequency, and amplitude, respectively, with the aim of selecting the most appropriate oscillation parameters according to the machine oscillation capability and process parameters for heavy-duty vertical turning machines. They proposed a methodology to characterize the oscillation capability of the machine and to automatically select the F-MAM parameters [14].
The tool wear, surface roughness, and temperature variation generated by the application of this chip-breaking technique were also analyzed by different authors. Smith et al. [15] concluded that as MAM involves an air-cutting phase where the tool is cooled down, in this way, a reduction in the wear can be obtained, in comparison to conventional turning. Mann et al. [9] analyzed the chip formation and the benefits of the modulation-assisted machining, including the tool wear and surface texture, concluding that the production of short chips facilitates the reach of the coolant to the cutting edge, resulting in reduced wear. Gao et al. [16,17] developed a model for the prediction of the surface topography and thermal effects, showing that MAM can reduce the average tool temperature by 30%, compared to conventional machining. However, the beforementioned MAM applications were conducted in small-size lathes with extremely low chip loads. Therefore, the conclusions may not be extrapolated to heavy-duty machining.
Finally, although the modulation of the tool path in the feed direction is a powerful tool for chip breaking, it cannot be applied to threads machining. The main difference for threading operations is that the tool does not encounter the same material surface from the previous revolution. Specifically, as the feed per revolution of the operation is equal to the thread pitch, there is no overlapping with the previous revolution.
As an answer to this limitation, Berglind et al. [18] proposed a variation in the depth of cut direction (D-MAM) for threading operations. This modulation was carried out by means of the machine’s ordinary drives through modulated tool path programming. Therefore, two different ways to apply MAM have been proposed in literature, but the performances of these techniques have not been compared.
The present paper evaluates and compares different MAM techniques for achieving chip breakage during the turning of low machinability materials. First, the industrial implementation of MAM techniques is analyzed, identifying optimized parameters for the application of both D-MAM and F-MAM techniques on big-diameter parts. Then, the evaluation of the performances of such techniques in comparison to conventional turning is carried out on 17-4 PH stainless steel in terms of chip formation, tool wear, and surface roughness. Results indicate that, in contrast to some works in the bibliography [9], both MAM techniques evaluated reduce tool life in comparison to conventional turning, especially the F-MAM technique. Moreover, significantly higher surface roughness values are achieved with this last technique in comparison to the conventional and D-MAM techniques. Finally, the conclusions for the presented work are drawn, indicating further research lines for the application of MAM techniques.
2. Modulation-Assisted Machining
The chip-breaking methods used in the present work are based on nullifying the undeformed chip thickness on the cutting tools, thanks to the harmonic modulation of the tool paths. Considering the kinematics of cylinder turning operations, the modulation of the tool path can be generated either in the feed direction (F-MAM) or in the depth of cut direction (D-MAM), as shown in Figure 1. The implementation of harmonic modulations in both the axial and radial directions using the machine drives is shown in Section 2.1 and Section 2.2, respectively.

Figure 1.
Diagram for a cylinder turning operation and directions for the harmonic modulation.
2.1. Modulation-Assisted Machining through Feed Variation (F-MAM)
To generate a variable feed turning tool path, a harmonic vibration is added to the tool trajectory in the axial direction of the part. The harmonic oscillation applied on the tool generates an interference between successive passes in the axial direction. Depending on the frequency relationship between the spindle rotation and the frequency of the harmonic modulation, this interference can nullify the chip load when the axial maximum from a previous pass and the axial minimum of the present pass coincide or intersect. In order to achieve this point with the minimum amplitude, the frequency relationship must correspond to an integer +0.5 (i.e., 0.5, 1.5, or 2.5) [7]. Figure 2 shows the tool paths for a conventional turning and for an F-MAM, with an oscillation frequency relationship of 1.5.

Figure 2.
Tool path when applying an F-MAM turning in comparison to conventional turning.
Additionally, the harmonic modification of the tool feed enables the total material removal rate (MRR) to be kept, in comparison to a conventional turning. However, the undeformed chip thickness on the tool varies from zero to double the nominal feed per revolution () value, which generates oscillations on the chip load on the tool. Figure 3a shows the chip load calculated for both conventional turning and the F-MAM operation with a depth of cut ( of 0.5 mm and a feed per revolution ( of 0.15 mm/rev. For a conventional turning operation, the chip load grows as the tool completely enters the part, reaching the nominal value of 0.075 mm2, and decreases down to zero as the tool exists in the part. In the F-MAM turning operation, the chip load follows a similar pattern, but its value oscillates from zero to double the value for conventional turning along the entire turning process. In this way, as the feed per revolution is doubled, the maximum pressure is also doubled in the same differential element of the cutting edge (Figure 3b).

Figure 3.
(a) Chip load values (/ = 1) and (b) pressure variations in the cutting edge for conventional (black arrows) and F-MAM (red arrows) turnings.
In previous works [13,14], a method to evaluate the machine oscillation capability was introduced, together with a procedure for the automatic selection of the oscillation parameters when applying a variable feed turning operation. The present work follows this approach for the application of the F-MAM technique during the experimental analysis (Section 3).
2.2. Modulation-Assisted Machining through Depth of Cut Variation (D-MAM)
When the depth of cut direction MAM is applied in longitudinal turning operations, an oscillation is applied over the radial direction of the workpiece, creating a variation in the actual diameter machined by the tool (Figure 4). This way, the tool leaves the workpiece at some circumferential locations, creating discontinuous chips. Nevertheless, this strategy does not generate a cylindrical shape or, at least, a cylindrical shape coaxial to the starting cylindrical part. Therefore, a second pass without modulation is required to generate a final coaxial cylindrical shape after the execution of an initial variable pass.

Figure 4.
Tool path when applying a D-MAM in comparison to conventional turning (/ = 1).
The length of such discrete chips is dependent upon the oscillation frequency (). When this frequency is equal to the workpiece rotational frequency (), the length of the chip will be the same as the perimeter of the part, producing an eccentric part. Higher oscillation frequencies will generate shorter chips.
In order to compare the D-MAM strategy with conventional turning, the material removal rate (MRR) must be kept constant. Therefore, the maximum depth of cut value in the D-MAM must be double that used during conventional turning. This is shown in Figure 5, where the straight black and blue lines are the cumulative depths of cut for the first and second conventional (as well as F-MAM) machining operations, respectively, while the red and green sinusoidal lines represent the depths of cut for the first and second D-MAM processes, respectively. It must be highlighted that only the first D-MAM machining has a modulated path, while the second one has a conventional trajectory. The non-circumferential shape generated in the first pass makes this second pass generate discontinuous chips with a conventional turning trajectory. This second conventional pass also has a variable chip thickness, due to the effect of the first non-conventional D-MAM pass. Notice that the sum of the depth of cuts of the successive cuts in a certain angular cut is constant (see Figure 5).

Figure 5.
Depth of cut values for two conventional and variable depth of cut passes, depending on the part circumferential angle, for a dimensionless oscillation ratio equal to 1.
In the case of the variable depth of cut MAM, the dimensionless oscillation frequency (/) must be an integer (i.e., 1, 2, 3, …). In case of an uneven relationship between both frequencies, while discontinuous chips will be produced, an interference is created between tool trajectories at different axial locations. Figure 6 shows the X–Y view of the variable depth of cut trajectories for dimensionless oscillation (/) relations of 3 and 1.5. As it can be seen, in the case of an integer relationship, the radial location of the tool trajectory for a circumferential position of the part is kept constant. In the case of an uneven relationship, this radial location is variable. This leads to interferences between the tool and the material left by passes in different axial locations, which makes the chip load on the tool increase over the nominal value. In addition, the value of such an integer must be defined according to the machine’s oscillation capacity and by selecting the highest possible value to produce the shortest possible chips.
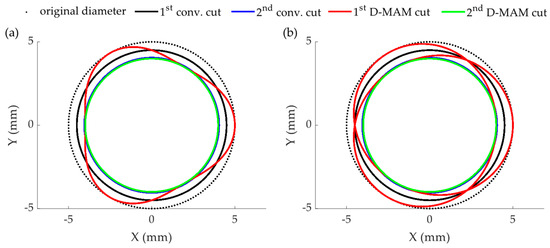
Figure 6.
Tool trajectories for the D-MAM process with different frequency relations: (a) / = 3, and (b) / = 1.5.
The application of D-MAM to achieve a discontinuous chip requires a specific oscillation frequency that can be calculated from the workpiece diameter and the cutting speed. In addition, oscillation frequency is inversely proportional to the workpiece diameter, so in small diameter parts, the oscillation frequency increases. In this way, to apply the MAM technique in small parts (D < 50 mm), linear motors or FTSs are generally needed to reach the required frequency. However, when the size of the part approaches the region of heavy-duty industrial applications (D > 1000 mm), the typical drives used in large-size machine tools can reach the necessary frequency to generate discontinuous chips. Therefore, when large-diameter workpieces are produced, both MAM methods can be applied using the ordinary drives of the machine, no matter the material being cut.
Figure 7a shows the calculated chip load for a D-MAM trajectory when using a 0.15 mm/rev feed per revolution () and a variable depth of cut () of 0–1 mm. As it can be seen, the chip load for the case of an integer frequency relationship (/ = 1) is variable from zero to double the chip load for a conventional turning operation (0.075 mm2). In the case of an uneven, dimensionless (/ = 1.5) oscillation frequency, the chip load can take values up to four times the chip load for conventional turning, which can lead to excessive loads on the cutting tool and generate its breakage. According to the pressure generated in the cutting edge when the D-MAM technique is applied, although a variation in the depth of cut is generated, the maximum pressure on each differential element of the cutting edge has the same value as in the conventional case (black and red arrows in Figure 7b).
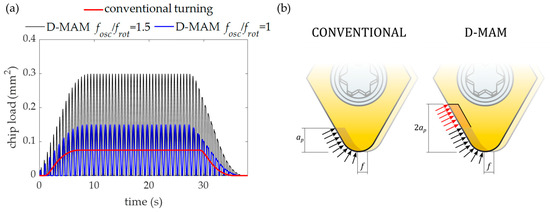
Figure 7.
(a) Chip load values for a conventional turning and a D-MAM with relations of / = 1.5 and / = 1. (b) Pressure variations in the cutting edge for conventional (black arrows) and D-MAM turnings (additional load represented by red arrows).
Regarding the practical implementation of the depth of cut direction MAM, oscillatory trajectories are programmed in the NC code, following the next relationship:
In Equation (1), is the diametral position of the tool, is the diameter of the workpiece, is the depth of cut and is the spindle speed. In order to avoid synchronization issues between axes, the spindle speed is kept constant during the tests.
However, the oscillation of the tool trajectory in the depth of cut direction () generates longer tool path lengths than in conventional turning for a workpiece revolution. Coupled with the differential displacement applied in the feed direction (), the motion in the direction generates an additional displacement that increases the actual tool path length (Figure 8).

Figure 8.
Tool path of the part revolution when applying D-MAM. Differential displacement between red dots highlighted by black lines.
If the programmed feed per revolution value is kept constant, this longer tool path would generate longer machining times than conventional turning, as well as a variable undeformed chip thickness on the tool. To avoid such issues, the programmed feed must be modified too, considering the tool motions in both and directions. For that purpose, the feed per revolution at each trajectory location () can be calculated according to Equation (2), using the modulus of the velocity vector formed by the displacements in the and directions.
3. Experimental Validation
In order to evaluate the performance of the chip-breaking methods in comparison to conventional turning operations, as well as their impact on tool life, turning tests were carried out. A 900 mm diameter rolled ring made of 17-4 PH precipitation-hardened stainless steel in H900 condition (45 ± 1 HRC) was used as the workpiece material, while conventional, oil-based coolant (5% concentration) was used as the cutting fluid. Cylinder turning tests were performed in a Soraluce (FMT-4000,Bergara, Spain) multitasking machine using feed and depth of cut MAM techniques, as well as conventional turning. Table 1 shows the cutting parameters and tools employed during the tests.

Table 1.
Cutting parameters employed during the experimental tests.
Regarding the cutting parameters, the chip load values were selected based on data from the bibliography [19]. The cutting speed was chosen to achieve a tool life of approximately 0.5 h in conventional turning, thereby avoiding excessively long tests. It should be noted that the selected insert had a chip-breaker geometry but could not generate chip breakage during conventional turning. To allow a fair comparison between the results from each test, they were divided into different passes, keeping the removed material (Q) constant for each pass (100 cm3). Three repetitions were performed for each machining strategy.
Regarding the oscillation parameters, their selection should keep the chip length similar in both MAM strategies to perform a fair comparison. However, F-MAM requires oscillation frequencies that are 0.5, 1.5, 2.5… times the rotational frequency to break the chips with the minimum variation [13]. On the contrary, D-MAM requires oscillation frequencies that are integer multiples of the rotational frequency. Therefore, it is not possible to achieve similar chip lengths for the same workpiece diameter. Bearing in mind machine drive limitations and the high mass of the machine components, the lowest dimensionless oscillation frequencies of 1.5 and 1 were selected for F-MAM and D-MAM, respectively, to avoid synchronization errors and to ensure accurate MAM oscillations.
3.1. Chip Generation
During conventional cutting tests, big chip nests were generated around the cutting tool. Figure 9a shows highlighted by a yellow circle one of these chip nests entangled between the part and the cutting tool. On the contrary, during the use of both MAM techniques, the generation of discrete-length chips was achieved, leaving the cutting zone free from chip nests (Figure 9b). The chips obtained for each test were collected to evaluate the capability of the applied modulation-assisted machining techniques to improve the chip control, in comparison to conventional turning operations (Figure 10). As it can be seen, the conditions employed during the conventional turning operation were unable to generate chip breakage, leading to long chips. During the execution of the machining tests, such long chips were rolled around the part and the fixture, generating impacts on the tool, as well as in the machine head and enclosure. Moreover, the chip nests stuck in the cutting zone would scratch the machined surface during the turning operation.

Figure 9.
Execution of machining tests for (a) conventional turning where a chip nest entangled between the part and the tool can be seen and (b) F-MAM.
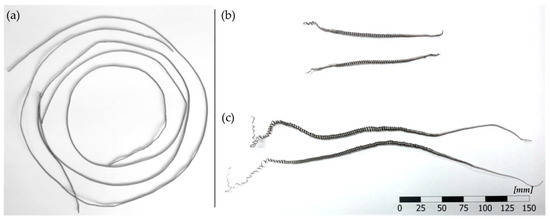
Figure 10.
Examples of chips obtained during (a) conventional turning, (b) F-MAM, and (c) D-MAM.
In the case of MAM, discontinuous chips were obtained during the feed and depth of cut modulation tests, as shown in Figure 10b and Figure 10c, respectively. In both cases, the chips showed variable thicknesses, from thin ends to a sturdy center, corresponding to the variable chip load generated when applying the MAM techniques. The different chip lengths were related to the optimum oscillation parameters, as different / ratios must be used for chip breakage in both techniques. With the employed ratios, D-MAM produced one chip per revolution, while 1.5 chips were generated with F-MAM.
While significantly lower-sized chips were reported in the bibliography [4,9,18], those results were obtained with low-mass and high-dynamic Swiss-type turning centers. The chip lengths obtained in the present work, adapting the MAM techniques to the oscillation capabilities of heavy-duty machines, were adequate to avoid the issues related to chip entanglement and control indicated above.
3.2. Tool Wear
After each machining pass, images of the flank and rake faces of the tools were obtained using a Koolertron 5 MP 20–300 × USB microscope(Hong Kong Karstone Technology Co., Shenzhen, China). Figure 11 shows images obtained for the rake faces of the tools after one machining pass for conventional, F-MAM, and D-MAM tests. The yellow lines overlaid on the images highlight the tool–chip contact area on the rake face on the tools. As it can be seen, the tool–chip contact area obtained for MAM tests increased consistently with the direction of the applied oscillation in comparison to conventional turning. When the oscillation was applied in the axial direction (F-MAM), the undeformed chip thickness increased, while the chip width on the tool was kept constant. The contrary can be observed for the case of radial oscillations (D-MAM), where the chip width was increased, while the chip thickness was kept constant.

Figure 11.
Images of the rake faces of tools from (a) conventional turning, (b) F-MAM, and (c) D-MAM. The yellow lines indicate the tool-chip contact area for each case.
Regarding the tool flank wear (VB), Figure 12 shows the evolution for the mean values of different repetitions after each machining pass for each tested condition, together with the associated 3σ error bars. While the classical criteria to stop the machining tests are based on reaching VB = 0.3 mm [20], the performed tests could not reach such a limit, due to the appearance of catastrophic failure on the cutting edges. As it can be seen, conventional turning generated lower tool wear than tested MAM techniques, from which the variable feed technique generated the highest VB values. The achievable removed material volumes were 300, 400, and 500 cm3 for variable feed, variable depth of cut, and conventional turning, respectively. It is also noteworthy that the variable feed technique showed the highest variabilities for the VB values obtained from different test repetitions.
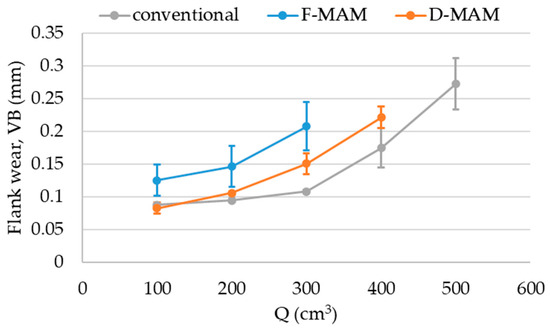
Figure 12.
Tool flank wear (VB) evolution along the cutting tests.
In contrast to the results in the bibliography [9], both MAM techniques increased the tool wear in comparison to conventional turning. The oscillatory movements of the MAM techniques can induce higher thermo-mechanical fatigue on the tool, which could lead to the higher wear results observed in comparison to conventional turning. Both MAM techniques presented in the manuscript generated oscillations on the chip load to achieve chip discontinuities. However, F-MAM increased the uncut chip thickness up to double the nominal value to generate the chip discontinuities. In comparison to F-MAM, D-MAM also doubled the chip load, but it was redistributed along the longer tool edge without increasing the uncut chip thickness (Figure 11). Since the tool wear did not follow a linear relationship with the uncut chip thickness, the higher uncut chip thickness values generated with F-MAM can be the reason for the higher tool wear generated in comparison to D-MAM. In addition, the chip generated in the present study was long, compared to the studies presented in literature [9], due to the limitations of the machine dynamics, and therefore, the tool life cannot be improved, due to the better lubrication condition generated by a more efficient chip breakage.
3.3. Surface Roughness
Concerning the generated surfaces, the roughness of the machined surface was measured axially on different circumferential locations of the part using a Mitutoyo SurfTest SJ-210(Mitutoyo Corporation, Kawasaki, Kanagawa, Japan) surface roughness tester. As in the case of the tool wear measurements, these measurements were performed after each machining pass, with three measurement repetitions at four equidistant circumferential angles of the part. The parameters for the roughness measurements were a sampling length of 0.8 mm and an evaluation length of 4 mm, according to the ISO 4288:1996 standard [21].
The evolutions of the measured mean surface roughness (Ra) and maximum surface height (Rz) are displayed in Figure 13. The mean values and 3σ error bars for the values obtained after each pass from the different repetitions for each test are shown. While the Ra and Rz values for conventional turning and D-MAM were close to each other, the F-MAM technique generated substantially higher mean values for both Ra and Rz measurements. In addition, high scatter can be observed in the roughness values for the F-MAM technique, generating considerably wider 3σ error bars.
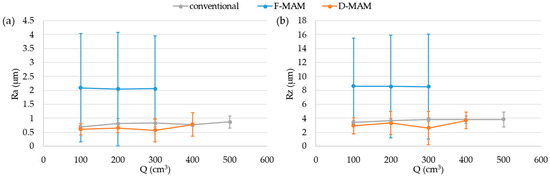
Figure 13.
Mean surface roughness (Ra) (a) and maximum surface height (Rz) (b) evolutions along the cutting tests.
The origin of this scatter is related to the kinematic dependency of the surface roughness in turning operations, with the surface roughness dependent partially on the feed per revolution and the nose radius of the tool. Therefore, a variation in the feed per revolution generated a variable surface roughness in the part. As this variation was generated in all the peripheries of the part, different roughness values were generated around the part. In addition, as the feed per revolution was doubled in some areas, the overall roughness value was also increased. This behavior was confirmed by roughness measurements at different angular locations of the part (Figure 14), as well as results reported in the bibliography [9,16]. In summary, while the conventional turning and D-MAM techniques yielded similar values for the roughness parameters at different parts of circumferential locations, the values obtained for the F-MAM technique varied. This was the main reason behind the high variability of the roughness values of the F-MAM technique in Figure 13.

Figure 14.
(a) Mean surface roughness (Ra) and (b) maximum surface height (Rz) along the circumferential angle of the part.
4. Conclusions
Different machining path modulation strategies were compared, using the machine’s own drives to produce an oscillation either in the direction of the feed or the depth of cut, to produce discontinuous chips in turning operations. The applications of both MAM techniques tested can generate discontinuous chips, avoiding the chip control issues observed during the tests performed with conventional turning. The required drive bandwidth for the generation of the modulation is dependent on the workpiece diameter and material being cut. In the case of heavy-duty parts (D > 1000 mm), the ordinary drives of the machine can be used to produce the modulation in both the F-MAM and D-MAM methods.
As the modulation in the depth of cut direction creates an oval surface, a second machining operation is needed to obtain the final part geometry. Therefore, the process planning must be modified for its application. However, this technique allows chip breaking in threading operations, which cannot be achieved by the feed variation MAM.
Under tested conditions, the chip-breaking functionality of MAM techniques have the cost of reducing tool life in comparison to conventional turning. F-MAM showed higher wear values than D-MAM, possibly due to the overload of the cutting edge when the uncut chip thickness was doubled to break the chip. In the case of the D-MAM, the chip width was increased, with the generated wear being an intermediate value between the F- MAM and the conventional turning. It is noteworthy to mention that the results may vary depending on the chip-breaking application. Although the tendency was clear under the tested conditions, in some applications, the results may differ, due to the improved lubrication of the cutting edge when chips are properly broken. Therefore, the relationship between the wear due to overstress in the cutting edge and the one due to improper lubrication will define the overall wear.
Regarding the surface roughness, D-MAM showed similar values to the ones obtained from conventional turning. When F-MAM was applied, surface roughness values were higher, due to the need to double the feed per revolution to keep the MRR constant while breaking the chips. As the roughness of turning operations is directly related to the feed per revolution value, its increase in chip breaking entailed the beforementioned surface roughness value increase. Additionally, this behavior resulted in a variable surface roughness along the part’s angular positions.
As a general conclusion, considering the effects of MAM techniques on the tool wear and surface roughness, they should be applied in cases where the chip control is the main cause of inefficiencies and time losses or is detrimental to the final quality and integrity of high added value parts. Comparing both MAM strategies, both are successful in generating discontinuous chips, but D-MAM can be more advantageous than F-MAM, as it produces lower tool wear and better surface roughness. However, F-MAM can provide higher flexibility for its application, while D-MAM would require creating tool trajectories with computer-aided manufacturing (CAM), as well as a modification of the production plan, as a secondary machining is needed to eliminate the non-circumferential geometry.
Clarifying the effect of MAM techniques during the process design phases would require further evaluation of their effects on the tool wear and surface roughness. Further research should be performed by analyzing the variable thermo-mechanical loads generated and their relationship with the fatigue behavior of the tool and the increased tool wear.
Author Contributions
Conceptualization, M.H.F. and J.M.; methodology, I.L.; software, A.R and I.M.; validation, A.R., A.A. and I.L.; formal analysis, I.L. and J.M.; investigation, A.A and I.L.; resources, A.A. and I.M.; data curation, A.R. and A.A.; writing—original draft preparation, A.R. and A.A.; writing—review and editing, I.M. and J.M.; visualization, A-R. and A.A.; supervision, M.H.F.; project administration, J.M.; funding acquisition, I.M. and J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded from the European Union’s Horizon 2020 Research and Innovation. Programme under the project InterQ (grant agreement No. 958357), and it is an initiative of the Factories-of-the-Future (FoF) Public Private Partnership
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shaw, M.C. Metal Cutting Principles, 2nd ed; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Güllü, A.; Karabulut, S. Dynamic chip breaker design for Inconel 718 using positive angle tool holder. Mater. Manuf. Process. 2008, 23, 852–857. [Google Scholar] [CrossRef]
- Shamoto, E.; Aoki, T.; Sencer, B.; Suzuki, N.; Hino, R.; Koide, T. Control of chip flow with guide grooves for continuous chip disposal and chi-pulling turning. CIRP Ann. 2011, 60, 125–128. [Google Scholar] [CrossRef]
- Bergs, T.; Splettstößer, A.; Schraknepper, D. Pulsating high-pressure cutting fluid supply for chip control in finish turning of Inconel 718. In Proceedings of the 15th International Conference on High Speed Machining (MM Science Journal), Prague, Czech Republic, 8–9 October 2019. [Google Scholar] [CrossRef]
- Splettstoesser, A.; Schraknepper, D.; Bergs, T. Influence of the frequency of pulsating high-pressure cutting fluid jets on the resulting chip length and surface finish. Int. J. Adv. Manuf. Technol. 2021, 117, 2185–2196. [Google Scholar] [CrossRef]
- Satel, E.A.; Podurev, V.N.; Kamelov, V.S.; Bezborodov, A.M. Potentialities of vibratory turning. Stank. Instrum. 1961, 32, 45–50. [Google Scholar]
- Ostwald, P.F. Dynamic Chip Breaking—An Evaluation of the Effects Upon Surface Microgeometry and Free Chip Dimensions. Ph.D. Thesis, Oklahoma State University, Stillwater, OK, USA, 1966. [Google Scholar]
- Skelton, R.C. Turning with an oscillating tool. Int. J. Mach. Tool Des. Res. 1968, 8, 239–259. [Google Scholar] [CrossRef]
- Mann, J.B.; Guo, Y.; Saldana, C.; Compton, W.D.; Chandrasekar, S. Enhancing material removal processes using modulation-assisted machining. Tribol. Int. 2011, 44, 1225–1235. [Google Scholar] [CrossRef]
- Laporte, S.; De Castelbajac, C. Major breakthrough in multi material drilling, using low frequency axial vibration assistance. SAE Int. J. Mater. Manuf. 2013, 6, 11–18. [Google Scholar] [CrossRef]
- Chhabra, N.; Ackroyd, B.; Compton, W.D.; Chandrasekar, S. Low-frequency modulation-assisted drilling using linear drives. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2002, 216, 321–330. [Google Scholar] [CrossRef]
- Woody, B.A.; Smith, K.S.; Adams, D.J.; Barkman, W.E. Assessment of the process parameters and their effect on the chip length when using CNC toolpaths to provide chip breaking in turning operations. In Proceedings of the ASME 2008 International Manufacturing Science and Engineering Conference, Evanston, IL, USA, 7–10 October 2008; pp. 533–540. [Google Scholar] [CrossRef]
- Astarloa, A.; Beudaert, X.; Dombovari, Z.; Fernandes, M.H.; Munoa, J. Application of machine drive oscillations for chip breaking in heavy duty turning operations. Procedia CIRP 2021, 101, 110–113. [Google Scholar] [CrossRef]
- Astarloa, A.; Beudaert, X.; Ealo, J.A.; Álvarez, J.; Fernandes, M.H.; Munoa, J. Chip breaking system or turning applications using machine drive oscillations. DYNA 2020, 95, 100–106. [Google Scholar] [CrossRef]
- Smith, S.; Woody, B.; Barkman, W.; Tursky, D. Temperature control and machine dynamics in chip breaking using CNC toolpaths. CIRP Ann. 2009, 58, 97–100. [Google Scholar] [CrossRef]
- Gao, Y.; Mann, J.B.; Chandrasekar, S.; Sun, R.; Leopold, J. Modelling of tool temperature in modulation-assisted machining. Procedia CIRP 2017, 58, 204–209. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, R.; Chen, Y.; Leopold, J. Analysis of chip morphology and surface topography in modulation assisted machining. Int. J. Mech. Sci. 2016, 111, 88–100. [Google Scholar] [CrossRef]
- Berglind, L.; Ziegert, J. Modulated tool path (MTP) machining for threading applications. Procedia Manuf. 2015, 1, 546–555. [Google Scholar] [CrossRef][Green Version]
- Leksycki, K.; Feldshtein, E.; Lisowicz, J.; Chudy, R.; Mrugalski, R. Cutting Forces and Chip Shaping When Finish Turning of 17-4 PH Stainless Steel under Dry, Wet, and MQL Machining Conditions. Metals 2020, 10, 1187–1201. [Google Scholar] [CrossRef]
- ISO 3685:1993; Tool-Life Testing with Single-Point Turning Tools. International Organization for Standardization: Geneva, Switzerland, 1993.
- ISO 4288:1996; Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Rules and Procedures for the Assessment of Surface Texture. International Organization for Standardization: Geneva, Switzerland, 1996.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).