Droplet Formation and Energy Input during Induction Wire Melting with Pulsed and Constant Generator Power
Abstract
1. Introduction
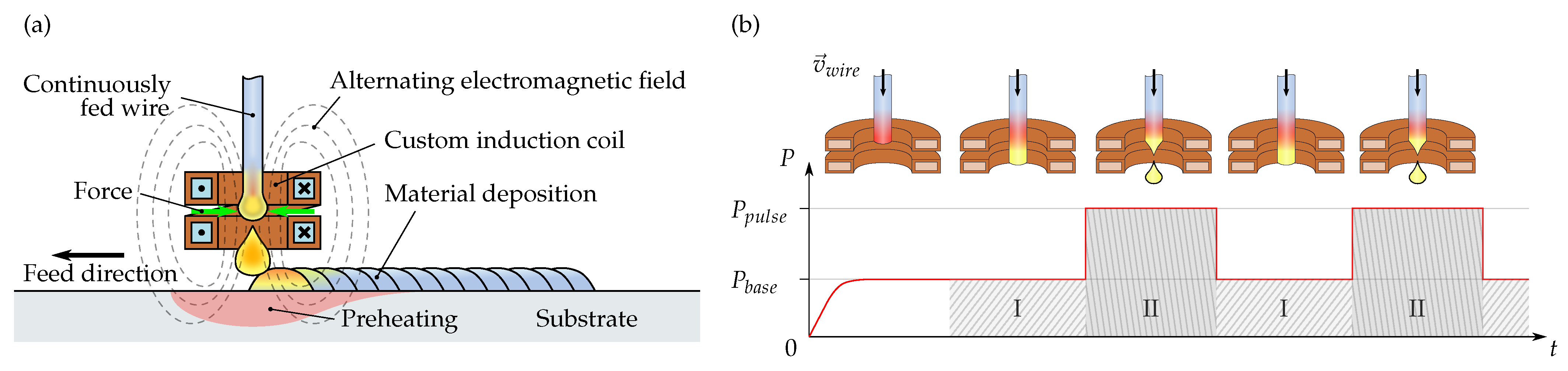
2. Materials and Methods
3. Results and Discussion
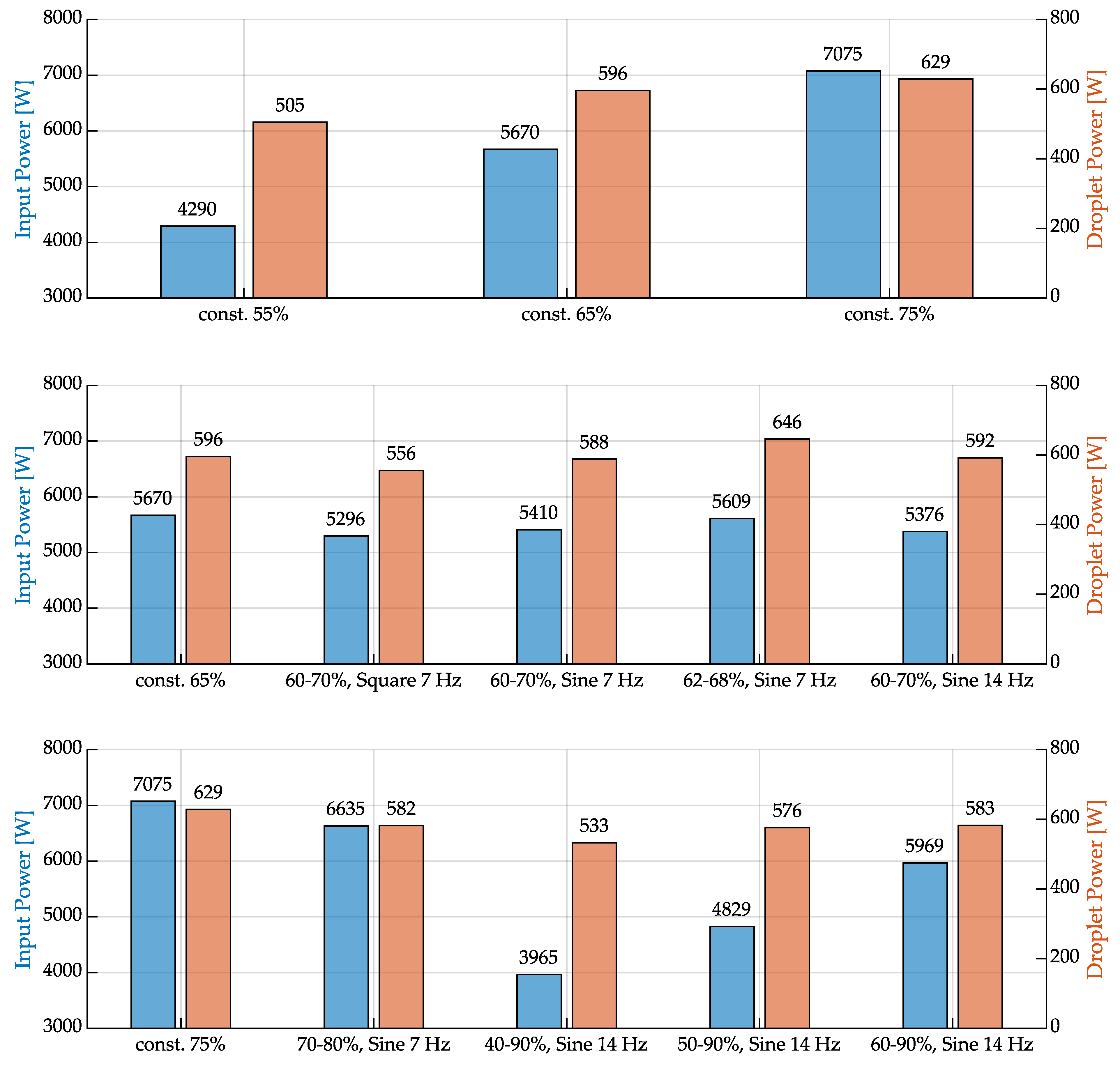
3.1. Generator Response Behavior
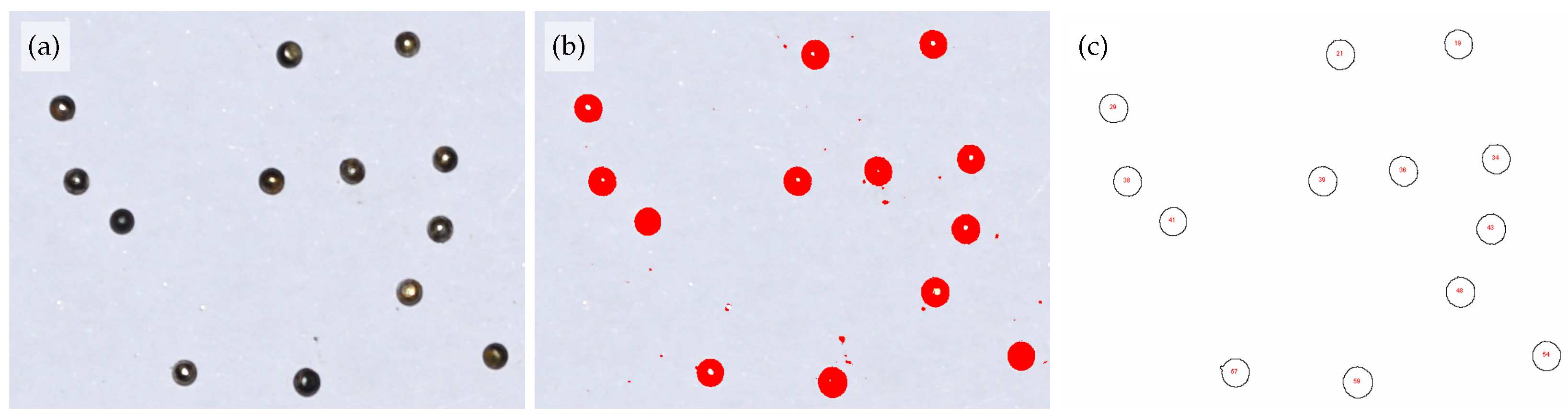
3.2. Droplet Formation and Detachments
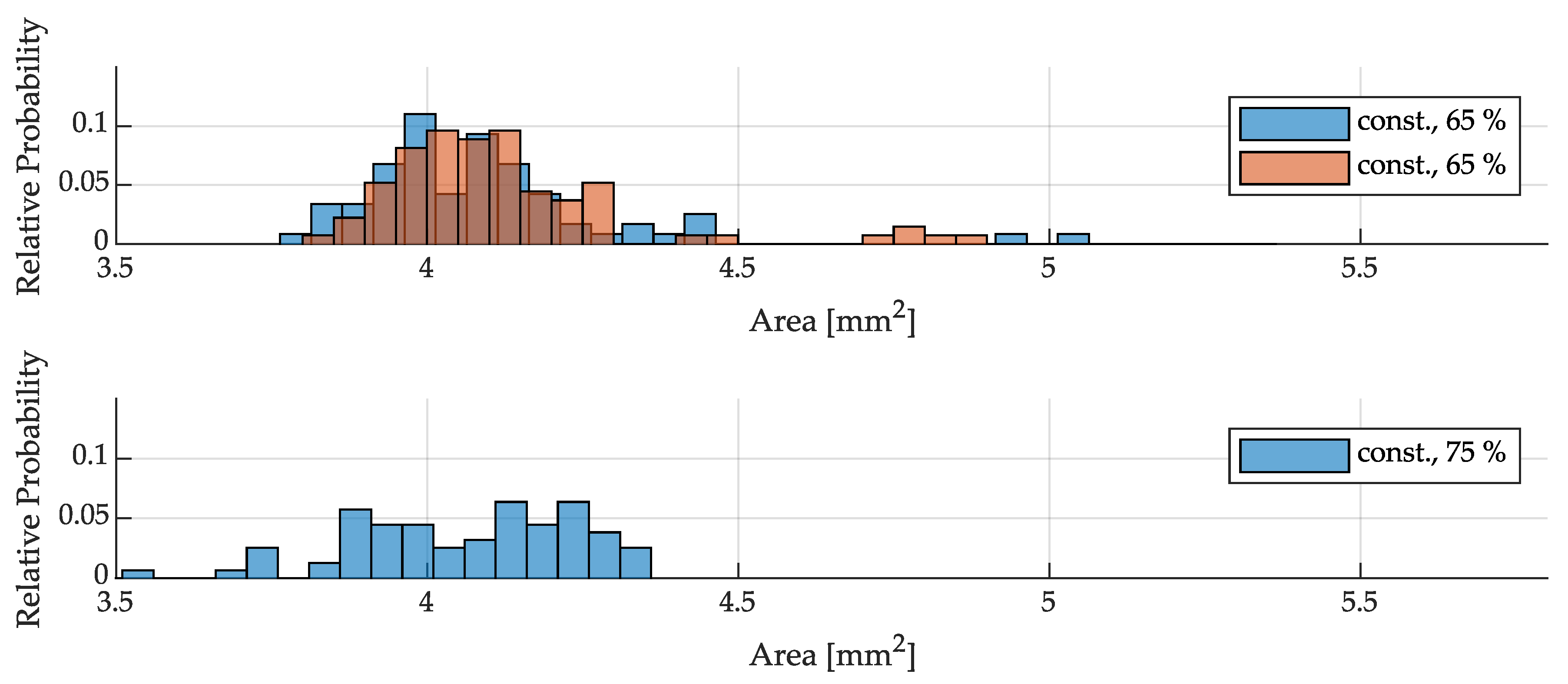
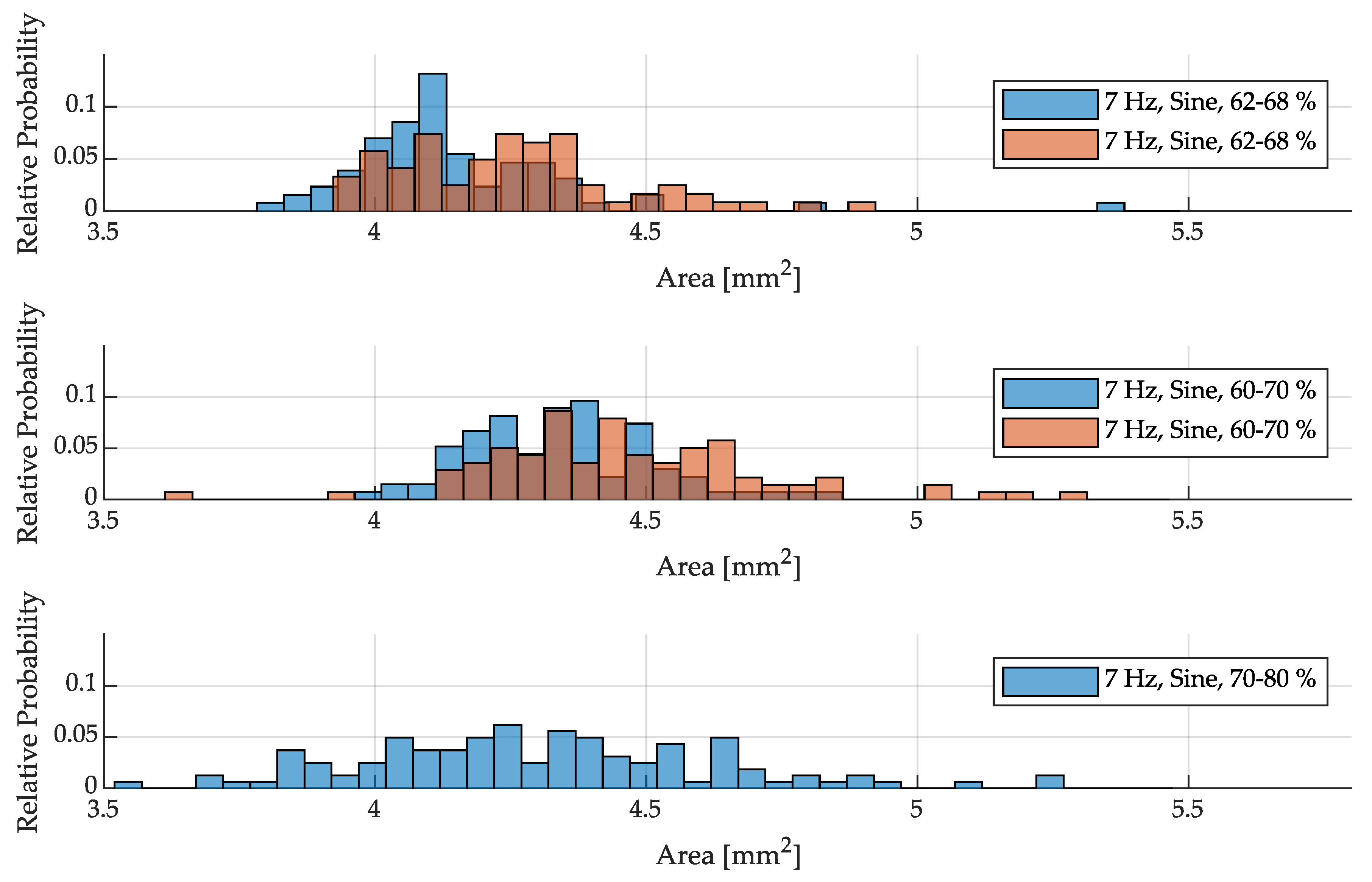
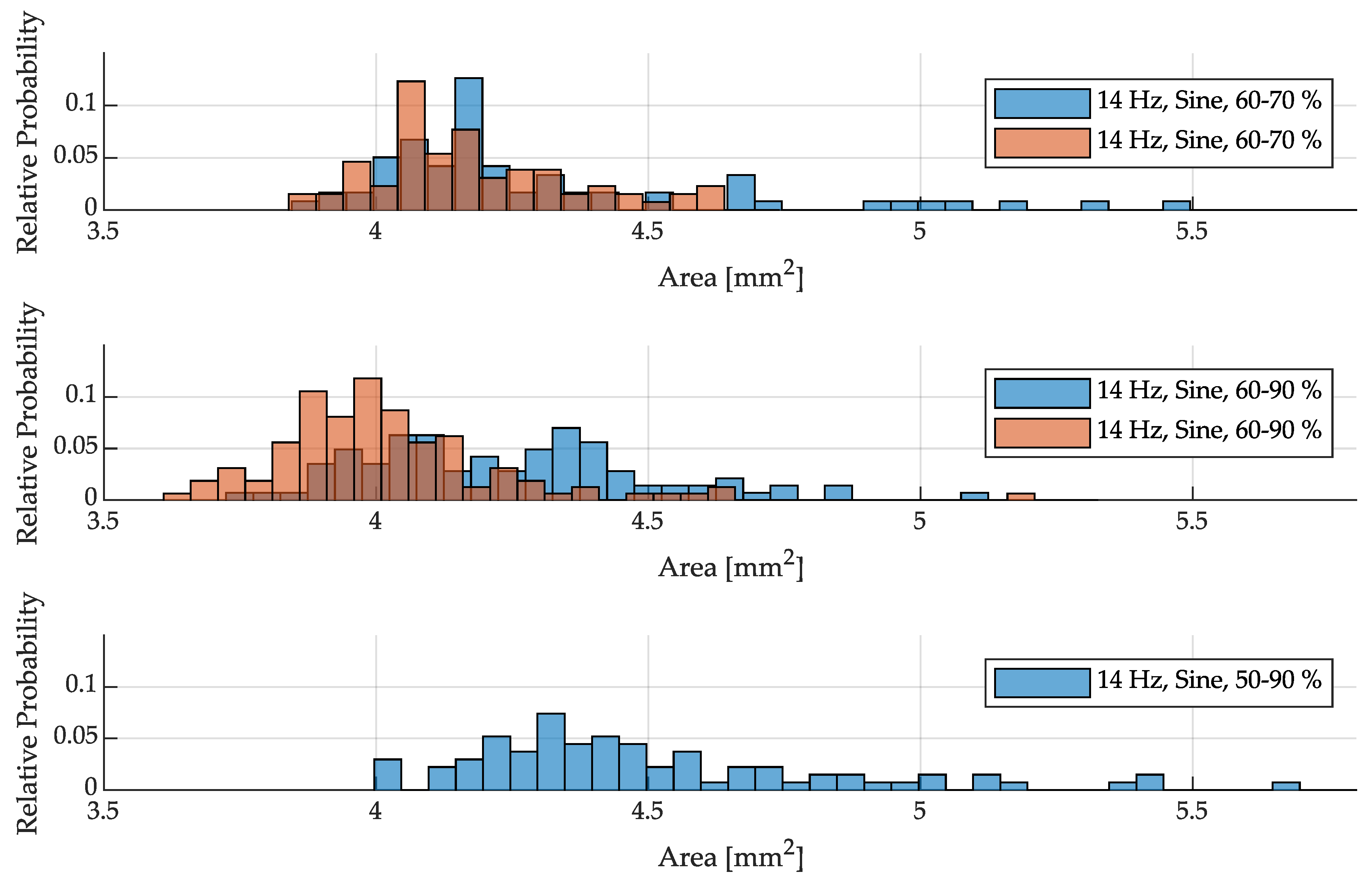
3.3. Size Distribution of Drops
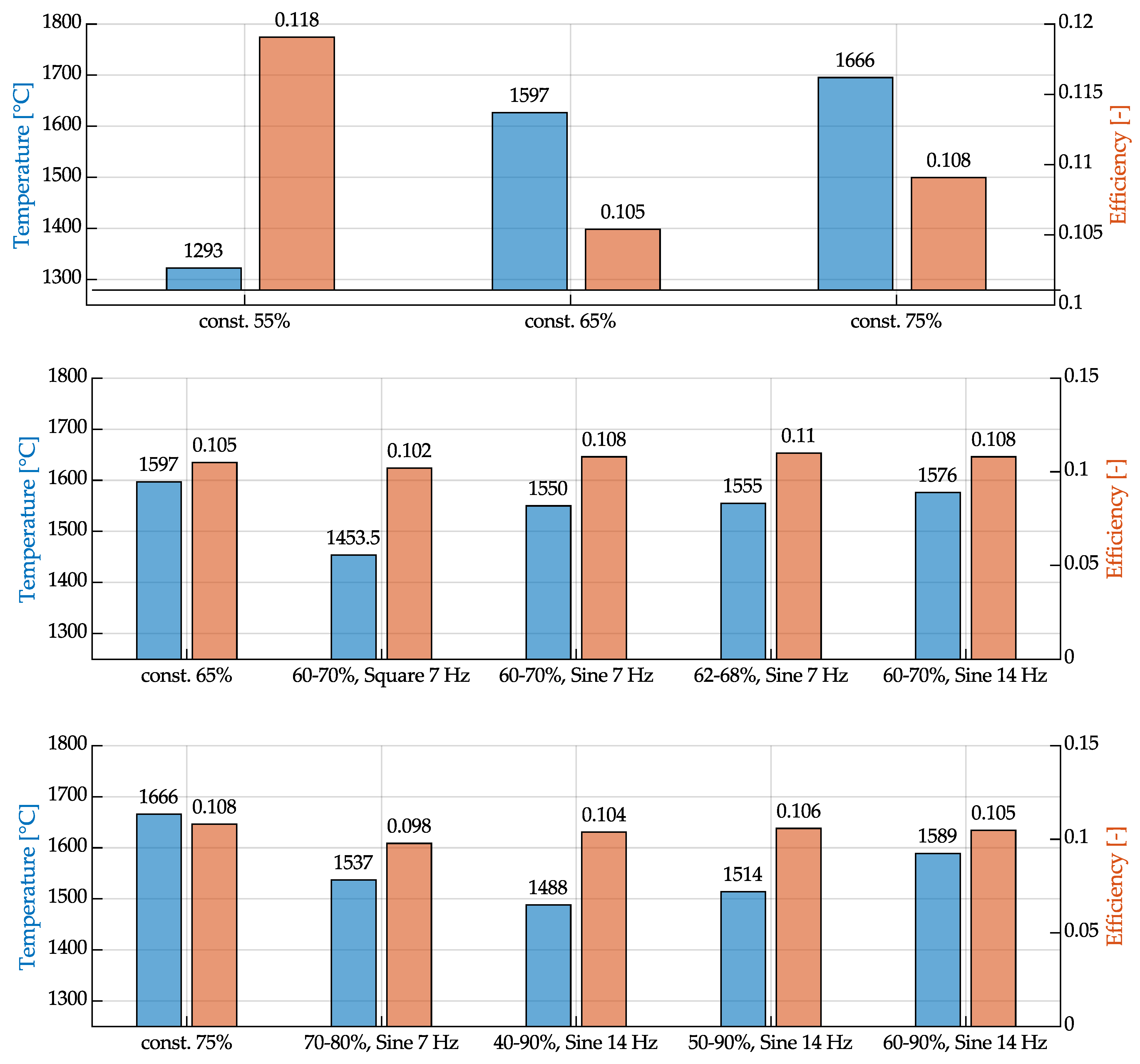
3.4. Droplet Temperature and Efficiency
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wohlers, T.T.; Campbell, I.; Diegel, O.; Huff, R.; Kowen, J. Wohlers Report 2022: 3D Printing and Additive Manufacturing Global State of the Industry; Technical Report; Wohlers Associates: Fort Collins, CO, USA, 2022. [Google Scholar]
- Vafadar, A.; Guzzomi, F.; Rassau, A.; Hayward, K. Advances in Metal Additive Manufacturing: A Review of Common Processes, Industrial Applications, and Current Challenges. Appl. Sci. 2021, 11, 1213. [Google Scholar] [CrossRef]
- Steenhuis, H.J.; Pretorius, L. Consumer additive manufacturing or 3D printing adoption: An exploratory study. J. Manuf. Technol. Manag. 2016, 27, 990–1012. [Google Scholar] [CrossRef]
- Bhavar, V.; Kattire, P.; Patil, V.; Khot, S.; Gujar, K.; Singh, R. A review on powder bed fusion technology of metal additive manufacturing. In Additive Manufacturing Handbook, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 251–253. [Google Scholar] [CrossRef]
- Abd-Elaziem, W.; Elkatatny, S.; Abd-Elaziem, A.E.; Khedr, M.; Abd El-baky, M.A.; Hassan, M.A.; Abu-Okail, M.; Mohammed, M.; Järvenpää, A.; Allam, T.; et al. On the current research progress of metallic materials fabricated by laser powder bed fusion process: A review. J. Mater. Res. Technol. 2022, 20, 681–707. [Google Scholar] [CrossRef]
- Sing, S.L.; Yeong, W.Y. Laser powder bed fusion for metal additive manufacturing: Perspectives on recent developments. Virtual Phys. Prototyp. 2020, 15, 359–370. [Google Scholar] [CrossRef]
- Chowdhury, S.; Yadaiah, N.; Prakash, C.; Ramakrishna, S.; Dixit, S.; Gupta, L.R.; Buddhi, D. Laser powder bed fusion: A state-of-the-art review of the technology, materials, properties & defects, and numerical modelling. J. Mater. Res. Technol. 2022, 20, 2109–2172. [Google Scholar] [CrossRef]
- Kumar, S. Additive Manufacturing Solutions; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Ding, D.; Pan, Z.; Cuiuri, D.; Li, H. Wire-feed additive manufacturing of metal components: Technologies, developments and future interests. Int. J. Adv. Manuf. Technol. 2015, 81, 465–481. [Google Scholar] [CrossRef]
- Gisario, A.; Kazarian, M.; Martina, F.; Mehrpouya, M. Metal additive manufacturing in the commercial aviation industry: A review. J. Manuf. Syst. 2019, 53, 124–149. [Google Scholar] [CrossRef]
- Rudnev, V.; Loveless, D.; Cook, R.L. Handbook of Induction Heating, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Hofmann, C.; Frohlich, A.; Kimme, J.; Wiemer, M.; Otto, T. A Novel Method for Mems Wafer-Level Packaging: Selective and Rapid Induction Heating for Copper-Tin Slid Bonding. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems and Eurosensors XXXIII, TRANSDUCERS 2019 and EUROSENSORS XXXIII, Berlin, Germany, 23–27 June 2019. [Google Scholar] [CrossRef]
- Kräusel, V.; Fröhlich, A.; Kroll, M.; Rochala, P.; Kimme, J.; Wertheim, R. A highly efficient hybrid inductive joining technology for metals and composites. CIRP Ann. 2018, 67, 5–8. [Google Scholar] [CrossRef]
- Kimme, J.; Zeisig, J.; Fröhlich, A.; Kräusel, V. Technology Innovation for the Manual Laser Cladding of High-Alloy Tool Steels. Metals 2021, 11, 1820. [Google Scholar] [CrossRef]
- Vega, E.J.; Cabezas, M.G.; Muñoz-Sánchez, B.N.; Montanero, J.M.; Gañán-Calvo, A.M. A novel technique to produce metallic microdrops for additive manufacturing. Int. J. Adv. Manuf. Technol. 2014, 70, 1395–1402. [Google Scholar] [CrossRef]
- Fang, X.; Du, J.; Wei, Z.; Wang, X.; He, P.; Bai, H.; Wang, B.; Chen, J.; Geng, R.; Lu, B. Study on Metal Deposit in the Fused-coating Based Additive Manufacturing. Procedia CIRP 2016, 55, 115–121. [Google Scholar] [CrossRef]
- Du, J.; Wei, Z.; Wang, X.; Fang, X.; Zhao, G. A novel high-efficiency methodology for metal additive manufacturing. Appl. Phys. A 2016, 122, 945. [Google Scholar] [CrossRef]
- Jayant, H.; Arora, M. Induction Heating Based 3D Metal Printing of Eutectic Alloy Using Vibrating Nozzle. In Advances in Additive Manufacturing, Modeling Systems and 3D Prototyping, Proceedings of the AHFE 2019 International Conference on Additive Manufacturing, Modeling Systems and 3D Prototyping, Washington, DC, USA, 24–28 July 2019; Springer International Publishing: Cham, Switzerland, 2020; Volume 975, pp. 108–118. [Google Scholar] [CrossRef]
- Sharma, G.K.; Pant, P.; Jain, P.K.; Kankar, P.K.; Tandon, P. On the suitability of induction heating system for metal additive manufacturing. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 219–229. [Google Scholar] [CrossRef]
- Sharma, G.K.; Pant, P.; Jain, P.K.; Kankar, P.K.; Tandon, P. Analysis of novel induction heating extruder for additive manufacturing using aluminum filament. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 1961–1970. [Google Scholar] [CrossRef]
- Englert, L.; Klumpp, A.; Ausländer, A.; Schulze, V.; Dietrich, S. Semi-solid wire-feed additive manufacturing of AlSi7Mg by direct induction heating. Addit. Manuf. Lett. 2022, 3, 100067. [Google Scholar] [CrossRef]
- Hascoët, J.Y.; Parrot, J.; Mognol, P.; Willmann, E. Induction heating in a wire additive manufacturing approach. Weld. World 2018, 62, 249–257. [Google Scholar] [CrossRef]
- Sun, R.; Shi, Y.; Wang, X.; Guo, Y.; Zhou, X. Understanding the thermal process during laser assisted ultra-high frequency induction deposition with wire feeding. Int. J. Heat Mass Transf. 2020, 153, 119536. [Google Scholar] [CrossRef]
- Sun, R.; Shi, Y.; Yang, Y.; Wang, X.; Zhou, X. Microstructure, element segregation and performance of Inconel 625 metal layer deposited by laser assisted ultra-high frequency induction deposition. Surf. Coatings Technol. 2021, 405, 126715. [Google Scholar] [CrossRef]
- Fang, X.; Wei, Z.; Du, J.; Bingheng, L.; He, P.; Wang, B.; Chen, J.; Geng, R. Forming metal components through a novel fused-coating based additive manufacturing. Rapid Prototyp. J. 2017, 23, 893–903. [Google Scholar] [CrossRef]
- Jayant, H.K.; Arora, M. Influence of Workpiece Height on Induction Heating Process for Printing 3D Metal Structures. In Industry 4.0 and Advanced Manufacturing; Springer: Singapore, 2020; pp. 247–259. [Google Scholar] [CrossRef]
- Sharma, G.K.; Pant, P.; Jain, P.K.; Kankar, P.K.; Tandon, P. Numerical and experimental analysis of heat transfer in inductive conduction based wire metal deposition process. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 2395–2407. [Google Scholar] [CrossRef]
- Choubey, R.K.; Patil, M.; Jain, P.K. Tailoring Coil Geometry for Achieving Uniform Heating Through Coil Shape Optimization for Induction Heating-Based Metal Wire Additive Manufacturing. SSRN Electron. J. 2023; in press. [Google Scholar] [CrossRef]
- Prasad, A.K.; Kapil, S.; Bag, S. Critical conditions for melting of metallic wire in induction heating system through numerical simulation and experiments. J. Manuf. Processes 2022, 77, 678–693. [Google Scholar] [CrossRef]
- Prasad, A.K.; Kapil, S.; Bag, S. Tailoring coil geometry for secondary heating of substrate towards the development of induction heating-based wire additive manufacturing. Sci. Technol. Weld. Join. 2023, 28, 209–217. [Google Scholar] [CrossRef]
- Kimme, J.; Fröhlich, A.; Kroll, M.; Kräusel, V. Novel Process Approach for Additive Manufacturing Using Inductive Wire Melting by Forced Droplet Detachment. BHM Berg Hüttenmännische Monatshefte 2023, 168, 226–232. [Google Scholar] [CrossRef]
- Praveen, P.; Yarlagadda, P.; Kang, M. Advancements in pulse gas metal arc welding. J. Mater. Process. Technol. 2005, 164–165, 1113–1119. [Google Scholar] [CrossRef]
- Kimme, J.; Gruner, J.; Fröhlich, A.; Kroll, M. Study of an additive manufacturing technology using pulsed inductive wire melting. Int. J. Appl. Electromagn. Mech. 2024, 1–12. [Google Scholar] [CrossRef]
- DIN EN ISO 14341:2020; Schweißzusätze—Drahtelektroden und Schweißgut zum Metall-Schutzgasschweißen von Unlegierten Stählen und Feinkornstählen. Beuth Verlag: Berlin, Germany, 2020.
- Haelsig, A.; Kusch, M.; Mayr, P. Calorimetric analyses of the comprehensive heat flow for gas metal arc welding. Weld. World 2015, 59, 191–199. [Google Scholar] [CrossRef]
- Malin, V.; Sciammarella, F. Controlling heat input by measuring net power. Weld. J. 2006, 85, 44–50. [Google Scholar]
- JMatPro; v. 6.1; Sente Software Ltd.: Guildford, UK, 2010.
- Rasband, W. ImageJ; v. 1.54f; NIH: Bethesda, MD, USA, 2023. [Google Scholar]
- Matlab; v. 2023b; MathWorks, Inc.: Natick, MA, USA, 2023.
- Benkowsky, G. Induktionserwärmung, 5th ed.; Verl. Technik: Berlin, Germany, 1990; p. 259. [Google Scholar]
- Nacke, B.; Baake, E. Induktives Erwärmen: Wärmen, Härten, Glühen, Löten, Schweißen, 1st ed.; Vulkan-Verlag GmbH: Essen, Germany, 2013; p. 276. [Google Scholar]







| Authors | Year | Material | Melting Temperature [°C] | Wire Diameter [mm] | Frequency [kHz] | Power [kW] | Wire Feed Rate [m/min] |
|---|---|---|---|---|---|---|---|
| Vega et al. [15] | 2014 | Sn95Ag4Cu1 | 217 | 1.5 | 750…1150 | 1.68…2.13 | 0.84…1.8 |
| Fang et al. [16,25] | 2016 | Sn63Pb37 | 183 | n.a. | n.a. | 0.7 | n.a. |
| Hascoët et al. [22] | 2018 | 316L | 1450 | n.a. | n.a. | 4.5 | 0.1…0.12 |
| Jayant et al. [18,26] | 2020 | Sn99Cu1 | 227 | n.a. | 166 | 0.15 | n.a. |
| Sun et al. [23,24] | 2020 | Inconel 625 | 1350 | 2.0 | 700…800 | n.a. | 0.72 |
| Sharma et al. [19,27,28] | 2021 | AlSi5 | 632 | 1.6 | 100 | 1 | 0.12 |
| Englert et al. [21] | 2022 | AlSi7Mg | 625 | 1.2 | 1500 | 10…12 | 0.9…1.4 |
| Prasad et al. [29,30] | 2023 | mild steel | 1350 | 2.0 | 353 | 10 | n.a. |
| C | Si | Mn | P | S | Ni | Cr | Mo | V | Cu | Al | Ti+Zr |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.06…0.14 | 0.7…1.0 | 1.3…1.6 | 0.025 | 0.025 | 0.15 | 0.15 | 0.15 | 0.03 | 0.35 | 0.02 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kimme, J.; Gruner, J.; Hälsig, A.; Hensel, J. Droplet Formation and Energy Input during Induction Wire Melting with Pulsed and Constant Generator Power. J. Manuf. Mater. Process. 2024, 8, 80. https://doi.org/10.3390/jmmp8020080
Kimme J, Gruner J, Hälsig A, Hensel J. Droplet Formation and Energy Input during Induction Wire Melting with Pulsed and Constant Generator Power. Journal of Manufacturing and Materials Processing. 2024; 8(2):80. https://doi.org/10.3390/jmmp8020080
Chicago/Turabian StyleKimme, Jonas, Jonas Gruner, André Hälsig, and Jonas Hensel. 2024. "Droplet Formation and Energy Input during Induction Wire Melting with Pulsed and Constant Generator Power" Journal of Manufacturing and Materials Processing 8, no. 2: 80. https://doi.org/10.3390/jmmp8020080
APA StyleKimme, J., Gruner, J., Hälsig, A., & Hensel, J. (2024). Droplet Formation and Energy Input during Induction Wire Melting with Pulsed and Constant Generator Power. Journal of Manufacturing and Materials Processing, 8(2), 80. https://doi.org/10.3390/jmmp8020080







