Kerf Geometry and Surface Roughness Optimization in CO2 Laser Processing of FFF Plates Utilizing Neural Networks and Genetic Algorithms Approaches
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Full Quadratic Regression Models for CO2 Laser Cutting Objectives
3.2. Validation
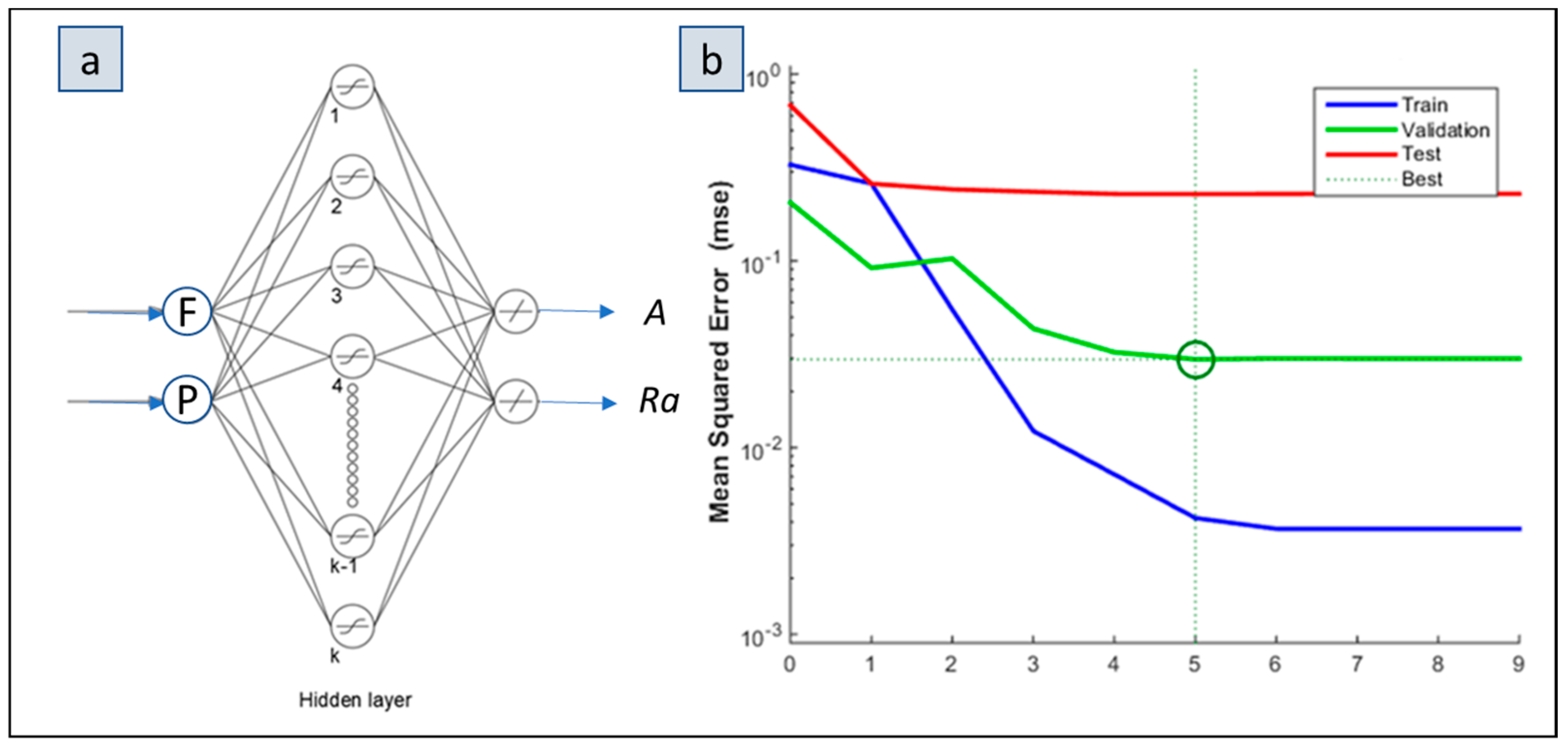
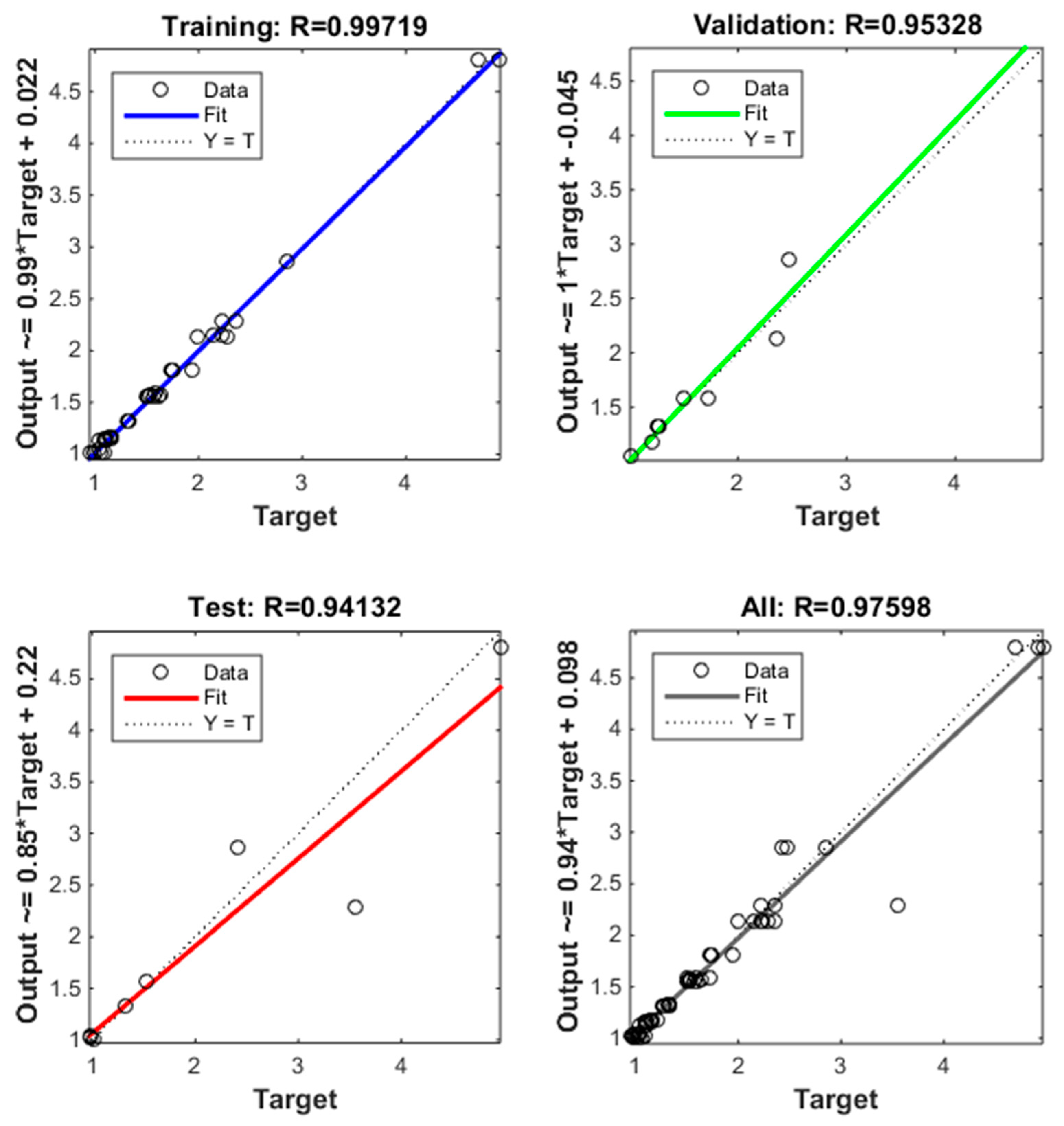
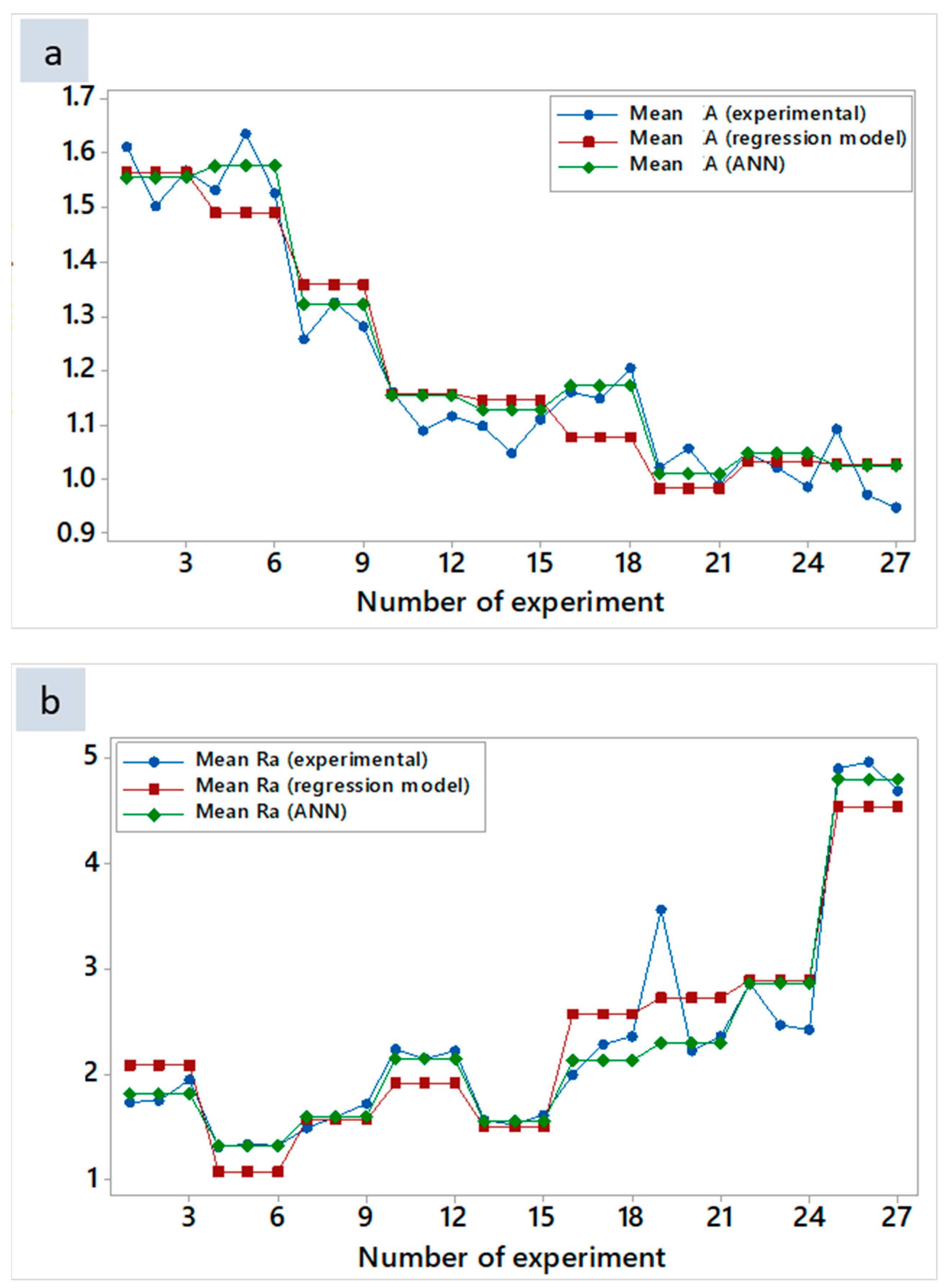
3.3. Neural Network Prediction
3.4. Multi-Objective Optimization of CO2 LC Parameters
4. Conclusions
- The kerf angle and Ra of the PLA 3DP samples cut by the CO2 laser are affected by the direction of the filament strands during the 3DP, as well as feed (F) and power (P) parameters.
- In general, when laser feed increases or the power decreases, the energy per unit area decreases, resulting in smaller bottom kerf widths and energy redistribution inside the cutting area.
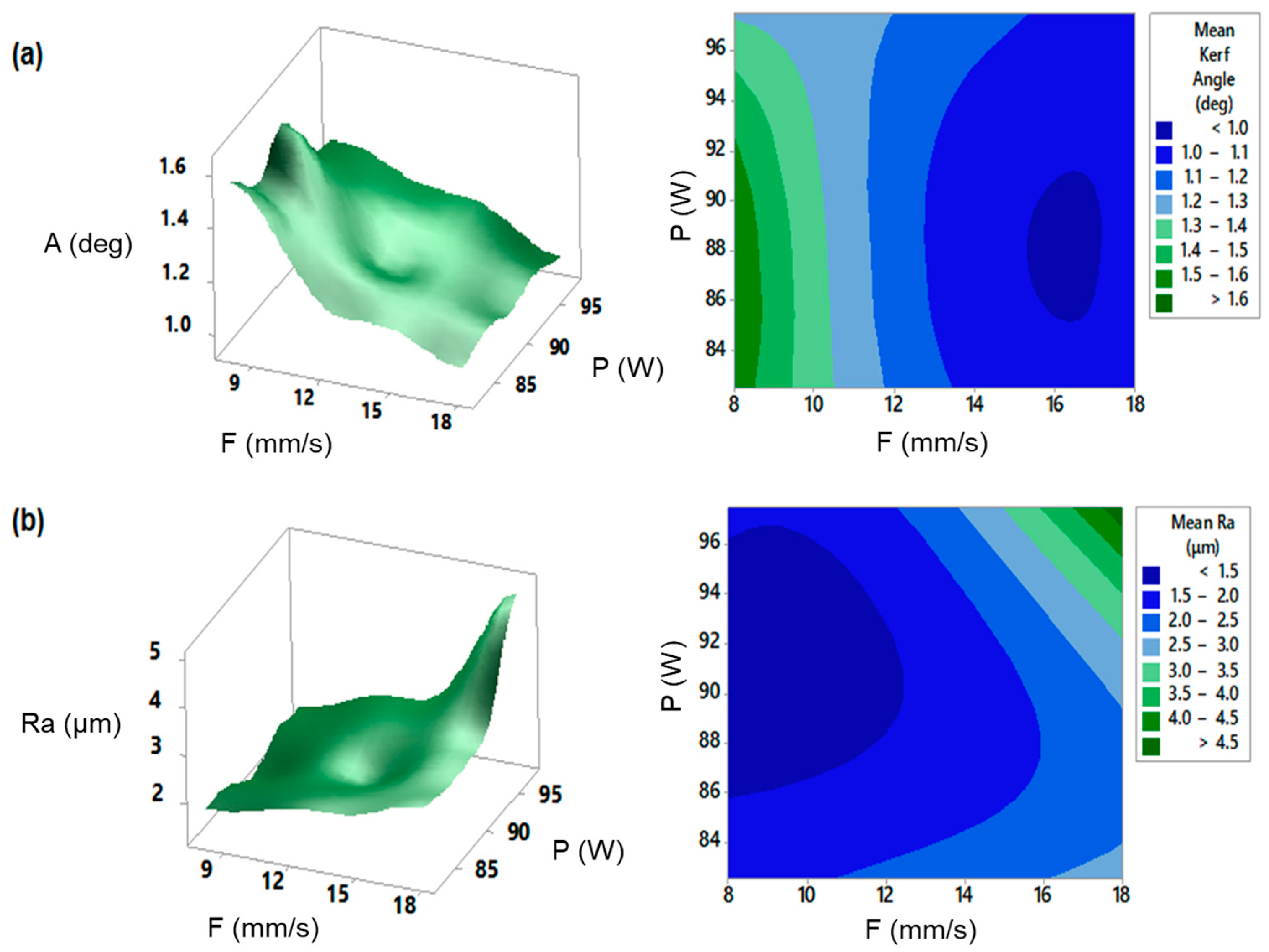
- ANOVA and statistics show that feed is the dominant parameter for both responses, having the power to be rather significant for mean Ra. By examining the contour plots and response surfaces, we concluded that the interaction between laser feed and power is synergistic for mean A and antagonistic for mean Ra.
- The feed parameter exhibits approximately 77% contribution in terms of its effect on the mean kerf angle. This contribution is followed by the effect of the square term of feed (6.66%), the interaction effect between feed and power (3.93%), and the effect of power (2.42%). Therefore, the correlation coefficient for the regression model to predict mean A was equal to 90.25%.
- The feed parameter also exhibits a high contribution percentage for the response of mean Ra (51.69%). The second contribution effect is seen through the interaction between feed and power (14.54%), followed by the square term of power (11.63%). The rest of the parameter effects are less significant for mean Ra. The correlation coefficient for the regression model to predict mean A is equal to 89.54%.
- The topology of 2-8-2 for the layers of a backpropagation ANN seems to be quite promising in predicting the responses of mean A and Ra, with high correlation.
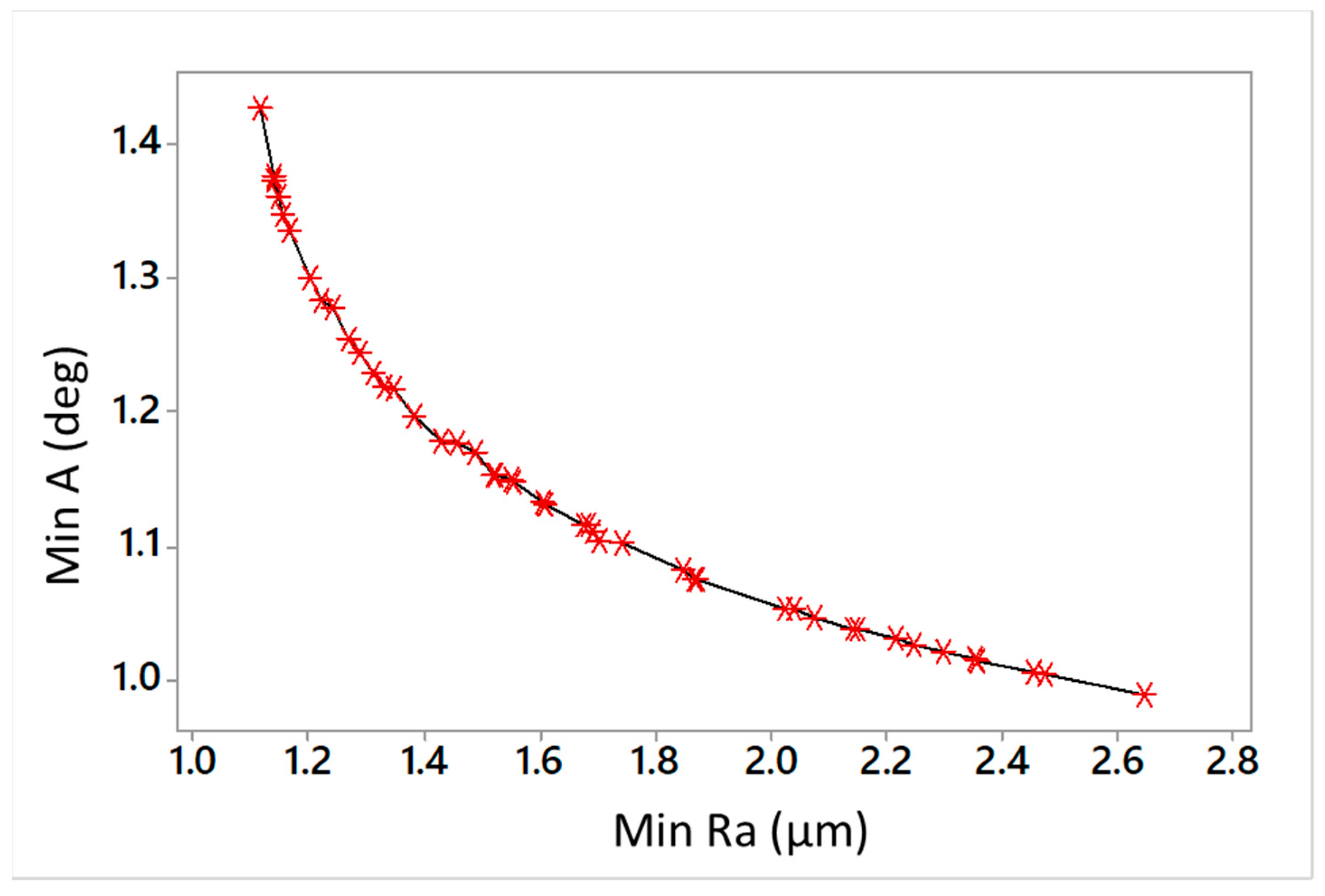
- The non-dominated set of Pareto optimal solutions seems advantageous for different importance degrees among mean kerf angle and surface roughness. Their inherent trade-off results from the nonlinear behavior, mainly owing to feed. A general range in terms of the overall gain by employing some indicative optimal solutions is between 10 and 55%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stavropoulos, P.; Koutsomichalis, A.; Vaxevanidis, N. Laser-Based Manufacturing Processes for Aerospace Applications. In Materials Science and Engineering; IGI Global: Hershey, PA, USA, 2017; pp. 374–391. [Google Scholar] [CrossRef]
- Mushtaq, R.T.; Wang, Y.; Rehman, M.; Khan, A.M.; Mia, M. State-of-the-Art and Trends in CO2 Laser Cutting of Polymeric Materials—A Review. Materials 2020, 13, 3839. [Google Scholar] [CrossRef] [PubMed]
- Ninikas, K.; Kechagias, J.; Salonitis, K. The Impact of Process Parameters on Surface Roughness and Dimensional Accuracy during CO2 Laser Cutting of PMMA Thin Sheets. J. Manuf. Mater. Process. 2021, 5, 74. [Google Scholar] [CrossRef]
- Förster, D.J.; Jäggi, B.; Michalowski, A.; Neuenschwander, B. Review on Experimental and Theoretical Investigations of Ultra-Short Pulsed Laser Ablation of Metals with Burst Pulses. Materials 2021, 14, 3331. [Google Scholar] [CrossRef] [PubMed]
- Sing, S.L.; Kuo, C.N.; Shih, C.T.; Ho, C.C.; Chua, C.K. Perspectives of Using Machine Learning in Laser Powder Bed Fusion for Metal Additive Manufacturing. Virtual Phys. Prototyp. 2021, 16, 372–386. [Google Scholar] [CrossRef]
- Al-Ahmari, A.M.A.; Rasheed, M.S.; Mohammed, M.K.; Saleh, T. A Hybrid Machining Process Combining Micro-EDM and Laser Beam Machining of Nickel–Titanium-Based Shape Memory Alloy. Mater. Manuf. Process. 2016, 31, 447–455. [Google Scholar] [CrossRef]
- Buj-Corral, I.; Bagheri, A.; Sivatte-Adroer, M. Effect of Printing Parameters on Dimensional Error, Surface Roughness and Porosity of FFF Printed Parts with Grid Structure. Polymers 2021, 13, 1213. [Google Scholar] [CrossRef]
- Elkaseer, A.; Schneider, S.; Scholz, S.G. Experiment-Based Process Modeling and Optimization for High-Quality and Resource-Efficient FFF 3D Printing. Appl. Sci. 2020, 10, 2899. [Google Scholar] [CrossRef]
- Fountas, N.A.; Kechagias, J.D.; Manolakos, D.E.; Vaxevanidis, N.M. Single and Multi-Objective Optimization of FDM-Based Additive Manufacturing Using Metaheuristic Algorithms. Procedia Manuf. 2020, 51, 740–747. [Google Scholar] [CrossRef]
- Kim, H.; Lin, Y.; Tseng, T.-L.B. A Review on Quality Control in Additive Manufacturing. Rapid Prototyp. J. 2018, 24, 645–669. [Google Scholar] [CrossRef]
- Milovanovic, S.; Pajnik, J.; Lukic, I. Tailoring of Advanced Poly (Lactic Acid)-based Materials: A Review. J. Appl. Polym. Sci. 2022, 139, 51839. [Google Scholar] [CrossRef]
- Gul, J.Z.; Sajid, M.; Rehman, M.M.; Siddiqui, G.U.; Shah, I.; Kim, K.-H.; Lee, J.-W.; Choi, K.H. 3D Printing for Soft Robotics—A Review. Sci. Technol. Adv. Mater. 2018, 19, 243–262. [Google Scholar] [CrossRef] [PubMed]
- Buj-Corral, I.; Sánchez-Casas, X.; Luis-Pérez, C.J. Analysis of AM Parameters on Surface Roughness Obtained in PLA Parts Printed with FFF Technology. Polymers 2021, 13, 2384. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.V.; Hernandez, A. A Review of Additive Manufacturing. ISRN Mech. Eng. 2012, 2012, 208760. [Google Scholar] [CrossRef]
- Pham, D.T.; Gault, R.S. A comparison of rapid prototyping technologies. Int. J. Mach. Tools Manuf. 1998, 38, 1257. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Zaoutsos, S.P. Optimising Fused Filament Fabrication Surface Roughness for a Dental Implant. Mater. Manuf. Process. 2023, 38, 954–959. [Google Scholar] [CrossRef]
- Kechagias, J.; Chaidas, D. Fused Filament Fabrication Parameter Adjustments for Sustainable 3D Printing. Mater. Manuf. Process. 2023, 38, 933–940. [Google Scholar] [CrossRef]
- Faludi, J.; Bayley, C.; Bhogal, S.; Iribarne, M. Comparing Environmental Impacts of Additive Manufacturing vs. Traditional Machining via Life-Cycle Assessment. Rapid Prototyp. J. 2015, 21, 14–33. [Google Scholar] [CrossRef]
- Correa-Pacheco, Z.N.; Black-Solís, J.D.; Ortega-Gudiño, P.; Sabino-Gutiérrez, M.A.; Benítez-Jiménez, J.J.; Barajas-Cervantes, A.; Bautista-Baños, S.; Hurtado-Colmenares, L.B. Preparation and Characterization of Bio-Based PLA/PBAT and Cinnamon Essential Oil Polymer Fibers and Life-Cycle Assessment from Hydrolytic Degradation. Polymers 2019, 12, 38. [Google Scholar] [CrossRef]
- Nofar, M.; Salehiyan, R.; Sinha Ray, S. Rheology of Poly (Lactic Acid)-Based Systems. Polym. Rev. 2019, 59, 465–509. [Google Scholar] [CrossRef]
- Fortelny, I.; Ujcic, A.; Fambri, L.; Slouf, M. Phase Structure, Compatibility, and Toughness of PLA/PCL Blends: A Review. Front. Mater. 2019, 6, 206. [Google Scholar] [CrossRef]
- Davim, J.P.; Barricas, N.; Conceição, M.; Oliveira, C. Some Experimental Studies on CO2 Laser Cutting Quality of Polymeric Materials. J. Mater. Process. Technol. 2008, 198, 99–104. [Google Scholar] [CrossRef]
- Caiazzo, F.; Curcio, F.; Daurelio, G.; Minutolo, F.M.C. Laser Cutting of Different Polymeric Plastics (PE, PP and PC) by a CO2 Laser Beam. J. Mater. Process. Technol. 2005, 159, 279–285. [Google Scholar] [CrossRef]
- Choudhury, I.A.; Shirley, S. Laser Cutting of Polymeric Materials: An Experimental Investigation. Opt. Laser Technol. 2010, 42, 503–508. [Google Scholar] [CrossRef]
- Kechagias, J.; Ninikas, K.; Stavropoulos, P.; Salonitis, K. A Generalised Approach on Kerf Geometry Prediction during CO2 Laser Cut of PMMA Thin Plates Using Neural Networks. Lasers Manuf. Mater. Process. 2021, 8, 372–393. [Google Scholar] [CrossRef]
- Stankova, N.; Nikolov, A.; Iordanova, E.; Yankov, G.; Nedyalkov, N.; Atanasov, P.; Tatchev, D.; Valova, E.; Kolev, K.; Armyanov, S.; et al. New Approach toward Laser-Assisted Modification of Biocompatible Polymers Relevant to Neural Interfacing Technologies. Polymers 2021, 13, 3004. [Google Scholar] [CrossRef]
- Zhou, B.H.; Mahdavian, S.M. Experimental and Theoretical Analyses of Cutting Nonmetallic Materials by Low Power CO2-Laser. J. Mater. Process. Technol. 2004, 146, 188–192. [Google Scholar] [CrossRef]
- Moradi, M.; Karami Moghadam, M.; Shamsborhan, M.; Bodaghi, M.; Falavandi, H. Post-Processing of FDM 3D-Printed Polylactic Acid Parts by Laser Beam Cutting. Polymers 2020, 12, 550. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Fountas, N.A.; Ninikas, K.; Petousis, M.; Vidakis, N.; Vaxevanidis, N. Surface Characteristics Investigation of 3D-Printed PET-G Plates during CO2 Laser Cutting. Mater. Manuf. Process. 2021, 37, 1446–1462. [Google Scholar] [CrossRef]
- Kechagias, J.; Ninikas, K.; Petousis, M.; Vidakis, N. Laser Cutting of 3D Printed Acrylonitrile Butadiene Styrene Plates for Dimensional and Surface Roughness Optimization. Int. J. Adv. Manuf. Technol. 2022, 119, 2301–2315. [Google Scholar] [CrossRef]
- Kechagias, J.; Ninikas, K.; Petousis, M.; Vidakis, N.; Vaxevanidis, N. An Investigation of Surface Quality Characteristics of 3D Printed PLA Plates Cut by CO2 Laser Using Experimental Design. Mater. Manuf. Process. 2021, 36, 1544–1553. [Google Scholar] [CrossRef]
- Yang, L.; Wei, J.; Ma, Z.; Song, P.; Ma, J.; Zhao, Y.; Huang, Z.; Zhang, M.; Yang, F.; Wang, X. The Fabrication of Micro/Nano Structures by Laser Machining. Nanomaterials 2019, 9, 1789. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Vidakis, N.; Ninikas, K.; Petousis, M.; Vaxevanidis, N.M. Hybrid 3D Printing of Multifunctional Polylactic Acid/Carbon Black Nanocomposites Made with Material Extrusion and Post-Processed with CO2 Laser Cutting. J. Adv. Manuf. Technol. 2023, 124, 1843–1861. [Google Scholar] [CrossRef]
- Shakeri, Z.; Benfriha, K.; Shirinbayan, M.; Ahmadifar, M.; Tcharkhtchi, A. Mathematical Modeling and Optimization of Fused Filament Fabrication (FFF) Process Parameters for Shape Deviation Control of Polyamide 6 Using Taguchi Method. Polymers 2021, 13, 3697. [Google Scholar] [CrossRef] [PubMed]
- Bedi, R.; Mehta, B. Adaptive Neuro Fuzzy Inference System in Modelling/Detecting Cracks and Porosity Using Liquid Penetrant Test. Int. J. Exp. Des. Process Optim. 2016, 5, 117. [Google Scholar] [CrossRef]
- Jones, B.; Montgomery, D.C. Alternatives to Resolution IV Screening Designs in 16 Runs. Int. J. Exp. Des. Process Optim. 2010, 1, 285. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Aslani, K.-E.; Fountas, N.A.; Vaxevanidis, N.M.; Manolakos, D.E. A Comparative Investigation of Taguchi and Full Factorial Design for Machinability Prediction in Turning of a Titanium Alloy. Measurement 2020, 151, 107213. [Google Scholar] [CrossRef]
- Madić, M.; Petrović, G.; Petković, D.; Antucheviciene, J.; Marinković, D. Application of a Robust Decision-Making Rule for Comprehensive Assessment of Laser Cutting Conditions and Performance. Machines 2022, 10, 153. [Google Scholar] [CrossRef]
- Haddadi, E.; Moradi, M.; Karimzad Ghavidel, A.; Karimzad Ghavidel, A.; Meiabadi, S. Experimental and Parametric Evaluation of Cut Quality Characteristics in CO2 Laser Cutting of Polystyrene. Optik 2019, 184, 103–114. [Google Scholar] [CrossRef]
- Tamrin, K.F.; Nukman, Y.; Sheikh, N.A. Laser Spot Welding of Thermoplastic and Ceramic: An Experimental Investigation. Mater. Manuf. Process. 2015, 30, 1138–1145. [Google Scholar] [CrossRef]
- Kurt, M.; Kaynak, Y.; Bagci, E.; Demirer, H.; Kurt, M. Dimensional Analyses and Surface Quality of the Laser Cutting Process for Engineering Plastics. Int. J. Adv. Manuf. Technol. 2009, 41, 259–267. [Google Scholar] [CrossRef]
- Andriushchenko, E.; Kallaste, A.; Belahcen, A.; Vaimann, T.; Rassõlkin, A.; Heidari, H.; Tiismus, H. Optimization of a 3D-Printed Permanent Magnet Coupling Using Genetic Algorithm and Taguchi Method. Electronics 2021, 10, 494. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Tsiolikas, A.; Petousis, M.; Ninikas, K.; Vidakis, N.; Tzounis, L. A robust methodology for optimizing the topology and the learning parameters of an ANN for accurate predictions of laser-cut edges surface roughness. Simul. Model. Pract. Theory 2022, 114, 102414. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.D.S. Multi-Objective Grey Wolf Optimizer: A Novel Algorithm for Multi-Criterion Optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]


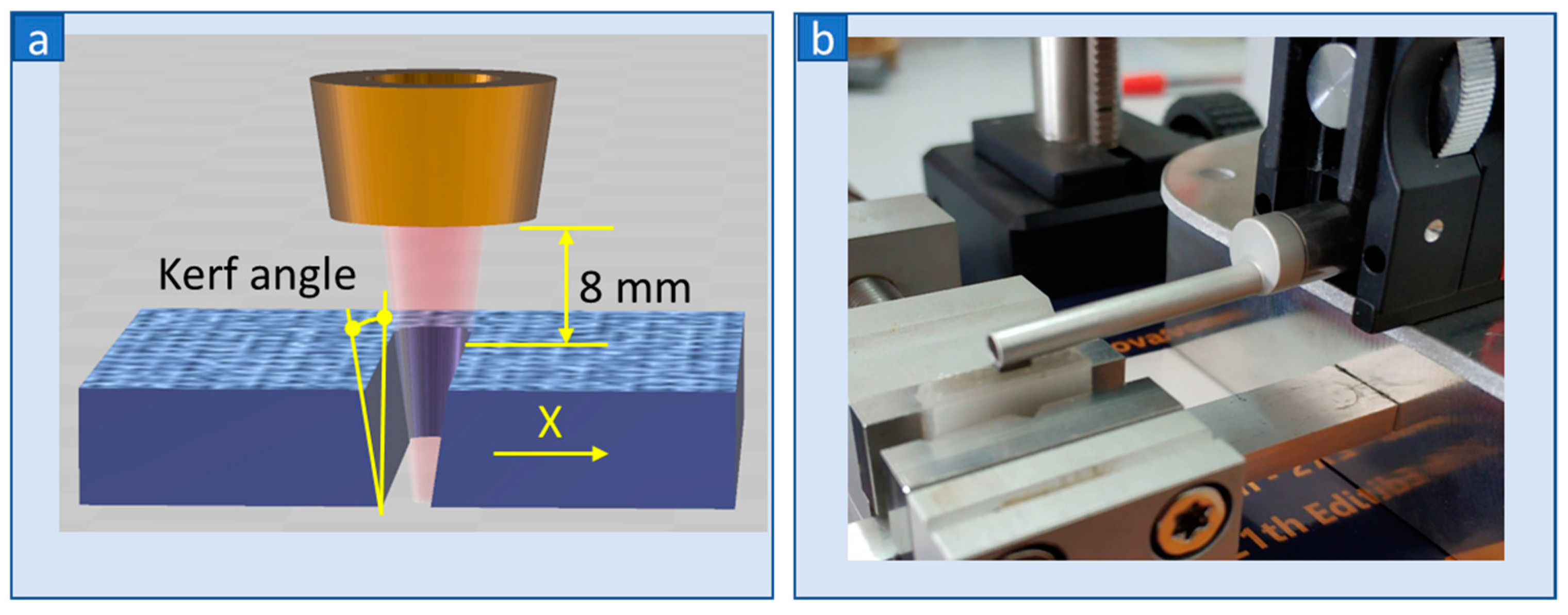

| Laser Parameters | Symbol | Levels | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Feed | F (mm/s) | 8 | 13 | 18 |
| Power | P (W) | 82.5 | 90.0 | 97.5 |
| a/a | F (mm/s) | P (W) | Mean A (°) | Mean Ra (μm) |
|---|---|---|---|---|
| 1 | 8 | 82.5 | 1.596 | 1.72 |
| 2 | 8 | 82.5 | 1.438 | 1.74 |
| 3 | 8 | 82.5 | 1.519 | 1.88 |
| 4 | 8 | 90.0 | 1.465 | 1.51 |
| 5 | 8 | 90.0 | 1.612 | 1.50 |
| 6 | 8 | 90.0 | 1.537 | 1.42 |
| 7 | 8 | 97.5 | 1.216 | 0.81 |
| 8 | 8 | 97.5 | 1.307 | 0.88 |
| 9 | 8 | 97.5 | 1.259 | 1.06 |
| 10 | 13 | 82.5 | 1.108 | 1.16 |
| 11 | 13 | 82.5 | 1.054 | 1.04 |
| 12 | 13 | 82.5 | 1.094 | 1.05 |
| 13 | 13 | 90.0 | 1.076 | 0.92 |
| 14 | 13 | 90.0 | 1.012 | 1.00 |
| 15 | 13 | 90.0 | 1.094 | 1.07 |
| 16 | 13 | 97.5 | 1.088 | 1.09 |
| 17 | 13 | 97.5 | 1.079 | 2.08 |
| 18 | 13 | 97.5 | 1.102 | 1.46 |
| 19 | 18 | 82.5 | 0.965 | 4.42 |
| 20 | 18 | 82.5 | 1.012 | 2.23 |
| 21 | 18 | 82.5 | 0.894 | 2.53 |
| 22 | 18 | 90.0 | 0.989 | 2.61 |
| 23 | 18 | 90.0 | 0.945 | 2.42 |
| 24 | 18 | 90.0 | 0.917 | 2.37 |
| 25 | 18 | 97.5 | 1.009 | 6.15 |
| 26 | 18 | 97.5 | 0.897 | 6.19 |
| 27 | 18 | 97.5 | 0.884 | 5.92 |
| Source | DF | Seq.SS | % Contribution | Adj.SS | Adj.MS | F-Value | P-Value |
|---|---|---|---|---|---|---|---|
| F(mm/s) | 1 | 0.93298 | 76.86 | 0.93298 | 0.932978 | 165.59 | 0.000 |
| P(W) | 1 | 0.02936 | 2.42 | 0.02936 | 0.029363 | 5.21 | 0.033 |
| F2 | 1 | 0.08089 | 6.66 | 0.08089 | 0.080891 | 14.36 | 0.001 |
| P2 | 1 | 0.00461 | 0.38 | 0.00461 | 0.004611 | 0.82 | 0.376 |
| F × P | 1 | 0.04775 | 3.93 | 0.04775 | 0.047754 | 8.48 | 0.008 |
| Error | 21 | 0.11832 | 9.75 | 0.11832 | 0.005634 | ||
| Total | 26 | 1.21392 | 100.00 | ||||
| A model R2 | 90.25% | ||||||
| F(mm/s) | 1 | 14.706 | 51.69 | 14.706 | 14.7063 | 103.73 | 0.000 |
| P(W) | 1 | 1.905 | 6.69 | 1.905 | 1.9045 | 13.43 | 0.001 |
| F2 | 1 | 1.421 | 4.99 | 1.421 | 1.4211 | 10.02 | 0.005 |
| P2 | 1 | 3.308 | 11.63 | 3.308 | 3.3078 | 23.33 | 0.000 |
| F × P | 1 | 4.136 | 14.54 | 4.136 | 4.1360 | 29.17 | 0.000 |
| Error | 21 | 2.977 | 10.46 | 2.977 | 0.1418 | ||
| Total | 26 | 28.453 | 100.00 | ||||
| Ra model R2 | 89.54% | ||||||
| Sol. No. | Optimization Objectives | Control Parameters | ||
|---|---|---|---|---|
| minA (°) | minRa (μm) | F (mm/s) | P (W) | |
| 1 | 0.98822 | 2.64480 | 17.48111 | 82.50000 |
| 2 | 1.07466 | 1.87228 | 14.92668 | 86.77339 |
| 3 | 1.42772 | 1.11480 | 08.53595 | 90.92663 |
| 4 | 1.27861 | 1.23830 | 10.71434 | 89.29454 |
| 5 | 1.33577 | 1.16668 | 09.66419 | 91.03837 |
| 6 | 1.02117 | 2.29789 | 16.40072 | 83.83890 |
| 7 | 1.07543 | 1.86701 | 14.91328 | 87.15281 |
| 8 | 1.03065 | 2.21364 | 16.11121 | 84.18711 |
| 9 | 1.29996 | 1.20229 | 10.20007 | 90.76634 |
| 10 | 1.00332 | 2.47574 | 16.99961 | 83.21187 |
| 11 | 1.10474 | 1.70393 | 14.09902 | 87.58292 |
| 12 | 1.00525 | 2.45430 | 16.91170 | 83.22919 |
| 13 | 1.19700 | 1.38032 | 12.04552 | 89.16643 |
| 14 | 1.11602 | 1.67524 | 13.84686 | 86.67821 |
| 15 | 1.15247 | 1.52201 | 13.01707 | 87.74314 |
| 16 | 1.01505 | 2.35604 | 16.64665 | 83.78354 |
| 17 | 1.03745 | 2.15047 | 16.00275 | 84.95377 |
| 18 | 1.11079 | 1.68988 | 13.96640 | 86.86978 |
| 19 | 1.05329 | 2.02306 | 15.53363 | 85.66028 |
| 20 | 1.37699 | 1.13618 | 09.18147 | 90.72416 |
| 21 | 1.36152 | 1.14691 | 09.41792 | 90.46029 |
| 22 | 1.37215 | 1.13903 | 09.24583 | 90.70076 |
| 23 | 1.08154 | 1.84548 | 14.70373 | 86.03587 |
| 24 | 1.21654 | 1.34745 | 11.76379 | 88.63053 |
| 25 | 1.14929 | 1.54881 | 13.11347 | 87.17124 |
| 26 | 1.13218 | 1.60573 | 13.47646 | 87.05567 |
| 27 | 1.13155 | 1.60924 | 13.49164 | 87.01271 |
| 28 | 1.28392 | 1.22144 | 10.53108 | 90.08822 |
| 29 | 1.21911 | 1.33139 | 11.64764 | 89.29424 |
| 30 | 1.22900 | 1.31082 | 11.46317 | 89.46176 |
| 31 | 1.14719 | 1.55199 | 13.15207 | 87.25544 |
| 32 | 1.11552 | 1.68425 | 13.86107 | 86.47686 |
| 33 | 1.10185 | 1.73947 | 14.18546 | 86.43617 |
| 34 | 1.17593 | 1.45489 | 12.55105 | 87.87838 |
| 35 | 1.17909 | 1.42963 | 12.42239 | 88.69144 |
| 36 | 1.34805 | 1.15551 | 09.57331 | 90.58348 |
| 37 | 1.24481 | 1.28694 | 11.24017 | 89.20021 |
| 38 | 1.03864 | 2.14012 | 15.97860 | 85.07588 |
| 39 | 1.24427 | 1.28737 | 11.24562 | 89.22634 |
| 40 | 1.15305 | 1.51632 | 12.99429 | 87.91324 |
| 41 | 1.01524 | 2.35420 | 16.64214 | 83.79649 |
| 42 | 1.25371 | 1.26658 | 11.03781 | 89.70594 |
| 43 | 1.05238 | 2.03865 | 15.49707 | 85.07198 |
| 44 | 1.24447 | 1.28734 | 11.24459 | 89.20843 |
| 45 | 1.24447 | 1.28734 | 11.24459 | 89.20843 |
| 46 | 1.04677 | 2.07469 | 15.71065 | 85.26258 |
| 47 | 1.02666 | 2.24627 | 16.28398 | 84.26596 |
| 48 | 1.24447 | 1.28734 | 11.24459 | 89.20843 |
| 49 | 1.16961 | 1.48469 | 12.70009 | 87.44660 |
| 50 | 1.24447 | 1.28734 | 11.24459 | 89.20843 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kechagias, J.D.; Fountas, N.A.; Ninikas, K.; Vaxevanidis, N.M. Kerf Geometry and Surface Roughness Optimization in CO2 Laser Processing of FFF Plates Utilizing Neural Networks and Genetic Algorithms Approaches. J. Manuf. Mater. Process. 2023, 7, 77. https://doi.org/10.3390/jmmp7020077
Kechagias JD, Fountas NA, Ninikas K, Vaxevanidis NM. Kerf Geometry and Surface Roughness Optimization in CO2 Laser Processing of FFF Plates Utilizing Neural Networks and Genetic Algorithms Approaches. Journal of Manufacturing and Materials Processing. 2023; 7(2):77. https://doi.org/10.3390/jmmp7020077
Chicago/Turabian StyleKechagias, John D., Nikolaos A. Fountas, Konstantinos Ninikas, and Nikolaos M. Vaxevanidis. 2023. "Kerf Geometry and Surface Roughness Optimization in CO2 Laser Processing of FFF Plates Utilizing Neural Networks and Genetic Algorithms Approaches" Journal of Manufacturing and Materials Processing 7, no. 2: 77. https://doi.org/10.3390/jmmp7020077
APA StyleKechagias, J. D., Fountas, N. A., Ninikas, K., & Vaxevanidis, N. M. (2023). Kerf Geometry and Surface Roughness Optimization in CO2 Laser Processing of FFF Plates Utilizing Neural Networks and Genetic Algorithms Approaches. Journal of Manufacturing and Materials Processing, 7(2), 77. https://doi.org/10.3390/jmmp7020077




_Kechagias.jpg)




