3D Hybrid Numerical Model of Residual Stresses: Numerical—Sensitivity to Cutting Parameters When Turning 15-5PH Stainless Steel
Abstract
:1. Introduction
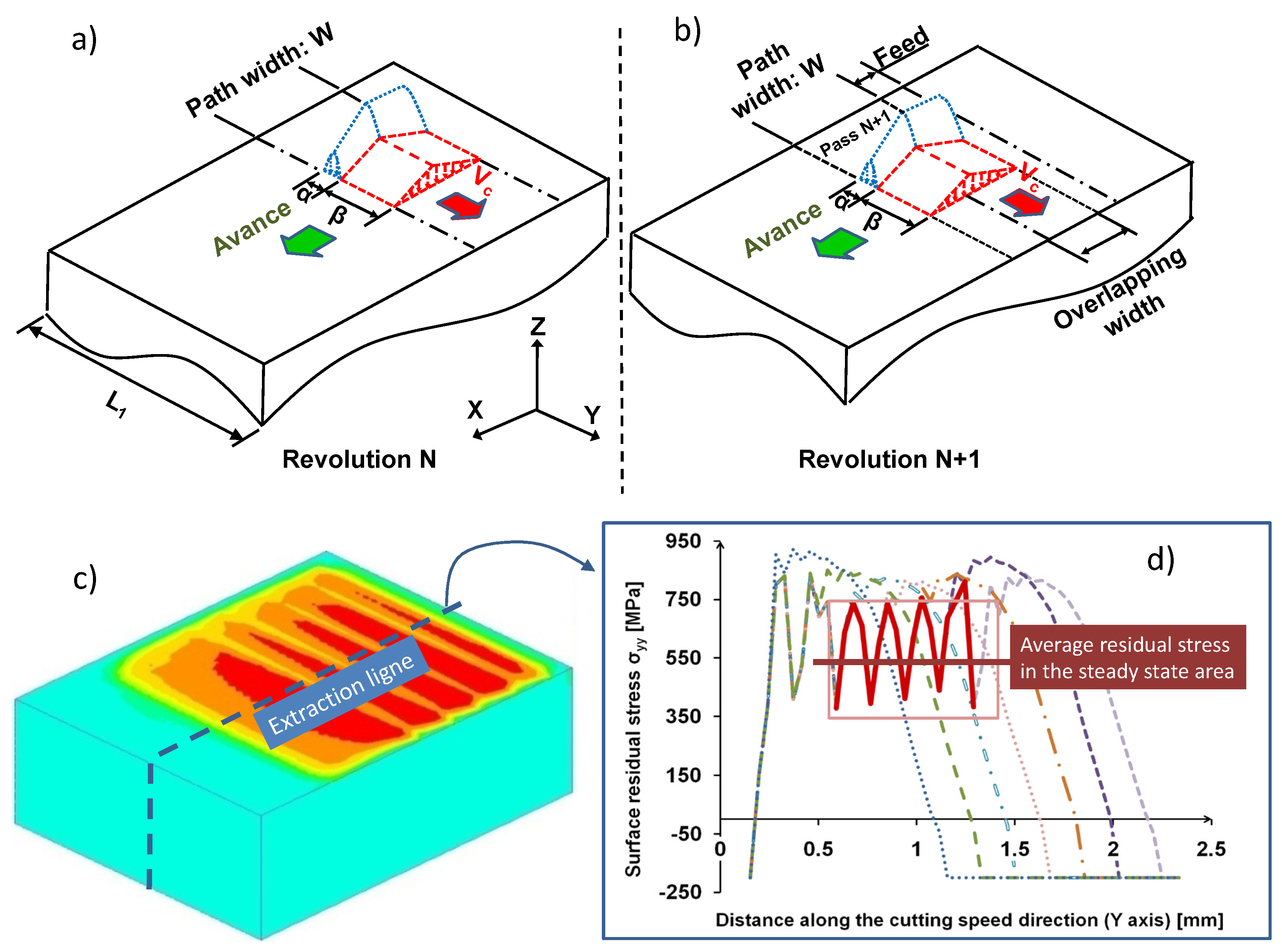
2. Experimental Database and Residual Stresses Measurements
3. Hybrid Model Computation
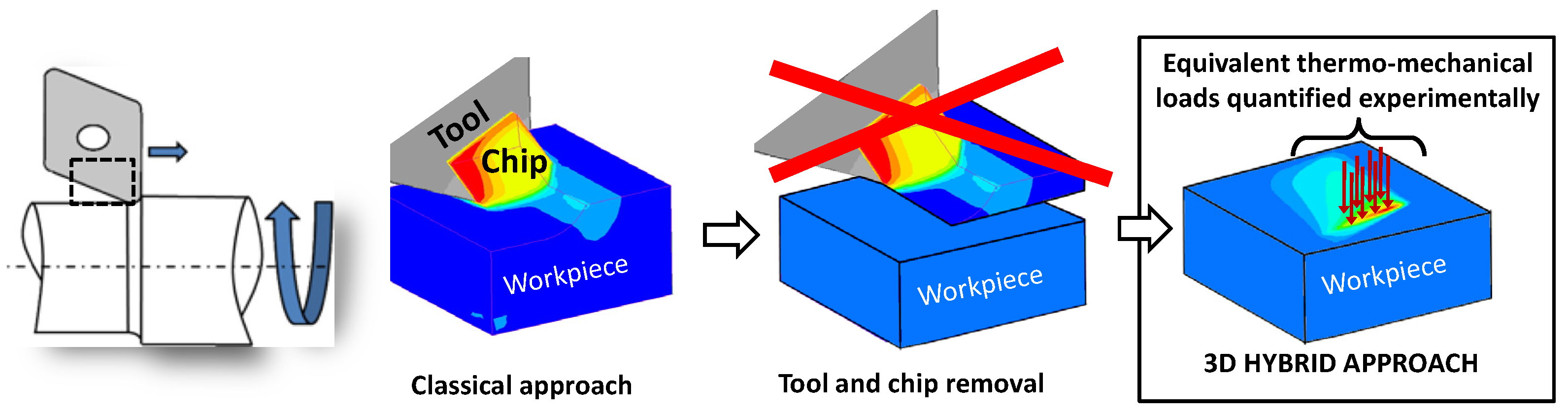
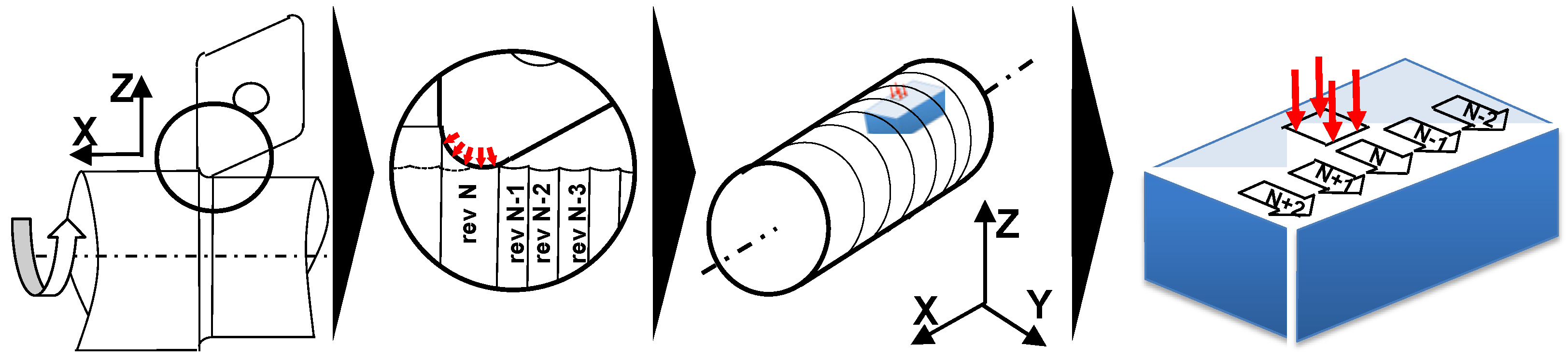
3.1. Principle of the 3D Hybrid Model
3.2. Numerical Model Design
3.3. Input Data for the Model
- Experimental parameters, measured during and after orthogonal cutting tests;
- Tribological parameters;
- Geometrical parameters.
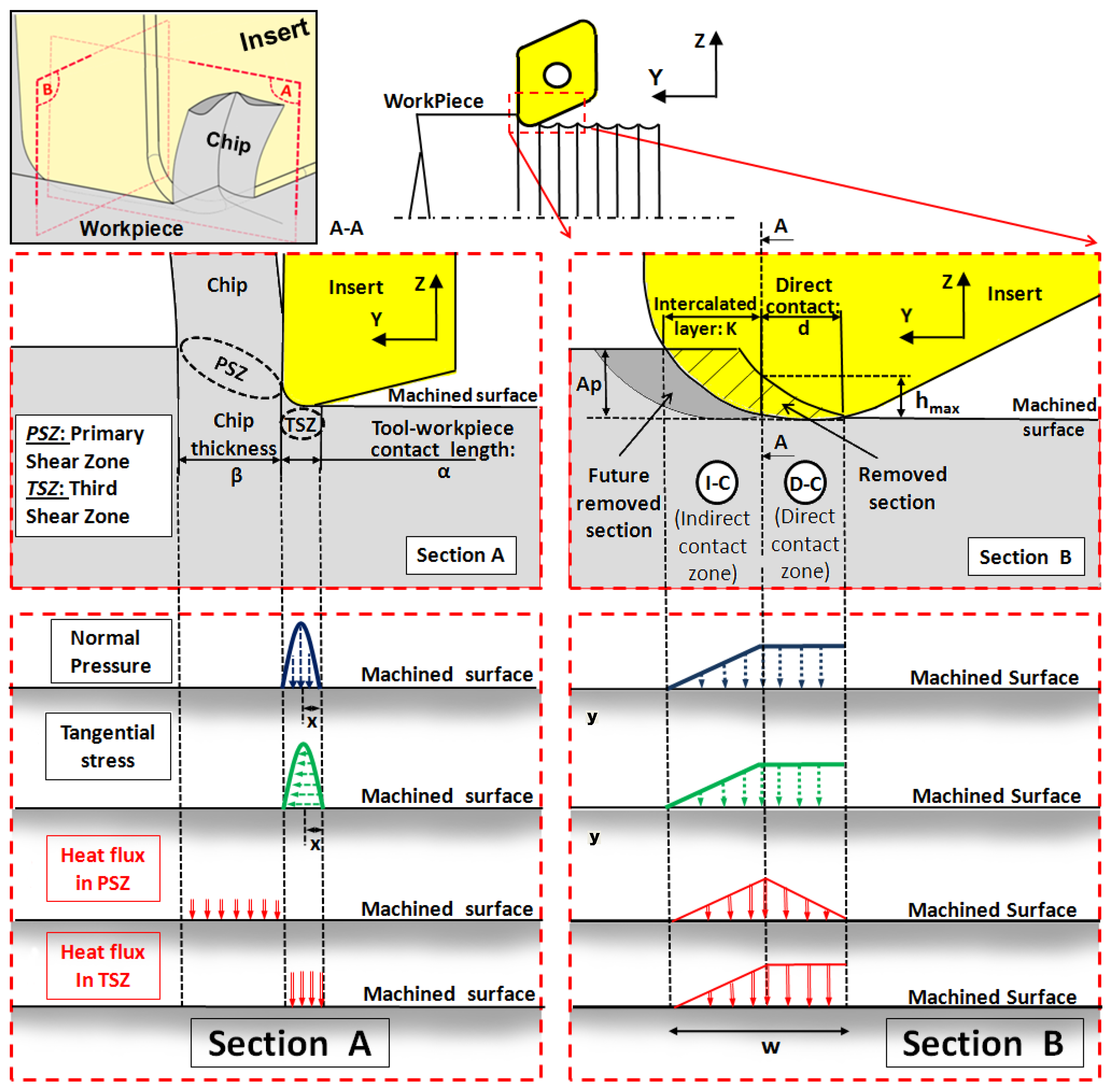
3.3.1. Experimental Parameters
- The average chip thickness: β;
- The contact length on the flank face in the TSZ: α.
3.3.2. Tribological Parameters
- μ = 2.12Vs − 0.45 with 10 m/min < Vs < 300 m/min
- μ = 0.15 with 300 m/min < Vs
- Λ3 = 0.25 with Vs < 25 m/min
- Λ3 = 2.3Vs − 0.63 with 25 m/min < Vs < 300 m/min
- Λ3 = 0.08 with Vs > 300 m/min
3.3.3. Geometrical Parameters
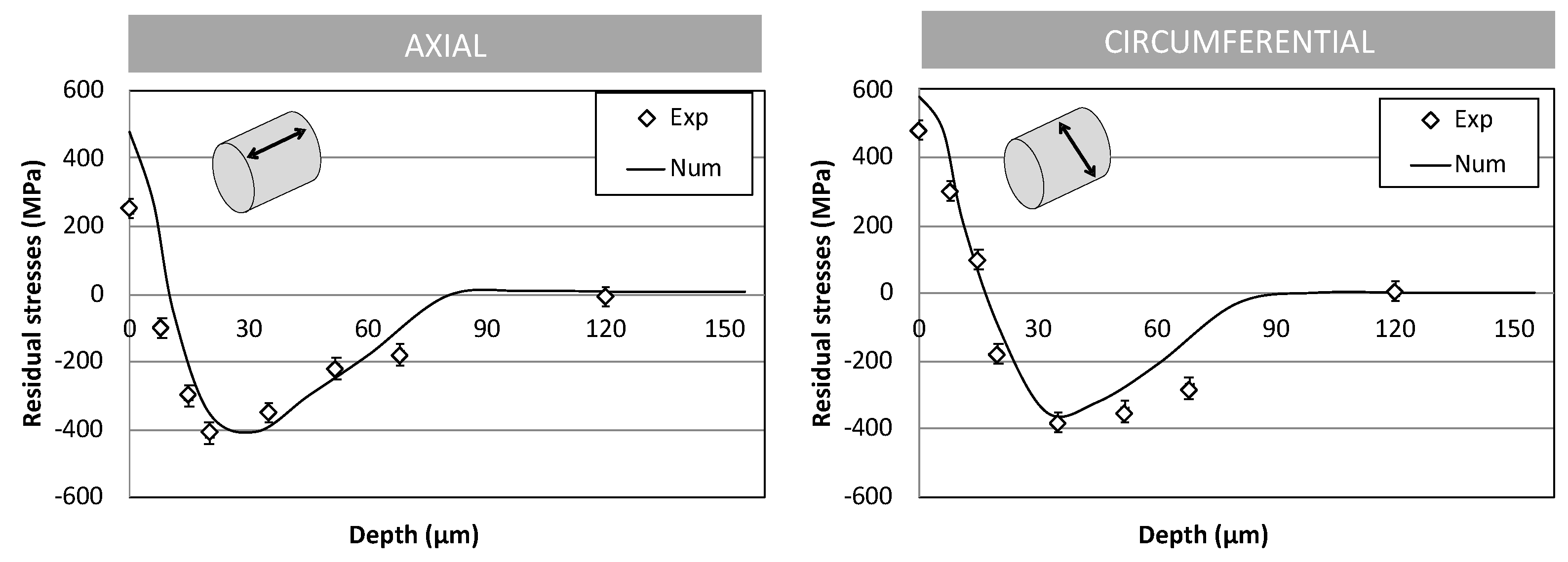
4. Simulation of Numerical Residual Stresses and Comparison to Experimental Values
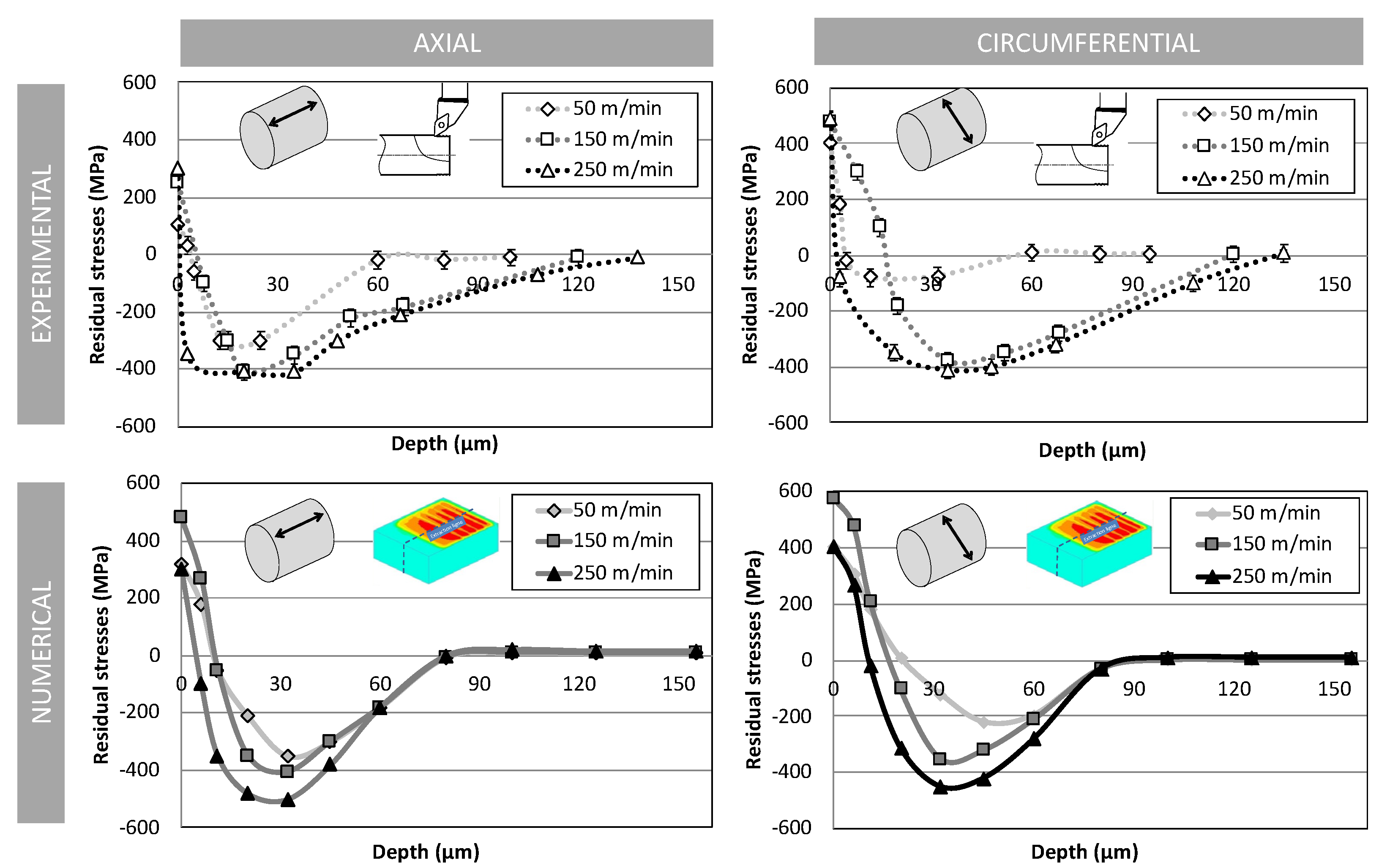
4.1. Sensitivity to Cutting Speed
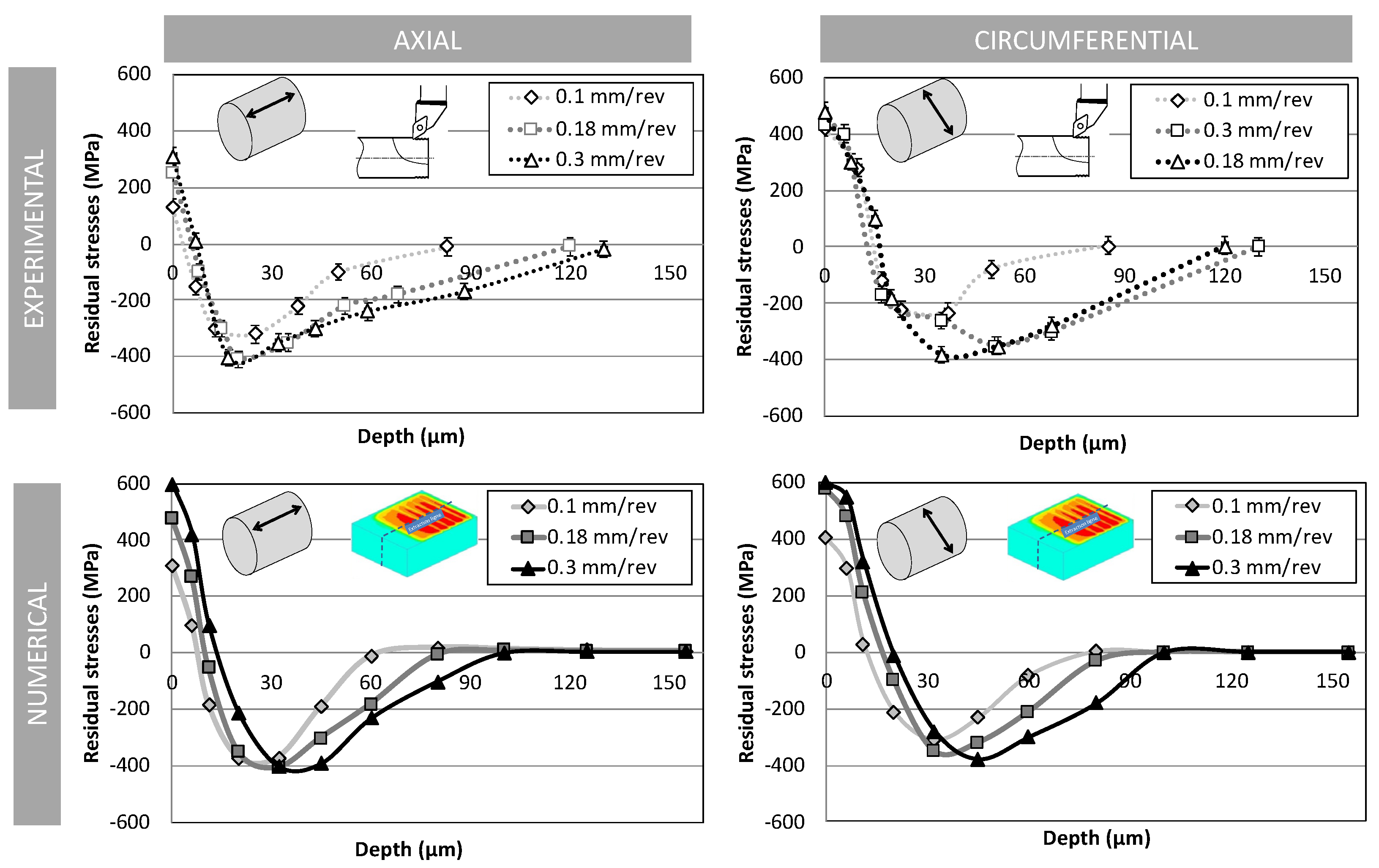
4.2. Sensitivity to Feed
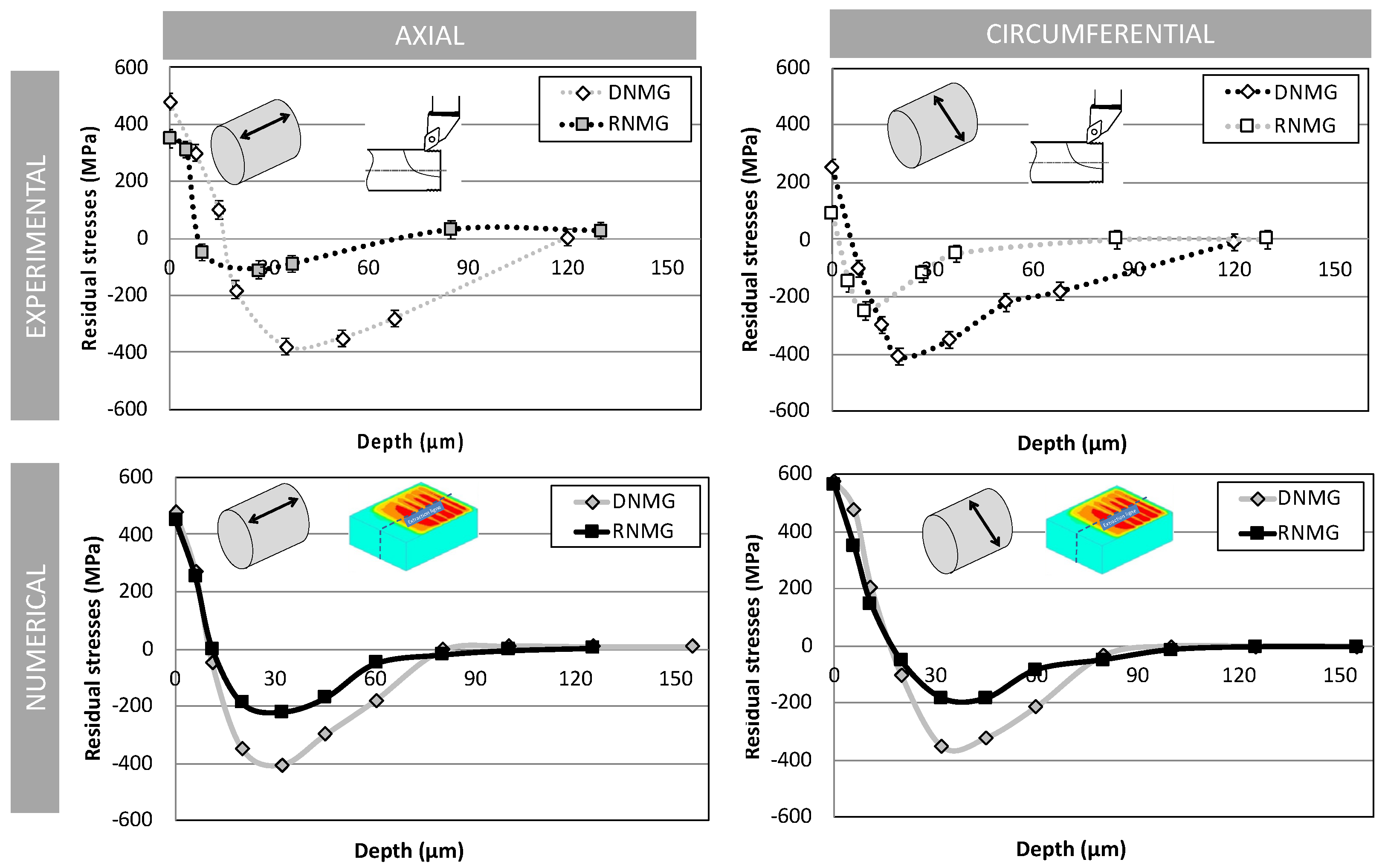
4.3. Sensitivity to Insert Geometry
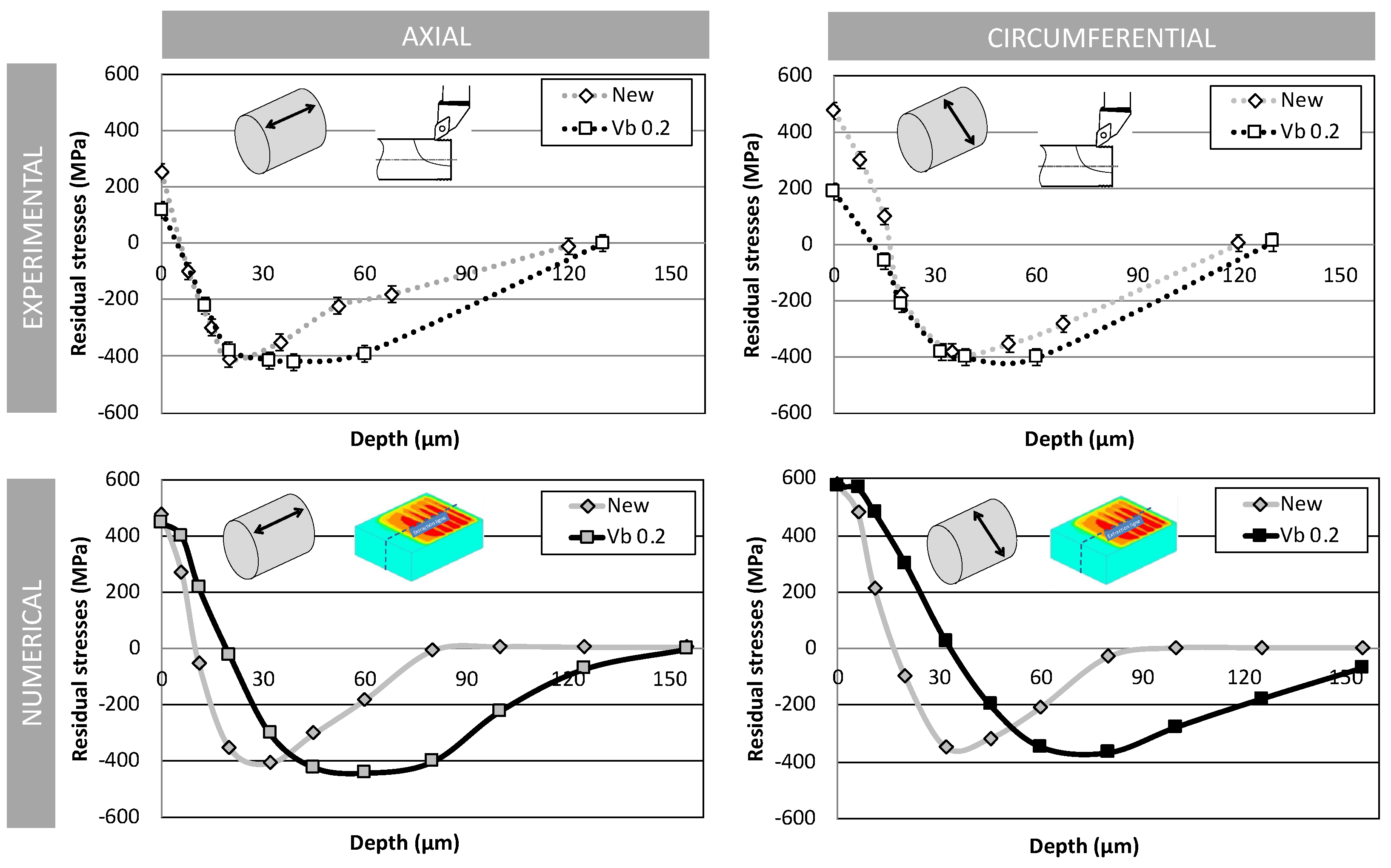
4.4. Sensitivity to Tool Wear in the Flank Face
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, S.; Melkote, S.N.; Lara-Curzio, E.; Watkins, T.R.; Allard, L.; Riester, L. Effect of surface integrity of hard turned AISI 52100 steel on fatigue performance. Mater. Sci. Eng. A 2007, 459, 337–346. [Google Scholar] [CrossRef]
- Davim, J.P. Machining-Fundamentals and Recent Advances; Springer: London, UK, 2008; pp. 59–96. ISBN 978-1-84800-213-5. [Google Scholar]
- Bissey-Breton, S.; Farr, J.; Vignal, V.; Mary, N. Impact des conditions d’usinage sur la zone du matériau affecté par le procédé. Méc. Ind. 2007, 8, 193–197. [Google Scholar] [CrossRef]
- Griffiths, B. Manufacturing Surface Technology—Surface Integrity and Functional Performance; Penton Press: London, UK, 1971; ISBN 18571-8029-1. [Google Scholar]
- Jawahir, I.; Brinksmeier, E.; M’Saoubi, R.; Aspinwall, D.; Outeiro, J.; Meyer, D.; Umbrello, D.; Jayal, A. Surface integrity in material removal processes: Recent advances. CIRP Ann. 2011, 60, 603–626. [Google Scholar] [CrossRef]
- Yang, X.; Richard Liu, C.; Grandt, A.F. An experimental study on fatigue life variance, residual stress variance, and their correlation of face-turned and ground Ti6Al4V samples. J. Manuf. Sci. Eng. 2002, 124, 809–819. [Google Scholar] [CrossRef]
- Liu, C.R.; Yang, X. The scatter of surface residual stresses produced by face turning and grinding. Mach. Sci. Technol. 2001, 5, 1–21. [Google Scholar] [CrossRef]
- Javidi, A.; Rieger, U.; Eichlseder, W. The effect of machining on the surface integrity and fatigue life. Int. J. Fatigue 2008, 30, 2050–2055. [Google Scholar] [CrossRef]
- Chomienne, V.; Verdu, C.; Rech, J.; Valiorgue, F. Influence of surface integrity of 15-5PH on the fatigue life. Procedia Eng. 2013, 66, 274–281. [Google Scholar] [CrossRef] [Green Version]
- Denkena, B.; Grove, T.; Maiß, O. Influence of the cutting edge radius on surface integrity in hard turning of roller bearing inner rings. Prod. Eng. Res. Dev. WGP 2015, 9, 299–305. [Google Scholar] [CrossRef]
- Sun, J.; Wang, T.; Su, A.; Chen, W. Surface integrity and its influence on fatigue life when turning nickel alloy GH4169. Procedia CIRP 2020, 71, 478–483. [Google Scholar] [CrossRef]
- Withers, P.J. Residual stress and its role in failure. Rep. Prog. Phys. 2007, 70, 2211–2264. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Warren, A.; Hashimoto, F. The basic relationships between residual stress, white layer, and fatigue life of hard turned and ground surfaces in rolling contact. CIRP J. Manuf. Sci. Technol. 2010, 2, 129–134. [Google Scholar] [CrossRef]
- Dumas, M.; Valiorgue, F.; Van Robaeys, A.; Rech, J. Interaction between a roughing and a finishing operation on the final surface integrity in turning. Procedia CIRP 2018, 71, 396–400. [Google Scholar] [CrossRef]
- Ulutan, D.; Erdem Alaca, B.; Lazoglu, I. Analytical modelling of residual stresses in machining. J. Mater. Process. Technol. 2007, 183, 77–87. [Google Scholar] [CrossRef]
- Ulutan, D.; Ozel, T. Machining induced surface integrity in titanium and nickel alloys: A review. Int. J. Mach. Tools Manuf. 2011, 51, 250–280. [Google Scholar] [CrossRef]
- Shet, C.; Deng, X. Residual stresses and strains in orthogonal metal cutting. Int. J. Mach. Tools Manuf. 2003, 43, 573–587. [Google Scholar] [CrossRef]
- Salio, M.; Berruti, T.; De Poli, G. Prediction of residual stress distribution after turning in turbine disks. Int. J. Mech. Sci. 2006, 48, 976–984. [Google Scholar] [CrossRef]
- Ee, K.; Dillon, O.; Jawahir, I. Finite element modeling of residual stresses in machining induced by cutting using a tool with finite edge radius. Int. J. Mech. Sci. 2005, 47, 1611–1628. [Google Scholar] [CrossRef]
- Guo, Y.B.; Liu, C.R. FEM analysis of mechanical state on sequentially machined surfaces. Mach. Sci. Technol. 2002, 6, 21–41. [Google Scholar] [CrossRef]
- Liu, C.R.; Guo, Y. Finite element analysis of the effect of sequential cuts and tool-chip friction on residual stresses in a machined layer. Int. J. Mech. Sci. 2000, 42, 1069–1086. [Google Scholar] [CrossRef]
- Nasr, M.N.; Ng, E.G.; Elbestawi, M. Modelling the effects of tool-edge radius on residual stresses when orthogonal cutting AISI 316L. Int. J. Mach. Tools Manuf. 2007, 47, 401–411. [Google Scholar] [CrossRef]
- Mondelin, A.; Valiorgue, F.; Rech, J.; Coret, M.; Feulvarch, E. Hybrid model for the prediction of residual stresses induced by 15-5PH steel turning. Int. J. Mech. Sci. 2012, 58, 69–85. [Google Scholar] [CrossRef] [Green Version]
- Sasahara, H.; Obikawa, T.; Shirakashi, T. Prediction model of surface residual stress within a ma- chined surface by combining two orthogonal plane models. Int. J. Mach. Tools Manuf. 2004, 44, 815–822. [Google Scholar] [CrossRef]
- Attanasio, A.; Ceretti, E.; Giardini, C. 3D FE modelling of superficial residual stresses in turning operations. Mach. Sci. Technol. 2009, 13, 317–337. [Google Scholar] [CrossRef]
- Mondelin, A. Modélisation de L’intégrité des Surfaces Usinées. Ph.D. Thesis, Ecole Centrale de Lyon, Écully, France, 2012. Available online: https://tel.archives-ouvertes.fr/tel-00838512/ (accessed on 26 September 2013).
- Rech, J.; Arrazola, P.J.; Claudin, C.; Courbon, C.; Pusavec, F.; Kopac, J. Characterisation of friction and heat partition coefficients at the tool-workmaterial interface in cutting. CIRP Ann. Manuf. Technol. 2013, 62, 79–82. [Google Scholar] [CrossRef]
- Madariaga, A.; Kortabarria, A.; Hormaetxe, E.; Garay, A.; Arrazola, P.J. Influence of tool wear on residual stresses when turning Inconel 718. Procedia CIRP 2016, 45, 267–270. [Google Scholar] [CrossRef] [Green Version]



| Test Number | Cutting Speed, Vc (m/min) | Feed, f (mm/rev) | Depth of Cut, ap (mm) | Flank Wear, VB (mm) | Insert | Cutting Fluid |
|---|---|---|---|---|---|---|
| 1 | 50 | 0.18 | 0.6 | 0 | DNMG 15 06 12 | Emulsion |
| 2 | 150 | 0.18 | 0.6 | 0 | DNMG 15 06 12 | Emulsion |
| 3 | 250 | 0.18 | 0.6 | 0 | DNMG 15 06 12 | Emulsion |
| 4 | 150 | 0.1 | 0.6 | 0 | DNMG 15 06 12 | Emulsion |
| 5 | 150 | 0.3 | 0.6 | 0 | DNMG 15 06 12 | Emulsion |
| 6 | 150 | 0.18 | 0.6 | 0.2 | DNMG 15 06 12 | Emulsion |
| 7 | 150 | 0.18 | 0.6 | 0 | RNMG 09 03 00 | Emulsion |
| Parameter | Temperature | Value |
|---|---|---|
| Thermal conductivity λ [W·m−1·°C−1] | 0 | 8.7 |
| 1200 | 29.2 | |
| Specific heat Cp [J·kg−1·°C−1] | 0 | 248 |
| 1200 | 1400 | |
| Density ρ [kg·m3] | 0 | 7810 |
| 1200 | 7450 | |
| Young’s Modulus E [MPa] | 20 | 197,000 |
| 1200 | 128,600 | |
| Thermal expansion coefficient α [°C−1] | −73 | 0.0000104 |
| 1200 | 0.0000145 | |
| Poisson’s coefficient ν [−] | 0.272 |
| Parameter | Value |
|---|---|
| Thermal conductivity K [W m−1 °C−1] | 110 |
| Specific heat C [J kg−1 °C−1] | 288 |
| Density ρ [Kg m3] | 14,600 |
| Young’s Modulus E [MPa] | 620,000 |
| Thermal expansion coefficient α [°C−1] | 0.0000049 |
| Poisson’s coefficient ν [−] | 0.235 |
| Temperature [°C] | σy [MPa] | C | γ |
|---|---|---|---|
| 20 | 530 | 421,405 | 730 |
| 300 | 382 | 284,420 | 508 |
| 600 | 197 | 120,000 | 600 |
| Cutting Speed, Vc (m/min) | Feed Per Revolution, f (mm/rev) | Cutting Force, Fc (N) | Feed Force, Ff (N) | Tool-Machined Surface Contact Length, a (mm) | Chip Thicness, b (mm) | |
|---|---|---|---|---|---|---|
| Reference | 150 | 0.18 | 432 | 603 | 0.075 | 0.06 |
| Low Cutting Speed | 50 | 0.18 | 447 | 630 | 0.075 | 0.06 |
| High Cutting Speed | 250 | 0.18 | 366 | 585 | 0.075 | 0.06 |
| Low Feed | 150 | 0.10 | 296 | 559 | 0.075 | 0.05 |
| High Feed | 150 | 0.30 | 699 | 690 | 0.075 | 0.10 |
| Worn Insert | 150 | 0.18 | 523 | 1180 | 0.220 | 0.06 |
| Round Insert | 150 | 0.18 | 268 | 550 | 0.075 | 0.04 |
| μPSZ | μTSZ | Λ3 | |
|---|---|---|---|
| Reference | 0.22 | 0.30 | 0.12 |
| Low Cutting Speed | 0.36 | 0.50 | 0.18 |
| High Cutting Speed | 0.18 | 0.24 | 0.08 |
| Low Feed | 0.22 | 0.46 | 0.12 |
| High Feed | 0.22 | 0.25 | 0.12 |
| Worn Insert | 0.26 | 0.30 | 0.25 |
| Round Insert | 0.22 | 0.64 | 0.12 |
| Insert | Cutting Speed, Vc (m/min) | Feed per Rev, f (mm/rev) | Depth of Cut, ap (mm) | Edge Prep., Rβ (mm) | Uncut Chip Thick., hmax (mm) | Direct Contact Length, d (mm) | Indirect Contact Length, k (mm) | |
|---|---|---|---|---|---|---|---|---|
| Reference | DNMG | 150 | 0.18 | 0.6 | 56 | 0.030 | 0.18 | 0.96 |
| Low Cutting Speed | DNMG | 50 | 0.18 | 0.6 | 56 | 0.030 | 0.18 | 0.96 |
| High Cutting Speed | DNMG | 250 | 0.18 | 0.6 | 56 | 0.030 | 0.18 | 0.96 |
| Low Feed | DNMG | 150 | 0.10 | 0.6 | 56 | 0.008 | 0.10 | 0.97 |
| High Feed | DNMG | 150 | 0.30 | 0.6 | 56 | 0.075 | 0.30 | 0.88 |
| Worn Insert | DNMG | 150 | 0.18 | 0.6 | 60 | 0.030 | 0.18 | 0.96 |
| Round Insert | RNMG | 150 | 0.18 | 0.6 | 56 | 0.003 | 0.18 | 2.10 |
| Normal Stress (MPa) | Tangential Stress (MPa) | Heat Flux in the TSZ (W) | Heat Flux Density in the TSZ (W/mm2) | Heat Flux in the PSZ (W) | Heat Flux Density in the PSZ (W/mm2) | |
|---|---|---|---|---|---|---|
| Reference | 2771 | 616 | 248 | 1001 | 68 | 366 |
| Low Cutting Speed | 2725 | 994 | 280 | 1130 | 190 | 101 |
| High Cutting Speed | 2842 | 502 | 353 | 1427 | 97 | 523 |
| Low Feed | 2572 | 572 | 230 | 929 | 41 | 320 |
| High Feed | 2987 | 664 | 267 | 1079 | 123 | 405 |
| Worn Insert | 2072 | 546 | 550 | 758 | 49 | 264 |
| Round Insert | 2416 | 537 | 216 | 873 | 36 | 313 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mondelin, A.; Valiorgue, F.; Rech, J.; Coret, M. 3D Hybrid Numerical Model of Residual Stresses: Numerical—Sensitivity to Cutting Parameters When Turning 15-5PH Stainless Steel. J. Manuf. Mater. Process. 2021, 5, 70. https://doi.org/10.3390/jmmp5030070
Mondelin A, Valiorgue F, Rech J, Coret M. 3D Hybrid Numerical Model of Residual Stresses: Numerical—Sensitivity to Cutting Parameters When Turning 15-5PH Stainless Steel. Journal of Manufacturing and Materials Processing. 2021; 5(3):70. https://doi.org/10.3390/jmmp5030070
Chicago/Turabian StyleMondelin, Alexandre, Frédéric Valiorgue, Joël Rech, and Michel Coret. 2021. "3D Hybrid Numerical Model of Residual Stresses: Numerical—Sensitivity to Cutting Parameters When Turning 15-5PH Stainless Steel" Journal of Manufacturing and Materials Processing 5, no. 3: 70. https://doi.org/10.3390/jmmp5030070
APA StyleMondelin, A., Valiorgue, F., Rech, J., & Coret, M. (2021). 3D Hybrid Numerical Model of Residual Stresses: Numerical—Sensitivity to Cutting Parameters When Turning 15-5PH Stainless Steel. Journal of Manufacturing and Materials Processing, 5(3), 70. https://doi.org/10.3390/jmmp5030070







