Search for the Optimal Build Direction in Additive Manufacturing Technologies: A Review
Abstract
1. Introduction
2. Objective Functions
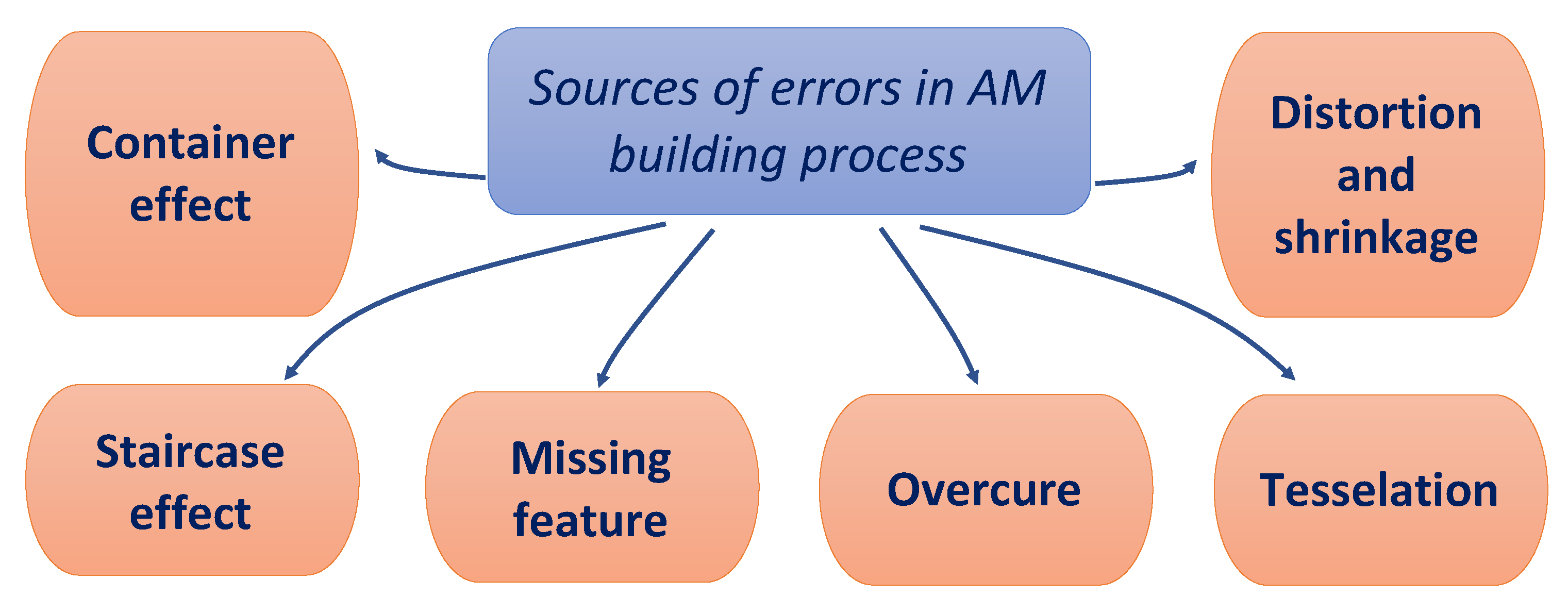
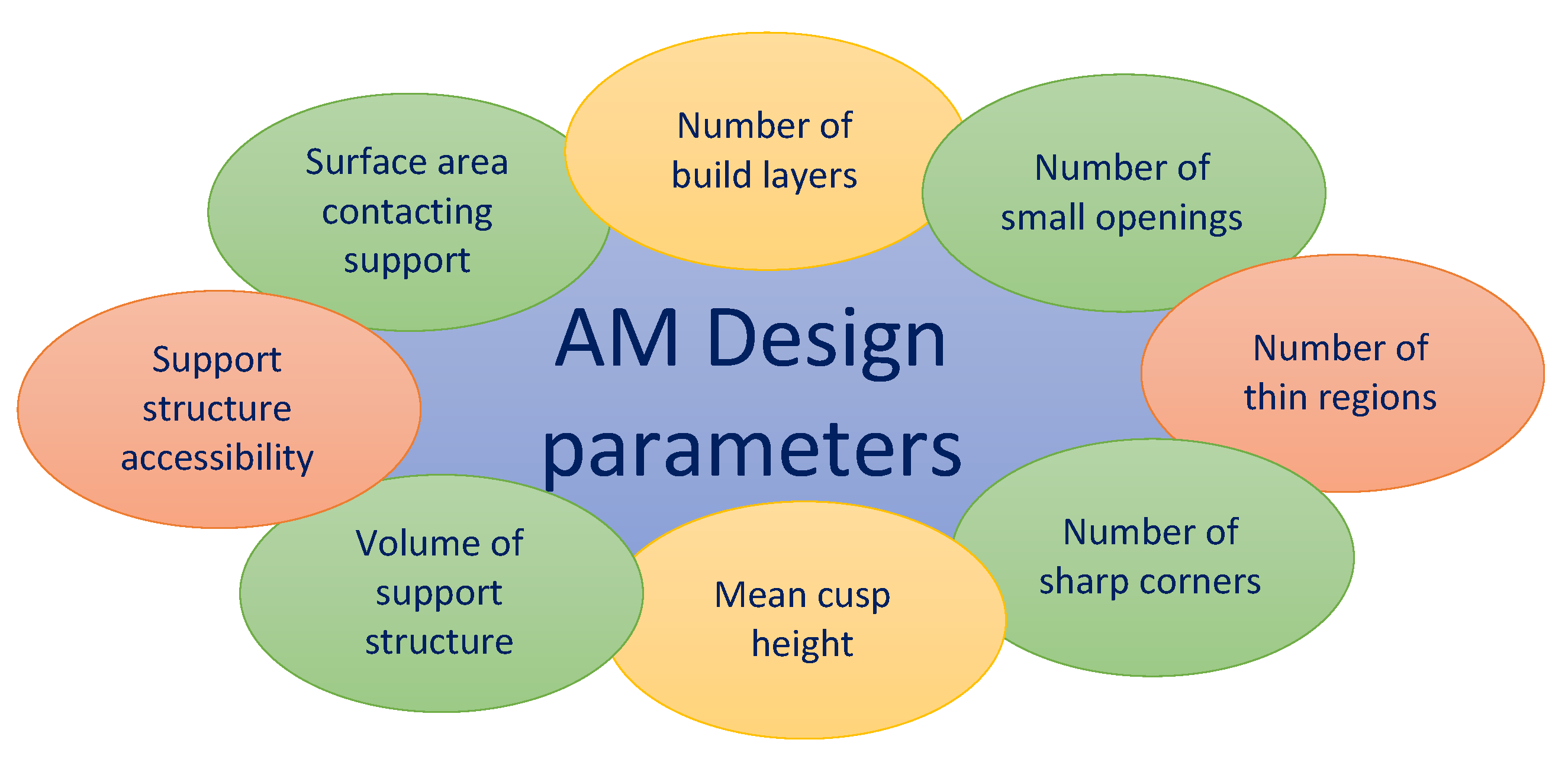
2.1. Part Quality
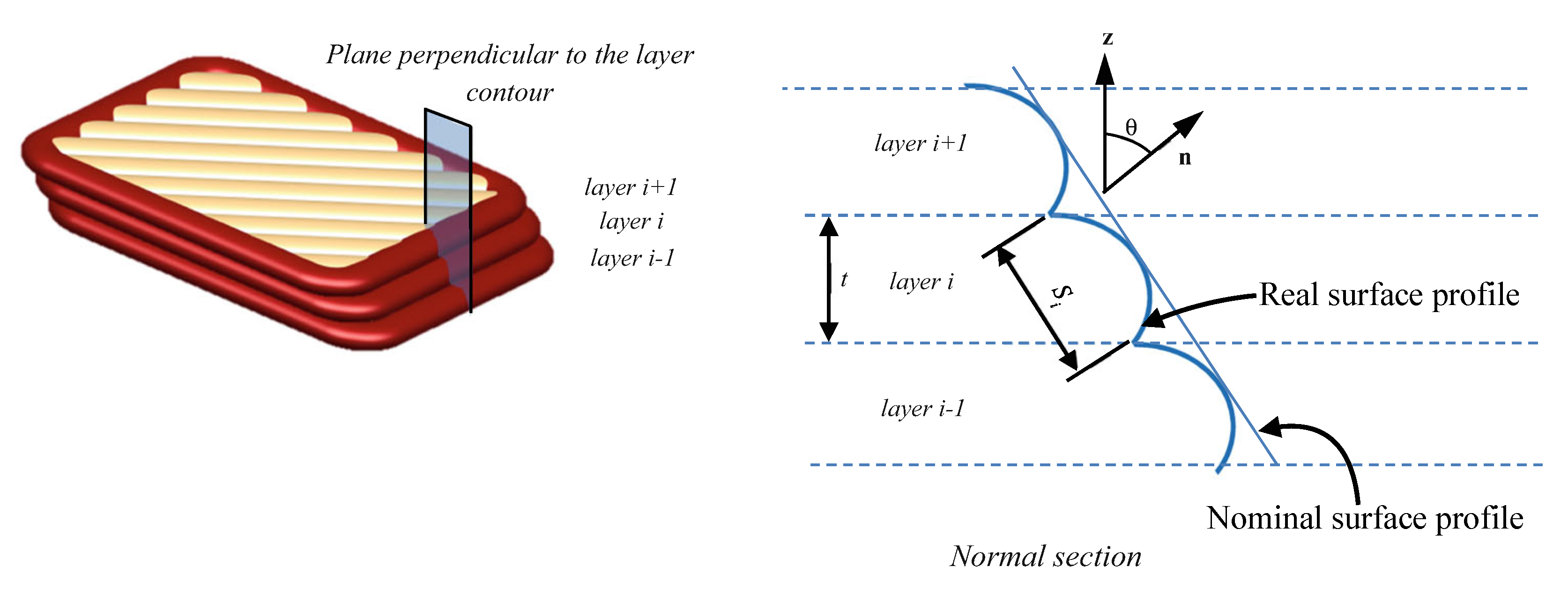
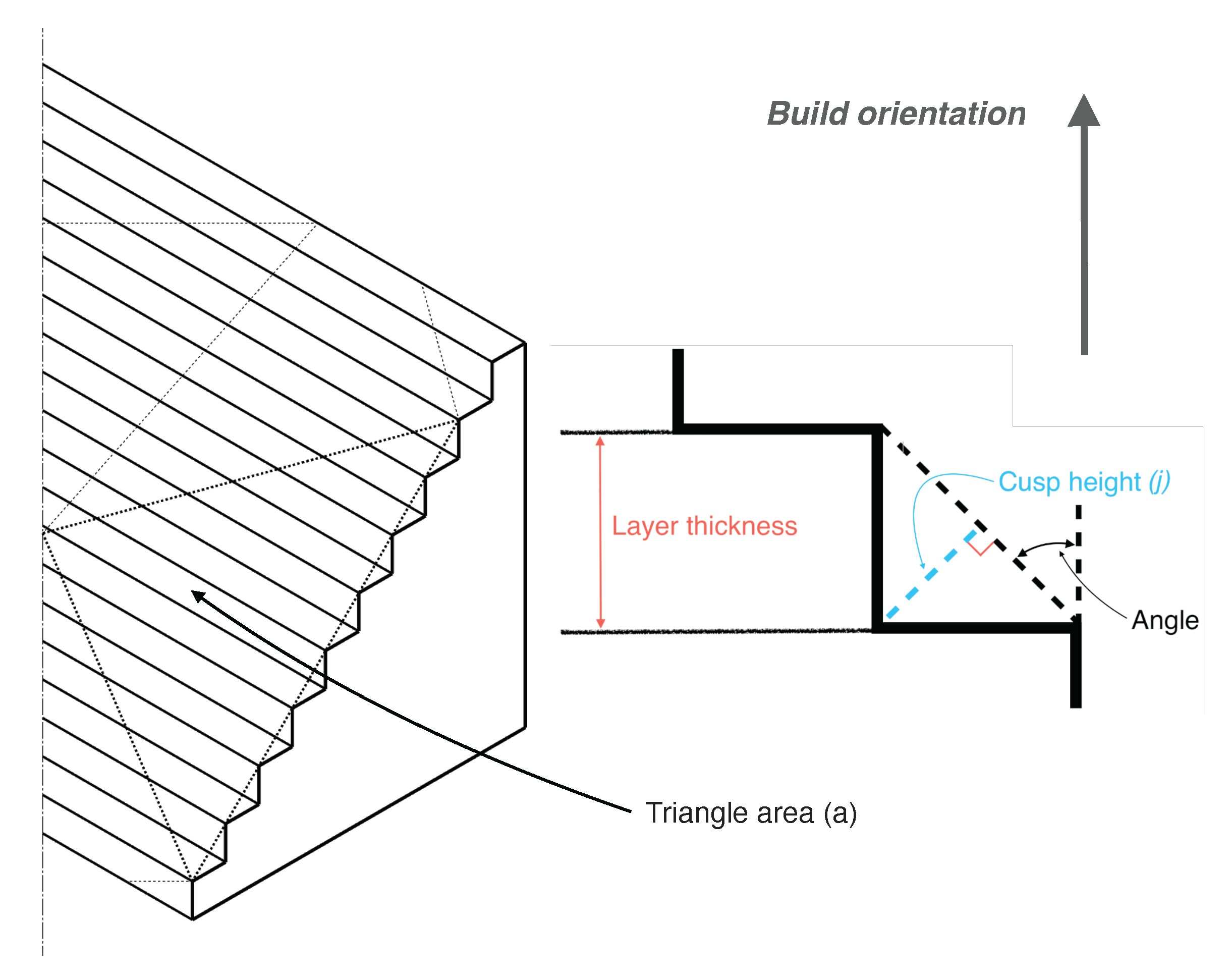
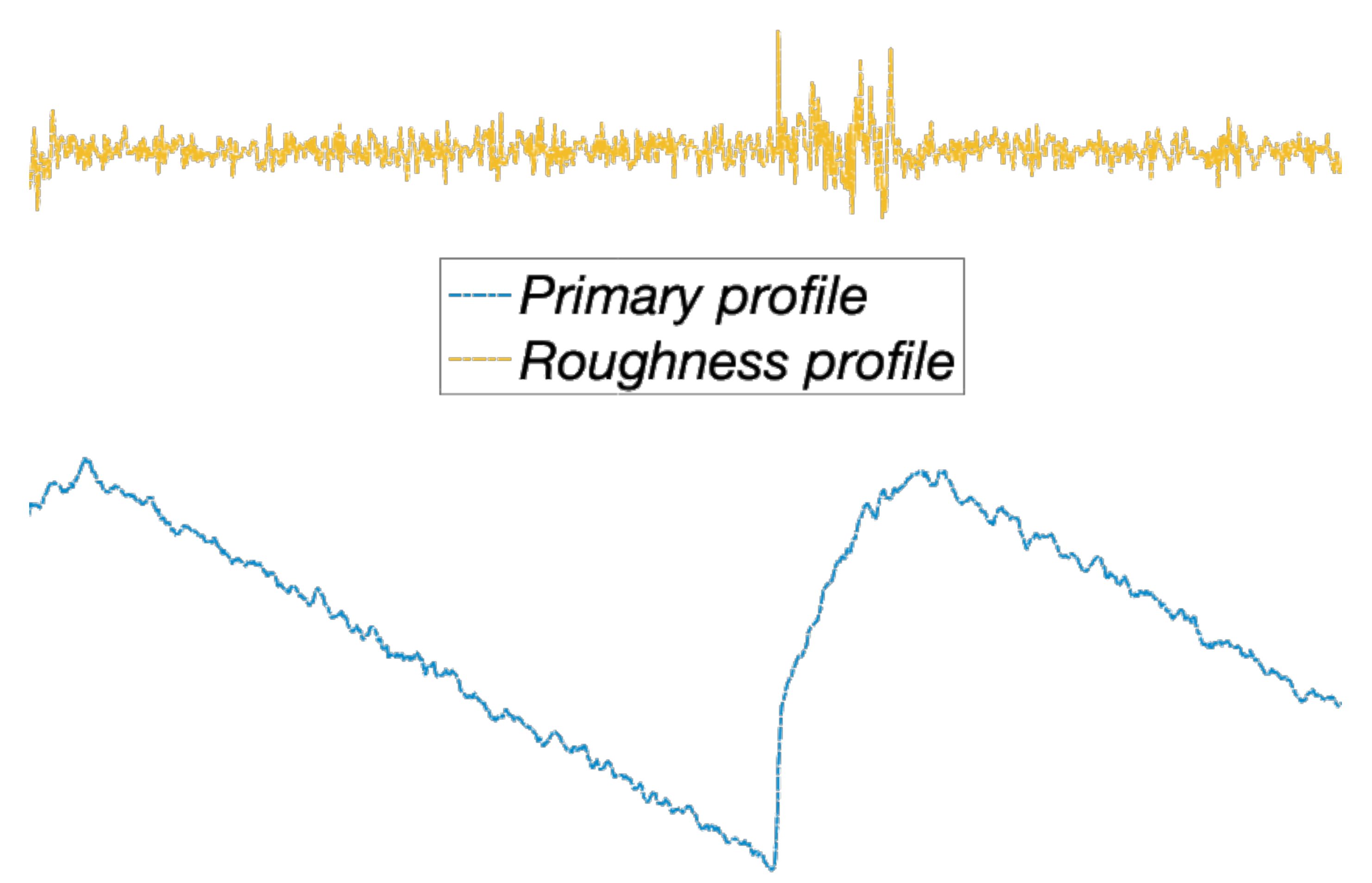
2.2. Surface Quality
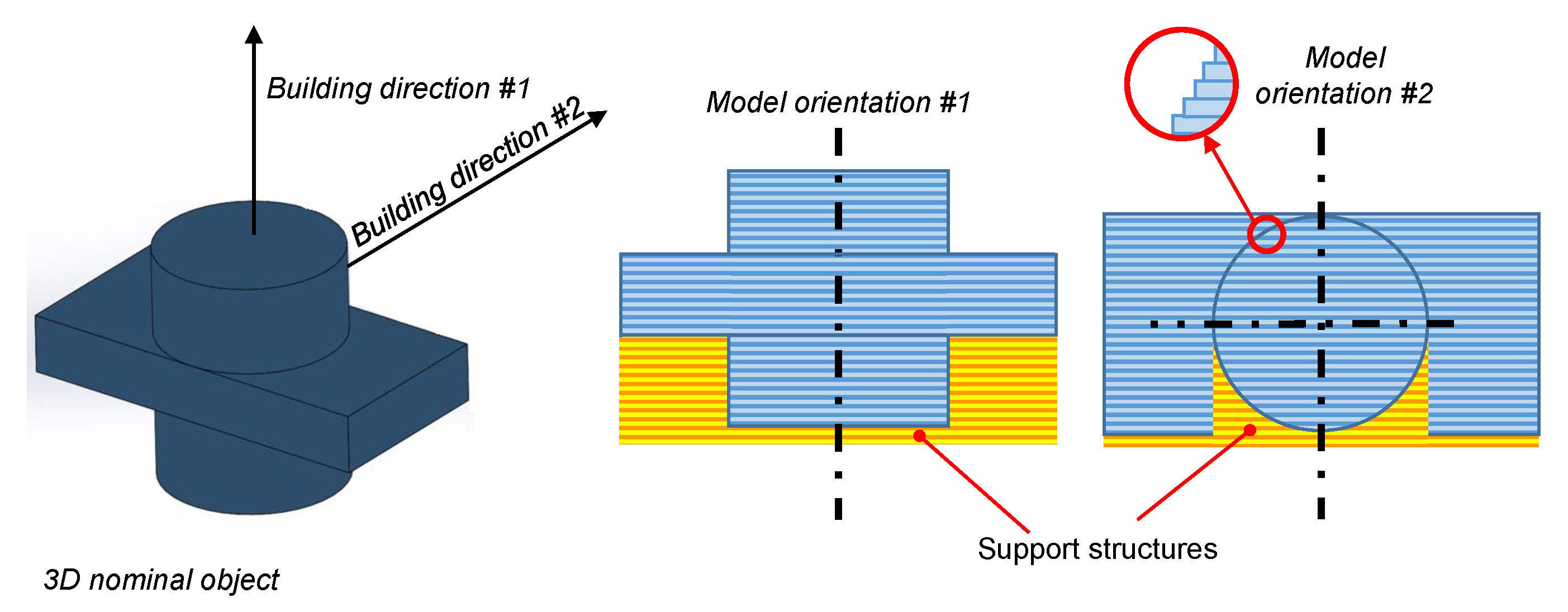
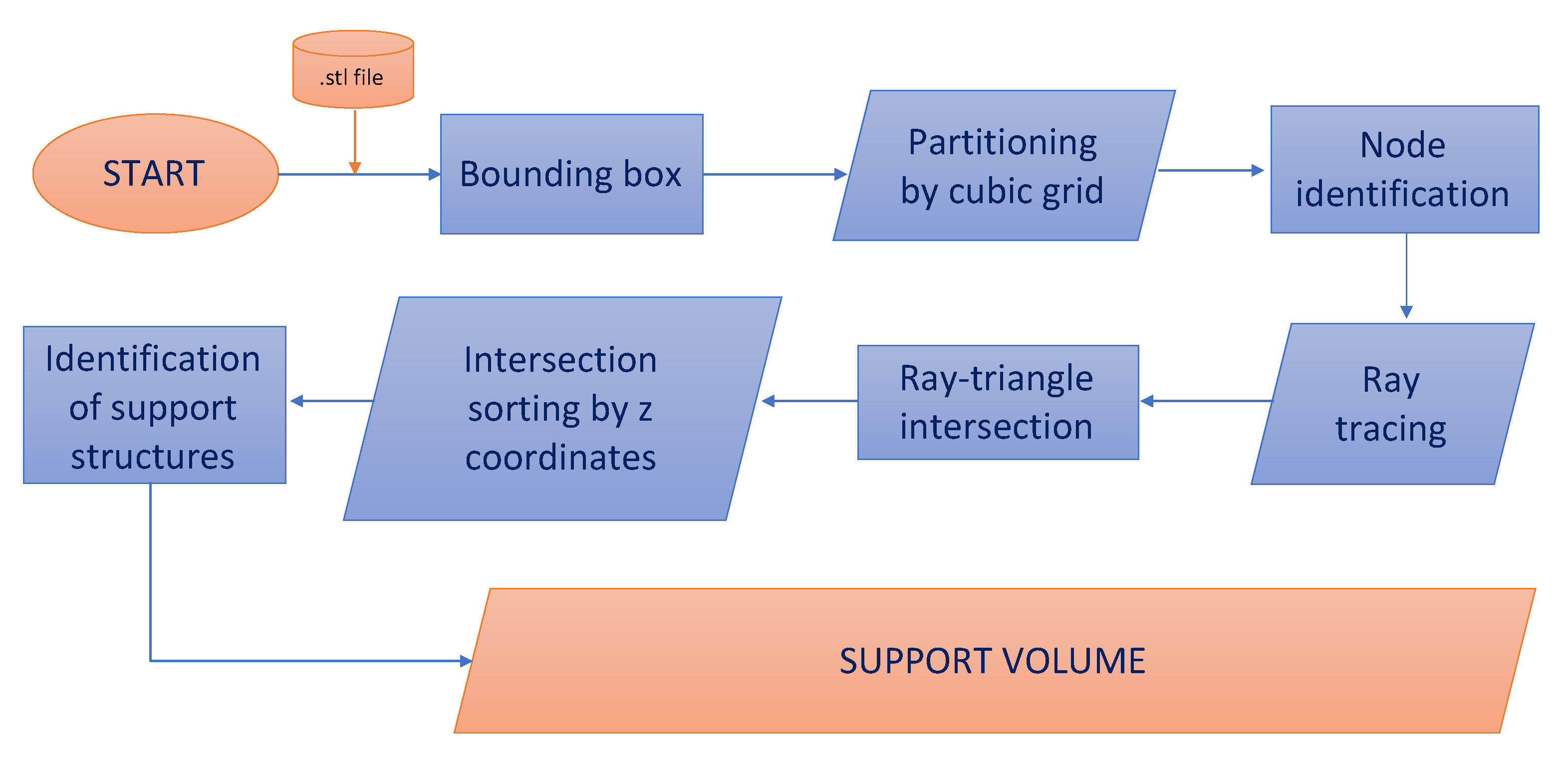
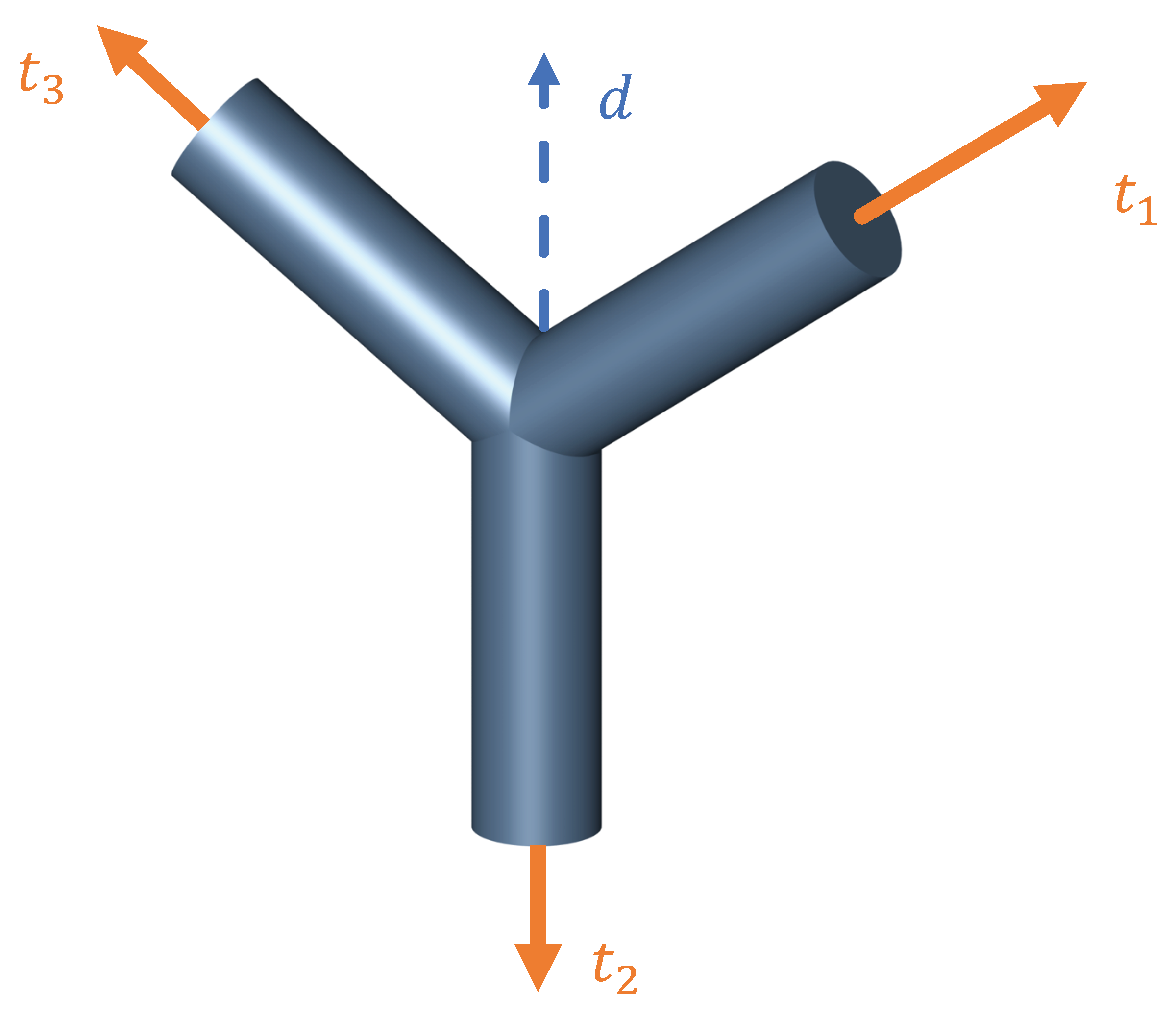
2.3. Support Structure
- discretization of the NURBS surface into fine points and extraction of the normal at these points;
- identification of points requiring supports by means of the dot product between normal and build direction;
- projection of identified points onto the X–Y plane;
- iterative Quadtree decomposition of X–Y plane until a pre-defined threshold value is met.
2.4. Build Time
2.5. Cost
| material cost | |
| operative cost | |
| labour cost | |
| build time | |
| pre-processing time | |
| post-processing time |
2.6. Mechanical Properties
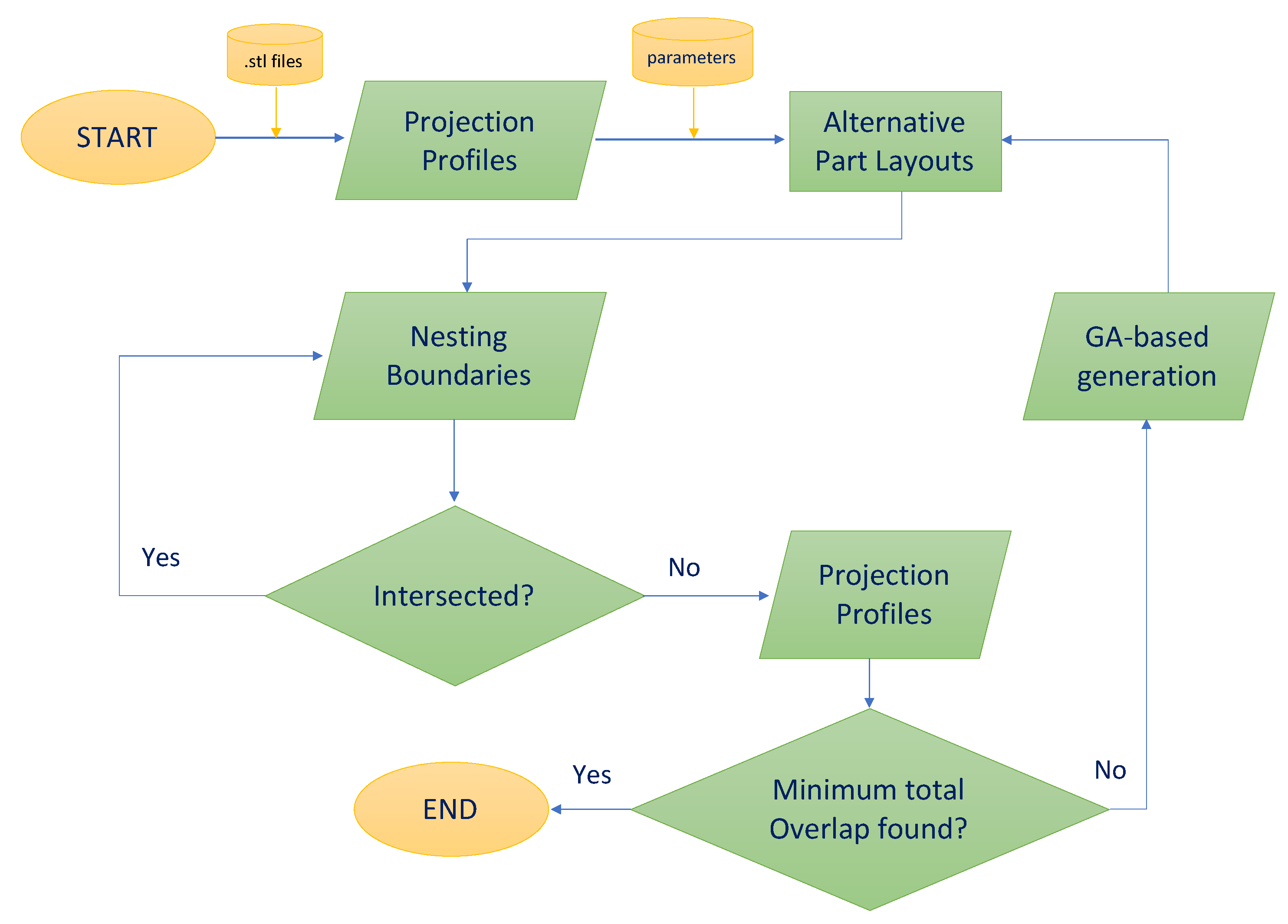
2.7. Multi-Part Job
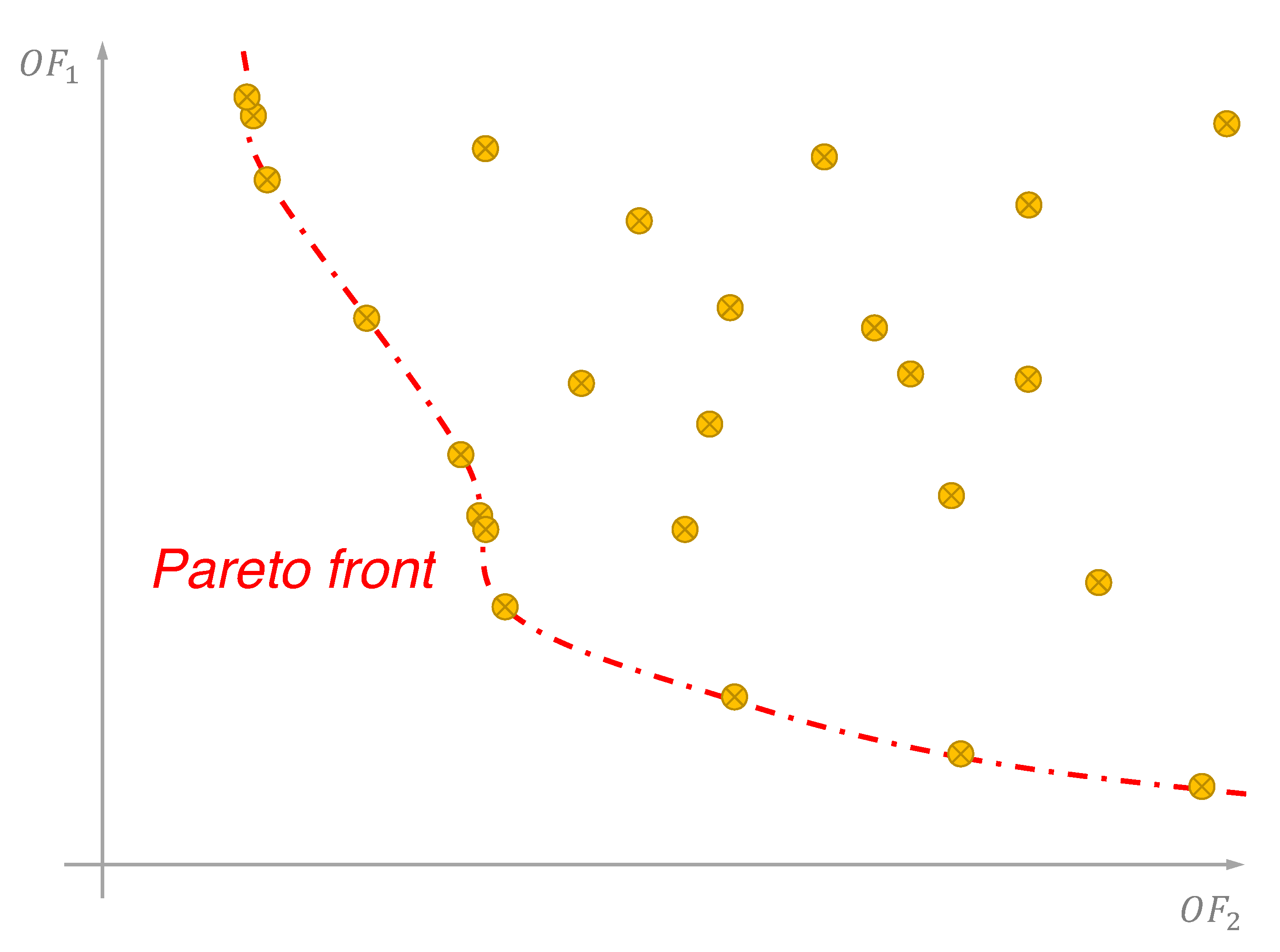
3. Optimization Methods and Decision Criteria
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| stereolitography file format | |
| additive manufacturing | |
| artificial neural network | |
| a | area of triangle |
| external surface area of the part | |
| supported area of the part | |
| computer-aided design | |
| computer-aided manufacturing | |
| material cost | |
| operative cost | |
| build cost | |
| labour cost | |
| post-processing cost | |
| pre-processing cost | |
| build direction | |
| externally supported feature | |
| functionally graded materials | |
| fused deposition modeling | |
| h | height of the part with respect to the build direction |
| iterative tabu search procedure | |
| j | cusp height |
| l | layer path length |
| layer external path length | |
| layer supports path length | |
| N | number of repositioning of deposition tool during the building process |
| non-dominate sorting genetic algorithm-II | |
| non-uniform rational basis spline | |
| n | number of layers |
| objective function | |
| arithmetic mean of the primary profile | |
| powder bed fusion | |
| part build orientation | |
| particle swarm-based optimizer | |
| S | contour area |
| stereolitography apparatus | |
| support structure accessibility | |
| s | scanning speed |
| roughness index | |
| T | layer thickness |
| technique for order of preference by similarity to ideal solution | |
| build time | |
| pre-processing time | |
| post-processing time | |
| recoating time for each layer | |
| V | number of voxel |
| volume of part | |
| volume of supports | |
| triangle normal | |
| z | z-component of triangle |
References
- ISO/ASTM. INTERNATIONAL STANDARD ISO/ASTM 52900 Additive Manufacturing—General Principles—Terminology; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar] [CrossRef]
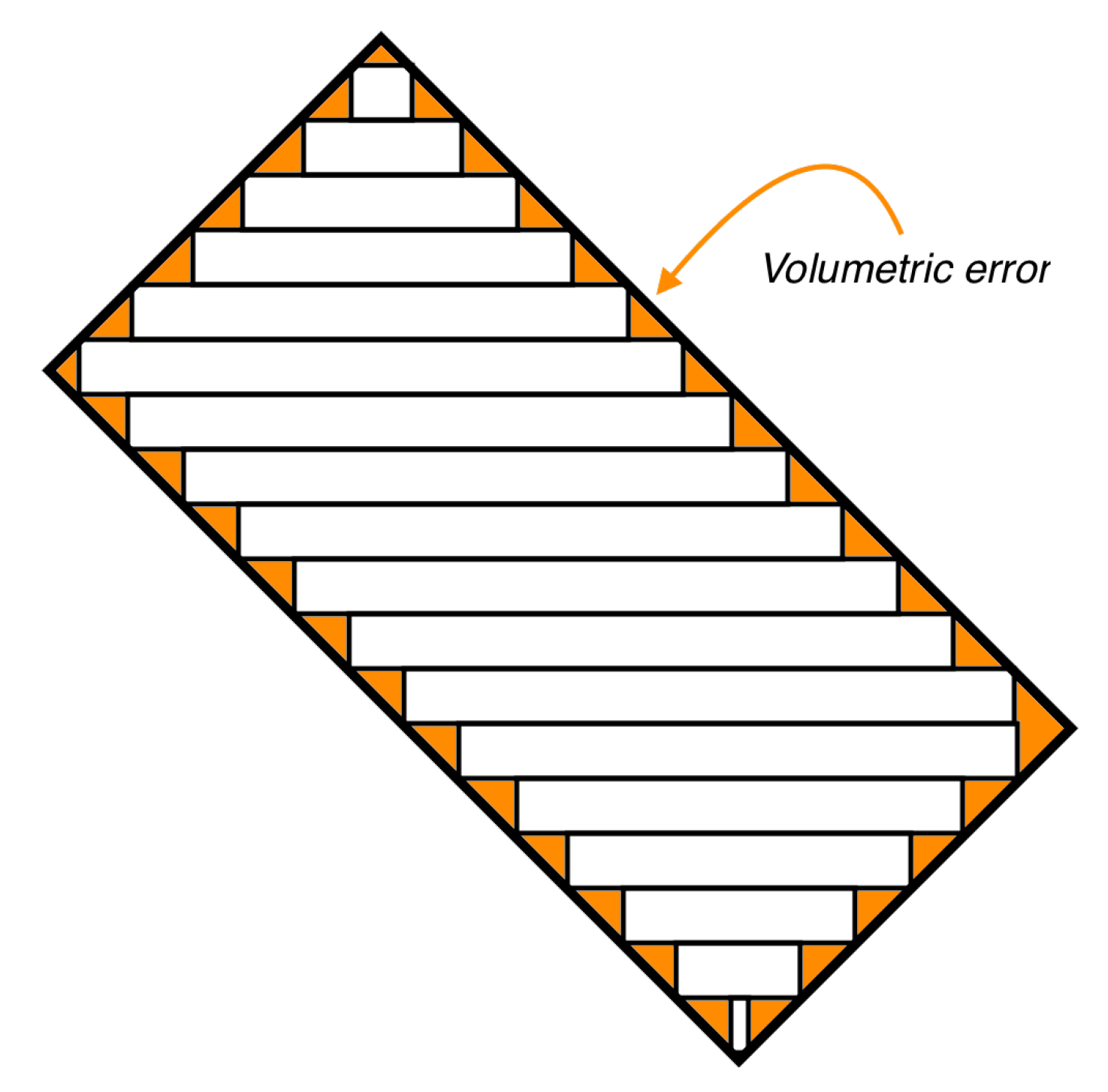
- Masood, S.H.; Rattanawong, W.; Iovenitti, P. Part build orientations based on volumetric error in fused deposition modelling. Int. J. Adv. Manuf. Technol. 2000, 16, 162–168. [Google Scholar] [CrossRef]
- Guo, N.; Leu, M.C. Additive manufacturing: Technology, applications and research needs. Front. Mech. Eng. 2013, 8, 215–243. [Google Scholar] [CrossRef]
- Lovo, J.F.P.; Fortulan, C.A.; Da Silva, M.M. Optimal deposition orientation in fused deposition modeling for maximizing the strength of three-dimensional printed truss-like structures. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 1206–1215. [Google Scholar] [CrossRef]
- Angelo, L.D.; Stefano, P.D.; Guardiani, E. A build time estimator for Additive Manufacturing. In Proceedings of the 2019 II Workshop on Metrology for Industry 4.0 and IoT (MetroInd4.0&IoT), Naples, Italy, 4–6 June 2019; pp. 344–349. [Google Scholar] [CrossRef]
- Di Angelo, L.; Di Stefano, P.; Marzola, A. Surface quality prediction in FDM additive manufacturing. Int. J. Adv. Manuf. Technol. 2017, 93, 3655–3662. [Google Scholar] [CrossRef]
- Lan, P.T.; Chou, S.Y.; Chen, L.L.; Gemmill, D. Determining fabrication orientations for rapid prototyping with Stereolithography apparatus. Comput.-Aided Des. 1997, 29, 53–62. [Google Scholar] [CrossRef]
- McClurkin, J.E.; Rosen, D.W. Computer-aided build style decision support for stereolithography. Rapid Prototyp. J. 1998. [Google Scholar] [CrossRef]
- Pham, D.T.; Dimov, S.S.; Gault, R.S. Part orientation in stereolithography. Int. J. Adv. Manuf. Technol. 1999, 15, 674–682. [Google Scholar] [CrossRef]
- Hur, S.M.; Choi, K.H.; Lee, S.H.; Chang, P.K. Determination of fabricating orientation and packing in SLS process. J. Mater. Process. Technol. 2001, 112, 236–243. [Google Scholar] [CrossRef]
- Thrimurthulu, K.; Pandey, P.M.; Reddy, N.V. Optimum part deposition orientation in fused deposition modeling. Int. J. Mach. Tools Manuf. 2004, 44, 585–594. [Google Scholar] [CrossRef]
- Kim, H.C.; Lee, S.H. Reduction of post-processing for stereolithography systems by fabrication- direction optimization. CAD Comput. Aided Des. 2005, 37, 711–725. [Google Scholar] [CrossRef]
- Byun, H.S.; Lee, K.H. Determination of the optimal build direction for different rapid prototyping processes using multi-criterion decision making. Robot. Comput.-Integr. Manuf. 2006, 22, 69–80. [Google Scholar] [CrossRef]
- Canellidis, V.; Giannatsis, J.; Dedoussis, V. Genetic-algorithm-based multi-objective optimization of the build orientation in stereolithography. Int. J. Adv. Manuf. Technol. 2009, 45, 714–730. [Google Scholar] [CrossRef]
- Singhal, S.K.; Jain, P.K.; Pandey, P.M.; Nagpal, A.K. Optimum part deposition orientation for multiple objectives in SL and SLS prototyping. Int. J. Prod. Res. 2009, 47, 6375–6396. [Google Scholar] [CrossRef]
- Phatak, A.M.; Pande, S.S. Optimum part orientation in rapid prototyping using genetic algorithm. Trans. North Am. Manuf. Res. Inst. SME 2012, 40, 708–716. [Google Scholar] [CrossRef]
- Paul, R.; Anand, S. Optimization of layered manufacturing process for reducing form errors with minimal support structures. J. Manuf. Syst. 2015, 36, 216–223. [Google Scholar] [CrossRef]
- Das, P.; Chandran, R.; Samant, R.; Anand, S. Optimum Part Build Orientation in Additive Manufacturing for Minimizing Part Errors and Support Structures. Procedia Manuf. 2015, 1, 343–354. [Google Scholar] [CrossRef]
- Moroni, G.; Syam, W.P.; Petrò, S. Functionality-based part orientation for additive manufacturing. Procedia CIRP 2015, 36, 217–222. [Google Scholar] [CrossRef]
- Brika, S.E.; Zhao, Y.F.; Brochu, M.; Mezzetta, J. Multi-Objective Build Orientation Optimization for Powder Bed Fusion by Laser. J. Manuf. Sci. Eng. Trans. ASME 2017, 139. [Google Scholar] [CrossRef]
- Chen, C.B.; Klein, C.M. An efficient approach to solving fuzzy MADM problems. Fuzzy Sets Syst. 1997, 88, 51–67. [Google Scholar] [CrossRef]
- Chowdhury, S.; Mhapsekar, K.; Anand, S. Part Build Orientation Optimization and Neural Network-Based Geometry Compensation for Additive Manufacturing Process. J. Manuf. Sci. Eng. 2018, 140. [Google Scholar] [CrossRef]
- Cheng, W.; Fuh, J.; Nee, A.; Wong, Y.; Loh, H.; Miyazawa, T. Multi-objective optimization of part- building orientation in stereolithography. Rapid Prototyp. J. 1995, 1, 12–23. [Google Scholar] [CrossRef]
- Alexander, P.; Allen, S.; Dutta, D. Part orientation and build cost determination in layered manufacturing. Comput. Aided Des. 1998, 30, 343–356. [Google Scholar] [CrossRef]
- Singhal, S.K.; Pandey, A.P.; Pandey, P.M.; Nagpal, A.K. Optimum Part Deposition Orientation in Stereolithography. Comput.-Aided Des. Appl. 2005, 2, 319–328. [Google Scholar] [CrossRef]
- Ahn, D.; Kim, H.; Lee, S. Fabrication direction optimization to minimize post-machining in layered manufacturing. Int. J. Mach. Tools Manuf. 2007, 47, 593–606. [Google Scholar] [CrossRef]
- Ezair, B.; Massarwi, F.; Elber, G. Orientation analysis of 3D objects toward minimal support volume in 3D-printing. Comput. Graph. 2015, 51, 117–124. [Google Scholar] [CrossRef]
- Delfs, P.; Tows, M.; Schmid, H.J. Optimized build orientation of additive manufactured parts for improved surface quality and build time. Addit. Manuf. 2016, 12, 314–320. [Google Scholar] [CrossRef]
- Luo, N.; Wang, Q. Fast slicing orientation determining and optimizing algorithm for least volumetric error in rapid prototyping. Int. J. Adv. Manuf. Technol. 2016, 83, 1297–1313. [Google Scholar] [CrossRef]
- Pereira, S.; Vaz, A.I.; Vicente, L.N. On the optimal object orientation in additive manufacturing. Int. J. Adv. Manuf. Technol. 2018, 98, 1685–1694. [Google Scholar] [CrossRef]
- Mele, M.; Campana, G.; Lenzi, F.; Cimatti, B. Optimisation of build orientation to achieve minimum environmental impact in Stereo-lithography. Procedia Manuf. 2019, 33, 145–152. [Google Scholar] [CrossRef]
- Nezhad, A.S.; Barazandeh, F.; Rahimi, A.R.; Vatani, M. Pareto-based optimization of part orientation in stereolithography. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 1591–1598. [Google Scholar] [CrossRef]
- Padhye, N.; Deb, K. Multi-objective optimisation and multi-criteria decision making in SLS using evolutionary approaches. Rapid Prototyp. J. 2011, 17, 458–478. [Google Scholar] [CrossRef]
- Strano, G.; Hao, L.; Everson, R.M.; Evans, K.E. Multi-objective optimization of selective laser sintering processes for surface quality and energy saving. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 1673–1682. [Google Scholar] [CrossRef]
- Huang, R.; Dai, N.; Li, D.; Cheng, X.; Liu, H.; Sun, D. Parallel non-dominated sorting genetic algorithm-II for optimal part deposition orientation in additive manufacturing based on functional features. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 3384–3395. [Google Scholar] [CrossRef]
- Khodaygan, S.; Golmohammadi, A.H. Multi-criteria optimization of the part build orientation (PBO) through a combined meta-modeling/NSGAII/TOPSIS method for additive manufacturing processes. Int. J. Interact. Des. Manuf. (IJIDeM) 2018, 12, 1071–1085. [Google Scholar] [CrossRef]
- Asadollahi-Yazdi, E.; Gardan, J.; Lafon, P. Multi-Objective Optimization of Additive Manufacturing Process. IFAC-PapersOnLine 2018, 51, 152–157. [Google Scholar] [CrossRef]
- Cheng, L.; To, A. Part-scale build orientation optimization for minimizing residual stress and support volume for metal additive manufacturing: Theory and experimental validation. CAD Comput. Aided Des. 2019, 113, 1–23. [Google Scholar] [CrossRef]
- Raju, M.; Gupta, M.K.; Bhanot, N.; Sharma, V.S. A hybrid PSO–BFO evolutionary algorithm for optimization of fused deposition modelling process parameters. J. Intell. Manuf. 2019, 30, 2743–2758. [Google Scholar] [CrossRef]
- Di Angelo, L.; Di Stefano, P.; Dolatnezhadsomarin, A.; Guardiani, E.; Khorram, E. A reliable build orientation optimization method in additive manufacturing: The application to FDM technology. Int. J. Adv. Manuf. Technol. 2020, 108, 263–276. [Google Scholar] [CrossRef]
- Zhang, Y.; Bernard, A.; Gupta, R.K.; Harik, R. Feature based building orientation optimization for additive manufacturing. Rapid Prototyp. J. 2016, 22, 358–376. [Google Scholar] [CrossRef]
- Zhang, Y.; Gupta, R.K.; Bernard, A. Two-dimensional placement optimization for multi-parts production in additive manufacturing. Robot. Comput.-Integr. Manuf. 2016, 38, 102–117. [Google Scholar] [CrossRef]
- Jaiswal, P.; Patel, J.; Rai, R. Build orientation optimization for additive manufacturing of functionally graded material objects. Int. J. Adv. Manuf. Technol. 2018, 96, 223–235. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Kim, N. Multi-criteria selection problem of part orientation in 3D fused deposition modeling based on analytic hierarchy process model: A case study. In Proceedings of the 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 10–13 December 2017; pp. 1455–1459. [Google Scholar] [CrossRef]
- Golmohammadi, A.H.; Khodaygan, S. A framework for multi-objective optimisation of 3D part-build orientation with a desired angular resolution in additive manufacturing processes. Virtual Phys. Prototyp. 2019, 14, 19–36. [Google Scholar] [CrossRef]
- Qin, Y.; Qi, Q.; Scott, P.J.; Jiang, X. Determination of optimal build orientation for additive manufacturing using Muirhead mean and prioritised average operators. J. Intell. Manuf. 2019, 30, 3015–3034. [Google Scholar] [CrossRef]
- Qin, Y.; Qi, Q.; Shi, P.; Scott, P.J.; Jiang, X. Automatic generation of alternative build orientations for laser powder bed fusion based on facet clustering. Virtual Phys. Prototyp. 2020, 15, 1–18. [Google Scholar] [CrossRef]
- Senthilkumaran, K.; Pandey, P.M.; Rao, P.V. Statistical modeling and minimization of form error in SLS prototyping. Rapid Prototyp. J. 2012. [Google Scholar] [CrossRef]
- Aslani, K.E.; Kitsakis, K.; Kechagias, J.D.; Vaxevanidis, N.M.; Manolakos, D.E. On the application of grey Taguchi method for benchmarking the dimensional accuracy of the PLA fused filament fabrication process. SN Appl. Sci. 2020, 2, 1016. [Google Scholar] [CrossRef]
- Masood, S.H.; Rattanawong, W.; Iovenitti, P. A generic algorithm for a best part orientation system for complex parts in rapid prototyping. J. Mater. Process. Technol. 2003, 24, 2799–2812. [Google Scholar] [CrossRef]
- Xu, F.; Wong, Y.; Loh, H.; Fuh, J.; Miyazawa, T. Optimal orientation with variable slicing in stereolithography. Rapid Prototyp. J. 1997, 3, 76–88. [Google Scholar] [CrossRef]
- Barari, A.; Kishawy, H.; Kaji, F.; Elbestawi, M. On the surface quality of additive manufactured parts. Int. J. Adv. Manuf. Technol. 2017, 89, 1969–1974. [Google Scholar] [CrossRef]
- Di Angelo, L.; Di Stefano, P.; Guardiani, E. A Build-Time Estimator for Additive Manufactured Objects. In International Conference on Design, Simulation, Manufacturing: The Innovation Exchange; Springer: Cham, Switzerland, 2020; pp. 925–935. [Google Scholar]
- Ahn, D.; Kweon, J.H.; Kwon, S.; Song, J.; Lee, S. Representation of surface roughness in fused deposition modeling. J. Mater. Process. Technol. 2009, 209, 5593–5600. [Google Scholar] [CrossRef]
- Reeves, P.E.; Cobb, R.C. Reducing the surface deviation of stereolithography using in-process techniques. Rapid Prototyp. J. 1997. [Google Scholar] [CrossRef]
- Ahn, D.; Kim, H.; Lee, S. Surface roughness prediction using measured data and interpolation in layered manufacturing. J. Mater. Process. Technol. 2009, 209, 664–671. [Google Scholar] [CrossRef]
- Reeves, P.E.; Cobb, R.C.; Dickens, P.M. Surface Deviation Modelling of LMT Processes—A Comparative Analysis, European conference. In Proceedings of the Fifth European Conference on Rapid Prototyping and Manufacturing, Helsinki, Finland, 4–6 June 1996; pp. 59–76. [Google Scholar]
- Pandey, P.M.; Reddy, N.V.; Dhande, S.G. Improvement of surface finish by staircase machining in fused deposition modeling. J. Mater. Process. Technol. 2003, 132, 323–331. [Google Scholar] [CrossRef]
- Boschetto, A.; Bottini, L. Accuracy prediction in fused deposition modeling. Int. J. Adv. Manuf. Technol. 2014, 73, 913–928. [Google Scholar] [CrossRef]
- ISO 4287. Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Terms, Definitions and Surface Texture Parameters; International Organization for Standardization: Geneva, Switzerland, 1997. [Google Scholar]
- Zhang, Y.; Bernard, A.; Harik, R.; Karunakaran, K.P. Build orientation optimization for multi-part production in additive manufacturing. J. Intell. Manuf. 2017, 28, 1393–1407. [Google Scholar] [CrossRef]
- Ga, B.; Gardan, N.; Wahu, G. Methodology for part building orientation in additive manufacturing. Comput.-Aided Des. Appl. 2019, 16. [Google Scholar]
- Zwier, M.P.; Wits, W.W. Design for additive manufacturing: Automated build orientation selection and optimization. Procedia CIRP 2016, 55, 128–133. [Google Scholar] [CrossRef]
- Qie, L.; Jing, S.; Lian, R.; Chen, Y.; Liu, J. Quantitative suggestions for build orientation selection. Int. J. Adv. Manuf. Technol. 2018, 98, 1831–1845. [Google Scholar] [CrossRef]
- Bacciaglia, A.; Ceruti, A.; Liverani, A. A systematic review of voxelization method in additive manufacturing. Mech. Ind. 2019, 20, 630. [Google Scholar] [CrossRef]
- Karim, K.F.; Hazry, D.; Zulkifli, A.; Ahmed, S.F.; Razlan, Z.M.; Wan, K.; Bakar, S.A. Feature Extraction and Optimum Part Deposition Orientation for FDM. Appl. Mech. Mater. 2015, 793, 642–646. [Google Scholar] [CrossRef]
- Griffiths, V.; Scanlan, J.P.; Eres, M.H.; Martinez-Sykora, A.; Chinchapatnam, P. Cost-driven build orientation and bin packing of parts in Selective Laser Melting (SLM). Eur. J. Oper. Res. 2019, 273, 334–352. [Google Scholar] [CrossRef]
- Schwerdt, J.; Smid, M.; Janardan, R.; Johnson, E. Protecting critical facets in layered manufacturing: Implementation and experimental results. CAD Comput. Aided Des. 2003, 35, 647–657. [Google Scholar] [CrossRef]
- Garzaniti, N.; Golkar, A.; Fortin, C. Optimization of multi-part 3D printing build strategies for lean product and process development. IFIP Adv. Inf. Commun. Technol. 2018, 540, 488–497. [Google Scholar] [CrossRef]
- Kok, Y.; Tan, X.P.; Wang, P.; Nai, M.L.; Loh, N.H.; Liu, E.; Tor, S.B. Anisotropy and heterogeneity of microstructure and mechanical properties in metal additive manufacturing: A critical review. Mater. Des. 2018, 139, 565–586. [Google Scholar] [CrossRef]
- Egan, P.F.; Bauer, I.; Shea, K.; Ferguson, S.J. Mechanics of Three-Dimensional Printed Lattices for Biomedical Devices. J. Mech. Des. Trans. ASME 2019, 141, 1–12. [Google Scholar] [CrossRef]
- Canellidis, V.; Dedoussis, V.; Mantzouratos, N.; Sofianopoulou, S. Pre-processing methodology for optimizing stereolithography apparatus build performance. Comput. Ind. 2006, 57, 424–436. [Google Scholar] [CrossRef]
- Martinez-Sykora, A.; Alvarez-Valdes, R.; Bennell, J.; Ruiz, R.; Tamarit, J. Matheuristics for the irregular bin packing problem with free rotations. Eur. J. Oper. Res. 2017, 258, 440–455. [Google Scholar] [CrossRef]
- Deb, K. Multi Objective Optimization using Evlutionary Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 19, 45–76. [Google Scholar] [CrossRef]
| Authors | Objective Functions (OFs) | Optimization Phase | Remarks |
|---|---|---|---|
| Weighted sum based methods | |||
| Lan et al., 1997 [7] | AM features. | Customized | |
| McClurkin et al., 1998 [8] | Cost, Surface quality, Support volume, Supported area. | Customized | |
| Pham et al., 1999 [9] | AM features, Build time, Cost, Support volume, Supported area. | Customized | |
| Hur et. Al 2001 [10] | Build height, Cross-section length. | Genetic Algorithm | |
| Thrimurthulu et al., 2004 [11] | Build time, Surface roughness. | Genetic Algorithm | |
| Kim et al., 2005 [12] | Cost, Build height, Build time. | Genetic Algorithm | Cost is an index of Surface roughness due to post-treatments. |
| Byun et al., 2006 [13] | Build time, Cost, Surface roughness | Customized | |
| Canellidis et al., 2009 [14] | Build time, Surface roughness. | Genetic Algorithm | |
| Singhal et al., 2009 [15] | Build time, Supported area, Surface roughness | Optimization toolbox of Matlab (FMINCON) | More efficient than classical GA-based methodologies. |
| Phatak et al., 2012 [16] | Build height, Material utilizzation factor, Surface roughness, Support volume, Supported area | Genetic Algorithm | |
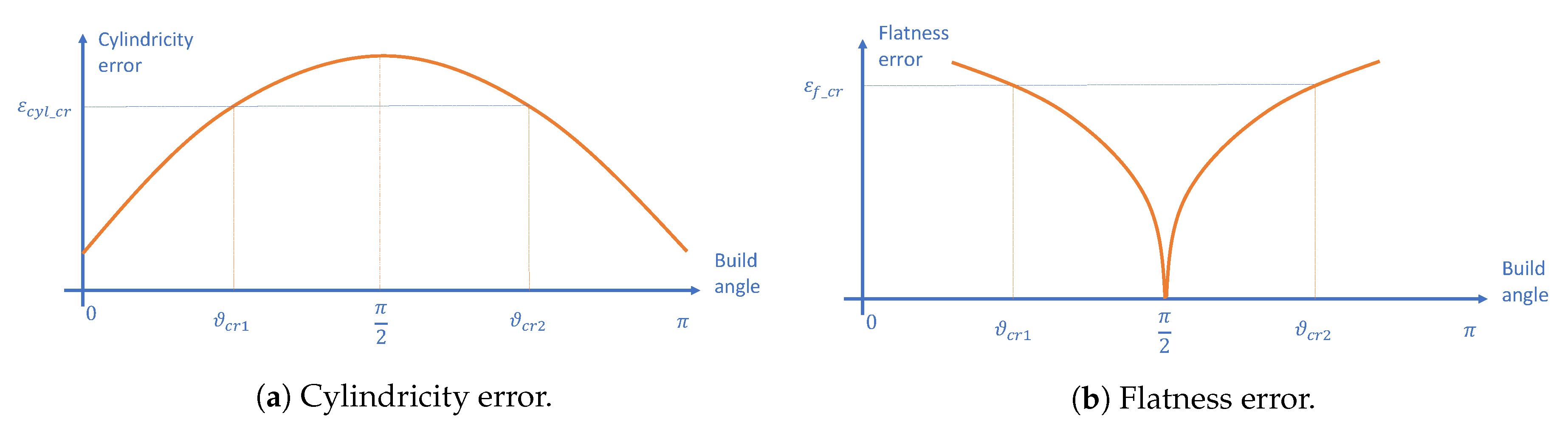
| Paul et al., 2015 [17] | Cylindricity error, Flatness error. | Customized | |
| Das et al., 2015 [18] | Angularity error, Cylindricity error, Flatness error, Parallelism error, Perpendiculary error, Support volume. | Optimization toolbox of Matlab (FMINCON) | Valid for NURBS models. |
| Moroni et al., 2015 [19] | Cylindrical features. | Genetic Algorithm | Optimal orientation of cylindrical features to maximize assembly accuracy. |
| Brika et al., 2017 [20] | Build time, Cost, Mechanical properties, Surface roughness, Support volume | Genetic Algorithm | OFs weights are defined using a Fuzzy methodology ([21]). |
| Chowdhury et al., 2018 [22] | Build height, Manufacturability features, Surface quality, Support volume, Supported area. | Artificial Neural Network-based | |
| Primary and secondary objectives based methods | |||
| Cheng et al., 1995 [23] | Build time, Part accuracy, stability. | Customized | |
| Alexander et al., 1998 [24] | Build height, Surface quality, Support volume, Supported area. | Customized | Direction choise is user-driven. |
| Singhal et al., 2005 [25] | Surface quality. | Trust Region Driven | |
| Ahn et al., 2007 [26] | Surface roughness. | Genetic Algorithm | |
| Ezair et al., 2015 [27] | Support volume. | Customized | A customized and high-efficient algorithm GPU-based for support evaluation is proposed. |
| Delfs et al., 2016 [28] | Build time, Surface quality. | Optimization tool of Magics | Very time-consuming. |
| Luo et al., 2016 [29] | Part accuracy. | Principal components analysis | |
| Pereira et al., 2018 [30] | Build time, Part accuracy, Supported area. | Global Derivative-free Optimization (PSwarm) | |
| Lovo et al., 2019 [4] | Mechanical properties. | Sequential Quadratic Programming (SQP) | |
| Mele et al., 2019 [31] | Environmental Impact. | Genetic Algorithm | |
| Pareto front based methods | |||
| Nezhad et al., 2010 [32] | Build time, Surface quality, Support Volume. | Genetic Algorithm | |
| Padhye et al., 2011 [33] | Build time, Surface roughness. | Genetic Algortithm; Particle Swarm Optimization | Two different optimization procedures are compared in this research, evidencing similar results. |
| Strano et al., 2011 [34] | Energy consumption, Surface roughness. | Customized | A self-defined procedure, more efficient than GA, is described. |
| Huang et al., 2018 [35] | Build time, Surface roughness. | Genetic Algorithm | A GA based on Compute Unified Device Architecture is used to increase solving speed. |
| Khodaygan et al., 2018 [36] | Build time, Surface quality. | Genetic Algorithm | |
| Yazdi et al., 2018 [37] | Build time, Material utilizzation. | Genetic Algorithm | Some technical requirements are defined as constrains. |
| Cheng et al., 2019 [38] | Mechanical properties, Support volume. | Particle Swarm Optimization | |
| Raju et al., 2019 [39] | Mechanical properties, Surface quality. | Genetic Algorithm | |
| Di Angelo et al., 2020 [40] | Build cost, Surface quality. | Genetic Algorithm | Implements an analytical an general-purpose formulation of surface quality. |
| Other methods | |||
| Zhang et al., 2016 [41] | Part accuracy, Surface roughness, Support volume. | Customized | Euclidian distance and shape analysis, derived from Grey System theory, are performed to make final decision. |
| Zhang et al., 2016 [42] | Build time, Surface roughness. | Customized | Multi-part two dimensional job optimization. |
| Jaiswal et al 2018 [43] | Part accuracy. | Surrogate model toolbox of Matlab (MATSuMoTo) | A surrogate model is applied to reduce computational burden. |
| Ransikarbum et al., 2018 [44] | Cost, Build time, Mechanical properties, Part accuracy, Surface quality, Support volume. | AHP-based | Analytic Hierarchy Process is adopted as decision criteria. |
| Golmohammadi et al., 2019 [45]. | Build time, Surface quality. | Taguchi-based experiments | No need of calculating derivates, as required by gradient-based methods. |
| Qin et al., 2019 [46] | AM features, Build time, Cost, Surface roughness, Support volume. | Fuzzy-based | |
| Qin et al., 2020 [47] | Mechanical properties, Surface roughness, Support volume. | Facet-clustering | |
| Authors | Considered Cost Components | Technology |
|---|---|---|
| Lan et al., 1997 [7] | Build time (number of layers) | |
| Xu et al., 1997 [51] | Build time (number of layers) | |
| Alexander et al., 1998 [24] | Prebuild cost (positioning, defining process parameters, generating supports, slicing, computer and operator cost), Build cost (manufacturing time, idle time, machine cost, material cost), Postprocessing cost (remove supports, finish surface, post-processing treatments, extra materials, operator cost). | FDM, SLA |
| Thrimurthulu et al., 2004 [11] | Build time (number of layers, supported area). | FDM |
| Kim et al., 2005 [12] | Postprocessing cost (polishing, postcure, support removal, washing) | |
| Byun et al., 2006 [13] | Pre and postprocessing time (operator cost), build cost (drawing exterior contour, filling interior area, generate supports, unproductive time, material cost). | |
| Nezhad et al., 2010 [32] | Build time (path length determined after slicing). | |
| Strano et al., 2011 [34] | Energy cost (preheating and part sintering). | SLS |
| Phatak et al., 2012 [16] | Build time (number of layers), material utilizzation factor. | |
| Brika et al., 2017 [20] | Build time (number of layers, part volume, part support), energy cost, indirect cost (portion of build-plate). | PBF |
| Yazdi et al., 2018 [37] | Build time (Gcode), material cost (GCode). | |
| Khodaygan et al., 2018 [36] | Build time (number of layers, supported area). | |
| Garzaniti et al., 2018 [69] | Recurring cost (hourly machine cost, energy, material), Non recurring cost (capital expediture, operating expediture, non recurring cost related to manufacturing phase). | |
| Di Angelo et al., 2020 [40] | Energy cost, Fixed Cost, Post-processing cost, Support material’s cost. | FDM |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Angelo, L.; Di Stefano, P.; Guardiani, E. Search for the Optimal Build Direction in Additive Manufacturing Technologies: A Review. J. Manuf. Mater. Process. 2020, 4, 71. https://doi.org/10.3390/jmmp4030071
Di Angelo L, Di Stefano P, Guardiani E. Search for the Optimal Build Direction in Additive Manufacturing Technologies: A Review. Journal of Manufacturing and Materials Processing. 2020; 4(3):71. https://doi.org/10.3390/jmmp4030071
Chicago/Turabian StyleDi Angelo, Luca, Paolo Di Stefano, and Emanuele Guardiani. 2020. "Search for the Optimal Build Direction in Additive Manufacturing Technologies: A Review" Journal of Manufacturing and Materials Processing 4, no. 3: 71. https://doi.org/10.3390/jmmp4030071
APA StyleDi Angelo, L., Di Stefano, P., & Guardiani, E. (2020). Search for the Optimal Build Direction in Additive Manufacturing Technologies: A Review. Journal of Manufacturing and Materials Processing, 4(3), 71. https://doi.org/10.3390/jmmp4030071






