UAV Path Planning in Threat Environment: A*-APF Algorithm for Spatio-Temporal Grid Optimization
Abstract
Highlights
- A new global subdivided spatio-temporal grid system is proposed, which integrates the advantages of GeoSOT binary coding and BeiDou grid location code subdivision rules.
- Based on the above-mentioned spatio-temporal grid system, threat quantification models for ground units such as radars, artillery, and interference are constructed. The traditional A* algorithm and artificial potential field (APF) algorithm are improved to enable each to adapt to the constructed complex threat environment. Experimental results show that the proposed A* algorithm is superior to the traditional algorithm in terms of path length, calculation time, threat value, and number of search nodes; the improved APF algorithm achieves 100% safe obstacle avoidance in dynamic obstacle environments.
- The designed global subdivided spatio-temporal grid system has become a new way of spatio-temporal data storage, which can provide new ideas for the management and application of UAV swarms in complex threat environments.
- The proposed A*-APF algorithm effectively solves the challenges of low threat avoidance efficiency and poor global path adaptability in UAV path planning in threat environments, and provides a new solution for UAV path planning in complex scenarios.
Abstract
1. Introduction
2. Related Methods
2.1. Spatio-Temporal Grid Modeling
2.1.1. Spatial Grid Division
- Coding length and level identification. The coding length for each dimension is fixed at 32 binary digits. For a given level (N2 = 13), the effective number of bits is 16. Therefore, the latter 16 bits of the latitude coding (the level identification code element part) consist of 1 bit of “0” (indicating the end of the level) and 15 bits of “1” (padding bits). Similarly, the effective number of bits for the height level N3 = 16 is 18.
- Encoding Latitude and Longitude. For latitude (34°24′58.379″ N), the first code element: the Northern Hemisphere (N) is identified as “0”; the degree value (34°) is converted to a 9-bit binary number “000100010” (with leading zeros to make 9 bits); the minute value (24′) is converted to a 7-bit binary number “0101100”; the second value (58″) is converted to a 7-bit binary number “1110011”; the fractional part of the second (0.379″) is converted to an 8-bit binary number “01100001”. Combining these parts and adding a 1-bit level identifier (the first “0” in the last 16 bits mentioned in Step 1), we obtain the complete 32-bit latitude code “0001000100101100111001101100001”. Based on an effective bit length of 16, the latitude code under N2 = 13 is “00010001001011000111111111111111”. Similarly, the longitude (109°3′41.260″ E) is encoded as “00110110100000110111111111111111111”.
- Two-dimensional plane encoding. The obtained 32-bit latitude encoding and 32-bit longitude encoding are combined using Morton ordering to generate a unique 64-bit two-dimensional plane encoding. The result in this example is “0000011100010110010010001010010100111111111111111111111111111111”.
- Height encoding. Based on an effective bit length of 18, the height encoding under N3 = 16 is “00000001000110000001111111111111”. See Figure 3 for a detailed diagram of the encoding process.
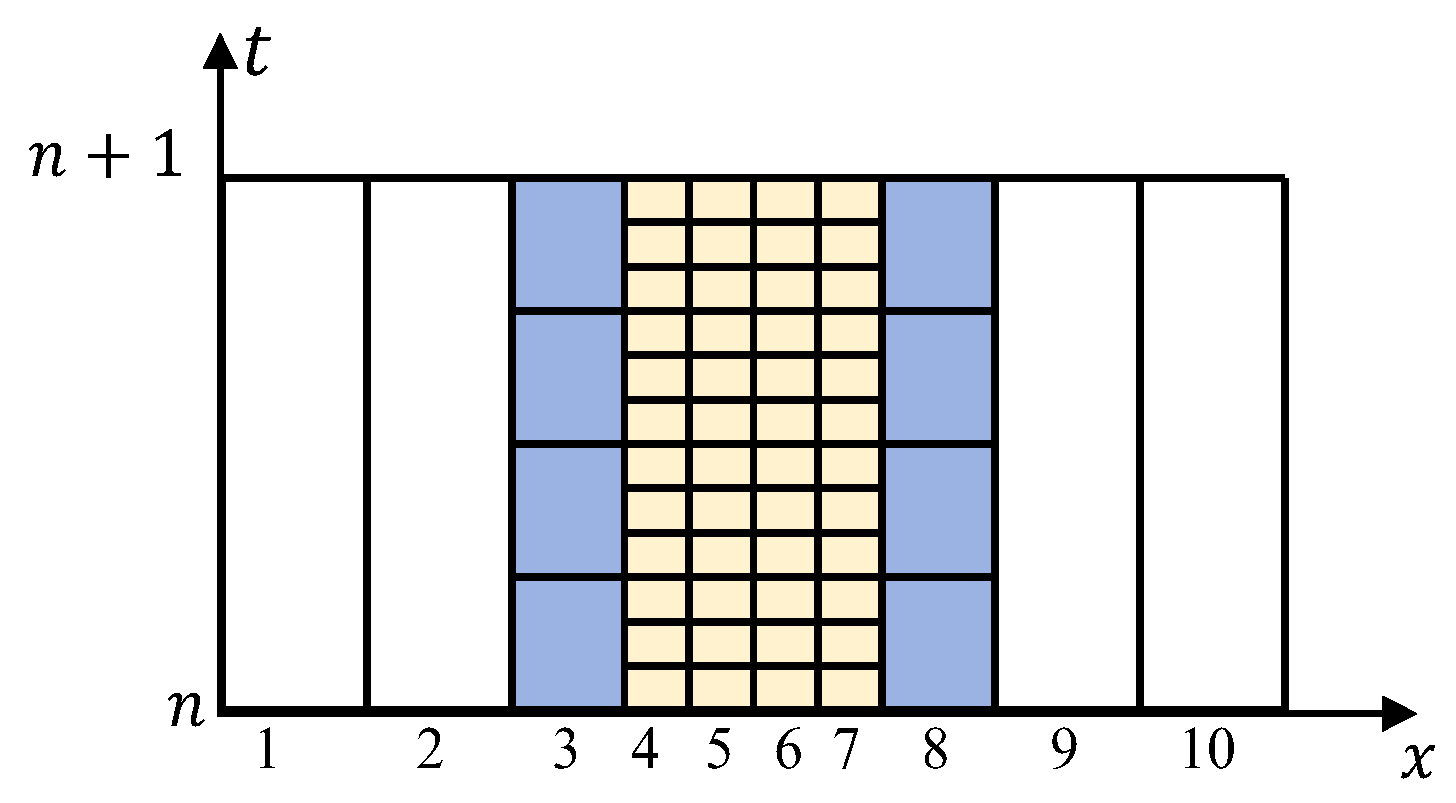
2.1.2. Temporal Grid Division
2.1.3. Multi-Granularity Spatio-Temporal Grid Division
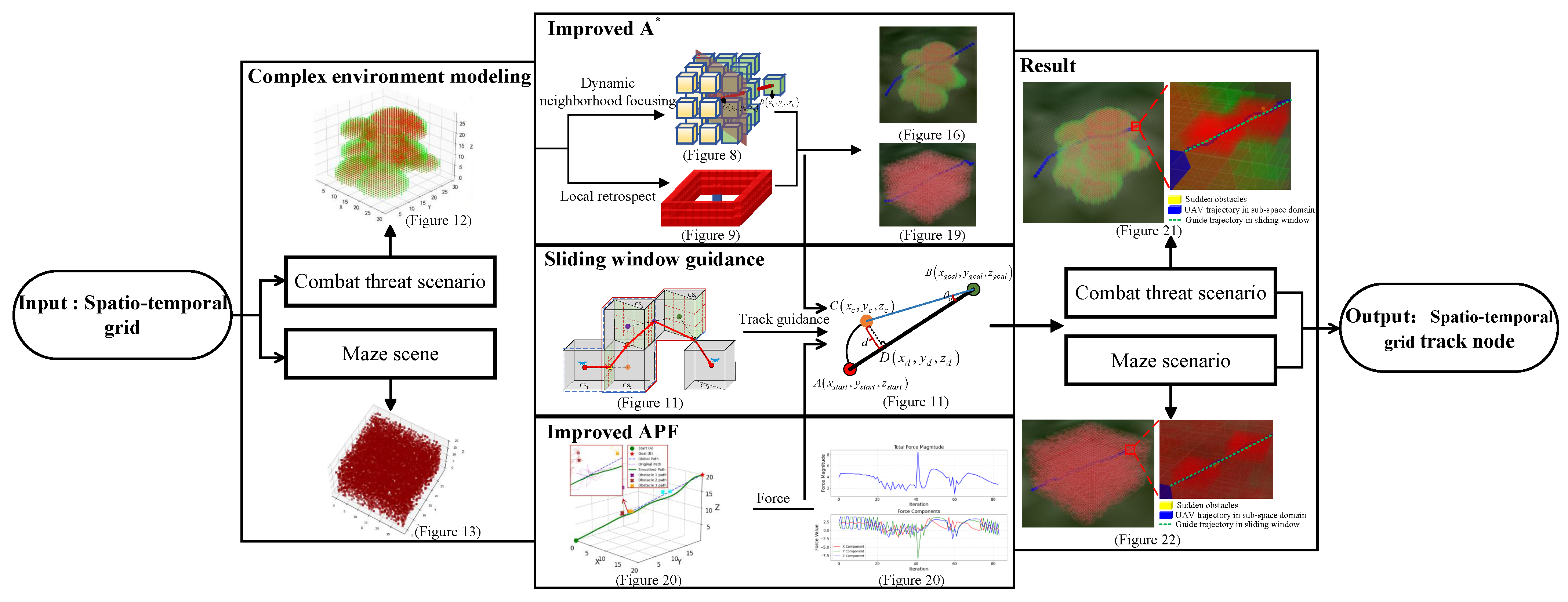
2.2. Complex Environment Modeling
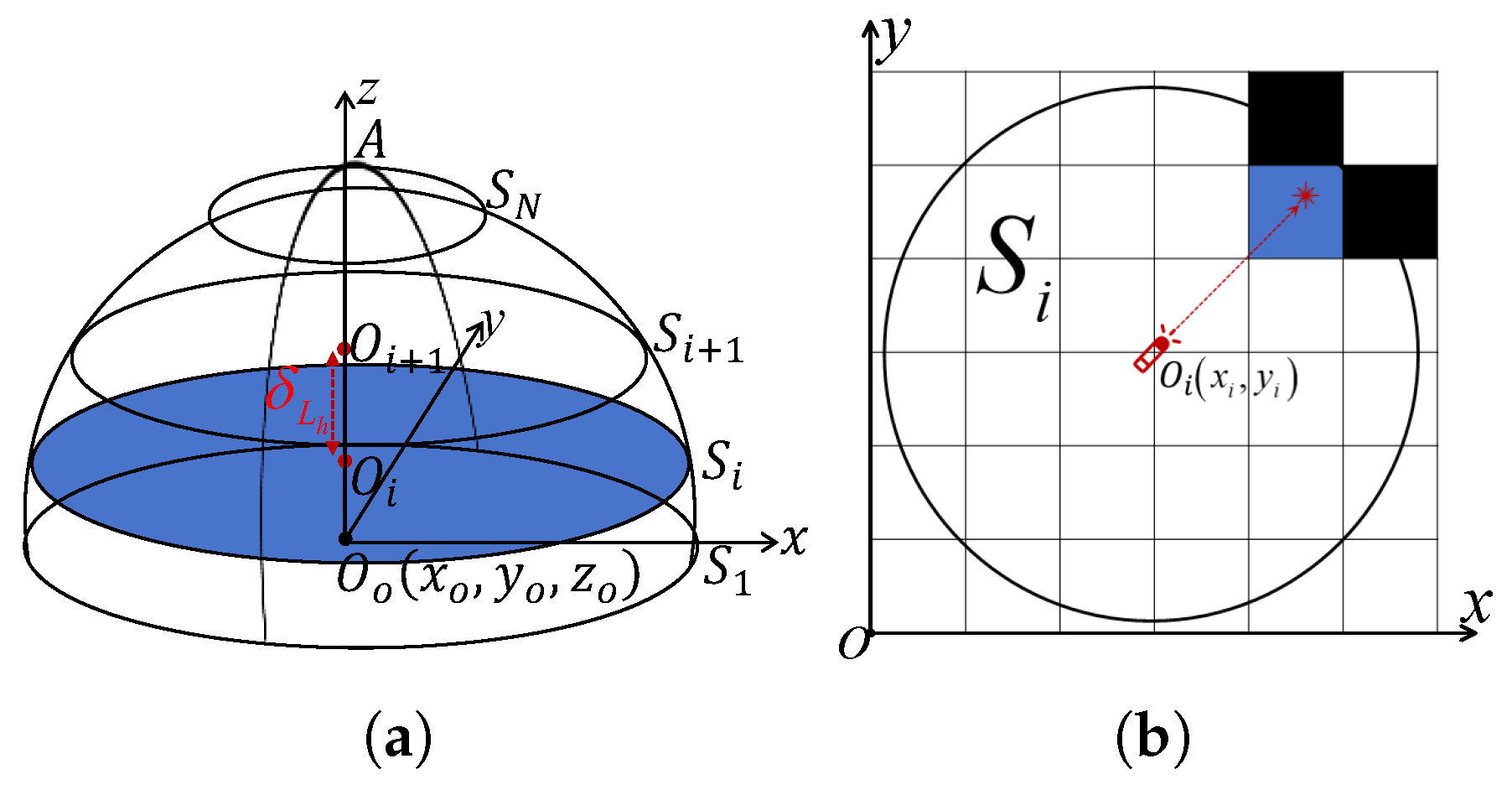
2.2.1. Threat Scenarios Modeling
2.2.2. Maze Scenario Modeling
2.3. Path Planning
2.3.1. Path Planning Among Sub-Airspaces Based on Improved A* Algorithm
Dynamic Constraints of Unmanned Aerial Vehicles
Optimizing Cost Function Design
- A and B represent the horizontal and vertical grid scales, respectively.
- The z-axis difference is scaled to match horizontal dimensions using .
- is the average threat value of detected nodes, estimating threat in unexplored areas.
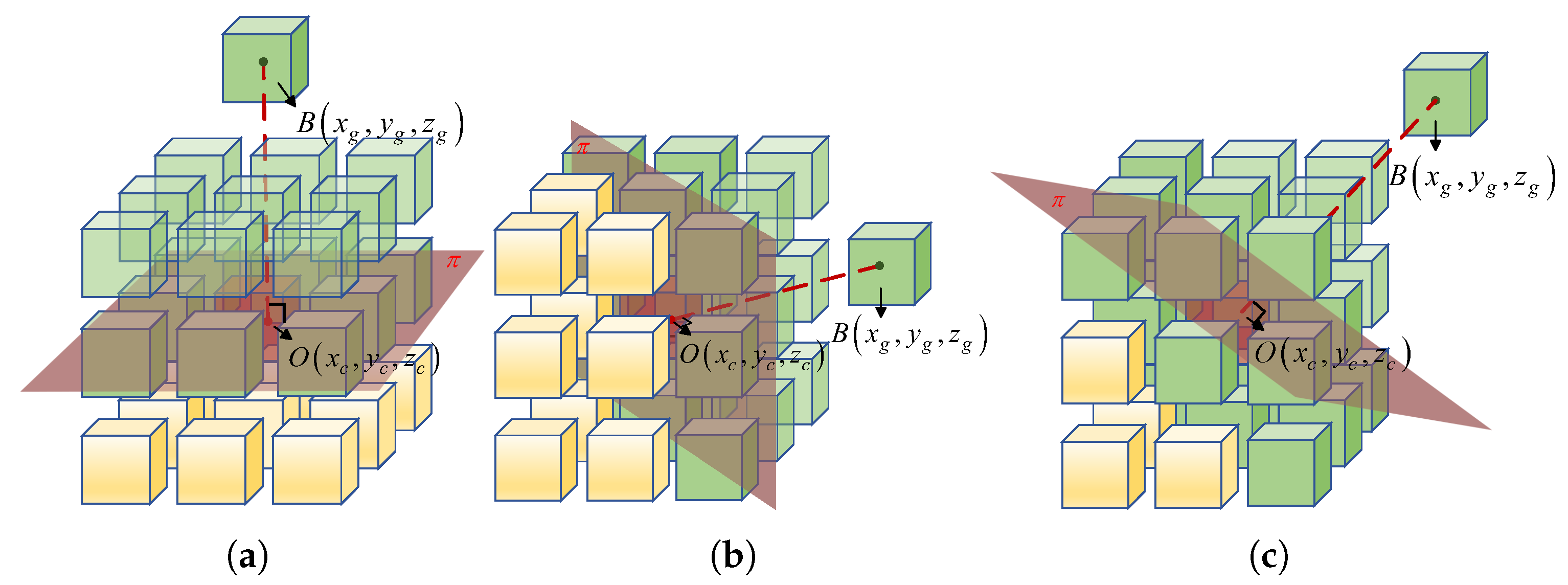
Dynamic Neighborhood Search
Design of Local Backtracking Mechanism
- represents the inverse of the average threat value within the UAV’s field of view.
- Local weights prioritize escape direction over path smoothness.
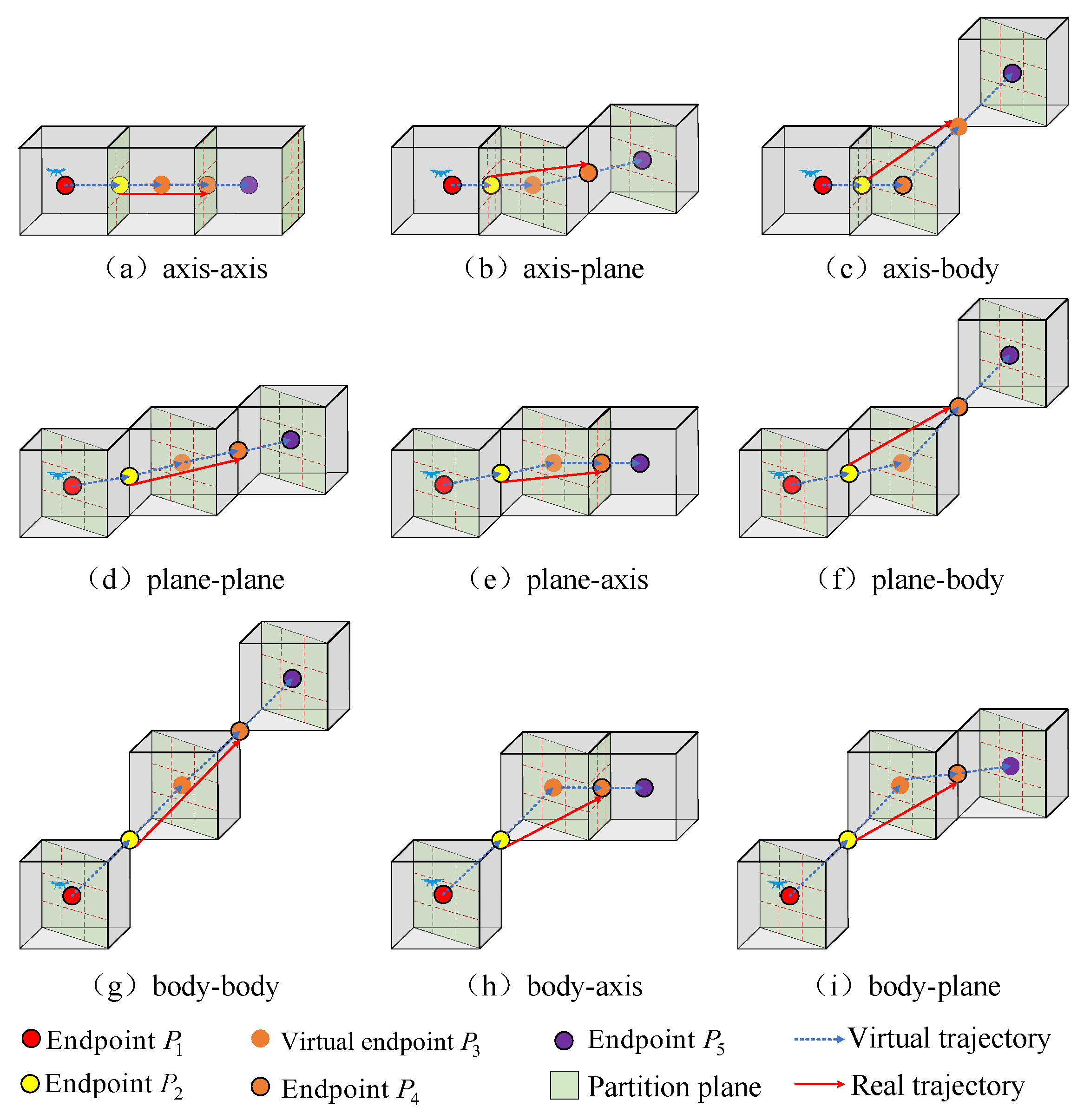
2.3.2. Design of Trajector Association Model Driven by Sliding Window
Sliding Window Design
- Actual path nodes: .
- Virtual path guidance nodes: .
Path Guidance Strategy
2.3.3. Path Planning in Sub-Airspace Based on an Improved APF Algorithm
Improved Gravitational Potential Field
Improved Repulsive Potential Field
UAV Motion Model in Sub-Airspace
3. Simulation Analysis
3.1. Environmental Settings
3.2. Plan Planning Among Sub-Airspaces
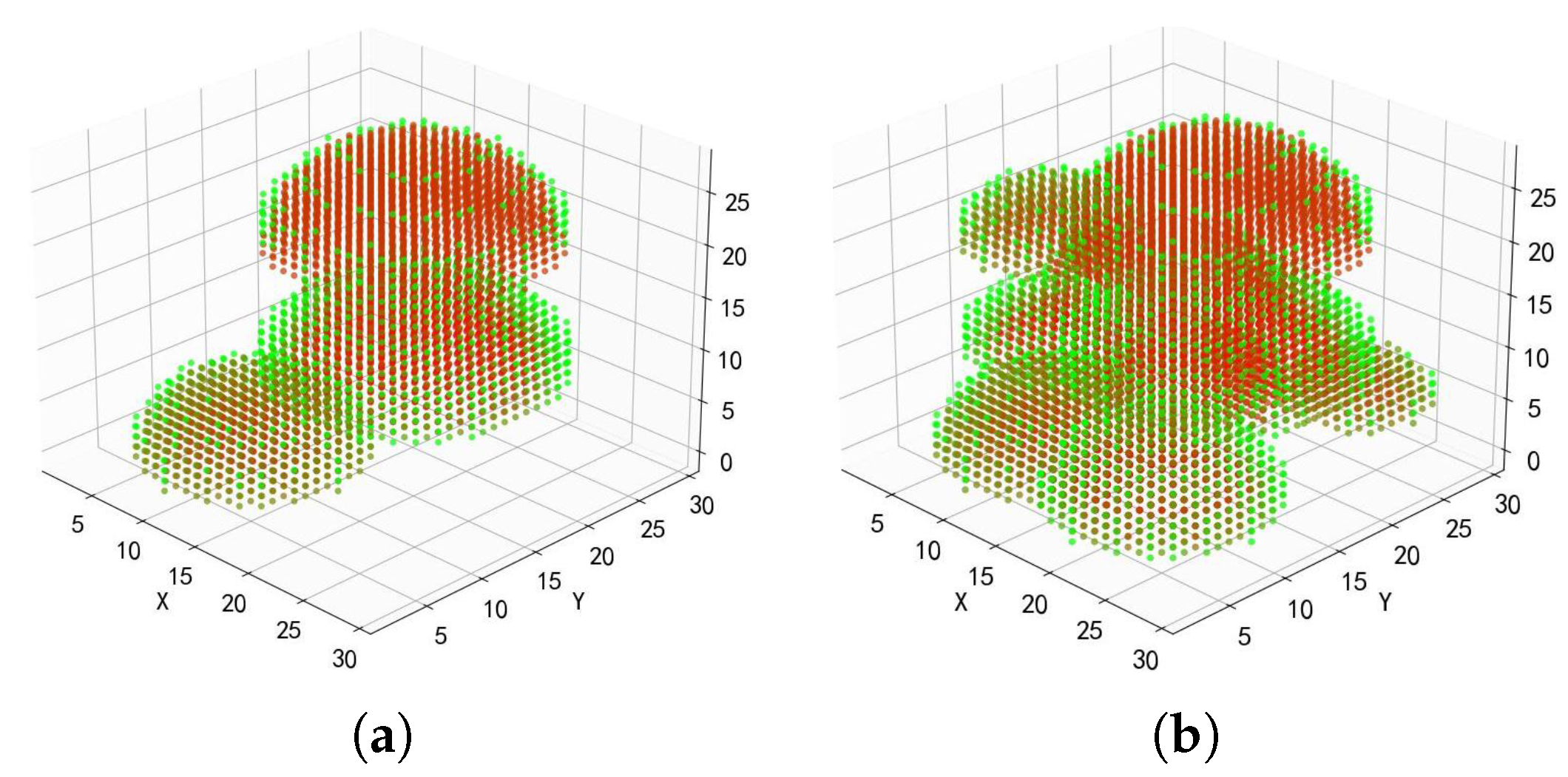
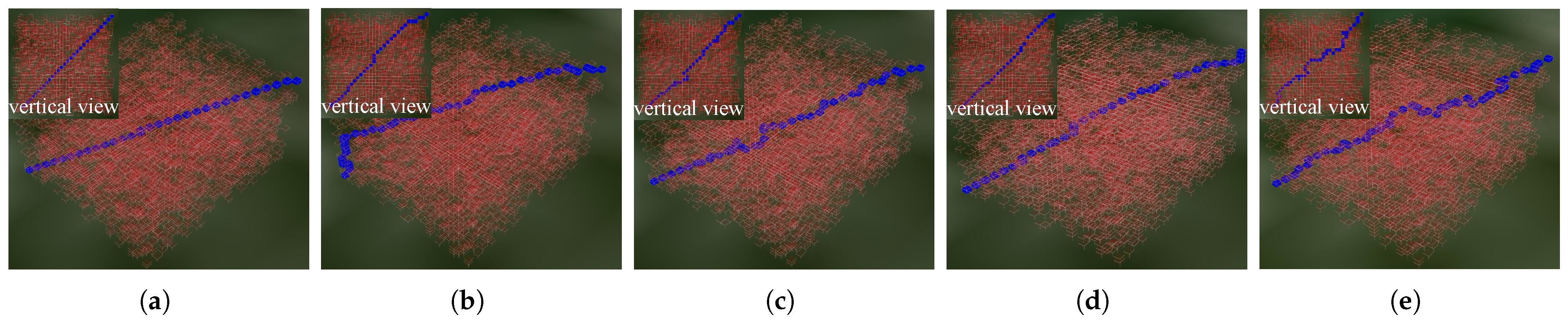
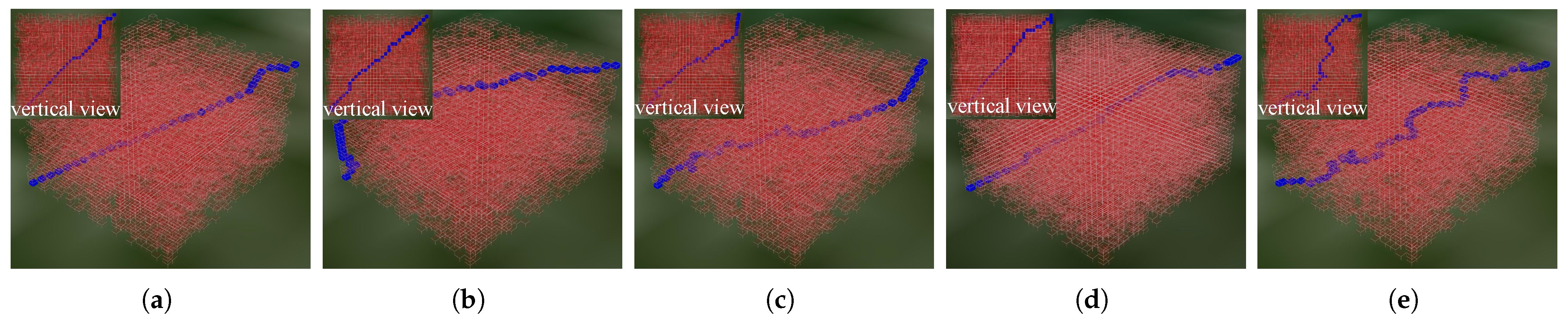
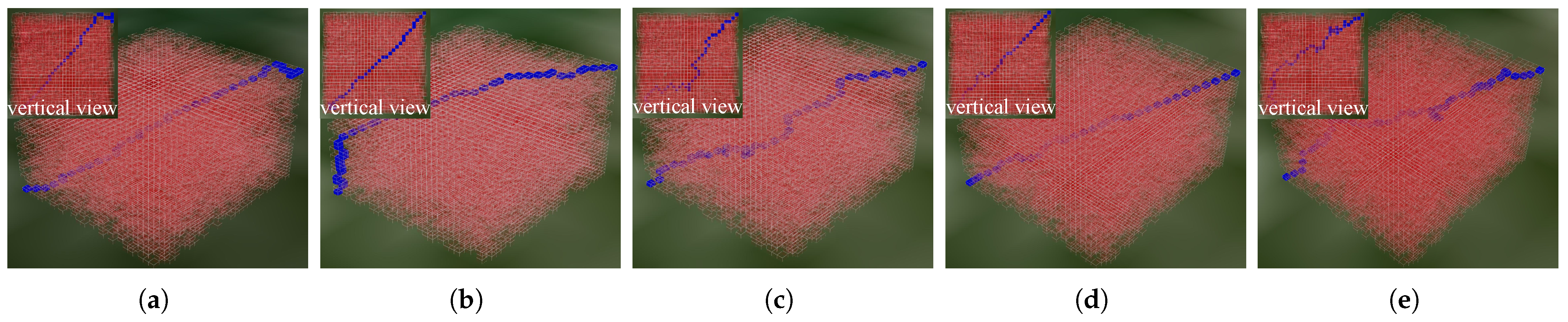
3.2.1. Ground Threat Scenario
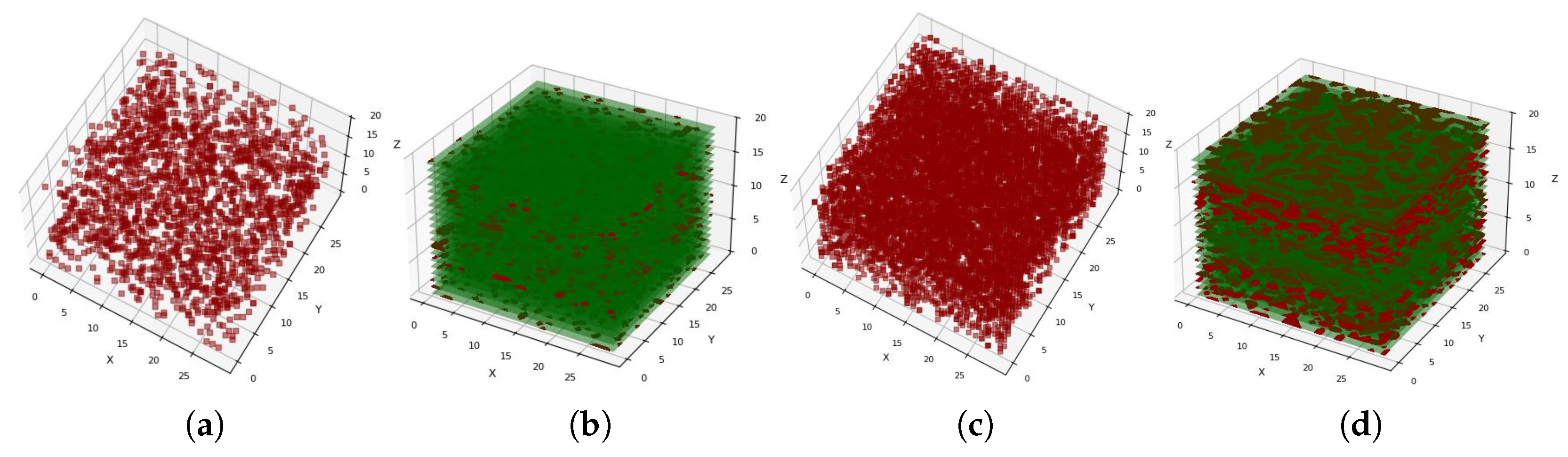
3.2.2. Maze Scenario
3.2.3. Result Analysis
Comparison with the Traditional A* Algorithm
Comparison with Other Intelligent Algorithms
- Path Length: Reduced by 18.18%, 11.79%, and 26.10% compared to GA, SA, and Q-learning, respectively;
- Computation Time: Decreased by 17.01%, 22.47%, and 83.95% compared to GA, SA, and Q-learning, respectively;
- Total Path Threat Value: Lowered by 50.21%, 50.37%, and 3.01% compared to GA, SA, and Q-learning, respectively.
- Path Length: Shortened by 21.00%, 15.31%, and 30.04% compared to GA, SA, and Q-learning, respectively;
- Computation Time: Reduced by 12.39%, 16.42%, and 75.71% compared to GA, SA, and Q-learning, respectively;
- Total Path Threat Value: Decreased by 42.86%, 53.75%, and 9.25% compared to GA, SA, and Q-learning, respectively.
- Path Length: Cut by 19.80%, 11.04%, and 30.69% compared to GA, SA, and Q-learning, respectively;
- Computation Time: Decreased by 11.67%, 20.20%, and 74.35% compared to GA, SA, and Q-learning, respectively;
- Total Path Threat Value: Reduced by 49.03%, 54.67%, and 43.00% compared to GA, SA, and Q-learning, respectively.
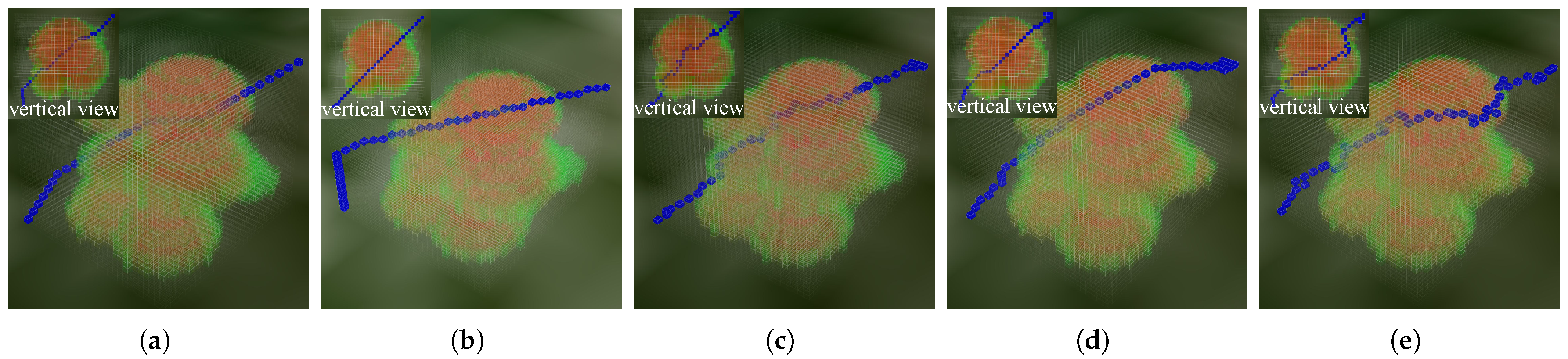
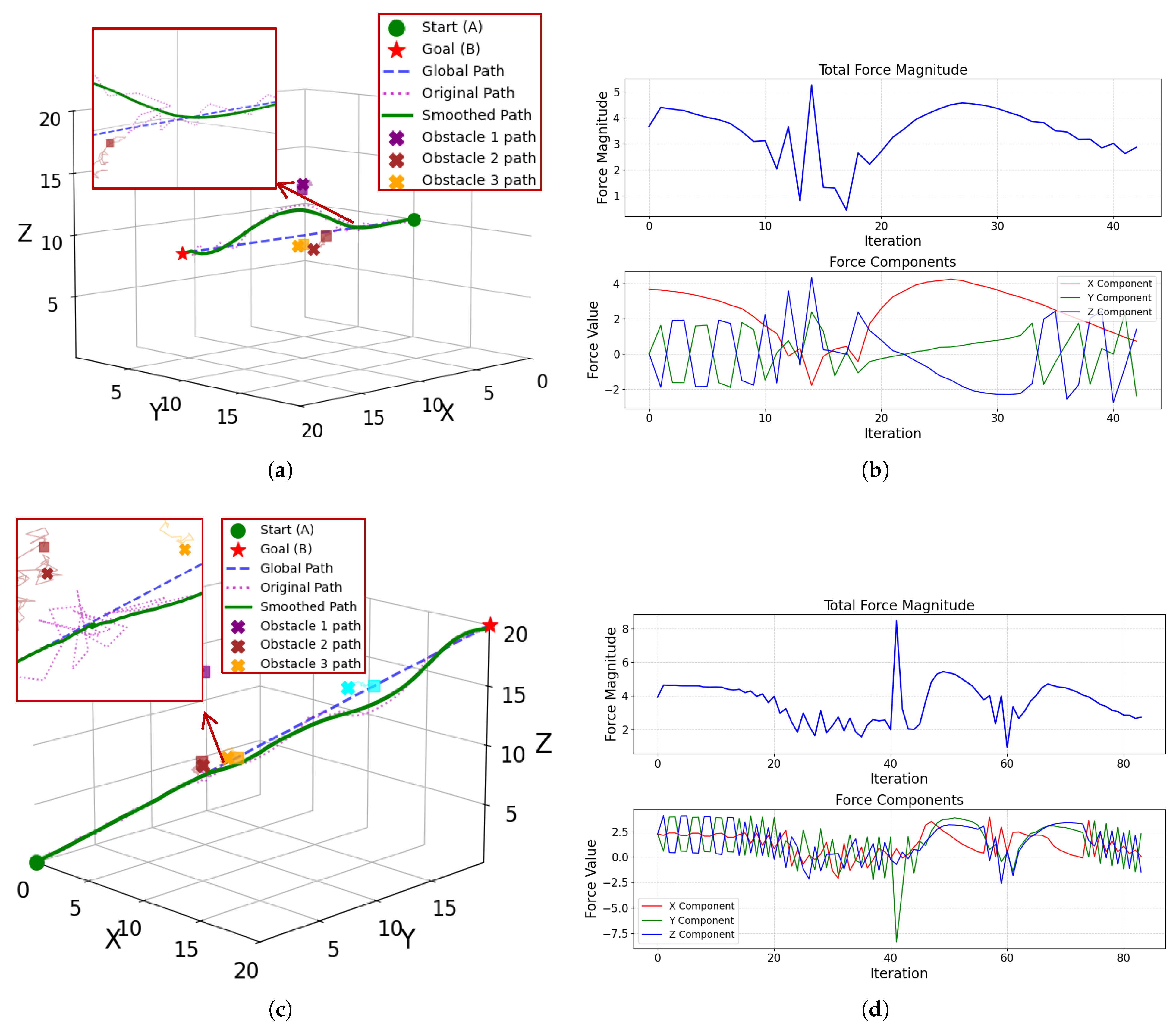
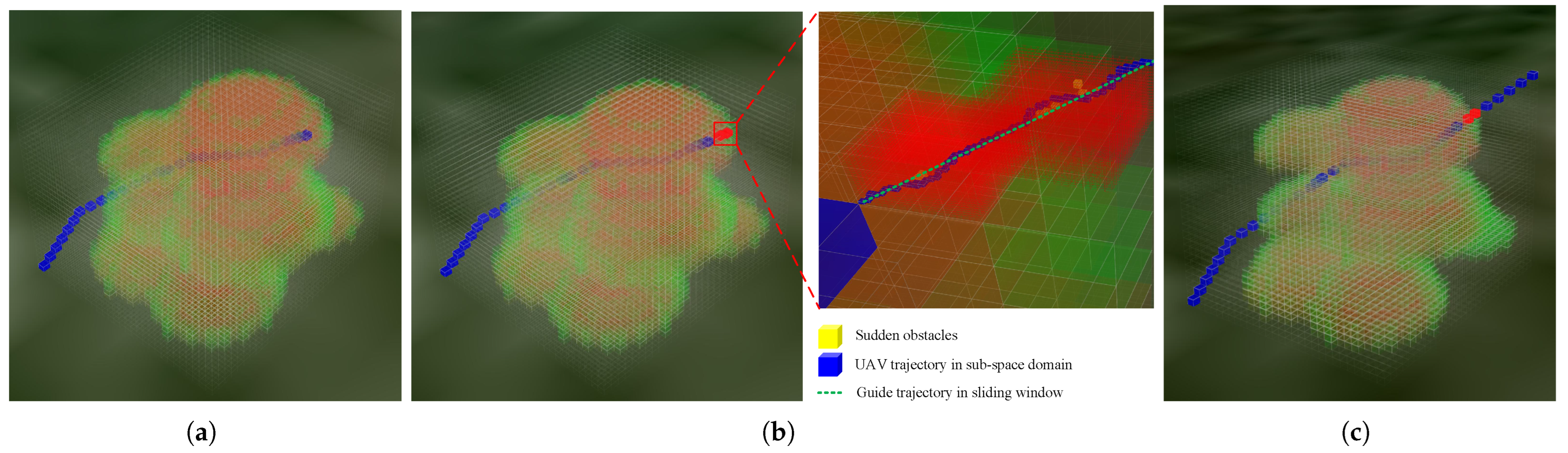
3.3. Path Planning in Sub-Airspace
3.4. Collaborative Path Planning
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jun, M.; D’Andrea, R. Path planning for unmanned aerial vehicles in uncertain and adversarial environments. In Cooperative Control: Models, Applications and Algorithms; Springer: Boston, MA, USA, 2003; pp. 95–110. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Guan, X.; Delahaye, D. Potential odor intensity grid based UAV path planning algorithm with particle swarm optimization approach. Math. Probl. Eng. 2016, 2016, 7802798. [Google Scholar] [CrossRef]
- Panov, A.I.; Yakovlev, K.S.; Suvorov, R. Grid path planning with deep reinforcement learning: Preliminary results. Procedia Comput. Sci. 2018, 123, 347–353. [Google Scholar] [CrossRef]
- Koay, T.B.; Chitre, M. Energy-efficient path planning for fully propelled AUVs in congested coastal waters. In Proceedings of the 2013 MTS/IEEE OCEANS-Bergen, Bergen, Norway, 10–14 June 2013; pp. 1–9. [Google Scholar] [CrossRef]
- Han, B.; Qu, T.; Tong, X.; Jiang, J.; Zlatanova, S.; Wang, H.; Cheng, C. Grid-optimized UAV indoor path planning algorithms in a complex environment. Int. J. Appl. Earth Obs. Geoinf. 2022, 111, 102857. [Google Scholar] [CrossRef]
- Sun, G.; Xu, Q.; Zhang, G.; Qu, T.; Cheng, C.; Deng, H. An Intelligent UAV Path-Planning Method Based on the Theory of the Three-Dimensional Subdivision of Earth Space. ISPRS Int. J. Geo-Inf. 2023, 12, 397. [Google Scholar] [CrossRef]
- Deng, C.; Cheng, C.; Qu, T.; Li, S.; Chen, B. A Method for Managing ADS-B Data Based on a 4D Airspace-Temporal Grid (GeoSOT-AS). Aerospace 2023, 10, 217. [Google Scholar] [CrossRef]
- Cao, J.; Shi, S.; Guo, Q.; Huang, G. Building Space Coding Based on Beidou Grid Position Code. Mob. Networks Appl. 2022, 27, 1700–1715. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. In Edsger Wybe Dijkstra: His Life, Work, and Legacy; ACM Digital Library: New York, NY, USA, 2022; pp. 287–290. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Noreen, I.; Khan, A.; Habib, Z. Optimal path planning using RRT* based approaches: A survey and future directions. Int. J. Adv. Comput. Sci. Appl. 2016, 7. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Yang, R.; Cheng, L. Path planning of restaurant service robot based on a-star algorithms with updated weights. In Proceedings of the 2019 12th International Symposium on Computational Intelligence and Design, Hangzhou, China, 14–15 December 2019; Volume 1, pp. 292–295. [Google Scholar] [CrossRef]
- Han, Z.; Chen, M.; Zhu, H.; Wu, Q. Ground threat prediction-based path planning of unmanned autonomous helicopter using hybrid enhanced artificial bee colony algorithm. Def. Technol. 2024, 32, 1–22. [Google Scholar] [CrossRef]
- Zhou, Z.; Guo, Y.; Wang, Y.; Lyu, J.; Gong, H.; Ye, X.; Li, Y. Multi-UAV Trajectory Optimization Under Dynamic Threats: An Enhanced GWO Algorithm Integrating a Priori and Real-Time Data. Int. J. Comput. Intell. Syst. 2025, 18, 1–21. [Google Scholar] [CrossRef]
- Zhang, M.; Su, C.; Liu, Y.; Hu, M.; Zhu, Y. Unmanned aerial vehicle route planning in the presence of a threat environment based on a virtual globe platform. ISPRS Int. J. Geo-Inf. 2016, 5, 184. [Google Scholar] [CrossRef]
- Li, W. An improved artificial potential field method based on chaos theory for UAV route planning. In Proceedings of the 2019 34th Youth Academic Annual Conference of Chinese Association of Automation, Jinzhou, China, 6–9 June 2019; pp. 47–51. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, B. AGV path planning based on improved artificial potential field method. In Proceedings of the 2021 IEEE International Conference on Power Electronics, Computer Applications, Shenyang, China, 22–24 January 2021; pp. 32–37. [Google Scholar] [CrossRef]
- Lu, S.; Li, E.; Guo, R. An obstacles avoidance algorithm based on improved artificial potential field. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation, Beijing, China, 13–16 October 2020; pp. 425–430. [Google Scholar] [CrossRef]
- Hu, H.; Liu, M.; Zhong, J.; Deng, X.; Cao, Y.; Fang, P. A Case Study of the 3D Water Vapor Tomography Model Based on a Fast Voxel Traversal Algorithm for Ray Tracing. Remote Sens. 2021, 13, 2422. [Google Scholar] [CrossRef]
- Chao, D.O.; Zhang, Y.; Ji, Z.; Li, Y.; Zhang, L.; Wu, Q. Three-dimension collision-free path planning of UAVs based on ADS-B information in low-altitude urban airspace. Chin. J. Aeronaut. 2025, 38, 103170. [Google Scholar] [CrossRef]
- He, X.; He, F.; Li, L.; Zhang, L.; Xiao, G. A route network planning method for urban air delivery. Transp. Res. Part E Logist. Transp. Rev. 2022, 166, 102872. [Google Scholar] [CrossRef]
- Jones, M.; Djahel, S.; Welsh, K. Path-planning for unmanned aerial vehicles with environment complexity considerations: A survey. ACM Comput. Surv. 2023, 55, 1–39. [Google Scholar] [CrossRef]









| Longitude | Latitude | Altitude | |
|---|---|---|---|
| Starting point | 110.000° | 25.000° | 0 m |
| Ending point | 110.042° | 25.042° | 3000 m |
| Grid size | 150 m | 150 m | 100 m |
| Algorithm | Performance Metrics | Threat Scenarios | ||
|---|---|---|---|---|
| Low-Level | Medium-Level | High-Level | ||
| Improved A* | Path length (m) | 7215.69 | 7008.39 | 7422.98 |
| Time (s) | 4.83 | 7.99 | 8.85 | |
| Total threat | 4.73 | 4.73 | 6.31 | |
| Search nodes | 18,909 | 22,353 | 33,290 | |
| Traditional A* | Path length (m) | 8089.11 | 8098.11 | 8098.11 |
| Time (s) | 18.12 | 21.02 | 42.85 | |
| Total threat | 6.31 | 6.31 | 14.54 | |
| Search nodes | 52,945 | 64,823 | 86,554 | |
| GA | Path length (m) | 8818.65 | 8871.40 | 9255.64 |
| Time (s) | 5.82 | 9.12 | 10.02 | |
| Total threat | 9.50 | 10.15 | 12.38 | |
| SA | Path length (m) | 8180.26 | 8275.64 | 8344.28 |
| Time (s) | 6.23 | 9.56 | 11.09 | |
| Total threat | 9.53 | 12.52 | 13.92 | |
| Q-learning | Path length (m) | 9764.62 | 10,017.86 | 10,709.81 |
| Time (s) | 30.10 | 32.90 | 34.50 | |
| Total threat | 4.98 | 6.38 | 11.07 | |
| Algorithm | Performance Metrics | Obstacle Density () | ||
|---|---|---|---|---|
| Improved A* | Path length (m) | 6878.71 | 7104.10 | 7990.92 |
| Time (s) | 0.15 | 0.34 | 0.51 | |
| Total threat | 0.00 | 0.00 | 0.00 | |
| Search nodes | 5599 | 10,953 | 12,993 | |
| Traditional A* | Path length (m) | 8190.52 | 8645.70 | 8701.37 |
| Time (s) | 0.23 | 0.48 | 1.32 | |
| Total threat | 0.00 | 0.00 | 0.00 | |
| Search nodes | 10,078 | 23,001 | 31,183 | |
| GA | Path length (m) | 7974.55 | 8636.20 | 9505.45 |
| Time (s) | 0.89 | 1.63 | 1.98 | |
| Total threat | 0.00 | 0.00 | 0.00 | |
| SA | Path length (m) | 7346.15 | 7835.70 | 10,016.26 |
| Time (s) | 20.90 | 23.82 | 25.76 | |
| Total threat | 0.00 | 0.00 | 0.00 | |
| Q-learning | Path length (m) | 9236.20 | 1015.05 | 10,484.05 |
| Time (s) | 30.10 | 31.87 | 33.50 | |
| Total threat | 0.00 | 0.00 | 0.00 | |
| Threat Scenario | Path Length | Computation Time | Path Threat Value | Number of Search Nodes |
|---|---|---|---|---|
| Low-threat | 10.90% | 73.34% | 25.04% | 64.29% |
| Medium-threat | 13.46% | 61.99% | 8.24% | 65.52% |
| High-threat | 8.34% | 79.35% | 56.60% | 61.54% |
| Threat Scenario | Index | Comparison with | ||
|---|---|---|---|---|
| GA | SA | Q-Learning | ||
| Low-threat | Path Length | 18.18% | 11.79% | 26.10% |
| Computation Time | 17.01% | 22.47% | 83.95% | |
| Path Threat Value | 50.21% | 50.37% | 3.01% | |
| Medium-threat | Path Length | 21.00% | 15.31% | 30.04% |
| Computation Time | 12.39% | 16.42% | 75.71% | |
| Path Threat Value | 42.86% | 53.75% | 9.25% | |
| High-threat | Path Length | 19.80% | 11.04% | 30.69% |
| Computation Time | 11.67% | 20.20% | 74.35% | |
| Path Threat Value | 49.03% | 54.67% | 43.00% | |
| Group 1 | Group 2 | Group 3 | Group 4 | ||||
|---|---|---|---|---|---|---|---|
| Spatial Node | Timestamp | Spatial Node | Timestamp | Spatial Node | Timestamp | Spatial Node | Timestamp |
| (0,0,0) | 00:00:00 | (19,23,19) | 00:25:00 | (33,24,23): (13,7,13) | 00:26:06 | (24,24,24): (10,15,9) | 00:27:21 |
| (0,1,1) | 00:01:00 | (20,23,20) | 00:26:00 | (33,24,23): (14,7,14) | 00:26:09 | (24,24,24): (11,15,9) | 00:27:24 |
| (0,2,2) | 00:02:00 | (21,23,21) | 00:24:00 | (33,24,23): (15,7,15) | 00:26:12 | (24,24,24): (11,15,10) | 00:27:27 |
| (0,3,3) | 00:03:00 | (22,23,22) | 00:25:00 | (33,24,23): (15,8,15) | 00:26:15 | (24,24,24): (12,16,10) | 00:27:30 |
| (0,4,4) | 00:04:00 | (23,24,23): (0,0,0) | 00:25:03 | (33,24,23): (16,8,16) | 00:26:18 | (24,24,24): (13,16,11) | 00:27:33 |
| (0,5,5) | 00:05:00 | (23,24,23): (1,0,1) | 00:25:06 | (33,24,23): (17,8,17) | 00:26:21 | (24,24,24): (13,17,12) | 00:27:36 |
| (0,6,6) | 00:06:00 | (23,24,23): (1,1,1) | 00:25:09 | (33,24,23): (17,9,17) | 00:26:24 | (24,24,24): (14,17,12) | 00:27:39 |
| (1,7,7) | 00:07:00 | (23,24,23): (1,1,2) | 00:25:12 | (33,24,23): (18,9,18) | 00:26:27 | (24,24,24): (14,17,13) | 00:27:42 |
| (2,8,8) | 00:08:00 | (23,24,23): (2,1,2) | 00:25:15 | (33,24,23): (19,9,19) | 00:26:30 | (24,24,24): (14,17,14) | 00:27:45 |
| (3,9,9) | 00:09:00 | (23,24,23): (3,1,3) | 00:25:18 | (24,24,24): (0,9,0) | 00:26:33 | (24,24,24): (14,17,15) | 00:27:48 |
| (4,10,10) | 00:10:00 | (23,24,23): (3,2,3) | 00:25:21 | (24,24,24): (1,0,1) | 00:26:36 | (24,24,24): (15,17,15) | 00:27:51 |
| (5,11,11) | 00:11:00 | (23,24,23): (4,2,4) | 00:25:24 | (24,24,24): (1,1,1) | 00:26:59 | (24,24,24): (15,18,16) | 00:27:54 |
| (6,12,12) | 00:12:00 | (23,24,23): (5,2,4) | 00:25:27 | (24,24,24): (2,1,1) | 00:26:42 | (24,24,24): (15,18,17) | 00:27:57 |
| (7,13,13) | 00:13:00 | (23,24,23): (6,3,5) | 00:25:30 | (24,24,24): (3,1,1) | 00:26:45 | (24,24,24): (16,18,17) | 00:28:00 |
| (8,13,14) | 00:14:00 | (23,24,23): (7,3,5) | 00:25:33 | (24,24,24): (3,1,2) | 00:26:48 | (24,24,24): (16,18,18) | 00:28:03 |
| (9,13,15) | 00:15:00 | (23,24,23): (8,3,5) | 00:25:36 | (24,24,24): (3,1,2) | 00:26:51 | (24,24,24): (17,18,18) | 00:28:06 |
| (10,14,16) | 00:16:00 | (23,24,23): (8,3,6) | 00:25:39 | (24,24,24): (3,1,3) | 00:26:54 | (24,24,24): (17,19,18) | 00:28:09 |
| (11,15,17) | 00:17:00 | (23,24,23): (9,3,6) | 00:25:42 | (24,24,24): (3,1,3) | 00:26:57 | (24,24,24): (18,19,19) | 00:28:12 |
| (12,16,17) | 00:18:00 | (23,24,23): (9,4,6) | 00:25:45 | (24,24,24): (4,1,4) | 00:27:00 | (24,24,24): (19,19,19) | 00:28:15 |
| (13,17,17) | 00:19:00 | (23,24,23): (10,4,7) | 00:25:48 | (24,24,24): (4,1,4) | 00:27:03 | (25,25,25) | 00:29:15 |
| (14,18,17) | 00:20:00 | (23,24,23): (11,4,8) | 00:25:51 | (24,24,24): (5,1,4) | 00:27:06 | (26,26,26) | 00:30:15 |
| (15,19,17) | 00:21:00 | (23,24,23): (12,5,10) | 00:25:54 | (24,24,24): (6,15,8) | 00:27:09 | (27,27,27) | 00:31:15 |
| (16,20,17) | 00:22:00 | (23,24,23): (12,6,11) | 00:25:57 | (24,24,24): (7,15,8) | 00:27:12 | (28,28,28) | 00:32:15 |
| (17,21,17) | 00:23:00 | (23,24,23): (13,6,12) | 00:26:00 | (24,24,24): (8,15,9) | 00:27:15 | (29,29,29) | 00:33:15 |
| (18,22,18) | 00:24:00 | (23,24,23): (13,6,13) | 00:26:03 | (24,24,24): (9,15,9) | 00:27:18 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Ru, L.; Wang, W.; Xi, H.; Zhu, R.; Li, S.; Zhang, Z. UAV Path Planning in Threat Environment: A*-APF Algorithm for Spatio-Temporal Grid Optimization. Drones 2025, 9, 661. https://doi.org/10.3390/drones9090661
Liu L, Ru L, Wang W, Xi H, Zhu R, Li S, Zhang Z. UAV Path Planning in Threat Environment: A*-APF Algorithm for Spatio-Temporal Grid Optimization. Drones. 2025; 9(9):661. https://doi.org/10.3390/drones9090661
Chicago/Turabian StyleLiu, Longhao, Le Ru, Wenfei Wang, Hailong Xi, Rui Zhu, Shiliang Li, and Zhenghao Zhang. 2025. "UAV Path Planning in Threat Environment: A*-APF Algorithm for Spatio-Temporal Grid Optimization" Drones 9, no. 9: 661. https://doi.org/10.3390/drones9090661
APA StyleLiu, L., Ru, L., Wang, W., Xi, H., Zhu, R., Li, S., & Zhang, Z. (2025). UAV Path Planning in Threat Environment: A*-APF Algorithm for Spatio-Temporal Grid Optimization. Drones, 9(9), 661. https://doi.org/10.3390/drones9090661






