An Algorithm for Planning Coverage of an Area with Obstacles with a Heterogeneous Group of Drones Using a Genetic Algorithm and Parameterized Polygon Decomposition
Abstract
1. Introduction
- Complex field geometries. Agricultural fields are often non-rectangular and may exhibit non-convex shapes (such as concave indentations) or other geometric peculiarities.
- Presence of obstacles within the field that are either inaccessible for flight or require no treatment (lakes, rocky areas, tall tree belts, farmyards). Additionally, obstacle areas may represent regions to be excluded from coverage (for instance, areas that do not require herbicide spraying). In this work, “obstacles” refer to zones within field boundaries that must be entirely excluded from flight paths—either because flying there is impossible or impractical.
- Heterogeneity of the UAV fleet. Different UAV models (multicopters, helicopter-type drones, fixed-wing aircraft) may exist within a single agricultural operation, each with distinct operational ranges, speeds, operational costs, payload capacities, and other characteristics.
- Use of a mobile ground platform (tractor, truck, pickup) that moves along the road at the edge of the field or traverses it via feasible paths. Such a platform enables more efficient logistics: drones can take off and land at various locations along the road instead of being limited to a single point, reducing total drone mileage and turnaround times for battery replacement or refueling.
- Account for geometry: complex field shapes and obstacles.
- Optimally allocate involved UAVs (considering their differing specifications).
- Plan an optimal route (or set of stops) for the ground platform to minimize overall mission duration.
- Reduce costs and time (two key metrics): where cost encompasses the total expenditure related to UAV wear and tear, depreciation, and personnel wages; and time refers to the duration of the entire operation, typically constrained by the working day or favorable weather window.
2. Related Work
3. Method
3.1. Baseline Approach to Coverage: Zamboni with Obstacle Avoidance
- (1)
- Zamboni route (zigzag traversal).The field is covered by parallel passes: the drone flies along a straight path, then makes a turn and moves back slightly offset from the previous stripe. This resembles the ice resurfacing pattern on hockey rinks or the operation of harvesting combines. Turns are usually performed at the field edges.
- (2)
- Obstacle avoidance (clockwise or counterclockwise).If the field contains a substantial obstacle area (e.g., a pond or tree belt), the classical method formally “cuts out” the obstacle contour from its route, circumnavigating it either clockwise or counterclockwise before resuming straight-line movement. This can introduce lengthy maneuvers around obstacles, creating additional turns and unnecessary segments. Practically, each obstacle encounter can split a single straight stripe into three or four separate segments.
- (3)
- Single drone or multiple identical drones.Typically, CPP tasks assume either a single drone or multiple identical drones (with uniform characteristics), all taking off from a single location. If refueling (or recharging) is required, the drone returns to the same point, then resumes the route from the point of interruption.
- (4)
- No ground-platform route optimization.Existing studies do not usually account for the potential use of a mobile platform. It is assumed to be stationary (or absent entirely), meaning there is no mechanism to shorten the drone’s path by moving the platform to points where the drone needs to land.
3.2. Concept of Coverage Algorithm with Obstacle Avoidance
- (1)
- Field division (with obstacles) into fractional zones:A field containing obstacles can be represented as an original polygon P minus the internal restricted areas (obstacles).Instead of covering the entire polygon with one continuous Zamboni route, we subdivide the field into subsets P1, P2,…, Pm so that they do not overlap and collectively cover the entire available area. Each Pi is assigned a fraction of the total area (for example, 30%, 20%, 50%, etc.).The rationale behind this subdivision is that certain areas (sub-polygons) might be more conveniently covered by tiltrotors (efficient for long, straight lines), while other areas (winding or fragmented) are better suited for multicopters. Additionally, subdividing the field into multiple blocks can help minimize the overall number of obstacle fly-arounds. This subdivision is performed using the pode library [53], implementing the algorithm from [54].
- (2)
- Two-stage optimization approach:Simultaneous optimization of polygon subdivision and flight parameters is infeasible, as changing the polygon subdivision (thus altering the overall zigzag shape) can render previously optimal flight parameters suboptimal. Thus, these two components must be optimized separately. The space of possible polygon subdivisions is continuous, with numerous possible variations; therefore, a discrete approach involving the separate optimization of flight parameters for every potential subdivision would be computationally expensive.
- In the first stage, multiple subdivision configurations are generated (each configuration represented by an area fraction vector summing to 1). For each subdivision, preliminary economic efficiency is evaluated through a set of random flight plans. The subdivision yielding minimal flight cost is selected as potentially optimal.
- In the second (main) stage, a genetic algorithm is employed: candidate solutions encode flight routes (including flight angle, entry point, drone assignment and sequence, mobile platform trajectory) based on the optimal polygon subdivision identified in the first stage. Iteratively selecting and combining candidates, the algorithm searches for an optimal route for the given polygon configuration excluding obstacles.
3.3. Detailed Algorithm Description
- Field polygon P,
- Set of obstacles {H1, H2,…, Hs}, each Hi⊂P,
- Road (or roads) D, along which the ground platform moves,
- Set of drones L = {L1,…, L1} with defined characteristics,
- Economic parameters: pilot hourly rate, takeoff fee, drone depreciation costs, etc.
- Stage 1 (Preliminary optimal subdivision search):
- (1)
- Select parameter N—number of partition vectors to test. Each subdivision consists of random fractions summing to 1.
- (2)
- For n from 1 to N:
- Generate random vector r = (r1,…,rm),with and random dimensionality m.
- Partition field into subsets {P1,…, Pm}, each with area Pi = ri × Aavailable using pode library.
- Generate M random flight configurations—flight angle, start point, drones, and landing points.
- Estimate total cost for each configuration (without full GA execution).
- Compute cost metrics (average + minimum).
- (3)
- Select subdivision r∗ yielding best cost metrics.
- Stage 2 (Genetic optimization based on best subdivision):
- (1)
- Input: optimal subdivision r∗.
- (2)
- Initialize GA population: each candidate encodes the following:
- θ—flight angle (0…360°);
- start_corner—one of («NW», «NE», «SW», «SE»);
- dronesList—ordered drone indices;
- carPointscarPointscarPoints—landing points along road (0 to 1 proportional positions);
- subPolygonsTraversalOrder—traversal order of sub-polygons r∗.
- (3)
- Each GA generation includes the following:
- Decoding: We convert each individual into a real-world route. Considering the subPolygonsTraversalOrder and angle θ, zigzag flight paths are constructed. Drone missions are simulated using the specified dronesList, takeoff and landing points from carPoints, and the initial start_corner position.
- Cost evaluation: We calculate operational expenses (flight costs, takeoff charges, and operator salaries) and apply a penalty Ppenalty if the total mission time Ttotal exceeds a predefined threshold.
- Selection: Individuals are sorted based on their objective value (total cost). The top-ranking individuals participate in crossover.
- Crossover: We randomly select pairs of individuals to exchange portions of their genomes (for instance, flight angle, part of drone order list, etc.).
- Mutation: With a certain probability, we adjust the flight angle, reorder drones, add or remove points in carPoints, etc.
- (4)
- Upon reaching the stopping criterion (either a sufficient number of generations or convergence of results), the individual with the best objective value is selected. This route is then used as the final coverage plan.
3.4. Formal Definition of the Objective Function
- —total operational costs of the UAV fleet (USD);
- —total wages for drone operators (pilots) (USD);
- —penalty function for violations of time or quality constraints (USD).
- —fixed cost per takeoff–landing cycle for drone i (USD);
- —cost per kilometer of flight for drone i (USD/km);
- —hourly operational cost for drone i (USD/h);
- —total distance traveled by drone i (km);
- —total flight duration of drone i (hours).
- T(x)—maximum flight duration among all drones (hours);
- —operator’s hourly wage rate (USD);
- —total number of drone takeoffs;
- —fixed operator payment per takeoff (USD).
3.5. Pseudocode of the Generalized Algorithm
| Algorithm 1: TWO_STAGE_GA_FOR_HETEROGENEOUS_UAV_COVERAGE |
| INPUT: P // field polygon OBSTACLES = {H1…Hs} ROAD // drivable path(s) for ground platform L // set of drones with parameters N, M, MAXGEN // search counts and GA generations T_MAX, T_BORDER // time thresholds for penalties COST_PARAMS // per-cycle, per-km, per-hour, salary, per-takeoff, etc. OUTPUT: BEST_PLAN // final coverage plan PROCEDURE TWO_STAGE_GA(P, OBSTACLES, ROAD, L, N, M, MAXGEN, T_MAX, T_BORDER, COST_PARAMS) RETURNS BEST_PLAN A_AVAIL <- AREA(P) - SUM_OVER(i=1…s){ AREA(Hi) } BEST_SCORE <- +INFINITY BEST_PART <- NULL // ---------- STAGE I: PARTITION SEARCH ---------- FOR n FROM 1 TO N DO R <- RANDOM_PARTITION_VECTOR() // dimension m chosen at random, SUM R[i] = 1 PART <- DIVIDE_WITH_OBSTACLES(P, OBSTACLES, R) // e.g., via PODE; produces {P1…Pm} SCORES <- EMPTY_LIST() FOR t FROM 1 TO M DO PLAN <- RANDOM_PLAN() // THETA, START_CORNER, DRONES_LIST, CAR_STOPS, SUBPOLY_ORDER COST_EST <- QUICK_EVALUATE(PLAN, PART, ROAD, L, COST_PARAMS) APPEND(SCORES, COST_EST) END FOR METRIC <- AGGREGATE(SCORES) // e.g., MIN(SCORES) + ALPHA * MEAN(SCORES) IF METRIC < BEST_SCORE THEN BEST_SCORE <- METRIC BEST_PART <- PART END IF END FOR // ---------- STAGE II: GENETIC OPTIMIZATION ---------- POP <- INITIALIZE_POPULATION() FOR g FROM 1 TO MAXGEN DO FOR EACH IND IN POP DO ROUTE <- DECODE(IND, BEST_PART, ROAD, L) // build sweeps by THETA and SUBPOLY_ORDER; assign launches/landings IND.FITNESS <- EVALUATE_COST(ROUTE, T_MAX, T_BORDER, COST_PARAMS) END FOR POP <- SELECT(POP) // e.g., tournament or rank selection POP <- CROSSOVER(POP) // exchange substrings: angle, drone order, stop subsets, etc. POP <- MUTATE(POP) // perturb angle, reorder drones, add/remove car stops, etc. END FOR BEST_PLAN <- ARGMIN_FITNESS(POP) RETURN BEST_PLAN END PROCEDURE // ---------- COST AND PENALTY MODEL ---------- PROCEDURE EVALUATE_COST(ROUTE, T_MAX, T_BORDER, COST_PARAMS) RETURNS TOTAL // DRONE OPERATING COSTS C_DRONE <- 0 FOR EACH DRONE i USED IN ROUTE DO D_i <- TOTAL_DISTANCE(i, ROUTE) // km T_i <- TOTAL_FLIGHT_TIME(i, ROUTE) // hours N_CYCLES_i <- NUM_TAKEOFFS(i, ROUTE) C_DRONE <- C_DRONE + (COST_PARAMS.PER_CYCLE[i] * N_CYCLES_i) + (COST_PARAMS.PER_KM[i] * D_i) + (COST_PARAMS.PER_HOUR[i] * T_i) END FOR // OPERATOR COSTS T_TOTAL <- MAX_OVER_DRONES{ TOTAL_FLIGHT_TIME(i, ROUTE) } // mission wall time N_STARTS <- TOTAL_TAKEOFFS(ROUTE) C_SALARY <- (T_TOTAL * COST_PARAMS.OP_HOURLY) + (N_STARTS * COST_PARAMS.OP_PER_TAKEOFF) // PENALTIES PEN <- 0 IF T_TOTAL > T_MAX THEN PEN <- (C_SALARY + C_DRONE) * POW(10, MIN(T_TOTAL - T_MAX, 10)) ELSE IF T_TOTAL > T_BORDER THEN PEN <- (C_SALARY + C_DRONE) * (T_TOTAL - T_BORDER) / (T_MAX - T_BORDER) END IF MISSED <- MISSED_WAYPOINTS(ROUTE) IF MISSED > 3 THEN PEN <- PEN + 1000000 END IF TOTAL <- C_DRONE + C_SALARY + PEN RETURN TOTAL END PROCEDURE // ---------- FAST PARTITION SCORING (STAGE I) ---------- PROCEDURE QUICK_EVALUATE(PLAN, PART, ROAD, L, COST_PARAMS) RETURNS COST_EST ROUTE_DRAFT <- DECODE(PLAN, PART, ROAD, L) // coarse simulation only COST_EST <- EVALUATE_COST_APPROX(ROUTE_DRAFT, COST_PARAMS) RETURN COST_EST END PROCEDURE |
4. Results
5. Discussion of Results
6. Conclusions and Future Research Directions
- the complex geometry of the field;
- the presence of internal obstacles;
- the heterogeneous composition of available UAVs;
- the ability (and desirability) to use a mobile ground platform.
- (1)
- Genetic algorithms are metaheuristics based on stochastic selection methods that do not guarantee finding a global optimum.
- (2)
- The results of computational experiments have not yet been tested in real missions
- (3)
- The implemented software is its inability to handle non-convex obstacles, due to technical constraints in the geometric libraries used for transformations and intersection checks.
- Incorporating detailed three-dimensional terrain and elevation variations (for example, when the drone can fly higher over tree belts, but at an increased energy cost).
- Enabling online route correction in response to changing conditions (weather factors, sudden drone failure).
- Investigating collision safety to ensure that the trajectories of different drones do not intersect at critically close distances during parallel operations.
- 3D simulation that takes into account the height of obstacles.
- Studying the influence of the initial partitioning of the field on the result of mission optimization.
- Investigating the problem of obstacle detection.
- Studying the influence of field relief on mission performance.
- Evaluation of simulation results during real missions.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Parameters of the Genetic Algorithm
- Input parameters
- Field polygon P,
- Set of obstacles {H1, H2,…, Hs}, each Hi⊂P,
- Road (or roads) D, along which the ground platform moves,
- Set of drones L = {L1,…, L1} with defined characteristics,
- —fixed cost per takeoff–landing cycle for drone i (USD);
- —cost per kilometer of flight for drone i (USD/km);
- —hourly operational cost for drone i (USD/h);
- —operator’s hourly wage rate (USD);
- —fixed operator payment per takeoff (USD).
- θ—flight angle (0…360°);
- start_corner—one of («NW», «NE», «SW», «SE»);
- dronesList—ordered drone indices;
- carPointscarPointscarPoints—landing points along road (0 to 1 proportional positions);
- subPolygonsTraversalOrder—traversal order of sub-polygons r∗.
- Selected parameters (parameters selected by stochastic search during the execution of the genetic algorithm)
- —total distance traveled by drone i (km);
- —total flight duration of drone i (hours).
- —total number of drone takeoffs;
- T(x)—maximum flight duration among all drones (hours);
- θ—flight angle (0…360°);
- start_corner—one of («NW», «NE», «SW», «SE»);
- dronesList—ordered drone indices;
- carPointscarPointscarPoints—landing points along road (0 to 1 proportional positions);
- subPolygonsTraversalOrder—traversal order of sub-polygons r∗.
- Calculated parameters
- —total operational costs of the UAV fleet (USD);
- —total wages for drone operators (pilots) (USD);
- Target value (the value to be minimized)
Appendix B
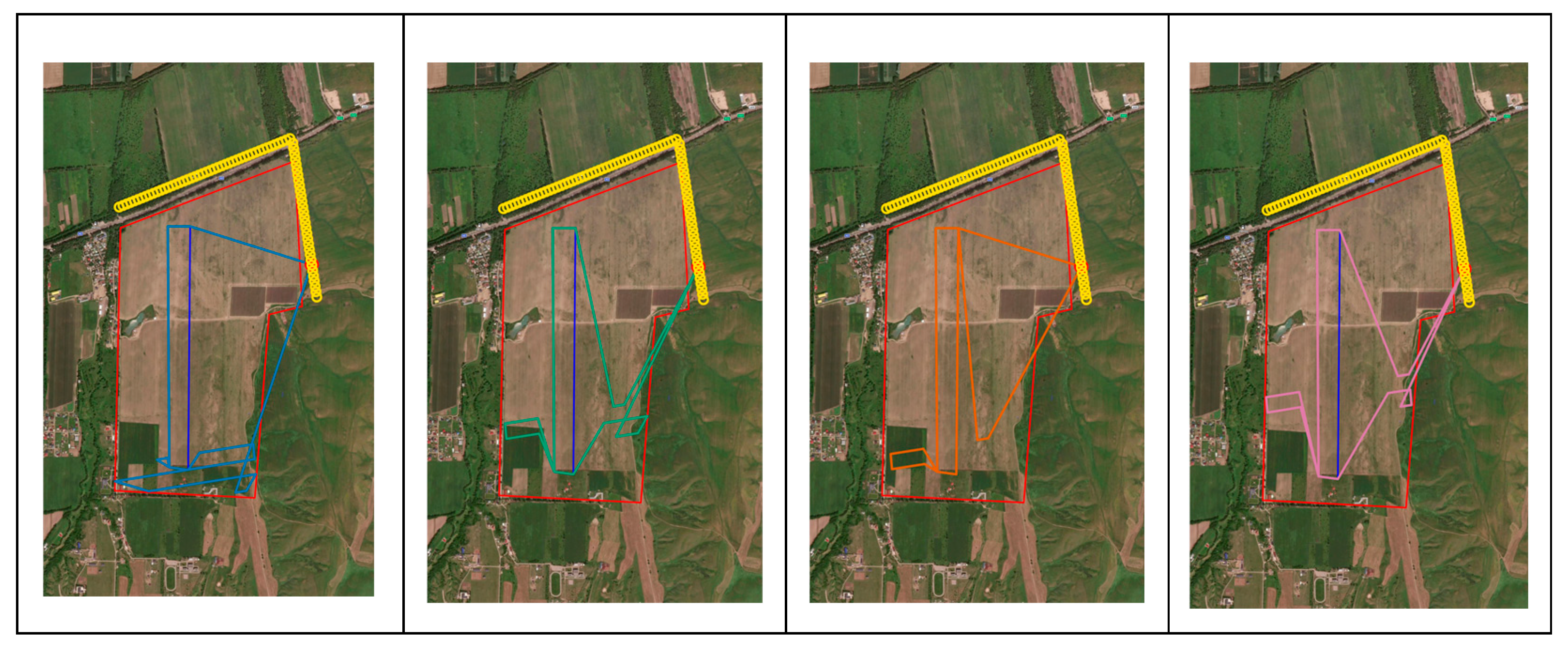

Appendix C
Appendix D
References
- Mogili, U.R.; Deepak, B.B.V.L. Review on Application of Drone Systems in Precision Agriculture. Procedia Comput. Sci. 2018, 133, 502–509. [Google Scholar] [CrossRef]
- Park, S.; Choi, Y. Applications of Unmanned Aerial Vehicles in Mining from Exploration to Reclamation: A Review. Minerals 2020, 10, 663. [Google Scholar] [CrossRef]
- Gailler, L.; Labazuy, P.; Régis, E.; Bontemps, M.; Souriot, T.; Bacques, G.; Carton, B. Validation of a New UAV Magnetic Prospecting Tool for Volcano Monitoring and Geohazard Assessment. Remote Sens. 2021, 13, 894. [Google Scholar] [CrossRef]
- Erdelj, M.; Król, M.; Natalizio, E. Wireless Sensor Networks and Multi-UAV Systems for Natural Disaster Management. Comput. Netw. 2017, 124, 72–86. [Google Scholar] [CrossRef]
- Mukhamediev, R.; Alexandrov, D.A.; Boukhanovsky, A.V.; Chugunov, A.V.; Kabanov, Y.; Koltsova, O.; Musabirov, I. Intelligent Unmanned Aerial Vehicle Technology in Urban Environments. In Digital Transformation and Global Society; Communications in Computer and Information Science; Springer: Cham, Switzerland, 2020; Volume 1242, pp. 312–325. [Google Scholar] [CrossRef]
- Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F. Fault-Tolerant Cooperative Navigation of Networked UAV Swarms for Forest Fire Monitoring. Aerosp. Sci. Technol. 2022, 123, 107494. [Google Scholar] [CrossRef]
- Hodgson, J.C.; Baylis, S.M.; Mott, R.; Herrod, A.; Clarke, R.H. Precision Wildlife Monitoring Using Unmanned Aerial Vehicles. Sci. Rep. 2016, 6, 22574. [Google Scholar] [CrossRef]
- Yuan, S.; Li, Y.; Bao, F.; Xu, H.; Yang, Y.; Yan, Q.; Lin, J. Marine Environmental Monitoring with Unmanned Vehicle Platforms: Present Applications and Future Prospects. Sci. Total Environ. 2023, 858, 159741. [Google Scholar] [CrossRef]
- Medvedev, A.; Telnova, N.; Alekseenko, N.; Koshkarev, A.; Kuznetchenko, P.; Asmaryan, S.; Narykov, A. UAV-Derived Data Application for Environmental Monitoring of the Coastal Area of Lake Sevan, Armenia with a Changing Water Level. Remote Sens. 2020, 12, 3821. [Google Scholar] [CrossRef]
- Jenssen, R.; Roverso, D. Intelligent Monitoring and Inspection of Power Line Components Powered by UAVs and Deep Learning. IEEE Power Energy Technol. Syst. J. 2019, 6, 11–21. [Google Scholar] [CrossRef]
- Jordan, S.; Moore, J.; Hovet, S.; Box, J.; Perry, J.; Kirsche, K.; Tse, Z.T.H. State-of-the-Art Technologies for UAV Inspections. IET Radar Sonar Navig. 2018, 12, 151–164. [Google Scholar] [CrossRef]
- Ham, Y.; Han, K.K.; Lin, J.J.; Golparvar-Fard, M. Visual Monitoring of Civil Infrastructure Systems via Camera-Equipped Unmanned Aerial Vehicles (UAVs): A Review of Related Works. Vis. Eng. 2016, 4, 1–8. [Google Scholar] [CrossRef]
- Khan, N.A.; Jhanjhi, N.Z.; Brohi, S.N.; Usmani, R.S.A.; Nayyar, A. Smart Traffic Monitoring System Using Unmanned Aerial Vehicles (UAVs). Comput. Commun. 2020, 157, 434–443. [Google Scholar] [CrossRef]
- Drone Inspections Help Cut Pollution by Half. Available online: https://gulfnews.com/uae/environment/drone-inspections-help-cut-pollution-by-half-1.2263928 (accessed on 16 September 2021).
- Mohsan, S.A.H.; Othman, N.Q.H.; Li, Y.; Alsharif, M.H.; Khan, M.A. Unmanned Aerial Vehicles (UAVs): Practical Aspects, Applications, Open Challenges, Security Issues, and Future Trends. Intell. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef] [PubMed]
- Telli, K.; Kraa, O.; Himeur, Y.; Ouamane, A.; Boumehraz, M.; Atalla, S.; Mansoor, W. A Comprehensive Review of Recent Research Trends on Unmanned Aerial Vehicles (UAVs). Systems 2023, 11, 400. [Google Scholar] [CrossRef]
- Erkec, T.Y.; Hajiyev, C. Swarm Architecture of UAVs. In Progress in Sustainable Aviation; Karakoc, T.H., Colpan, C.O., Dalkiran, A., Eds.; Sustainable Aviation; Springer: Cham, Switzerland, 2022; pp. 15–34. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the Unmanned Aerial Vehicles (UAVs): A Comprehensive Review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles (UAVs): A Survey on Civil Applications and Key Research Challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- On the Approval of the Rules for the Use of Unmanned Aerial Systems in the Airspace of the Republic of Kazakhstan. Available online: https://adilet.zan.kz/rus/docs/V2000022031 (accessed on 15 August 2025).
- Mukhamediev, R.I.; Symagulov, A.; Kuchin, Y.; Zaitseva, E.; Bekbotayeva, A.; Yakunin, K.; Assanov, I.; Levashenko, V.; Popova, Y.; Akzhalova, A.; et al. Review of Some Applications of Unmanned Aerial Vehicles Technology in the Resource-Rich Country. Appl. Sci. 2021, 11, 10171. [Google Scholar] [CrossRef]
- Wyngaard, J.; Barbieri, L.; Thomer, A.; Adams, J.; Sullivan, D.; Crosby, C.; Parr, C.; Klum, J.; Shrestha, S.R.; Bell, T. Emergent Challenges for Science sUAS Data Management: Fairness through Community Engagement and Best Practices Development. Remote Sens. 2019, 11, 1797. [Google Scholar] [CrossRef]
- Haghrah, A.A.; Ghaemi, S.; Badamchizadeh, M.A. Modeling and Solving Multi-Objective Path Planning Problem for Cooperative Cable-Suspended Load Transportation Considering the Time Variable Risk. IEEE Access 2025, 13, 11704–11719. [Google Scholar] [CrossRef]
- Ccari, L.F.C.; Yanyachi, P.R.; Luque, J.C.C.; Yanyachi, D. Distributed Robust Adaptive Control for Finite-Time Flight Formation of Multi-Quadcopter Systems with Large Lumped Uncertainties. IEEE Access 2024, 12, 113384–113405. [Google Scholar] [CrossRef]
- Bao, X.; Hu, Z.H.; Huang, Y. Routing a Fleet of Drones from a Base Station for Emission Detection of Moving Ships by Genetic Algorithm. J. Mar. Sci. Eng. 2024, 12, 891. [Google Scholar] [CrossRef]
- Alqudsi, Y.; Makaraci, M. UAV Swarms: Research, Challenges, and Future Directions. J. Eng. Appl. Sci. 2025, 72, 12. Available online: https://jeas.springeropen.com/articles/10.1186/s44147-025-00582-3 (accessed on 15 August 2025). [CrossRef]
- Muslimov, T.Z. Algorithms of Autonomous Fixed-Wing UAVs Formation Control via Vector Field Method. Syst. Control Commun. Secur. 2019, 4, 187–214. (In Russian) [Google Scholar]
- Huang, G.; Hu, M.; Yang, X.; Huang, F. Multi-UAV Cooperative Mission Assignment Based on Hybrid WAFC-RRAS Algorithm. IEEE Access 2023, 11, 98132–98152. [Google Scholar] [CrossRef]
- Martinez-Alpiste, I.; Golcarenarenji, G.; Wang, Q.; Alcaraz-Calero, J.M. Search and Rescue Operation Using UAVs: A Case Study. Expert Syst. Appl. 2021, 178, 114937. [Google Scholar] [CrossRef]
- Fang, Z.; Savkin, A.V. Strategies for Optimized UAV Surveillance in Various Tasks and Scenarios: A Review. Drones 2024, 8, 193. [Google Scholar] [CrossRef]
- Ahuraka, F.; Mcnamee, P.; Wang, Q.; Ahmadabadi, Z.N.; Hudack, J. Chaotic Motion Planning for Mobile Robots: Progress, Challenges, and Opportunities. IEEE Access 2023, 11, 134917–134939. [Google Scholar] [CrossRef]
- Kumar, K.; Kumar, N. Region Coverage-Aware Path Planning for Unmanned Aerial Vehicles: A Systematic Review. Phys. Commun. 2023, 59, 102073. [Google Scholar] [CrossRef]
- QGroundControl. Available online: http://qgroundcontrol.com/ (accessed on 7 November 2024).
- Dronekit. Available online: https://dronekit.io/ (accessed on 7 November 2024).
- Ardupilot. Available online: https://ardupilot.org/planner/docs/common-loading-firmware-onto-pixhawk.html (accessed on 7 November 2024).
- UgCS. Available online: https://www.sphengineering.com/flight-planning/ugcs (accessed on 7 November 2024).
- Vélez, S.; Mier, G.; Ariza-Sentís, M.; Valente, J. Integrated Framework for Multipurpose UAV Path Planning in Hedgerow Systems Considering the Biophysical Environment. Crop Prot. 2025, 187, 106992. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, D.; Li, C.; Zhang, Z. Multiple Fixed-Wing UAVs Collaborative Coverage 3D Path Planning Method for Complex Areas. Def. Technol. 2025, 47, 197–215. [Google Scholar] [CrossRef]
- Maaji, S.S.; Landa-Silva, D. UAV Path Planning for Area Coverage and Energy Consumption in Oil and Gas Exploration Environment. In Computational Logistics, Proceedings of the International Conference on Computational Logistics, Berlin, Germany, 6–8 September, 2023; Springer: Cham, Switzerland, 2023; pp. 467–481. [Google Scholar]
- Zhang, L.; Su, J.; Xu, C.; He, T. Coverage Path Planning with Minimum Cost Suitable for Sidewalk. In Proceedings of the 2023 3rd International Conference on Computer Science, Electronic Information Engineering and Intelligent Control Technology (CEI), Wuhan, China, 15–17 December 2023; pp. 801–805. [Google Scholar]
- Li, J.; Ren, W. A Multi-Machine Cooperation Full Coverage Path Planning Method in Agriculture. In Proceedings of the 2023 4th International Seminar on Artificial Intelligence, Networking and Information Technology (AINIT), Nanjing, China, 16–18 June 2023; pp. 713–716. [Google Scholar]
- Li, J.; Sheng, H.; Zhang, J.; Zhang, H. Coverage Path Planning Method for Agricultural Spraying UAV in Arbitrary Polygon Area. Aerospace 2023, 10, 755. [Google Scholar] [CrossRef]
- Plessen, M. Path Planning for Spot Spraying with UAVs Combining TSP and Area Coverages. arXiv 2024, arXiv:2408.08001. [Google Scholar] [CrossRef]
- Bine, L.M.S.; Boukerche, A.; Ruiz, L.B.; Loureiro, A.A.F. A Novel Ant Colony-Inspired Coverage Path Planning for Internet of Drones. Comput. Netw. 2023, 235, 109963. [Google Scholar] [CrossRef]
- Karthik, K.; Balasubramanian, C. Improved Green Anaconda Optimization Algorithm-Based Coverage Path Planning Mechanism for Heterogeneous Unmanned Aerial Vehicles. Sustain. Comput. 2024, 42, 100961. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Path Planning Techniques for Unmanned Aerial Vehicles: A Review Solutions and Challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Ahmadi, S.M.; Kebriaei, H.; Moradi, H. Constrained Coverage Path Planning: Evolutionary and Classical Approaches. Robotica 2018, 36, 904–924. [Google Scholar] [CrossRef]
- Önler, E. Comparative Analysis of Genetic and Greedy Algorithm for Optimal Drone Flight Route Planning in Agriculture. Anadolu Tarım Bilim. Derg. 2024, 39, 129–142. [Google Scholar] [CrossRef]
- Barzola, P.D.; Baños, E.H.; Baños, L.H.; Moreira, W.M.; Muentes, E.H. Review of Genetic Algorithms Applied to Agriculture. In Proceedings of the 2024 International Conference on Electrical, Computer and Energy Technologies (ICECET), Sydney, Australia, 25–27 July 2024; pp. 1–8. [Google Scholar]
- Mukhamediev, R.I.; Yakunin, K.; Aubakirov, M.; Assanov, I.; Kuchin, Y.; Symagulov, A.; Levashenko, V.; Zaitseva, E.; Sokolov, D.; Amirgaliyev, Y. Coverage Path Planning Optimization of Heterogeneous UAVs Group for Precision Agriculture. IEEE Access 2023, 11, 5789–5803. [Google Scholar] [CrossRef]
- Wen, J.; Wang, F.; Su, Y. A Bi-Layer Collaborative Planning Framework for Multi-UAV Delivery Tasks in Multi-Depot Urban Logistics. Drones 2025, 9, 512. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, W.; Ye, H.; Shi, Z. A Two-Stage Optimization Framework for UAV Fleet Sizing and Task Allocation in Emergency Logistics Using the GWO and CBBA. Drones 2025, 9, 501. [Google Scholar] [CrossRef]
- Pode Library. Available online: https://github.com/GeorgySk/pode (accessed on 7 November 2024).
- Hert, S.; Lumelsky, V. Polygon Area Decomposition for Multiple-Robot Workspace Division. Int. J. Comput. Geom. Appl. 1998, 8, 437–466. [Google Scholar] [CrossRef]



| Field | Baseline Approach | Partition Optimization | Improvement over the Baseline Approach (%) | Computation Time (s) | Number of Drones (Baseline/Partition Optimization) |
|---|---|---|---|---|---|
| Field 1—Large obstacle | 465.300863 | 399.7649577 | 14.08 | 234 | 2/2 |
| Field 2—Large elongated rectangular obstacle | 375.7315059 | 331.2337709 | 11.84 | 190 | 1/1 |
| Field 3—Two orthogonal rectangular obstacles | 391.0776317 | 394.5266994 | −0.88 | 178 | 3/2 |
| Field 4—Multiple small obstacles | 413.7058472 | 317.9067045 | 23.16 | 199 | 3/2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakunin, K.; Kuchin, Y.; Muhamedijeva, E.; Symagulov, A.; Mukhamediev, R.I. An Algorithm for Planning Coverage of an Area with Obstacles with a Heterogeneous Group of Drones Using a Genetic Algorithm and Parameterized Polygon Decomposition. Drones 2025, 9, 658. https://doi.org/10.3390/drones9090658
Yakunin K, Kuchin Y, Muhamedijeva E, Symagulov A, Mukhamediev RI. An Algorithm for Planning Coverage of an Area with Obstacles with a Heterogeneous Group of Drones Using a Genetic Algorithm and Parameterized Polygon Decomposition. Drones. 2025; 9(9):658. https://doi.org/10.3390/drones9090658
Chicago/Turabian StyleYakunin, Kirill, Yan Kuchin, Elena Muhamedijeva, Adilkhan Symagulov, and Ravil I. Mukhamediev. 2025. "An Algorithm for Planning Coverage of an Area with Obstacles with a Heterogeneous Group of Drones Using a Genetic Algorithm and Parameterized Polygon Decomposition" Drones 9, no. 9: 658. https://doi.org/10.3390/drones9090658
APA StyleYakunin, K., Kuchin, Y., Muhamedijeva, E., Symagulov, A., & Mukhamediev, R. I. (2025). An Algorithm for Planning Coverage of an Area with Obstacles with a Heterogeneous Group of Drones Using a Genetic Algorithm and Parameterized Polygon Decomposition. Drones, 9(9), 658. https://doi.org/10.3390/drones9090658







