A Feature-Aware Elite Imitation MARL for Multi-UAV Trajectory Optimization in Mountain Terrain Detection

Abstract

With the advancement of UAV trajectory planning and sensing technologies, unmanned aerial vehicles (UAVs) are now capable of performing high-performance ground detection and search tasks. Mountainous regions, due to their complex terrain, have long been a focal point in the field of remote sensing. Effective UAV search tasks in such areas must consider not only horizontal coverage but also variations in detection range and angle caused by changes in elevation. Conventional algorithms typically require complete prior knowledge of the environment for trajectory optimization and often depend on scenario-specific policy models, limiting their generalizability. To address these challenges, this paper proposes a Feature-Aware Elite Imitation Multi-Agent Reinforcement Learning (FA-EIMARL) algorithm that leverages partial terrain information to construct a feature extraction network. This approach enables batch training across diverse terrains without the need for full environmental maps. In addition, an elite imitation mechanism has been proposed for convergence acceleration and task performance enhancement. Simulation results demonstrate that the proposed method achieves superior reward performance, convergence rate, and computational efficiency while maintaining strong adaptability to varying terrains.

1. Introduction

With the development of infrared detection [1], action cameras [2], and beyond 5G communication technologies [3], unmanned aerial vehicles (UAVs) have been widely applied in the field of remote sensing [4]. Due to mobility, flexibility, and high temporal responsiveness, UAVs are capable of conducting aerial reconnaissance in mountainous or rugged terrains where ground personnel or vehicles cannot easily access [5]. Equipped with thermal infrared (IR) sensors, UAVs can perform surface mapping and accurately detect objects with temperatures higher than the surrounding environment [6]. Meanwhile, UAVs can be integrated with communication modules, enabling multiple UAVs to share data and synchronize task progress in real time [7]. In addition, a UAV range-finding module like Light Detection and Ranging (LiDAR) equips UAVs with the ability to measure terrain elevation [8]. These multifunctional capabilities prepare UAVs for a wide range of applications, including remote sensing, forest fire monitoring, and nighttime search and rescue operations [9,10,11].

In this work, we envision a multi-UAV collaborative system in which UAVs perform search and detection tasks in mountainous regions. UAVs depart from different positions and aim to achieve the highest coverage rate in the shortest time possible. During the flight tasks, each UAV can adjust its speed and flight direction [12]. Regarding the complexity of terrains, UAVs should focus on flight altitude to balance the field of view (FOV) and detection accuracy [13]. Due to limited battery capacities, the UAVs should complete their task before their battery runs out. UAVs are equipped with communication modules to broadcast coverage and location information to avoid collision and duplicate search [14].

In mountainous search, monitoring, or rescue missions, which are typically urgent in nature, it is essential to develop high-precision trajectory optimization models for UAVs [15,16,17]. Moreover, given the limited computational and storage capabilities of UAVs, lightweight and generalizable task models capable of adapting to terrains with varying steepness and elevations are desired. Under these circumstances, integrating environmental features into the model construction and optimization process is particularly valuable. The problem of UAV trajectory design has been extensively studied. Researchers have proposed various trajectory optimization approaches such as a heuristic-based approach [18], hybrid optimization [19], convex optimization [20], and deep reinforcement learning (DRL) based [21]. However, there are still limitations in these existing studies. First, heuristic and hybrid optimization methods struggle to adapt multi-dimensional speed direction and flexible velocity limitation. In addition, convex optimization is not suitable for trajectory problems with a multifaceted search space. On the other hand, the aforementioned methods only enable trajectory design when all environmental parameters are known, and cooperation among multiple UAVs remains insufficient. Although DRL can address complex uncertainty optimization problem [22], the existing models are designed to serve specific tasks in homogeneous scenarios, lacking the generalization ability to transfer to new environments.

In real-world environments, the joint trajectory design for UAVs is highly complex [23], which leads to a series of challenges [24]. From the UAV control perspective, UAVs must avoid collision with other UAVs [25] and maintain their cruising altitude for the balance of FOV and detection precision [26]. In addition, limited battery capacity and UAV dynamics need to be considered when making the joint decisions [27]. UAVs can establish inter-UAV wireless communication links to facilitate the exchange of positioning and environmental coverage record [28]. To address the limitations of existing UAV trajectory optimization methods in complex and dynamic environments, this work proposes a generalized Multi-Agent Reinforcement Learning (MARL) framework based on actor–critic networks. The term generalized refers to the capability of the proposed system to accommodate diverse trajectory constraints and to enable trained models to be deployed across multiple mountainous regions with varying altitudes and terrain complexities for detection tasks.

To jointly optimize key performance indicators—namely, coverage rate, energy consumption, and detection accuracy—we enhance standard deterministic MARL algorithms by introducing an elite imitation (EI) strategy. In this mechanism, the multi-agent system periodically conducts performance evaluations and selects the best-performing agent (elite). A portion of this elite agent’s parameters are then softly integrated into the policies of other agents. To prevent overfitting and encourage continuous exploration, the imitation frequency decreases gradually, and the parameter-sharing ratio is progressively reduced. Given the cooperative nature of the UAVs and the equivalence of their tasks, this strategy accelerates early-stage policy convergence and reduces the negative impact of poor initialization.

Building upon the EI-enhanced MARL framework, we further propose a Feature-Aware Elite Imitation Multi-Agent Reinforcement Learning (FA-EIMARL) algorithm that incorporates environmental information to improve adaptability in varying task scenarios. In FA-EIMARL, UAVs perform random sampling of ground elevation data and store it in a structured point array format. These arrays, labeled with scenario-specific attributes, are input into a classification pipeline composed of a Point Array Network (PAN) for multi-dimensional feature extraction, followed by a classification module. During training, multiple terrain scenarios are sampled at each time step. Extracted features are then fused with the UAVs’ state representations to support policy updates. This design enables FA-EIMARL to generalize effectively across terrain profiles with different altitudes and structural complexities.

In addition, evaluating the quality of IR-based mapping by calculating the geometric relationship between UAVs and the terrain they observe often requires extensive computation, especially when assessing the accuracy of terrain data acquisition in mountainous regions. To improve computational efficiency, we design a lightweight detection quality prediction network (DQPN) that estimates the reliability of mapping results based on partial ground elevation information and UAV altitude. Unreliable regions are subsequently flagged for re-sensing, thereby reducing unnecessary computation while maintaining overall mapping accuracy.

Our key contributions are as follows:

• We formulate the joint trajectory optimization system that simultaneously accounts for detection accuracy, UAV energy efficiency, and collision avoidance.
• We propose a generalized MARL framework incorporating the EI mechanism and the DQPN structure, which together enhance training stability, accelerate convergence, and reduce inference latency in detection tasks.
• We propose a novel FA-EIMARL algorithm that can rapidly adapt to dynamic task spaces based on the extracted environmental features. Experimental results demonstrate that this algorithm outperforms baselines.

The remainder of this paper is organized as follows. Section 2 reviews the related works. Section 3 introduces the exemplary scenario and methodology. Section 4 presents the system model. Section 5 proposes two novel algorithms. Section 6 presents the experiment. Finally, Section 7 concludes this work.

2. Related Works

Trajectory optimization plays a crucial role in UAV research. The most conventional studies focus on addressing the problems in a fixed and predefined task space. For example, the authors of [29] optimized trajectories for multi-UAV systems in a fixed 3D space to cover the 3D space cooperatively and avoid obstacles. In [30], the main objective of path planning is to visit some predetermined checkpoints in the operational area for the maximum target coverage rate. In [31], a multi-UAV coverage path planning approach is introduced for collaborative 3D space coverage in predetermined large-scale search tasks. In [32], UAV trajectory planning is employed to generate remote sensing image acquisition paths within predefined urban task areas. In [33], the selected task scenarios can be represented by the LiDAR data collected by UAVs. In [34], pre-setting terrain simulation data is used for UAV path design. Only a limited number of studies consider UAVs performing tasks in dynamic task spaces. For instance, [35] focuses on UAV trajectory design to cope with dynamic task scenarios. In [36], a novel approach was proposed to optimize UAV navigation in dynamic environments. However, these algorithms still face significant challenges when applied to real-world environments. On the one hand, their high computational complexity makes them unsuitable for time-sensitive applications. On the other hand, they typically rely more on enhancing algorithmic fault tolerance rather than task-specific adaptability. Building upon the aforementioned works, this study aims to extend the field by developing generalized solutions for diverse UAV task spaces.

Current research on UAV trajectory optimization primarily encompasses heuristic algorithms [37], hybrid optimization [38], convex optimization [39], and deep reinforcement learning (DRL) [40]. In [41], convex optimization was applied to address UAV placement and resource allocation. In [42], a hybrid Particle Swarm Optimization (PSO) approach was proposed to enhance UAV path planning efficiency. In [43], an Ant Colony Optimization (ACO) algorithm combined with A-star search was introduced to optimize UAV flight trajectories.

Compared to traditional heuristic- and optimization-based algorithms, DRL provides distinct advantages, including adaptability to dynamic environments, scalability to high-dimensional state and action spaces, support for online learning, and reduced computational overhead in multi-UAV decision-making. Several DRL variants have been successfully applied in UAV trajectory planning tasks. In [44], Twin Delayed Deep Deterministic Policy Gradient (TD3) was utilized to optimize UAV paths, demonstrating strong convergence properties and robustness in task performance. In [45], Deep Deterministic Policy Gradient (DDPG)—a continuous control algorithm—was shown to deliver lower computational complexity and faster decision-making compared to other DRL methods. In [46], Soft Actor–Critic (SAC) was adopted to maximize the communication sum-rate, with results indicating superior performance over Deep Q-Network (DQN), which is limited to discrete action spaces. Additionally, [47] applied Proximal Policy Optimization (PPO) for UAV obstacle avoidance, proving its feasibility and generalizability across various environments.

Building upon conventional DRL frameworks, several enhanced DRL variants have been developed to improve either service performance or task generalization. In [48], a Graph Neural Network (GNN) was integrated with DRL for multi-UAV trajectory planning in smart agriculture. By modeling the relationships between UAVs and IoT devices as graphs, the algorithm enables UAVs to extract useful spatial and temporal features in dynamic environments. In [49], a GNN-based MARL was proposed for the solution of UAV trajectory design. However, GNN-RL has several limitation. First, GNN-based RL requires continuously acquiring partial information from the environment, which typically relies on IoT or other specialized devices for sensing and transmission. In the context of UAV mountain rescue and exploration tasks studied in this work, UAVs cannot easily obtain such information, making GNN-based RL unsuitable. Second, the GNN architecture relies on convolutional layers, which significantly increase the computational and memory burden. Maintaining high-performance operations under these conditions is impractical for lightweight UAVs tasked with rapid search. Finally, GNN-based RL uses experience to extract features from the environment to guide training and prediction. In scenarios with multiple predefined conditions and a known exploration area, this approach offers no clear advantage. In [50], Soft Actor–Critic (SAC) and Twin Delayed DDPG (TD3) were combined with transfer learning to support UAV-assisted integrated sensing and communication in emergency rescue scenarios. The proposed method adapts effectively to situations where certain base stations (BSs) are out of service. Nonetheless, the learned policies are difficult to generalize to unrelated tasks such as payload delivery. In [51], a meta-RL framework was employed to optimize UAV service quality in wireless sensor networks. In [52], meta-RL was also applied for UAV energy distribution and trajectory design. Although meta-learning provides adaptability across multiple tasks, it presents several limitations in our scenario. Meta-learning enables UAVs to perform diverse tasks by fine-tuning network parameters. However, it struggles to balance the inherent trade-off between task-specific performance and generalization, resulting in potentially large variations in effectiveness across tasks. Additionally, achieving multi-task capability requires learning distinct strategies for each task, which entails an extra network for parameter adjustment. This increases computational complexity and may reduce overall task accuracy. In contrast, our scenario demands UAVs to adopt a single strategy capable of handling multiple predefined environments with a lightweight model while maintaining high performance. In terms of computational speed, model size, and task requirements, meta-learning deviates substantially from these needs.

In addition, to achieve more stable training performance, imitation learning has been applied in the RL field. In [53], a multi-virtual-agent imitation learning method was proposed to learn the dispatch policy under different power supply interruption periods. In [54], an imitation learning agent was proposed for a variety of learning approaches. In [55], a pre-training imitation model was applied to improve the learning performance of autonomous vehicles. However, the aforementioned methods merely apply the concept of agent imitation, using already established expert knowledge to achieve rapid learning in a specific environment and obtain better learning outcomes. These methods lack generality and are highly dependent on the constructed scenarios and the prior knowledge available.

Overall, existing DRL and imitation methods demonstrate satisfactory performance in homogeneous environments, and some have been extended to handle multiple task types. However, real-world UAV mission scenarios are inherently complex and demand adaptability to diverse and dynamic environmental conditions. To address these challenges, this paper proposes a novel imitation learning-based DRL framework named FA-EIMARL, which integrates a feature-aware model with a DQPN architecture. Compared to current DRLs, the FA module extracts the features from scenarios, enabling the training model to be adapted to complex known task spaces and achieve the total task performance reward. Compared to existing imitation learning modules, the EI module can adaptively select elite individuals and adjust the degree of learning according to the training process, thereby improving the model’s learning quality and convergence speed in complex environments. Moreover, this method does not rely on specific scenarios or prior knowledge. The DQPN can significantly reduces the UAVs’ inference time while maintaining computational accuracy, thereby ensuring high task efficiency. The proposed approach offers improved generalization, enhanced reward performance, and faster convergence, enabling effective deployment in varied and uncertain UAV task environments.

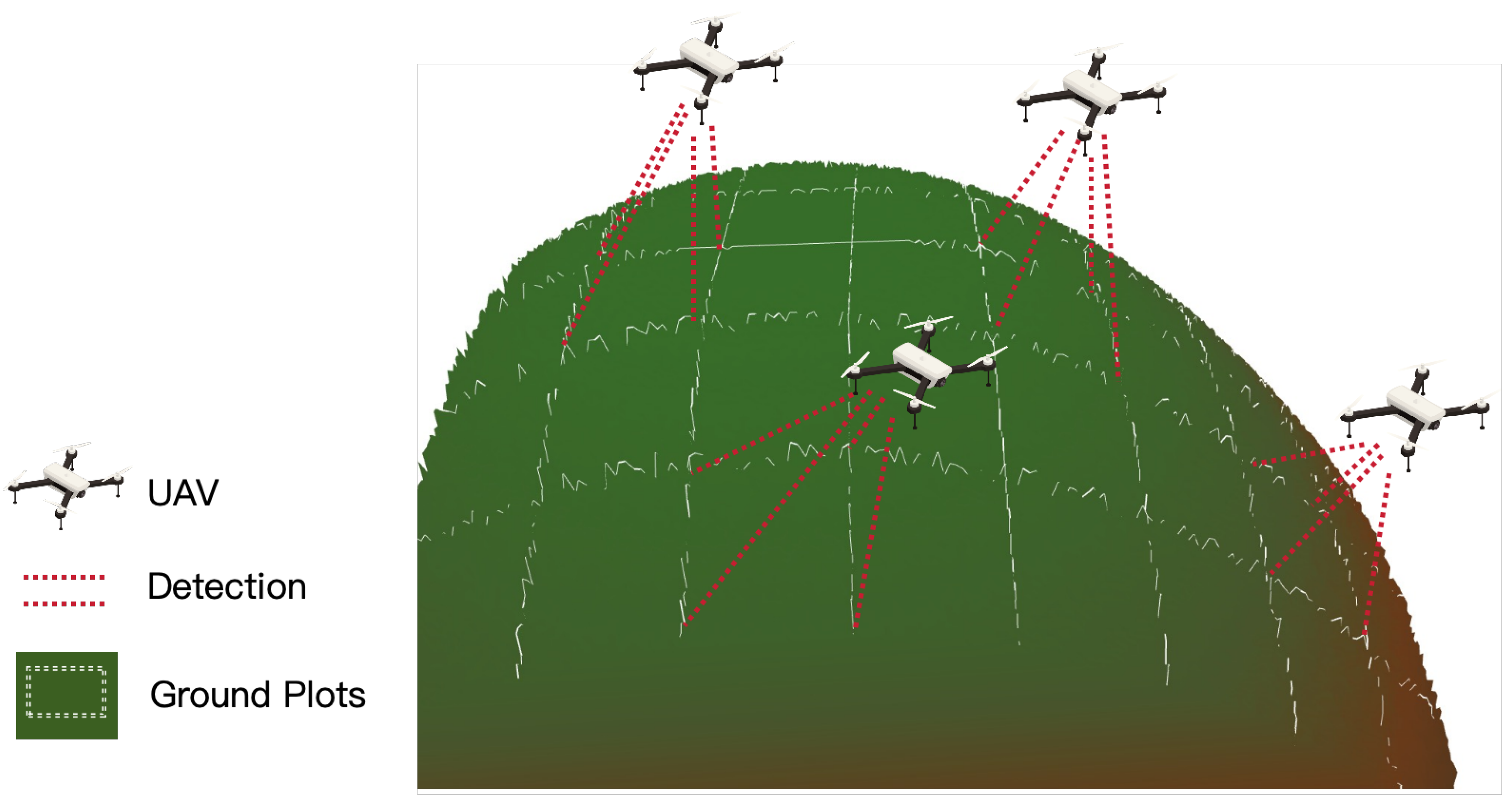
3. System Overview

This section demonstrates an exemplary scenario and introduces the employed methodology.

3.1. Exemplary Scenario

Figure 1 demonstrates an exemplary scenario located in a mountainous region, where a collaborative multi-UAV system is applied to perform the detection task. The system consists of $n_{\mathrm{UAV}}$ UAVs, and the set of UAVs is denoted as $\mathrm{UAV}=\{{\mathrm{UAV}}_1,{\mathrm{UAV}}_2,\dots ,{\mathrm{UAV}}_{n_{\mathrm{UAV}}}\}$. The position of ${\mathrm{UAV}}_i$ at time t can be represented as $\mathit{u}(i,t)=\{u_x(i,t),u_y(i,t),u_z(i,t)\}$, where $u_x(i,t)$, $u_y(i,t)$, and $u_z(i,t)$ represent the x, y, and z axis coordinates in the three-dimensional (3D) spatial coordinate system, respectively.

The choice of UAV flight altitude has a significant impact on both the sensing area and the quality of detection. Especially in complex terrain environments, optimizing altitude control becomes vital for achieving effective and accurate sensing performance. If the UAVs perform tasks at a low altitude, the limited FOV restricts the coverage area, leading to reduced detection efficiency and quality. Conversely, elevated UAV altitude increases the distance to the target area, which may degrade detection accuracy. Therefore, to balance detection precision and coverage, each ${\mathrm{UAV}}_i$ should maintain its cruising altitude $u_z(i,t)$ within a certain range $[u_{z-\min },u_{z-\max }]$, where t represents the current task time. During the flying tasks, each ${\mathrm{UAV}}_i$ departs from the starting point ${\mathit{u}}_{\mathrm{start}}\left(i\right)$ and explores mountainous task areas. We denote the start point as ${\mathit{u}}_{\mathrm{start}}\left(i\right)=\mathit{u}(i,0)$. To facilitate the statistical analysis and recording of the exploration status, we partition the mission area into detection plots DP of length and width $d_{\mathrm{DP}}$, and establish a visitation map $M_V\left(t\right)$. DP can be represented as $\mathrm{DP}={\mathrm{DP}}_{0,0},{\mathrm{DP}}_{0,1},\dots ,{\mathrm{DP}}_{n_x,n_y}$, where $n_x={\displaystyle \frac{u_{x-\max }-u_{x-\min }}{d_{DP}}}$ and $n_y={\displaystyle \frac{u_{y-\max }-u_{y-\min }}{d_{DP}}}$. The UAV performs reconnaissance over the mountainous terrain at an appropriate altitude and inspects the ground plots $\mathrm{DP}(u_x,u_y)$ corresponding to its position periodically every $t_d$ units of time. The UAV estimates the mapping results based on its own altitude, the ground elevation, and the terrain, and updates $M_V\left(t\right)$ according to the detection quality. Once $M_V\left(t\right)$ exceeds $M_{\mathrm{th}}$, we consider the detection to be sufficiently comprehensive, and the task can be terminated early. Here, $M_{\mathrm{th}}$ represents the detection threshold.

Also, we set a maximum task time $T_{\mathrm{end}}$ to ensure that the multi-UAV collaborative system can complete the detection task within $T_{\mathrm{end}}$. In addition, UAVs should fly within a 3D task space, which can be represented as ${\mathbb{R}}^3:\{x\in [u_{x-\min },u_{x-\max }],y\in [u_{y-\min },u_{y-\max }],z-EL(x,y)\in [u_{\{z-\min },u_{z-\max }]\}$, where $EL(x,y)$ denotes the ground elevation at coordinates $(x,y)$. The flying speed of ${\mathrm{UAV}}_i$ can be represented as $\mathit{v}(i,t)=[v_x(i,t),v_y(i,t),v_z(i,t)]$, where $v_x(i,t)$, $v_y(i,t)$, and $v_z(i,t)$ represent the velocity in the x, y, and z direction, where the value of $v_x(i,t)$ and $v_y(i,t)$ is constrained within the range of $[0,v_{\mathrm{horizon}}]$, while the value of $v_z(i,t)$ is constrained within the range of $[0,v_{\mathrm{vertical}}]$. In addition, with the limited onboard battery, each ${\mathrm{UAV}}_i$ should complete its task before the battery runs out. It is worth noting that, to ensure flight safety and task efficiency, each UAV predicts the movements of others based on shared positional information. When UAVs are close, they actively avoid overlapping task areas to prevent collisions and reduce redundant detections, thereby improving overall system performance.

In this work, we utilize 5G New Radio (NR) Vehicle-to-Everything (V2X) as the communication module. Specifically, the UAVs connect with each other and exchange information via 5G NR Vehicle-to-Vehicle (V2V) communication.

Above all, the joint path planning of the multi-UAV system in mountainous search scenarios faces several challenges. First, the complex and uncertain terrain requires dynamic trajectory adjustments to maximize area coverage. Second, UAVs must collaboratively plan their paths to maximize the coverage rate on the visitation map $M_V\left(t\right)$ within the limited mission time $T_{\mathrm{end}}$, while ensuring collision avoidance among UAVs. Finally, flight altitude significantly affects the FOV and detection quality: lower altitudes limit coverage due to a narrow FOV, whereas higher altitudes may reduce detection accuracy. Therefore, the path planning strategy must balance these factors by maintaining each UAV’s altitude within the allowable range $[u_{z-\min },u_{z-\max }]$ to achieve maximal coverage in minimal time.

3.2. Methodology

This work adopts a model-based, data-driven hybrid methodology. Specifically, it integrates two approaches: (i) model-based approaches, which involve the energy, communication, and detection models of the UAV system for environment construction and constraint design, and (ii) data-driven approaches, which utilize data analysis and machine learning to extract environmental features and support decision-making. By combining these approaches, the proposed method aims to enhance model robustness and accuracy through the joint exploitation of theoretical knowledge and empirical data.

As Figure 2 shows, the data and system model units are separated in this framework. In the data unit, diverse terrain data is utilized to generate an elevation map dataset for training the feature extraction model and providing the environment sample for UAV detection tasks. In the system model, the energy consumption, communication, and UAV detection models are installed to be connected with the environment for policy updating.

With the aforementioned data and system models as inputs, the core component of the proposed framework is a feature-aware MARL module, with which UAVs interact with the environment and learn trajectory planning policies. The proposed FA-EIMARL algorithm is detailed in Section 5. In a multi-agent Markov Decision Process (MDP), the key elements include agents, observations, actions, and rewards. To improve performance and generalization, we incorporate a feature extraction module into the MARL framework. In addition, an elite imitation strategy is introduced to enhance convergence speed and training stability. To further accelerate the computation of detection quality during environment interactions, we employ a DQPN architecture as a surrogate model for real-time prediction, avoiding costly explicit evaluations.

The following subsections provide a detailed explanation of these components.

As described earlier, the environment in this work is a collaborative multi-UAV system, where each UAV functions as an autonomous agent. An observation represents the state information perceived by a UAV from the environment, including its own position, destination coordinates, task progress indicators, and the current status of the visitation map. Observations define the agent’s state space. The action space consists of velocity components along the x, y, and z axes, allowing UAVs to adjust their trajectories in 3D space. The reward function provides feedback from the environment to guide learning. It captures multiple factors such as flight altitude, energy consumption, detection quality, task process, and penalties for boundary violations and collisions. The feature module processes data through a feature extraction network to obtain scenario-relevant representations that enhance policy learning and generalization. The UAVs learn policies that map observations and extracted features to actions, to maximize cumulative long-term rewards. During each iteration of the FA-EIMARL algorithm, agents select actions based on their current observations, extracted features, and learned policies. They then interact with the environment, receive corresponding rewards, and observe the resulting states, enabling continuous policy updates.

4. System Model

This section presents the energy consumption model, the communication model, and the formal problem formulation.

4.1. Energy Consumption

We assume that the total energy consumption includes the computational, communication, and flight energy consumption. The cumulative energy consumption $E(i,t)$ from task start to time t can be represented as

$$\mathcal{E}(i,t)={\mathcal{E}}_{\mathrm{cmp}}(i,t)+{\mathcal{E}}_{\mathrm{comm}}(i,t)+{\mathcal{E}}_{\mathrm{fly}}(i,t),$$

(1)

where ${\mathcal{E}}_{\mathrm{cmp}}(i,t)$, ${\mathcal{E}}_{\mathrm{comm}}(i,t)$, and ${\mathcal{E}}_{\mathrm{fly}}(i,t)$ represent the cumulative computation, communication, and flight energy consumption of ${\mathrm{UAV}}_i$, respectively.

The UAV’s cumulative computational energy consumption ${\mathcal{E}}_{\mathrm{cmp}}(i,t)$ can be represented as

$${\mathcal{E}}_{\mathrm{cmp}}(i,t)={\int }_0^t{P}_{\mathrm{cmp}}\mathrm{d}t,$$

(2)

$$P_{\mathrm{cmp}}=P_{\mathrm{static}}+P_{\mathrm{dynamic}}$$

(3)

$$P_{\mathrm{dynamic}}\approx C^{\ast }·V^2·f^{\ast }·{\alpha }^{\ast }$$

(4)

where $P_{\mathrm{cmp}}$ represents UAV computational power, $P_{\mathrm{static}}$ represents the static power of the computing module, $P_{\mathrm{dynamic}}$ represents the dynamic power of the computing module, $C^{*}$ represents the load capacitance, V represents voltage, $f^{*}$ represents clock frequency, and ${\alpha }^{*}$ represents the activity factor.

$${\mathcal{E}}_{\mathrm{comm}}(i,t)={\int }_0^t{P}_{\mathrm{comm}}\mathrm{d}t,$$

(5)

$$P_{\mathrm{comm}}=P_{\mathrm{TX}}+P_{\mathrm{RX}}=P_{\mathrm{TX}}(1+{\displaystyle \frac{G_t{G}_r}{\mathcal{L}}}),$$

(6)

where the constant $P_{\mathrm{comm}}$ represents the UAV communication power, $P_{\mathrm{TX}}$ represents UAV transmission power, $P_{\mathrm{RX}}$ represents UAV receiving power, $G_t$ represents transmission antenna gain, $G_r$ represents receiving antenna gain, and $\mathcal{L}$ represents system average path loss.

The UAV’s cumulative flight energy consumption ${\mathcal{E}}_{\mathrm{fly}}(i,t)$ can be represented as

$${\mathcal{E}}_{\mathrm{fly}}(i,t)={\int }_0^t{P}_{\mathrm{fly}}(i,t)\mathrm{d}t,$$

(7)

where $P_{\mathrm{fly}}(i,t)$ denotes the flight power of ${\mathrm{UAV}}_i$ at time t, which depends on the UAV’s structural parameters and flying speed. The detailed derivation is grounded in References [56,57], and it can be expressed as

$$P_{fly}(i,t)=\left\{\begin{array}{cc}{\displaystyle \frac{m_{\mathrm{UAV}}{g}^{3/2}}{\sqrt{2{\rho }_{\mathrm{air}}{A}_{\mathrm{UAV}}}\eta }},\hfill & \left|\mathit{v}(i,t)\right|<v_{\mathrm{th}},\hfill \\ c_1{\left|\mathit{v}(i,t)\right|}^2+{\displaystyle \frac{c_2}{g^2}}{\displaystyle \frac{{\left|\mathit{a}(i,t)\right|}^2}{\left|\mathit{v}\right(i,t\left)\right|}}+{\displaystyle \frac{2c_2}{g}}{\displaystyle \frac{{\mathit{a}}_z(i,t)}{\left|\mathit{v}\right(i,t\left)\right|}}+\hfill \\ c_2{\displaystyle \frac{v_x^2(i,t)+v_y^2(i,t)}{{\left|\mathit{v}(i,t)\right|}^3}}+mg\left|\mathit{v}(i,t)\right|+{\displaystyle \frac{1}{2}}m{\left|\mathit{a}(i,t)\right|}^2,\hfill & \left|\mathit{v}(i,t)\right|\ge v_{\mathrm{th}},\hfill \end{array}\right.$$

(8)

where $m_{\mathrm{UAV}}$ denotes the mass of the UAVs, g is the gravitational acceleration, ${\rho }_{\mathrm{air}}$ denotes the air density, $A_{\mathrm{UAV}}$ is the frontal area of the UAV, $\eta$ is the mechanical efficiency, $c_1$ and $c_2$ represent the drag and lift coefficients, respectively, and $\mathit{v}(i,t)$ denotes the velocity vector of ${\mathrm{UAV}}_i$ at time t. Components $v_x(i,t)$ and $v_y(i,t)$ represent the UAV’s velocity in the x and y directions, respectively. Component $\mathit{a}(i,t)$ represents the acceleration of ${\mathrm{UAV}}_i$, and $a_z(i,t)$ represents the z axis direction of the acceleration of ${\mathrm{UAV}}_i$. A speed threshold $v_{\mathrm{th}}$ is defined to distinguish between flying and hovering states, which differ significantly in terms of energy consumption. Parameters $c_1$, $c_2$, and $A_{\mathrm{UAV}}$ are given by

$$c_1={\displaystyle \frac{1}{2}}\rho ·A_{\mathrm{UAV}}·C_d,$$

(9)

$$c_2={\displaystyle \frac{m_{\mathrm{UAV}}^2}{\eta ·{\rho }_{\mathrm{air}}·n_{\mathrm{prp}}·\pi R_{\mathrm{prp}}^2}},$$

(10)

$$A_{\mathrm{UAV}}=A_{\mathrm{surf}}+n_{\mathrm{prp}}\pi R_{\mathrm{prp}}^2,$$

(11)

where $C_d$ denotes the air viscosity coefficient, $n_{\mathrm{prp}}$ denotes the number of UAV propellers, $R_{\mathrm{prp}}$ denotes the radius of the UAV propellers, and $A_{\mathrm{surf}}$ denotes the UAV surface area.

The remaining battery $\mathcal{B}(i,t)$ can be presented as

$$\mathcal{B}(i,t)={\mathcal{B}}^{\ast }-\mathcal{E}(i,t),$$

(12)

where ${\mathcal{B}}^{\ast }$ represents the battery capacity.

4.2. Communication

We assume that the communication among UAVs follows the 5G NR V2X standard as the underlying communication module.

The communication protocol consists of the following procedures:

• Each UAV periodically broadcasts its current geographic position and the updated visitation map to nearby UAVs according to a predefined broadcast interval $t_d$ in order to improve mission efficiency and avoid collisions.
• ${\mathrm{UAV}}_i$ continuously transmits the detection data to the remote mountain base stations. Upon successful reception, the base stations return an acknowledgment message to ${\mathrm{UAV}}_i$. If no acknowledgment is received within a certain timeout period $t_f$, ${\mathrm{UAV}}_i$ initiates retransmission.
• If retransmission attempts fail $n_f$ times and no acknowledgment is received, ${\mathrm{UAV}}_i$ sends a request to the nearest ${\mathrm{UAV}}_j$. Once ${\mathrm{UAV}}_j$ confirms the request, a communication link is established between the two UAVs. The data is then relayed to ${\mathrm{UAV}}_j$, which attempts to forward the information to the base station.

As for the channel model, we should firstly talk about the path loss $\mathcal{PL}$. Due to the large coverage area of the sensing region, the communication environment is highly complex, involving both Line-of-Sight (LoS) and Non-Line-of-Sight (NLoS), two communication modes. As with the 3GPP standard [58], $\mathcal{PL}$ can be represented as

$$\mathcal{PL}=\left\{\begin{array}{cc}28.0+22{log}_{10}\left(d_{\mathrm{TS}}\right)+20{log}_{10}\left(f_c\right)\hfill & LoS,\hfill \\ & \\ -17.5+20{log}_{10}\left({\displaystyle \frac{40\pi f_c}{3}}\right)+[46-71{log}_{10}\left(EL(u_x,u_y)\right)]{log}_{10}\left(d_{\mathrm{TS}}\right),\hfill & NLoS,\hfill \end{array}\right.$$

(13)

where $f_c$ represents the carrier frequency of the transmitters, and $d_{\mathrm{TS}}$ represents the distances between transmitters and receivers.

The received signal strength at the UAV or base station can be expressed as

$$\mathcal{S}=P_{\mathrm{comm}}-\mathcal{PL}=P_{\mathrm{TX}}(1+{\displaystyle \frac{G_t{G}_r}{\mathcal{L}}})-\mathcal{PL}.$$

(14)

To evaluate the quality of the received signal, we use the signal-to-noise ratio (SNR) as the metric, which is defined as

$$SNR={\displaystyle \frac{\mathcal{S}}{P_{\mathrm{thermal}}}},$$

(15)

where $P_{\mathrm{thermal}}$ represents the thermal noise, which can be denoted as

$$P_{\mathrm{thermal}}=k_B\times T_K\times Bw,$$

(16)

where $k_B$ represents Boltzmann constant, $T_K$ represents temperature in Kelvin, and $Bw$ represents bandwidth.

4.3. UAV Detection

To facilitate computation and assessment of UAV sensing quality, the detection plot is divided into $n_{\mathrm{grid}}\times n_{\mathrm{grid}}$ grids, as shown in Figure 3, which can be represented as $G=G_{0,0},G_{0,1}\dots ,G_{0,n_{\mathrm{grid}}}$.

The sensing quality of each grid is determined based on the UAV’s distance and viewing angle relative to the grid. The overall sensing quality of the plot is then obtained by aggregating the evaluation of all grids. Considering the mountainous terrain, the center height of each grid cell varies. Therefore, accurate distance estimation between the UAV and each grid cell requires LiDAR-based elevation sensing. Assume that the distance between gird $G_{l,m}$ and the task UAV can be denoted as $d_G(l,m)$. We define a distance threshold $d_{th}$. If the actual average distance $d_G(l,m)$ exceeds $d_{th}$ (i.e., $d_G(l,m)>d_{th}$), the sensing quality is considered poor; otherwise, it is deemed acceptable.

Meanwhile, as illustrated in Figure 4, the UAV sensing task must also consider the FOV. Specifically, we define a sensing angle threshold ${\theta }_f$. If the angle between the UAV’s Line-of-Sight and the normal direction ${\theta }_g(l,m,t)$ of the grid $G_{l,m}$ at time t exceeds ${\theta }_f$, the sensing quality is considered poor. The detection quality of each grid $G_{l,m}$ can be denoted as ${\mathcal{Q}}_{l,m,t}$. In this context, the detection quality ${\mathcal{Q}}_{\mathrm{overall}}(i,j,t)$ of the whole detection plot ${\mathrm{DP}}_{i,j}$ at time t can be represented as

$${\mathcal{Q}}_{\mathrm{overall}}(i,j,t)={\displaystyle \frac{{\sum }_{l=0}^{n_{\mathrm{grid}}}{\sum }_{m=0}^{n_{\mathrm{grid}}}\mathcal{Q}(l,m,t)}{n_{\mathrm{grid}}^2}},$$

(17)

We define a sensing quality threshold $\mathcal{Q}\mathrm{th}$. If the quality metric ${\mathcal{Q}}_{\mathrm{overall}}(i,j)$ does not exceed this threshold (i.e., ${\mathcal{Q}}_{\mathrm{overall}(i,j,t)}<\mathcal{Q}\mathrm{th}$), the sensing is considered unsuccessful.

4.4. Problem Formulation

In this work, the overall performance of the multi-UAV collaborative system is evaluated by jointly considering detection coverage effectiveness, appropriate flight altitude, energy consumption, and collision avoidance. To simplify computation, the time domain is discretized into uniform time steps of duration $t_{\mathrm{step}}$, with the discrete index denoted by k.

The detection coverage rate $M_V\left(t\right)$ at time t can be represented as

$$M_V\left(t\right)=\sum _{i=0}^{n_{\mathrm{x}}}\sum _{j=0}^{n_{\mathrm{y}}}{Q}_{\mathrm{overall}}(i,j,t),$$

(18)

We assume that the incremental detection coverage rate contributed by ${\mathrm{UAV}}_i$ at each time step k can be represented as $m_V(i,k)$. The final detection coverage rate $M_V\left(K_{\mathrm{end}}\right)$ can be expressed as

$$M_V\left(K_{\mathrm{end}}\right)=\sum _{i=0}^{n_{\mathrm{x}}}\sum _{j=0}^{n_{\mathrm{y}}}{Q}_{\mathrm{overall}}(i,j,K_{\mathrm{end}})=\sum _{i=0}^{n_{\mathrm{UAV}}}\sum _{k=0}^{K_{\mathrm{end}}}{m}_V(i,k),$$

(19)

$$K_{\mathrm{end}}=\lfloor {\displaystyle \frac{T_{\mathrm{end}}}{t_{\mathrm{step}}}}\rfloor ,$$

(20)

where $K_{\mathrm{end}}$ represents the discretized task completion time.

Once $M_V\left(k\right)$ exceeds $M_{\mathrm{th}}$, we consider the detection to be sufficiently comprehensive, and the task can be terminated early.

If at time step k, ${\mathrm{UAV}}_i$ visits a detection plot that has already been successfully sensed, the action is considered redundant and incurs a penalty $\mathcal{PR}$. The total number of redundant visits $N_{\mathrm{redundant}}^{\left(i\right)}$ made by ${\mathrm{UAV}}_i$ during the entire detection process can be defined as

$$N_{\mathrm{redundant}}^{\left(i\right)}=\sum _{k=0}^{K_{\mathrm{end}}}\mathbb{I}\left({\mathrm{DP}}_i\left(k\right)\in {\mathcal{DP}}_{\mathrm{visited}}\right),$$

(21)

where $\mathbb{I}(·)$ represents the indicator function, ${\mathrm{DP}}_i\left(k\right)$ represents the DP visited by ${\mathrm{UAV}}_i$ at time step k, and ${\mathcal{DP}}_{\mathrm{visited}}$ represents the set of visited DPs. In this context, the total penalty ${\mathcal{PR}}_{\mathrm{redundant}}$ caused by redundant visits during the entire detection process can be expressed as

$${\mathcal{PR}}_{\mathrm{redundant}}=\mathcal{PR}·(\sum _{i=0}^{n_{\mathrm{UAV}}}{N}_{\mathrm{redundant}}^{\left(i\right)}).$$

(22)

To describe the performance of ${\mathrm{UAV}}_i$ in maintaining flight altitude, the parameter $H_d\left(i\right)$ is defined as

$$H_d\left(i\right)=\sum _{k=0}^{K_{\mathrm{end}}-1}\left(h_d(i,k+1)-h_d(i,k)\right),$$

(23)

$$h_d(i,t)=u_z(i,t)-{\displaystyle \frac{u_{z-\min }+u_{z-\max }}{2}},$$

(24)

where $h_d(i,t)$ represents the height difference between the altitude of ${\mathrm{UAV}}_i$ at time t and the midpoint of the assumed flight altitude range.

The penalty ${\mathcal{PH}}_{\mathrm{height}}$ of flying at an inappropriate height can be expressed as

$${\mathcal{PH}}_{\mathrm{height}}=\mathcal{PH}·\sum _{i=0}^{n_{\mathrm{UAV}}}{H}_d\left(i\right),$$

(25)

where $\mathcal{PH}$ represents the penalty parameter.

To avoid UAVs from flying out of the task space, a penalty parameter $\mathcal{PO}$ is set. ${\mathrm{UAV}}_i$ denotes the total number $N_{\mathrm{flyout}}^{\left(i\right)}$ of UAVs flying out, which can be represented as

$$N_{\mathrm{flyout}}^{\left(i\right)}=\sum _{k=0}^{K_{\mathrm{end}}-1}\mathbb{I}(u(i,k)\notin {\mathbb{R}}^3),$$

(26)

The total penalty ${\mathcal{PO}}_{\mathrm{flyout}}$ caused by flying out of the task space throughout the detection process can be expressed as

$${\mathcal{PO}}_{\mathrm{flyout}}=\mathcal{PO}·(\sum _{i=0}^{n_{\mathrm{UAV}}}(N_{\mathrm{flyout}}^{\left(i\right)})),$$

(27)

To prevent UAV collisions and to improve efficiency by avoiding the clustering of multiple UAVs in the same region, a distance function $d_{\mathrm{UAV}}(i,t)$ is defined to represent the distance between ${\mathrm{UAV}}_i$ and its nearest neighboring UAV at time t. A penalty coefficient $\mathcal{PN}$ is defined to evaluate the duration and severity of danger triggered by a UAV. The penalty ${\mathcal{PN}}_{\mathrm{near}}$ for ${\mathrm{UAV}}_i$ can then be expressed as

$${\mathcal{PN}}_{\mathrm{near}}=\mathcal{PN}·(\sum _{k=1}^{K_{\mathrm{end}}}\mathbb{I}(d_{\mathrm{UAV}}(i,k)<d_{\mathrm{safety}}))(d_{\mathrm{UAV}}(i,k-1)-d_{\mathrm{UAV}}(i,k)),$$

(28)

To further prevent collisions between UAVs, a penalty parameter $\mathcal{PC}$ is set. The total number $N_{\mathrm{collision}}^{\left(i\right)}$ of ${\mathrm{UAV}}_i$ flying out can be represented as

$$N_{\mathrm{collision}}^{\left(i\right)}=\sum _{k=0}^{K_{\mathrm{end}}-1}\mathbb{I}(u(i,k)=u(j,k)|j\in [0,n_{\mathrm{UAV}}]),$$

(29)

The total penalty ${\mathcal{PC}}_{\mathrm{collision}}$ caused by UAV collisions throughout the detection process can be expressed as

$${\mathcal{PC}}_{\mathrm{collision}}=\mathcal{PC}·(\sum _{i=0}^{n_{\mathrm{UAV}}}(N_{\mathrm{collision}}^{\left(i\right)})),$$

(30)

In addition, the total energy consumption ${\mathcal{E}}_{\mathrm{consumption}}$ of the multi-UAV collaborative system can be expressed as

$${\mathcal{E}}_{\mathrm{consumption}}=\sum _{i=0}^{n_{\mathrm{UAV}}}{\int }_0^t\mathcal{E}(i,t)dt=\sum _{i=0}^{n_{\mathrm{UAV}}}\sum _{k=0}^{K_{\mathrm{end}}}\mathcal{E}(i,k).$$

(31)

The objective of our optimization problem is to jointly maximize the coverage rate but minimize the energy, while flying at an inappropriate height, avoiding flying out of the task space, flying near other UAVs, and avoiding collisions. We include the trajectory planning variable $\mathit{v}(i,k)$ as our decision variable. The optimization problem is formulated as follows:

$$\begin{array}{cc}\hfill \mathrm{Pro}:& \underset{\mathit{v}(i,t)}{max}{\alpha }_1·M_V\left(K_{\mathrm{end}}\right)-{\mathcal{PR}}_{\mathrm{redundant}}-{\mathcal{PR}}_{\mathrm{height}}-{\mathcal{PO}}_{\mathrm{flyout}}\hfill \\ \hfill & -{\mathcal{PN}}_{\mathrm{near}}-{\mathcal{PC}}_{\mathrm{collsion}}-{\alpha }_2·{\mathcal{E}}_{\mathrm{consumption}},\hfill & \hfill \left(32\mathrm{a}\right)\\ \hfill \mathrm{s}.\mathrm{t}.& \mathit{u}(i,k+1)=\mathit{u}(i,k)+\mathit{v}(i,k),\forall k\in \left[0,K_{\mathrm{end}}\right],\hfill & \hfill \left(32\mathrm{b}\right)\\ \hfill & 0\le v_x(i,k)\le v_{\mathrm{horizon}},\hfill & \hfill \left(32\mathrm{c}\right)\\ \hfill & 0\le v_y(i,k)\le v_{\mathrm{horizon}},\hfill & \hfill \left(32\mathrm{d}\right)\\ \hfill & 0\le v_z(i,k)\le v_{\mathrm{vertical}},\hfill & \hfill \left(32\mathrm{e}\right)\\ \hfill & \mathit{u}(i,0)={\mathit{u}}_{\mathrm{start}}\left(i\right),\hfill & \hfill \left(32\mathrm{f}\right)\\ \hfill & \mathit{u}(i,k)\in {\mathbb{R}}^3:\{x\in [u_{x-\min },u_{x-\max }],y\in [u_{y-\min },u_{y-\max }],\hfill \\ \hfill & z-EL(x,y)\in [u_{\{z-\min },u_{z-\max }]\},\hfill & \hfill \left(32\mathrm{g}\right)\\ \hfill & \mathcal{B}(i,k)\ge 0,\hfill & \hfill \left(32\mathrm{h}\right)\end{array}$$

where parameters ${\alpha }_1$ and ${\alpha }_2$ represent the weights assigned to different factors affecting task performance. Equation (32b) describes the relationship between the UAV’s position and velocity. Equations (32c), (32d), and (32e) ensure that UAV velocities remain within their maximum limits. Equation (32f) specifies the UAVs’ starting positions. Equation (32g) enforces that UAVs stay within the task space boundaries. Finally, Equation (32h) ensures that the UAVs do not run out of battery.

5. Feature-Aware Elite Imitation Multi-Agent Reinforcement Learning

This section introduces the proposed DQPN architecture and FA-EIMARL algorithm.

5.1. Multi-Agent Markov Decision Process

To solve Equations (32a)–(32h) through MARL, a multi-agent Markov Decision Process (MDP) is designed as follows:

• Observation of Each Agent $o_{i,k}$: In the considered scenario, the observation space should provide information of UAVs, including their current positions, the nearest UAV position and the distances between them, the detection status of PDs near the UAV, remain power, and the system coverage rate. The observation space can be represented as ${\mathit{o}}_{i,k}=\{u(i,k),u(j_n,k),d_{\mathrm{UAV}}(i,k),\left[\mathrm{DP}(i,k)\right],\mathcal{B}(i,k),M_V\left(k\right)\}$ where $j_n$ represents the nearest UAV of ${\mathrm{UAV}}_i$, and $\left[\mathrm{DP}\right(i,k\left)\right]$ represents the detection status of PDs near the ${\mathrm{UAV}}_i$.
• Action of Each Agent $a_{i,k}$: The action space, which describes the speed in the x, y, and z direction of ${\mathrm{UAV}}_i$, can be expressed as ${\mathit{a}}_{i,k}=\{v_x(i,k),v_y(i,k),v_z(i,k)\}$.
• Feature of the Environment $f_{i,k}$: The feature space describes the scenario features agent i obtains, which is introduced in Section 5.4.
• Reward of Each Agent $r_{i,k}$: The reward serves as the environmental feedback received by agent i when observing $\mathit{o}i,k$, extracting features $fi,k$, and executing action $\mathit{a}i,k$. Similarly to the objective function Pro in Equation (32a), the reward $ri,k$ guides UAV_i to improve detection coverage, maintain suitable flight altitude, reduce energy consumption, and avoid collisions. As shown in Equations (18) to (31), the reward can be defined as

  $$\begin{array}{c}\hfill r_{i,k}={\alpha }_1·[m_V(i,k)-m_V(i,k-1)]-\mathcal{PR}·\mathbb{I}(D{P}_i\left(k\right)\in {\mathcal{DP}}_{\mathrm{visited}})-\mathcal{PH}·H_d\left(i\right)\\ \hfill -\mathcal{PO}·\mathbb{I}(u(i,k)\in {\mathbb{R}}^3)-\mathcal{PN}·\mathbb{I}(d_{\mathrm{UAV}}(i,k)<d_{\mathrm{safety}}))(d_{\mathrm{UAV}}(i,k-1)-d_{\mathrm{UAV}}(i,k))\\ \hfill -\mathcal{PC}·\mathbb{I}(u(i,k)=u(j,k)|j\in [0,n_{\mathrm{UAV}}])-{\alpha }_2·\mathcal{E}(i,k).\end{array}$$

  (33)
• Set of Actions ${\mathit{A}}_k$: ${\mathit{A}}_k$ denotes the set of actions available to all agents at time step k, which can be formulated as

  $$A_k=\{a_{1,k},a_{2,k},...,a_{n_{\mathrm{UAV}},k}\},$$

  (34)
• The Return of Each Agent $R_i$: The objective of agent i’s policy is to maximize the expected cumulative reward, which is defined as

  $$R_i=\sum _{k=0}^{k_{\mathrm{end}}}{\gamma }^{k-1}{r}_{i,k},$$

  (35)

  where $\gamma$ denotes the discount factor that balances immediate and future rewards, with a value range of $\gamma \in [0,1]$. In long-term strategies, future rewards are expected to play a more significant role than immediate ones. Accordingly, the influence of immediate rewards gradually diminishes over time, as the term ${\gamma }^{k-1}$ decreases with increasing time step k.

5.2. Detection Quality Prediction Network

To simplify computation and reduce UAV inference time, we designed a DEPN to predict the detection quality of UAVs. The architecture of the DEPN is illustrated in Figure 5. The DEPN consists of convolutional layers and fully connected layers.

We generated a dataset ${\mathcal{S}}_p$ using the real terrain information and computed the real detection value. During the training process, we input a batch size $n_{\mathrm{batch}}$ of sample matrix $S_{pm}$, which consists of state vectors $S_{pv}$ for different samples of DPs. The state vector is composed of the UAV’s altitude difference relative to the lowest grid cell $G_{\mathrm{lowest}}$, the horizontal offset between the ${\mathrm{UAV}}_i$ and a reference grid cell $G_{0,0}$, and the altitude differences between $G_{\mathrm{lowest}}$ and the four corner grids, as well as the center grid at time t. It can be expressed as

$$\begin{array}{cc}\hfill S_{pv}=& \{[u_z(i,t)-EL\left(G_{\mathrm{lowest}}\right)],[u_x(i,t)-x\left(G_{0,0}\right)],[u_y(i,t)-y\left(G_{0,0}\right)],\hfill \\ & [EL\left(G_{0,0}\right)-EL\left(G_{\mathrm{lowest}}\right],[EL(G_{0,n_{\mathrm{grid}}})-EL\left(G_{\mathrm{lowest}}\right],[EL(G_{n_{\mathrm{grid}},0})-EL\left(G_{\mathrm{lowest}}\right]\},\hfill \\ & [EL(G_{n_{\mathrm{grid}},n_{\mathrm{grid}})}-EL\left(G_{\mathrm{lowest}}\right],[EL(G_{n_{{\displaystyle \frac{\mathrm{grid}}{2}}},n_{{\displaystyle \frac{\mathrm{grid}}{2}}}})-EL\left(G_{\mathrm{lowest}}\right]\}.\hfill \end{array}$$

(36)

We constructed a sample set $S_{pm}$ using various DP data points and computed the real ground detection effectiveness value $V_p$ for the dataset according to Equation (17). In this situation, we define $V_p=\{v_{p1},v_{p2},\dots ,v_{p{n}_{batch}}\}$, where $v_{pi}$ represents the ith sample. The system’s loss function can thus be defined as

$${\mathcal{J}}_{\mathrm{DQPN}}=\left|\right|V_p-V_r{\left|\right|}^2,$$

(37)

where $v_r$ represents the real detection quality value.

During actual UAV task execution, the estimation value $v_p$ is obtained directly by feeding the DP information as input into the DEPN module, denoted as $s_{pv}$.

We trained the DQPN ${\mathcal{N}}_{\mathrm{DQPN}}\left(S_{pm}\right|S_{pv})$ module by minimizing this loss function. Assuming the maximum epoch is ${\lambda }_{\max }$, the detailed training procedure is described as in Algorithm 1:

Algorithm 1 Detection Quality Prediction Model Generation

1: Input: The terrain dataset ${\mathcal{S}}_p$.   2: Initialize the DQPN ${\mathcal{N}}_{\mathrm{DQPN}}\left(S_{pm}\right|S_{pv})$ module.   3: for epoch $\lambda =1,2,\dots ,{\lambda }_{\max }$ do   4:    Extract a batch size $n_{\mathrm{batch}}$ of $S_{pm}$ from ${\mathcal{S}}_p$.   5:    Computation the Real value $V_r$ of $S_{pm}$.   6:    Input $S_{pm}$ to ${\mathcal{N}}_{\mathrm{DQPN}}\left(S_{pm}\right|S_{pv})$ to generate $V_p$.   7:    Compute the loss as Equation (37).   8:    Update ${\mathcal{N}}_{\mathrm{DQPN}}\left(S_{pm}\right|S_{pv})$.   9: end for 10: return The detection quality prediction model $mathcal{N}_{\mathrm{DQPN}}\left(S_{pv}\right)$.

5.3. Elite Imitation Mechanism

To accelerate the training process and enable agents to learn from high-performing individuals, we propose an elite imitation module. This mechanism is designed to help agents escape prolonged periods of low-reward exploration by imitating elite behavior.

We introduce a mimicry cycle factor, denoted by $\delta$. During certain episodes determined by this factor, each agent i does not update its policy network ${\pi }_i\left(\theta \right)$ directly. Instead, it generates action sequences ${\mathcal{A}}_i\{=a_{i,0},a_{i,1},\dots ,a_{i,K_{\mathrm{end}}}\}$ and interacts with the environment to obtain a corresponding reward vector ${\mathcal{R}}_i=\{r_{i,0},r_{i,1},\dots ,r_{i,K_{\mathrm{end}}}\}$.

The elite policy is then identified based on the mean ${\mu }_i$ and variance ${\sigma }^2$ of the rewards in ${\mathcal{R}}_i$. The evaluation metric can be defined as

$${\mathcal{RE}}_i={\beta }_1{\mu }_i+{\beta }_2{\sigma }^2.$$

(38)

Specifically, we select the agent $i^{\prime }$ with the best-performing reward profile as the elite individual.

Other agents update their policy networks by soft copying from the elite policy using a soft update parameter $\vartheta$. The update rule is formulated as

$${\theta }_i=(1-\vartheta ){\theta }_i+\vartheta {\theta }_i^{\prime },$$

(39)

where ${\theta }_i^{\prime }$ and ${\theta }_i$ denote the parameters of the elite and regular agents’ policy networks, respectively.

Furthermore, to maintain a certain level of exploration while benefiting from the elite imitation strategy, we gradually adjust the influence of the imitation process. Specifically, we gradually decrease $\vartheta$ and increase $\delta$. We initialize the values of $\vartheta$ and $\delta$ as ${\vartheta }^{\ast }$ and ${\delta }^{\ast }$. The detailed procedure of this algorithm is shown in Algorithm 2.

Algorithm 2 Elite Imitation Mechanism

1: Initialize policy network ${\pi }_i\left(\theta \right)$ for each agent i.   2: Initialize $\vartheta ={\vartheta }^{\ast }$ and $\delta ={\delta }^{\ast }$.   3: for episode ${\lambda }^{\prime }=1,2,\dots ,{\lambda }_{\max }^{\prime }$ do   4:    if ${\lambda }^{\prime }\mid \delta$ then   5:      for agent $i=1,2,\dots ,n_{\mathrm{UAV}}$ do   6:         Generate ${\mathcal{A}}_i$ from ${\pi }_i\left(\theta \right)$.   7:         Obtain Reward ${\mathcal{R}}_i$ from the interaction between agent i and the environment.   8:      end for   9:      Compute the maximum reward evaluation parameter ${\mathcal{RE}}_i$ as Equation (38). 10:      Update ${\pi }_i\left(\theta \right)$ as Equation (39). 11:      Update parameters $\vartheta ={\displaystyle \frac{1}{2}}\vartheta$ and $\delta =2\delta$. 12:    end if 13: end for

5.4. Feature-Aware MARL

To simulate the continuity of UAV actions, the proposed FA-MARL adopts an actor–critic framework. With the integration of environmental features $f_{i,k}$, the traditional actor–critic structure is extended by incorporating $f_{i,k}$ into the input of the critic network. Consequently, the critic estimates the action–state–feature value, denoted as $V(o_{i,k},a_{i,k},f_{i,k})$.

Let ${\mathcal{A}}_{\mathcal{B}}$, ${\mathcal{S}}_{\mathcal{B}}$, ${\mathcal{R}}_{\mathcal{B}}$, ${\mathcal{F}}_{\mathcal{B}}$, and ${\mathcal{S}}_{\mathcal{B}}^{\prime }$ denote the actions, states, rewards, environmental features, and next states in a sampled batch of experience, respectively. The policy (i.e., actor network) for agent i is represented by ${\pi }_i({\mathcal{S}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}})$.

To improve training stability and performance, two critic networks are employed, ${\mathcal{Q}}_1({\mathcal{S}}_{\mathcal{B}},{\mathcal{A}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}})$ and ${\mathcal{Q}}_2({\mathcal{S}}_{\mathcal{B}},{\mathcal{A}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}})$, along with their corresponding target critic networks, ${\mathcal{Q}}_1^{\prime }({\mathcal{S}}_{\mathcal{B}},{\mathcal{A}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}})$ and ${\mathcal{Q}}_2^{\prime }({\mathcal{S}}_{\mathcal{B}},{\mathcal{A}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}})$, which periodically copy parameters from their respective primary critic networks.

The enhanced actor–critic learning process for each agent i can then be implemented through the following steps:

• Initialize the update parameter for actor network $\theta$, the update parameters for critic networks ${\varphi }_1$ and ${\varphi }_2$, and the update parameters for target critic networks ${\varphi }_1^{\prime }$ and ${\varphi }_2^{\prime }$. Initialize the replay buffer $\mathcal{D}$.
• During an episode ${\lambda }^{\prime }$, let agent i interact with the environment and store observation ${\mathit{o}}_{i,k}$, action $a_{i,k}$, rewards $r_{i,k}$, and features $f_{i,k}$ to the replay buffer $\mathcal{D}$.
• Randomly sample one batch of data ${\mathcal{A}}_{\mathcal{B}}$, ${\mathcal{S}}_{\mathcal{B}}$, ${\mathcal{R}}_{\mathcal{B}}$, ${\mathcal{F}}_{\mathcal{B}}$, and ${\mathcal{S}}_{\mathcal{B}}^{\prime }$ from $\mathcal{D}$.
• Use the target critic networks and the current policy to compute the target value. Specifically, the target Q-values ${\mathcal{Y}}_{\mathcal{Q}}$ are calculated using the minimum of the two target critics, following the Clipped Double Q-learning strategy to mitigate overestimation bias. The formulation is as follows:

  $${\mathcal{Y}}_{\mathcal{Q}}={\mathcal{R}}_{\mathcal{B}}+\gamma min\left\{{\mathcal{Q}}_1^{\prime }({\mathcal{S}}_{\mathcal{B}}^{\prime },{\mathcal{A}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}}),{\mathcal{Q}}_2^{\prime }({\mathcal{S}}_{\mathcal{B}}^{\prime },{\mathcal{A}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}})\right\}.$$

  (40)
• Minimize the mean squared error (MSE) between the predicted Q-values and the target Q-values for the critic update. We update the primary and secondary critic networks by minimizing the loss function ${\mathcal{J}}_{\mathcal{Q}i}\left(\varphi \right)$:

  $${\mathcal{J}}_{\mathcal{Q}i}\left(\varphi \right)=\mathbb{E}\left[{\left({\mathcal{Q}}_i({\mathcal{S}}_{\mathcal{B}},{\mathcal{A}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}})-{\mathcal{Y}}_{\mathcal{Q}}\right)}^2\right],i\in \{1,2\},$$

  (41)

  where $\mathbb{E}[·]$ denotes the mathematical expectation.
• Update the actor network by maximizing the estimated Q-value from critic ${\mathcal{Q}}_1(·)$. The loss function ${\mathcal{J}}_{\pi }\left(\theta \right)$ is expressed as

  $${\nabla }_{\theta }{J}_{\pi }\left(\theta \right)=\mathbb{E}\left[{\nabla }_a{Q}_1({\mathcal{S}}_{\mathcal{B}},{\mathcal{A}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}}){|}_{{\mathcal{A}}_{\mathcal{B}}={\pi }_i({\mathcal{S}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}})}·{\nabla }_{\theta }{\pi }_i\left(\theta \right)\right].$$

  (42)
• Softly update the target critic networks to ensure training stability. Instead of directly copying the weights, the target networks are updated using a weighted average of the current and previous target weights:

  $${\varphi }_i^{\prime }=\xi {\varphi }_i+(1-\xi ){\varphi }_i^{\prime },i\in \{1,2\},$$

  (43)

  where $\xi$ is the soft update parameter.
• Repeat steps 2–7 in all training iterations until the policy converges.

We now proceed to detail the specific steps of the proposed FA-MARL algorithm, which utilizes a pre-trained feature extraction network (FEN) ${\mathcal{N}}_{\mathrm{FEN}}(\tilde{S},\tilde{X},\tilde{K})$ to generate environmental features, where $\tilde{S}$, $\tilde{X}$, and $\tilde{K}$ denote a batch size $n_{\mathrm{batch}}^{\prime }$ of the task space, dynamic grid positions detected by UAVs, and the discrete time step. $\tilde{S}=\{\widetilde{s_0},\widetilde{s_1},\dots ,\tilde{s_{n_{\mathrm{batch}}^{\prime }}}\}$. $\tilde{X}=\{\widetilde{x_0},\widetilde{x_1},\dots ,\tilde{x_{n_{\mathrm{batch}}^{\prime }}}\}$. $\tilde{K}=\{\widetilde{k_0},\widetilde{k_1},\dots ,\tilde{k_{n_{\mathrm{batch}}^{\prime }}}\}$.

To pre-train the FEN, we first construct a dataset $\mathcal{M}$ composed of point array samples $\{\tilde{s},\tilde{x},\tilde{k}\}$. Each sample includes elevation data from $n_{\mathrm{sample}}$. The label of the sample can be represented as $\{\tilde{s},\tilde{x}\}$. Figure 6 shows the structure of the feature extraction model pre-training process. First, the input triplet $\{\tilde{S},\tilde{X},\tilde{K}\}$ is passed through the feature extraction layers to generate environmental features $f_{i,k}$ for each agent i. The output of this module, denoted as ${\mathcal{F}}^{\prime }(\tilde{S},\tilde{X},\tilde{K})$, is subsequently fed into a series of sequential layers to produce a vectorized label $\tilde{L}(\tilde{S},\tilde{X},\tilde{K})$.

This predicted label vector is then transformed into the expected label $\{{\tilde{S}}^{\prime },{\tilde{X}}^{\prime }\}$. Assuming the true label vector is $\{\tilde{S},\tilde{X}\}$ and the feature extraction network is parameterized by $\omega$ as ${\mathcal{N}}_{\mathrm{FEN}}(\tilde{S},\tilde{X},\tilde{K})$, the corresponding loss function ${\mathcal{J}}_F\left(\omega \right)$ is defined as

$${\mathcal{J}}_F\left(\omega \right)={∥\{\tilde{S},\tilde{X}\}-\{{\tilde{S}}^{\prime },{\tilde{X}}^{\prime }\}∥}^2,$$

(44)

where $∥·∥$ denotes the Euclidean distance.

In the proposed FA-MARL framework, the network ${\mathcal{N}}_{\mathrm{FEN}}(\tilde{S},\tilde{X},\tilde{K})$ is pre-trained for ${\lambda }_{\max }^{\ast }$ epochs to ensure reliable environmental feature extraction. After that, $\{\tilde{S},\tilde{X},\tilde{K}\}$ is sampled as batch input data. In each episode ${\lambda }^{\prime }$, agents perform detection tasks within random task spaces $\tilde{s}$, with corresponding dynamic ground observations $\tilde{x}$ at time $\tilde{k}$.

The output ${\mathcal{N}}_{\mathrm{FEN}}(\tilde{s},\tilde{x},\tilde{k})$ is used as the feature component $f(i,k)$ of agent i, which is computed as

$$f(i,k)={\beta }_{\mathrm{F}}·{\mathcal{N}}_{\mathrm{FEN}}(\tilde{s},\tilde{x},\tilde{k}),$$

(45)

where ${\beta }_{\mathrm{F}}$ is a feature normalization coefficient. The complete design of the proposed FA-EIMARL algorithm is detailed in Algorithm 3.

Algorithm 3 Feature-Aware Elite Imitation Multi-Agent Reinforcement Learning

1: Input:$\pi (·)$, ${\mathcal{Q}}_1(·)$, ${\mathcal{Q}}_2(·)$, ${\mathcal{Q}}_1^{\prime }(·)$, ${\mathcal{Q}}_{\mathcal{T}}^{\prime }2(·)$, ${\mathcal{Q}}_2^{\prime }(·)$, ${\mathcal{N}}_{\mathrm{FEN}}(·)$, and ${\mathcal{N}}_{\mathrm{DQPN}}(·)$.   2: Initialize $\theta$, ${\varphi }_1$, ${\varphi }_2$, ${\varphi }_1^{\prime }$, ${\varphi }_2^{\prime }$, and $\omega$.   3: Pre-train ${\mathcal{N}}_{\mathrm{DQPN}}(·)$ as Algorithm 1   4: for epoch ${\lambda }^{\ast }=1,2,\dots ,{\lambda }_{\max }^{\ast }$ do   5:    Sample $\{\tilde{S},\tilde{X},\tilde{K}\}$   6:    Update ${\mathcal{N}}_{\mathrm{FEN}(·)}$ as (44)   7: end for   8: Initialize replay buffer $\mathcal{D}$   9: for episode ${\lambda }^{\prime }=1,2,\dots ,{\lambda }_{\max }^{\prime }$ do 10:    Update elite imitation strategy as Algorithm 2. 11:    Sample $n_{ts}$ task space set $\widetilde{S^{\prime }}$ from $\tilde{S}$. 12:    for scenario $\tilde{s}\in \widetilde{S^{\prime }}$ do 13:      for Agent $i=1,2,\dots ,n_{\mathrm{UAV}}$ do 14:         Reset $o_{i,0}$, $a_{i,0}$, $r_{i,0}$, and $f_{i,0}$. 15:      end for 16:      for time step $k=1,2,\dots ,k_{\max }$ do 17:         Calculate the observed environmental feature as (45). 18:         Update $o_{i,k}$, $a_{i,k}$, $r_{i,k}$, and $f_{i,k}$. 19:         Update ${\mathcal{Q}}_1(·)$ and ${\mathcal{Q}}_2(·)$ as (41). 20:         Update $\pi (·)$ as (42) 21:         Update ${\mathcal{Q}}_1^{\prime }(·)$ and ${\mathcal{Q}}_2^{\prime }(·)$ as (43). 22:         if Task End, when $M_V\left(k\right)$$M_{\mathrm{th}}$> then 23:           Break 24:         end if 25:      end for 26:    end for 27: end fo 28: return Policy $\pi (·)$.

6. Simulation Results

This section illustrates the experimental setup and simulation results.

6.1. Experimental Setup

We analyzed mountainous terrain data from OpenTopography [59] and constructed 10 UAV task spaces based on the Fujisan mountain dataset, with coordinates ranging from longitude $138.6^{\circ }$ to $138.8^{\circ }$ and from latitude $35.3^{\circ }$ to $35.4^{\circ }$, featuring varying elevations and steepness levels to simulate diverse environmental conditions for flight and sensing tasks.

Table 1. Environmental parameters for UAV task.

Symbol	Definition	Value	Unit
$u_{x-\min }$	Task Space Left Edge	0	m
$u_{x-\max }$	Task Space Right Edge	2000	m
$u_{y-\min }$	Task Space Back Edge	0	m
$u_{y-\max }$	Task Space Front Edge	2000	m
$u_{z-\min }$	Task Space Bottom Edge	50	m
$u_{z-\max }$	Task Space Top Edge	100	m
$T_{\mathrm{end}}$	Maximum Mission Time	2000	s
$t_d$	Detection Cycle	10	s
$n_x$	Number of DPs in x Direction	20	s
$n_y$	Number of DPs in y Direction	20	s
$v_{\mathrm{horizon}}$	Velocity Limitation at Horizontal Direction	10	m/s
$v_{\mathrm{vertical}}$	Velocity Limitation at Vertical Direction	5	m/s
$K_{\mathrm{end}}$	Discretized End Time	2000	-
$m_{\mathrm{UAV}}$	UAV Mass	0.2	kg
g	Gravitational Acceleration	9.8	m/s2
${\rho }_{\mathrm{air}}$	Air Density	1.225	kg/m3
$C_d$	Drag Coefficient	0.5	-
$A_{\mathrm{surf}}$	UAV Fuselage Area	0.01	m2
$n_{\mathrm{prp}}$	Propeller Number	4	-
$R_{\mathrm{prp}}$	Propeller Radius	0.1	m
$\eta$	Mechanical Efficiency	0.8	-
$P_{\mathrm{TX}}$	UAV Transmit Power	17	dBm
$G_t$	Transmit Antenna Gain	2	dBi
$G_r$	Receive Antenna Gain	2	dBi
$\mathcal{L}$	System Average Path Loss	2	-
$f_c$	UAV Communication Frequency	3.5	GHz
$k_B$	Boltzmann Constant	$1.38\times {10}^{-23}$	-
$T_K$	Temperature (Kelvin)	298	K
c	Speed of Light	$3\times {10}^8$	m/s
${\mathcal{B}}^{*}$	Battery Capacity	311,040	J
$P_{\mathrm{static}}$	Static Power	4	W
V	Voltage	5	V
$f^{*}$	Clock Frequency	$200\times {10}^6$	Hz
${\alpha }^{*}$	Activity Factor	0.5	-
$C^{*}$	Load Capacitance	6.4	nF
$n_{\mathrm{grid}}$	Grid Number at Each Direction of per DP	100	-
$M_{\mathrm{th}}$	Coverage Rate Threshold	0.85	-
$d_{\mathrm{th}}$	Distance Threshold	150	m
${\theta }_{\mathrm{f}}$	FOV Threshold	45	∘
$t_{\mathrm{step}}$	Uniform Time Step	1	s
$n_{\mathrm{UAV}}$	UAV Number	4, 6, 10, 12, 15	-

and

Table 2. Hyperparameters for reinforcement learning.

Symbol	Definition	Value
$\mathcal{PR}$	Penalty Parameter	5
$\mathcal{PH}$	Penalty Parameter	$0.02$
$\mathcal{PO}$	Penalty Parameter	50
$\mathcal{PN}$	Penalty Parameter	$0.01$
$\mathcal{PC}$	Penalty Parameter	50
${\alpha }_1$	Weight Parameter	20
${\alpha }_2$	Weight Parameter	$0.001$
$\gamma$	Discounted Factor	0.99
$r_a$	Learning Rate for Actor	${10}^{-5}$
$r_c$	Learning Rate for Critic	${10}^{-4}$
$n_{\mathrm{batch}}$	DQPN Training Batch Size	128
$n_{\mathrm{batch}}^{\prime }$	FEN Training Batch Size	128
$n_{\mathrm{batch}}^{*}$	MARL Training Batch Size	128
$\mathcal{D}$	Replay Buffer Size	$2^{16}$
${\lambda }_{\max }$	Maximum Training Epoch of DQPN	100
${\lambda }_{\max }^{\prime }$	Maximum Training Epoch of FEN	1000
${\lambda }_{\max }^{*}$	Maximum Training Episode of MARL	10,000
${\vartheta }^{*}$	Parameter Initial Value	1
${\delta }^{*}$	Parameter Initial Value	10
${\lambda }_{\max }$	Maximum Training Epoch	100
$\xi$	Soft Update Parameter	0.01
${\beta }_F$	Feature Normalization Coefficient	1
$\tilde{S}$	Scenario Number	10
$\tilde{X}$	Position Number	80

, respectively, summarize the environmental parameters and hyperparameters used in this work.

Based on the Fujisan mountain terrain data and the communication parameters in Table 1, and according to Equation (14), the communication SNR between UAVs mainly depends on the path loss $\mathcal{PL}$. According to 3GPP Standards [60,61], the extreme path loss at kilometer-scale distances in the Fujisan mountain terrain is approximately 130 dB, indicating that the SNR of task UAVs is far greater than 13 dB, which can be regarded as indicative of good communication quality.

We evaluate the proposed FA-EIMARL algorithm from four key perspectives: training performance, scalability and complexity analysis, ablation study, and 3D visualization. The following performance metrics are defined:

• Reward (M1): Measures the average reward received per agent during one episode.
• Detection Coverage Rate (M2): Measures the overall detection quality across an episode.
• Task Completion Time (M3): Measures the overall detection mission time across an episode.
• Convergence Time (M4): Measures the number of iterations required for the algorithm to converge.
• Stability and Generalization (M5): Measures post-convergence reward fluctuations to assess robustness.

In addition, we evaluate the inference time, defined as the duration required for agents to make decisions during execution. The following metrics are used to assess inference efficiency:

• Scalability (M6): Measures how inference time per time step changes with the number of UAVs.
• Policy Efficiency (M7): Measures the inference time of UAVs during the detection process.

6.2. Training Performance

In the regular experiment, we set $n_{\mathrm{UAV}}=4$. Since non-RL algorithms such as heuristics struggle to cope with continuous action and state space UAV trajectory optimization tasks, we compared the proposed FA-EIMARL just with DRL algorithms. We selected continuous action space MARL algorithms as baselines: MASAC, MATD3, MAPPO, and MADDPG. These algorithms are introduced in Section 2.

Evaluation of M1 (Reward): As shown in Figure 7, the proposed FA-EIMARL achieves significantly higher average rewards compared to all DRL baselines. MAPPO demonstrates the poorest performance, likely due to its on-policy learning strategy, which struggles in highly dynamic environments. In contrast, MADDPG, MATD3, and MASAC attain similar reward levels, outperforming MAPPO. These off-policy methods benefit from experience replay mechanisms that improve resource efficiency. However, they still face challenges in adapting to dynamically changing task spaces, resulting in lower overall performance compared to FA-EIMARL.

Evaluation of M2 (Detection Coverage Rate): As illustrated in Figure 8, FA-EIMARL achieves the task objectives more efficiently than all competing DRL methods. MAPPO again yields the worst results. MADDPG and MATD3 outperform MASAC, both surpassing MAPPO, indicating that the off-policy approaches better support spatial exploration, though still not as effectively as the proposed method.

Evaluation of M3 (Task Completion Time): As illustrated in

Table 3. The average task completion time comparison with DRL algorithms.

Algorithm	Average Task Completion Time
MADDPG	1842
MASAC	1927
MATD3	1839
MAPPO	>2000
FA-EIMARL	1236

, compared with other DRL algorithms, FA-EIMARL requires shorter task completion time and can accomplish the search mission more quickly and efficiently. TD3 and DDPG demonstrate better task time performance than SAC, while PPO fails to complete the task within the specified time.

Evaluation of M4 (Convergence Time): As shown in Figure 7, all baseline methods, except MAPPO, converge within 2000 episodes. Among them, FA-EIMARL exhibits the fastest convergence. This improvement is attributed to two key mechanisms: the elite imitation mechanism(Section 5.3) and the feature-aware extraction method (Section 5.4). The former allows agents to mimic expert-level trajectories during training, effectively narrowing the exploration space and accelerating policy optimization. By selecting and learning from elite individuals, the agent reduces the early-stage exploration cost, adjusting its parameters based on already acquired experience. Furthermore, the learning rate is gradually slowed to maintain sufficient freedom for exploration, ensuring a balanced trade-off between guided learning and autonomous discovery. The latter provides additional environmental features that help the critic more accurately evaluate the value of state–action pairs. This enables the agent to make more informed and reasonable assessments of its actions even during the early stages of training, thereby guiding the convergence direction more effectively and improving overall learning efficiency. Together, these mechanisms significantly enhance sample efficiency and lead to faster convergence compared to other DRL baselines.

Evaluation of M5 (Stability and Generalization): Moreover, the reward curves of the proposed FA-EIMARL are significantly smoother and more stable than those of all baseline methods. Compared to MADDPG and MATD3, FA-EIMARL exhibits higher stability and reduced variance across episodes. It also shows more consistent performance than MASAC and outperforms MAPPO by a large margin in both stability and generalization. This improvement is primarily driven by two core components: the elite imitation mechanism and the feature-aware extraction module. The elite imitation mechanism enables agents to imitate high-performing individuals, which not only reduces unnecessary exploration costs but also helps prevent convergence to suboptimal or biased policies. Meanwhile, the feature-aware extraction method allows UAVs to extract generalized environmental representations from diverse task spaces. This capability empowers agents to dynamically adapt their policies to different scenarios, thereby maintaining robust performance under varying environmental conditions.

Therefore, it can be concluded that the proposed FA-EIMARL achieves superior performance in M1 compared to all other DRL baselines (MADDPG, MATD3, MASAC, MAPPO). Moreover, it demonstrates clear advantages in terms of M2 and M3 metrics, outperforming state-of-the-art DRL approaches in both task efficiency and convergence speed.

6.3. Scalability and Complexity Analysis

In this experiment, we first varied $n_{\mathrm{UAV}}$ from 4 to 15 to observe the trend of inference time to analyze the computational complexity. Then, we discuss the impact of the DQPN on the performance of FA-EIMARL. After that, we set $n_{\mathrm{UAV}}=4$ and compare the inference time of the proposed FA-EIMARL and other baseline algorithms introduced in Section 6.2.

Evaluation of M6 (Scalability):

Table 4. The inference time changes as the agent number increases.

Agent Number	Inference Time
$n_{\mathrm{UAV}}=4$	34.71 ms
$n_{\mathrm{UAV}}=6$	35.36 ms
$n_{\mathrm{UAV}}=10$	37.28 ms
$n_{\mathrm{UAV}}=12$	37.42 ms
$n_{\mathrm{UAV}}=15$	39.61 ms

illustrates the relationship between the inference time of FA-EIMARL and the number of agents. The inference time remains relatively stable as the number of agents increases. This is because the information required for each UAV to perform its task does not increase with the number of agents, and the use of the DQPN further reduces the additional computational complexity.

Table 5. The total task rewards change as the agent number increases.

Agent Number	Task Rewards
$n_{\mathrm{UAV}}=4$	4541.68
$n_{\mathrm{UAV}}=6$	4356.57
$n_{\mathrm{UAV}}=10$	4069.32
$n_{\mathrm{UAV}}=12$	3932.35
$n_{\mathrm{UAV}}=15$	3614.98

illustrates the relationship between the total task rewards and number of agents. The task reward remains at a relatively high level overall but shows a slight decrease as the number of agents increases. This is primarily because, with more UAVs in the scenario, the likelihood of them approaching each other and entering the safety distance increases. Moreover, since the size of the exploration space remains fixed, a larger number of UAVs makes it more challenging to avoid previously explored areas, which in turn affects the task reward. In general, the increase in the number of agents does not exert a significant impact on the performance of the FA-EIMARL algorithm.

As shown in

Table 6. Improvement of time performance brought by DQPN.

Approach	Operation Time
DQPN Prediction	0.4442 ms
Direct Computation	525.9 ms

, due to the acceleration provided by the DQPN module, the calculation of DP detection quality has been significantly accelerated.

As shown in

Table 7. Function parameter of elite imitation module.

Average Overhead	Computational Parameter	Total Extra Overhead
85.09 ms	2300	872.2 ms

, the EI process performs elite selection and parameter replication based on the UAVs’ experience. Consequently, the number of parameters involved is proportional to the neuron parameters of the lightweight network. The resulting overhead is negligible compared with gradient computations during training and the inference time of UAVs, and thus has an insignificant impact on the overall time complexity of the training process.

As shown in Figure 9, the overhead of the FA module does not increase linearly with the number of sampling points; instead, its growth rate gradually decreases, and the overall overhead remains at a low level. Compared with the UAVs’ inference time, it is negligible.

The loss curve for training DQPN is shown as Figure 10. It can be obviously seen that, DQPN has a high level of reliability.

Evaluation of M7 (Policy Efficiency) We choose their minimum duration to achieve stable rewards as the inference time. As depicted in

Table 8. The performance comparison of inference time with baseline algorithms.

Algorithm	Inference Time
MADDPG	162.39 ms
MASAC	320.21 ms
MATD3	172.74 ms
MAPPO	59.79 ms
FA-EIMARL	34.76 ms

, it can be observed that FA-EIMARL introduces a slight increase in inference time due to its more complex network structure, FEN. However, since FEN is a lightweight convolutional network, the impact remains limited. Meanwhile, the core acceleration component, the DQPN structure, significantly reduces the time required for predicting UAV detection success rates. This high-precision reduction in inference time gives FA-EIMARL a substantial advantage over other algorithms.

In summary, there exists a trade-off between the richness of information that networks can extract and their computational complexity in deep reinforcement learning. The proposed FA-EIMARL algorithm, with the support of the DQPN module, achieves stable and superior inference time performance compared to other DRL methods.

6.4. Ablation Study

In this experiment, we set $n_{\mathrm{UAV}}=4$ and conducted an ablation study to evaluate the effectiveness of the proposed feature-aware (FA) and elite imitation (EI) mechanisms. As shown in Figure 11, the reward performance noticeably degrades when either the FA or EI module is removed. In particular, EIMARL, which lacks any feature extraction module, yields the lowest reward, highlighting the crucial role of the FA mechanism in guiding task perception.

Moreover, both EIMARL and FAMARL, which exclude the EI and FA modules, respectively, exhibit significant fluctuations in reward curves. This observation underscores the importance of both modules in enhancing training stability and convergence robustness. The EI mechanism helps reduce exploration overhead by guiding agents with prior expert behaviors, while the FA module improves the agents’ adaptability to varying task spaces through more informative environmental representations.

6.5. Three-Dimensional Visualization

In this experiment, we set $n_{\mathrm{UAV}}=4$ and present the visualization of UAV trajectories in 3D scenes. We simulate different mountainous areas as mentioned in Section 6.1, with different mountain heights and steepness levels. The visualization results for 10 scenarios are available at https://github.com/usainzhou0301/FA-EIMARL (accessed on 4 August 2025).

This section only presents exemplary virtualization results of trajectory optimization for a multi-UAV cooperative system in a certain mountainous area. As shown in Figure 12 and Figure 13, we can clearly observe that the multi-UAV exploration space has a high coverage rate with low trajectory overlap. Each UAV is able to find its own comfortable working space and to some extent fill the coverage gaps left by other UAVs. In addition, the drones can always maintain an appropriate flight altitude and adjust smoothly according to changes in elevation.

7. Conclusions

In this paper, we present a comprehensive study on trajectory optimization for multi-UAV collaborative systems operating in complex mountainous environments. The UAVs are tasked with performing search and detection tasks, aiming to maximize coverage while minimizing task completion time. To address the challenges posed by complex terrain, varying flight altitudes, limited battery capacity, and collision avoidance, we developed a model-based, data-driven methodology that jointly optimizes detection coverage, flight altitude, energy consumption, and collision avoidance.

To realistically reproduce the UAV flight process, we constructed UAV dynamics, communication, and detection models based on the existing literature and real UAV parameters. We formulated the problem and defined constraints for key aspects such as detection coverage, flight altitude, energy consumption, and collision avoidance.

To enhance training efficiency and stability, we introduce an EI mechanism, with which the top-performing agent periodically shares its parameters with others in a controlled manner, accelerating policy convergence while maintaining sufficient exploration. Building on this, we propose the FA-EIMARL algorithm, which integrates environmental features extracted from structured point arrays of terrain elevation. This enables the UAVs to adapt rapidly to dynamic and diverse task environments. Additionally, we designed a lightweight DQPN to efficiently estimate the reliability of terrain mapping, reducing unnecessary computation while ensuring mapping accuracy.

Experimental results demonstrate that the proposed FA-EIMARL significantly outperforms baseline methods, achieving shorter task completion times, higher coverage rates, and better adaptability in scenarios with varying terrain complexities.

Looking forward, we plan to further improve environmental feature extraction techniques to better capture terrain characteristics and enhance UAV decision-making. We also aim to increase scenario complexity, enabling multi-UAV systems to handle a broader range of tasks under dynamic conditions, thereby further improving their robustness, generalization, and operational efficiency in real-world search and rescue missions.