A Method for Orderly and Parallel Planning of Public Route Networks for Logistics Based on Urban Low-Altitude Digital Airspace Environment Risks
Abstract
Highlights
- A parallel system has been developed to facilitate the partitioning of airspace into vertical and horizontal grids, quantify risks, and construct a virtual planning environment for public route networks.
- An orderly planning framework for public route networks has been proposed, which achieves safe and conflict-free design of the route network.
- This paper presents a refined technical framework for planning urban low-altitude terminal public route networks, enhancing research on route network planning through a comprehensive consideration of global airspace resource allocation and multi-dimensional risk factors.
- Furthermore, it supports the planning of urban low-altitude public route networks characterized by high safety, minimal inflection points, and stringent segregation. This facilitates large-scale low-altitude terminal logistics operations and expands the application of parallel system theory in the context of spatially conflict-free route network planning.
Abstract
1. Introduction
1.1. Related Prior Work
1.2. Our Contributions
- (1)
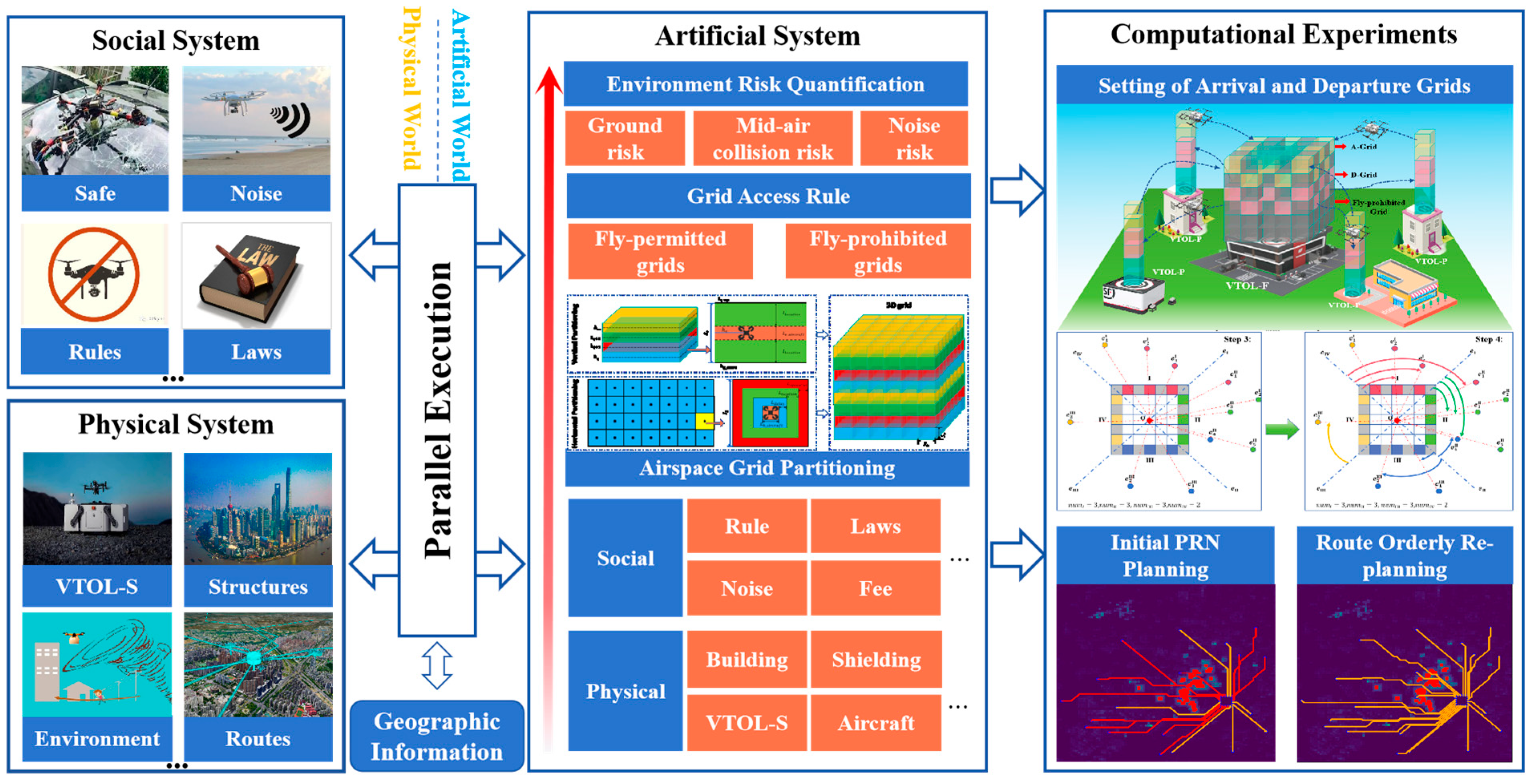
- A parallel system framework for PRN planning for UAVs in urban low-altitude terminal logistics is constructed. Physical and social elements associated with the hub-and-spoke PRN in the real world are parallelly mapped to the artificial system.
- (2)
- A quantitative assessment of airspace grid environmental risks in urban low-altitude digital airspace is conducted. On the basis of vertical–horizontal grid partitioning, differentiated grid flight access rules are formulated, and environmental risks in urban low-altitude airspace are quantified.
- (3)
- An orderly planning methodology for PRNs is proposed. By precisely configuring approach–departure grid (AD-Grid) resources in layered airspace, an accurate one-to-one matching between AD-Grids and take-off and landing points (VTOL-Ps) is achieved. Initial planning and iterative re-planning of the route network are performed sequentially, ultimately resulting in a safe, segregated, and conflict-free hub-and-spoke PRN.
- (4)
- Using Nanjing Liuhe District as an empirical research case, study analyses are conducted. These detailed studies analyses include systematic environmental risk assessment, average risk value analysis, statistical analysis of average inflection points, comprehensive cost calculation, algorithm complexity analysis, and PRN scale planning analysis.
2. Foundation of Research
2.1. Basic Concept and Problem Description
2.2. Research Hypothesis
- (1)
- All UAVs involved in this study process vertical take-off and landing capabilities, enabling them to meet the take-off and landing requirements in complex low-altitude environments.
- (2)
- Adverse weather conditions, such as thunderstorms and strong winds, are not considered to impact flight operations, as they can lead to significant suspensions or delays in urban terminal areas.
- (3)
- All goods are dispatched from VTOL-Fs and transported by UAVs to designated VTOL-Ps.
- (4)
- The planned PRN is confined to a single altitude layer within the layered airspace.
3. Establish Parallel System
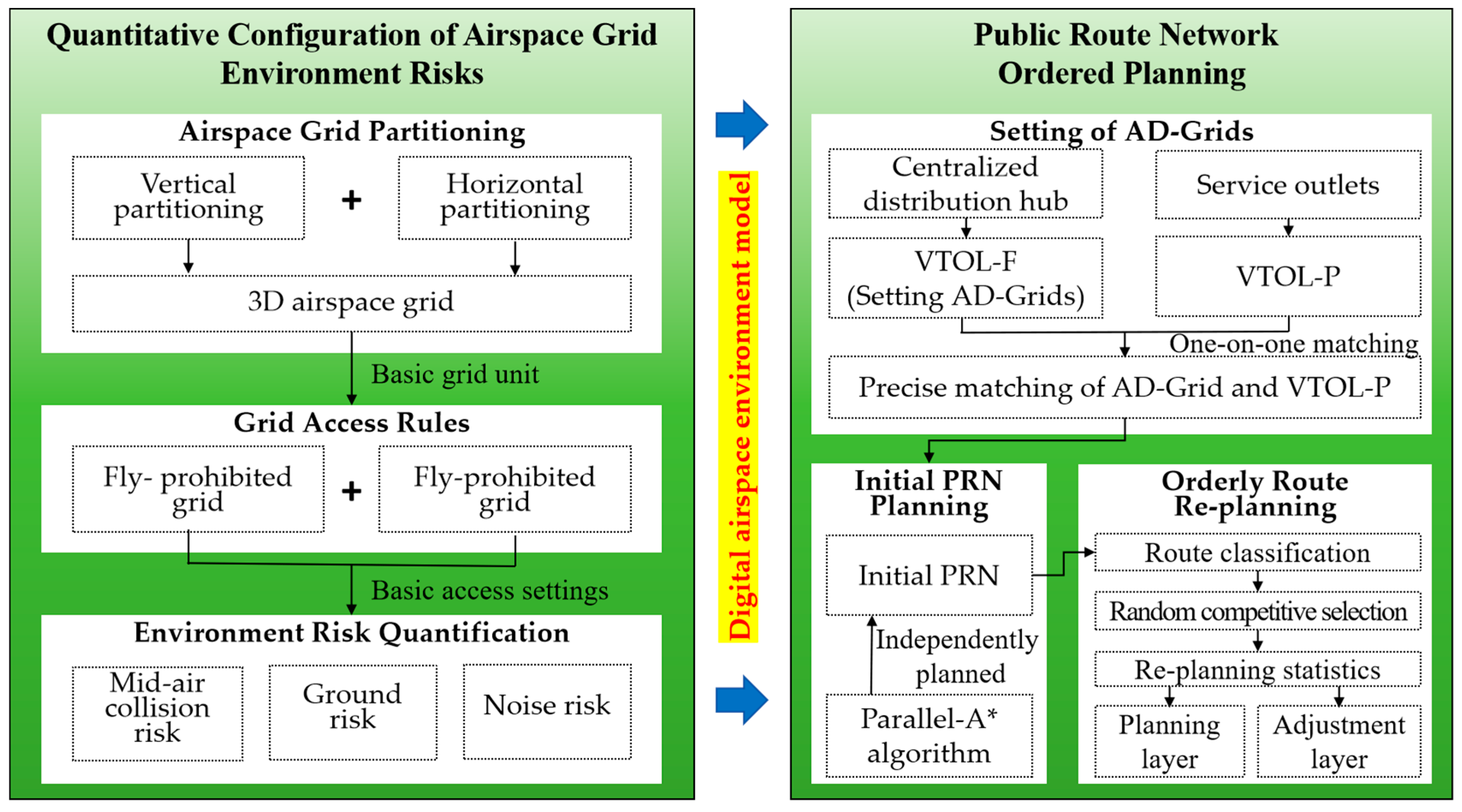
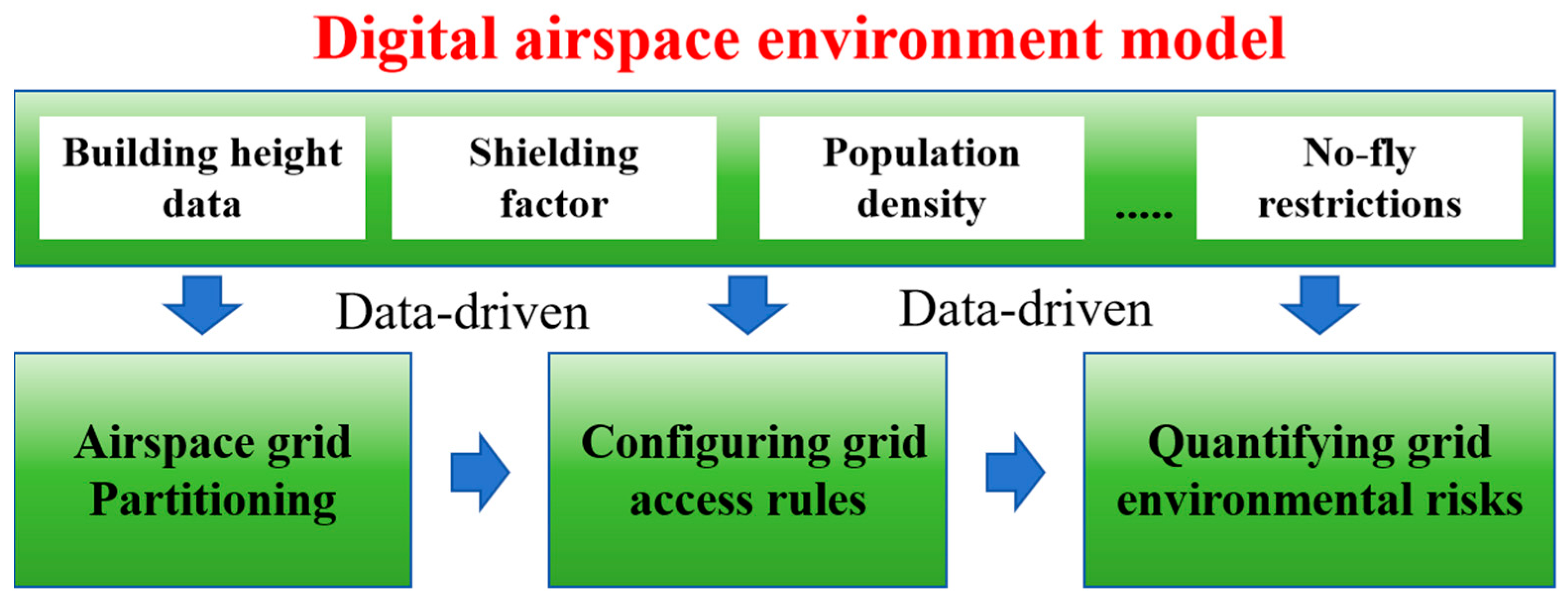
3.1. Quantitative Configuration of Airspace Grid Environment Risks
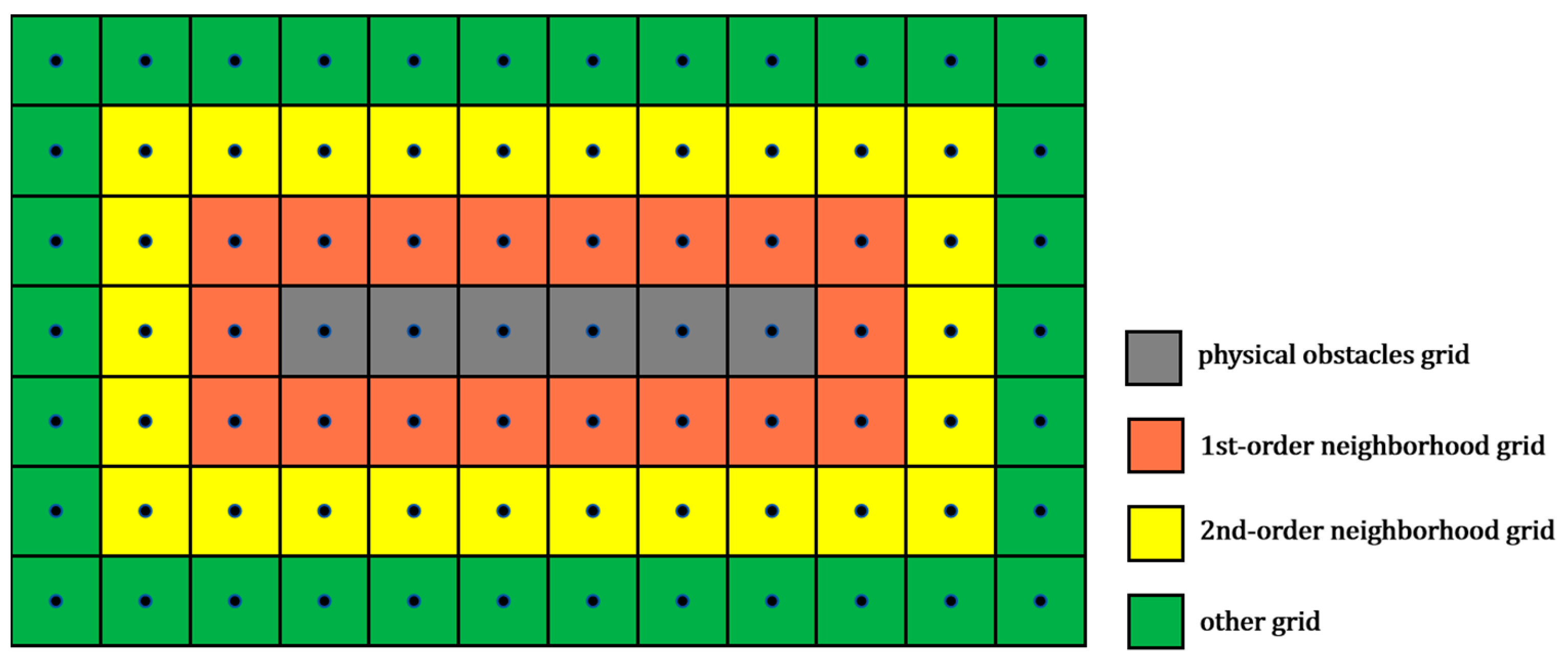
3.1.1. Airspace Grid Partitioning
3.1.2. Grid Access Rule
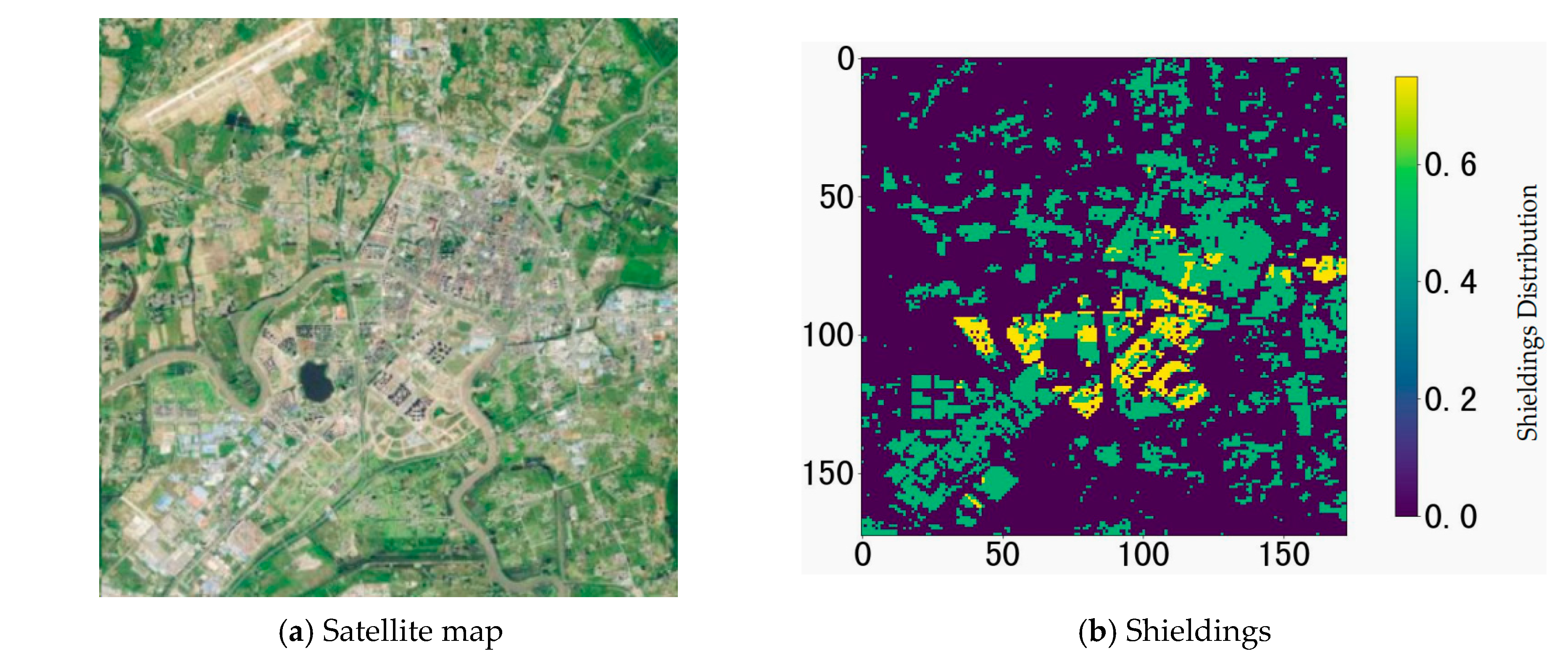
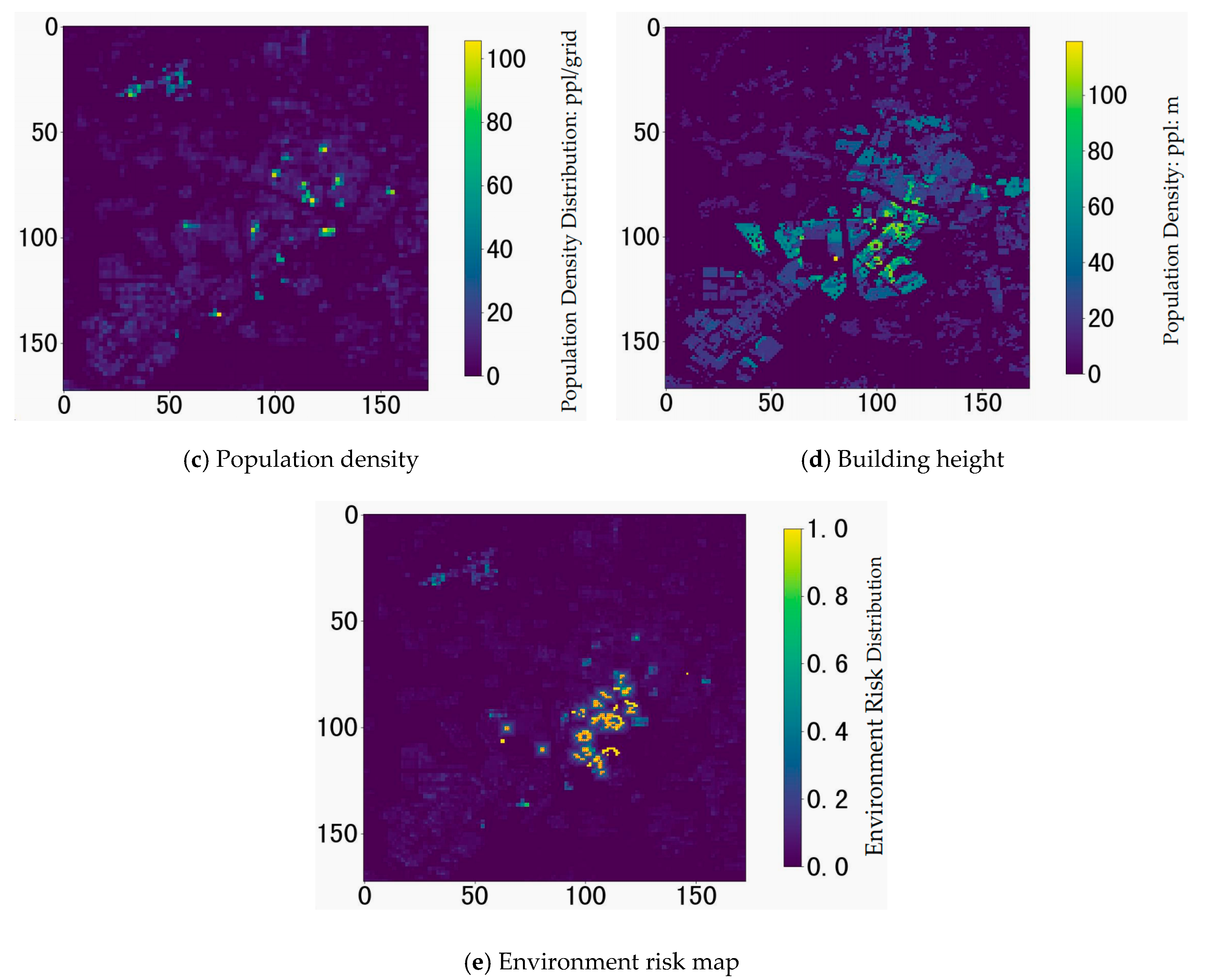
3.1.3. Environment Risk Quantification
- (1)
- Mid-air Collision Risk
- (2)
- Ground Risk
- (3)
- Noise Risk
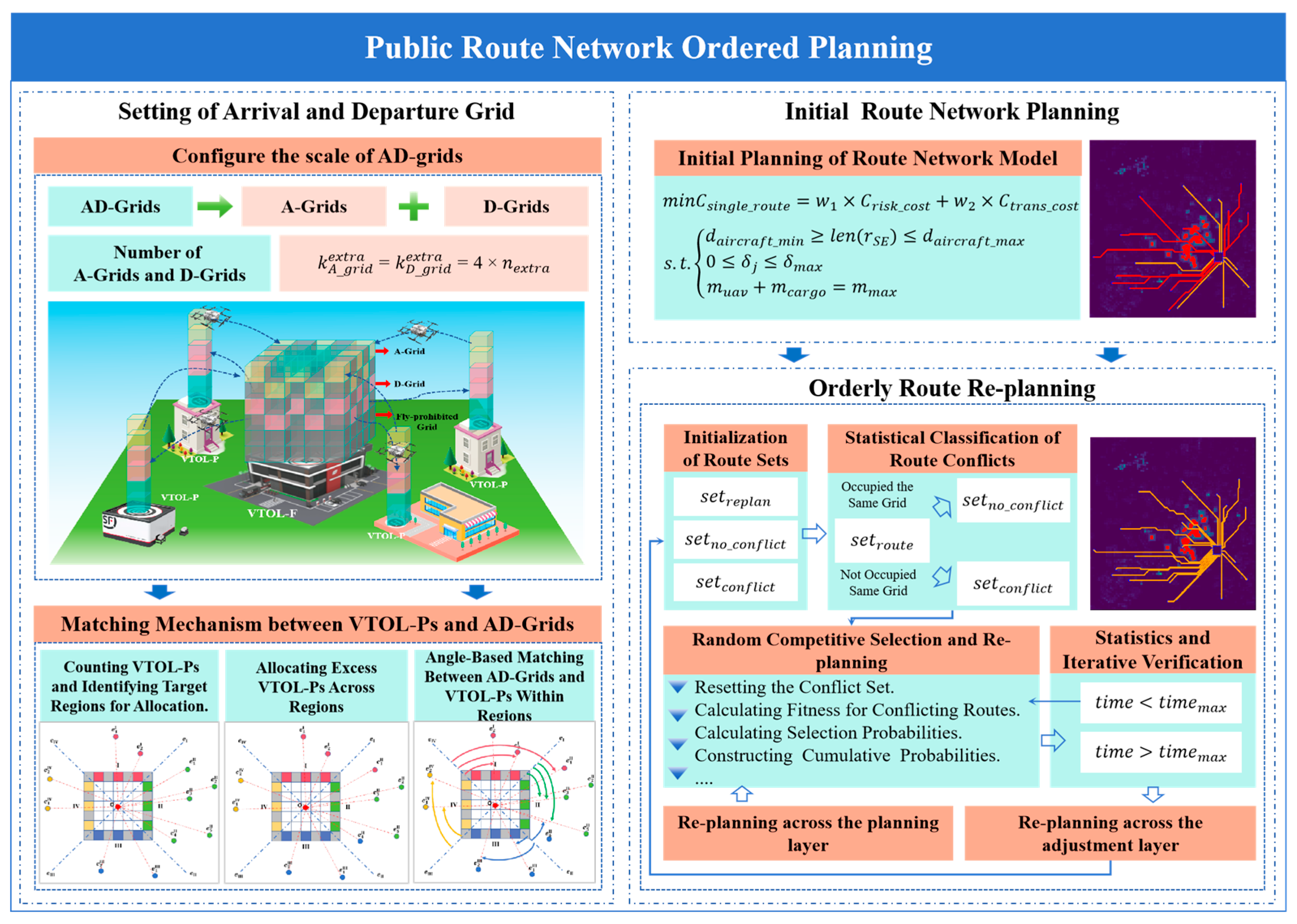
3.2. PRN Ordered Planning
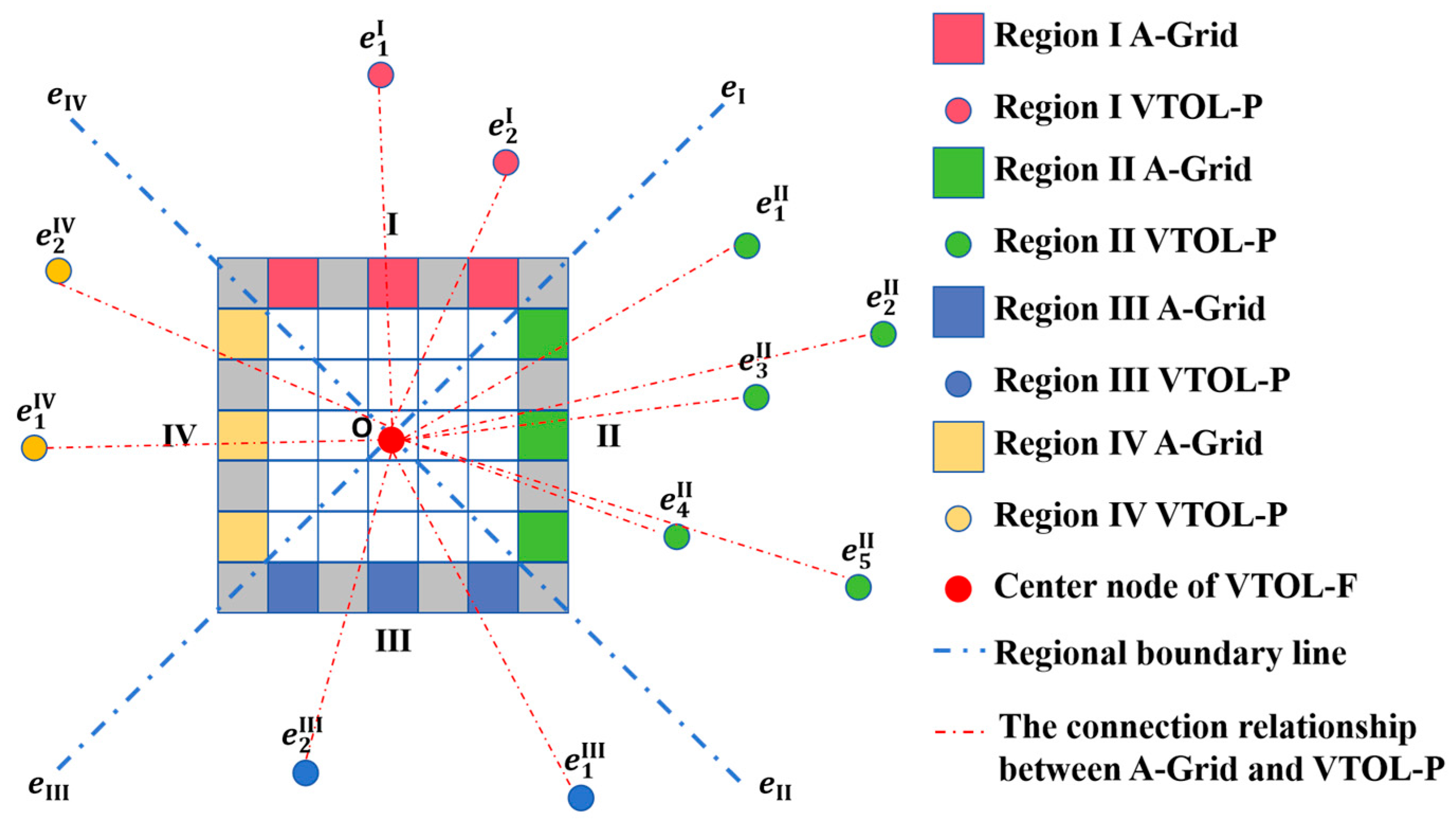
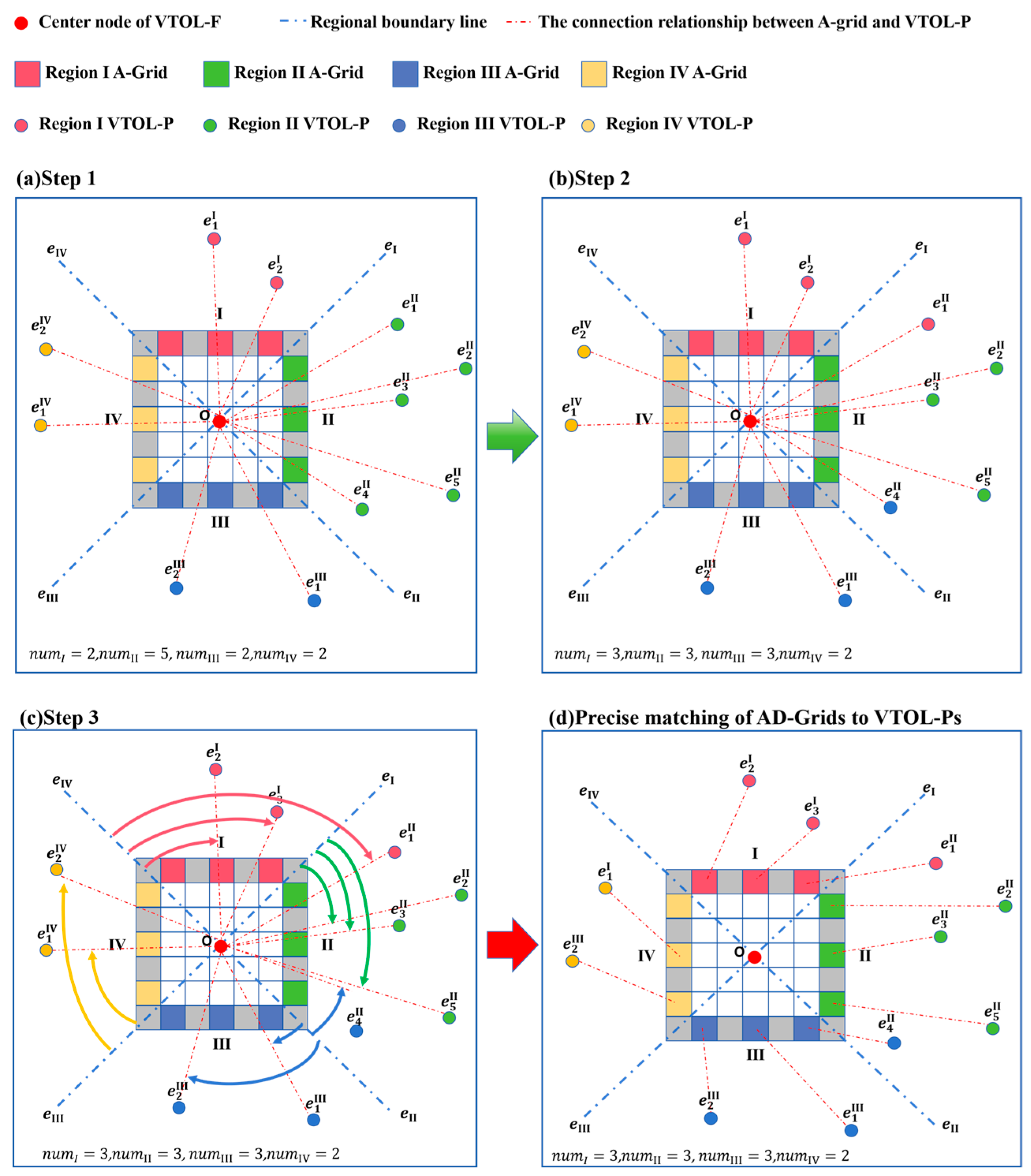
3.2.1. Setting of AD-Grids
3.2.2. Initial PRN Planning
- (1)
- Range Constraint
- (2)
- Steering Angle Constraint
- (3)
- Maximum Take-off Weight
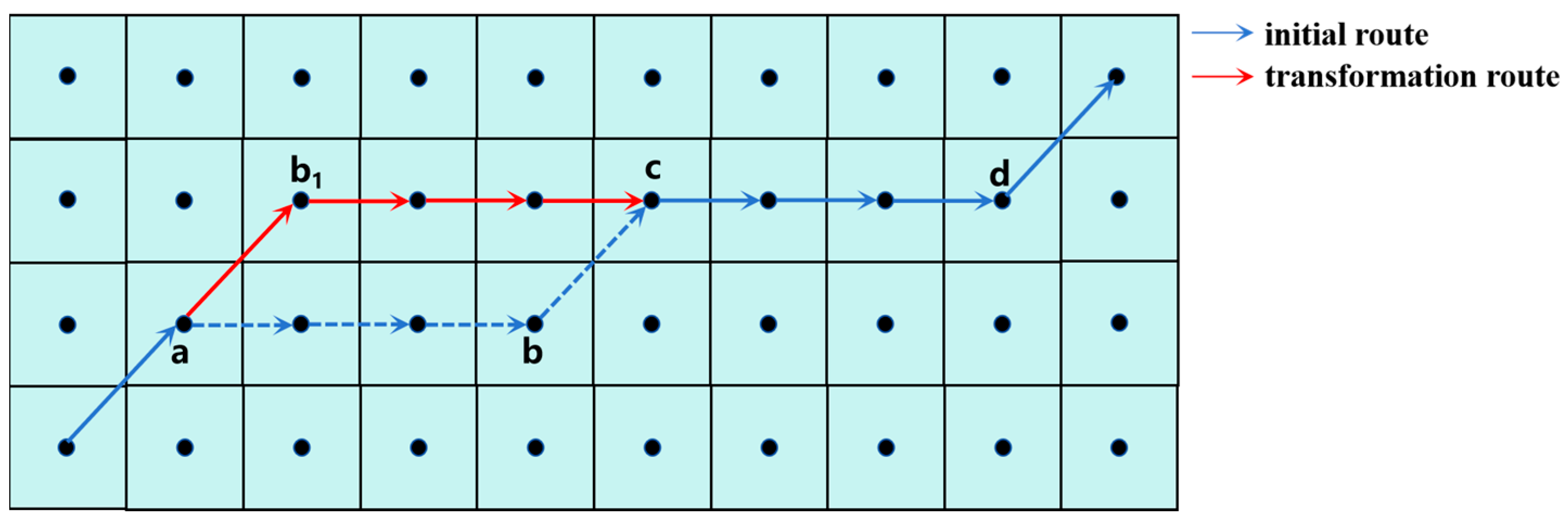
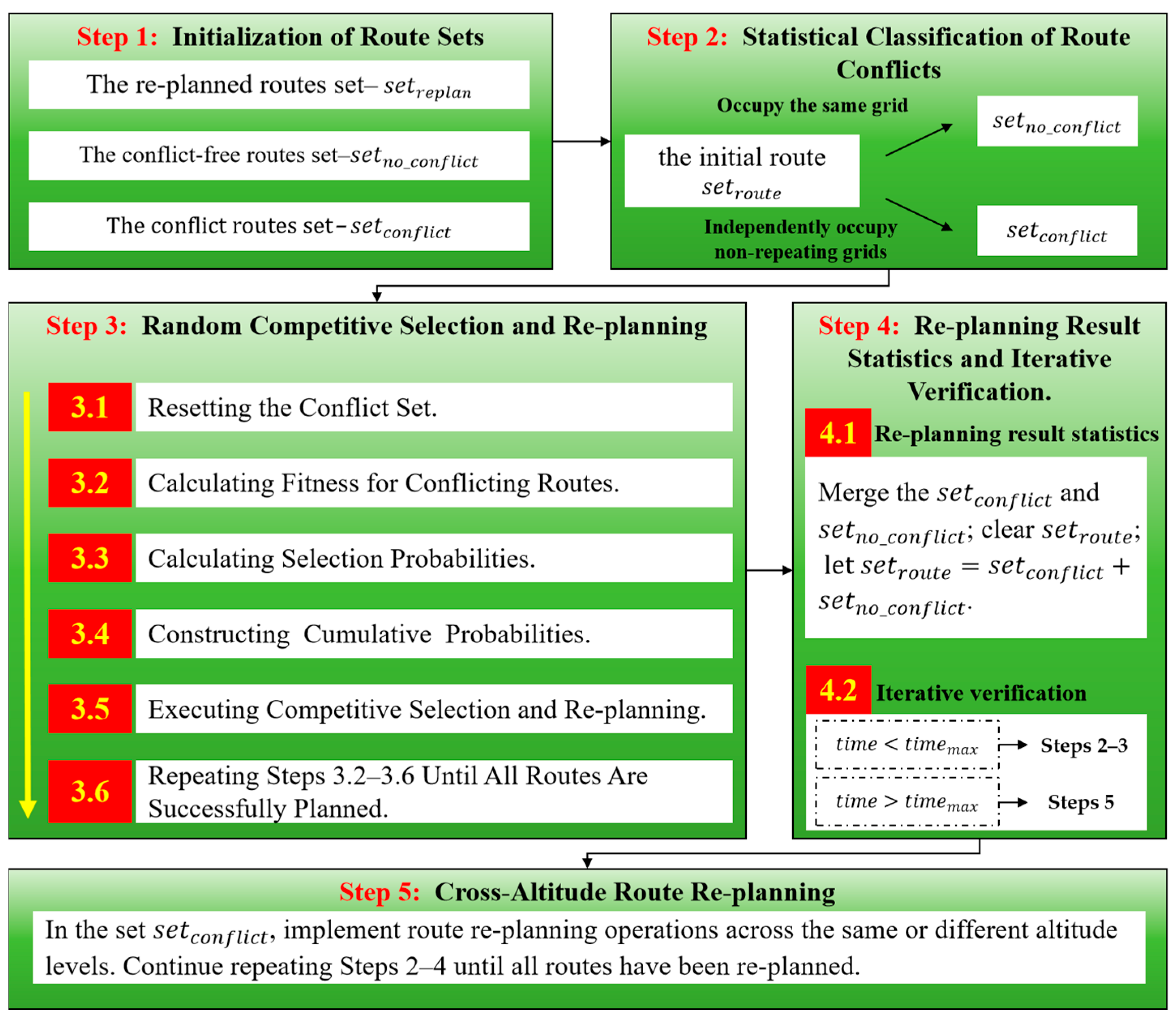
3.2.3. Orderly Route Re-Planning
- Constraint (25) ensures that for every intermediate grid point (excluding VTOL-Ps and AD-Grids), the out-degree is equal to the in-degree, thereby guaranteeing the continu-ity of the planned route.
- Constraints (26) and (27) collectively ensure that each route in the PRN originates from an A-Grid and terminates at a VTOL-P.
- Constraint (28) ensures that each grid is traversed by at most one route, thereby achieving conflict-free route segregation within the PRN.
- Constraint (29) restricts each edge to two states: selected or not selected.
3.2.4. Technical Process of the PRN Orderly Planning
4. Case Study Analysis
4.1. Parameter Settings
4.2. Environment Risk Analysis
4.3. Analysis of AD-Grid Configuration
- (1)
- The sequential matching method begins at the upper-right corner of the A-Grid, calculating the orientation of VTOL-Ps relative to D-Grids. It prioritizes linking A-Grids to VTOL-Ps with congruent orientations, thereby completing the matching while maintaining a regular directional distribution.
- (2)
- The greedy matching method first computes the Euclidean distance between each VTOL-P and the A-Grid centroid, then sorts them in ascending order of distance. Subsequently, it sequentially assigns each VTOL-P to the nearest A-Grid. Figure 15 illustrates the schematic diagrams of the three AD-Grid configuration strategies described above.
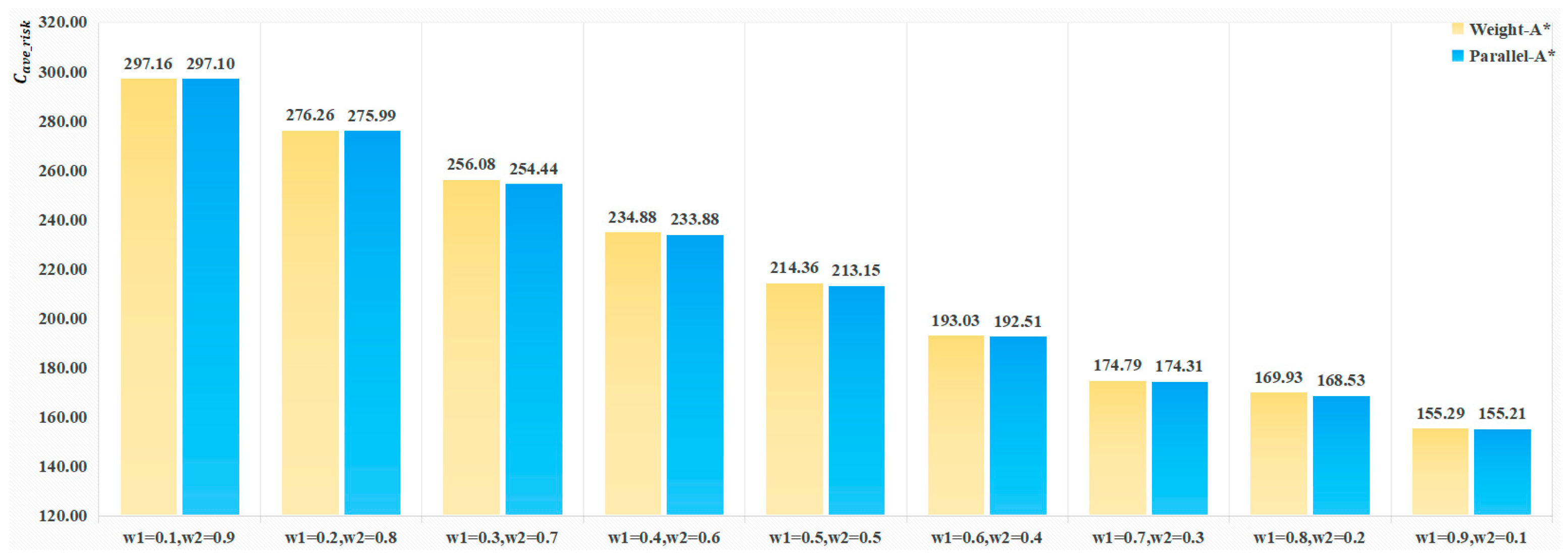
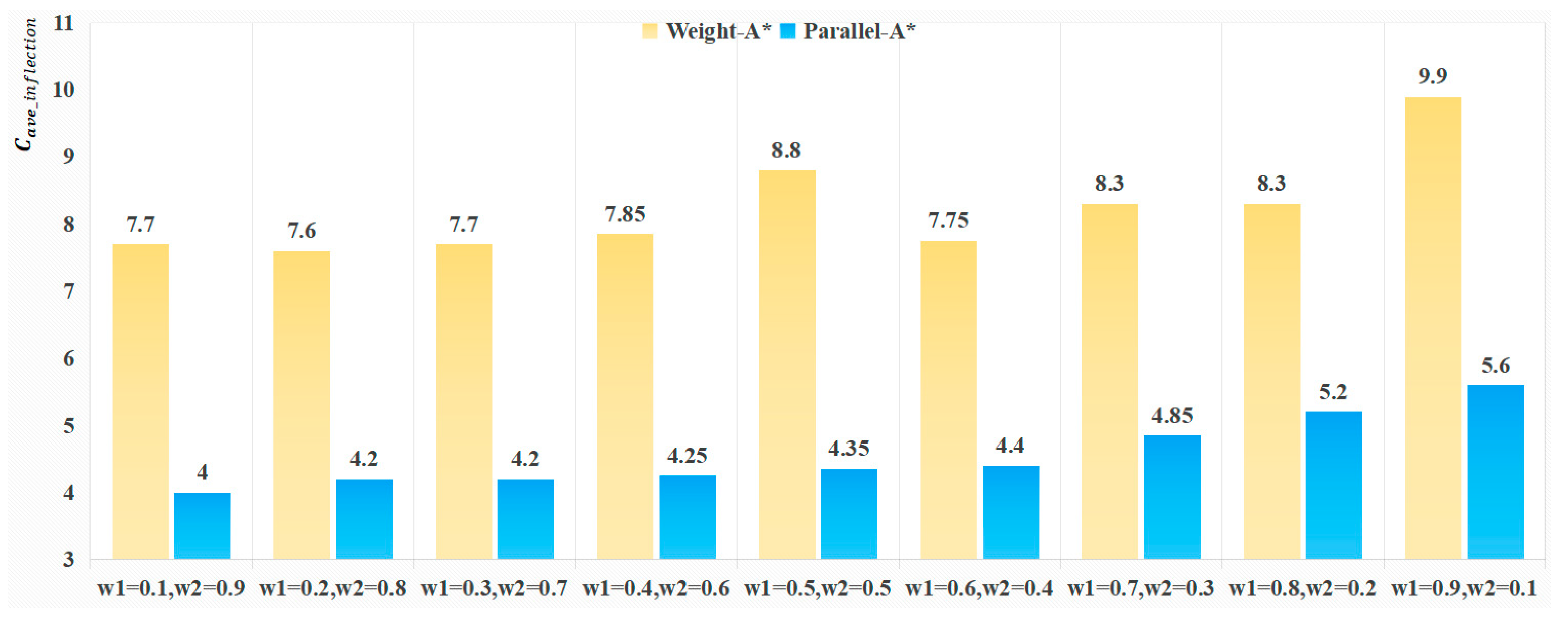
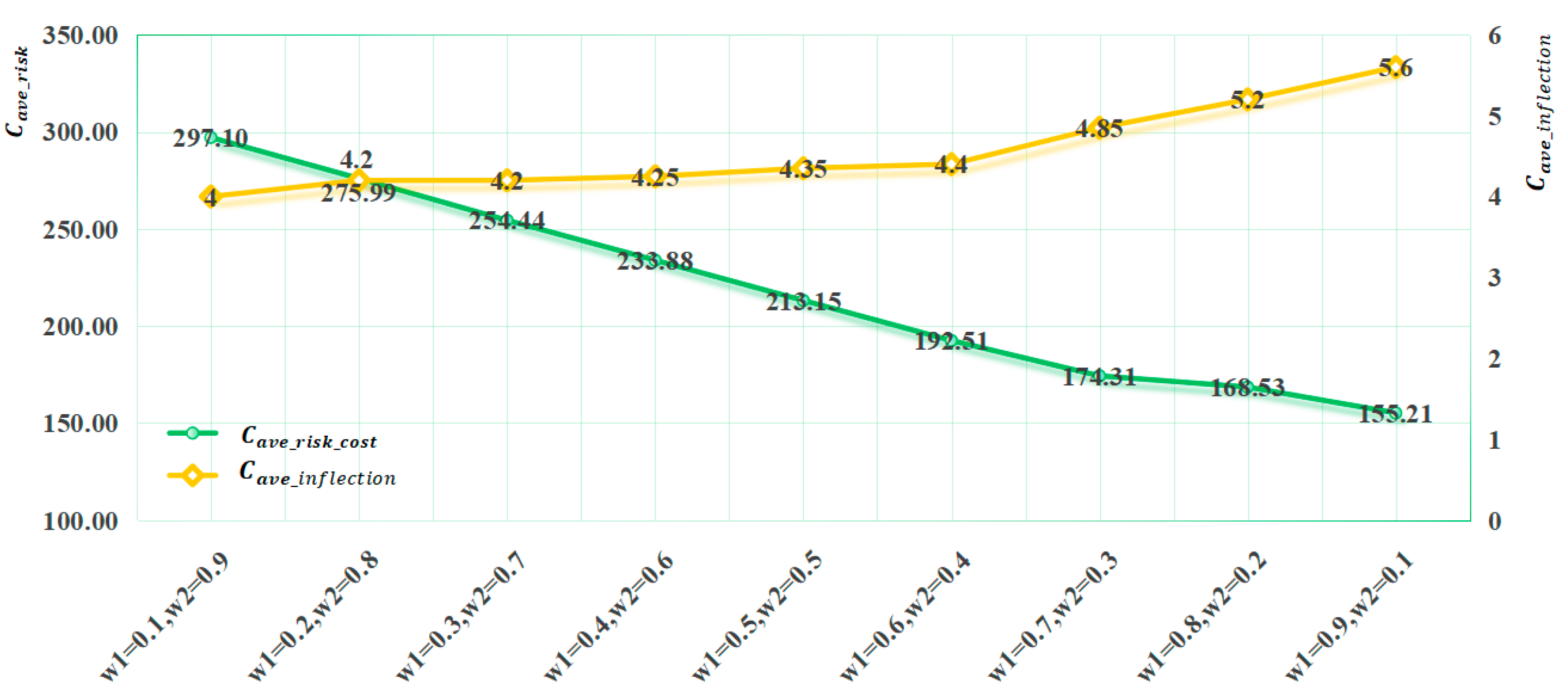
4.4. Analysis of Average Risk Cost and Average Inflection Point Cost
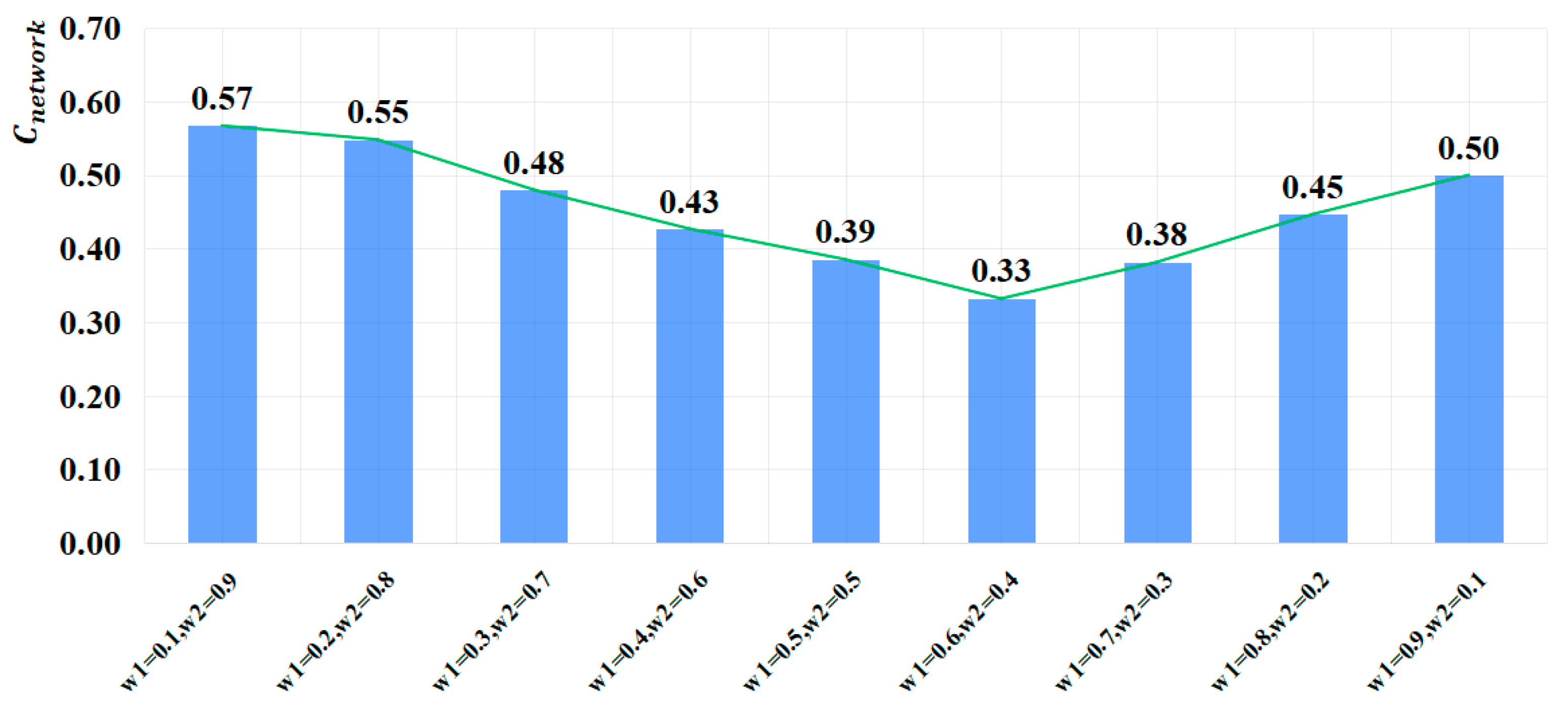
4.5. Analysis of Comprehensive Cost
4.6. Comparative Analysis
4.7. Algorithm Complexity Analysis and PRN Scale Planning Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| PRN | Public Route Network |
| CPSS | Cyber–Physical–Social System |
| CPS | Cyber–Physical System |
| GSO | Glowworm Swarm Optimization |
| 3D | Three-Dimensional |
| UAM | Urban Air Mobility |
| AD-Grid | Approach–Departure Grid |
| VTOL-S | Vertical Take-Off and Landing Site |
| VTOL-C | Vertical Take-Off and Landing Center |
| VTOL-F | Vertical Take-Off and Landing Field |
| VTOL-P | Vertical Take-Off and Landing Point |
| A-Grid | Arrival Grid |
| D-Grid | Departure Grid |
References
- Deng, M.; Yang, Q.; Peng, Y. A real-time path planning method for urban low-altitude logistics UAVs. Sensors 2023, 23, 7472. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Jeon, H.; Oh, J.; Lee, H. Dynamic Order Picking Method for Multi-UAV System in Intelligent Warehouse. Remote Sens. 2022, 14, 6106. [Google Scholar] [CrossRef]
- Liu, H.; Tsang, Y.P.; Lee, C. A cyber-physical social system for autonomous drone trajectory planning in last-mile superchilling delivery. Transp. Res. Part C Emerg. Technol. 2024, 158, 104448. [Google Scholar] [CrossRef]
- Shao, P. Risk assessment for UAS logistic delivery under UAS traffic management environment. Aerospace 2020, 7, 140. [Google Scholar] [CrossRef]
- Lyu, R.; Zhang, J.; Pang, J.; Zhang, J. Modeling the impacts of 2D/3D urban structure on PM2.5 at high resolution by combining UAV multispectral/LiDAR measurements and multi-source remote sensing images. J. Clean. Prod. 2024, 437, 140613. [Google Scholar] [CrossRef]
- Yang, C.; Zhu, W.; Sun, J.; Xu, X.; Wang, R.; Lu, Y.; Zhang, S.; Zhou, W. Assessing the effects of 2D/3D urban morphology on the 3D urban thermal environment by using multi-source remote sensing data and UAV measurements: A case study of the snow-climate city of Changchun, China. J. Clean. Prod. 2021, 321, 128956. [Google Scholar] [CrossRef]
- Yamashita, R.; Kidoguchi, K.; Oshima, T.; Ishigaki, A. Sustainable paddy farming in rural Japan: Leveraging farmer integration and agricultural UAVs for synergistic solutions. J. Clean. Prod. 2024, 475, 143685. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Chen, Y.; Zhang, G.; Liu, Z. Deep Learning-Based Target Point Localization for UAV Inspection of Point Cloud Transmission Towers. Remote Sens. 2024, 16, 817. [Google Scholar] [CrossRef]
- Tang, G.; Gu, J.; Zhu, W.; Claramunt, C.; Zhou, P. HD Camera-Equipped UAV Trajectory Planning for Gantry Crane Inspection. Remote Sens. 2022, 14, 1658. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Wang, Y.T.; Liu, Z.M.; Li, X.S.; Wang, F.Y. Parallel Intelligence and CPSS in 30 Years: An ACP Approach. Acta Autom. Sinica 2023, 49, 614–634. [Google Scholar]
- Wang, F.; Zheng, N.; Cao, D.; Martinez, C.M.; Li, L.; Liu, T. Parallel driving in CPSS: A unified approach for transport automation and vehicle intelligence. IEEE/CAA J. Autom. Sin. 2017, 4, 577–587. [Google Scholar] [CrossRef]
- Dong, H.; Zhu, H.; Li, Y.; Lv, Y.; Gao, S.; Zhang, Q.; Ning, B. Parallel intelligent systems for integrated high-speed railway operation control and dynamic scheduling. IEEE Trans. Cybern. 2018, 48, 3381–3389. [Google Scholar] [CrossRef]
- Aslam, M.M.; Shafik, W.; Hidayatullah, A.F.; Kalinaki, K.; Gul, H.; Zakari, R.Y.; Tufail, A. Intelligent Transportation Systems: A Critical Review of Integration of Cyber-physical Systems (CPS) and Industry 4.0. Digit. Commun. Netw. 2025; in press. [Google Scholar]
- Lu, Y.S.; Wang, F.Y.; Zhang, Y.; Zhang, X.D. Parallel cities: Framework, methodology, and application. Chin. J. Intell. Sci. Technol. 2019, 1, 311–317. [Google Scholar]
- Saritha, I.G.; Naveen, I.G.; Sowmyashree, M.S. CPS Secured Hybridization Technique for Healthcare in Smart Cities. In 5G Green Communication Networks for Smart Cities; Apple Academic Press: Palm Bay, FL, USA, 2025; pp. 77–93. [Google Scholar]
- Ma, S.; Liu, H.; Pan, N.; Wang, S. Study on an autonomous distribution system for smart parks based on parallel system theory against the background of Industry 5.0. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101608. [Google Scholar] [CrossRef]
- Liu, H.; Sun, Y.; Cao, J.; Chen, S.; Pan, N.; Dai, Y.; Pan, D. Study on UAV parallel planning system for transmission line project acceptance under the background of industry 5.0. IEEE Trans. Ind. Inform. 2022, 18, 5537–5546. [Google Scholar] [CrossRef]
- Wang, F.; Gao, Y.; Shang, X.; Zhang, J. Parallel manufacturing and industries 5.0: From virtual manufacturing to intelligent manufacturing. Sci. Technol. Rev. 2018, 36, 10–22. [Google Scholar]
- Aleisa, M.A. Enhancing Security in CPS Industry 5.0 using Lightweight MobileNetV3 with Adaptive Optimization Technique. Sci. Rep. 2025, 15, 18677. [Google Scholar] [CrossRef]
- Faiçal, B.S.; Marcondes, C.A.; Loubach, D.S.; Sbruzzi, E.F.; Verri, F.A.; Marques, J.C.; Pereira, L.A.; Maximo, M.R.; Curtis, V.V. A Cyber-Physical System’s Roadmap to Last-Mile Delivery Drones. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 6–16. [Google Scholar] [CrossRef]
- Mohamed Salleh, M.F.B.; Wanchao, C.; Wang, Z.; Huang, S.; Tan, D.Y.; Huang, T.; Low, K.H. Preliminary concept of adaptive urban airspace management for unmanned aircraft operations. In Proceedings of the 2018 AIAA Information Systems-AIAA Infotech@ Aerospace, Kissimmee, FL, USA, 8–12 January 2018; American Institute of Aeronautics and Astronautics: Kissimmee, FL, USA, 2018; p. 2260. [Google Scholar]
- Xu, X.Y.; Wan, L.J.; Chen, P.; Dai, J.B.; Cai, M. An Airspace Raster Representation Method Based on GeoSOT Grid. J. Air Force Eng. Univ. (Nat. Sci. Ed.) 2021, 22, 15–22. [Google Scholar]
- Feng, O.; Zhang, H.; Tang, W.; Wang, F.; Feng, D.; Zhong, G. Digital Low-Altitude Airspace Unmanned Aerial Vehicle Path Planning and Operational Capacity Assessment in Urban Risk Environments. Drones 2025, 9, 320. [Google Scholar] [CrossRef]
- Martin, T.; Huang, Z.F.; McFadyen, A. Airspace risk management for UAVs a framework for optimising detector performance standards and airspace traffic using JARUS SORA. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; IEEE: New York, NY, USA, 2018; pp. 1516–1525. [Google Scholar]
- CAAC Management Regulations for Trial Operation of Specific Types of UAVs. Available online: https://www.caac.gov.cn/XXGK/XXGK/GFXWJ/201902/t20190201_194511.html (accessed on 1 February 2019).
- Jiao, Q.; Liu, Y.; Zheng, Z.; Sun, L.; Bai, Y.; Zhang, Z.; Sun, L.; Ren, G.; Zhou, G.; Chen, X. Ground risk assessment for unmanned aircraft systems based on dynamic model. Drones 2022, 6, 324. [Google Scholar] [CrossRef]
- Han, P.; Zhao, Y.F.; Liu, H. Assessment system construction and trend foresight of UAV ground impact risk. J. Civ. Aviat. Univ. China 2021, 39, 40–47. [Google Scholar]
- Banerjee, P.; Gorospe, G.; Ancel, E. 3D representation of UAV-obstacle collision risk under off-nominal conditions. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021; IEEE: New York, NY, USA, 2021; pp. 1–7. [Google Scholar]
- Jie, C.; Yuan, Z.; Cheng-long, L.I.; Bo, J.; Dong-lai, L. Minimum Risk Path Planning Algorithm for Urban Very-low-level Logistics Scenarios. Sci. Technol. Eng. 2023, 23, 690–698. [Google Scholar]
- Han, P.; Zhou, B.; Zhang, E.Y. Air Collision Risk of Manned Drones in Multiple Scenarios in the Terminal Area. J. Xihua Univ. (Nat. Sci. Ed.) 2022, 41, 8–11. [Google Scholar]
- Li, J.; Zhong, G.; Zhang, X.W.; Zhang, H.H. Research on calculation method of aerial collision risk of urban low-altitude UAV. Mod. Transp. Metall. Mater. 2022, 2, 20–30. [Google Scholar]
- Kutpanova, Z.; Kadhim, M.; Zheng, X.; Zhakiyev, N. Multi-UAV path planning for multiple emergency payloads delivery in natural disaster scenarios. J. Electron. Sci. Technol. 2025, 23, 100303. [Google Scholar] [CrossRef]
- Re, X.; Cheng, C. Construction and application of third-party risk model for unmanned aerial vehicle operation in urban environment. China Saf. Sci. J. 2021, 31, 15–20. [Google Scholar]
- Pang, B.; Hu, X.; Dai, W.; Low, K.H. UAV path optimization with an integrated cost assessment model considering third-party risks in metropolitan environments. Reliab. Eng. Syst. Saf. 2022, 222, 108399. [Google Scholar] [CrossRef]
- Jiang, C.; Blom, H.A.; Sharpanskykh, A. Third party risk indicators and their use in safety regulations for UAS operations. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020; p. 2901. [Google Scholar]
- Xu, C.; Liao, X.; Ye, H.; Yue, H. Iterative construction of low-altitude UAV air route network in urban areas: Case planning and assessment. J. Geogr. Sci. 2020, 30, 1534–1552. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, T.; Feng, O.; Wu, S.; Zhong, G. Research on Public Air Route Network Planning of Urban Low-Altitude Logistics Unmanned Aerial Vehicles. Sustainability 2023, 15, 12021. [Google Scholar] [CrossRef]
- Li, S.; Zhang, H.; Yi, J.; Liu, H. A bi-level planning approach of logistics unmanned aerial vehicle route network. Aerosp. Sci. Technol. 2023, 141, 108572. [Google Scholar] [CrossRef]
- Hu, Z.; Huang, Y.; Li, Y.; Bao, X. Drone-Based Instant Delivery Hub-and-Spoke Network Optimization. Drones 2024, 8, 247. [Google Scholar] [CrossRef]
- Gao, C.; Hu, Z.; Wang, Y. Optimizing the Hub-and-Spoke Network with Drone-Based Traveling Salesman Problem. Drones 2023, 7, 6. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Lu, J.; Wang, S. Air Route Network Planning Method of Urban Low-Altitude Logistics UAV with Double-Layer Structure. Drones 2025, 9, 193. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, H.; Pu, F.; Zhang, Y.; He, W. Research of Airspace Gridding Method and Its Application in Air Traffic Management. Adv. Aeronaut. Sci. Eng. 2021, 12, 12–24. [Google Scholar]
- Liao, X.; Xu, C.; Ye, H.; Tan, X.; Fang, S.; Huang, Y.; Lin, J. Critical Infrastructures for Developing UAVs’ Applications and Low-altitude Public Air-route Network Planning. Bull. Chin. Acad. Sci. 2022, 37, 977–988. [Google Scholar]
- Fraga-Lamas, P.; Fernández-Caramés, T.M.; Da Cruz, A.M.R.; Lopes, S.I. An Overview of Blockchain for Industry 5.0: Towards Human-centric, Sustainable and Resilient Applications. IEEE Access 2024, 12, 116162–116201. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Feng, D.; Du, S.; Zhong, G.; Deng, C.; Zhou, J. A Logistics UAV Parcel-Receiving Station and Public Air-Route Planning Method Based on Bi-Layer Optimization. Appl. Sci. 2023, 13, 1842. [Google Scholar] [CrossRef]
- Primatesta, S.; Rizzo, A.; la Cour-Harbo, A. Ground risk map for unmanned aircraft in urban environments. J. Intell. Robot. Syst. 2020, 97, 489–509. [Google Scholar] [CrossRef]
- Alexander, W.N.; Whelchel, J. Flyover noise of multi-rotor sUAS. In Proceedings of the Inter-Noise and Noise-Con Congress and Conference Proceedings, Madrid, Spain, 30 September 2019; Institute of Noise Control Engineering: Madrid, Spain, 2019; Volume 259, pp. 2548–2558. [Google Scholar]
- Zhang, Q.; Xu, W.; Zhang, H.; Zou, Y.; Chen, Y. Path planning for logistics UAV in complex low-altitude airspace. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1275–1286. [Google Scholar]







| Property | Grid Access Rules |
|---|---|
| Communication signal blind spots | |
| Electromagnetic interference area | |
| Physical obstacles | |
| Buildings | |
| Government and military key areas | |
| Special event areas | |
| Temporary no-fly zones established under dynamic demand conditions | |
| Other |
| Shielding Type | Value |
|---|---|
| No Shelters | 0.00 |
| Scattered Trees | 0.25 |
| Vehicles and Low-rise Structures | 0.50 |
| High-rise Structures | 0.75 |
| Industrial Structures | 1.00 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 95 | 10 | /(¥·) | 1.2 | ||
| 2.36 | 5 | 3 | |||
| 4 | /(m/s) | 0.5 | |||
| 1.2 | 10 | 30 | |||
| 16.3 | 95 | 20 | |||
| 1.4 | 9.14 | 10 | |||
| 10.36 | 100 | ||||
| 64 | 12 | ||||
| /° | 180 |
| Number | Coordinates | Number | Coordinates | Number | Coordinates | Number | Coordinates |
|---|---|---|---|---|---|---|---|
| 1 | (69, 142) | 6 | (161, 137) | 11 | (162, 90) | 16 | (92, 32) |
| 2 | (43, 155) | 7 | (138, 23) | 12 | (132, 27) | 17 | (86, 96) |
| 3 | (71, 162) | 8 | (143, 41) | 13 | (113, 4) | 18 | (55, 51) |
| 4 | (125, 151) | 9 | (145, 83) | 14 | (119, 47) | 19 | (64, 85) |
| 5 | (142, 163) | 10 | (164, 81) | 15 | (110, 96) | 20 | (58, 132) |
| Type | Connectivity Rate Before Optimization | Connectivity Rate After Optimization |
|---|---|---|
| The method in this paper | 30% | 100% |
| The sequential matching method | 30% | 70% |
| The greedy matching method | 5% | 20% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, O.; Zhang, H.; Wang, F.; Tang, W.; Zhong, G. A Method for Orderly and Parallel Planning of Public Route Networks for Logistics Based on Urban Low-Altitude Digital Airspace Environment Risks. Drones 2025, 9, 634. https://doi.org/10.3390/drones9090634
Feng O, Zhang H, Wang F, Tang W, Zhong G. A Method for Orderly and Parallel Planning of Public Route Networks for Logistics Based on Urban Low-Altitude Digital Airspace Environment Risks. Drones. 2025; 9(9):634. https://doi.org/10.3390/drones9090634
Chicago/Turabian StyleFeng, Ouge, Honghai Zhang, Fei Wang, Weibin Tang, and Gang Zhong. 2025. "A Method for Orderly and Parallel Planning of Public Route Networks for Logistics Based on Urban Low-Altitude Digital Airspace Environment Risks" Drones 9, no. 9: 634. https://doi.org/10.3390/drones9090634
APA StyleFeng, O., Zhang, H., Wang, F., Tang, W., & Zhong, G. (2025). A Method for Orderly and Parallel Planning of Public Route Networks for Logistics Based on Urban Low-Altitude Digital Airspace Environment Risks. Drones, 9(9), 634. https://doi.org/10.3390/drones9090634









