A Multi-UAV Distributed Collaborative Search Algorithm Based on Maximum Entropy Mechanism
Abstract
1. Introduction
- (1)
- A search mechanism based on dynamic entropy guides UAVs to explore unknown areas. An entropy matrix is constructed to quantify the exploration value of the mission area, and a dynamic entropy model is established in the environment update function: the entropy value of explored areas decays exponentially, while unexplored areas maintain high entropy values. By using entropy to reflect regional uncertainty, UAVs are guided to high-entropy regions, enabling efficient multi-UAV search.
- (2)
- A cooperative framework based on DMPC is combined with a receding horizon optimization model to quickly implement the Observe-Orient-Decide-Act (OODA) closed-loop mechanism. Through a dynamic prediction model, each UAV solves for the optimal heading angle based on existing environmental information, realizing local information interaction in the Observe phase, search direction plan adjustment in the Orient phase, decision selection in the Decide phase, and final action execution in the Act phase.
- (3)
- A multi-objective optimization function based on dynamic weights was designed to address the issues of multi-machine collaborative obstacle avoidance and coverage balancing. Through adaptive weight adjustment, a dynamic balance is achieved between rapid coverage in the initial stage and fine search in the later stage, and Adaptive Differential Evolution (ADE) is used to solve the optimal heading angle sequence in real time, improving search intelligence.
2. System Model
2.1. Problem Description
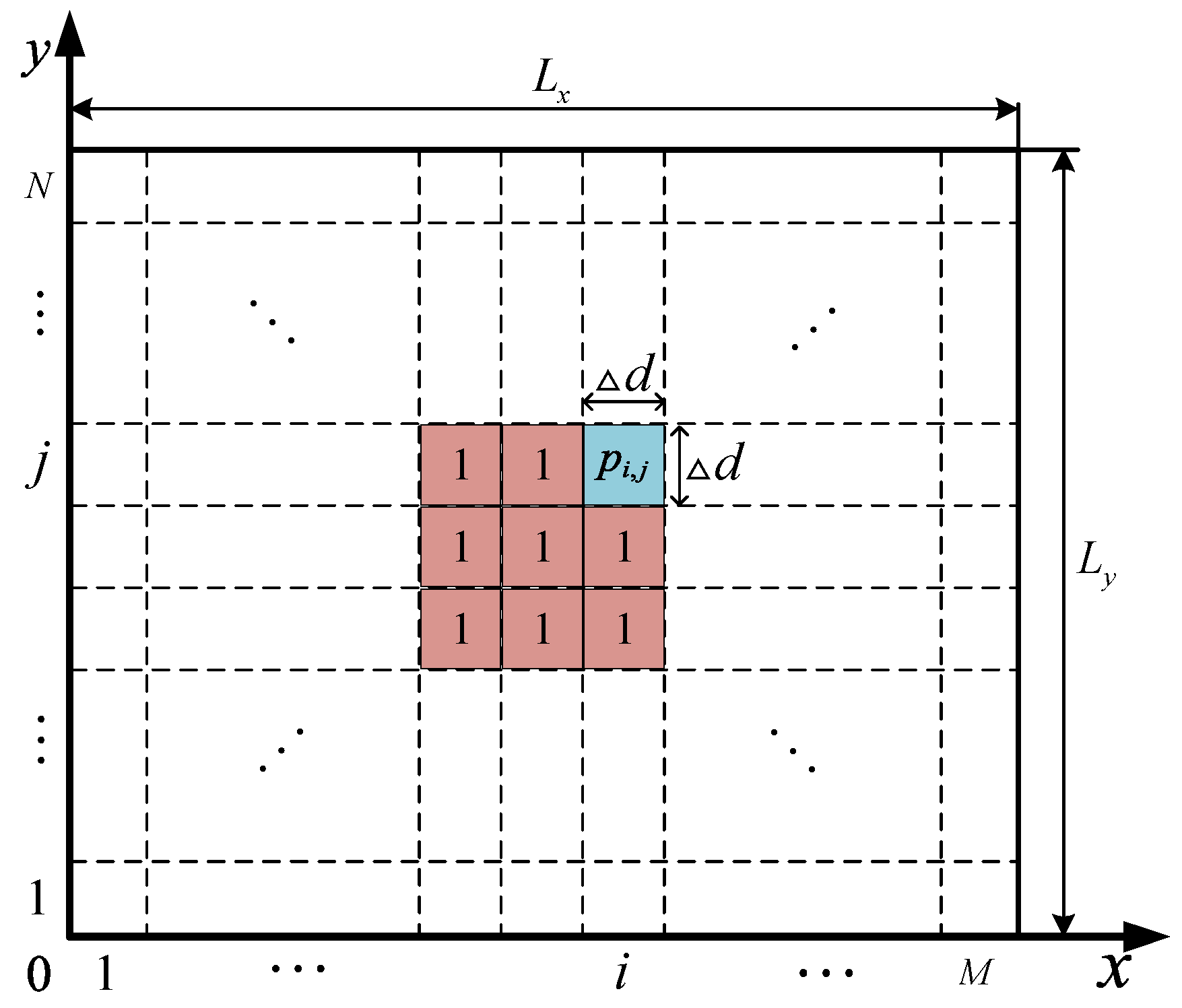
2.2. UAV Mission Space Model
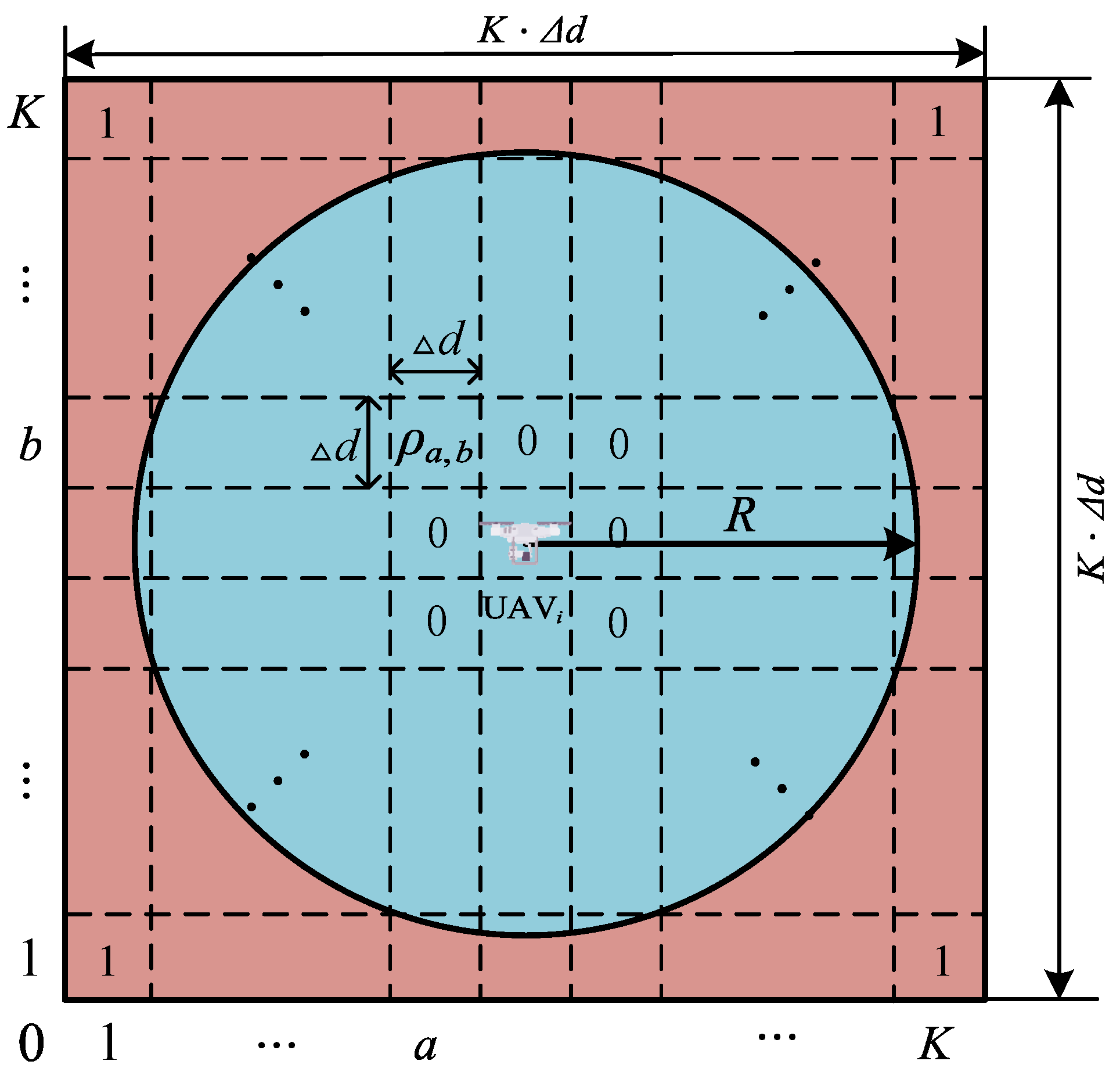
2.3. UAV Model
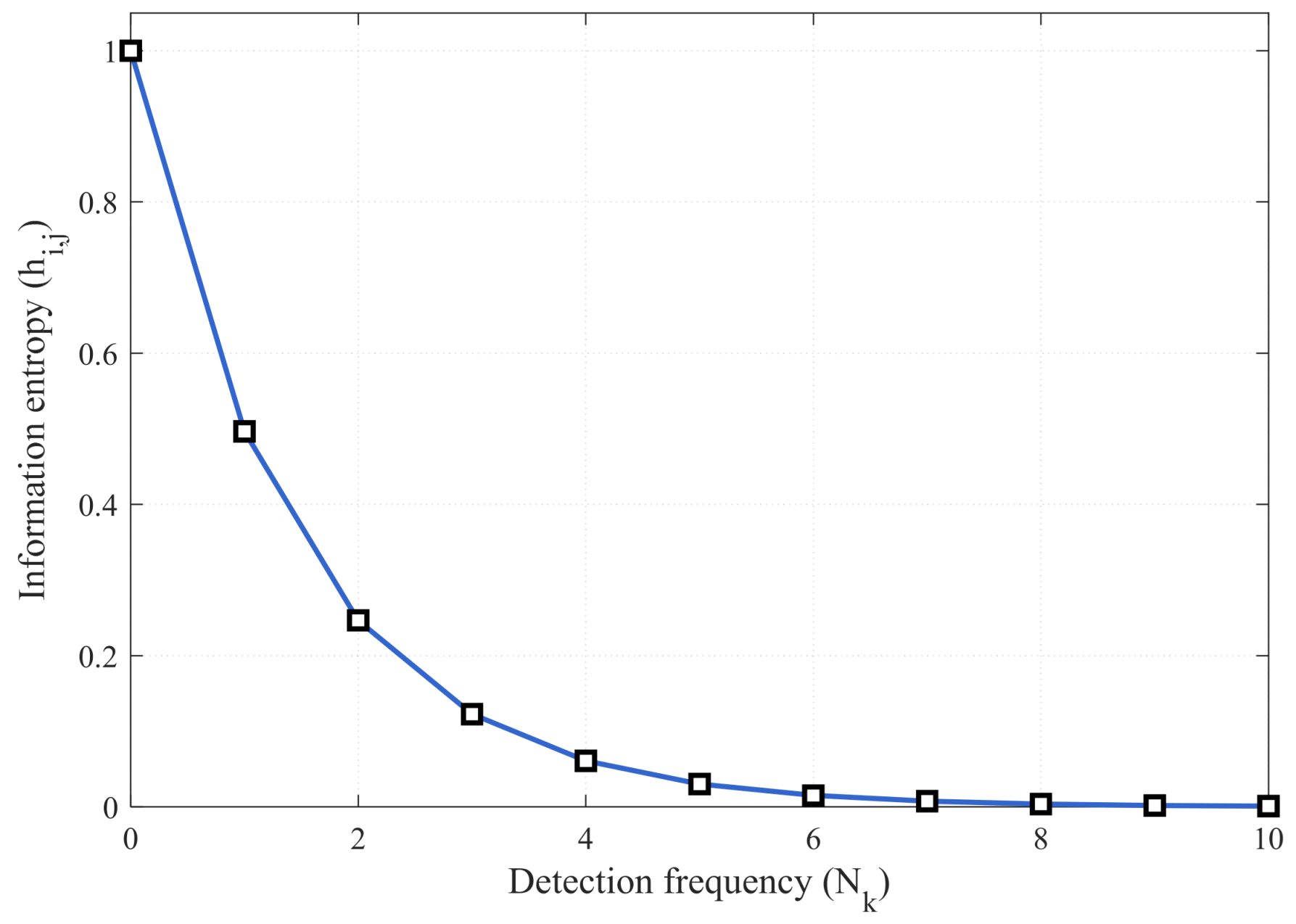
2.4. Maximum Entropy Model
3. Cooperative Decision-Making Optimization Framework Based on Maximum Entropy Mechanism
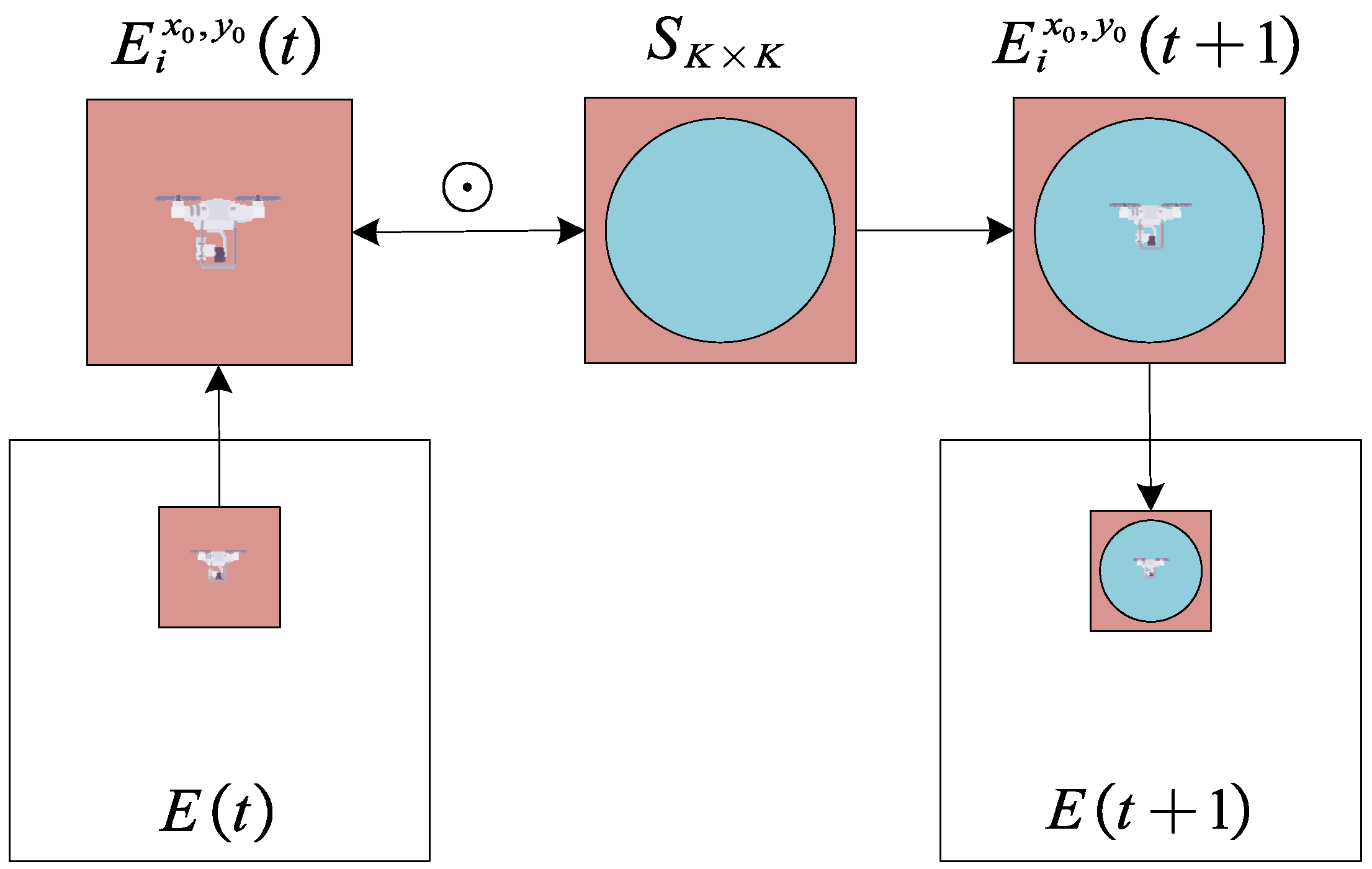
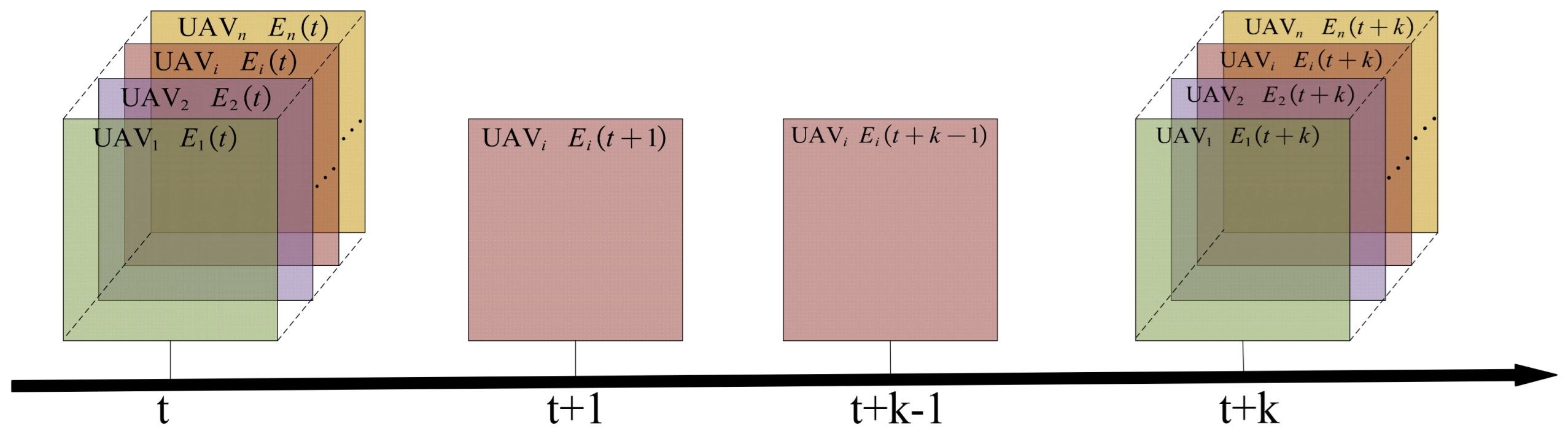
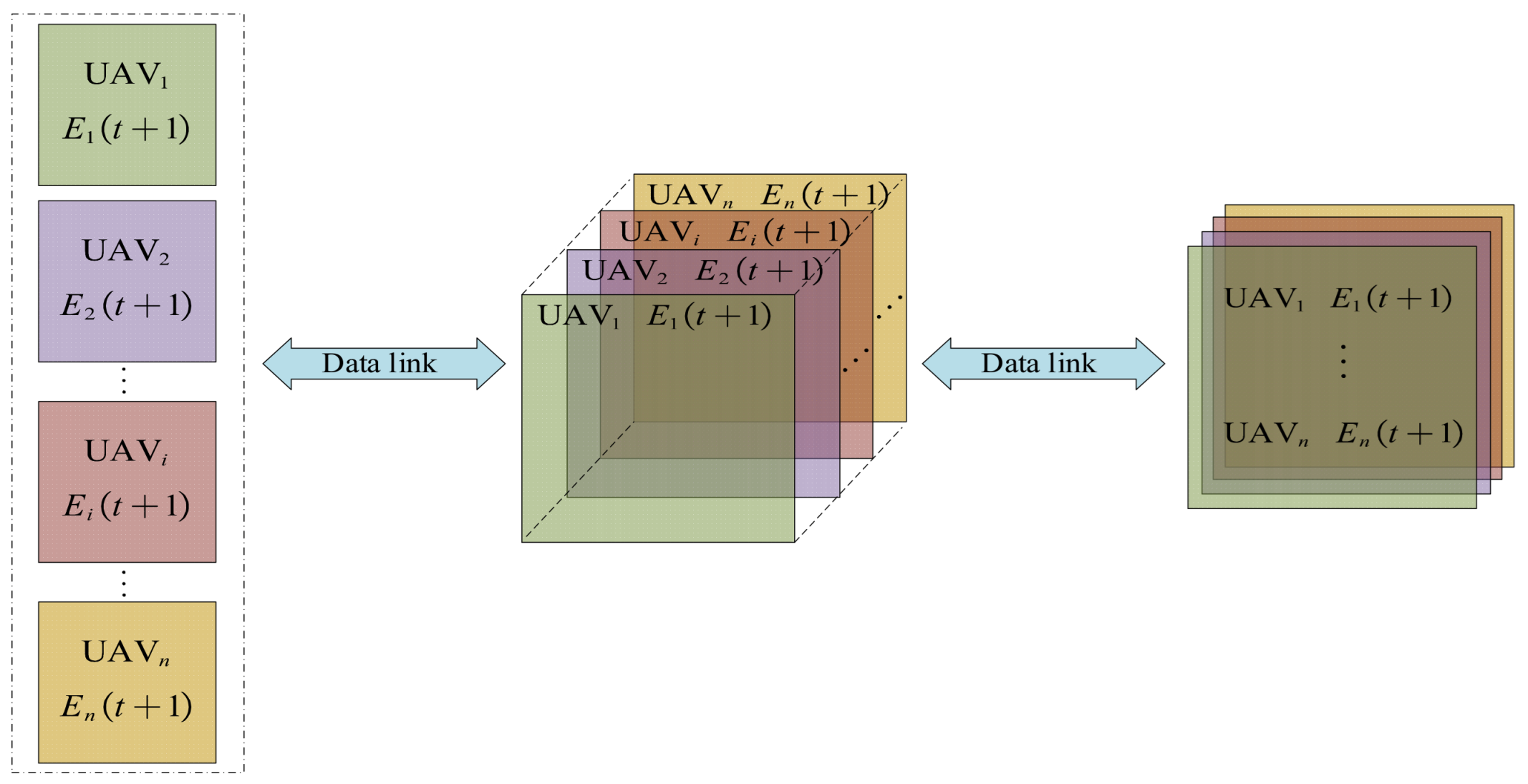
3.1. Update and Fusion of Environmental Maps
3.2. Search Benefit Function
- (1)
- Coverage increment: Each UAV in the cluster will prioritize the direction with the largest increment in coverage area when adjusting its flight angle, so as to complete the search task in a shorter time. The coverage rate of the mission area at the corresponding time is obtained by calculating at that time:
- (2)
- Entropy gain: Entropy reflects the uncertainty in the mission area rather than a simple coverage state [45,46,47]. The search potential field generated by the gradient characteristics of the entropy field drives UAVs to search in high-entropy areas. The corresponding entropy gain is as shown in Formula (14):
- (3)
- Yaw angle constraint: The yaw angle is the main control variable in the entire search task, but a larger yaw angle is accompanied by greater energy consumption, which affects endurance time. Therefore, this yaw angle constraint is designed to reduce the negative impact caused by excessively large turning angles, as shown in Formula (15):
- (4)
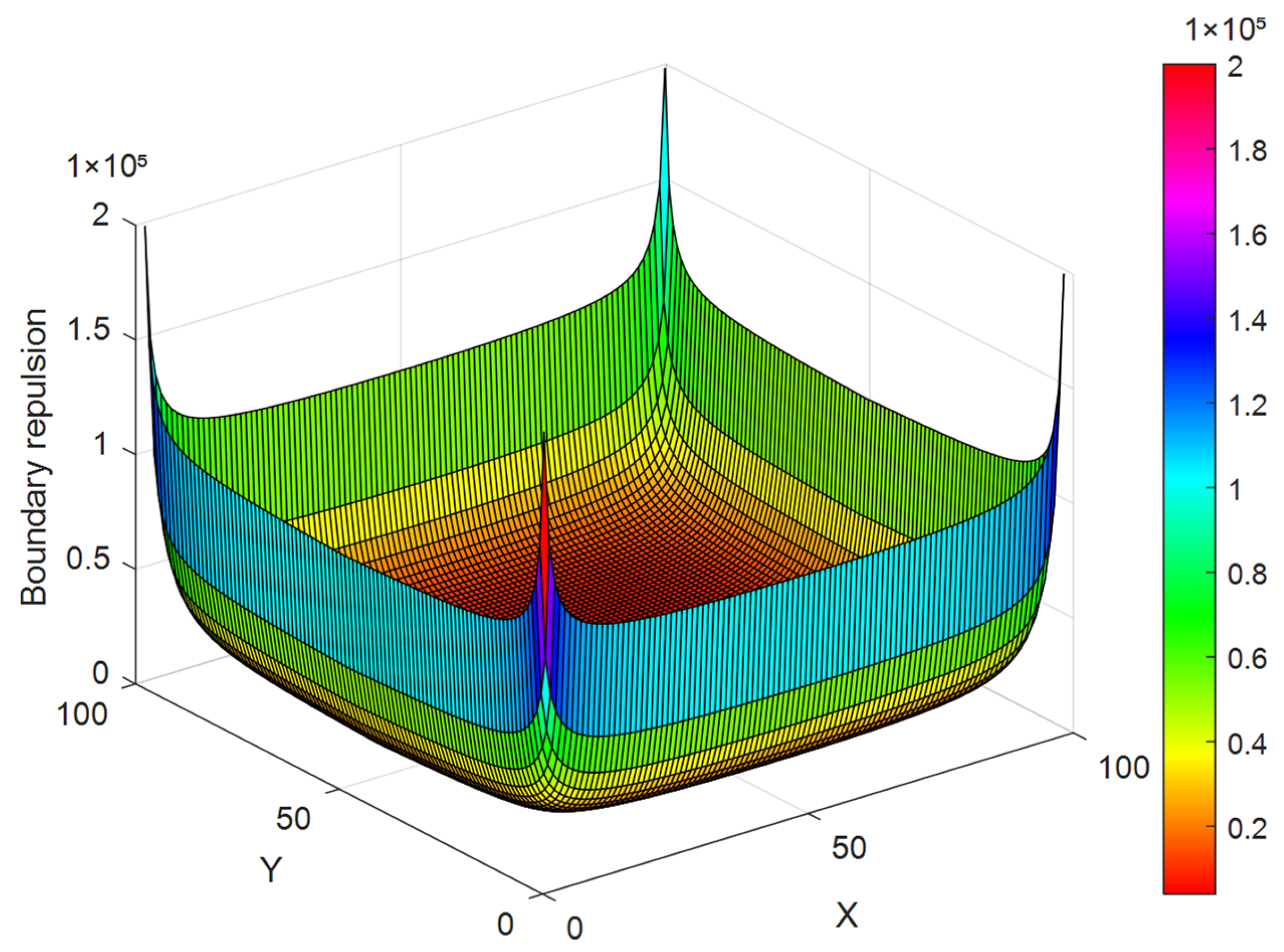
- Boundary constraint: When explores near the boundary, the effective search area of the UAV will be reduced. A virtual potential field is designed to provide boundary repulsion to prevent this situation [48]. The magnitude of the boundary repulsion is inversely proportional to the distance from the UAV to the boundary; the closer the distance, the greater the repulsion, as shown in Formula (16) and Figure 8:
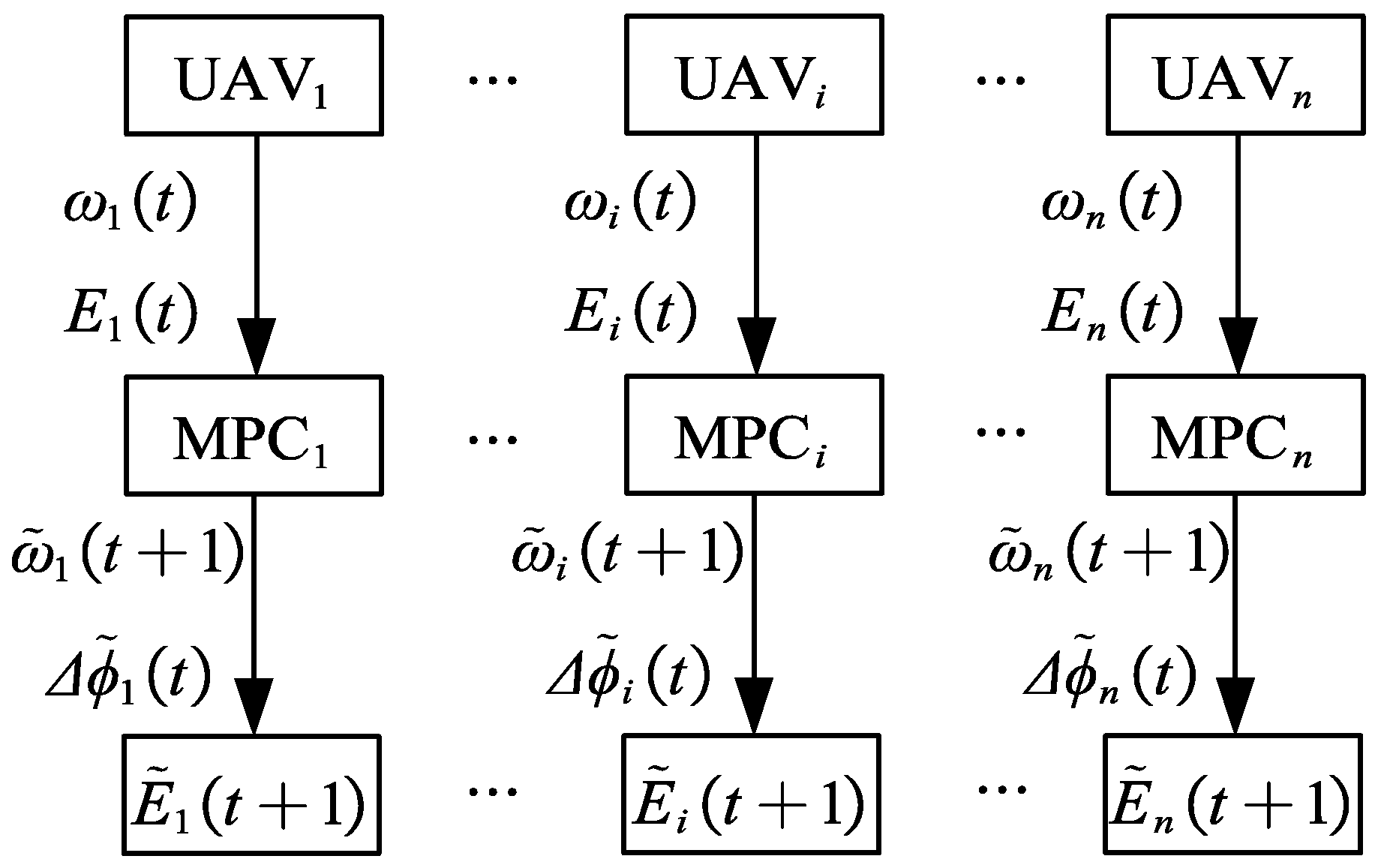
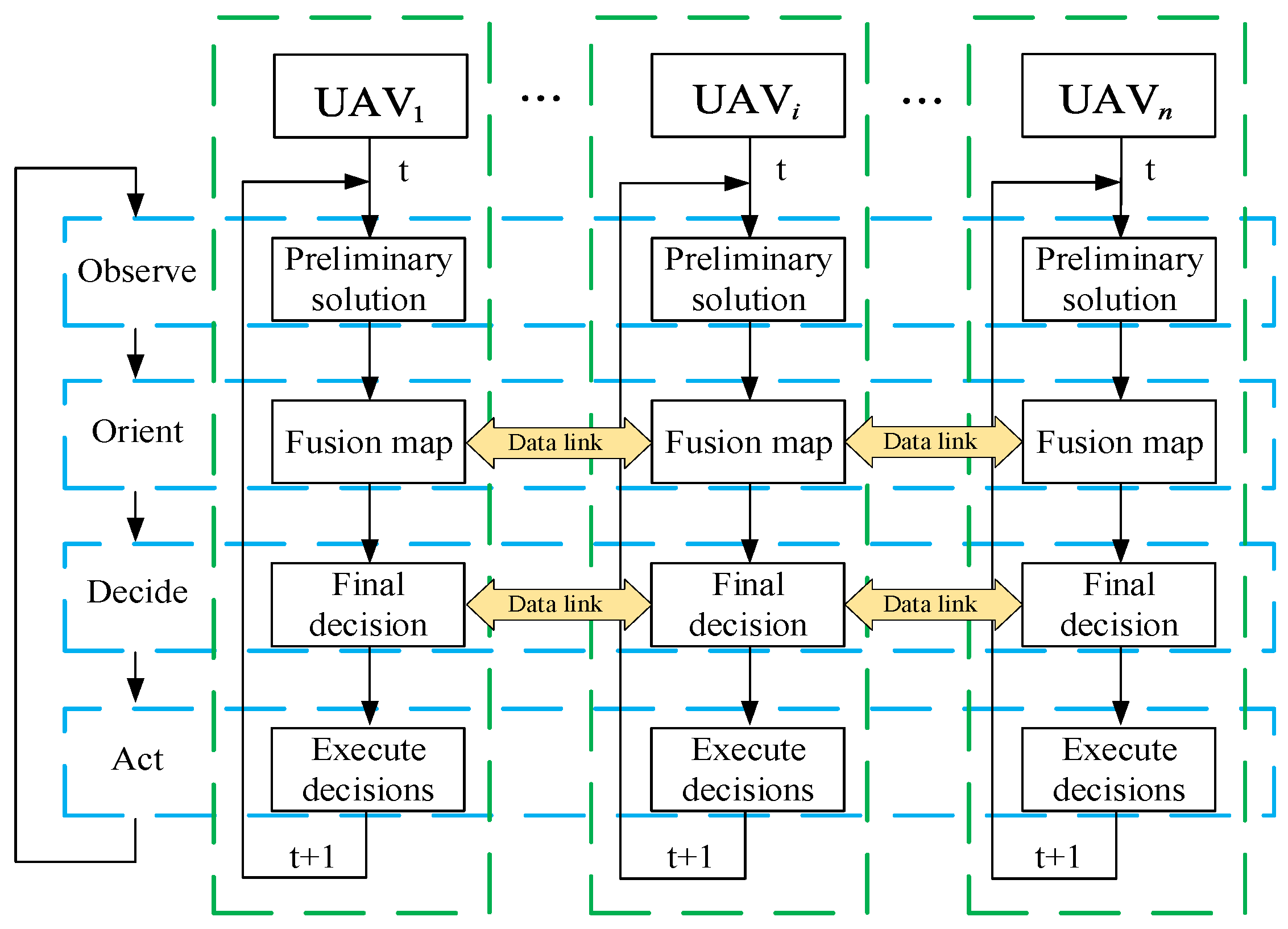
3.3. Decision Optimization and Solution of DMPC-OODA Based on Maximum Entropy Mechanism
| Algorithm 1 Solution of DMPC-OODA based on maximum entropy mechanism |
| Initialization task parameters: UAV state equation , Environmental matrix , Grid state , Entropy matrix for t = 1: for i = 1: Calculate the UAV state equation and preliminary control input according to Equation (4) and Equation (20) Calculate the environment matrix and entropy matrix according to Equation (2) and Equation (8) end for Communication network sharing and sending , . Receive , from other machine for i = 1: Update according to Equation (10) Based on calculation, the final decision is update end for Update the global if set threshold break end if end for |
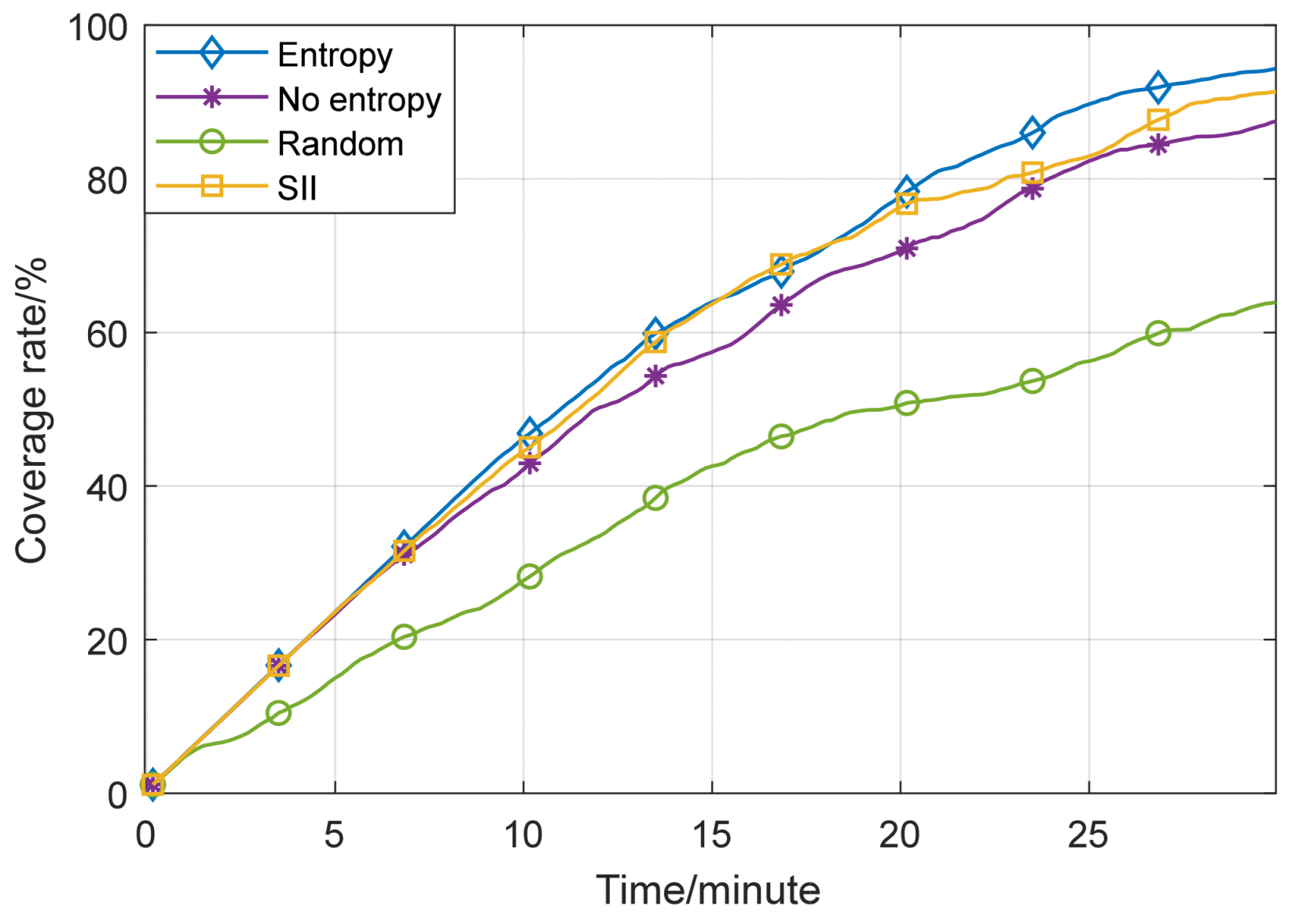
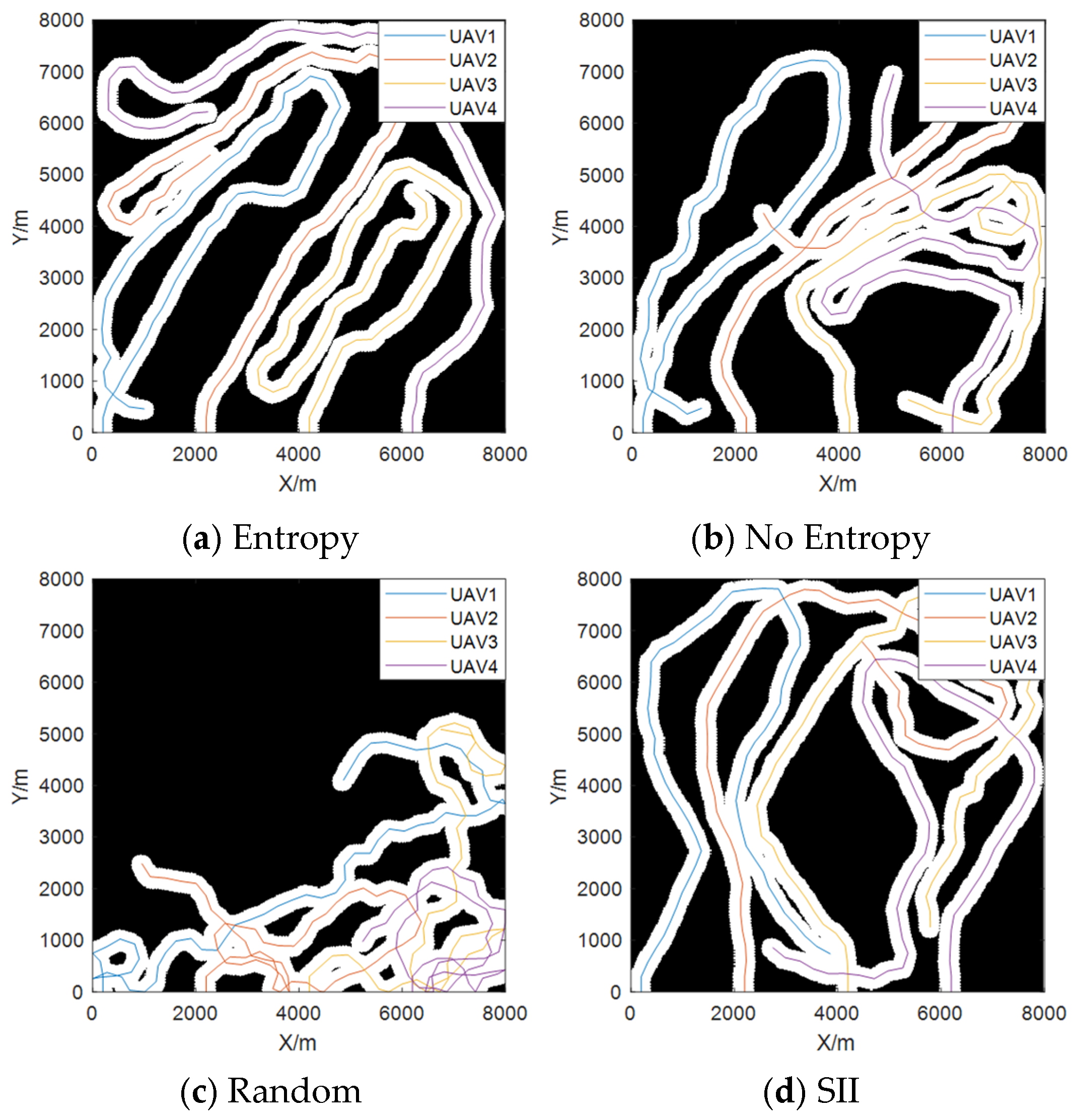
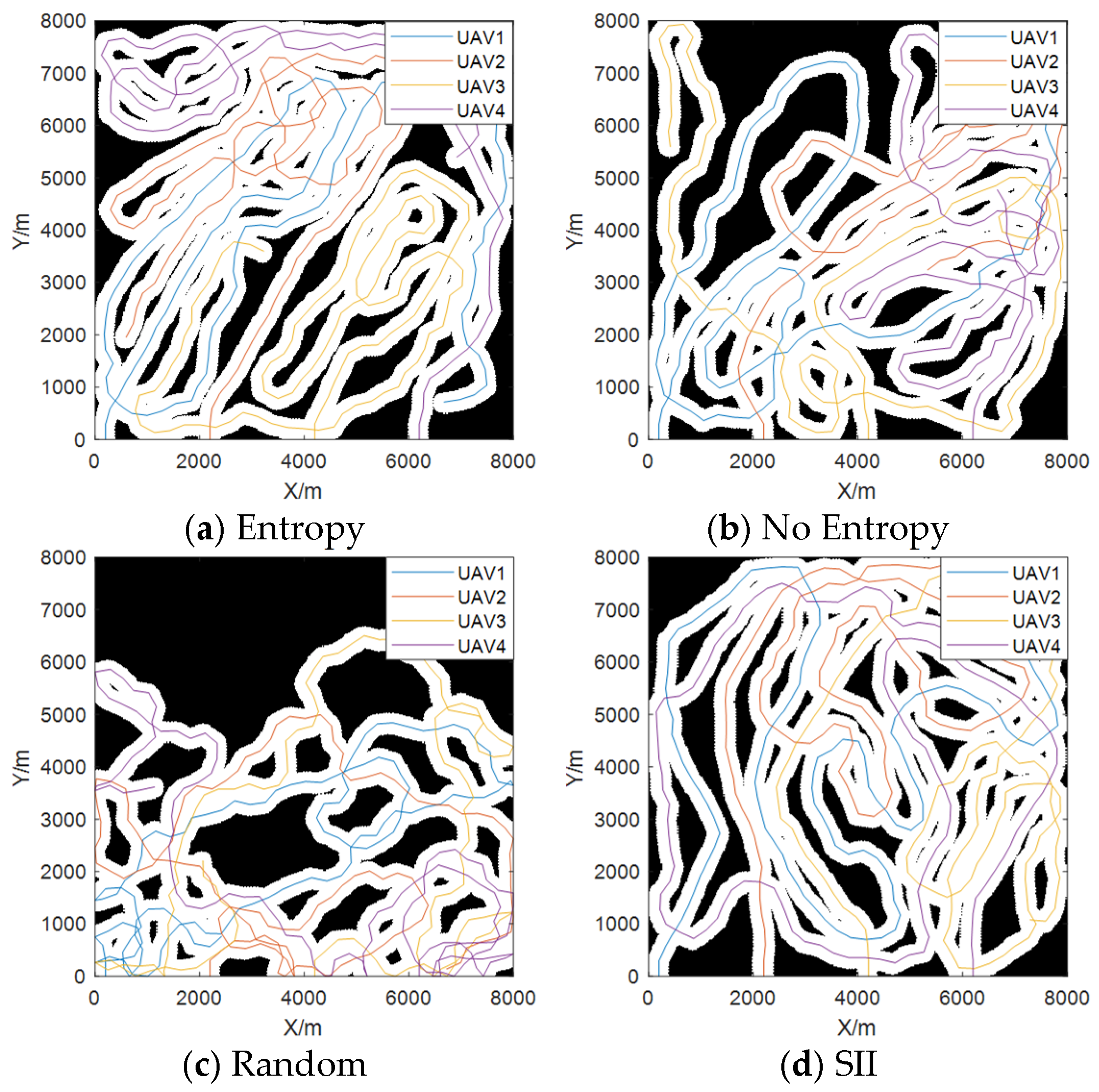
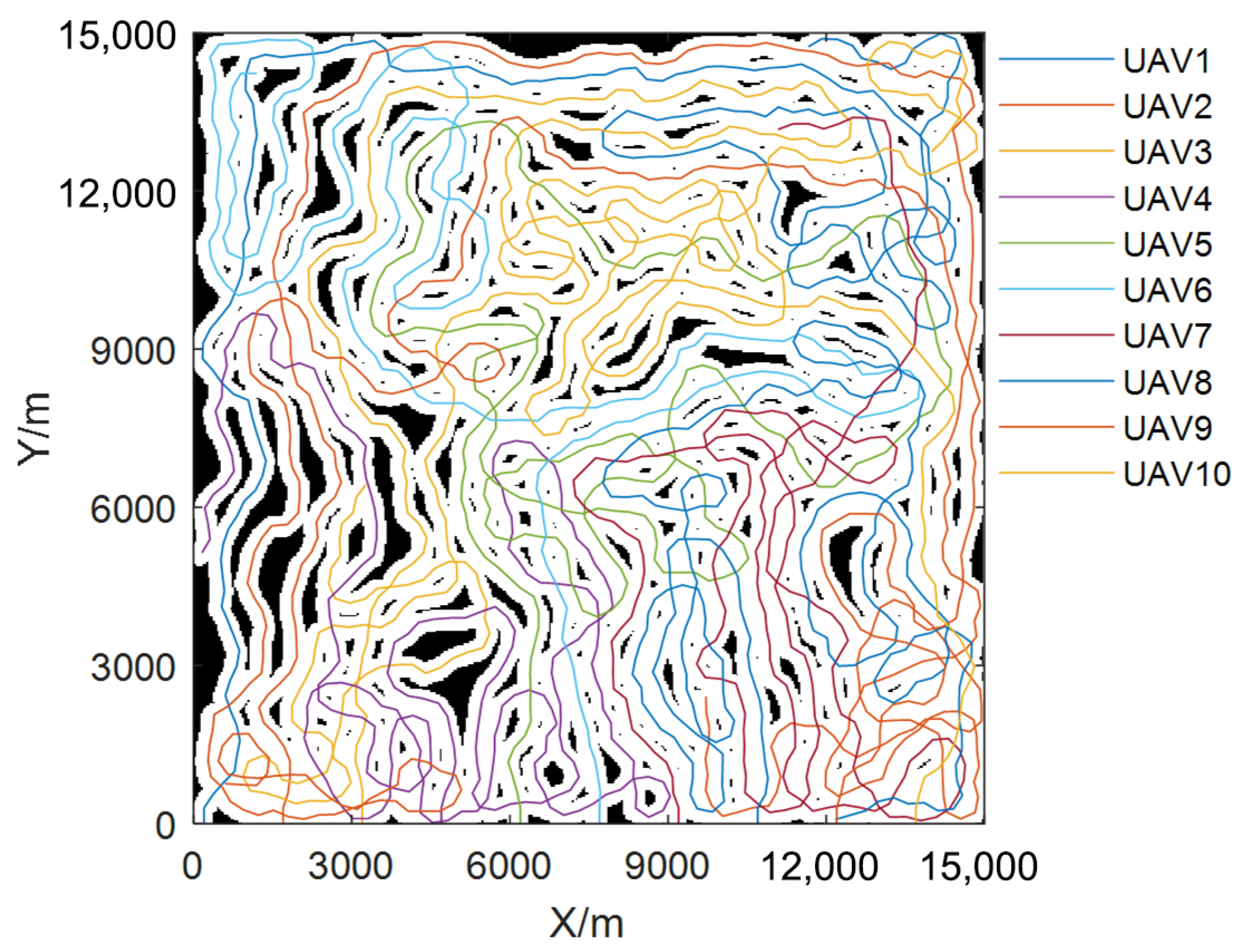
4. Simulation Experiments
5. Summary
- (1)
- Dynamic Exponentially Decaying Entropy Model: An entropy model is constructed to quantify environmental uncertainty, effectively guiding UAVs toward high-entropy (high-uncertainty) regions.
- (2)
- Integration of DMPC and OODA Decision Loop: DMPC is innovatively integrated with the OODA Decision Loop and achieves rapid updating and fusion of environmental maps through element-by-element multiplication operations, resulting in a highly efficient rolling time-domain co-optimization framework.
- (3)
- Adaptive Dynamic Weight Function: A dynamic weight function is designed to balance coverage gain and entropy gain, facilitating a smooth transition of strategies from “rapid coverage” to “accurate exploration”.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Xin, B.; Dou, L.-H.; Chen, J.; Hirota, K. A Review of Cooperative Path Planning of an Unmanned Aerial Vehicle Group. Front. Inf. Technol. Electron. Eng. 2020, 21, 1671–1694. [Google Scholar] [CrossRef]
- Zhou, Y.; Rao, B.; Wang, W. UAV Swarm Intelligence: Recent Advances and Future Trends. IEEE Access 2020, 8, 183856–183878. [Google Scholar] [CrossRef]
- Li, H.; Sun, H.; Zhou, R.; Zhang, H. Hybrid TDOA/FDOA and track optimization of UAV swarm based on A-optimality. Syst. Engin. Electron. 2023, 34, 149–159. [Google Scholar] [CrossRef]
- Sheng, L.; Shi, M.H.; Qi, Y.C.; Li, H.; Pang, M.J. Dynamic offense and defense of UAV swarm based on situation evolution game. Syst. Engin. Electron. 2023, 45, 2332–2342. [Google Scholar]
- Fan, X.; Li, H.; Chen, Y.; Dong, D. A Path-Planning Method for UAV Swarm under Multiple Environmental Threats. Drones 2024, 8, 171. [Google Scholar] [CrossRef]
- Fan, X.; Li, H.; Chen, Y.; Dong, D. UAV Swarm Search Path Planning Method Based on Probability of Containment. Drones 2024, 8, 132. [Google Scholar] [CrossRef]
- Cheng, Z.; Yang, J.; Sun, J.; Zhao, L. Trajectory Planning of Unmanned Aerial Vehicles in Complex Environments Based on Intelligent Algorithm. Drones 2025, 9, 468. [Google Scholar] [CrossRef]
- Hao, L.; Xiangyu, F.; Manhong, S. Research on the cooperative passive location of moving targets based on improved particle swarm optimization. Drones 2023, 7, 264. [Google Scholar] [CrossRef]
- Wang, W.; Bai, P.; Li, H.; Liang, X. Optimal configuration and path planning for UAV swarms using a novel localization approach. Appl. Sci. 2018, 8, 1001. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, B.; Zhang, Q.; Gao, C.; Feng, J.; Yue, L. Large-area coverage path planning method based on vehicle–UAV collaboration. Appl. Sci. 2025, 15, 1247. [Google Scholar] [CrossRef]
- Lun, Y.; Wang, H.; Wu, J.; Liu, Y.; Wang, Y. Target Search in Dynamic Environments With Multiple Solar-Powered UAVs. IEEE Trans. Veh. Technol. 2022, 71, 9309–9321. [Google Scholar] [CrossRef]
- Fei, B.; Bao, W.; Zhu, X.; Liu, D.; Men, T.; Xiao, Z. Autonomous Cooperative Search Model for Multi-UAV With Limited Communication Network. IEEE Internet Things J. 2022, 9, 19346–19361. [Google Scholar] [CrossRef]
- Chai, S.; Yang, Z.; Huang, J.; Li, X.; Zhao, Y.; Zhou, D. Cooperative UAV search strategy based on DMPC-AACO algorithm in restricted communication scenarios. Def. Technol. 2024, 31, 295–311. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, Z.; Li, J.; Wang, L.; Zhang, X.; Gao, H. Communication-Constrained UAVs’ Coverage Search Method in Uncertain Scenarios. IEEE Sens. J. 2024, 24, 17092–17101. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Bai, Z.; Lin, W.; Ding, W.R. Cooperative Search Method for Ground Moving Targets Using Multiple UAVs. Syst. Eng. Electron. 2018, 40, 1498–1505. [Google Scholar] [CrossRef]
- Li, Y. Research on Cooperative Formation Control of Multi-UAVs Based on Distributed Search and Capture Algorithm. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Luo, L. Research on the Strategy of Cooperative Search for Moving Targets by UAV Swarm Based on Search Benefit Balance. Master’s Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2024. [Google Scholar] [CrossRef]
- Xie, P.Z.; Wei, C. Research on Multi-UAV Scanning Line Search Method Based on Unilateral Region Segmentation. Aero Weapon. 2020, 27, 67–72. [Google Scholar]
- Chen, X.L.; Peng, X.H.; Kong, J.T. Cooperative Search and Experimental Verification of Multi-UAVs Under Limited Information Conditions. Control Eng. 2025, 1–8. [Google Scholar] [CrossRef]
- Niu, Z.; Jia, X.; Yao, W. Communication-Free MPC-Based Neighbors Trajectory Prediction for Distributed Multi-UAV Motion Planning. IEEE Access 2022, 10, 13481–13489. [Google Scholar] [CrossRef]
- Du, J.Y.; Zhang, F.M.; Mao, H.B.; Liu, H.W.; Mao, Y.Y. Game Theory Model and Fast Solution Method for Multi-UAV Cooperative Search. J. Shanghai Jiaotong Univ. 2013, 47, 667–673. [Google Scholar]
- Wu, A.; Yang, R.N.; Liang, X.L.; Hou, Y.Q. Cooperative Search Algorithm for UAV Swarm Based on Pheromone Decision. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 814–827. [Google Scholar] [CrossRef]
- Li, C. Research on Autonomous Cooperative Search Using UAV Swarms. Master’s Thesis, Zhejiang University, Hangzhou, China, 2019; pp. 1–8. [Google Scholar]
- Wang, W.; Chen, Y.; Zhang, Y.; Chen, Y.; Du, Y. Collaborative Search Algorithm for Multi-UAVs Under Interference Conditions: A Multi-Agent Deep Reinforcement Learning Approach. Drones 2025, 9, 445. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, S.; Wang, C.; Liu, Y.; Ding, Y.; Wang, H. Integrated Reinforcement Learning Framework for UAV Swarm Two-Stage Cooperative Multitarget Detection Tasks. IEEE Internet Things J. 2025, 12, 9435–9448. [Google Scholar] [CrossRef]
- Dong, P.; Liu, J.; Tao, H.; Ruby, R.; Jian, M.; Luo, H. An Optimized Scheduling Scheme for UAV-USV Cooperative Search via Multi-Agent Reinforcement Learning Approach. In Proceedings of the 2024 20th International Conference on Mobility, Sensing and Networking (MSN), Harbin, China, 20–22 December 2024; pp. 172–179. [Google Scholar] [CrossRef]
- Zou, L.; Tan, Y. Collaborative Search Planning of UAV Swarms Based on Deep Reinforcement Learning. In Proceedings of the 2023 5th International Conference on Intelligent Control, Measurement and Signal Processing (ICMSP), Chengdu, China, 19–21 May 2023; pp. 1184–1187. [Google Scholar] [CrossRef]
- Guo, K.; Luo, H.; Tao, H.; Ruby, R.; Qin, Z.; Liu, K. Multi-UAVs Collaborative Search Scheme in Marine Environments using Deep Reinforcement Learning. In Proceedings of the 2023 Eleventh International Conference on Advanced Cloud and Big Data (CBD), Danzhou, China, 18–19 December 2023; pp. 39–44. [Google Scholar] [CrossRef]
- Ni, J.; Tang, G.; Mo, Z.; Cao, W.; Yang, S.X. An Improved Potential Game Theory Based Method for Multi-UAV Cooperative Search. IEEE Access 2020, 8, 47787–47796. [Google Scholar] [CrossRef]
- Ma, T.; Jiang, J.; Liu, X.; Liu, R.; Sun, H. Target Search of UAV Swarm Based on Improved Wolf Pack Algorithm. In Proceedings of the 2023 6th International Symposium on Autonomous Systems (ISAS), Nanjing, China, 23–25 June 2023; pp. 1–6. [Google Scholar]
- Hou, Y.Q.; Liang, X.L.; He, L.L.; Liu, L. Cooperative Area Search Algorithm for UAV Swarm in Unknown Environment. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 347–356. [Google Scholar]
- Wang, N.; Li, Z.; Liang, X.L.; Hou, Y.; Wu, A. Cooperative Search Algorithm for UAV Swarm Based on Search Intention Interaction. J. Beijing Univ. Aeronaut. Astronaut. 2022, 48, 454–463. [Google Scholar]
- Zheng, H.J. Investigation on the UAV Path Planning Problem of Area Reconnaissance. Master’s Thesis, National University of Defense Technology, Changsha, China, 2011; pp. 5–8. [Google Scholar]
- Liu, C.; Gao, X.G.; Fu, X.W. Distributed Cooperative Target Search Algorithm for Multi-UAVs With Controllable Revisit Mechanism Based on Digital Pheromone. Syst. Eng. Electron. 2017, 39, 1999–2010. [Google Scholar]
- Shen, D.; Wei, R.X.; Qi, X.M.; Guan, X. Receding Horizon Decision Method Based on MTPM and DPM for Multi-UAVs Cooperative Large Area Target Search. Acta Autom. Sin. 2014, 40, 1391–1403. [Google Scholar]
- Qin, Y.; Zhao, F.Y.; Li, X.Z.; Wei, D.; Chen, S.; Li, Z. Prediction of Flight Status of Logistics UAVs Based on an Information Entropy Radial Basis Function Neural Network. Sensors 2021, 21, 3651. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Yang, Z.H.; Liu, T.; Zhang, Y.; Zhang, N. An Information-Entropy-Based Hierarchical Serialization Allocation Method for UAV Tracking in 6G Networks. Wirel. Commun. Mob. Comput. 2022, 2022, 1–15. [Google Scholar] [CrossRef]
- Xuan, Y.L.; Jiang, G.D.; Sun, T.; Tan, L.; Wang, L.F. Template-Guided Frequency Attention and Adaptive Cross-Entropy Loss for UAV Visual Tracking. Chin. J. Aeronaut. 2023, 36, 299–312. [Google Scholar]
- Ju, R.; Zhang, H.; Han, W.; Ge, S.S. Maximum Entropy Searching. CAAI Trans. Intell. Technol. 2019, 4, 1–8. [Google Scholar] [CrossRef]
- Singh, C.; Sharma, A. Modified Online Newton Step Based on Element Wise Multiplication. Comput. Intell. 2020, 36, 1010–1025. [Google Scholar] [CrossRef]
- Ozel, M.; Varol, D. On the Lower Bounds for the Minimum Eigenvalue of the Hadamard Product of an M-Matrix and Its Inverse. Linear Algebra Appl. 2021, 28, 439–443. [Google Scholar]
- Zou, R.; Guo, C.C.; Chen, X.C.; Li, F.; Yi, D.; Wu, Y. Genetic Algorithm Optimised Hadamard Product Method for Inconsistency Judgement Matrix Adjustment in AHP and Automatic Analysis System Development. Expert Syst. Appl. 2023, 211, 118689. [Google Scholar]
- Tian, W.Y.; Liu, L.; Wang, Q.S. Fast Search Method for Moving Targets Using Multiple UAVs Cooperative Searching. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022. [Google Scholar]
- Wu, W.C.; Huang, C.Q.; Song, L.; Tang, S.Q.; Bai, R.C. Cooperative Search and Path Planning of Multi-Unmanned Air Vehicles in Uncertain Environment. Acta Armamentarii 2011, 32, 1337–1342. [Google Scholar]
- Zhang, S.Q.; Yang, H.T. Quantitative Description of Uncertainty and Entropic Uncertainty Relation. Acta Phys. Sin. 2023, 72. [Google Scholar] [CrossRef]
- Deng, Z.Y.; Yuan, H.; Wang, D.; Yuan, H.; Yang, J.; Ye, L. Experimental Investigation of Entropic Uncertainty Relations and Coherence Uncertainty Relations. Phys. Rev. A 2020, 101, 032101. [Google Scholar] [CrossRef]
- Floerchinger, S.; Haas, T.; Hoeber, B. Relative Entropic Uncertainty Relation. Phys. Rev. A 2021, 103, 062209. [Google Scholar] [CrossRef]
- Fu, Q.X.; Liang, X.L.; Zhang, J.Q. Design and Implementation of Autonomous Flight Unmanned Aircraft System Geo-Fence Algorithm. J. Xi’an Jiaotong Univ. 2019, 53, 167–175. [Google Scholar]
- Bryant, D. Rethinking OODA: Toward a Modern Cognitive Framework of Command Decision Making. Mil. Psychol. 2006, 18, 183–206. [Google Scholar] [CrossRef]
- Huang, Y.Y. Modeling and Simulation Method of the Emergency Response Systems Based on OODA. Knowl.-Based Syst. 2015, 89, 527–540. [Google Scholar] [CrossRef]
- Wu, W.L.; Zhou, X.S.; Shen, B. Comprehensive Evaluation of the Intelligence Levels for Unmanned Swarms Based on the Collective OODA Loop and Group Extension Cloud Model. Connect. Sci. 2022, 34, 630–651. [Google Scholar] [CrossRef]
- Revay, M.; Liska, M. OODA Loop in Command & Control Systems. In Proceedings of the 2017 Communication and Information Technologies (KIT), Vysoke Tatry, Slovakia, 4–6 October 2017; pp. 127–130. [Google Scholar]
- Huang, J.; Zhou, N.; Cao, M. Adaptive Fuzzy Behavioral Control of Second-Order Autonomous Agents With Prioritized Missions: Theory and Experiments. IEEE Trans. Ind. Electron. 2019, 66, 9612–9622. [Google Scholar] [CrossRef]
- Brezocnik, L.; Fister, I.; Podgorelec, V. Swarm Intelligence Algorithms for Feature Selection: A Review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef]
- Chen, X.F.; Ye, C.M. Improved Teaching-Learning Optimization Algorithm Based on Nonlinear Convergence Factor and Benchmarking Management. J. Shanghai Univ. Sci. Technol. 2022, 44, 508–518. [Google Scholar]


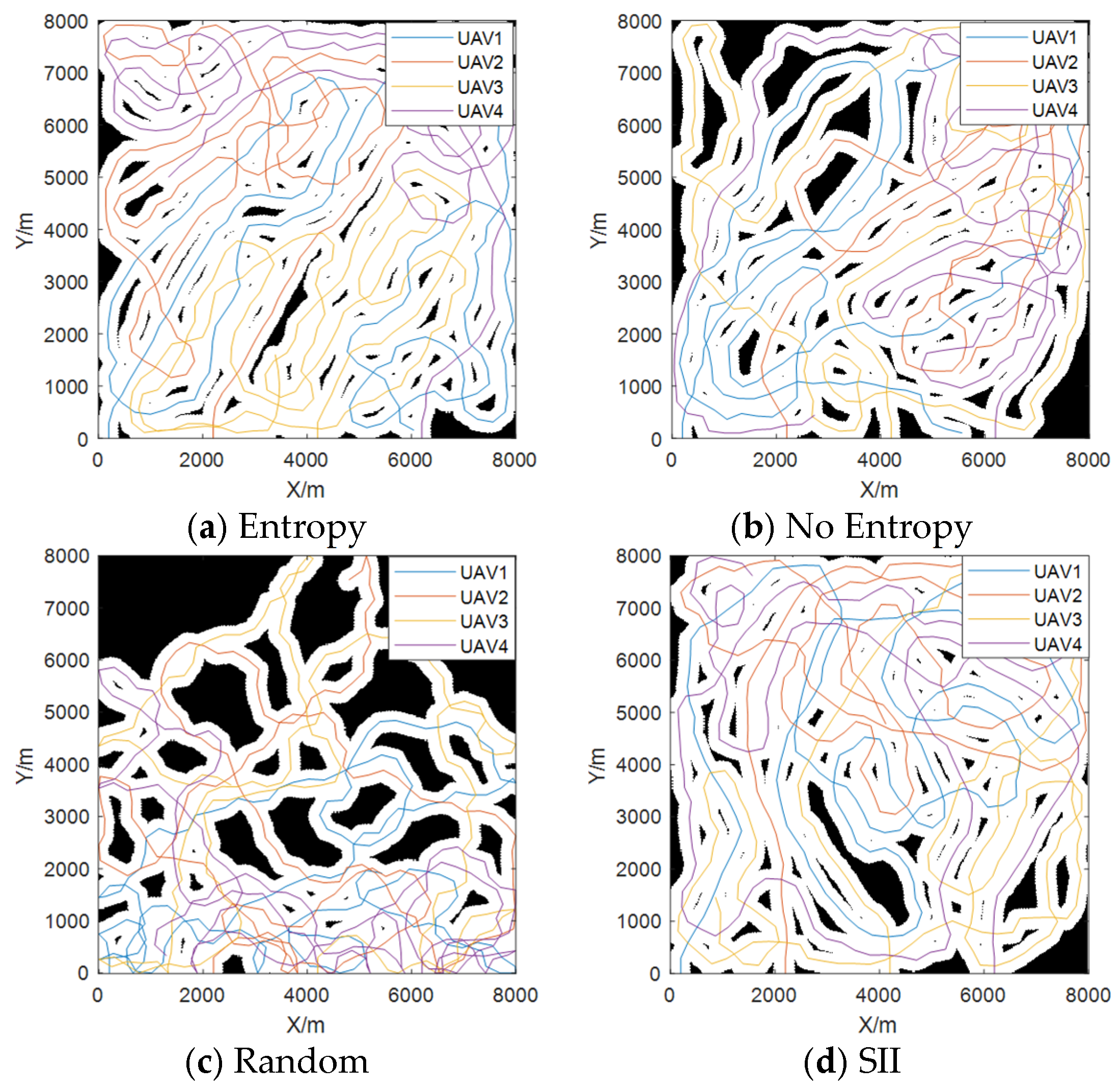
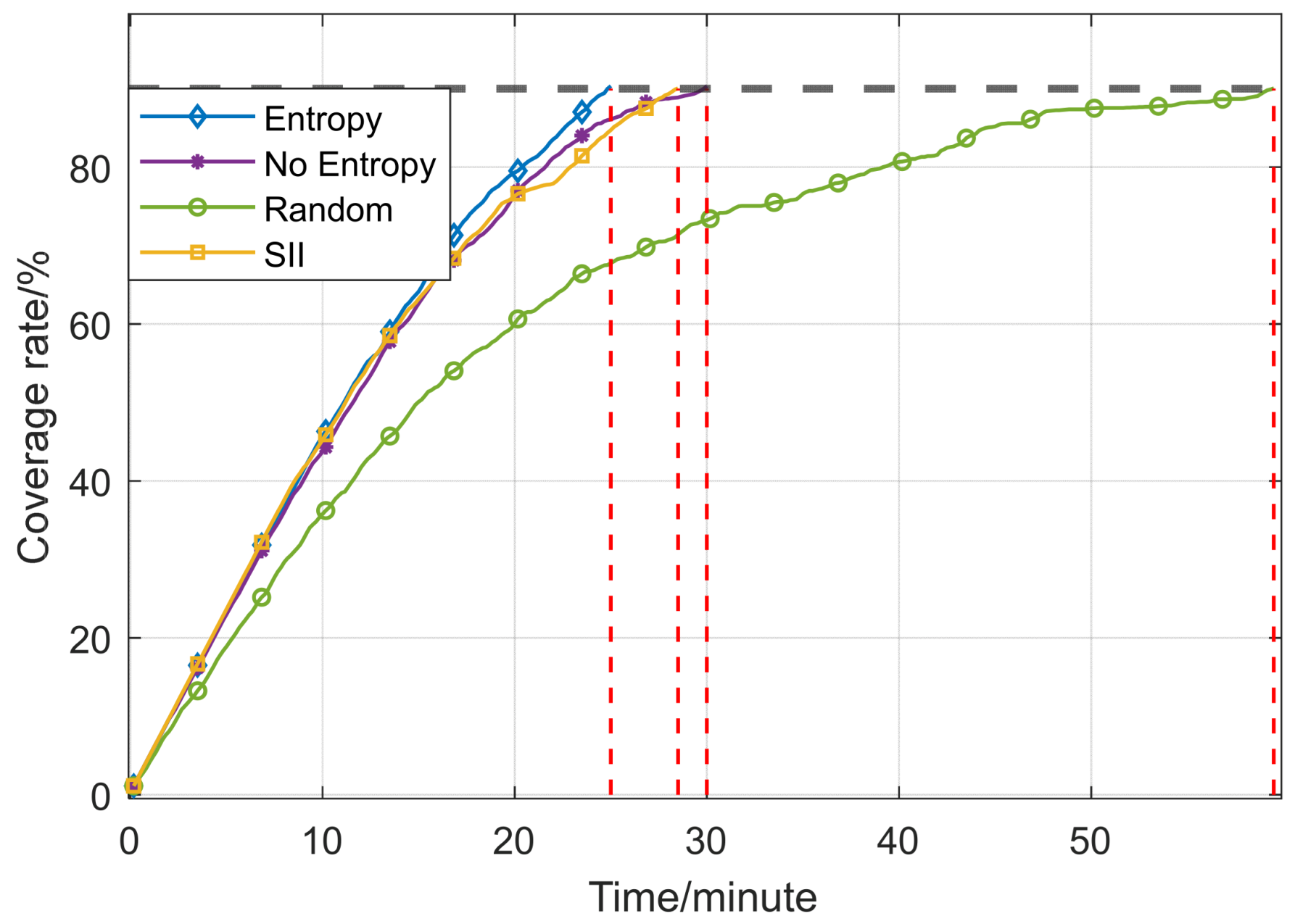
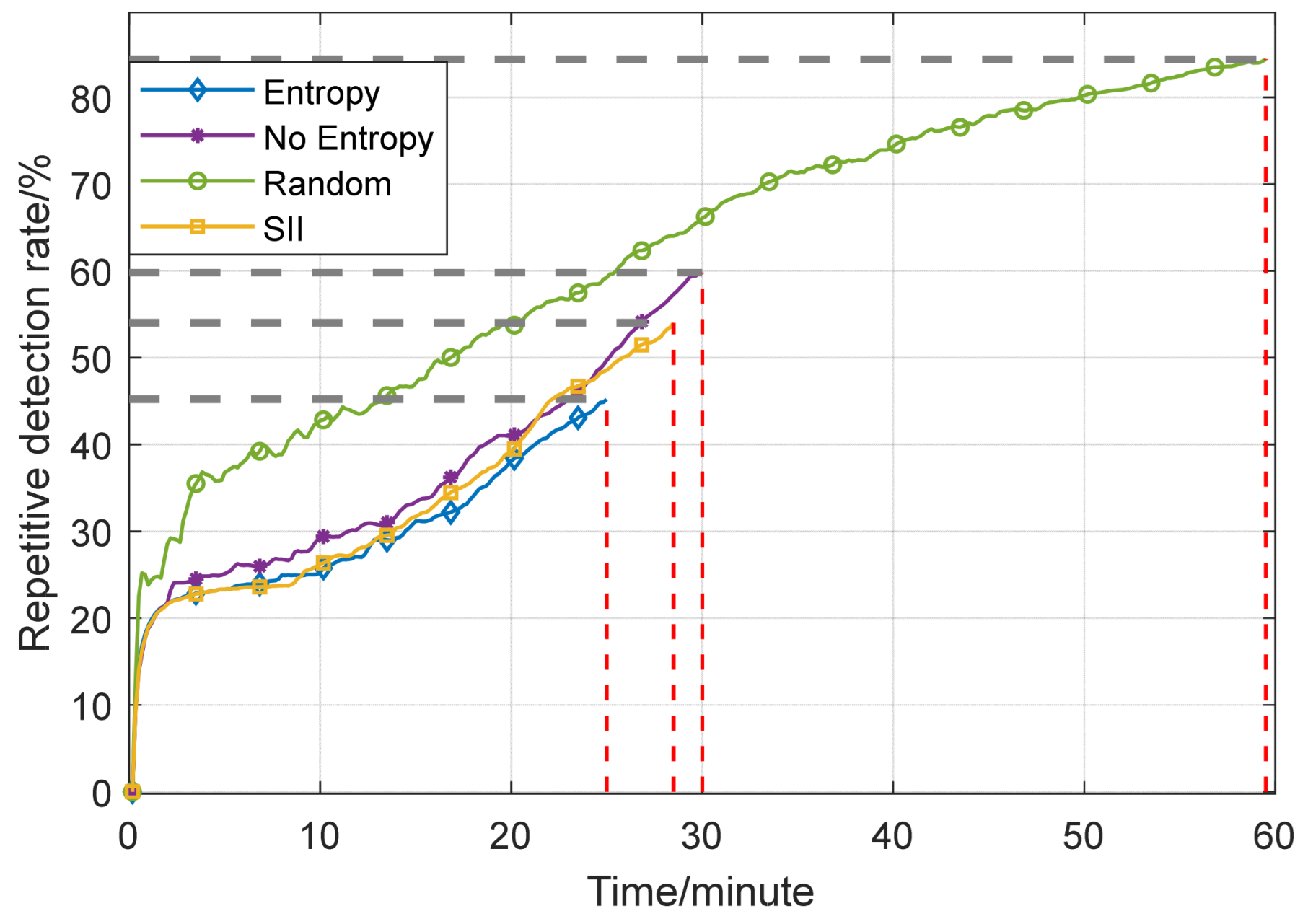
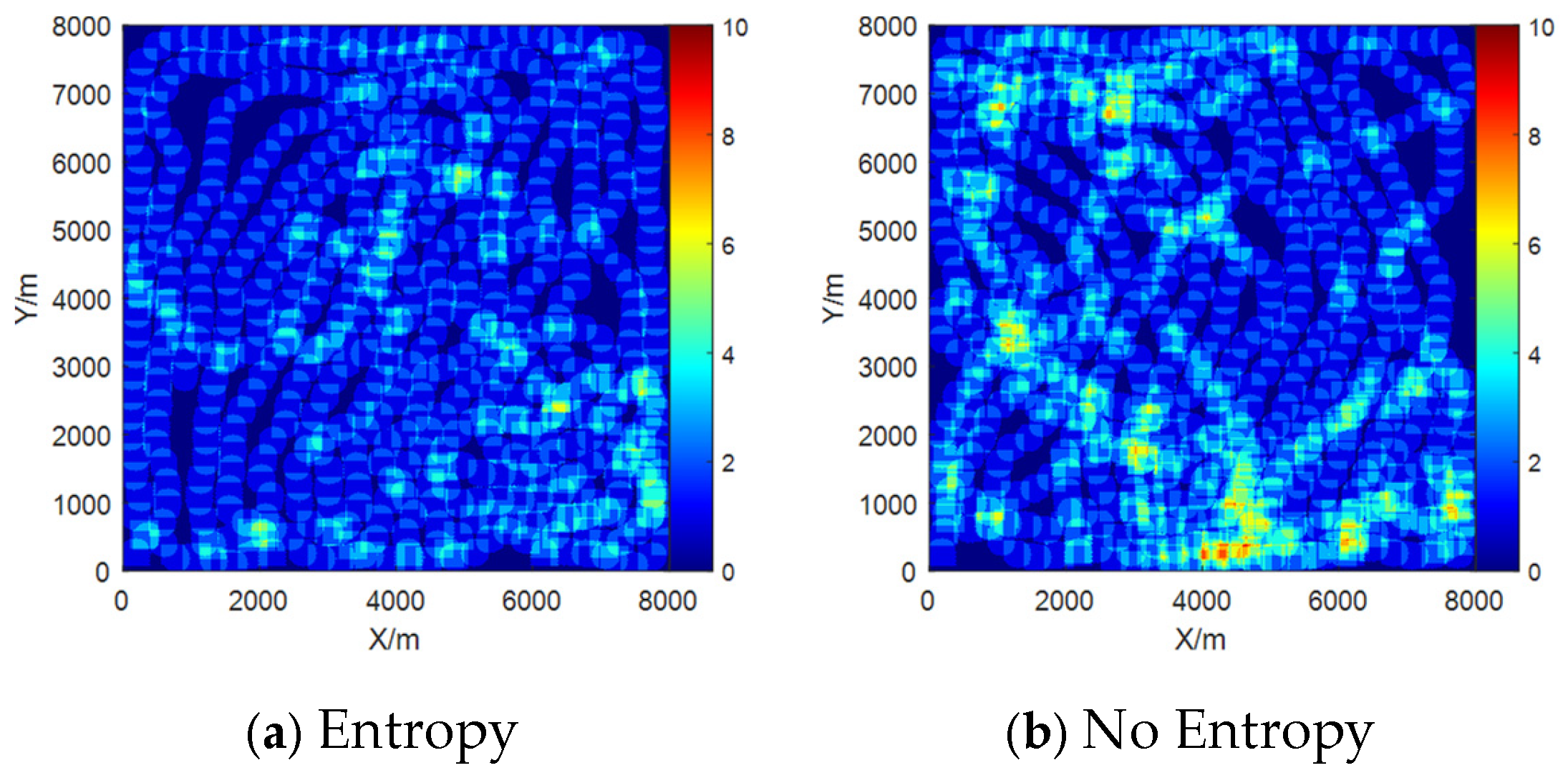
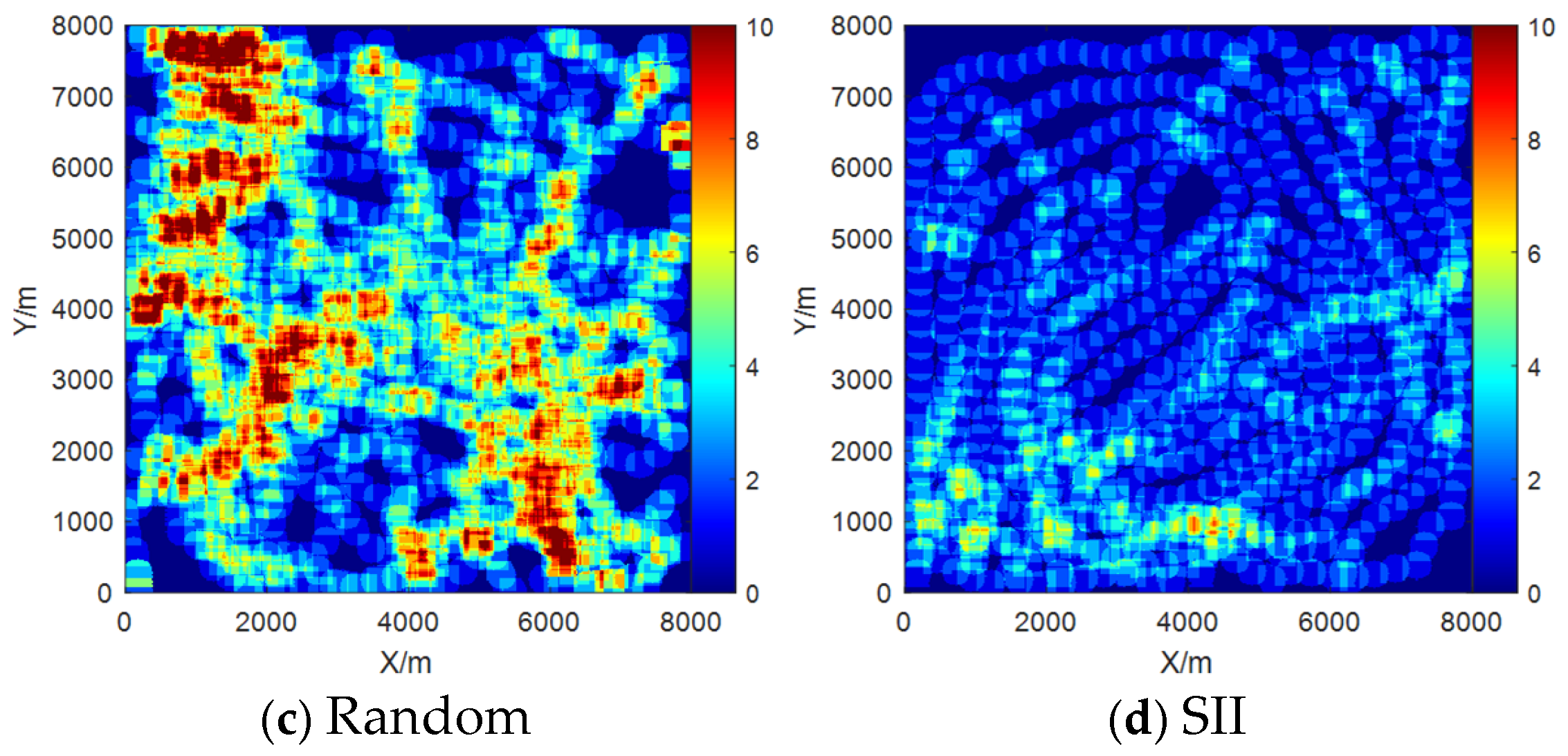
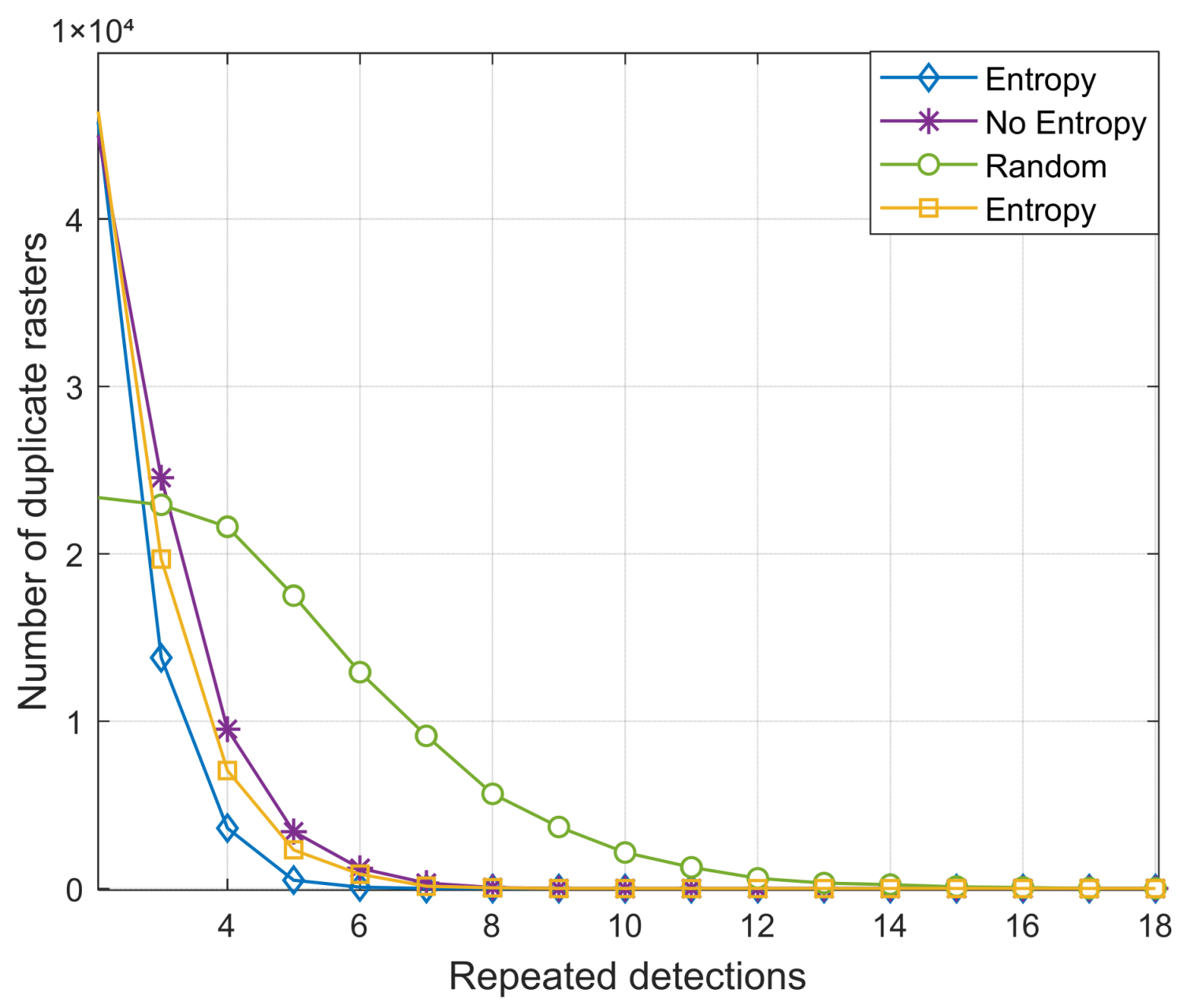
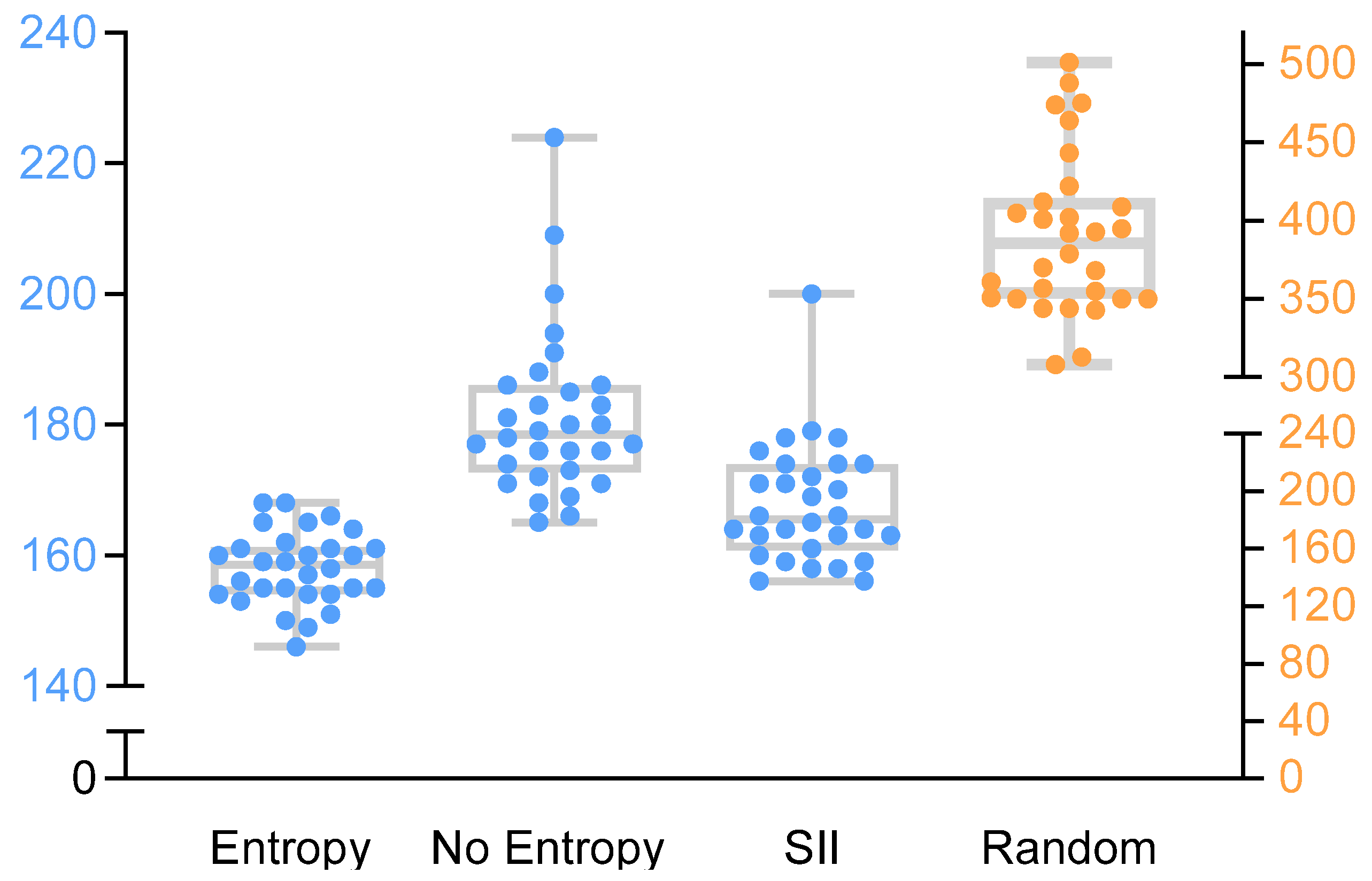
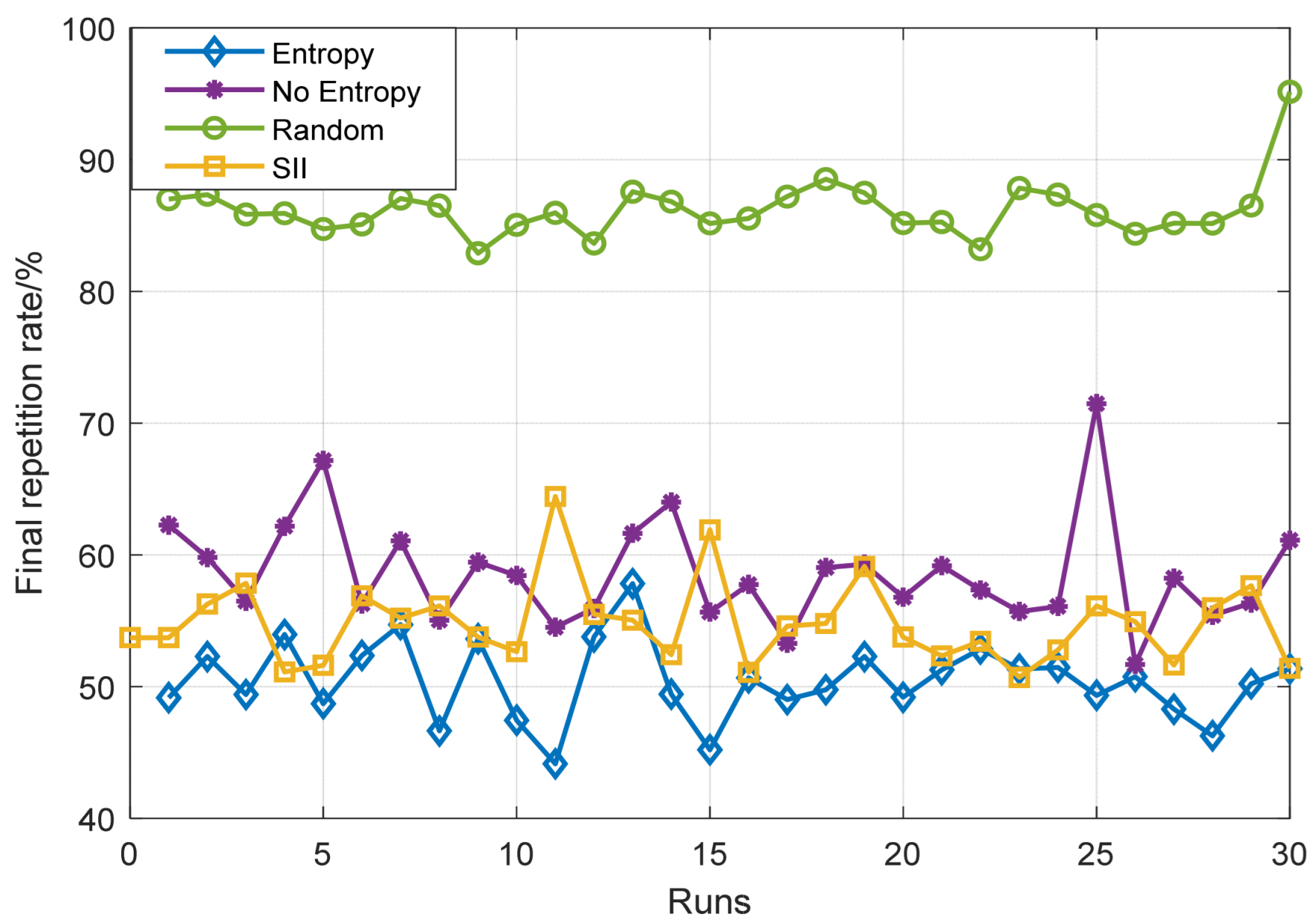


| Parameters | Variable Symbol | Value |
|---|---|---|
| Environmental length | Lx | 8000 m |
| Environmental width | Ly | 8000 m |
| Grid step size | ∆d | 20 m |
| Number of grids | M × N | 400 × 400 |
| Detecting radius | R | 200 m |
| UAV speed | v | 30 m/s |
| Step size during simulation | ∆t | 10 s |
| Maximum steering angle | ϕmax | |
| Predict the number of steps | k | 5 |
| Coverage area weight | λA | 0.5/0.3 |
| Entropy gain weight | λB | 0.3/0.5 |
| Yaw angle constraint weight | λC | 0.1 |
| Boundary constraint weight | λD | 0.1 |
| Starting point A | - | [200, 0] |
| Starting point B | - | [2200, 0] |
| Starting point C | - | [4200, 0] |
| Starting point D | - | [6200, 0] |
| Vlaue | Mode | Average | SD | Min | Max | Median |
|---|---|---|---|---|---|---|
| Simulation steps | Entropy | 158 | 5.59 | 146 | 168 | 158.5 |
| No entropy | 180 | 12.72 | 165 | 224 | 178.5 | |
| Random | 390 | 51.34 | 308 | 501 | 394 | |
| SII | 168 | 9.20 | 156 | 200 | 165.5 | |
| Repetition rate | Entropy | 50.43 | 2.60 | 44.14 | 54.71 | 50.44 |
| No entropy | 58.60 | 3.88 | 53.29 | 71.48 | 58.03 | |
| Random | 86.04 | 2.65 | 81.27 | 90.98 | 85.46 | |
| SII | 54.59 | 3.60 | 50.71 | 64.43 | 53.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, S.; Li, H.; Fan, X.; Ni, L.; Hou, J. A Multi-UAV Distributed Collaborative Search Algorithm Based on Maximum Entropy Mechanism. Drones 2025, 9, 592. https://doi.org/10.3390/drones9080592
Cui S, Li H, Fan X, Ni L, Hou J. A Multi-UAV Distributed Collaborative Search Algorithm Based on Maximum Entropy Mechanism. Drones. 2025; 9(8):592. https://doi.org/10.3390/drones9080592
Chicago/Turabian StyleCui, Siyuan, Hao Li, Xiangyu Fan, Lei Ni, and Jiahang Hou. 2025. "A Multi-UAV Distributed Collaborative Search Algorithm Based on Maximum Entropy Mechanism" Drones 9, no. 8: 592. https://doi.org/10.3390/drones9080592
APA StyleCui, S., Li, H., Fan, X., Ni, L., & Hou, J. (2025). A Multi-UAV Distributed Collaborative Search Algorithm Based on Maximum Entropy Mechanism. Drones, 9(8), 592. https://doi.org/10.3390/drones9080592






