Cluster Characteristics Analysis of UAV Air-to-Air Channels Based on Ray Tracing and Wasserstein Generative Adversarial Network with Gradient Penalty
Abstract
1. Introduction
- A UAV A2A channel dataset is constructed for various representative built-up area scenarios using ray tracing (RT) simulations. An automatic clustering algorithm based on kernel power density (KPD) is applied to group MPCs, where the conventional Euclidean distance is replaced by the multipath component distance (MCD), resulting in more accurate clustering performance.
- In addition to providing empirical distribution expressions, a Wasserstein generative adversarial network with gradient penalty (WGAN-GP) is introduced to perform generative modeling of intra-cluster azimuth and elevation angle offsets using a large number of angular offset data.
- Based on the clustering results, the cluster characteristics of UAV A2A channels are systematically analyzed, including the number of sub-paths per cluster, the total number of clusters, intra-cluster delay and angular spreads, angular offsets, cluster Rician K-factor, and angular distributions. The numerical results demonstrate that the generated angular offset distributions closely match the RT data and outperform conventional empirical methods, validating the effectiveness of the generative model in improving modeling accuracy.
2. RT-Based Channel Data Acquisition and Clustering
2.1. UAV A2A Channel Description
2.2. Scenario Setup and RT Simulation
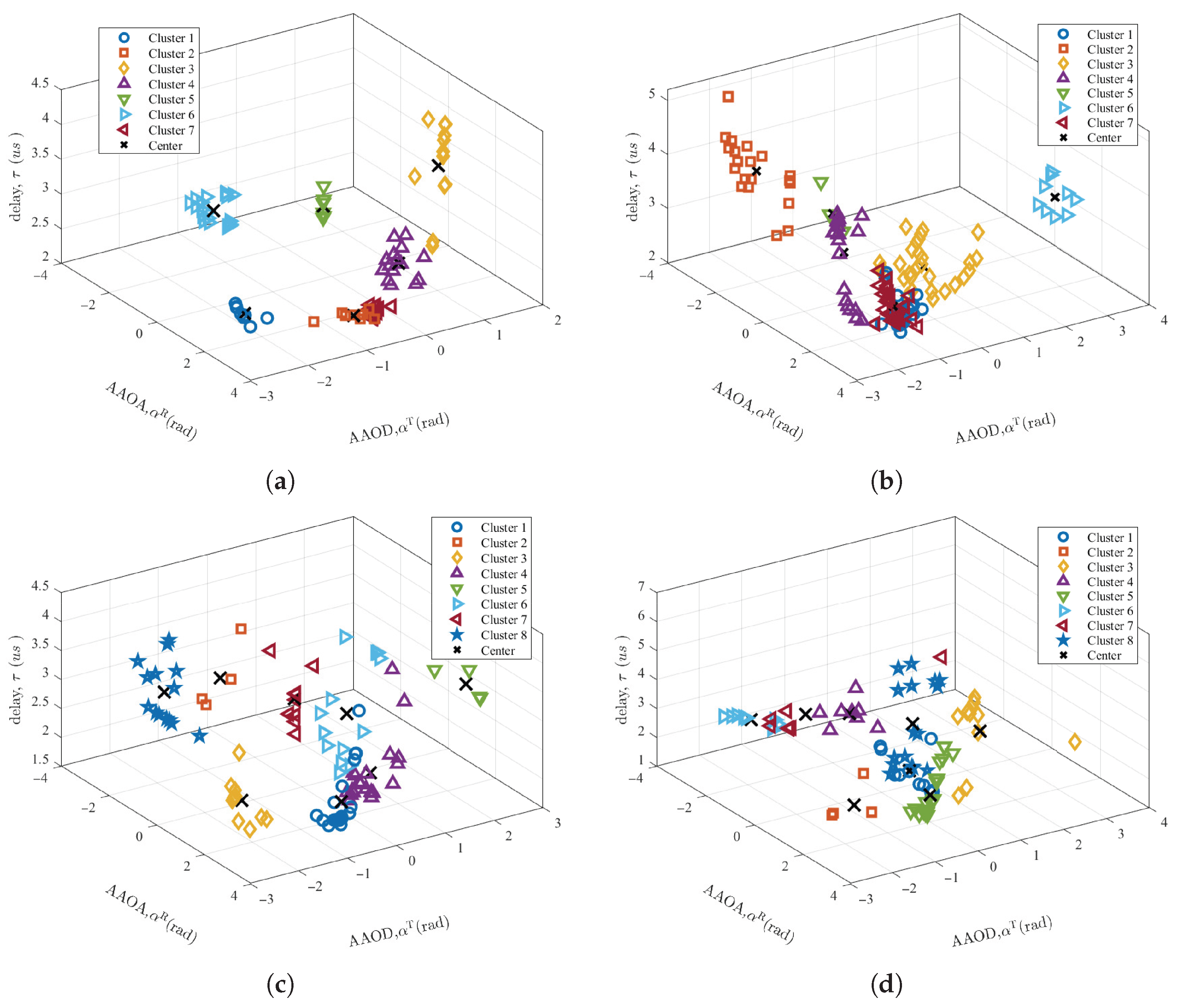
2.3. KPD Clustering Algorithm
| Algorithm 1 KPD Clustering Algorithm. |
|
3. Empirical Fitting and Generation Method
3.1. Cluster Parameter and Distribution Fitting Methods
3.2. WGAN-GP-Based Intra-Cluster Angle Generation
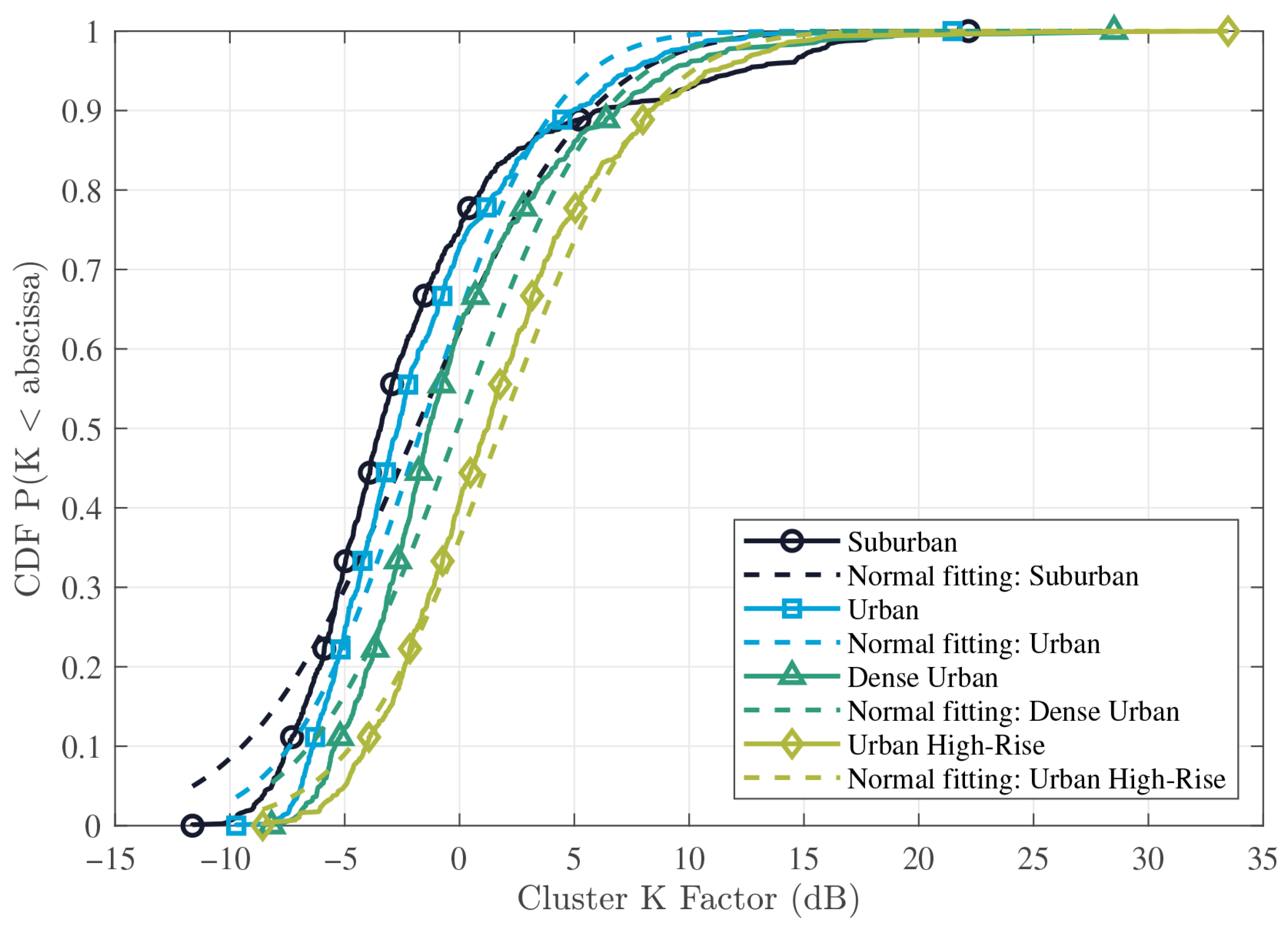
4. Numerical Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hua, B.; Han, L.; Zhu, Q.; Wang, C.X.; Mao, K.; Bao, J.; Chang, H.; Tang, Z. Ultra-Wideband Nonstationary Channel Modeling for UAV-to-Ground Communications. IEEE Trans. Wirel. Commun. 2025, 24, 4190–4204. [Google Scholar] [CrossRef]
- Jiang, H.; Shi, W.; Zhang, Z.; Pan, C.; Wu, Q.; Shu, F.; Liu, R.; Chen, Z.; Wang, J. Large-Scale RIS Enabled Air-Ground Channels: Near-Field Modeling and Analysis. IEEE Trans. Wirel. Commun. 2025, 24, 1074–1088. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Q.; Lin, Z.; Chen, J.; Ding, G.; Wu, Q.; Gu, G.; Gao, Q. Sparse Bayesian Learning-Based Hierarchical Construction for 3D Radio Environment Maps Incorporating Channel Shadowing. IEEE Trans. Wirel. Commun. 2024, 23, 14560–14574. [Google Scholar] [CrossRef]
- Lian, Z.; Zhang, W.; Wang, Y.; Su, Y.; Zhang, B.; Jin, B.; Wang, B. Physics-Based Channel Modeling for IRS-Assisted mmWave Communication Systems. IEEE Trans. Commun. 2024, 72, 2687–2700. [Google Scholar] [CrossRef]
- Ede, B.; Kaplan, B.; Kahraman, İ.; Keşir, S.; Yarkan, S.; Ekti, A.R.; Baykaş, T.; Görçin, A.; Çırpan, H.A. Measurement-Based Large Scale Statistical Modeling of Air–to–Air Wireless UAV Channels via Novel Time–Frequency Analysis. IEEE Wirel. Commun. Lett. 2022, 11, 136–140. [Google Scholar] [CrossRef]
- Guo, L.; Guan, K.; Liu, T.; He, D.; Zhang, H.; Zhu, Q.; Lu, J.; Zhang, M. Obtaining electromagnetic properties of multi-type media in realistic environments: State-of-the-art and prospects. China Commun. 2025, 22, 25–40. [Google Scholar] [CrossRef]
- Zhu, G.; Liu, Y.; Li, S.; Mao, K.; Zhu, Q.; Briso-Rodríguez, C.; Liang, J.; Ye, X. Semantic-Based Channel State Information Feedback for AAV-Assisted ISAC Systems. IEEE Internet Things J. 2025, 12, 4981–4991. [Google Scholar] [CrossRef]
- Liu, X.; Zhong, W.; Wang, X.; Duan, H.; Fan, Z.; Jin, H.; Huang, Y.; Lin, Z. Deep Reinforcement Learning-Based 3D Trajectory Planning for Cellular Connected UAV. Drones 2024, 8, 199. [Google Scholar] [CrossRef]
- Molisch, A.; Tufvesson, F. Propagation Channel Models for Next-Generation Wireless Communications Systems. IEICE Trans. Commun. 2014, 97, 2022–2034. [Google Scholar] [CrossRef]
- Zeng, L.; Liao, X.; Ma, Z.; Liu, W.; Jiang, H.; Chen, Z. Toward More Adaptive UAV-to-UAV GBSMs: Introducing the Extended vMF Distribution. IEEE Wirel. Commun. Lett. 2025, 14, 260–264. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Y.; Zhang, P.; Jiang, H.; Xiao, Y.; Huang, L. Physical Layer Security Improvement for Hybrid RIS-Assisted MIMO Communications. IEEE Commun. Lett. 2024, 28, 2493–2497. [Google Scholar] [CrossRef]
- Lee, J. Cluster-Based Millimeter-Wave Outdoor-to-Indoor Propagation Characteristics Based on 32 GHz Measurement Analysis. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 73–77. [Google Scholar] [CrossRef]
- Liu, L.; Oestges, C.; Poutanen, J.; Haneda, K.; Vainikainen, P.; Quitin, F.; Tufvesson, F.; Doncker, P.D. The COST 2100 MIMO channel model. IEEE Wirel. Commun. 2012, 19, 92–99. [Google Scholar] [CrossRef]
- 3GPP. Enhanced LTE Support for Aerial Vehicles; Technical Report TR 36.777; Sophia Antipolis, France. 2018. Available online: https://www.3gpp.org/dynareport/36777.htm (accessed on 1 June 2025).
- Bai, L.; Huang, Z.; Cheng, X. A non-stationary model with time-space consistency for 6G massive MIMO mmWave UAV channels. IEEE Trans. Wirel. Commun. 2022, 22, 2048–2064. [Google Scholar] [CrossRef]
- Ge, C.; Zhang, R.; Jiang, Y.; Li, B.; He, Y. A 3-D Dynamic Non-WSS Cluster Geometrical-Based Stochastic Model for UAV MIMO Channels. IEEE Trans. Veh. Technol. 2022, 71, 6884–6899. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; Gu, F.; Ma, D.; Wei, J. An extended 3-D ellipsoid model for characterization of UAV air-to-air channel. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Ma, Z.; Ai, B.; He, R.; Zhong, Z.; Yang, M. A non-stationary geometry-based MIMO channel model for millimeter-wave UAV networks. IEEE J. Sel. Areas Commun. 2021, 39, 2960–2974. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, H.; Zhang, C.; Yu, X.; Dong, Y. Three-dimensional geometry-based stochastic model for sub-terahertz air-to-air UAV-MIMO channels. In Proceedings of the 2023 IEEE/CIC International Conference on Communications in China (ICCC), Dalian, China, 10–12 August 2023; pp. 1–6. [Google Scholar]
- Hua, B.; Deng, Q.; Zhu, Q.; Wang, C.X.; Han, L.; Briso-Rodríguez, C.; Tang, Z.; Mao, K. A Novel A2A Channel Model Incorporating Rooftop Specular Reflection and Airframe Occlusion. IEEE Trans. Wirel. Commun. 2025. [Google Scholar] [CrossRef]
- Hua, B.; Han, L.; Deng, Q.; Zhu, Q.; Li, H.; Qu, Y.; Briso-Rodríguez, C.; Mao, K. AAV Air-to-Air Channel: Statistical Properties and Experimental Verification. IEEE Internet Things J. 2025, 12, 25790–25803. [Google Scholar] [CrossRef]
- Huang, C.; He, R.; Ai, B.; Molisch, A.F.; Lau, B.K.; Haneda, K.; Liu, B.; Wang, C.X.; Yang, M.; Oestges, C.; et al. Artificial Intelligence Enabled Radio Propagation for Communications—Part I: Channel Characterization and Antenna-Channel Optimization. IEEE Trans. Antennas Propag. 2022, 70, 3939–3954. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, R.; Ai, B.; Lian, Z.; Zeng, L.; Niyato, D.; Peng, Y. Deep Reinforcement Learning for Energy Efficiency Maximization in RSMA-IRS-Assisted ISAC System. IEEE Trans. Veh. Technol. 2025, 1–6. [Google Scholar] [CrossRef]
- Luo, J.; Liao, X.; Wang, Y.; Zhang, J.; Yu, Z.; Wang, G.; Li, X. An Entropy-Based Adaptive DBSCAN Clustering Algorithm and Its Application in THz Wireless Channels. IEEE Trans. Antennas Propag. 2023, 71, 9830–9837. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, R.; Pan, J.; Jiang, Y.; Zhai, D. A Framework of Multipath Clustering Based on Space-Transformed Fuzzy c-Means and Data Fusion for Radio Channel Modeling. IEEE Trans. Veh. Technol. 2020, 69, 4–15. [Google Scholar] [CrossRef]
- Zhou, T.; Qiao, Y.; Salous, S.; Liu, L.; Tao, C. Machine Learning-Based Multipath Components Clustering and Cluster Characteristics Analysis in High-Speed Railway Scenarios. IEEE Trans. Antennas Propag. 2022, 70, 4027–4039. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Wang, C.X.; Chang, H.; Bian, J.; Zhang, J. Machine Learning Based Clustering and Modeling for 6G UAV-to-Ground Communication Channels. IEEE Trans. Veh. Technol. 2024, 73, 14113–14126. [Google Scholar] [CrossRef]
- Cui, Z.; Guan, K.; Oestges, C.; Briso-Rodríguez, C.; Ai, B.; Zhong, Z. Cluster-Based Characterization and Modeling for UAV Air-to-Ground Time-Varying Channels. IEEE Trans. Veh. Technol. 2022, 71, 6872–6883. [Google Scholar] [CrossRef]
- Lyu, Y.; Xue, B.; Wang, W. A Genetic Algorithm-Based Iterative Channel Estimation Method for Ranging Applications in Closely Spaced Multipath Environment. IEEE Antennas Wirel. Propag. Lett. 2025, 24, 1327–1331. [Google Scholar] [CrossRef]
- Lyu, Y.; Wang, W.; Chen, P. Fixed-Wing UAV-Based Air-to-Ground Channel Measurement and Modeling at 2.7 GHz in a Rural Environment. IEEE Trans. Antennas Propag. 2025, 73, 2038–2052. [Google Scholar] [CrossRef]
- ITU-R. Propagation Data and Prediction Methods for the Design of Terrestrial Broadband Millimetric Radio Access Systems; Recommendation ITU-R P.1410-2; International Telecommunication Union: Geneva, Switzerland, 2003; Available online: https://www.itu.int/rec/R-REC-P.1410/en (accessed on 1 June 2025).
- Du, F.; Zhao, X.; Zhang, Y.; Wen, Y.; Fu, Z.; Geng, S.; Qin, P.; Zhou, Z.; Xu, C.; Liu, Y.; et al. SVM-Assisted Adaptive Kernel Power Density Clustering Algorithm for Millimeter Wave Channels. IEEE Trans. Antennas Propag. 2022, 70, 4014–4026. [Google Scholar] [CrossRef]
- Czink, N.; Cera, P.; Salo, J.; Bonek, E.; Nuutinen, J.P.; Ylitalo, J. Improving clustering performance using multipath component distance. Electron. Lett. 2006, 42, 33–35. [Google Scholar] [CrossRef]
- He, R.; Li, Q.; Ai, B.; Geng, Y.L.A.; Molisch, A.F.; Kristem, V.; Zhong, Z.; Yu, J. A Kernel-Power-Density-Based Algorithm for Channel Multipath Components Clustering. IEEE Trans. Wirel. Commun. 2017, 16, 7138–7151. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Meinilä, J.; Kyösti, P.; Hentilä, L.; Jämsä, T.; Suikkanen, E.; Kunnari, E.; Narandžić, M. Document Title: D5. 3: WINNER+ Final Channel Models 2010. Available online: https://www.researchgate.net/publication/261467821 (accessed on 1 June 2025).
- Mao, K.; Zhu, Q.; Wang, C.X.; Ye, X.; Gomez-Ponce, J.; Cai, X.; Miao, Y.; Cui, Z.; Wu, Q.; Fan, W. A Survey on Channel Sounding Technologies and Measurements for UAV-Assisted Communications. IEEE Trans. Instrum. Meas. 2024, 73, 1–24. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of wasserstein GANs. In Proceedings of the Advances in Neural Information Processing Systems, Red Hook, NY, USA, 4–9 December 2017; pp. 5769–5779. [Google Scholar]
- Ziółkowski, C.; Kelner, J.M. Empirical models of the azimuthal reception angle—Part I: Comparative analysis of empirical models for different propagation environments. Wirel. Pers. Commun. 2016, 91, 771–791. [Google Scholar] [CrossRef]







| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Scenario | Suburban, urban, dense urban, urban high-rise | Tx altitude | 150 m |
| Building area ratio | 0.1, 0.3, 0.5, 0.5 | Rx altitude | 140 m, 120 m, 100 m, 80 m |
| Building density | 750/km2, 500/km2, 300/km2, 300/km2 | Frequency | 2.4 GHz |
| Average building height | 8 m, 15 m, 20 m, 50 m | Antenna type | Omnidirectional |
| Building width | 11.6 m, 24.5 m, 40.8 m, 40.8 m | Transmit power | 0 dBm |
| Street width | 24.9 m, 20.2 m, 16.9 m, 16.9 m | Concrete | One-layer dielectric |
| Building location/height distribution | Uniform/Rayleigh distribution | Wet earth | Dielectric half-space |
| Methods | Effectiveness Indexes | |
|---|---|---|
| Silhouette Coefficient | Calinski–Harabasz Index | |
| KPD | 0.71 | 311.94 |
| K-means | 0.55 | 245.77 |
| KPM | 0.66 | 262.77 |
| Cluster Parameters | Statistical Distribution | Suburban | Urban | Dense Urban | Urban High-Rise |
|---|---|---|---|---|---|
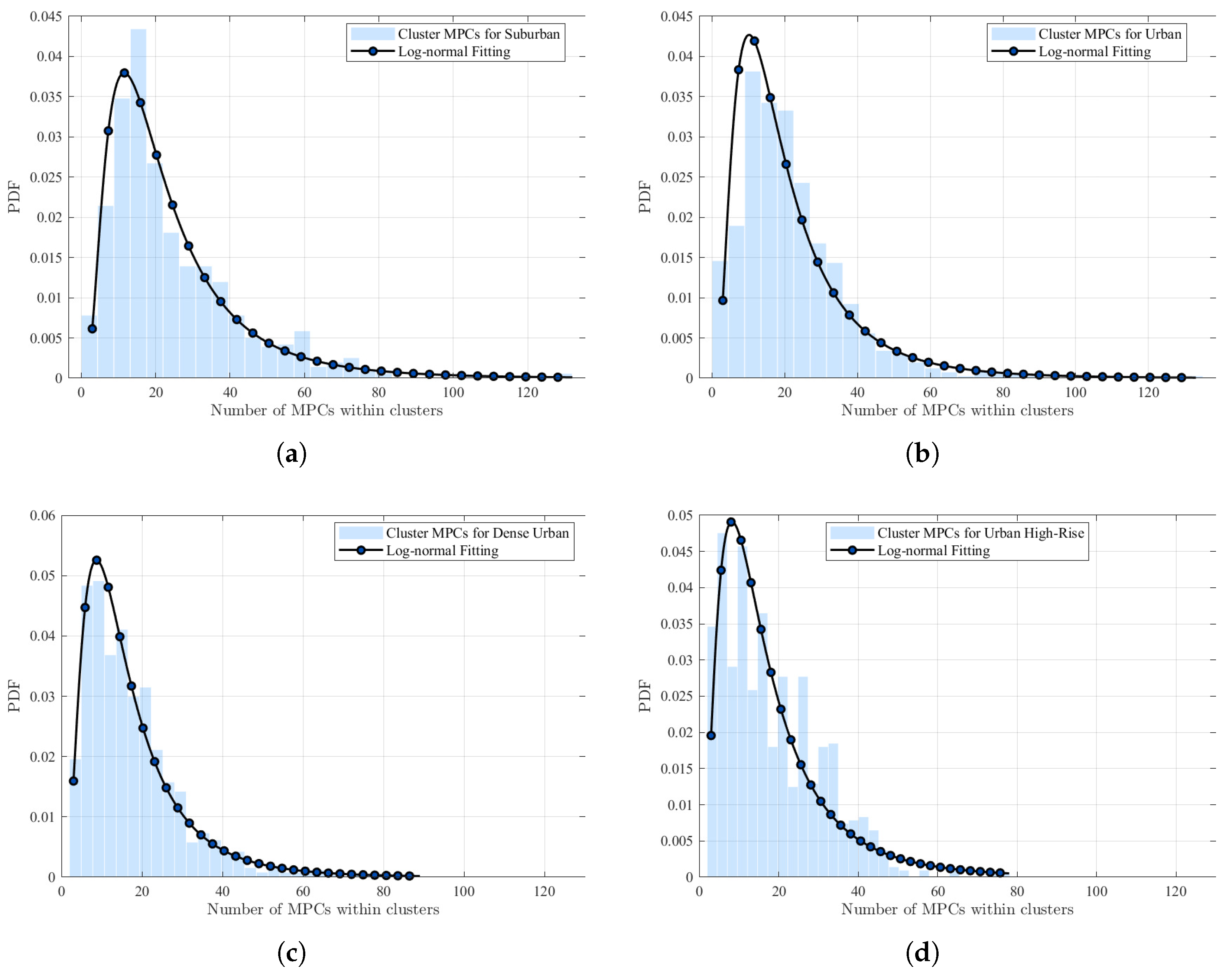
| Number of intra-cluster MPCs | Log-normal | ||||
| Cluster Rician K-factor (dB) | Normal | ||||
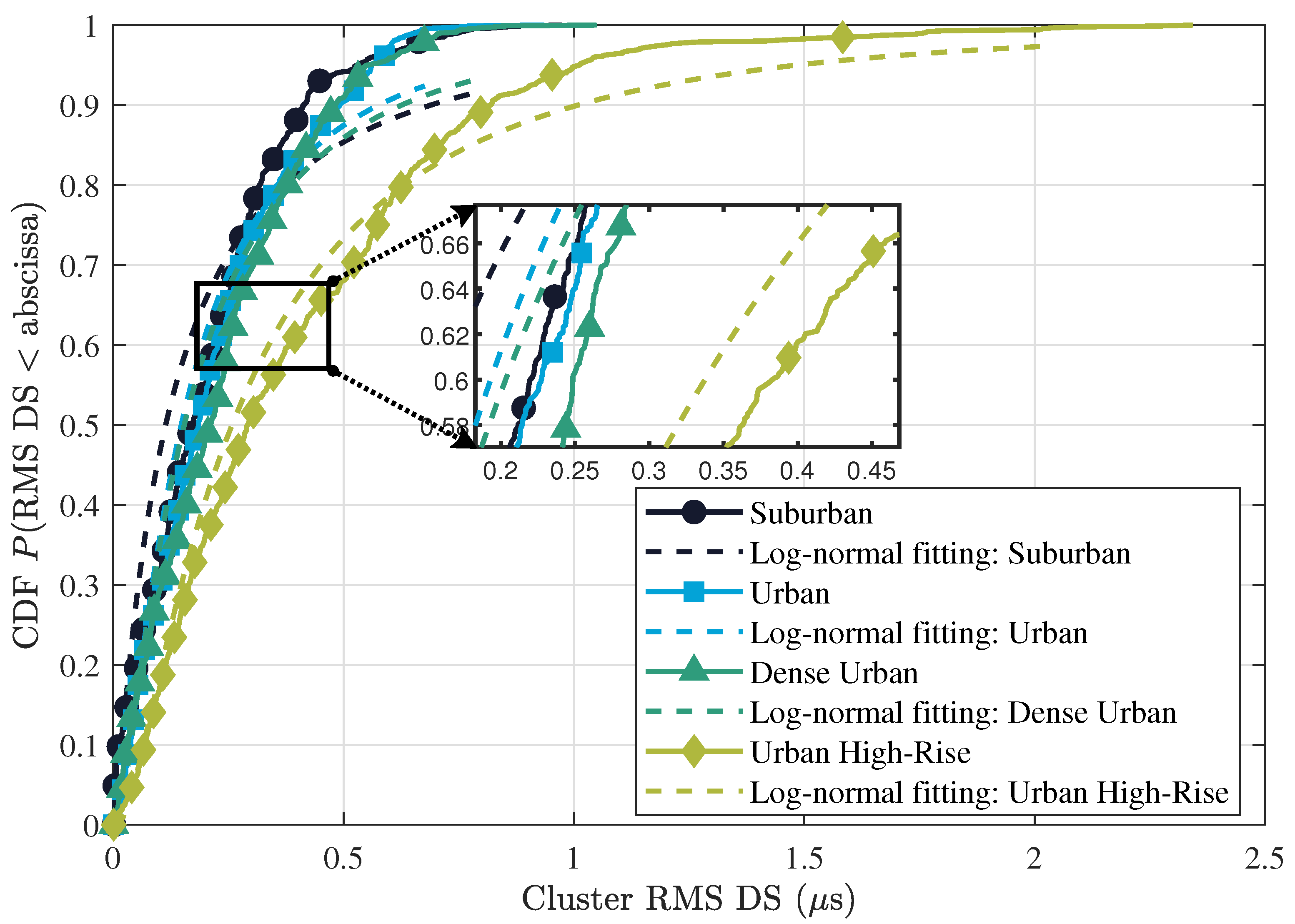
| RMS-DS (s) | Log-normal | ||||
| RMS-AAS (rad) | Log-normal | ||||
| RMS-EAS (rad) | Log-normal | ||||
| RMS-ADS (rad) | Log-normal | ||||
| RMS-EDS (rad) | Log-normal | ||||
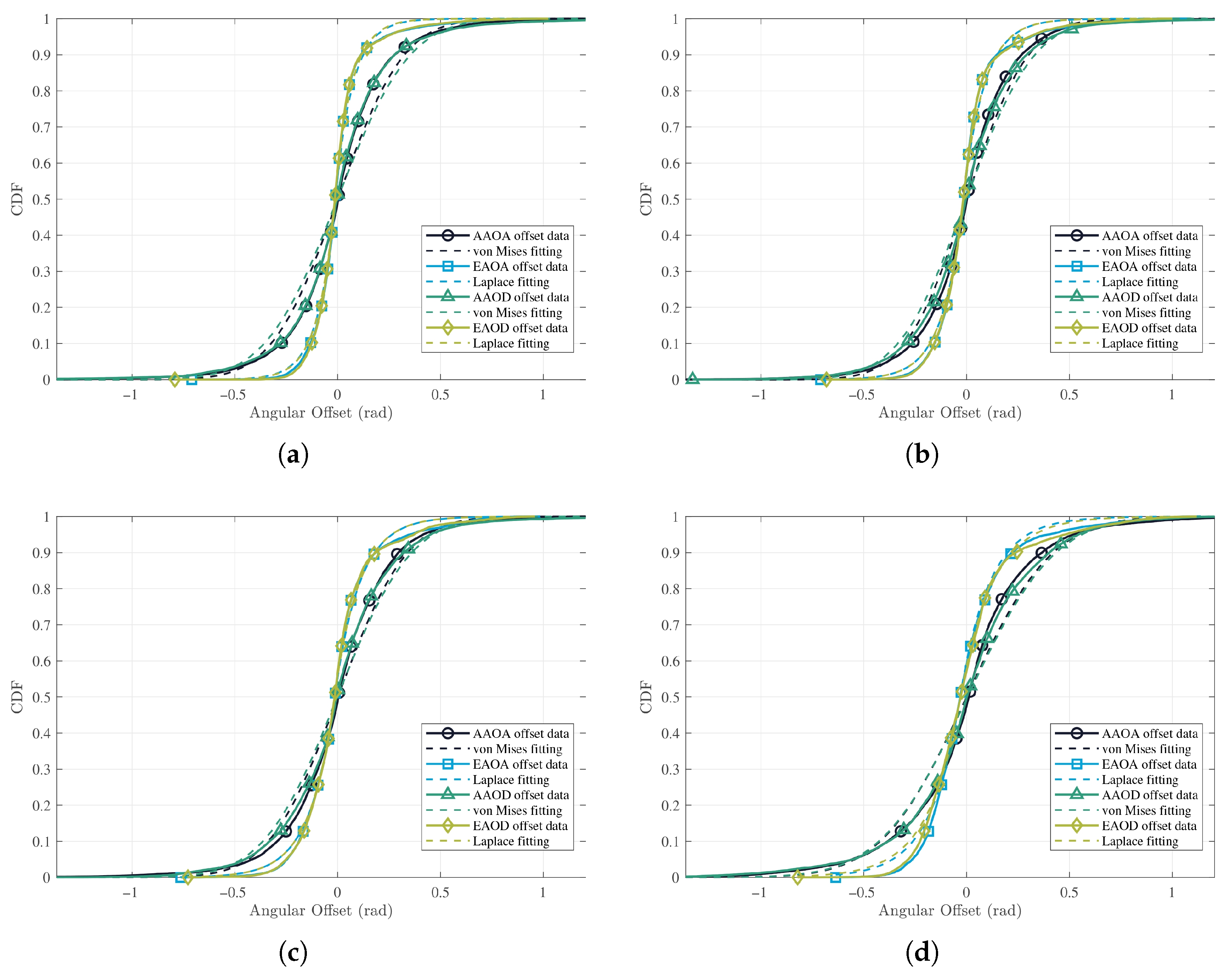
| AAOA offset (rad) | von Mises | ||||
| AAOD offset (rad) | von Mises | ||||
| EAOA offset (rad) | Laplace | ||||
| EAOD offset (rad) | Laplace | ||||
| Scenario | Kolmogorov–Smirnov | Cramer–von Mises | ||
|---|---|---|---|---|
| Fit vs. RT | Generated vs. RT | Fit vs. RT | Generated vs. RT | |
| Suburban | 0.06709 | 0.02787 | 0.00165 | 0.00006 |
| Urban | 0.06292 | 0.03456 | 0.00123 | 0.00011 |
| Dense urban | 0.05592 | 0.02232 | 0.00118 | 0.00007 |
| Urban high-rise | 0.07588 | 0.02487 | 0.00230 | 0.00007 |
| Scenario | Kolmogorov–Smirnov | Cramer–von Mises | ||
|---|---|---|---|---|
| Fit vs. RT | Generated vs. RT | Fit vs. RT | Generated vs. RT | |
| Suburban | 0.03299 | 0.03268 | 0.00031 | 0.00005 |
| Urban | 0.04447 | 0.03200 | 0.00045 | 0.00007 |
| Dense urban | 0.02605 | 0.01790 | 0.00033 | 0.00002 |
| Urban high-rise | 0.04179 | 0.01698 | 0.00065 | 0.00002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Chen, X.; Hua, B.; Deng, Q.; Mao, K.; Zhong, W.; Zhu, Q. Cluster Characteristics Analysis of UAV Air-to-Air Channels Based on Ray Tracing and Wasserstein Generative Adversarial Network with Gradient Penalty. Drones 2025, 9, 586. https://doi.org/10.3390/drones9080586
Han L, Chen X, Hua B, Deng Q, Mao K, Zhong W, Zhu Q. Cluster Characteristics Analysis of UAV Air-to-Air Channels Based on Ray Tracing and Wasserstein Generative Adversarial Network with Gradient Penalty. Drones. 2025; 9(8):586. https://doi.org/10.3390/drones9080586
Chicago/Turabian StyleHan, Liwei, Xiaomin Chen, Boyu Hua, Qingzhe Deng, Kai Mao, Weizhi Zhong, and Qiuming Zhu. 2025. "Cluster Characteristics Analysis of UAV Air-to-Air Channels Based on Ray Tracing and Wasserstein Generative Adversarial Network with Gradient Penalty" Drones 9, no. 8: 586. https://doi.org/10.3390/drones9080586
APA StyleHan, L., Chen, X., Hua, B., Deng, Q., Mao, K., Zhong, W., & Zhu, Q. (2025). Cluster Characteristics Analysis of UAV Air-to-Air Channels Based on Ray Tracing and Wasserstein Generative Adversarial Network with Gradient Penalty. Drones, 9(8), 586. https://doi.org/10.3390/drones9080586







