A Computational Method for the Nonlinear Attainable Moment Set of Tailless UAVs in Flight-Control-Oriented Scenarios
Abstract
1. Introduction
- Incomplete integration of the constraints from the admissible control set. During the design of the flight control system, the AMS must be tightly coupled with control algorithms. Therefore, AMS innovations should consider the constraints from the admissible control set, including but not limited to deflection angle and angular rate limitations.
- Inadequate consideration of nonlinear characteristics. Aerodynamic moments and deflection angles of control surfaces typically exhibit nonlinear relationships. Algorithms based on classical AMS frameworks fail to produce accurate results due to linear assumptions.
- Insufficient handling of multivariable coupling. Moment computation for control surfaces involves multiple coupled variables and parameters, such as deflection angles, angle of attack, flight velocity, and altitude. The intricate interdependencies among these variables necessitate comprehensive multifactor integration in AMS calculations.
- Mapping the constraints from the admissible control set for enhanced AMS reliability. We map the constraints from the admissible control set, including deflection angle and angular rate limits, to aerodynamic moment amplitude and bandwidth boundaries. This mapping process enhances the reliability and accuracy of the AMS.
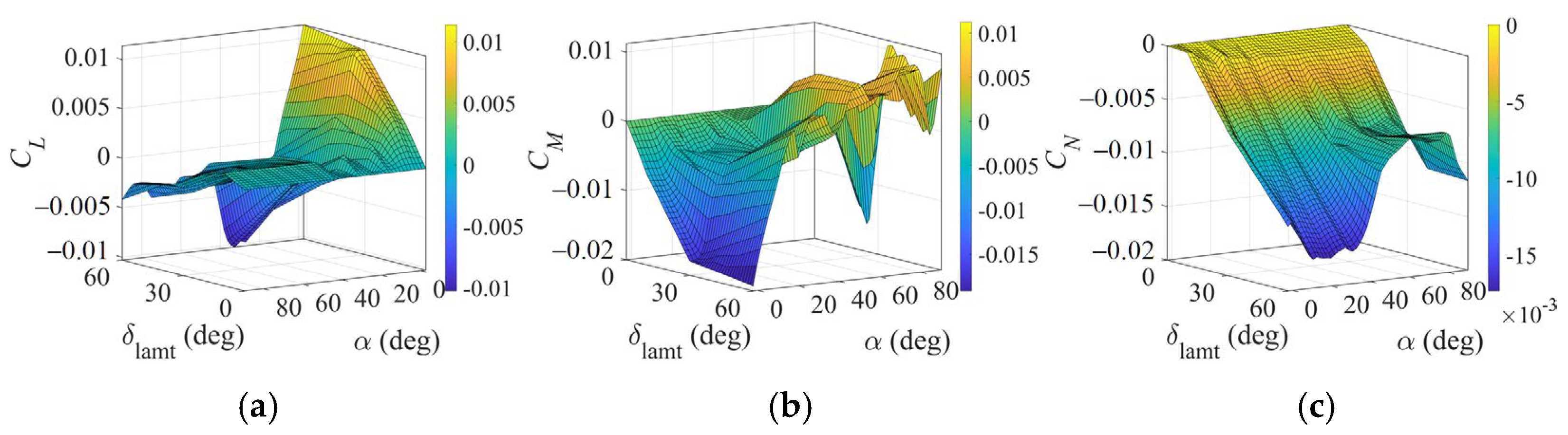
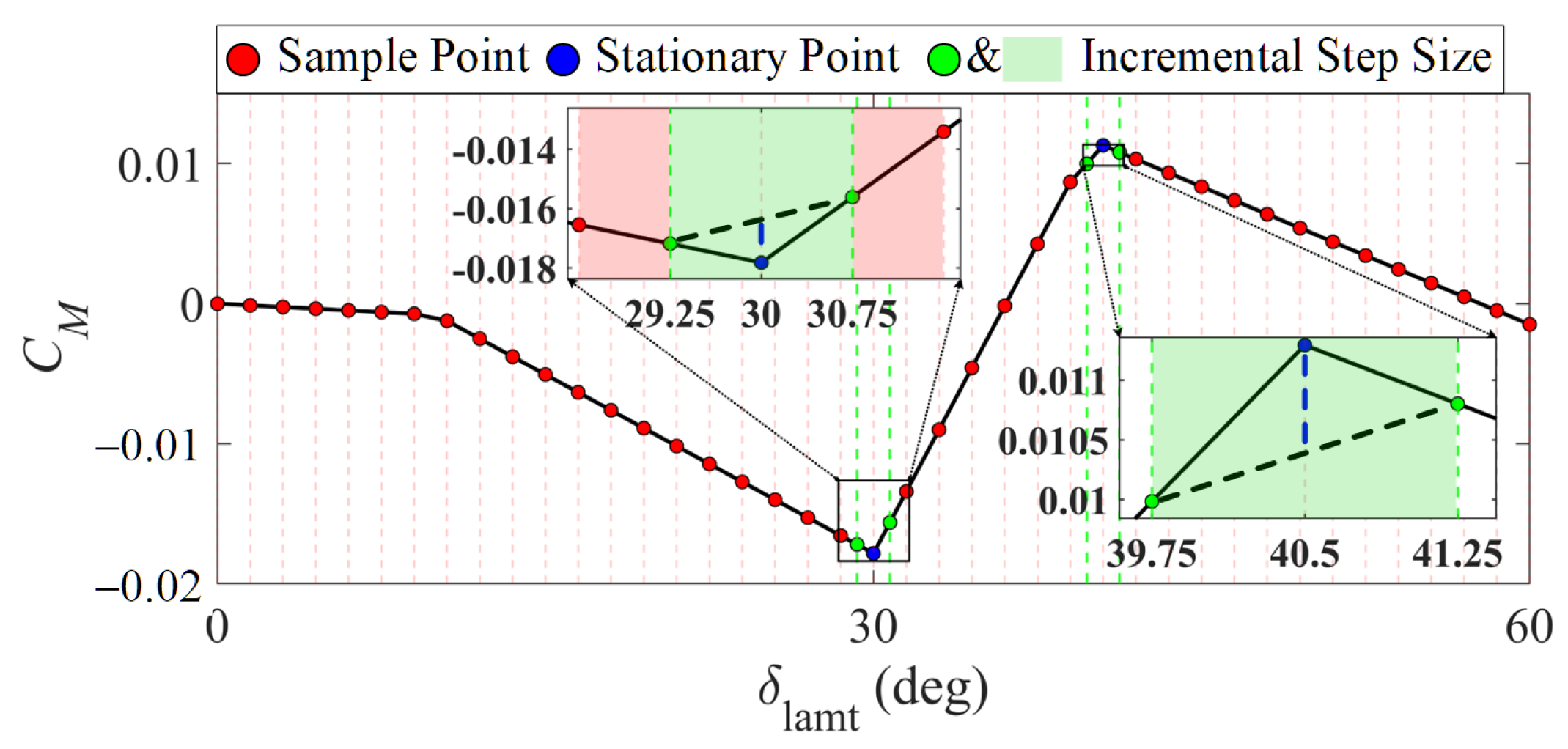
- Nonlinear AMS computation with a nonlinear aerodynamic model. We develop a dedicated NAMS algorithm to address nonlinear aerodynamic effectiveness and control surface coupling. The non-monotonic characteristics in the aerodynamic effectiveness function are addressed by fitting functions and calculating stationary points.
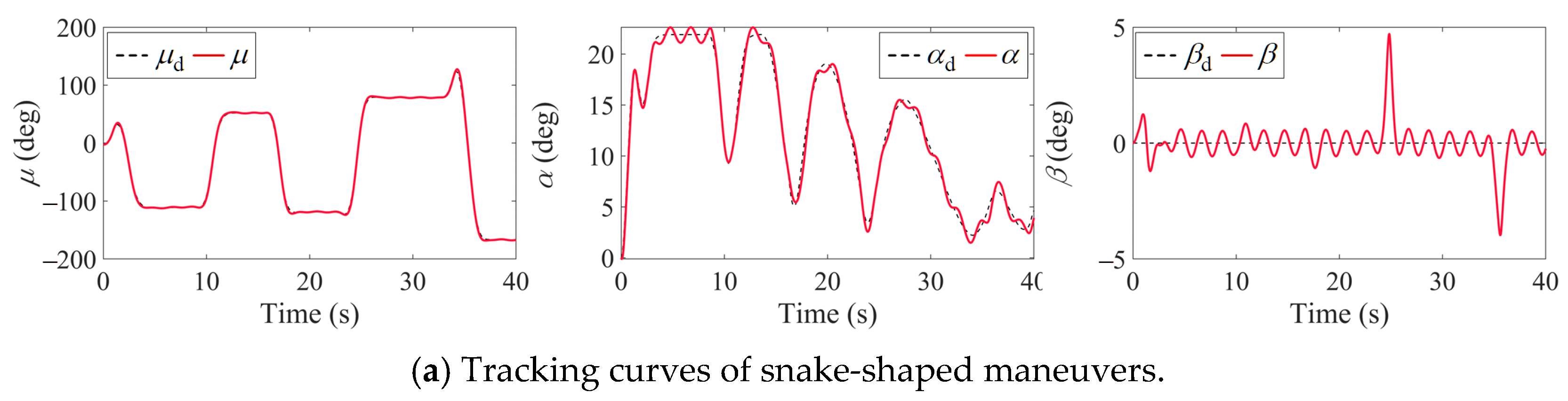
- Dynamic nonlinear AMS computation and validation. The algorithm dynamically computes the nonlinear AMS by integrating real-time control parameters. We conduct flight control simulations to validate feasibility and effectiveness. These simulations utilize the admissible control set derived from the nonlinear AMS to quantify residual moments of tailless UAVs.
2. Problem Formulation and Preliminaries
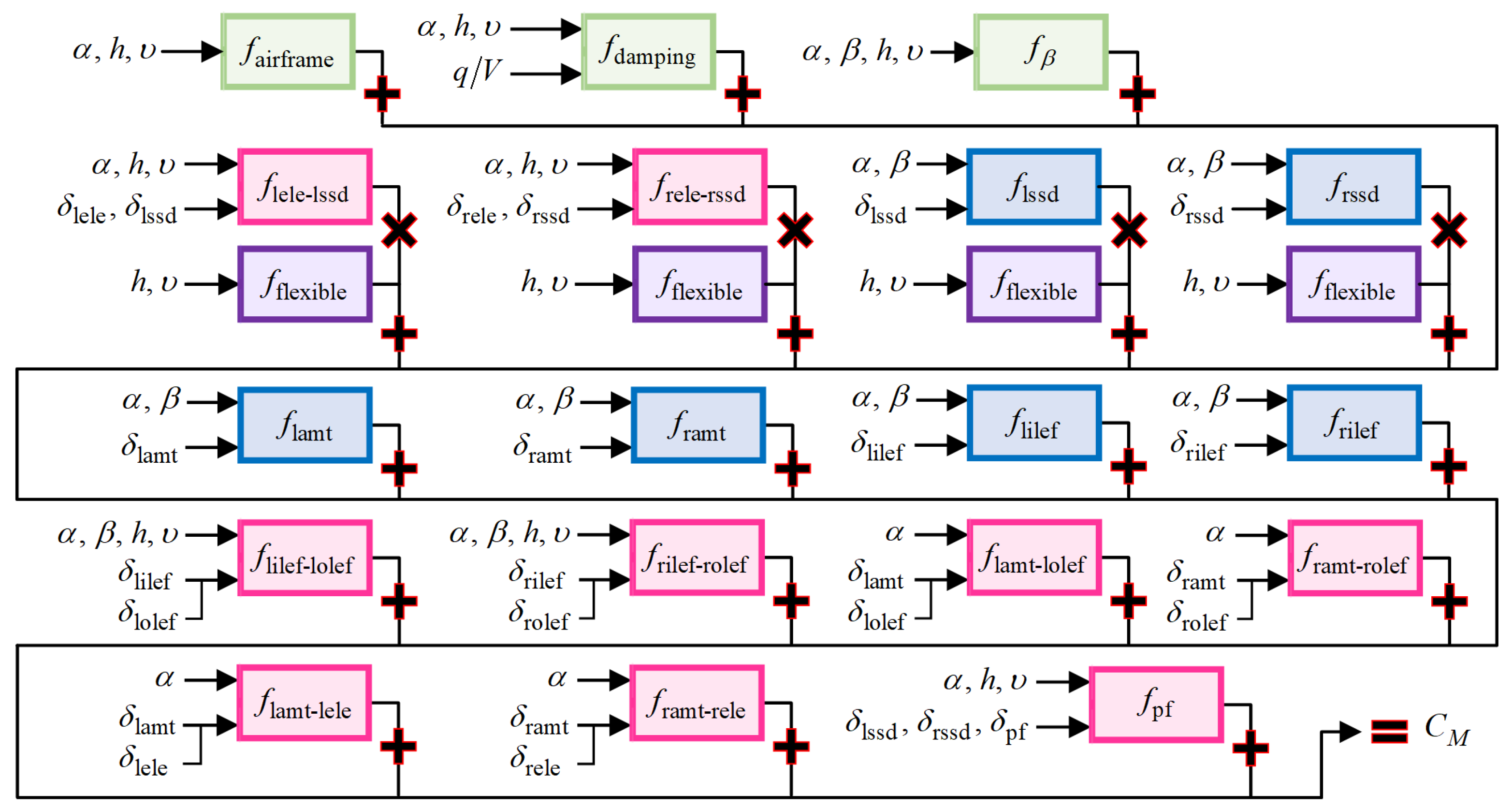
3. Computational Method for the Nonlinear Attainable Moment Set
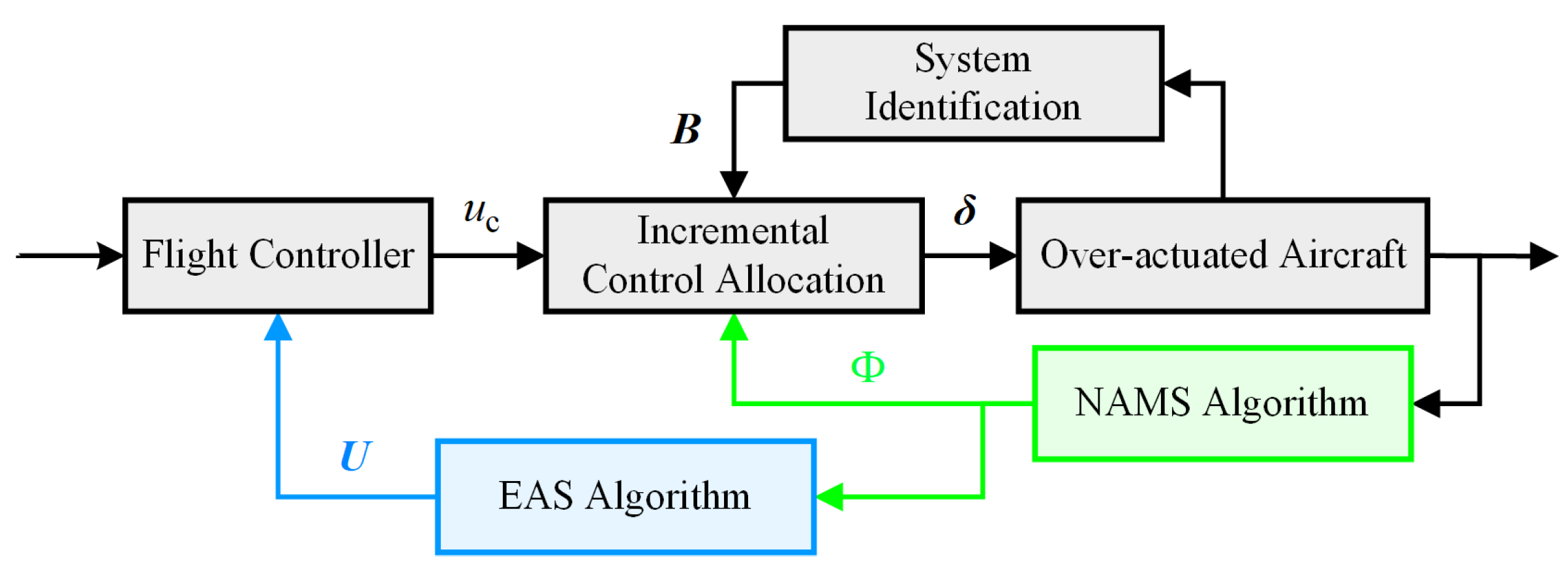
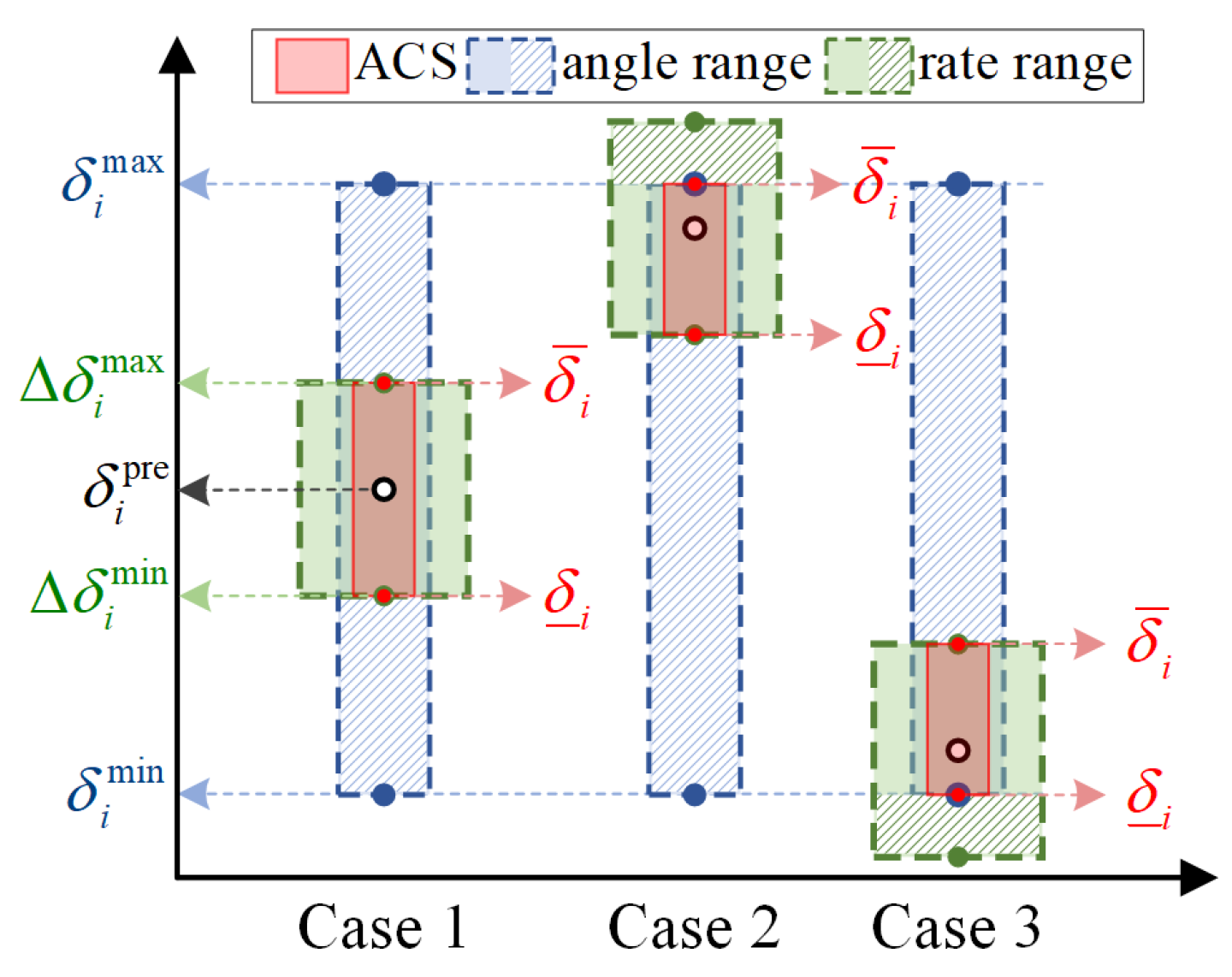
3.1. Flight-Control-System-Dynamics-Integrated AMS Computation Under the Constraints of the Admissible Control Set
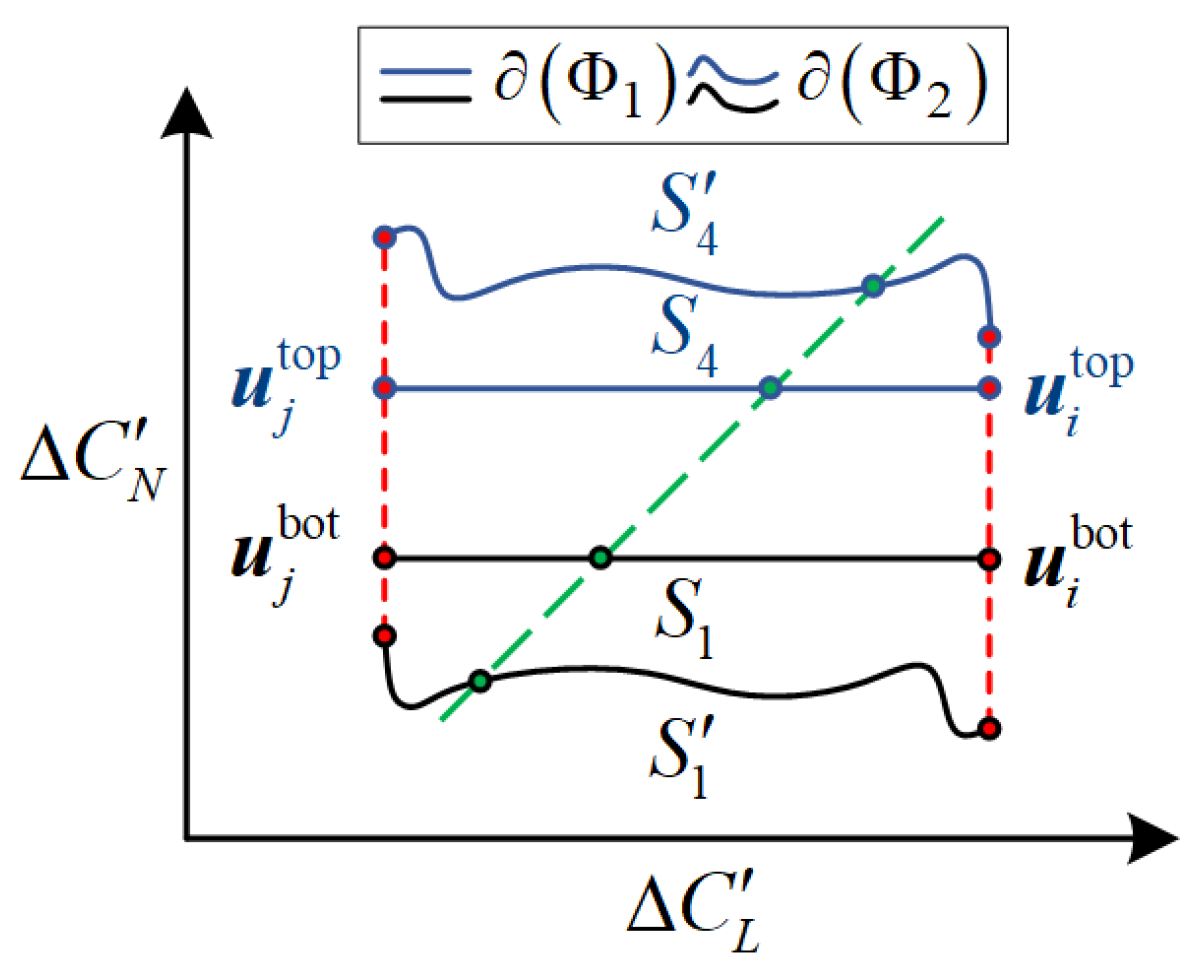
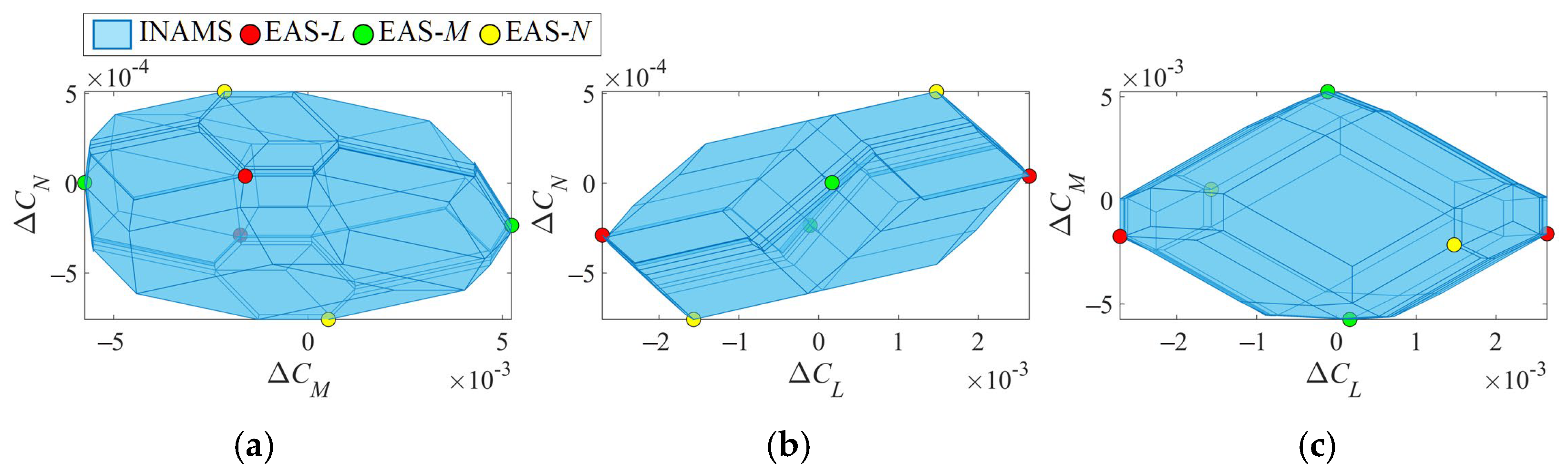
3.2. Incremental Nonlinear Attainable Moment Set (INAMS)
| Algorithm 1 Incremental Nonlinear Attainable Moment Set |
 |
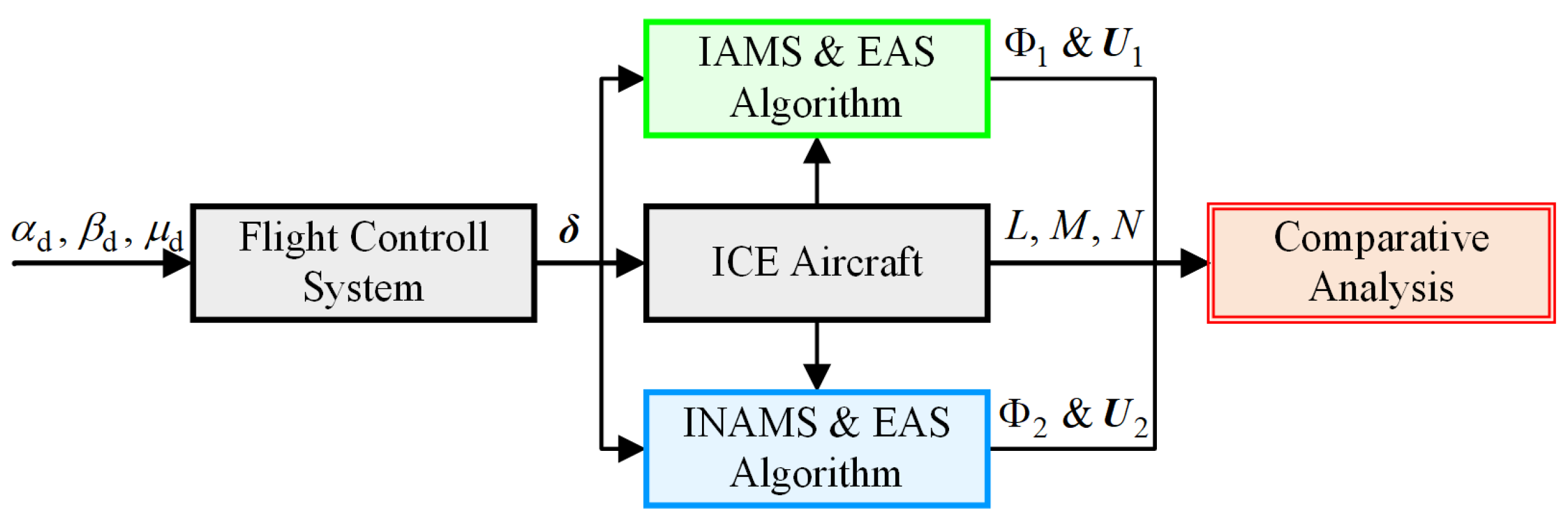
4. Experiment Evaluation and Comparison
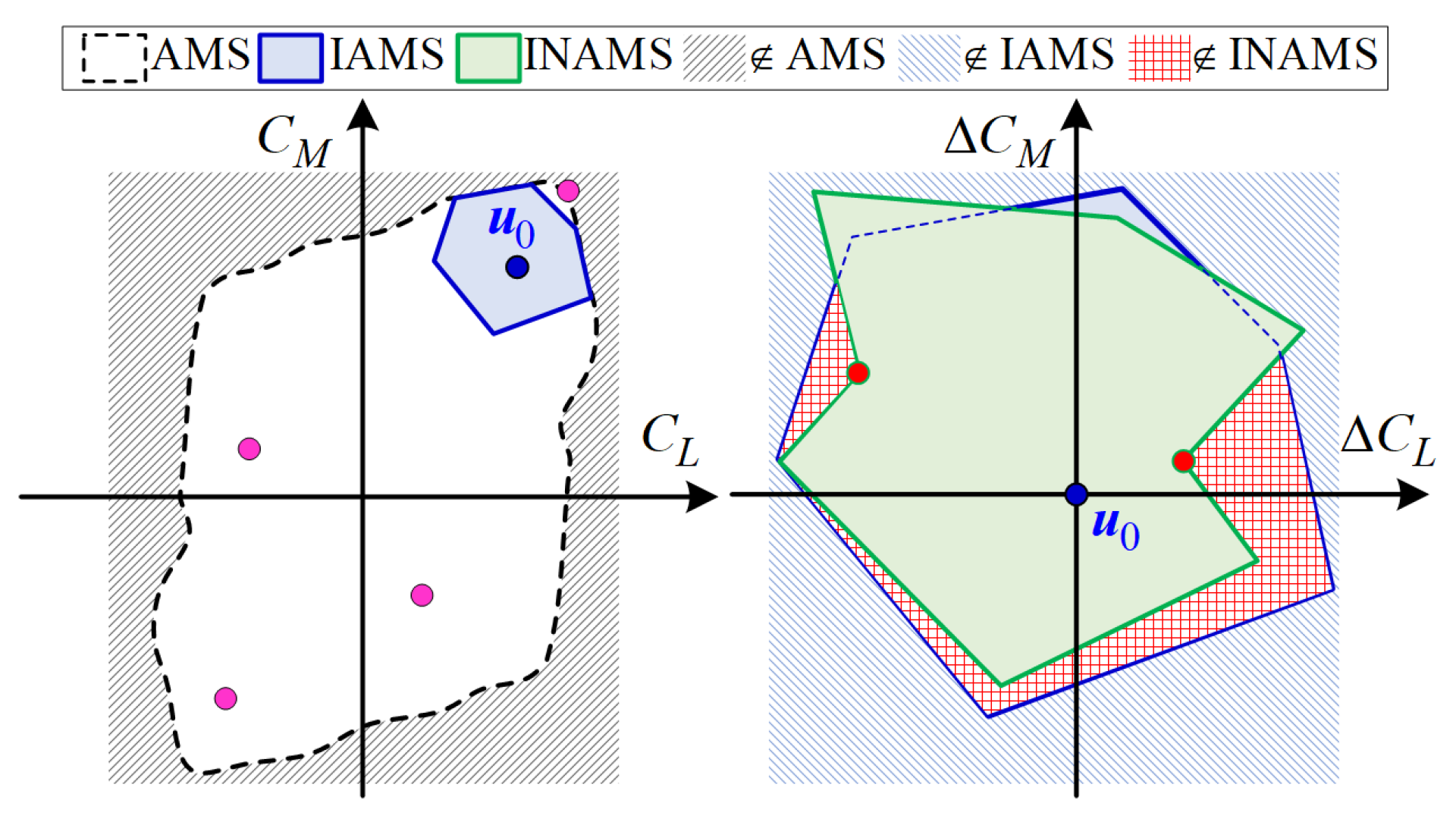
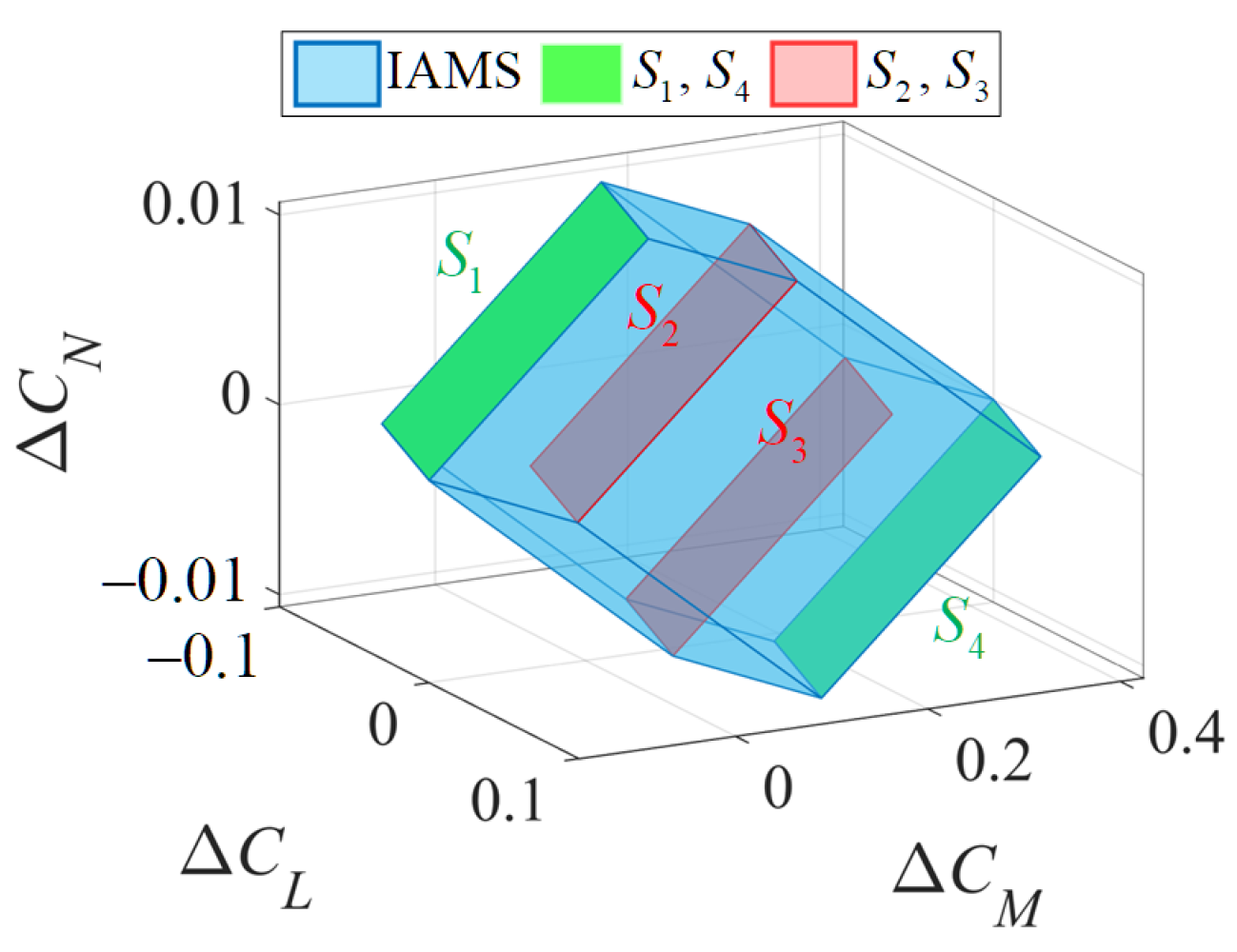
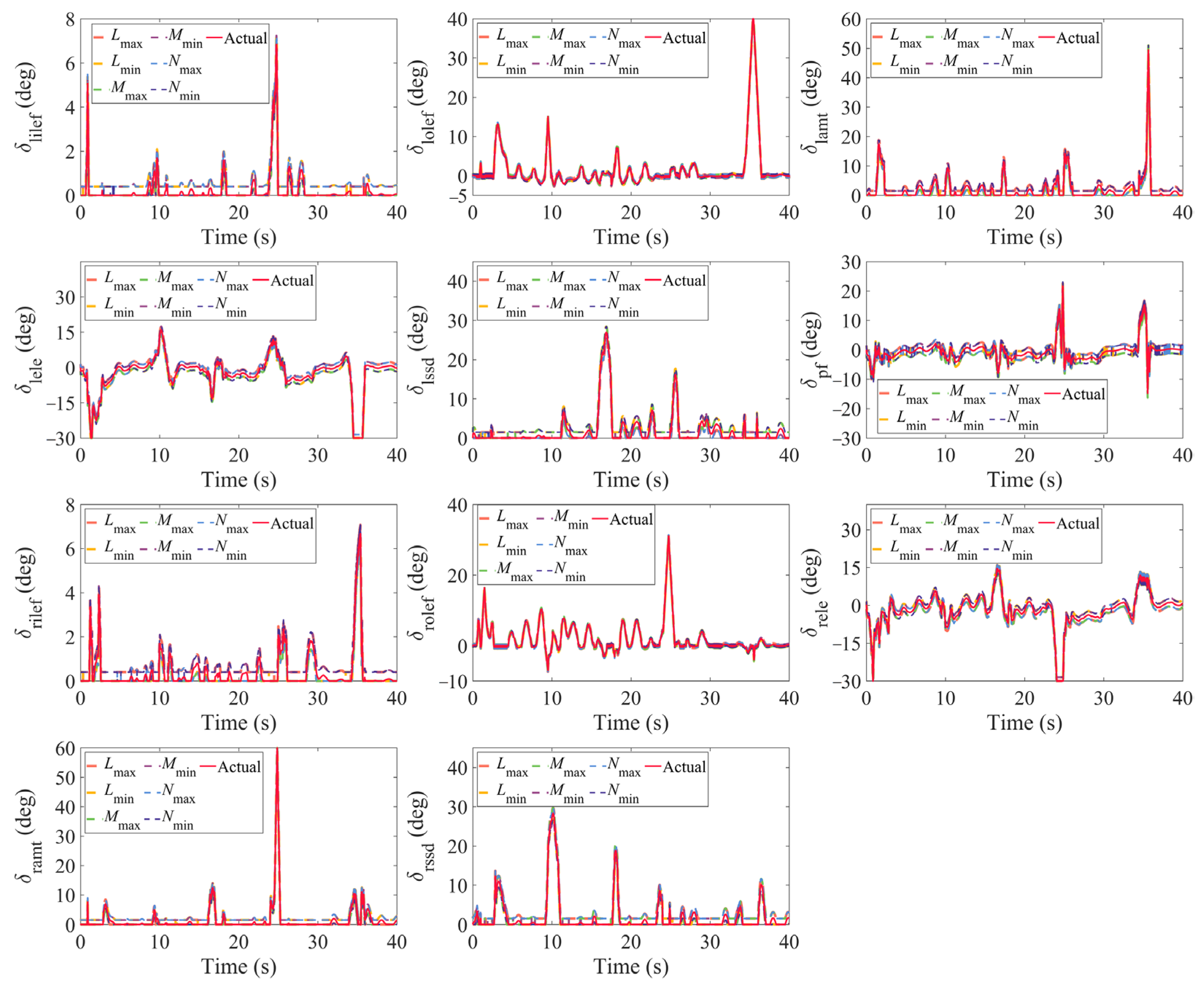
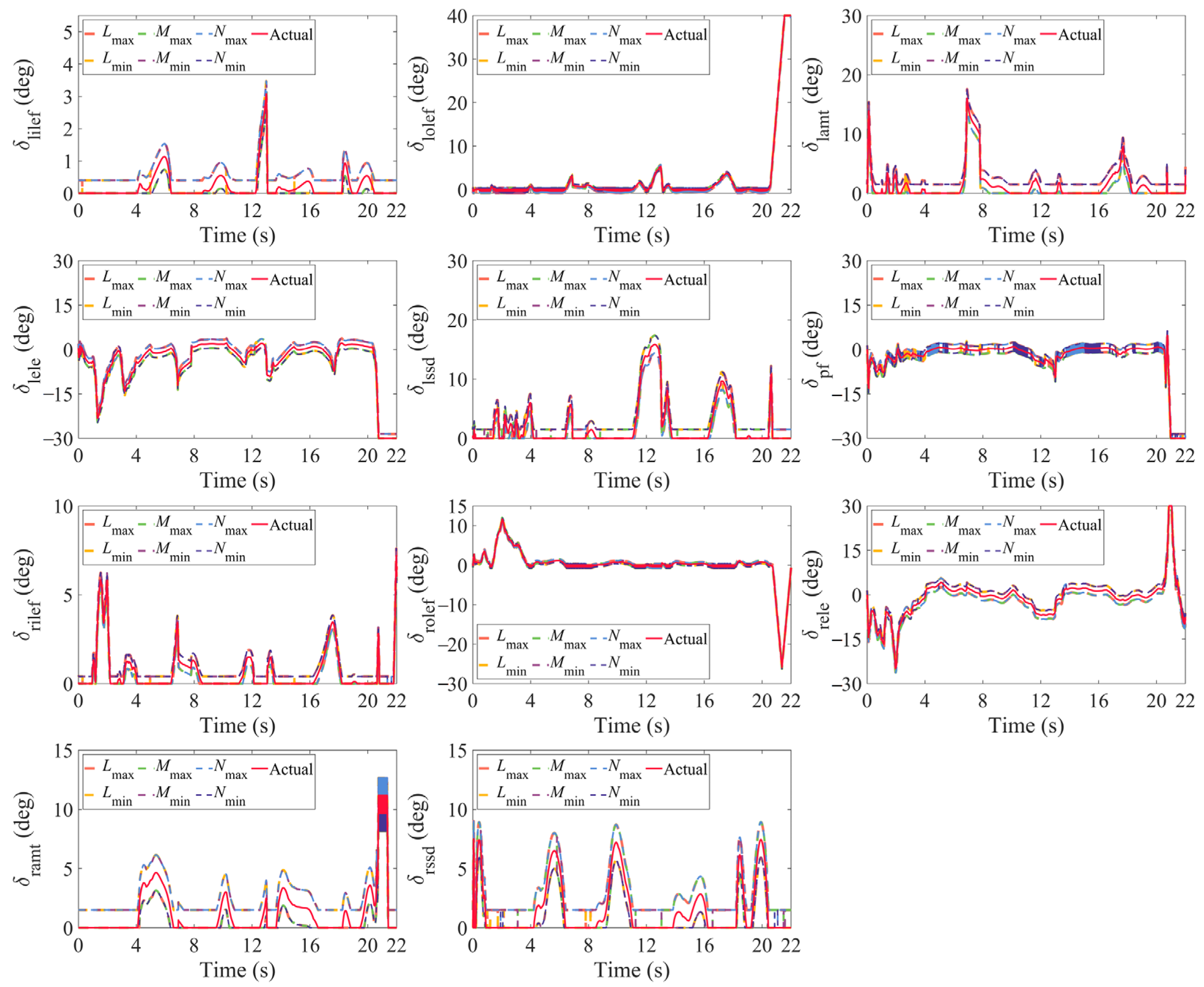
4.1. Comparative Simulations of the AMS and IAMS
4.2. Comparative Simulations of the IAMS and INAMS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, J.; He, R.; Tang, G.; Bao, W. Pendulum Maneuvering Strategy for Hypersonic Glide Vehicles. Aerosp. Sci. Technol. 2018, 78, 62–70. [Google Scholar] [CrossRef]
- Yu, Z.; Li, Y.; Lv, M.; Pei, B.; Xu, W.; Bu, X. Fixed-Time Adaptive Fuzzy Fault-Tolerant Attitude Control for Tailless Aircraft Without Angular Velocity Measurements. IEEE Trans. Fuzzy Syst. 2024, 32, 2458–2470. [Google Scholar] [CrossRef]
- Lei, H.; Chen, B.; Liu, Y.; Lv, Y. Modified Kalman Particle Swarm Optimization: Application for Trim Problem of Very Flexible Aircraft. Eng. Appl. Artif. Intell. 2021, 100, 104176. [Google Scholar] [CrossRef]
- Lu, Z.; Hong, H.; Diepolder, J.; Holzapfel, F. Maneuverability Set Estimation and Trajectory Feasibility Evaluation for eVTOL Aircraft. J. Guid. Control Dyn. 2023, 46, 1184–1196. [Google Scholar] [CrossRef]
- Durham, W.C. Attainable Moments for the Constrained Control Allocation Problem. J. Guid. Control Dyn. 1994, 17, 1371–1373. [Google Scholar] [CrossRef]
- Varriale, C. Flight Mechanics and Performance of Direct Lift Control. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2022. [Google Scholar]
- Kaloust, J.; Doman, D.B. Computing Trimmable Angle of Attack for Aircraft with Control Failures. In Proceedings of the 2003 IEEE Aerospace Conference Proceedings (Cat. No.03TH8652), Big Sky, MT, USA, 8–15 March 2003; IEEE: Big Sky, MT, USA, 2003; Volume 6, pp. 6_2801–6_2807. [Google Scholar] [CrossRef]
- Zhong, L. Contribution to Fault Tolerant Flight Control Under Actuator Failures. Ph.D. Thesis, INSA de Toulouse, Toulouse, France, 2014. [Google Scholar]
- Söpper, M.; Zhang, J.; Bähr, N.; Holzapfel, F. Required Moment Sets: Enhanced Controllability Analysis for Nonlinear Aircraft Models. Appl. Sci. 2021, 11, 3456. [Google Scholar] [CrossRef]
- Yu, Y.; Li, R.; Ji, W.; Lu, Z.; Tian, G. Refinements of the Dynamic Inversion Part of Hierarchical 4WIS/4WID Trajectory Tracking Controllers. SAE Int. J. Adv. Curr. Prac. Mobil. 2024, 6, 898–912. [Google Scholar] [CrossRef]
- Lu, Z.; Hong, H.; Schweighofer, F.; Holzapfel, F. Controllability Evaluation for VTOL Aircraft in Velocity Envelope: A Distance-Based Metric. J. Guid. Control Dyn. 2024, 47, 1620–1633. [Google Scholar] [CrossRef]
- Bolender, M.A.; Doman, D.B. Method for Determination of Nonlinear Attainable Moment Sets. J. Guid. Control Dyn. 2004, 27, 907–914. [Google Scholar] [CrossRef]
- Hu, Q.; Tan, X.; Akella, M.R. Closed-Loop-Based Control Allocation for Spacecraft Attitude Stabilization with Actuator Fault. J. Guid. Control Dyn. 2018, 41, 944–953. [Google Scholar] [CrossRef]
- Zhu, Z.; Guo, H.; Ma, J. Aerodynamic Layout Optimization Design of a Barrel-Launched UAV Wing Considering Control Capability of Multiple Control Surfaces. Aerosp. Sci. Technol. 2019, 93, 105297. [Google Scholar] [CrossRef]
- Zheng, F.; Liu, L.; Chen, Z.; Chen, Y.; Cheng, F. Hybrid Multi-Objective Control Allocation Strategy for Compound High-Speed Rotorcraft. ISA Trans. 2020, 98, 207–226. [Google Scholar] [CrossRef] [PubMed]
- Varriale, C.; Voskuijl, M. A Trim Problem Formulation for Maximum Control Authority Using the Attainable Moment Set Geometry. CEAS Aeronaut. J. 2022, 13, 251–266. [Google Scholar] [CrossRef]
- Pfeifle, O.; Fichter, W. Incremental Control Allocation with Axis Prioritization on the Boundary of the Attainable Control Set. In AIAA SCITECH 2023 Forum; American Institute of Aeronautics and Astronautics: National Harbor, MD, USA, 2023. [Google Scholar] [CrossRef]
- Pfeifle, O.; Fichter, W. Minimum Power Control Allocation for Incremental Control of Over-Actuated Transition Aircraft. J. Guid. Control Dyn. 2023, 46, 286–300. [Google Scholar] [CrossRef]
- Bolander, C.R.; Hunsaker, D.F.; Myszka, D.; Joo, J.J. Attainable Moment Set and Actuation Time of a Bio-Inspired Rotating Empennage. In AIAA SCITECH 2022 Forum; AIAA: San Diego, CA, USA, 2022. [Google Scholar]
- Wahler, N.F.; Varriale, C.; La Rocca, G. Impact of Control Allocation Methods on the Design of Control Surface Layouts for Box-Wing Aircraft under Flying Qualities Constraints. In AIAA AVIATION 2023 Forum; American Institute of Aeronautics and Astronautics: San Diego, CA, USA, 2023. [Google Scholar] [CrossRef]
- Zhang, J.; Söpper, M.; Holzapfel, F.; Zhang, S. Four-Dimensional Generalized AMS Optimization Considering Critical Engine Inoperative for an eVTOL. Aerospace 2024, 11, 990. [Google Scholar] [CrossRef]
- Jonasson, M.; Andreasson, J.; Jacobson, B.; Trigell, A.S. Global Force Potential of Over-Actuated Vehicles. Veh. Syst. Dyn. 2010, 48, 983–998. [Google Scholar] [CrossRef]
- Han, L.; Hu, J.; Wang, Y.; Cong, J.; Zhang, P. Design of Pseudo-Command Restricted Controller for Tailless Unmanned Aerial Vehicles Based on Attainable Moment Set. Drones 2024, 8, 101. [Google Scholar] [CrossRef]
- Stolk, A.R.J. Minimum Drag Control Allocation for the Innovative Control Effector Aircraft. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
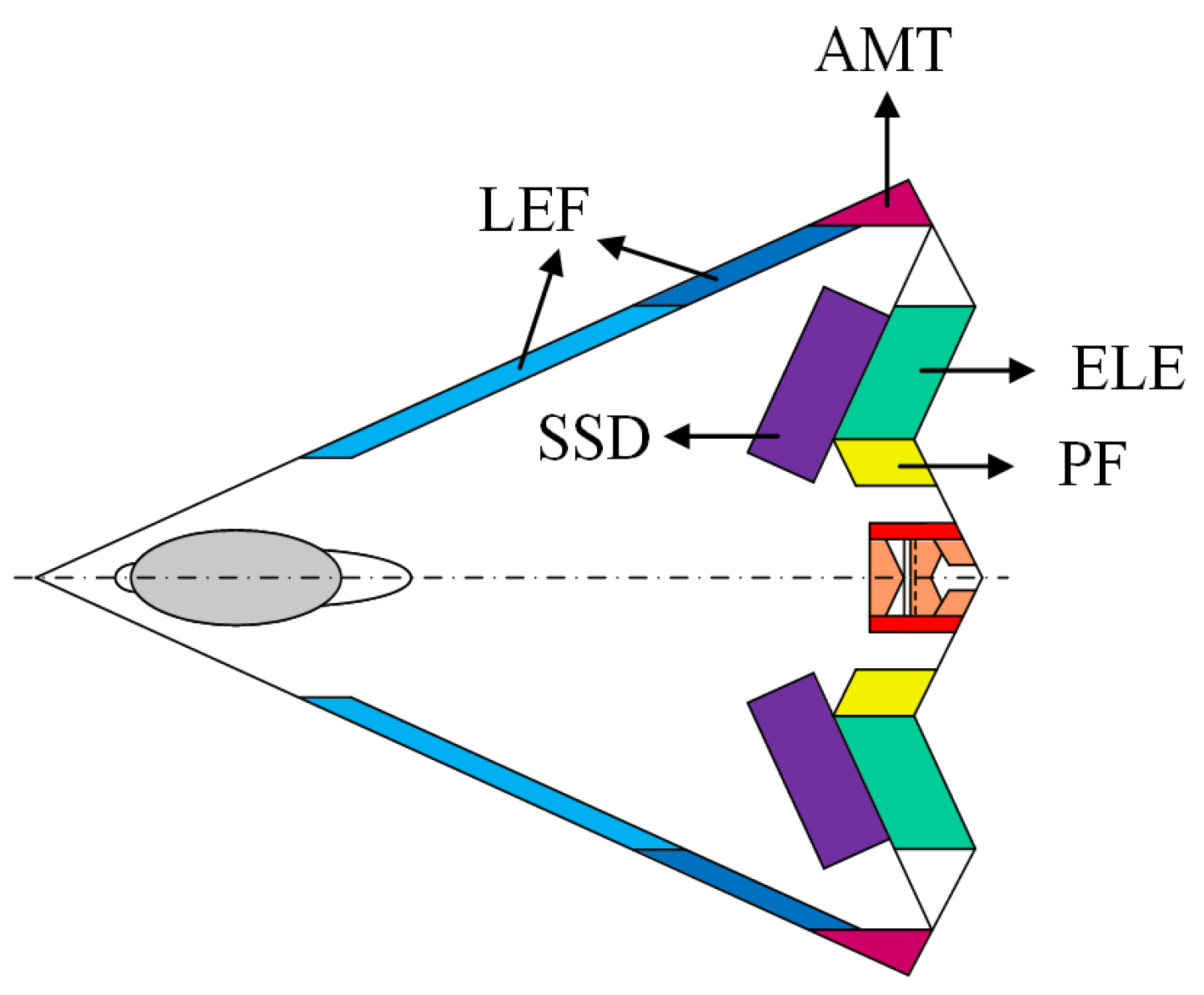


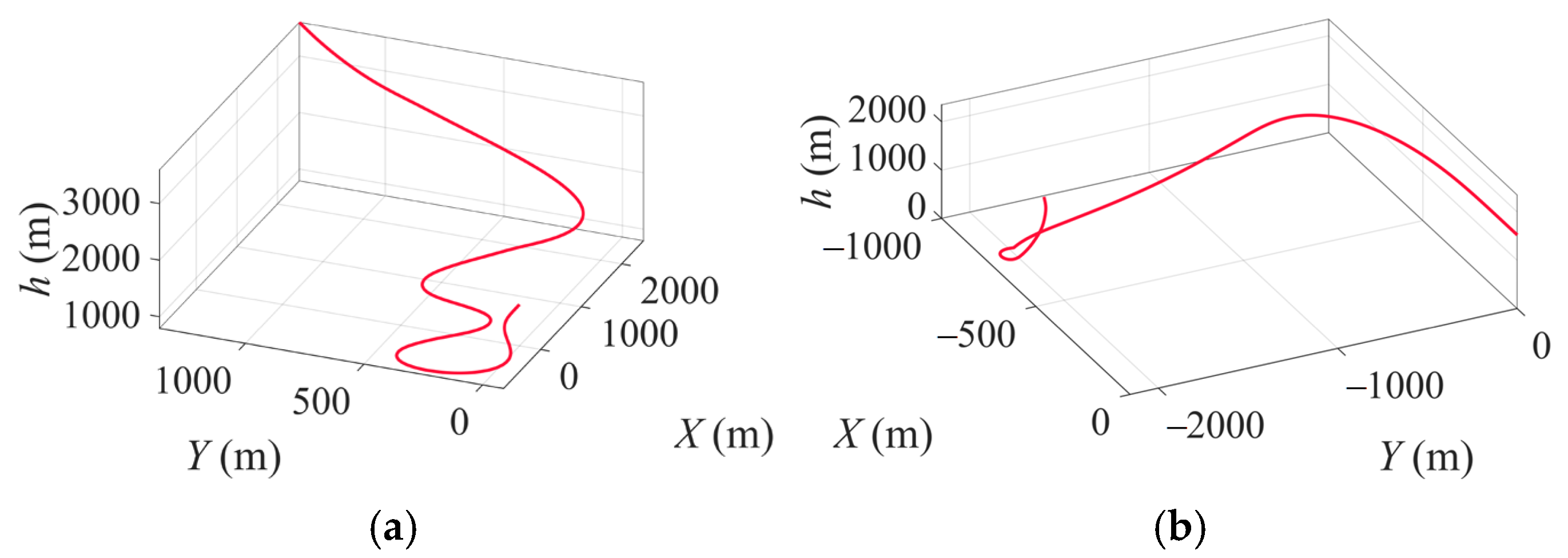

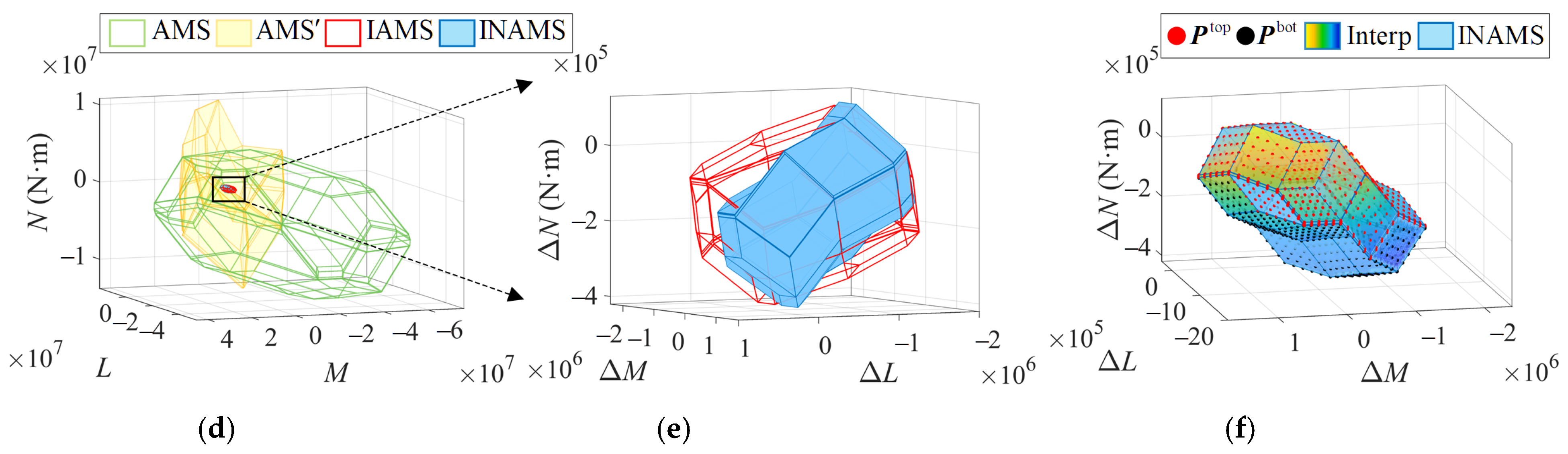
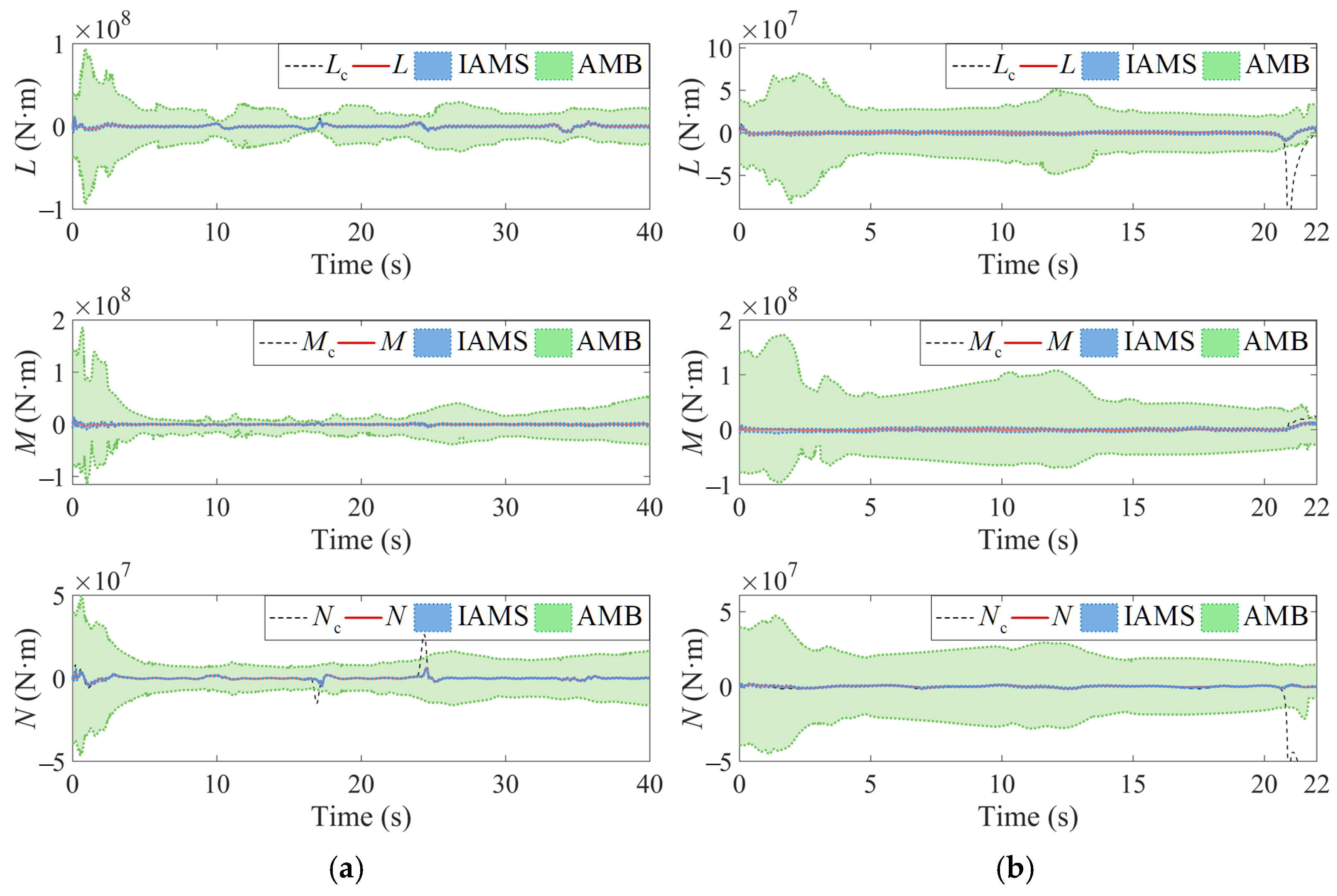
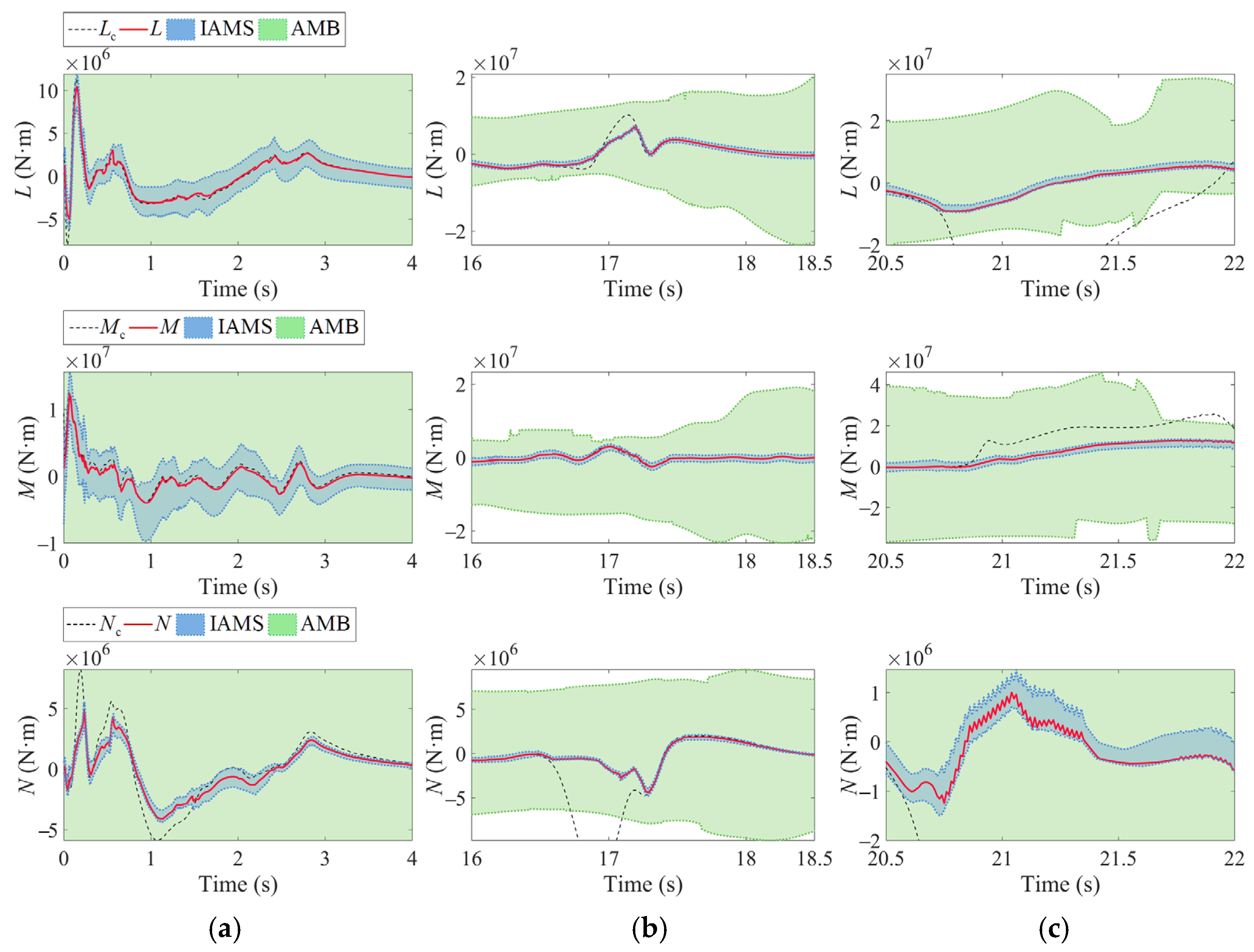

| Parameters | Value | Unit |
|---|---|---|
| c | ||
| Effectors | Angle Limits (deg) | Angle Rate Limits (deg/ms) |
|---|---|---|
| lilef | [0, 40] | [−0.04, 0.04] |
| lolef | [−40, 40] | [−0.04, 0.04] |
| lamt | [0, 60] | [−0.15, 0.15] |
| lele | [−30, 30] | [−0.15, 0.15] |
| lssd | [0, 60] | [−0.15, 0.15] |
| pf | [−30, 30] | [−0.15, 0.15] |
| rilef | [0, 40] | [−0.04, 0.04] |
| rolef | [−40, 40] | [−0.04, 0.04] |
| ramt | [0, 60] | [−0.15, 0.15] |
| rele | [−30, 30] | [−0.15, 0.15] |
| rssd | [0, 60] | [−0.15, 0.15] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Zhang, P.; Wang, Y.; Bian, Y.; Hu, J. A Computational Method for the Nonlinear Attainable Moment Set of Tailless UAVs in Flight-Control-Oriented Scenarios. Drones 2025, 9, 585. https://doi.org/10.3390/drones9080585
Han L, Zhang P, Wang Y, Bian Y, Hu J. A Computational Method for the Nonlinear Attainable Moment Set of Tailless UAVs in Flight-Control-Oriented Scenarios. Drones. 2025; 9(8):585. https://doi.org/10.3390/drones9080585
Chicago/Turabian StyleHan, Linxiao, Peng Zhang, Yingyang Wang, Yuan Bian, and Jianbo Hu. 2025. "A Computational Method for the Nonlinear Attainable Moment Set of Tailless UAVs in Flight-Control-Oriented Scenarios" Drones 9, no. 8: 585. https://doi.org/10.3390/drones9080585
APA StyleHan, L., Zhang, P., Wang, Y., Bian, Y., & Hu, J. (2025). A Computational Method for the Nonlinear Attainable Moment Set of Tailless UAVs in Flight-Control-Oriented Scenarios. Drones, 9(8), 585. https://doi.org/10.3390/drones9080585






