Path Planning for Unmanned Aerial Vehicle: A-Star-Guided Potential Field Method †
Abstract
1. Introduction
2. Traditional Path Planning Algorithm
2.1. A-Star Algorithm
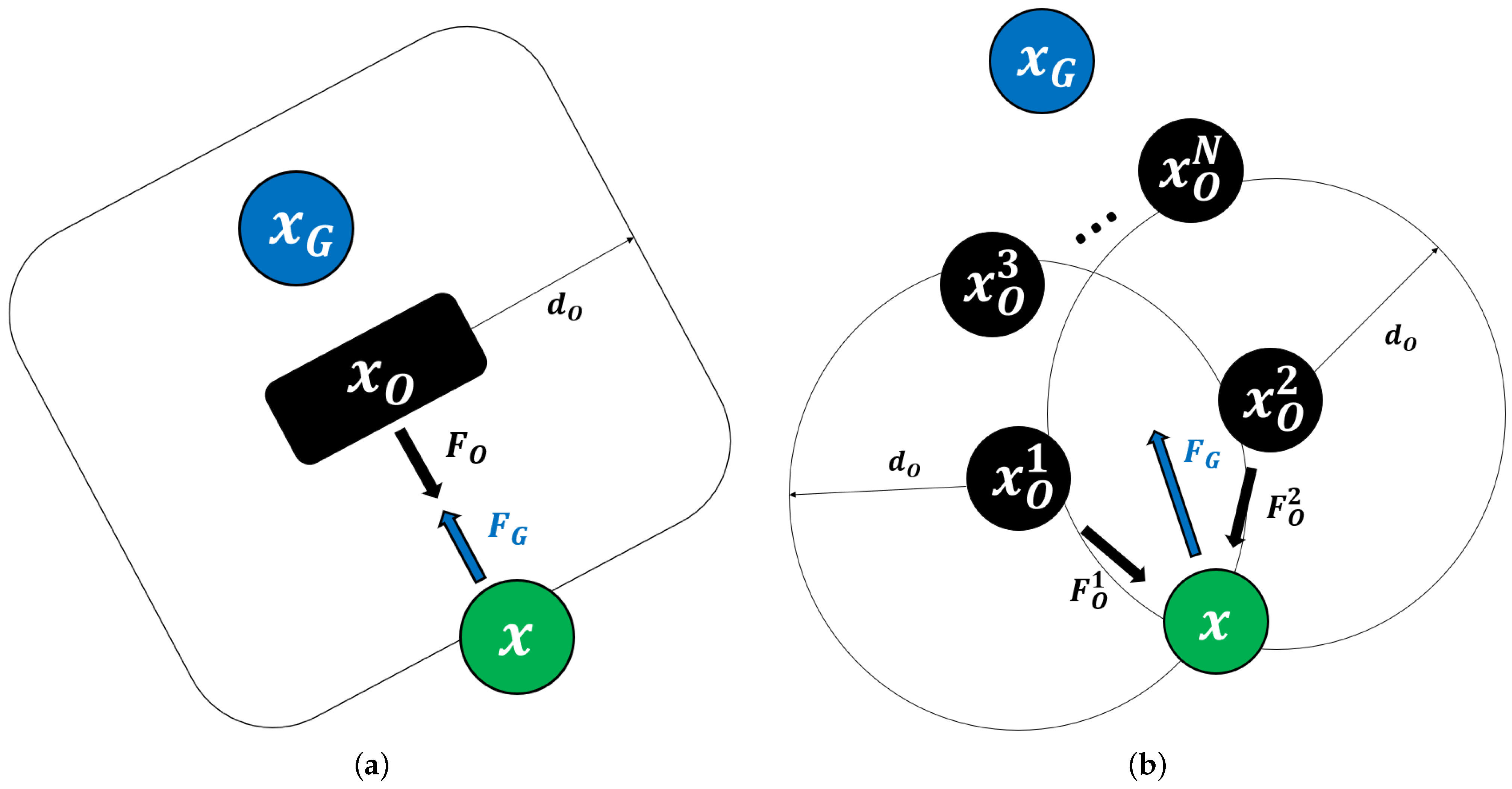
2.2. Artificial Potential Field Algorithm
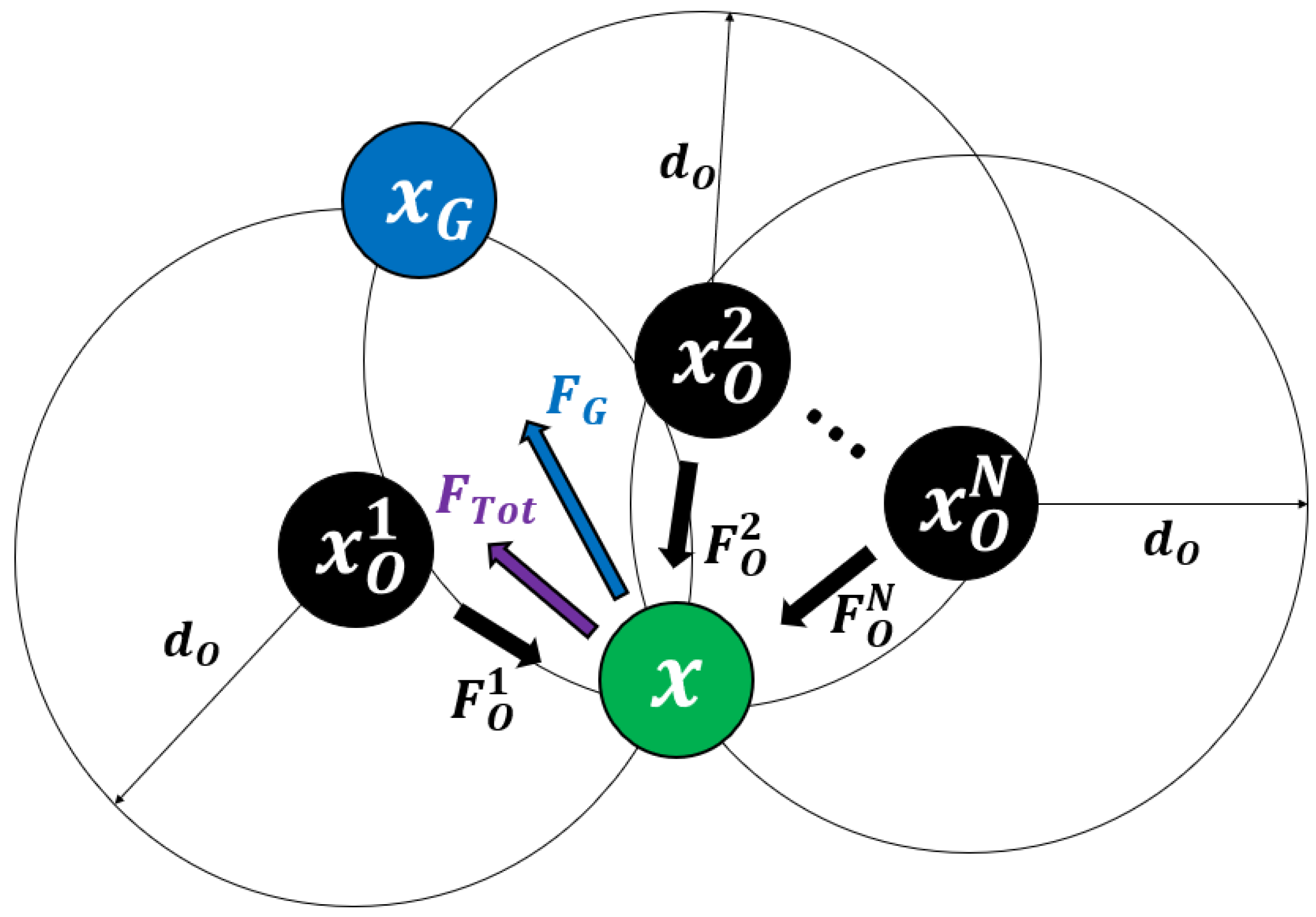
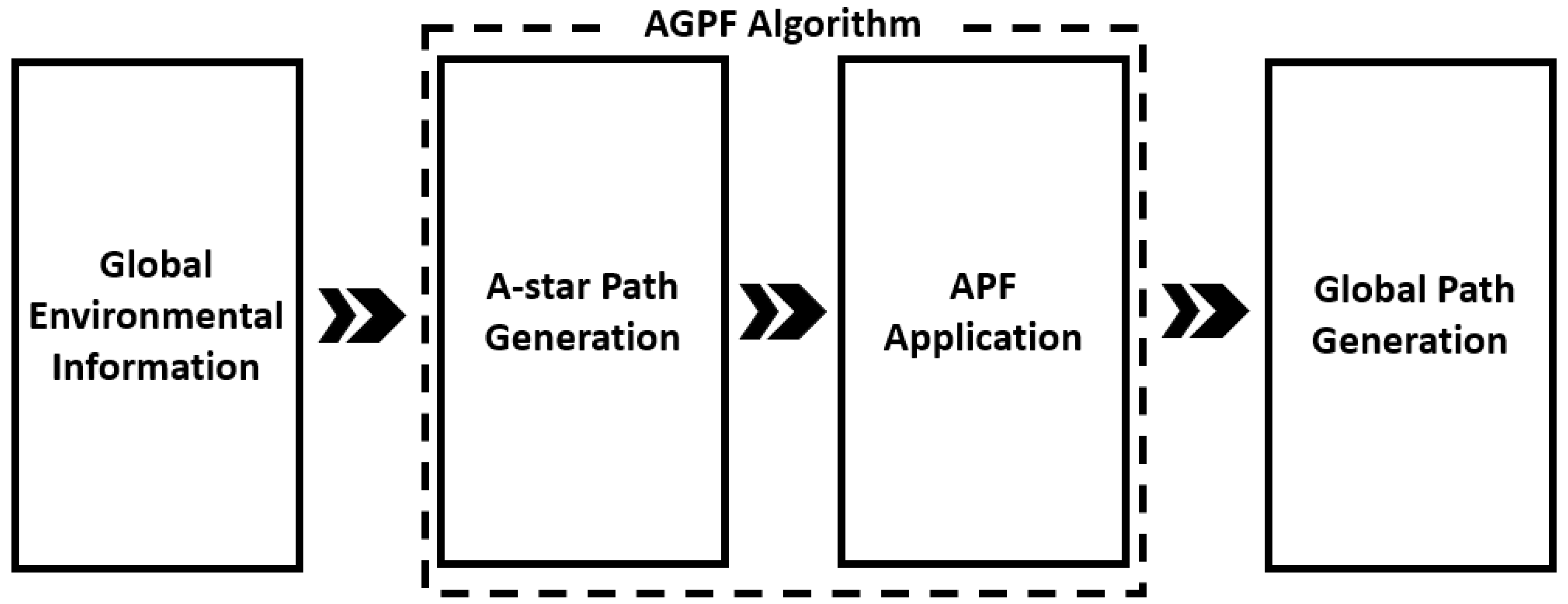
3. A-Star-Guided Potential Field Algorithm
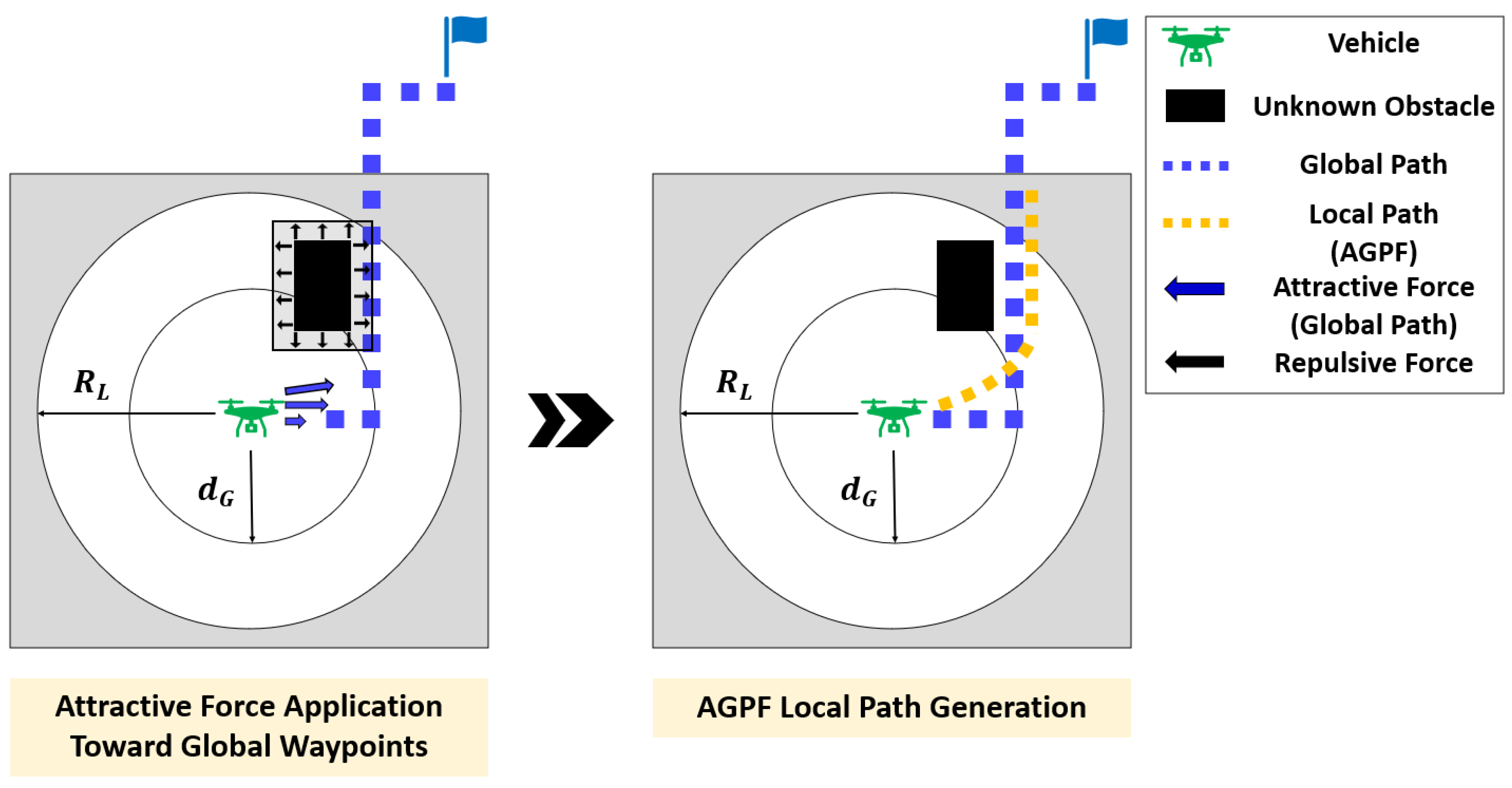
3.1. AGPF for Global Path Planning
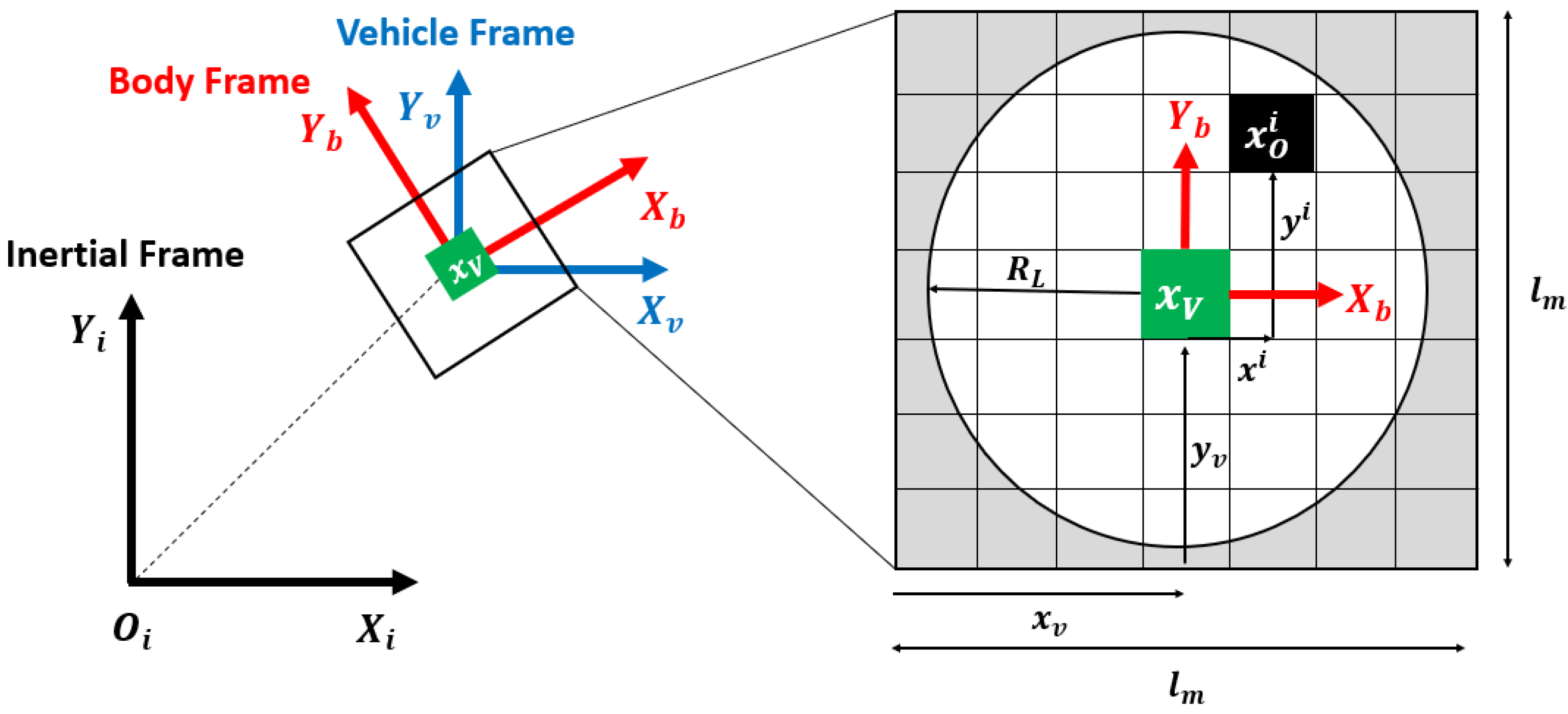
3.2. AGPF for Local Path Planning
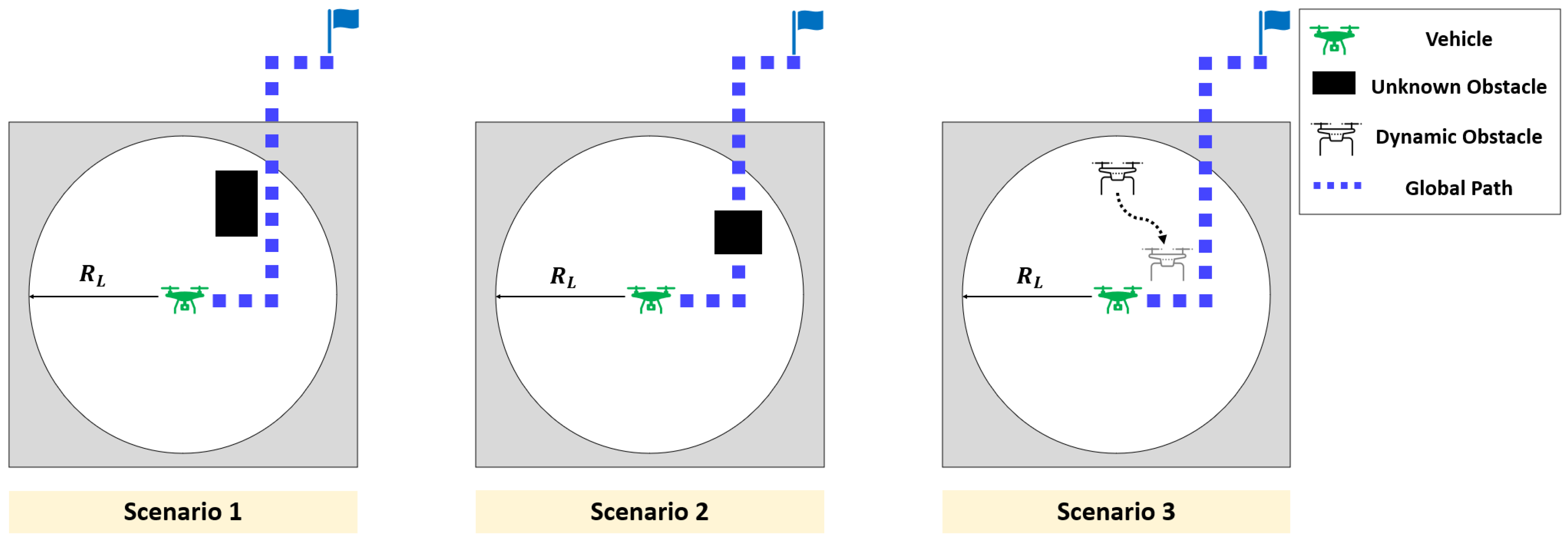
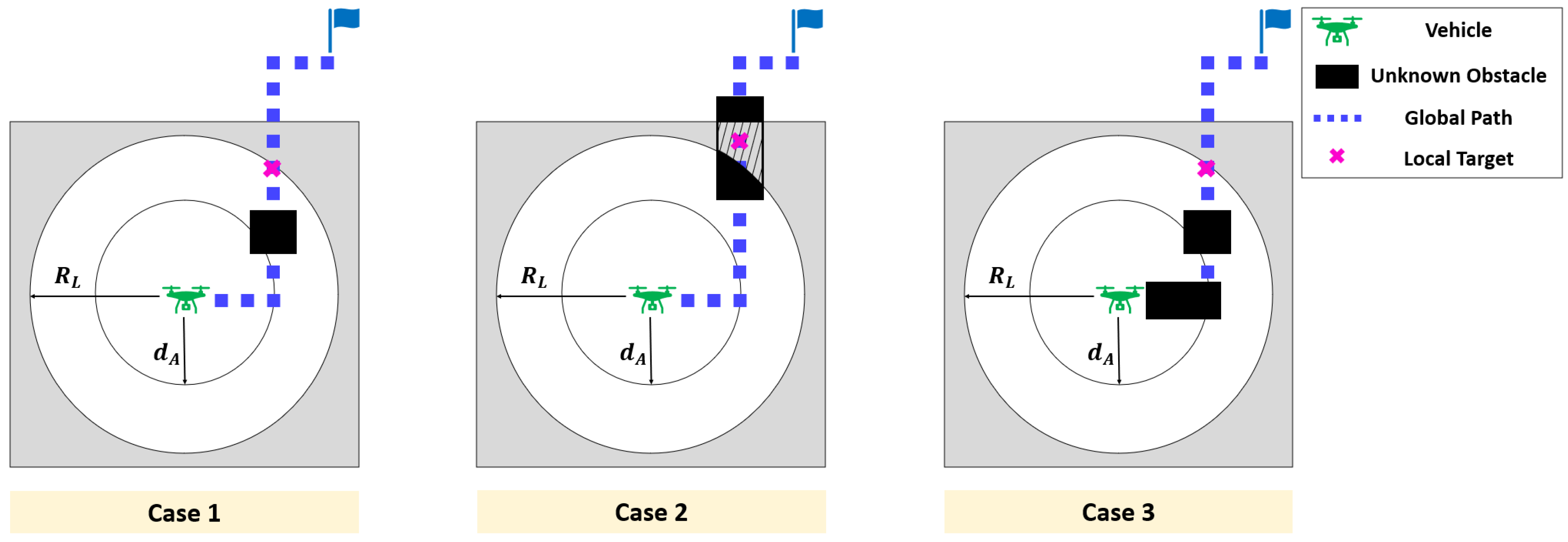
3.2.1. Avoidance of Obstacle
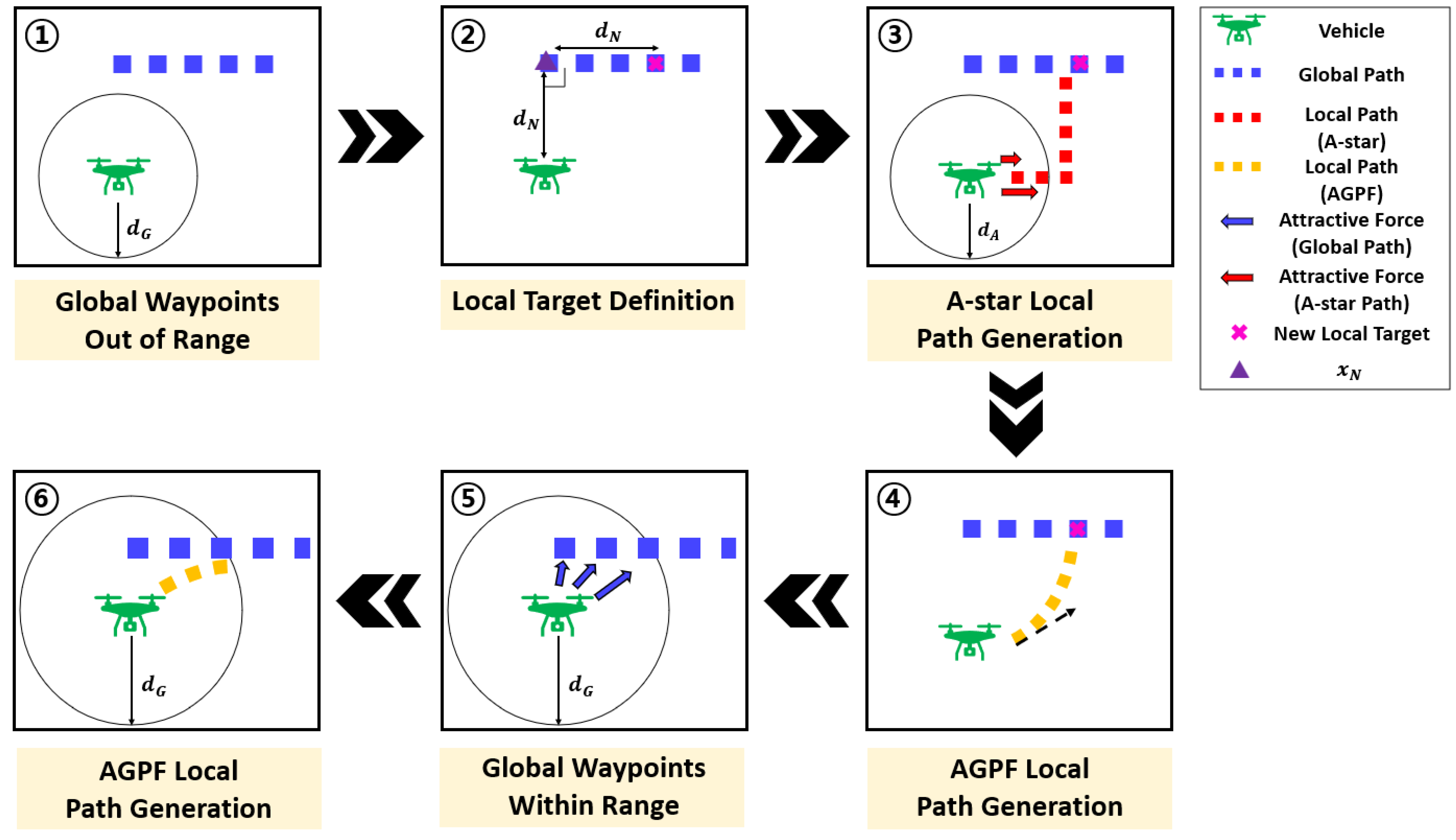
3.2.2. Return to Global Path
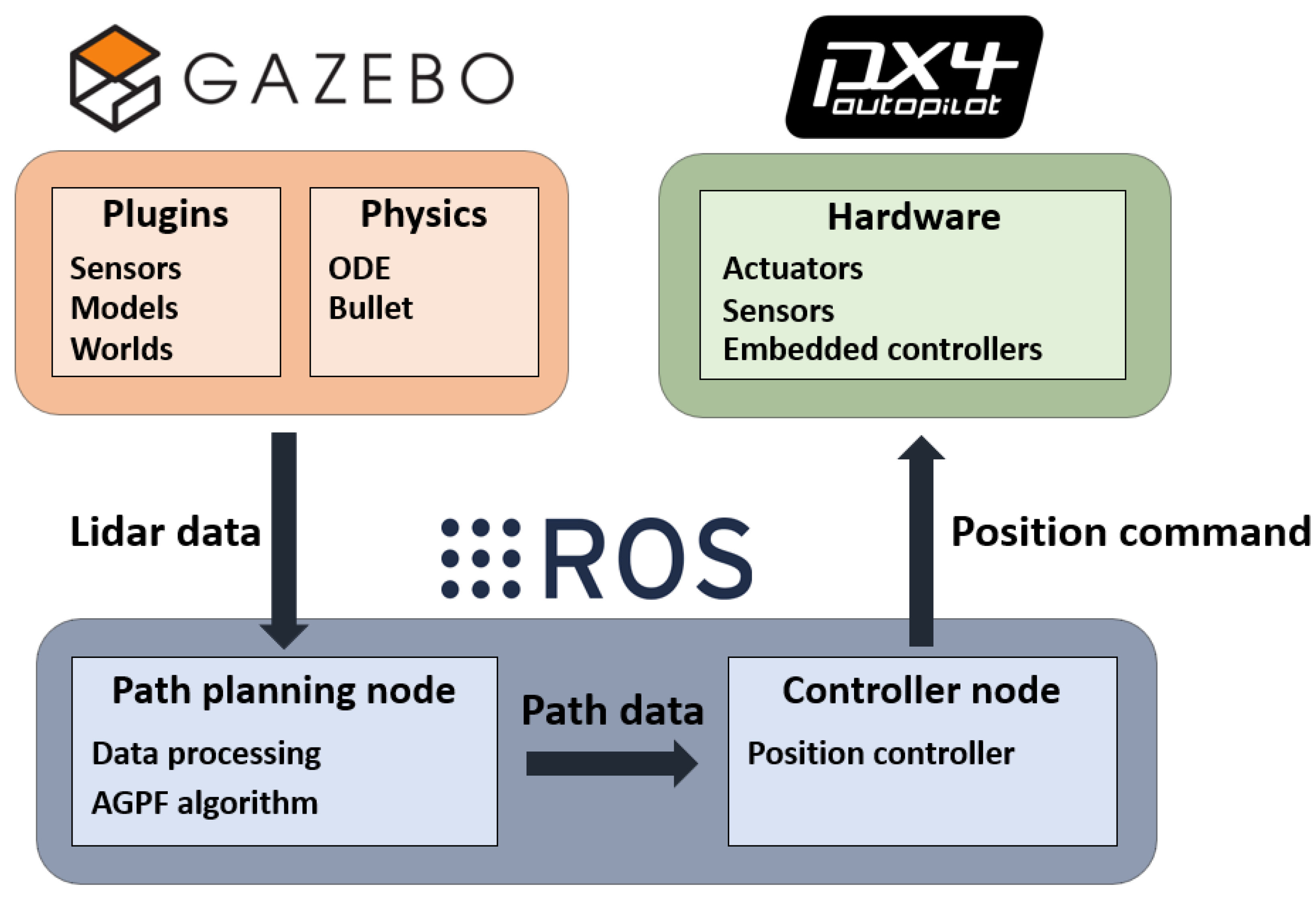
4. Simulation
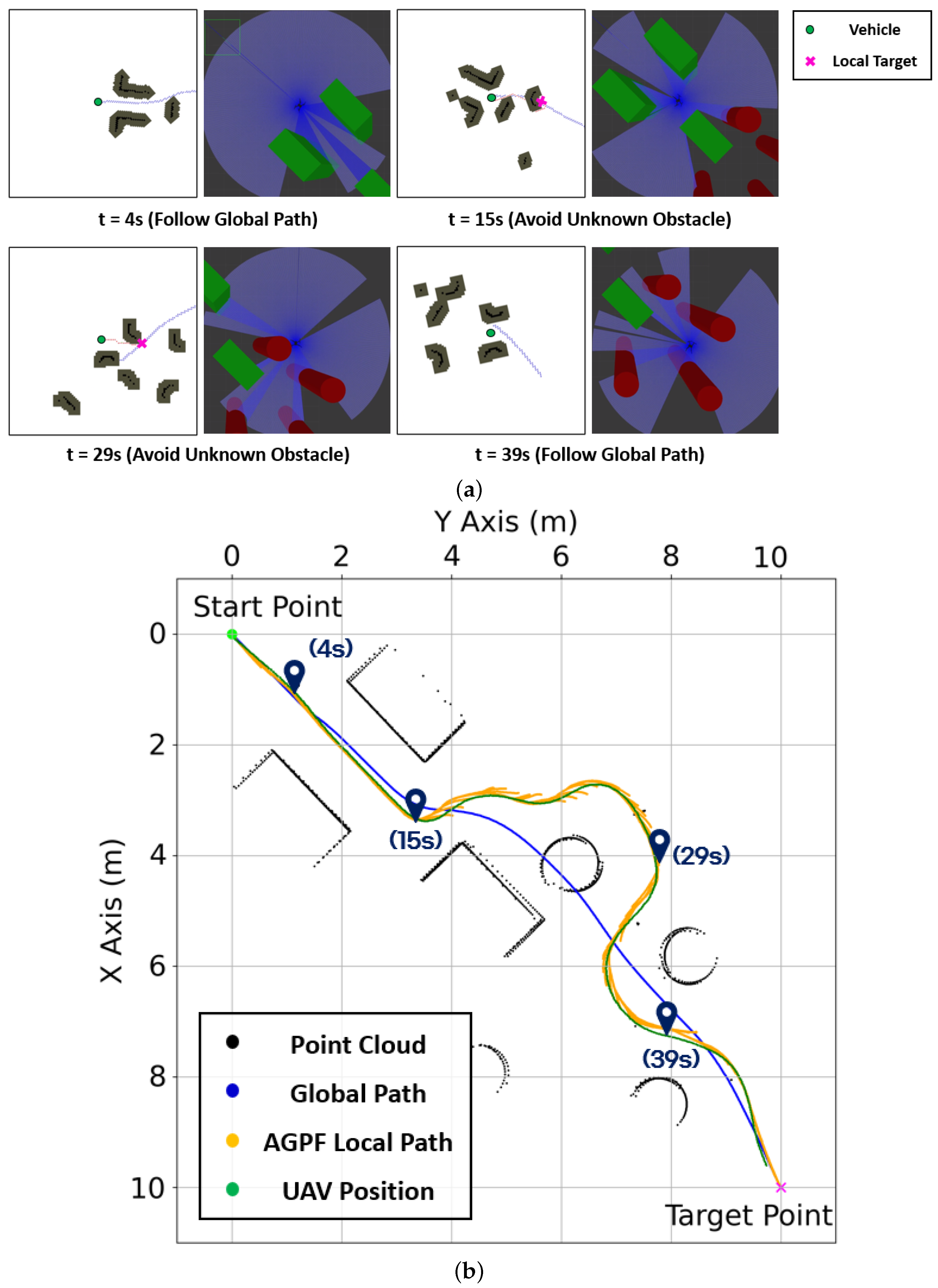
4.1. Global Path Planning
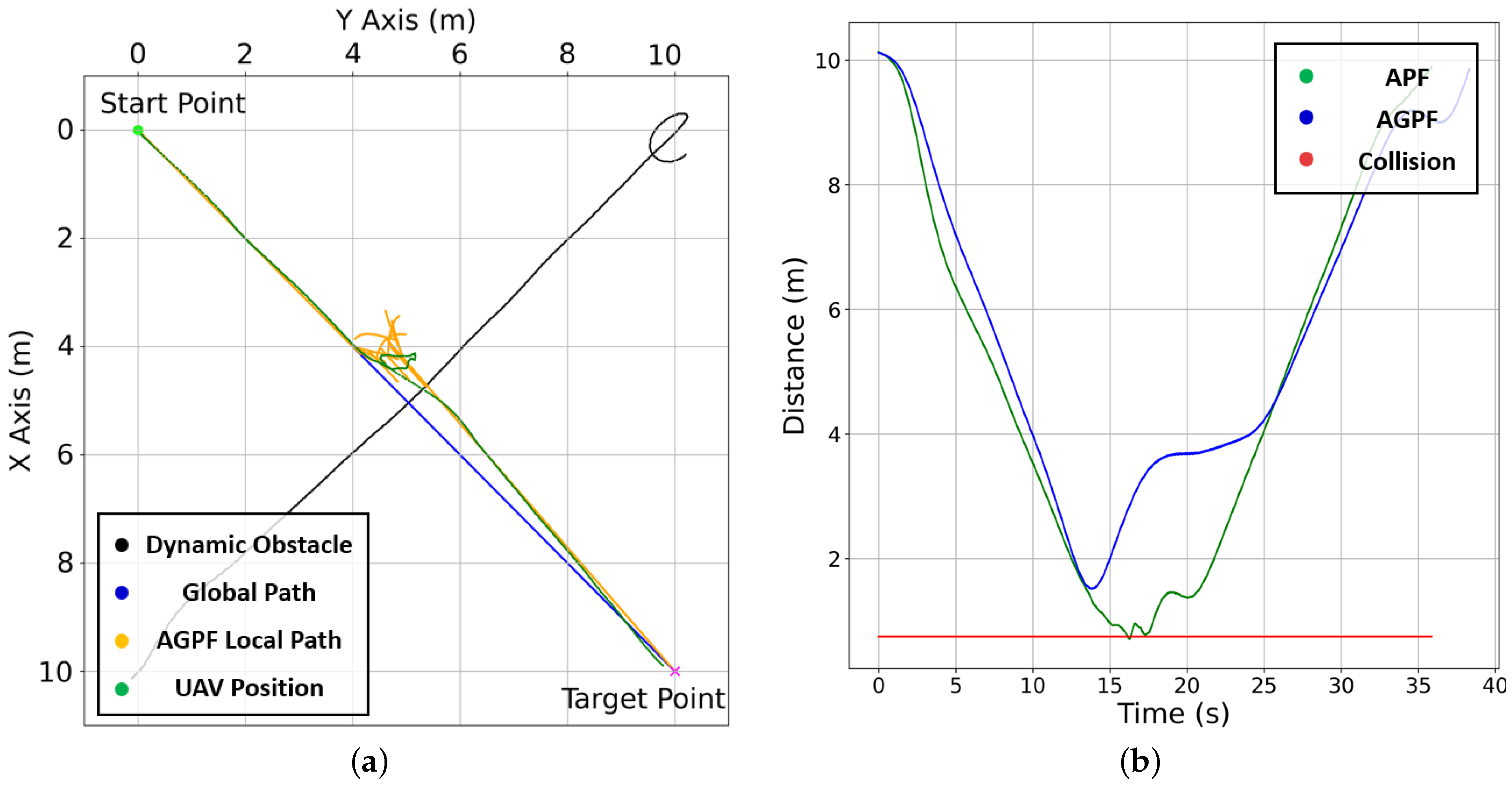
4.2. Local Path Planning
4.2.1. Avoidance of Unknown Obstacle
4.2.2. Avoidance of Dynamic Obstacle
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| c | Maximum allowable heading angle change |
| Distance threshold for A-star waypoints attraction | |
| Distance threshold for dynamic obstacle | |
| Distance from vehicle for local target selection | |
| Distance threshold for repulsive force | |
| Heuristic function in A-star | |
| Attraction force toward A-star waypoints | |
| Attraction force toward A-star waypoint | |
| Total attraction force | |
| Attractive force components along the x-axis | |
| Attractive force components along the y-axis | |
| Attractive force toward goal | |
| Repulsive force from obstacle in APF | |
| Repulsive force from obstacle in AGPF | |
| Repulsive force from obstacle in APF | |
| Repulsive force from obstacle in AGPF | |
| Component of the repulsive force parallel to from the obstacle | |
| Component of the repulsive force perpendicular to from the obstacle | |
| Total repulsive force | |
| Force along the vehicle’s heading direction | |
| Actual cost of the path from the start to the current node | |
| Estimated cost calculated by Euclidean | |
| Attractive potential field coefficient for A-star waypoints in AGPF | |
| Attractive potential field coefficient for goal in APF | |
| Velocity-aligned force coefficient in AGPF | |
| Size of the local grid map | |
| Coefficient defining the shape of the repulsive force | |
| Rotation matrix used to transform the local target | |
| Detection range of LiDAR sensor | |
| Attractive field toward A-star waypoints in AGPF | |
| Attractive field toward goal in APF | |
| Repulsive field from obstacle | |
| Velocity of dynamic obstacle | |
| Velocity of vehicle | |
| Relative velocity between the vehicle and the dynamic obstacle | |
| x-coordinate of the relative position to the obstacle in the local grid map | |
| Position vector of the A-star waypoint | |
| x-axis of the body frame | |
| Position vector of the dynamic obstacle | |
| x-coordinate of the goal | |
| Position vector of the goal | |
| Position vector of the node in the local grid map | |
| x-axis of the inertial frame | |
| Position vector of the local target in the local grid map | |
| Position vector from to in the local grid map | |
| x-coordinate of the node | |
| Position vector of the obstacle | |
| x-coordinate of the obstacle in the local grid map | |
| Position vector of the vehicle in the local grid map | |
| x-coordinate of the vehicle in the local grid map | |
| x-axis of the Vehicle frame | |
| y-coordinate of the relative position to the obstacle in the local grid map | |
| y-axis of the body frame | |
| y-coordinate of the goal | |
| y-axis of the inertial frame | |
| y-coordinate of the node | |
| y-coordinate of the obstacle in the local grid map | |
| y-coordinate of the vehicle in the local grid map | |
| y-axis of the Vehicle frame | |
| Angle between and | |
| Step size | |
| Vector from the current position to the A-star waypoint | |
| Vector from the current position to the dynamic obstacle | |
| Vector from the current position to the goal | |
| Vector from the current position to the obstacle | |
| Angle between and |
References
- Davies, S.; Pettersson, T.; Öberg, M. Organized violence 1989–2021 and drone warfare. J. Peace Res. 2022, 59, 593–610. [Google Scholar] [CrossRef]
- Xiaoning, Z. Analysis of military application of UAV swarm technology. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 1200–1204. [Google Scholar]
- Daud, S.M.S.M.; Yusof, M.Y.P.M.; Heo, C.C.; Khoo, L.S.; Singh, M.K.C.; Mahmood, M.S.; Nawawi, H. Applications of drone in disaster management: A scoping review. Sci. Justice 2022, 62, 30–42. [Google Scholar] [CrossRef]
- Mishra, B.; Garg, D.; Narang, P.; Mishra, V. Drone-surveillance for search and rescue in natural disaster. Comput. Commun. 2020, 156, 1–10. [Google Scholar] [CrossRef]
- Kunertova, D. The war in Ukraine shows the game-changing effect of drones depends on the game. Bull. At. Sci. 2023, 79, 95–102. [Google Scholar] [CrossRef]
- Abrahamsen, H.B. A remotely piloted aircraft system in major incident management: Concept and pilot, feasibility study. BMC Emerg. Med. 2015, 15, 1–12. [Google Scholar] [CrossRef]
- Seguin, C.; Blaquière, G.; Loundou, A.; Michelet, P.; Markarian, T. Unmanned aerial vehicles (drones) to prevent drowning. Resuscitation 2018, 127, 63–67. [Google Scholar] [CrossRef] [PubMed]
- Anwar, N.; Izhar, M.A.; Najam, F.A. Construction monitoring and reporting using drones and unmanned aerial vehicles (UAVs). In Proceedings of the Tenth International Conference on Construction in the 21st Century (CITC-10), Colombo, Sri Lanka, 2–4 July 2018; Volume 8, pp. 2–4. [Google Scholar]
- Mangiameli, M.; Muscato, G.; Mussumeci, G.; Milazzo, C. A GIS application for UAV flight planning. IFAC Proc. Vol. 2013, 46, 147–151. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Tang, G.; Tang, C.; Claramunt, C.; Hu, X.; Zhou, P. Geometric A-star algorithm: An improved A-star algorithm for AGV path planning in a port environment. IEEE Access 2021, 9, 59196–59210. [Google Scholar] [CrossRef]
- Erke, S.; Bin, D.; Yiming, N.; Qi, Z.; Liang, X.; Dawei, Z. An improved A-Star based path planning algorithm for autonomous land vehicles. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420962263. [Google Scholar] [CrossRef]
- Li, J.; Liao, C.; Zhang, W.; Fu, H.; Fu, S. UAV path planning model based on R5DOS model improved A-star algorithm. Appl. Sci. 2022, 12, 11338. [Google Scholar] [CrossRef]
- Stentz, A. Optimal and efficient path planning for partially-known environments. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 3310–3317. [Google Scholar]
- Stentz, A. The focussed d* algorithm for real-time replanning. In Proceedings of the International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Volume 95, pp. 1652–1659. [Google Scholar]
- Koenig, S.; Likhachev, M.; Furcy, D. Lifelong planning A. Artif. Intell. 2004, 155, 93–146. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. Fast replanning for navigation in unknown terrain. IEEE Trans. Robot. 2005, 21, 354–363. [Google Scholar] [CrossRef]
- Guan, W.; Wang, K. Autonomous collision avoidance of unmanned surface vehicles based on improved A-star and dynamic window approach algorithms. IEEE Intell. Transp. Syst. Mag. 2023, 15, 36–50. [Google Scholar] [CrossRef]
- Liao, T.; Chen, F.; Wu, Y.; Zeng, H.; Ouyang, S.; Guan, J. Research on Path Planning with the Integration of Adaptive A-Star Algorithm and Improved Dynamic Window Approach. Electronics 2024, 13, 455. [Google Scholar] [CrossRef]
- He, Z.; Liu, C.; Chu, X.; Negenborn, R.R.; Wu, Q. Dynamic anti-collision A-star algorithm for multi-ship encounter situations. Appl. Ocean Res. 2022, 118, 102995. [Google Scholar] [CrossRef]
- Nash, A.; Daniel, K.; Koenig, S.; Felner, A. Theta*: Any-angle path planning on grids. In Proceedings of the Twenty-Second Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–26 July 2007; Volume 7, pp. 1177–1183. [Google Scholar]
- Liu, Y.; Wang, L. AGV Path Planning: An Improved A* Algorithm Based on Bézier Curve Smoothing. In Proceedings of the 2024 39th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Dalian, China, 7–9 June 2024; pp. 243–247. [Google Scholar]
- Jayaweera, H.M.; Hanoun, S. Path planning of unmanned aerial vehicles (UAVs) in windy environments. Drones 2022, 6, 101. [Google Scholar] [CrossRef]
- Aldao, E.; González-de Santos, L.M.; González-Jorge, H. LiDAR based detect and avoid system for UAV navigation in UAM corridors. Drones 2022, 6, 185. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, X.; Nie, Z. A real-time collision avoidance strategy in dynamic airspace based on dynamic artificial potential field algorithm. IEEE Access 2019, 7, 169469–169479. [Google Scholar] [CrossRef]
- Rimon, E. Exact Robot Navigation Using Artificial Potential Functions; Yale University: New Haven, CT, USA, 1990. [Google Scholar]
- Bounini, F.; Gingras, D.; Pollart, H.; Gruyer, D. Modified artificial potential field method for online path planning applications. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 180–185. [Google Scholar]
- Hao, G.; Lv, Q.; Huang, Z.; Zhao, H.; Chen, W. Uav path planning based on improved artificial potential field method. Aerospace 2023, 10, 562. [Google Scholar] [CrossRef]
- Ruchti, J.; Senkbeil, R.; Carroll, J.; Dickinson, J.; Holt, J.; Biaz, S. Unmanned aerial system collision avoidance using artificial potential fields. J. Aerosp. Inf. Syst. 2014, 11, 140–144. [Google Scholar] [CrossRef]
- Qixin, C.; Yanwen, H.; Jingliang, Z. An evolutionary artificial potential field algorithm for dynamic path planning of mobile robot. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–13 October 2006; pp. 3331–3336. [Google Scholar]
- Ge, S.S.; Cui, Y.J. Dynamic motion planning for mobile robots using potential field method. Auton. Robot. 2002, 13, 207–222. [Google Scholar] [CrossRef]
- Sheng, J.; He, G.; Guo, W.; Li, J. An improved artificial potential field algorithm for virtual human path planning. In Proceedings of the Entertainment for Education. Digital Techniques and Systems: 5th International Conference on E-learning and Games, Edutainment 2010, Changchun, China, 16–18 August 2010; Proceedings 5. Springer: Berlin/Heidelberg, Germany, 2010; pp. 592–601. [Google Scholar]
- Li, G.; Yamashita, A.; Asama, H.; Tamura, Y. An efficient improved artificial potential field based regression search method for robot path planning. In Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012; pp. 1227–1232. [Google Scholar]
- Ju, C.; Luo, Q.; Yan, X. Path planning using artificial potential field method and A-star fusion algorithm. In Proceedings of the 2020 Global Reliability and Prognostics and Health Management (PHM-Shanghai), Shanghai, China, 16–18 October 2020; pp. 1–7. [Google Scholar]
- Liu, J.; Yan, Y.; Yang, Y.; Li, J. An improved artificial potential field UAV path planning algorithm guided by RRT under environment-aware modeling: Theory and simulation. IEEE Access 2024, 12, 12080–12097. [Google Scholar] [CrossRef]
- Xu, D.; Yang, J.; Zhou, X.; Xu, H. Hybrid path planning method for USV using bidirectional A* and improved DWA considering the manoeuvrability and COLREGs. Ocean Eng. 2024, 298, 117210. [Google Scholar] [CrossRef]
- Choi, J.W.; Choi, Y.H. Fusion Algorithm of A-star and Artificial Potential Field for Path Planning. In Proceedings of the 1st International Conference on on Drones and Unmanned Systems (DAUS’ 2025), Granada, Spain, 19–21 February 2025. [Google Scholar]











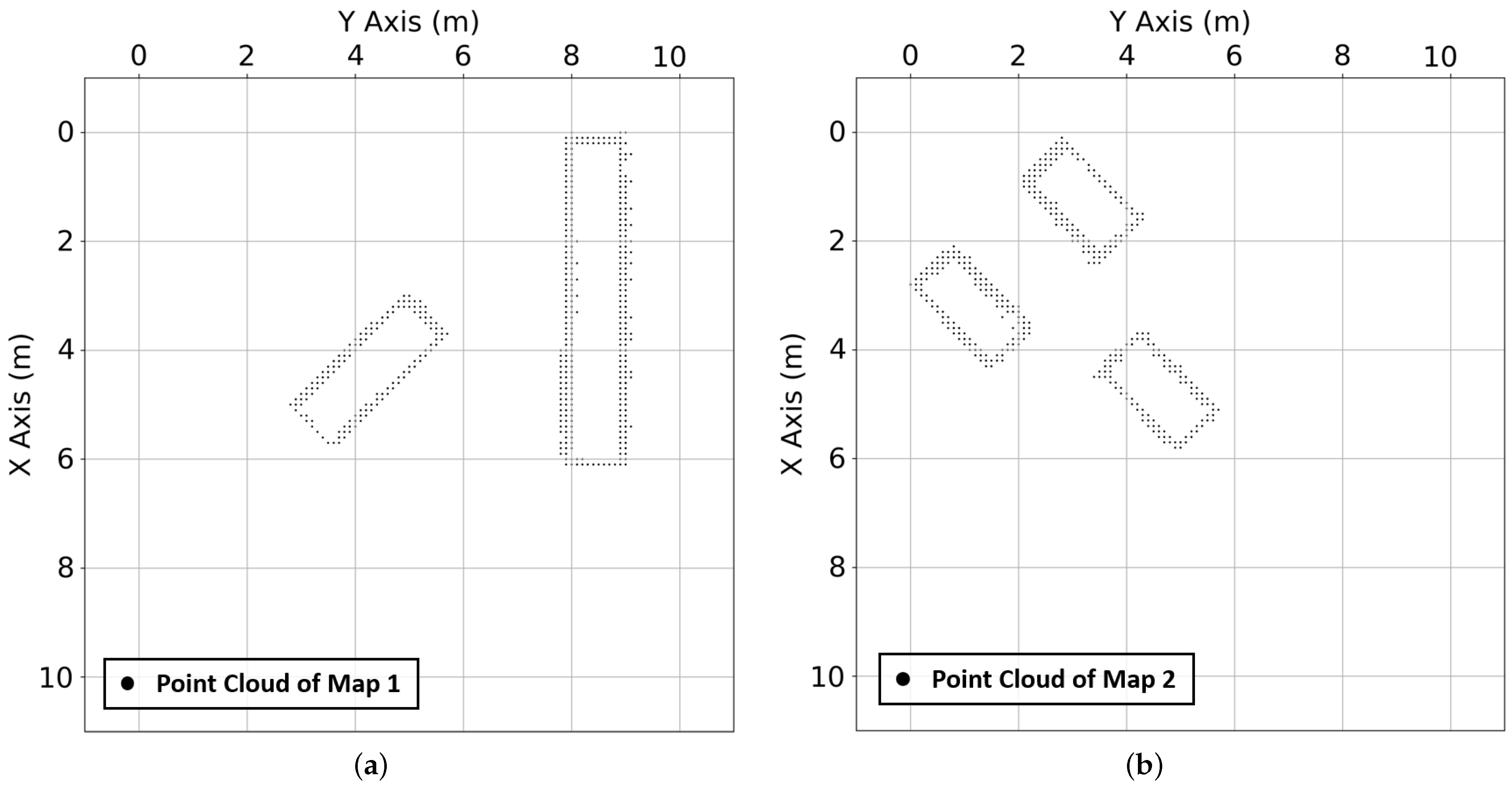

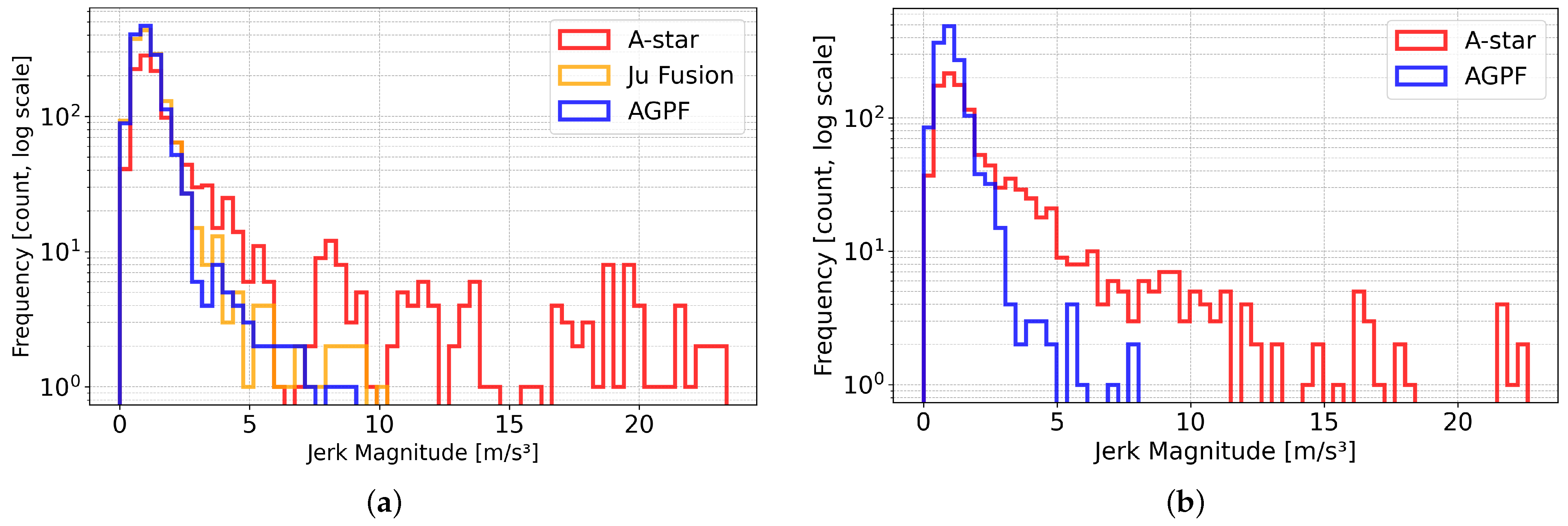
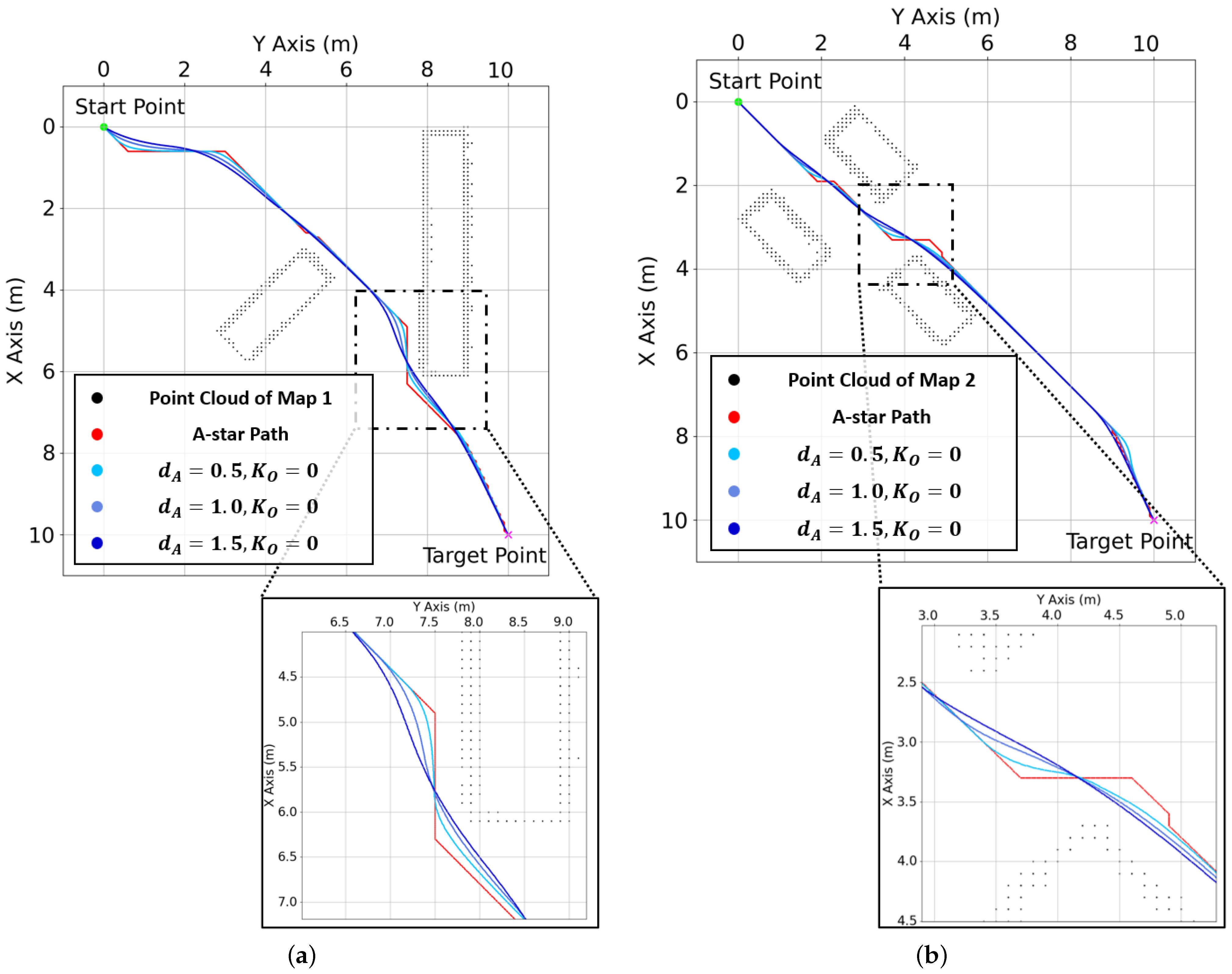






| Coefficient | A-Star | APF | Ju’s Fusion | AGPF | Unit |
|---|---|---|---|---|---|
| Grid size | 0.1 | - | 0.1 | 0.1 | m |
| - | 10 | - | - | - | |
| - | 1 | 1 | 1 | - | |
| - | 1.5 | 1.5 | 1.5 | - | |
| - | 1.5 | 1.5 | 1.5 | m | |
| - | - | 20 | 20 | - | |
| - | - | 1 | 1 | m | |
| 0.01 | 0.01 | 0.01 | 0.01 | m |
| Map | Data | A-star | APF | Ju’s Fusion | AGPF | Unit |
|---|---|---|---|---|---|---|
| Map 1 | Path length | 15.665 | - | 15.090 | 15.050 | m |
| Time | 0.409 | - | 3.309 | 3.313 | s | |
| Map 2 | Path length | 14.904 | - | - | 14.470 | m |
| Time | 0.171 | - | - | 2.714 | s |
| Coefficient | LiDAR and Grid Map | Unit |
|---|---|---|
| Range | 5 | m |
| Range resolution | 0.1 | m |
| 11 | m | |
| Min angle and Max angle | −180 and 180 | deg |
| Horizontal resolution | 1 | deg |
| Grid size | 0.1 | m |
| Coefficient | AGPF | Unit |
|---|---|---|
| Grid size | 0.1 | m |
| Local path length | 0.8 | m |
| 1 | - | |
| 1.5 | - | |
| 1.5 | m | |
| 2 | - | |
| 1 | m | |
| 0.01 | m | |
| 10 | - | |
| 0.8 | m | |
| 1 | m | |
| c | 30 | deg |
| 0.5 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.; Choi, Y. Path Planning for Unmanned Aerial Vehicle: A-Star-Guided Potential Field Method. Drones 2025, 9, 545. https://doi.org/10.3390/drones9080545
Choi J, Choi Y. Path Planning for Unmanned Aerial Vehicle: A-Star-Guided Potential Field Method. Drones. 2025; 9(8):545. https://doi.org/10.3390/drones9080545
Chicago/Turabian StyleChoi, Jaewan, and Younghoon Choi. 2025. "Path Planning for Unmanned Aerial Vehicle: A-Star-Guided Potential Field Method" Drones 9, no. 8: 545. https://doi.org/10.3390/drones9080545
APA StyleChoi, J., & Choi, Y. (2025). Path Planning for Unmanned Aerial Vehicle: A-Star-Guided Potential Field Method. Drones, 9(8), 545. https://doi.org/10.3390/drones9080545






