Highway Autonomous Driving Decision Making Using Reweighting Ego-Attention and Driver Assistance Module

Abstract

Decision making is challenging in autonomous driving (AD) under highway scenarios because of the unpredictable behaviors of neighbor vehicles, leading to the necessity of accurately modelling interactions between vehicles. Though ego-attention, a variant of self-attention, provides a way for object interaction extraction, its feature expression still needs to improve. This paper improves the original ego-attention by reweighting the encoding vehicle features, forcing them to pay more attention to significant features. Moreover, we designed a rule-based driver assistance module (DAM) to alleviate mis-decisions by constraining action space. Finally, we constructed our final AD decision-making model by integrating the proposed reweighting ego-attention and the DAM into the dual-input decision-making framework trained by enhanced deep reinforcement learning (DRL). We evaluated our decision-making model on highway scenarios. The results show that our model achieves better performance in success step (39.95 steps/episode), speed (29.15 m/s), lane-changing times (5.64 times/episode), and task completion rate (98%) than existing models, including DRL-GAT-SA, AE-D3QN-DA, and ego-attention-based ones, implying the competitive driving accuracy, safety, and comfort of our model.

1. Introduction

Decision making, the core of autonomous driving (AD), selects a discrete, high-level action by taking the environmental representation around a vehicle as input [1]. The importance of decision making safety becomes even more crucial in highway scenarios, where passengers need safer decisions than in low-speed tasks, such as automatic parking [2,3].

Existing AD decision-making technologies encompass rule-based and learning-based approaches. While rule-based decision making, often implemented through if–then rules [4] or a finite-state machine [5,6], offers good interpretability, it is limited by the breadth of predefined rules to the range of road scenarios. Since prior knowledge in many AD situations falls short, there is a growing necessity to integrate learning-based methods into decision making.

The existing learning-based AD decision making includes imitation learning (IL) and deep reinforcement learning (DRL). IL models AD behavior by learning expert demonstrations, e.g., behavior clone [7,8,9,10,11,12,13], inverse reinforcement learning [14,15], and generative adversarial imitation learning [16,17]. The IL paradigm is time-consuming due to the requirement of elaborating a dataset manually in advance. In contrast, DRL, combining deep learning (DL) and reinforcement learning (RL), generates driving policies without using massive amounts of data [18]. With the development of DL, self-attention mechanisms [19] are introduced to bolster the model’s understanding of critical vehicles by effectively filtering out irrelevant interactions, enhancing the AD safety performance of DRL decision-making models [20,21]. However, the self-attention mechanism alone is insufficient for enhancing safety in highway scenarios [22,23] because the RL’s self-exploration nature during training may excessively emphasize actions and state spaces unrelated to safe driving [24,25]. Furthermore, the trained decision-making model may produce unreasonable actions caused by the function approximation [26]. These limitations underscore the need for better solutions in AD decision making.

In the realm of RL, the subfield of safe RL is dedicated to ensuring the safety of RL models throughout their learning and deployment processes [27]. This is achieved by introducing a safety layer, a component that checks potentially unsafe actions and modifies them to safe ones. The safety layer can be implemented using either a neural network models or a rule-based model. The neural network-based safety layer requires extensive data for training a predictor [28,29]. In contrast, the rule-based safety layer does not need expert demonstrations. Moreover, such rule-based methods are more explainable than neural network ones. Therefore, existing AD models prefer appending a rule-based safety layer to enhance their decision safety [30,31,32]. However, it is important to note that existing simple rule-based constraints may hinder a DRL model from finding the optimal driving strategies because they do not take into account the principle in [33], which states that a driver-assistance module (DAM) should not introduce too many additional actions that would disrupt the stability of a DRL decision-making model.

This paper aims to support the making of accurate and safe AD decisions. We constructed our AD decision maker by integrating reweighting ego-attention and a DAM into the dual-input decision-making framework [34] trained by DRL. Our first contribution is the design of a novel self-attention, reweighting ego-attention, to identify vehicles that significantly influence an ego vehicle, increasing the accuracy and safety of the model. Our second contribution lies in designing a rule-based DAM, which detects and corrects unreasonable decisions to improve decision safety further while preserving the model’s intelligence. To improve the convergence of our model, we introduce DAM’s influence to the reward function of DRL, which is our third contribution.

The organization of the paper is as follows. Section 2 reviews the dual-input decision-making model. Section 3 details the proposed model, including the reweighting ego-attention, the DAM, the reward function, and the loss function. Section 4 presents experimental results and analysis. Section 5 concludes the work and suggests future work.

2. Dual-Input Decision-Making Model and Its Limitation

2.1. Dual-Input Decision-Making Model

We constructed our model under an ego-attention-based dual-input decision-making frame. Since ego-attention, a self-attention variant, can ensure a safe and accurate decision making by capturing the relative importance of each participant, some AD decision makers introduce it due to the complex interaction between vehicles. An ego-attention mechanism was proposed to capture vehicle-to-ego dependencies exclusively in decision making using the vector-based state input by modifying the query matrix of self-attention [35]. Later, the ego-attention-based model was extended to a dual-input one by incorporating image information as the other input besides the vector state input, thereby demonstrating the limitation in generalization capability of single-input models [34].

As shown in Figure 1, the dual-input decision-making model efficiently processes vector and image inputs through two branches. The vector-based branch sequentially applies a multi-layer perceptrons (MLPs) encoder and an ego-attention module to the vector state input. In parallel, the image-based branch sequentially applies a convolutional neural network (CNN) and a non-local mean operation [36] to the image input. The two branches are then merged via concatenation. Next, linear layers efficiently decode the concatenating features to acquire the action values of each action. Finally, the epsilon-greedy algorithm selects the final action to be executed by the ego vehicle. For details of the model, one can refer to [34]. The two branches employ ego-attention and non-local block to extract interactions between the ego vehicle and other vehicles. Since the non-local block is just a simple extension of ego-attention to process image information, we proceed to describe the details of ego-attention.

Figure 2 presents the ego-attention module. This module first encodes features from the ego vehicle and its N − 1 neighbors using linear layers L_q, L_k, and L_v. It then generates a query matrix $Q \mathsf{ϵ} {\mathbb{R}}^{1\times d}$, a key matrix $K \mathsf{ϵ} {\mathbb{R}}^{N\times d}$, and a value matrix $V \mathsf{ϵ} {\mathbb{R}}^{N\times d}$.

The attention weight of the ego vehicle to others, $a_e$, is then computed by (1).

$$a_e=softmax\left(score\left(Q,K\right)\right),$$

(1)

where $score\left(·\right)$ given in (2) is the attention score between the ego vehicle and its neighbors.

$$score\left(Q,K\right)={\displaystyle \frac{Q\times K^T}{\sqrt{d_K}}},$$

(2)

where $K^T$ is the transpose of $K$. $d_k$ is the dimensionality of the K matrix.

With $a_e$ at hand, the updated ego vehicle features $\widehat{V}$ are obtained by (3).

$$\widehat{V}=a_e\times V,$$

(3)

where $\widehat{V}$ is the updated vehicle’s feature.

Furthermore, we can extend the practical single-head ego-attention to multi-head via a simple concatenation, as given in (4), obtaining the final output of the vector-based branch. This allows the model to pay attention to information from different representation subspaces [19].

$${output}_1=Concat({\widehat{V}}_1,{\widehat{V}}_2),$$

(4)

where ${\widehat{V}}_1$ and ${\widehat{V}}_2$ computed by (3) are the updated features of the first and the second attention heads. $Concat(·)$ represents the concatenation operation.

2.2. Ego-Attention’s Limitation in AD

We analyzed ego-attention’s limitation in AD from the perspective of its attention score. Figure 2 and (2) show that ego-attention obtains the interactions between the ego vehicle and the i-th neighbor by multiplying the query matrix, $Q$, with the i-th row of the key matrix, $k_i^T$. Ego-attention adopts the similarity of two vehicles as the interaction information. When calculating the similarity, ego-attention treats a vehicle as a whole while ignoring the significance of the individual feature component on the final decision. It is worth noting that feature components probably contribute differently [37]. For example, when calculating the dependencies of an ego vehicle on its preceding vehicle in the same lane, the longitudinal features, such as the longitudinal position and driving speed, are more important than the lateral ones. Therefore, the current approach of ego-attention, which overlooks the importance of individual feature components, is a significant limitation that needs to be addressed in AD.

3. The Proposed Decision-Making Model

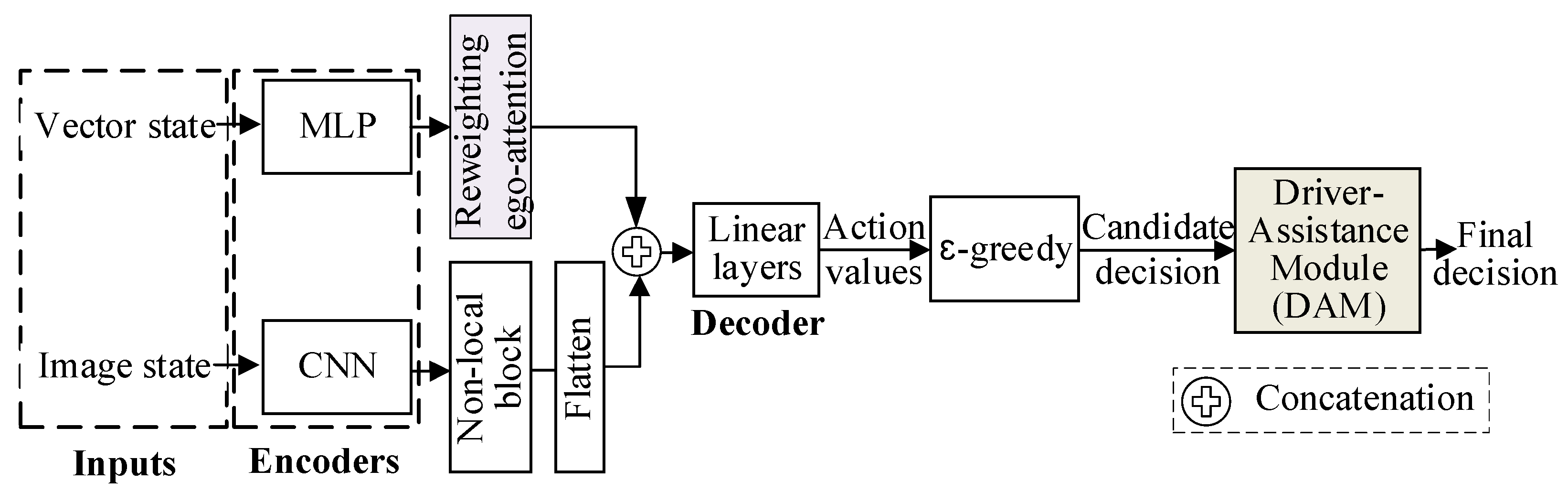
As shown in Figure 3, we improved the dual-input decision-making model. By reweighting ego-attention and appending a driver-assistance module (DAM), we enhanced the model’s performance. Since images provide more intuitional representations of the relative positions of vehicles, the non-local block, an extension to image data of ego-attention, in the image input branch effectively captures vehicle-to-ego interactions [34,38]. Therefore, we first enhanced ego-attention in the vector state input branch to improve the model’s decision-making performance by capturing more vehicle-to-ego dependencies. The additional DAM is a key safety feature. It adopts candidate safety-checking rules to improve AD safety, ensuring dangerous decision actions are checked and substituted with safe ones, providing reassurance and confidence in the decision safety. The whole model is trained by the double deep Q-learning (DDQN) [39], a DRL algorithm, with a modified reward function.

3.1. Reweighting Ego-Attention

As mentioned in Section 2.2, conventional dot-product attention struggles to fully capture the structured and asymmetric interactions among vehicles, particularly in spatially considered highway environments. To address this, prior work [40,41] has introduced Gaussian-weighted multi-head self-attention, which enhances attention expressiveness by incorporating spatial priors.

Specifically, these methods construct a Gaussian weight matrix $G\in {\mathbb{R}}^{N\times N}$, where each element $g_{ij}$ depends solely on the longitudinal distance $∆x_{ij}$ between vehicle $i$ and vehicle $j$. This matrix is then used to modulate the attention score matrix in (2) via element-wise multiplication:

$${score}_G=G·\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right).$$

(5)

This mechanism effectively emphasizes spatially closer agents, refining attention distribution to focus on nearby tokens. However, we identify two critical limitations when applying this technique to AD decision making:

First, in prior Gaussian-weighted methods, attention scores are modulated based on the relative longitudinal distance between the ego vehicle and surrounding vehicles. However, in multi-lane highway scenarios, such distance-only weighting can lead to misaligned attention allocation. For example, suppose the ego vehicle faces two leading vehicles: one in the same lane (veh_same) and another in an adjacent lane (veh_adj), with relative distances Δx₁ and Δx₂, respectively. Even if veh_same is farther ahead (Δx₁ > Δx₂), it poses a greater impact on the ego’s driving decision due to its lane relevance. Gaussian weighting, however, assigns more attention to veh_adj merely due to its shorter longitudinal distance, neglecting lateral context. This often results in unnecessarily conservative behaviors, such as premature braking or lane-keeping.

Second, Gaussian weighting typically applies object-level scaling—each vehicle as a whole receives a single attention modulation factor. This approach fails to account for the differentiated significance of features (e.g., velocity) within a single vehicle. In decision-critical contexts, such coarse-grained modulation is insufficient, as the policy requires fine-grained, feature-level discrimination to balance safety and efficiency.

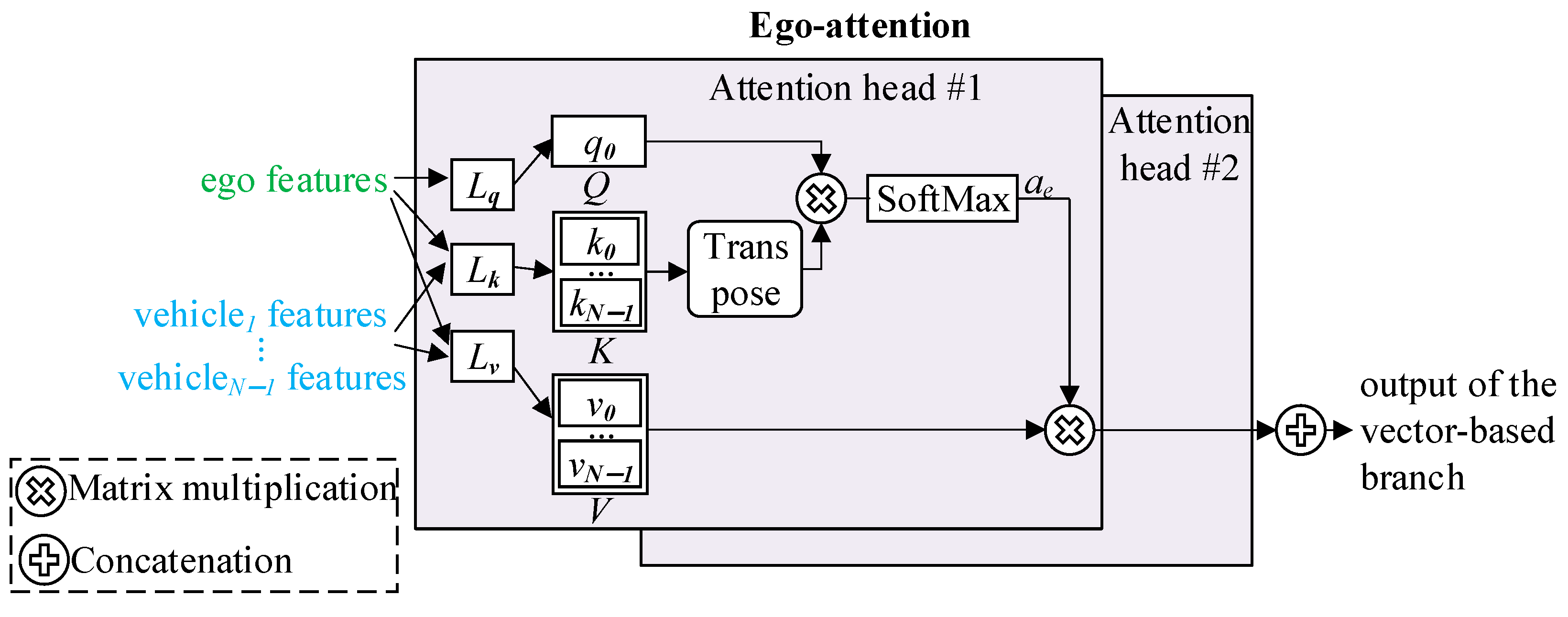
To address the limitations of Gaussian-weighted methods in AD decision making, we propose a novel feature-wise attention mechanism inspired by [37,42]. Specifically, we adopted a learnable matrix W into the K^T of attention score. This learnable matrix enables the attention mechanism to adaptively capture vehicles’ features that are critical for decision making, such as driving speed and relative lateral distance, rather than focusing solely on relative longitudinal distance. Consequently, it allows the model to autonomously extract and utilize a broader range of informative state features.

Specifically, the attention score of the proposed reweighting ego-attention is given in (6).

$${score}^{\prime }\left(Q,K\right)={\displaystyle \frac{Q\times \left(W{·K}^T\right)}{\sqrt{d_K}}},$$

(6)

where ${score}^{\prime }(·)$ is the novel proposed attention score, and Q, K, K^T, and d_K are the same as in (2). × and · denote matrix multiplication and Hadamard (element-wise) product, respectively. W is the learnable weight matrix, whose dimension is the same with K^T. Here, each element of W represents the importance of the corresponding encoding feature in K. It is worth pointing out that (6) adopts the Hadamard product due to its excellent feature-expressing capability [43] and light calculation cost.

3.2. DAM

An inadequately designed reward function may induce the model to exhibit unsafe behaviors. For example, underweighting the safety component could cause the ego vehicle to overemphasize efficiency, resulting in overly aggressive decisions and a heightened risk of hazardous scenarios. Although a carefully balanced reward function can theoretically address such issues, its design typically demands considerable domain expertise and incurs substantial retraining costs due to the need for extensive parameter tuning.

Therefore, it is essential to provide the model with explicit guidance—such as the restriction of unsafe actions—to prevent undesirable behaviors. Such guidance serves as a practical and efficient complement to reward design, especially in scenarios where the reward function alone fails to enforce critical safety constraints. Moreover, the intrinsic self-exploratory mechanism of DRL, along with the approximation of policy [26], may result in dangerous actions during training and deployment. These unsafe behaviors significantly compromise the safety of autonomous driving systems.

To address the safety challenges, we propose DAM, a safety module based on rules designed to check dangerous actions given by the decision-making model. After checking, DAM replaces a dangerous action to a safe one.

3.2.1. The Dangerous Decision Analysis Without DAM

We thus introduced three representative types of dangerous scenarios, where although no actual collisions occur, the likelihood of collision would be extremely high without human intervention. These scenarios served as the foundation for the design of our DAM module, which is detailed in Section 3.2.2.

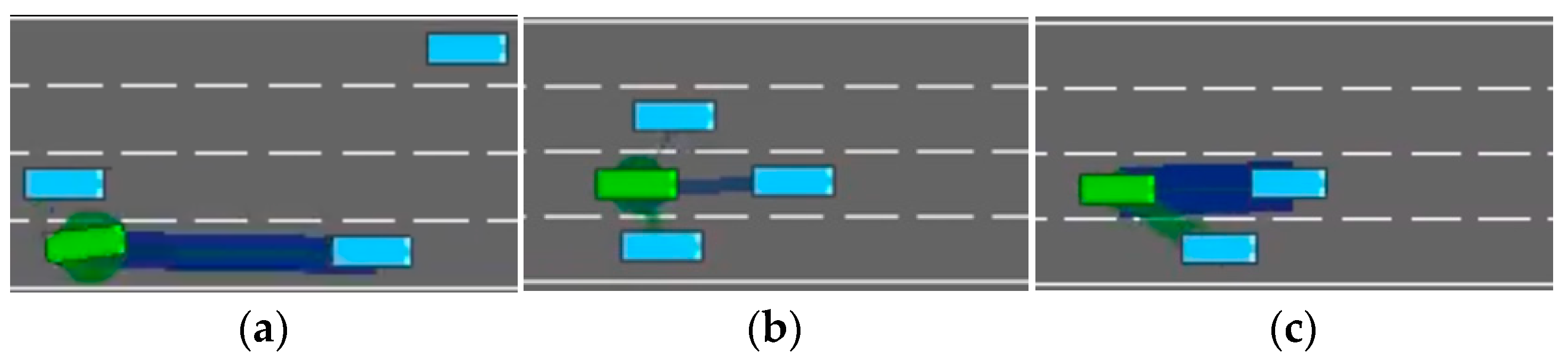
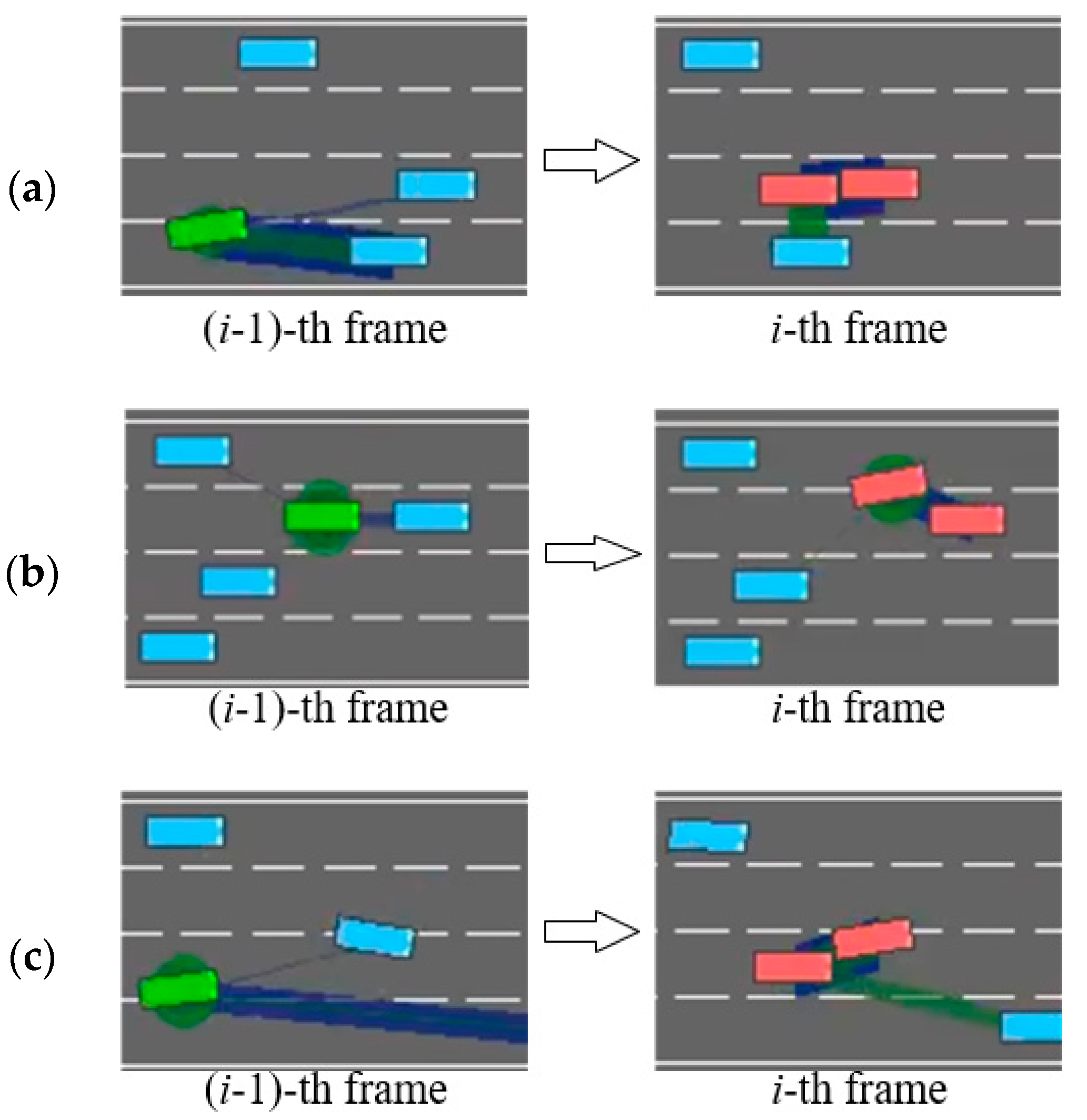
The first type of scenario, illustrated in Figure 4a, occurs when a leading vehicle in the same lane as the ego vehicle decelerates; the model may choose to execute a risky lane-changing instead of the safer option of slowing down, in an attempt to maintain driving efficiency. However, if the vehicle in the target lane does not yield, this behavior can result in a collision. The second scenario, as shown in Figure 4b, involves the ego vehicle traveling at a speed similar to that of vehicles in the adjacent lanes, while the preceding car suddenly decelerates. In this case, if the leading vehicle continues to decelerate, the ego vehicle cannot avoid a collision by simple slowing, as vehicles on both sides block any possible lane changes, and we configure the minimum speed of non-ego vehicles to be lower than that of the ego vehicle to effectively simulate overtaking scenarios. The root cause of such scenarios lies in the fact that past decisions made by the DRL model may potentially endanger the ego vehicle. In pursuit of driving efficiency, the model can exhibit short-term behavior and miss the optimal moment for deceleration, thereby falling into the above driving traps. In the third scenario, as illustrated in Figure 4c, the ego vehicle is too close to the leading vehicle in the same lane. If the model fails to respond promptly with lane-changing or slowing actions, a collision may ultimately occur.

These three scenarios also provide practical insights for the design of Level-2 driver-assistance systems aimed at enhance driving safety in real-world settings. For example, as illustrated in Figure 4a, a driver may initiate a lane change without checking the rear-view mirror or due to mirror blind spots. In Figure 4b, when driving in the leftmost lane on a highway (with guardrails on the left and traffic flow on the right), maintaining insufficient following distance poses significant risks. Should the lead vehicle suddenly decelerate or change lanes due to emergent conditions, the following vehicle may lack adequate reaction time, substantially increasing collision risk. In Figure 4c, distraction may prevent the driver from promptly detecting an imminent hazard, such as a pedestrian or another road user suddenly appearing in the vehicle’s path. In all of these cases, the proposed DAM module is capable of issuing timely risk alerts to help prevent accidents.

3.2.2. Design of DAM

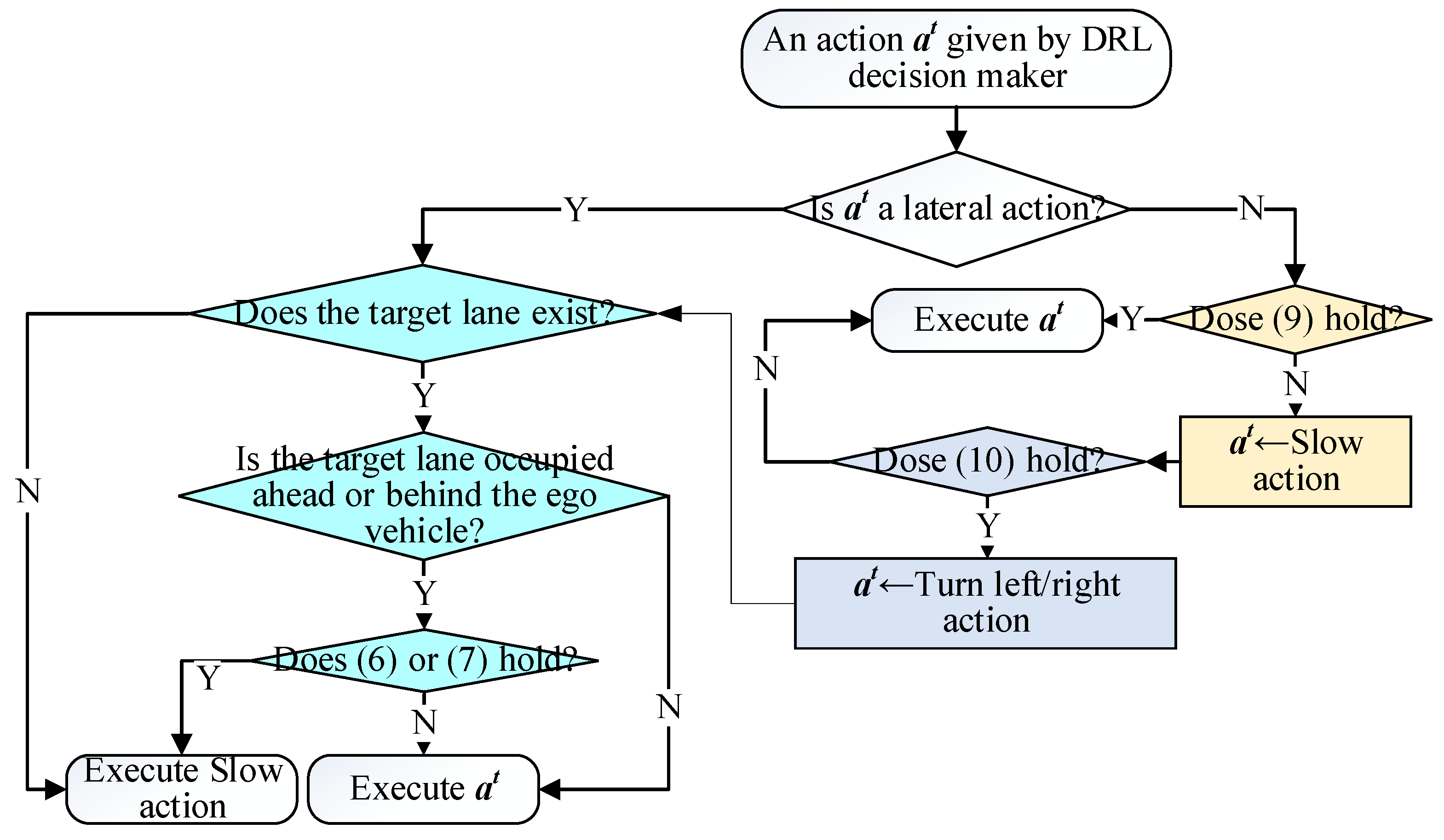
We designed a rule-based DAM, as shown in Figure 5. In order to avoid local optimization at the cost of safety caused by DAM interventions, we (1) carefully calibrated the DAM parameters adhering to the principle in [33] through extensive experiments to ensure that they both guarantee safety and allow the DRL agent sufficient flexibility to explore and (2) adopted a soft penalty mechanism (incorporating the DAM into reward function) instead of hard constraint termination. This design encourages the DRL model to weigh the trade-off between exploring better policies and incurring minor penalties rather than entirely avoiding such regions.

As illustrated in Figure 5, the DAM operates downstream of the DRL-based decision-making framework. Upon receiving actions generated by the DRL model, DAM executes distinct logic depending on whether the action involves lateral or longitudinal control commands.

To prevent the model from pursuing overly aggressive lane-changing that could lead to dangerous scenarios like Figure 4a, DAM implements the following safety protocol for lateral decisions: (1) When the DRL model outputs a lateral control command, DAM assesses the target lane-changing lane. If the requested lane change is infeasible (e.g., when the ego vehicle already occupies the rightmost/leftmost lane but attempts a rightward/leftward lane-changing), DAM immediately triggers a deceleration intervention. Otherwise, DAM examines the relative distances to both the preceding and following vehicles in the target lane, as in (7) and (8).

If conditions (7) and (8) are held, indicating an insufficient gap for lane-changing, DAM will override the DRL-generated action with a brake action. Otherwise, it will execute the lateral action given by DRL.

$$x_{front}^{targetlane}\left(t+1\right)-{x_{ego}^{targetlane}\left(t+1\right)-l\le \theta }_{lat\_front},$$

(7)

$$x_{ego}^{targetlane}\left(t+1\right)-x_{rear}^{targetlane}\left(t+1\right)-l\le {\theta }_{lat\_rear},$$

(8)

where $x_{front}^{target lane}(t+1)$ and $x_{rear}^{target lane}(t+1)$ are the next time step location of the front and the rear vehicles on the target lane. $x_{ego}^{target lane}(t+1)$ given in (9) is the location of the ego vehicle after executing action. We assume all vehicles are with the same length of $l$.

Assuming the speed remains constant during the maneuver, the lateral dynamic model of a vehicle is given in (9) [44].

$$x_{ego}^{target lane}(t+1)=x\left(t\right)+v∆t,$$

(9)

where $x\left(t\right)$ is the vehicle location in the current lane. $v$ is the current vehicle speed. $∆t$ = 0.5 s is the simulation time step.

When the DRL model outputs a longitudinal control action rather than a lateral maneuver, DAM verifies compliance with (10) to ensure the ego vehicle maintains a safe following distance from the leading vehicle. This safety constraint prevents the accumulation of myopic control decisions that could result in hazardous situations, such as the dangerous close-following scenario depicted in Figure 4b. If condition (10) is held, the ego will execute the longitudinal action given by DRL. Otherwise, the DAM will check (11).

$$TTC\left(t\right)={\displaystyle \frac{x_{\mathrm{preceding}}\left(t\right)-x_{\mathrm{ego}}\left(t\right)-l}{v_{\mathrm{ego}}\left(t\right)-v_{\mathrm{preceding}}\left(t\right)}}>{\theta }_{long},$$

(10)

where TTC(t) is the time to collision (TTC) at time instant t. x_preceding and x_ego are the locations of the preceding vehicle and the ego, whose rates are v_preceding and v_ego, respectively.

DAM checks (11) to address the situation depicted in Figure 4c. As demonstrated in [45], human drivers typically initiate steering maneuvers rather than relying solely on braking when facing imminent hazards during high-speed driving. To imitate this behavior, DAM activates an emergency collision avoidance maneuver when (11) is satisfied; otherwise, the system defaults to executing only slow maneuvers.

$$x_{preceding}-x_{ego}\le x_{min}\hspace{0.17em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{0.17em}{v}_{ego}>v_{preceding},$$

(11)

where x_preceding and x_ego are the positions of the preceding vehicle and the ego vehicle, respectively. x_min is the acceptable minimal car-following distance. v_ego and v_preceding are the current rates of the ego and the preceding vehicle.

3.3. Training with DDQN

3.3.1. State Space

Our model’s state space falls into vector state $S_v\in {\mathbb{R}}^{N\times F}$ and image state $S_{img}\in {\mathbb{R}}^{w\times h\times c}$, with w, h, and c being the input image’s width, height, and channel number. We chose w = h = 128 to balance the efficiency and the performance. The input image is single-channel, c = 1, aligning with the configuration in [34] because only the vehicles’ position is considered.

The state representation of the i-th vehicle in the vector-based input is $s_i\in {\mathbb{R}}^{1\times F}$. Here, F is the state number of the vehicle, and $s_0$ represents the ego vehicle. Consequently, an N × F matrix $S_v$ in (12) constitutes the state space of vector-based inputs [35].

$$S_v={\left[presence, x_i,y_i,v_x^i,v_y^i \right]}_{N\times F},$$

(12)

where presence is an indicator that the i-th vehicle is observed (presence = 1) or is not observed (presence = 0) by the ego vehicle. ($x_i$, $y_i$) and ($v_x^i$, $v_y^i$) represent the position and speed of the i-th vehicle, respectively. N denotes the total number of vehicles, and N − 1 is the vehicle number that can be observed by the ego vehicle, with the perception distance of D. In the case that the observed vehicles are less than N − 1, the model will populate the corresponding state with all-zero vectors.

3.3.2. Action Space

The proposed model’s discrete action space represents the output of DRL agents, including both lateral and longitudinal commands for the ego vehicle. These commands consist of no action, left LC, right LC, acceleration, and deceleration [34,35]. At any time step, the ego vehicle receives only one lateral or longitudinal action command.

3.3.3. Reward Function

The reward function is critical to the convergence of the RL model [22,30]. Therefore, we carefully consider the influence of the DAM on the model when designing the reward function R, which is given in (13).

$$R=r_{\mathrm{collision}}+r_{\mathrm{speed}}+\beta ·\tilde{r},$$

(13)

where $\tilde{r}$ is experimentally determined. $r_{\mathrm{collision}}$ = 0 or −1 indicates whether the ego vehicle is colliding with others. $r_{\mathrm{speed}}\in$ [0, 0.8] is proportional to the ego vehicle speed. $\beta$ is a Boolean value set to 1 when the DAM confirms the current decision is dangerous and 0 otherwise.

3.3.4. Training Method

We use a value-based DRL algorithm, double deep Q-learning (DDQN) [39], to find an optimal policy to maximize the discounted return. As an extension of DQN, DDQN implements Q-learning [46] that approximates the action-value function using neural networks with weights ω.

As introduced in Section 3.1, we incorporate a learnable weight matrix W into the attention mechanism. To mitigate gradient saturation [47] and ensure stable training dynamics [48], W is initialized with values sampled from a Gaussian distribution (μ = 0, σ² = 0.01). The matrix parameters are optimized using the DDQN loss function during training. We introduce L1 regularization to the loss function to improve the matrix’s feature discrimination capability. Formally, the loss function of the DDQN is in (14).

$$L_i\left({\omega }_i\right)=E_{s,a,R,s^{\prime }}[\left(y_i-Q\left(s,a;{\omega }_i\right){)}^2\right]+{\lambda \left|\left|W\right|\right|}_1,$$

(14)

where L_i(·) is the loss of the model at the ith training epoch. a, s, and s′ are the action and the state at the current time step and the next, respectively. R is the immediate reward. E(·) is the mathematical expectation. y_i is the target value given in (15). Q(·) is the action-value function denoting the expected return of a given action at each state. ${\omega }_i$ is the parameter of the online network. ${\left|\left|W\right|\right|}_1$ is the sum of the absolute values of all elements in the matrix. λ controls regularization strength.

$$y_i=R+\gamma Q(s^{\prime },\underset{a^{\prime }}{argmax}Q(s^{\prime },a^{\prime }{;\omega }_i){;\omega }_{\mathrm{target}}),$$

(15)

where ${\omega }_{\mathrm{target}}$ is the parameter of the target network. $\gamma \in [0, 1]$ is a discount factor.

Our online and target networks share the structure illustrated in Figure 3.

4. Experimental Results and Analysis

We trained our model using the ADAM optimizer, whose learning rate, replay buffer size, and batch size are 5 × 10⁻⁴, 1.5 × 10⁴, and 64, respectively. The discount factor $\gamma$ in (14) is 0.99. We adopted ɛ-greedy exploration to induce novel behaviors. The initial ɛ = 0.95 for training and ɛ = 0 for evaluation. The regularization strength λ was set to 0.01, determined through cross-validation to balance model complexity and generalization performance.

We evaluated our model on scenes with 51 vehicles produced by the highway-env simulator [35]. Figure 6 shows an example scene from the simulator. All vehicles adhere to the bicycle model. Except for the ego vehicle, their behavior is governed by the intelligent driver model (IDM) [49] and minimizing overall braking induced by lane change (MOBIL) [50]. For details of the simulator, please refer to [51]. We trained the model with 4000 episodes and tested it with 100 episodes.

We used five metrics for quantitative evaluation, i.e., average driving score (Avg score), average driving speed (Avg speed), average success step (Avg SS) [22], average lane change times (Avg LCT), and task completion rate (TCR). Avg score is the mean of the driving returns of all episodes, reflecting the similarity between the driving process of a model and an expected one. Avg speed is the mean of the driving speeds of all episodes, measuring the vehicle’s driving efficiency. Avg SS averages the driving steps in all episodes, measuring the model safety. The driving step is the number of completed actions in one episode. Avg LTC measures the driving comfort level. Finally, the TCR is the ratio of the number of times the episode completed all pre-defined actions to the total test episodes, which also measures driving safety.

4.1. Parameter Determination

The vehicle number N; the state dimension F in (11); the DAM hyper-parameters in (6), (7), (9), and (10); and $\tilde{r}$ in (12) are crucial to our model. We used a variable-controlling approach to evaluate their influences on the model.

We first fixed DAM hyper-parameters and the vehicle number N, studying the influence of the state dimension F. Following the principle that DAM hyper-parameters should have minor impacts on the decision [33], we fixed θ_long, x_min, θ_{lat_front}, θ_{lat_rear}, and $\tilde{r}$ in (6), (7), (9), (10), and (12) as 2 s, 7.5 m, 2.5 m, 0 m, and −0.08 after several tries. We let the ego vehicle have the perception distance D = 180 m (refer to [52]), observing 15 surrounding vehicles, i.e., N = 15.

Besides the elements presence, x, y, v_x, and v_y in (11), a vehicle’s heading angle φ is a possible state feature element of the vehicle [51], often characterized by cosφ and sinφ. We experimentally compared the impact of a vehicle state vector with and without the heading angle on our decision-making model. The results in

Table 1. The influence of the heading angle feature on the performance of our model. F = 5 and 7, respectively, mean the feature vector excludes and includes (cosφ, sinφ).

F	Avg Score	Avg Speed	Avg SS	Avg LCT	TCR
5	37.81	29.15	39.95	5.64	98
7	34.26	27.88	38.57	25.99	89

imply that excluding heading angle gains improvements on all five metrics. Therefore, as given in (11), we adopted the state vector with five elements, i.e., F = 5.

Then, we studied parameter N using fixed F and DAM hyper-parameters. In [22,34], the authors assumed N to be 5 and 15, respectively. Based on their studies, we further refined N = 5, 10, and 15, listing the results in

Table 2. The performance of our model with different vehicle number N.

N	Avg Score	Avg Speed	Avg SS	Avg LCT	TCR
5	37.33	29.04	39.31	12.81	94
10	37.97	29.35	39.45	23.52	95
15	37.81	29.15	39.95	5.64	98

. We found that increasing the number of observable vehicles benefits driving safety. Moreover, the ego showed the best balance of speed, TCR, and LCT when N = 15, meaning the best driving safety and comfort, which is consistent with common sense: “Given perception distance D, the more vehicles the ego vehicle observes, the better it understands the scene”. Thus, we chose N = 15.

Next,

Table 3. The performance of our model with different DAM hyper-parameters.

θlong	xmin	θlat_front	θlat_rear	Avg Score	Avg Speed	TCR
4	10	5	0	36.35	28.56	97
3	7.5	2.5	0	36.57	29.04	91
2	7.5	2.5	0	37.81	29.15	98
1.5	7.5	2.5	0	36.33	28.34	96

presents the experimental results of our model, showcasing the impact of different DAM hyper-parameters. We chose θ_long = 2 s, x_min = 7.5 m, θ_{lat_front} = 2.5 m, and θ_{lat_rear} = 0 m based on these results.

Finally, the results in

Table 4. The performance of our model with different $\tilde{r}$.

$\tilde{\mathit{r}}$	Avg Score	Avg Speed	Avg SS	Avg LCT	TCR
−0.04	34.83	27.50	39.32	11.25	94
−0.05	37.47	28.92	39.69	17.12	97
−0.08	37.81	29.15	39.95	5.64	98
−0.1	37.39	29.17	39.34	5.61	94

illustrates the impact of $\tilde{r}$ on driving speed and driving safety. We see that decreasing $\tilde{r}$ benefits driving speed and LCT, but driving safety is compromised when $\tilde{r}=-1$. We chose $\tilde{r}$= −0.08, which nicely balances driving speed and safety. To summarize, the parameters we used are D = 180 m, N = 15, F = 5, θ_long = 2 s, x_min = 7.5 m, θ_{lat_front} = 2.5 m, θ_{lat_rear} = 0 m, and $\tilde{r}$= −0.08.

4.2. Comparison with Other Methods

We next compared the proposed model with the dual-input decision-making model (DI-DM) [34], DRL-GAT-SA [22], AE-D3QN-DA [53], and ego-attention (EA) [35]. For fairness, all methods had the same episode duration and lane count. Note that all vehicles except for the ego vehicle followed traditional rule-based models, such as IDM [49] and MOBIL [50], by default in the highway-env simulator. Consequently, if the ego vehicle was also configured to use these methods, its behavior would largely mirror that of other vehicles in the environment, resulting in minimal interaction or decision-making complexity. Thus, such a comparison would not provide additional insight into the benefits of the proposed learning-based approach. We therefore focused our evaluations on decision-making tasks where DRL models can actively respond to and coordinate with rule-based traffic participants.

Table 5. Comparison results with different methods. - means the corresponding metric is missing in the original work.

Model	Avg Speed	Avg SS	Avg LCT	TCR
DRL-GAT-SA [22]	24.48	39.36	-	-
AE-D3QN-DA [53]	-	39.33	-	97
EA [35]	27.15	35.68	17.51	73
DI-DM [34]	29.01	35.80	28.41	71
Ours	29.15	39.95	5.64	98

presents the experimental results. Although AE-D3QN-DA provided Avg speed [53], we still do not present it for its unique speed settings. Our model performed best regarding the four metrics. Comparing with the DI-DM, our model improved Avg speed and Avg SS by 0.14 m/s and 4.15, respectively, indicating that the K matrix in (6) efficiently improved the driving efficiency. These results also illustrate that (7), (8), and (11) given in DAM ensure the ego vehicle’s safety while barely compromising the intelligence of DRL. Moreover, our method greatly reduced Avg LCT, which means much greater driving comfort. It reduced Avg LCT by 22.77 and 11.87 compared to DI-DM and EA, respectively. This suggests that the conservative driving strategy of avoiding clustering in (10) plays a certain role, and the K matrix contributes more foresight to the driving decisions. Finally, our model increased the TCR by 27%, 25%, and 1%, respectively, compared to DI-DM, EA, and AE-D3QN-DA while increasing the Avg SS by 0.59 compared with DRL-GAT-SA, demonstrating the effectiveness of the reweighting strategy and the DAM on boosting driving safety.

4.3. Ablation Studies

Our method’s highlights include the design of the reweighting ego-attention and the DAM. Thus, to evaluate each module’s contribution, we compared four variants: our final model (Ours), the final model without DAM (w/o DAM), the final model with DAM only being deployed during testing (w/o DAM-t), and the final model with ego-attention rather than the reweighting one (w/o R).

Table 6. Results from three variants of our model.

	Avg Score	Avg Speed	Avg SS	Avg LCT	TCR
Ours	37.81	29.15	39.95	5.64	98
w/o DAM	38.70	29.60	39.64	21.60	96
w/o DAM-t	37.02	28.47	39.69	6.34	97
w/o R	30.91	26.98	36.64	15.32	75

provides the results. Our final model’s Avg score and Avg speed, though slightly lower than the one without DAM, outperformed in Avg SS, Avg LCT, and TCR. This suggests that DAM, by slightly reducing the driving speed, achieves a more conservative driving strategy that is advantageous for hidden driving risk identification, driving safety, and driving comfort. As illustrated in Figure 5, our DAM prefers deceleration to avoid high driving speeds, thereby reducing LCT. When DAM was deployed solely during the testing phase, the model exhibited inferior performance across speed, comfort, and safety metrics compared to our proposed method. This degradation occurs because DAM’s intervention merely avoids unsafe actions without propagating their consequences back to the training process, preventing the model from learning to intrinsically improve its decision making. Importantly, our final model demonstrated superiority over the model without the reweighting attention strategy on all metrics, highlighting the enhanced accuracy of our reweighting strategy in capturing the interaction information between vehicles compared to the original ego-attention.

4.4. The Analysis of Generalization Ability

We next explored the generalization capability of driving models by modulating the interaction parameters of surrounding vehicles. Specifically, we varied the politeness factor p in the MOBIL model from 0 to 1 to simulate a spectrum of driver behaviors ranging from selfish to cooperative, thereby capturing the diversity and complexity of real-world traffic dynamics, as shown in

Table 7. The decision-making performance with different politeness coefficient.

p	Avg Score	Avg Speed	Avg SS	Avg LCT	TCR
0	37.81	29.15	39.95	5.64	98
0.5	36.64	28.33	38.16	10.45	94
1	36.91	29.02	38.73	12.95	95

.

From the experimental results, it can be observed that the decision-making model exhibited consistently robust performance under varying politeness coefficients of surrounding vehicles. Specifically, the TCR showed little change across all tested settings, indicating that the model generalizes well to diverse driving behaviors, from aggressive to highly courteous. While the Avg LCT and Avg speed exhibited moderate fluctuations, these variations reflect the model’s adaptive behavior rather than performance degradation.

4.5. Failure Cases

Although our DAM significantly improves driving safety, it still cannot avoid certain wrong decisions. Our model’s decision failures fall into three cases. As shown in Figure 7a, when the ego turns left, a potential danger will occur if the vehicle on its left front is near and moving slowly. In this case, a collision will occur if the DAM only considers the distance between the two vehicles without caring about their speeds. Figure 7b shows another failure case. The two vehicles will probably collide if the ego executes a lateral action without considering its preceding vehicle. Similarly, as depicted in Figure 7c, if two vehicles change lanes simultaneously, they will probably collide when the rear car moves faster than the one in the front.

5. Conclusions

This paper proposes a new AD decision-making model for highway scenarios. Our model reweights the original ego-attention to accurately capture the interactions between the ego vehicle and its neighbors. Moreover, our model appends a DAM combined with the reward function of the DDQN to check and correct unreasonable decisions.

The proposed AD decision-making model was evaluated based on the highway scenarios simulated by the highway-env simulator. The quantitative experimental results conclude that our model exhibits a performance superior to the existing AD decision makers, such as DRL-GAT-SA, AE-D3QN-DA, EA, and DI-DM, particularly in terms of driving safety. Furthermore, the evaluation of the variants of our model confirms that the reweighting ego-attention effectively captures the interaction between the ego vehicle and its neighbors, significantly enhancing the AD performance. The DAM not only enhances driving safety without significantly compromising driving efficiency but also enhances the decision-making model’s foresight, thereby improving driving comfort.

However, from the failure cases in Figure 7, it can be observed that although we designed the DAM to enhance safety, it still cannot fully guarantee collision-free driving. For example, the ego vehicle may perform risky lane-changing maneuvers (Figure 7a,b), or collisions may occur when two vehicles simultaneously attempt to change into the same lane (Figure 7c). This may be because (1) the reweighting ego-attention requires more data for training, increasing model uncertainty and thereby resulting in dangerous driving behaviors, and though the DAM mitigates such danger, it does not care about the source of uncertainty; (2) there is a lack of coordination among surrounding vehicles in the scenario. In the future, we will integrate uncertainty details such as using distributional DRL and ensemble technology into the DAM to capture the aleatoric and epistemic uncertainty, encouraging the model to produce context-dependent decisions with appropriately calibrated risk levels. Additionally, we aim to explore cooperative strategies by establishing communication between the ego vehicle and surrounding vehicles, such as through V2V technology, or developing predictive models of other drivers’ behaviors to support multi-agent decision making.