Coordinated Heterogeneous UAVs for Trajectory Tracking and Irregular Payload Transportation Using Sliding Mode Control

Abstract

Heterogeneous UAVs offer unique advantages in multi-agent systems due to their varying capabilities including (a) different payload capacities, (b) maneuverability, and (c) flight endurance. These properties made them particularly well suited for complex operations such as lifting and transporting irregularly shaped payloads with even mass distribution. Homogeneous UAV systems may face limitations. By utilizing these capabilities, heterogeneous UAVs enable efficient resource utilization, adaptability to dynamic conditions, and precise coordination for challenging missions. This paper presents a distributed sliding mode control (DSMC) strategy, designed to achieve stable trajectory tracking and synchronized irregular-shaped payload lifting by heterogeneous UAVs. The proposed approach ensures maintaining stability throughout the operation. The framework dynamically adjusts roll, pitch, and yaw angles to achieve precise payload lifting, while maintaining stability during transportation. Additionally, we conduct a comparative analysis between DSMC and PID controller, evaluating their performance in terms of trajectory tracking accuracy, payload stability, and safety distance between the drones. Simulation results demonstrate the effectiveness of the proposed method in minimizing trajectory tracking errors, achieving smooth payload transportation, and ensuring robust performance. The findings highlight the potential of DSMC as a reliable control strategy for multi-UAV coordination in complex payload transportation scenarios.

1. Introduction

The rapid growth in unmanned aerial vehicles (UAVs) has revolutionized a broader range of applications such as: (a) including logistics, (b) environmental monitoring, (c) disaster management, and (d) industrial automation [1]. The concept of heterogeneous UAV systems gained attention among the recent advancements in UAVs due to their ability to perform complex and dynamic tasks more effectively than homogeneous UAVs [2]. Heterogeneous systems are characterized by their various payload capacities, flight endurance, and maneuvering capabilities, providing and efficient solution for multi-agent operations that demand different performance attributes. For example, the mission involved coordination in lifting and transportation of irregularly shaped payloads benefits significantly from UAVs, which can support each other’s strength, offering operational robustness and flexibility [3].

In recent years, the logistics industry has seen growth in demand for aerial delivery systems capable of handling different payloads efficiently [4]. The use of UAVs for lifting and transporting irregular payloads is a challenging issue, as it introduces different complexities in terms of dynamic stability, trajectory tracking, and synchronization between the UAVs [5]. These challenges are further amplified in heterogeneous UAVs due to differences in their characteristics, such as (a) thrust, (b) weight, (c) lifting capability, and (d) flight dynamics [6]. Despite these complexities, heterogeneous UAVs provide significant advantages in terms of scalability, adaptability to diverse missions, and optimized resource allocation.

One of the main aspects of multi-UAV coordination is the ability to maintain synchronized operations while ensuring the stability of the payload [7]. There are several challenges to maintaining synchronization during the transportation of irregularly shaped payloads, due to their uneven mass distribution and aerodynamic properties. Different advanced control schemes were used for accurate trajectory tracking and stable lifting of irregularly shaped payloads to handle the aforementioned issues. The avoidance of collisions between heterogeneous UAVs is important during the whole operation. This necessitates robust control techniques, which can manage predefined safety distance between them during any uncertainties.

Communication delays and external disturbances are inevitable in real-world operations of UAVs. Delays in communication between the UAVs lead to a lack of stability, which affects the overall mission success [8]. Similarly, environmental disturbances can also affect the UAV’s ability to maintain its trajectory and payload stability. Addressing these challenges requires advanced control techniques that are not only robust to disturbances but also capable of dynamically adapting to different missions.

Sliding mode control (SMC) emerged as a powerful tool that addresses these challenges [9]. Its inherent robustness to model uncertainties and external disturbances made it suitable for multi-UAV systems tasked with lifting and delivering irregularly shaped payloads. Different traditional control schemes often struggle to attain the desired performance in the presence of such complexities, while SMC ensures stability by driving the system dynamics to a predefined sliding surface. At that point, the control objectives are met despite uncertainties and disturbances [10]. Moreover, the distributed sliding mode control (DSMC) approach enables decentralized control of UAVs. This offers scalable and efficient coordination in multi-UAV systems [11].

The focus of the research lies in the development of a DSMC framework specifically designed for heterogeneous UAV systems engaged in coordinated payload lifting and delivering operations. Unlike homogeneous UAV systems, where identical UAVs share the same dynamic properties, heterogeneous systems introduce an additional layer of complexity due to the varying capabilities of the UAVs [12]. Real-time inter-UAV communication is utilized to facilitate coordination between them, while advanced algorithms are employed to manage roll, pitch, and yaw synchronization during mission [13].

The proposed work is motivated by the need for a robust and scalable heterogeneous UAV coordination structure that can handle real-world challenges. The proposed strategy not only ensures precise trajectory tracking and synchronization but also addresses safety concerns by maintaining a predefined safety distance between the UAVs. By incorporating the proposed DSMC framework, the research demonstrates significant improvements in system robustness, adaptability, and operational performance.

In order to validate the effectiveness of the proposed strategy, simulations are conducted under realistic conditions, including delays in communication. The results demonstrate the proposed framework’s ability to minimize trajectory tracking errors, maintain safety distance between them, maintain irregularly shaped payload stability, and ensure robust synchronization between heterogeneous UAVs. These results show the potential of the proposed methodology for advancing the capabilities of heterogeneous UAV systems in complex and dynamic environments.

2. Literature Review

In recent years, the coordination of heterogeneous UAVs for complex tasks such as trajectory tracking and varying payload delivery has received significant attention from researchers. The integration of SMC in addressing these challenges is associated with the no-linear dynamics and external environmental disturbances inherent in UAV missions [14]. Sliding mode control is known for its robustness against uncertainties and external disturbances, making it the best choice for controlling UAVs with complex dynamics [15]. In [16], authors introduced an adaptive fuzzy-based global SMC strategy for UAVs, improving trajectory tracking performance under parameter uncertainties and external disturbances. The integration of fuzzy logic with SMC effectively overcomes control chattering and removes the reach phase, resulting in improved robustness and tracking accuracy.

A high-order sliding mode observer-based trajectory tracking control for quadrotor UAVs was developed in [17]. By employing high-order sliding mode observers to estimate slang disturbances, the proposed method achieved enhanced trajectory tracking performance and showed the efficiency of SMC in handling UAV dynamics. The deployment of heterogeneous UAVs, characterized by varying capabilities and configurations, offers enhanced flexibility and efficiency in performing complex missions.

In [18], the authors investigated predefined time cooperative formation control of heterogeneous unmanned surface vehicle (USV)–UAV systems. Using virtual leader tracking methods and robust adaptive algorithms, the study addressed the challenges posed by various structural parameters and external disturbances, contributing to improved coordination efficiency and reliability in maritime domains. In the context of marine aerial–surface heterogeneous systems, coordinated trajectory-tracking control schemes have been developed to manage the interactions between UAVs and unmanned surface vehicles (USVs). For instance, a novel coordinated trajectory-tracking control scheme was proposed to solve the accurate trajectory-tracking problem in systems composed of a quadrotor UAV and a USV with heterogeneity, in unknown dynamics, and disturbances [19].

The transportation of payloads, especially those with irregular shapes, introduces additional complexities in UAV control due to altered dynamics and stability concerns. Recent advancements have focused on developing control strategies that ensure precise trajectory tracking while compensating for the challenges posed by payload variations. A novel continuous sliding mode control strategy was introduced for transporting a hanging payload by a UAV [20]. This approach addressed the longstanding challenge of stabilizing both actuated and underactuated states in underactuated systems, ensuring stable payload transportation.

Reliable communication is essential for effective coordination between multiple drones, but communication delays can negatively impact system performance. To address this challenge, event-triggered sliding mode control methods have been introduced to improve consensus tracking in multi-rotor drone swarms [21]. In addition, the synthesized sliding mode control strategies were applied to quadcopter drones to increase their robustness against sudden and external disturbances. These strategies incorporate adaptive laws well suited to real applications that involve drones with small moments of inertia, such as quad rotors, thus improving their ability to reject disturbances [22].

Non-linear control techniques have been introduced to better manage the complexity of quadrotor dynamics, particularly in underactuated systems [23] where classical methods fall short. Nonlinear approaches, such as feedback militarization and back-stepping control, aim to directly address the system nonlinearity by transforming the nonlinear system into a linear one or designing controllers that can manage the nonlinearity in a more direct way. Predictive control schemes [24], which anticipate the future behavior of the system based on its current state, have also been applied to quadrotors.

DSMC is a promising method to address the challenges associated with coordinating heterogeneous drones. DSMC offers robustness against disturbances and uncertainties [25], making it well suited for complex multi-agent systems. The formulation of DSMC involves designing individual controllers for each drone while ensuring that they coordinate effectively to handle the dynamic interactions between the drones and the payload. In DSMC, each drone follows a sliding surface that allows the system to maintain stability despite disturbances like wind gusts. The main advantage of DSMC over traditional control techniques is its stability to handle both the nonlinearity of the system and uncertainties introduced by the heterogeneous drone dynamics. The sliding mode formulation ensures that the system stays on the sliding surface, reducing the effect of disturbance and ensuring that the drone remains in a stable operation region. The robust approach allows real-time adaptation to changes in system behavior, making DSMC particularly useful in disturbances in unknown environments [26].

A novel approach to cooperative control of heterogeneous UAVs was introduced in [27], where the authors proposed a decentralized control system with distributed sliding mode control. This system aimed to enhance the adaptability of the UAV fleet to changing payload weights and real-time communication delays. The experimental results showed that this method was effective in improving the stability and trajectory-tracking accuracy of the UAVs under various operating conditions. Furthermore, the authors in [28] introduced a deep reinforcement learning (DRL)-based algorithm for UAV trajectory planning and payload delivery. By leveraging DRL, the system was able to learn optimal flight paths in real time, accounting for payload shifts and environmental uncertainties, while ensuring minimal control effort and smooth operations.

Furthermore, the integration of real-time data and adaptive control strategies is becoming a key trend in enhancing UAV coordination. In [29], the authors presented an adaptive fuzzy sliding mode control (AFSMC) technique, with prescribed performance. This approach was shown to improve the system’s robustness to external disturbances, such as wind and turbulence, by continuously updating the control parameters based on sensor data.

There are still challenges in the coordination of heterogeneous UAVs for complex missions, despite significant advancements. The integration of advanced control strategies, such as DSMC, with real-time communication and decision-making algorithms, is necessary to improve system robustness and adaptability. Future research should focus on developing scalable control techniques that can accommodate a larger number of heterogeneous UAVs, ensuring efficient coordination in dynamic conditions and uncertain environments.

DSMC for heterogeneous UAV coordination showed promising capabilities in improving accuracy in trajectory tracking and irregularly shaped payload delivery efficiently. Ongoing research continues to address the challenges related to communication delays, system uncertainties, and dynamic environmental conditions, paving the way for more robust and adaptable UAV systems.

Main contributions of this research work are listed as follows:

• A DSMC framework is designed specifically for coordinated trajectory tracking and stable transportation of irregular shape payload using heterogeneous UAVs with varying thrust and dynamic capabilities.
• The proposed control scheme ensures synchronized lifting and stable transportation while maintaining a predefined safety distance to prevent collisions between the UAVs.
• The DSMC framework incorporates real-time inter-UAV coordination to ensure a predefined safety distance between UAVs, reducing the risk of mid-air collisions. This ensures smooth and safe operation, which is essential for multi-drone payload transportation and formation flying.

The rest of the paper is organized as follows: Section 3 presents the detailed mathematical modeling of heterogeneous drones. Section 4 describes controller design. Section 5 provides an in-depth analysis of the simulation results, evaluating the proposed framework’s performance in terms of trajectory tracking accuracy, payload stability, safety distance maintenance, and disturbance rejection. Finally, Section 6 concludes the paper by summarizing the key findings and suggesting future research directions.

3. System Dynamics

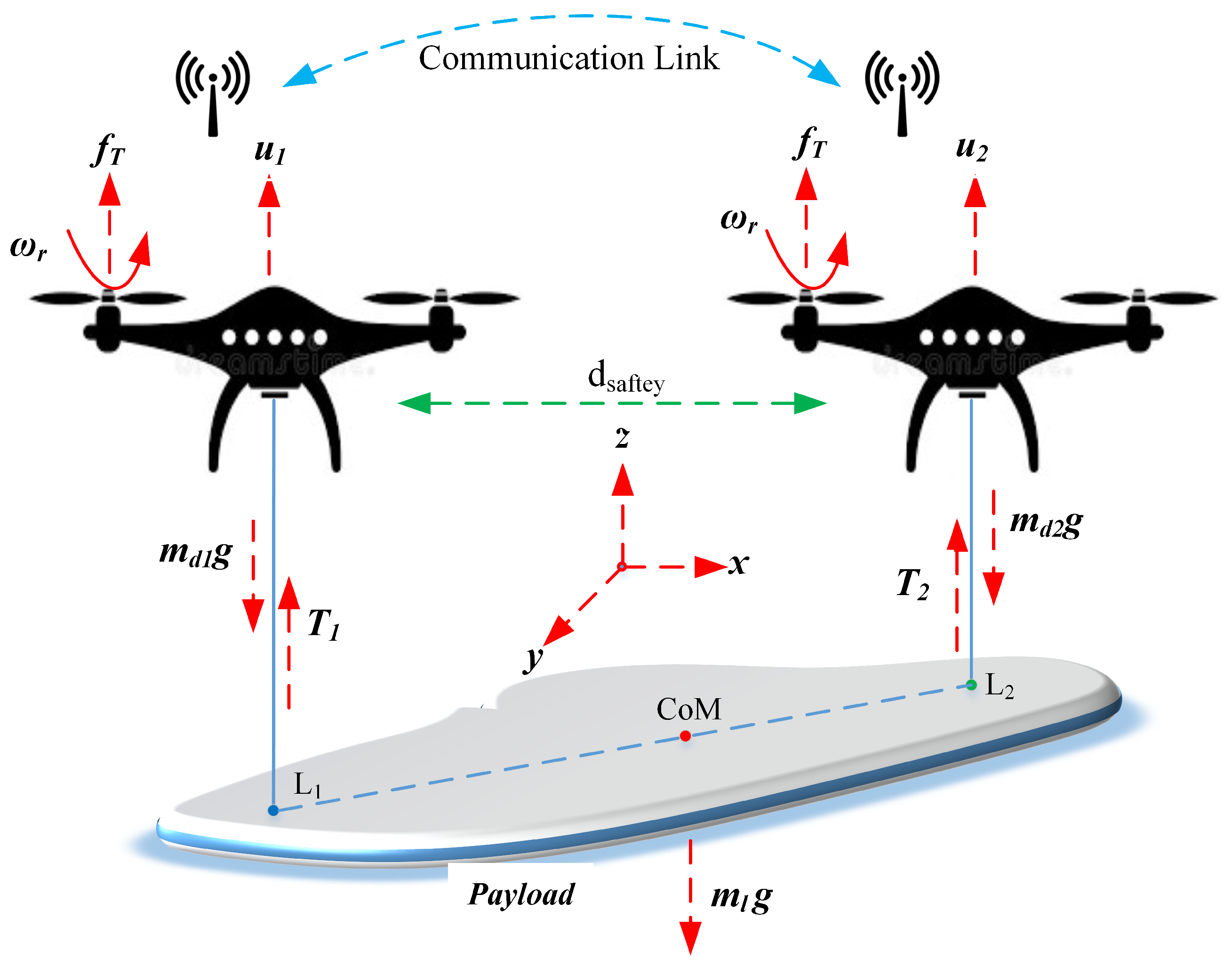
Figure 1 shows two heterogeneous UAVs that are coordinated together to lift and deliver an irregularly shaped payload. The payload is assumed to have an even mass distribution, which helps the UAVs to distribute the load evenly among each other and maintain balance during the whole mission. Each drone is attached to the payload through a point $L_1$ and $L_2$ for UAV 1 and UAV 2, respectively. UAV 1, with a mass $m_1$, generates a tension force $T_1$, while the second UAV, with mass $m_2$, generates a tension force of $T_2$. UAVs are controlled by their respective control inputs $u_1$ and $u_2$, which represent the thrust and torque needed to stabilize the UAVs and guide them throughout the mission. The control forces $f_T$ are responsible for ensuring that each UAV maintains its trajectory while supporting an irregularly shaped payload. The CoM of the irregularly shaped payload is crucial in finding the forces applied by each UAV. There is a communication link between the two heterogeneous UAVs to facilitate real-time coordination, allowing them to adjust their positions and forces based on the status of the payload. The safe distance between the UAVs, denoted by $d_{saftey}$ ensures that they do not collide during operation. The subscript ‘i’ corresponds to the $i\mathrm{th}$ UAVs (i = 1, 2, 3, …, n) throughout the paper. The following assumptions are provided to ensure a thorough and precise design and analysis of the subsequent controller [30]:

• The quadrotor UAV structure is rigid, without internal forces or deformations.
• The quadrotor is symmetrical.
• The center of mass coincides with the origin of the body frame.
• The earth frame is an inertial frame.
• The cable used is inelastic, with negligible mass compared to the load and quadrotor.
• The cable tension is positive throughout the mission.

The system dynamics of the heterogeneous UAVs engaged in coordinated trajectory tracking and payload delivery are derived based on Newton–Euler equations. The modeling considers the translational and rotational motion of each quadrotor while incorporating the effects of external disturbances, inter-UAV communication, and control inputs.

The orientation of each UAV is described using Euler angles ${\mathit{\eta }}_i={[{\varphi }_i,{\theta }_i,{\psi }_i]}^T$. The relationship between the Euler angle rates ${\dot{\mathit{\eta }}}_i$ and the angular velocity ${\mathit{\omega }}_i={[p_i,q_i,r_i]}^T$ in the body-fixed frame is given by:

$${\dot{\mathit{\eta }}}_i={\mathbf{T}}_i^{-1}\left({\mathit{\eta }}_i\right){\mathit{\omega }}_i,$$

(1)

where ${\mathbf{T}}_i\left({\mathit{\eta }}_i\right)$ is the transformation matrix:

$${\mathbf{T}}_i\left({\mathit{\eta }}_i\right)=\left[\begin{array}{ccc}1& sin{\varphi }_{i}tan{\theta }_i& cos{\varphi }_{i}tan{\theta }_i\\ 0& cos{\varphi }_i& -sin{\varphi }_i\\ 0& sin{\varphi }_{i}sec{\theta }_i& cos{\varphi }_{i}sec{\theta }_i\end{array}\right]$$

(2)

The rotation matrix ${\mathbf{R}}_i$ transforms a vector from the body-fixed frame to the inertial frame:

$${\mathbf{R}}_i={\mathbf{R}}_z\left({\psi }_i\right){\mathbf{R}}_y\left({\theta }_i\right){\mathbf{R}}_x\left({\varphi }_i\right),$$

(3)

where:

$${\mathbf{R}}_x\left({\varphi }_i\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos{\varphi }_i& -sin{\varphi }_i\\ 0& sin{\varphi }_i& cos{\varphi }_i\end{array}\right],$$

(4)

$${\mathbf{R}}_y\left({\theta }_i\right)=\left[\begin{array}{ccc}cos{\theta }_i& 0& sin{\theta }_i\\ 0& 1& 0\\ -sin{\theta }_i& 0& cos{\theta }_i\end{array}\right],$$

(5)

$${\mathbf{R}}_z\left({\psi }_i\right)=\left[\begin{array}{ccc}cos{\psi }_i& -sin{\psi }_i& 0\\ sin{\psi }_i& cos{\psi }_i& 0\\ 0& 0& 1\end{array}\right].$$

(6)

By combining Equations (4)–(6), Equation (3) can be rewritten as:

$$R_i=\left[\begin{array}{ccc}cos{\theta }_{i}cos{\psi }_i& cos{\theta }_{i}sin{\psi }_i& -sin{\theta }_i\\ sin{\varphi }_{i}sin{\theta }_{i}coc{\psi }_i-coc{\varphi }_{i}sin{\psi }_i& sin{\varphi }_{i}sin{\theta }_{i}sin{\psi }_i+cos{\varphi }_{i}cos{\psi }_i& sin{\varphi }_{i}cos{\theta }_i\\ cos{\varphi }_{i}sin{\theta }_{i}cos{\psi }_i+sin{\varphi }_{i}sin{\psi }_i& cos{\varphi }_{i}sin{\theta }_{i}sin{\psi }_i-sin{\varphi }_{i}cos{\psi }_i& cos{\varphi }_{i}cos{\theta }_i\end{array}\right].$$

The thrust ${\mathbf{F}}_i^{\mathrm{body}}$ and torque ${\mathit{\tau }}_i^{\mathrm{body}}$ generated by the rotors of UAV i are:

$${\mathbf{F}}_i^{\mathrm{body}}=\left[\begin{array}{c}0\\ 0\\ F_{z,i}\end{array}\right],{\mathit{\tau }}_i^{\mathrm{body}}=\left[\begin{array}{c}{\tau }_{\varphi ,i}\\ {\tau }_{\theta ,i}\\ {\tau }_{\psi ,i}\end{array}\right].$$

(7)

The translational dynamics of $i\mathrm{th}$ UAV in the inertial frame are:

$$m_i{\ddot{\mathbf{r}}}_i={\mathbf{R}}_i{\mathbf{F}}_i^{\mathrm{body}}-m_{i}g{\mathbf{e}}_3+{\mathbf{F}}_{\mathrm{ext},i},$$

(8)

where ${\mathbf{e}}_3={[0,0,1]}^T$.

The rotational dynamics of $i\mathrm{th}$ UAV in the body-fixed frame are:

$${\mathbf{I}}_i{\dot{\mathit{\omega }}}_i+{\mathit{\omega }}_i\times {\mathbf{I}}_i{\mathit{\omega }}_i={\mathit{\tau }}_i^{\mathrm{body}}+{\mathit{\tau }}_{\mathrm{ext},i}.$$

(9)

The complete dynamic model for $i\mathrm{th}$ UAV is:

$$\left[\begin{array}{cc}{m}_i{\mathbf{I}}_3& \mathbf{0}\\ \mathbf{0}& {\mathbf{I}}_i\end{array}\right]\left[\begin{array}{c}{\ddot{\mathbf{r}}}_i\\ {\dot{\mathit{\omega }}}_i\end{array}\right]+\left[\begin{array}{c}\mathbf{0}\\ {\mathit{\omega }}_i\times {\mathbf{I}}_i{\mathit{\omega }}_i\end{array}\right]=\left[\begin{array}{c}{\mathbf{R}}_i{\mathbf{F}}_i^{\mathrm{body}}-m_{i}g{\mathbf{e}}_3+{\mathbf{F}}_{\mathrm{ext},i}\\ {\mathit{\tau }}_i^{\mathrm{body}}+{\mathit{\tau }}_{\mathrm{ext},i}\end{array}\right].$$

(10)

The payload dynamics are:

$$m_p{\ddot{\mathbf{r}}}_p=\sum _{i=1}^2{\mathbf{T}}_i-m_{p}g{\mathbf{e}}_3+{\mathbf{F}}_{\mathrm{ext},p},$$

(11)

where ${\mathbf{T}}_i$ is the tension force exerted by UAV i on the payload.

The tension forces ${\mathbf{T}}_i$ are modeled as:

$${\mathbf{T}}_i=k({\mathbf{r}}_i-{\mathbf{r}}_p-{\mathbf{L}}_i)+c({\dot{\mathbf{r}}}_i-{\dot{\mathbf{r}}}_p).$$

(12)

Algorithm 1 calculates the Center of Mass (CoM) for an irregular shape with even mass distribution. The first step involves defining the number of vertices, N, of the irregular polygon, and then storing the ordered coordinates of these vertices, $P=\{(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)\}$, in a list. The second step uses the Shoelace Theorem to calculate the total area A of the polygon. This theorem works by summing the cross-products of the x and y coordinates of consecutive vertices and computing the absolute value of the result to find the area.

$$A={\displaystyle \frac{1}{2}}\left|\sum _{i=1}^{N-1}(x_i{y}_{i+1}-x_{i+1}{y}_i)+(x_N{y}_1-x_1{y}_N)\right|$$

(13)

In the third step, the algorithm calculates the coordinates of the center of mass. The x-coordinate of the CoM is calculated using a weighted sum of the coordinates, and similarly, the y-coordinate of the CoM is computed using the same method. These relations sum the terms based on the vertices’ coordinates and the area calculated in Equation (13). Afterward, the computed center of mass, calculated as ${\mathbf{x}}_{\mathrm{com}}=(x_{\mathrm{com}},y_{\mathrm{com}})$, and it can be displayed for further process. The CoM can be visualized by plotting the 2D shape and marking the CoM.

$$x_{\mathrm{com}}={\displaystyle \frac{1}{6A}}\sum _{i=1}^N(x_i+x_{i+1})(x_i{y}_{i+1}-x_{i+1}{y}_i)$$

(14)

$$y_{\mathrm{com}}={\displaystyle \frac{1}{6A}}\sum _{i=1}^N(y_i+y_{i+1})(x_i{y}_{i+1}-x_{i+1}{y}_i)$$

(15)

The result provides the exact center of mass (CoM) of the irregular shape, which can be visualized for validation. This method is useful in applications where objects have uniform density and complex boundaries.

Algorithm 1. Center of Mass Calculation for an Irregular Shape

1. Input Polygon Vertices and Assumptions

a. The shape is assumed to be a closed 2D polygon with uniform mass distribution.

b. Define the number of vertices N of the irregular shape.

c. Ensure the vertices are ordered counterclockwise to maintain a consistent orientation.

d. Store the ordered vertex coordinates:

$P=\{(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)\}$

2. Compute the Area of the Irregular Shape

a. The area calculation is based on the Shoelace Theorem, which applies to simple polygons (non-self-intersecting).

b. Compute the total area A:

$A={\displaystyle \frac{1}{2}}\left|{\sum }_{i=1}^{N-1}(x_i{y}_{i+1}-x_{i+1}{y}_i)+(x_N{y}_1-x_1{y}_N)\right|$

c. Ensure that the computed area is nonzero to avoid division errors in the center of mass calculations.

3. Compute the Center of Mass (CoM) Coordinates

a. The center of mass formula assumes a constant surface mass density, meaning the CoM is purely a geometric property.

b. Compute the x-coordinate of the center of mass:

$x_{\mathrm{com}}={\displaystyle \frac{1}{6A}}{\sum }_{i=1}^N(x_i+x_{i+1})(x_i{y}_{i+1}-x_{i+1}{y}_i)$

c. Compute the y-coordinate of the center of mass:

$y_{\mathrm{com}}={\displaystyle \frac{1}{6A}}{\sum }_{i=1}^N(y_i+y_{i+1})(x_i{y}_{i+1}-x_{i+1}{y}_i)$

d. Validate the computed CoM by checking whether it lies inside the polygon. If not, verify the ordering of vertices.

4. Output Center of Mass

a. Store or display the CoM position:

${\mathbf{x}}_{\mathrm{com}}=(x_{\mathrm{com}},y_{\mathrm{com}})$

5. Visualize the Center of Mass (Optional but Recommended)

a. Plot the irregular shape using the stored vertices.

b. Mark the computed CoM to verify correctness visually.

6. End

Algorithm 2 explains a simulation for multi-UAV helix trajectory tracking with irregularly shaped payload with an even distribution of mass. It starts by initializing basic simulation parameters such as the simulation time, UAV initial states, and trajectory tracking errors. A reference helix trajectory is computed for the drones to follow, where one UAV is positioned slightly offset from the other to track the same path. The required thrust for each UAV is calculated based on their positions relative to the predefined reference trajectory. The inter-UAV distance is also calculated to ensure they maintain a safe distance between them throughout the mission. The irregularly shaped payload with an even distribution of mass is modeled by generating random points with assigned mass values, and the CoM is calculated in 2D. The lifting points for the UAVs are defined relative to the CoM to ensure balanced payload lifting. The algorithm then simulates the motion, computes thrust variations, and plots results. These results are analyzed for accuracy and stability, with the simulation ending after the visualization of the data.

Algorithm 2. Multi-Drone Helix Trajectory Tracking with Payload

Start

1. Initialization

a. Define simulation parameters:

i. Time range $t\in [0,T]$, with step size $\mathsf{\Delta }t$.

ii. Initialize drone states:

positions ${\mathbf{x}}_1\left(0\right),{\mathbf{x}}_2\left(0\right)$, velocities ${\mathbf{v}}_1\left(0\right),{\mathbf{v}}_2\left(0\right)$, and thrust $F_1\left(0\right),F_2\left(0\right)$.

iii. Define initial tracking errors $e_1\left(0\right),e_2\left(0\right)$ and inter-drone distance $d_{12}\left(0\right)$.

2. Compute Reference Helix Trajectory

a. Generate time-dependent reference trajectory:

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathbf{x}}_r\left(t\right)={\left[\begin{array}{ccc}Rcos\left({\displaystyle \frac{2\pi t}{T}}\right)& Rsin\left({\displaystyle \frac{2\pi t}{T}}\right)& {\displaystyle \frac{z_{\max }}{T}}t\end{array}\right]}^T$$ where R, $z_{\max }$, and T define the helix geometry.

3. Compute Control Inputs for Drones

a. Define tracking control law based on position error:

i. Compute errors: $e_1\left(t\right)={\mathbf{x}}_r\left(t\right)-{\mathbf{x}}_1\left(t\right)$, $e_2\left(t\right)={\mathbf{x}}_r\left(t\right)-{\mathbf{x}}_2\left(t\right)$.

ii. Compute desired control force: ${\mathbf{u}}_i=K_p{e}_i+K_d{\dot{e}}_i+mg{\mathbf{e}}_z$

where $K_p,K_d$ are controller gains.

4. Update Drone Dynamics

a. Integrate equations of motion for each drone:

i. Compute accelerations: ${\mathbf{a}}_i={\displaystyle \frac{{\mathbf{u}}_i}{m_i}}-g{\mathbf{e}}_z$.

ii. Update velocities and positions using numerical integration.

5. Compute Inter-Drone Distance

a. Calculate inter-drone distance constraint:

i. $d_{12}\left(t\right)=\parallel {\mathbf{x}}_1\left(t\right)-{\mathbf{x}}_2\left(t\right)\parallel$.

ii. Apply corrective control if $d_{12}\left(t\right)$ deviates from the desired formation spacing.

6. Simulate Irregular Payload and Compute Center of Mass (COM)

a. Generate random payload mass distribution:

i. Define set of N points with masses $m_i$ distributed non-uniformly.

ii. Compute COM: $${\mathbf{x}}_{\mathrm{com}}={\displaystyle \frac{\sum m_i{\mathbf{x}}_i}{M_{\mathrm{total}}}},M_{\mathrm{total}}=\sum m_i.$$ 7. Define Lifting Points Based on COM

a. Assign lifting positions to drones:

i. ${\mathbf{x}}_{\mathrm{lift},1}={\mathbf{x}}_{\mathrm{com}}+{\left[\begin{array}{cc}-d& 0\end{array}\right]}^T$.      ii. ${\mathbf{x}}_{\mathrm{lift},2}={\mathbf{x}}_{\mathrm{com}}+{\left[\begin{array}{cc}d& 0\end{array}\right]}^T$.

iii. Assign drones to lifting points based on computed tension forces.

8. Analyze System Performance

a. Evaluate trajectory tracking accuracy:

i. Compute root mean square (RMS) error of tracking.

ii. Assess control effort required for stability.

iii. Evaluate robustness of formation maintenance.

9. Output Results and Visualization

i. 3D visualization of trajectory.

ii. Plots of tracking errors and thrust variations.

iii. Analysis of inter-drone coordination and stability.

End

4. Controller Design and Stability Analysis

To address the challenges faced during cooperative trajectory tracking and irregular payload transportation using heterogeneous UAVs, a novel DSMC strategy is proposed, unlike the traditional SMC technique. The proposed control scheme explicitly deals with variations in UAV dynamics, thrust limits, and payload influence. It also incorporates real-time inter-UAV coordination to ensure synchronized lifting and safe flight operation by maintaining a predefined safety distance between the UAVs. This made the proposed control scheme robust and coordinated in complex multi-UAV scenarios. The control laws for i-th drone is defined as:

$${\mathbf{F}}_i=m{\ddot{\mathbf{r}}}_{i,d}-m\lambda {\dot{\mathbf{e}}}_i-ktanh\left({\displaystyle \frac{{\mathbf{s}}_i}{ϵ}}\right),$$

(16)

The sliding surface g for the i-th drone can be written as:

$${\mathbf{s}}_i=\lambda ({\mathbf{r}}_i-{\mathbf{r}}_{i,d})+{\dot{\mathbf{r}}}_i-{\dot{\mathbf{r}}}_{i,d},$$

(17)

Lyapunov-Based Stability Analysis for Distributed Sliding Mode Controller

Theorem 1. 

The sliding surface dynamics for the i-th UAV defined in Equation (16) are globally asymptotically stable under the control law defined by Equation (17), if the control gain satisfies $k>{\displaystyle \frac{\mathsf{\Delta }}{ϵ}}$, where Δ is the upper bound.

Proof. 

Consider the Lyapunov function for the sliding surface ${\mathbf{s}}_i$:

$$V_i={\displaystyle \frac{1}{2}}{\mathbf{s}}_i^T{\mathbf{s}}_i,$$

which is positive definite ($V_i>0$) when ${\mathbf{s}}_i\ne 0$, and $V_i=0$ at ${\mathbf{s}}_i=0$.

The time derivative of $V_i$ is:

$${\dot{V}}_i={\mathbf{s}}_i^T{\dot{\mathbf{s}}}_i.$$

The sliding surface dynamics are given by:

$${\dot{\mathbf{s}}}_i=\lambda {\dot{\mathbf{e}}}_i+{\ddot{\mathbf{e}}}_i.$$

Substituting the tracking error dynamics:

$${\ddot{\mathbf{e}}}_i={\displaystyle \frac{1}{m}}({\mathbf{F}}_i+{\mathbf{F}}_{\mathrm{disturbance}})-{\ddot{\mathbf{r}}}_{i,d},$$

we obtain:

$${\dot{\mathbf{s}}}_i=-{\displaystyle \frac{k}{m}}tanh\left({\displaystyle \frac{{\mathbf{s}}_i}{ϵ}}\right)+{\displaystyle \frac{{\mathbf{F}}_{\mathrm{disturbance}}}{m}}.$$

Substituting ${\dot{\mathbf{s}}}_i$ into ${\dot{V}}_i$:

$${\dot{V}}_i={\mathbf{s}}_i^T\left(-{\displaystyle \frac{k}{m}}tanh\left({\displaystyle \frac{{\mathbf{s}}_i}{ϵ}}\right)+{\displaystyle \frac{{\mathbf{F}}_{\mathrm{disturbance}}}{m}}\right).$$

□

Lemma 1. 

If the disturbance satisfies the bound $\parallel {\mathbf{F}}_{disturbance}\parallel \le \mathsf{\Delta }$, then:

$${\dot{V}}_i\le -{\displaystyle \frac{\parallel {\mathbf{s}}_i\parallel }{m}}\left(k-{\displaystyle \frac{\mathsf{\Delta }}{ϵ}}\right).$$

Proof. 

Using the bound $\parallel {\mathbf{F}}_{\mathrm{disturbance}}\parallel \le \mathsf{\Delta }$:

$${\mathbf{s}}_i^T{\displaystyle \frac{{\mathbf{F}}_{\mathrm{disturbance}}}{m}}\le {\displaystyle \frac{\parallel {\mathbf{s}}_i\parallel \mathsf{\Delta }}{m}}.$$

Thus:

$${\dot{V}}_i\le -{\displaystyle \frac{k}{m}}\parallel {\mathbf{s}}_i\parallel +{\displaystyle \frac{\parallel {\mathbf{s}}_i\parallel \mathsf{\Delta }}{m}}.$$

Factoring out $\parallel {\mathbf{s}}_i\parallel$:

$${\dot{V}}_i\le -{\displaystyle \frac{\parallel {\mathbf{s}}_i\parallel }{m}}\left(k-{\displaystyle \frac{\mathsf{\Delta }}{ϵ}}\right).$$

If the control gain $k>{\displaystyle \frac{\mathsf{\Delta }}{ϵ}}$, for all ${\mathbf{s}}_i\ne 0$, ensuring that ${\dot{V}}_i<0$. By Lyapunov’s theorem, this guarantees the global asymptotic stability of ${\mathbf{s}}_i$, which means that $s_i\to 0$ as $t\to \infty .$ This implies that trajectory tracking error asymptotically vanish, proving the effectiveness of the control law. □

Theorem 2. 

The proposed distributed sliding mode control (DSMC) framework ensures that the tracking error ${\mathbf{e}}_i=\mathbf{r}i-{\mathbf{r}}_{i,d}$ globally asymptotically converges to zero under the control law:

$${\mathbf{F}}_i=m{\ddot{\mathbf{r}}}_{i,d}-m\lambda {\dot{\mathbf{e}}}_i-ktanh\left({\displaystyle \frac{{\mathbf{s}}_i}{ϵ}}\right),$$

the tracking error ${\mathbf{e}}_i={\mathbf{r}}_i-{\mathbf{r}}_{i,d}$ converges to zero globally asymptotically, provided that:

$$k>{\displaystyle \frac{\mathsf{\Delta }}{ϵ}}.$$

Proof. 

From Lemma 1, if $k>{\displaystyle \frac{\mathsf{\Delta }}{ϵ}}$, the Lyapunov derivative satisfies:

$${\dot{V}}_i<0\forall {\mathbf{s}}_i\ne 0.$$

This implies that ${\mathbf{s}}_i$ converges to zero as $t\to \infty$, leading to:

$${\mathbf{e}}_i\to 0\mathrm{and}{\dot{\mathbf{e}}}_i\to 0\mathrm{as}t\to \infty .$$

Thus, the tracking error ${\mathbf{e}}_i$ is globally asymptotically stable.

Theorem 2 plays a crucial role in validating the robustness and stability of the proposed control strategy. While Theorem 1 established the asymptotic stability of the sliding surface dynamics, it did not explicitly confirm the convergence of the position tracking error ${\mathbf{e}}_i$ to zero. Theorem 2 fills this gap by proving that, under the designed control law, the UAV’s position $\mathbf{r}i$ will track the desired trajectory $\mathbf{r}i,d$ globally and asymptotically. □

Remark. 

The control gain k must satisfy $k>{\displaystyle \frac{\mathsf{\Delta }}{ϵ}}$ to ensure robustness against bounded disturbances. A higher k improves disturbance rejection but increases control effort.

5. Results and Discussion

In this section, heterogeneous UAVs with varying capabilities such as (a) payload capacity, (b) maneuverability, and (c) flight endurance were modeled to evaluate the performance of the proposed DSMC technique. The scenario focused on lifting and transporting an irregularly shaped payload with an even distribution of mass, a task that poses a significantly heterogeneous UAV system due to the difference in their capabilities. The UAVs were equipped with GPS for accurate position tracking and inertial measurement units to maintain stability during flight. The DSMC strategy was applied to ensure stable trajectory tracking and precise synchronization between the UAVs throughout the operation. The proposed control approach allowed the UAVs to work cohesively, overcoming the inherent challenges of coordinating heterogeneous UAVs while achieving efficient payload transportation and maintaining stability under dynamic conditions. UAVs dynamically adjusted their roll, pitch, and yaw angles to ensure smooth and stable irregularly shaped payload transportation while maintaining coordination. Key metrics such as trajectory tracking accuracy, thrust variations, and inter-UAV distances were analyzed in the simulations. The results show the effectiveness of the DSMC strategy in achieving efficient payload transportation by minimizing trajectory tracking errors confirming DSMC’s potential as a reliable control method for multi-UAV coordination in complex scenarios.

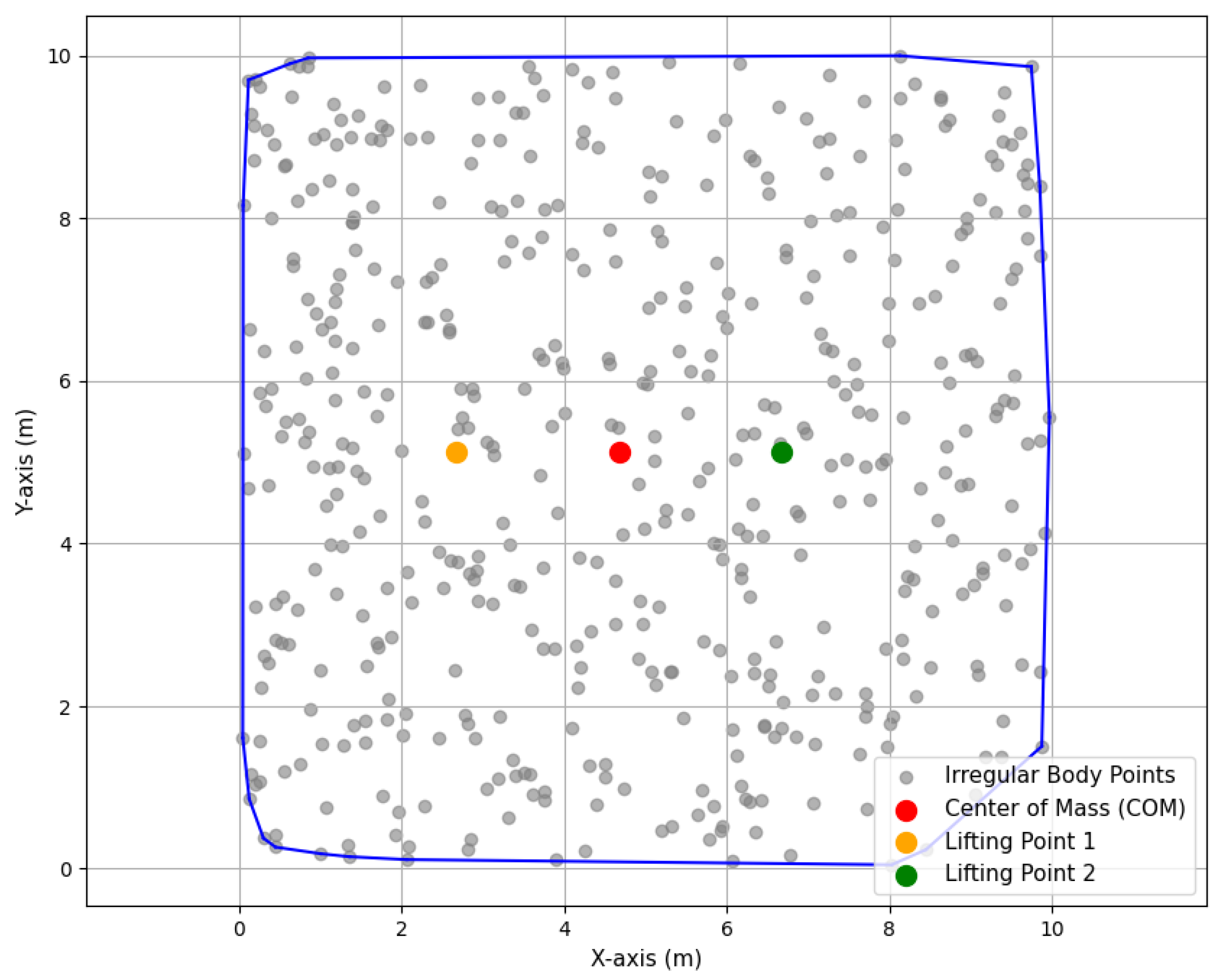
Figure 2 shows the irregular shape body, the CoM, and the lifting points determined for two heterogeneous drones. The boundary of the irregular shape is outlined using its convex hull. The placement of the lifting points ensures a proper load distribution among the heterogeneous UAVs during flight, which is critical to maintaining stability and reducing the effort to control. The two-dimensional view sets the stage for understanding the payload interaction and how drones adjust to stabilize the irregularly shaped payload while maintaining trajectory tracking. A precise lifting point selection is crucial because any misalignment can introduce significant oscillations in the payload, affecting overall trajectory tracking performance. Furthermore, real-world applications of this method include search and rescue operations and industrial logistics, where UAVs transport loads of varying shapes and weights. One limitation of this approach is that it assumes an even mass distribution, which may not always be the case in real applications, requiring adaptive load redistribution strategies.

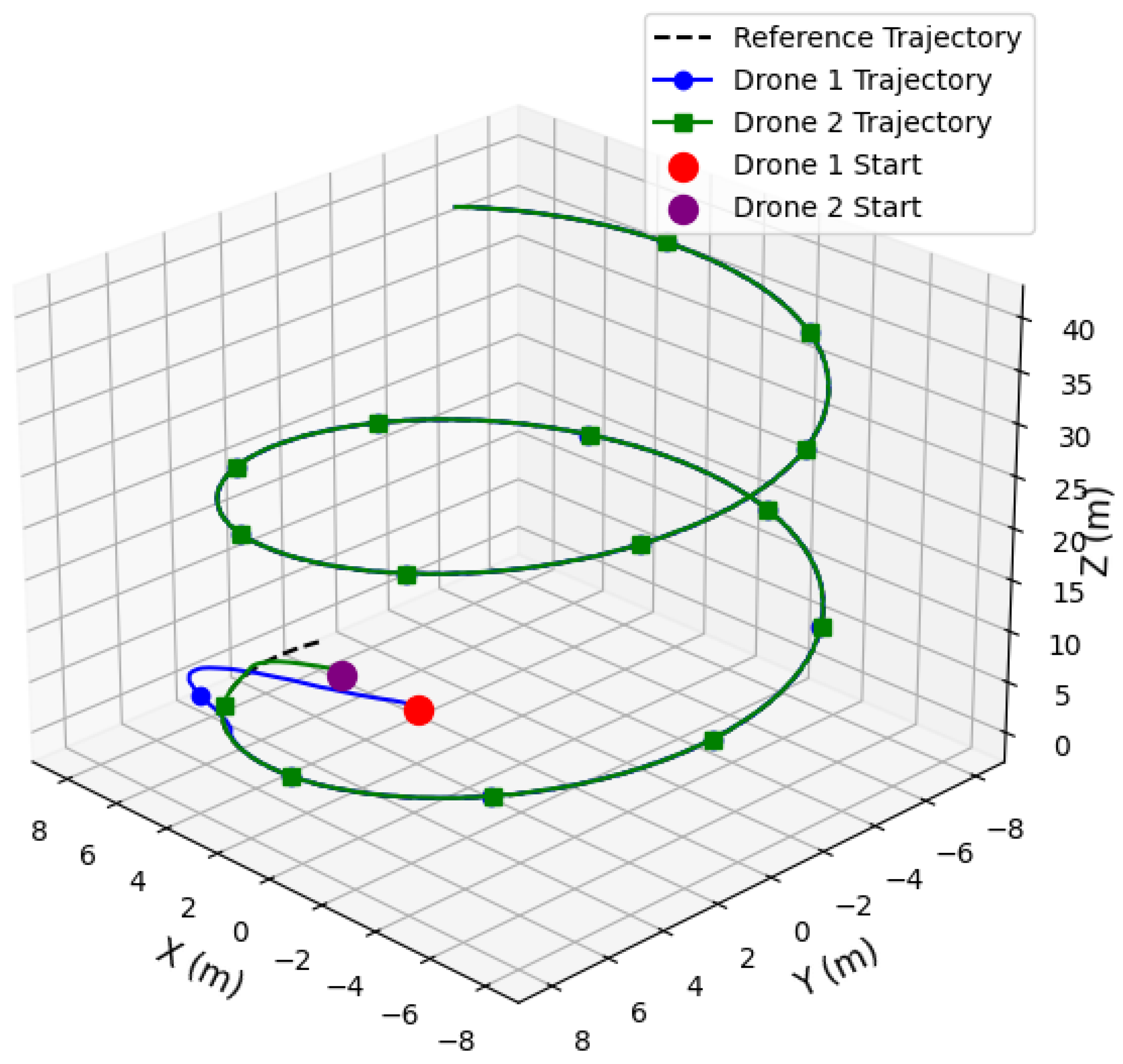
Figure 3 shows the 3D trajectory tracking of two heterogeneous UAVs engaged in lifting and transporting an irregularly shaped payload with an even distribution of mass. The dotted line shows the reference helix trajectory, which is the path that the UAVs are supposed to follow. The solid lines show the actual trajectories of both UAVs, with each UAV starting at its respective initial positions. The trajectories of both UAVs are calculated to closely match the desired path, highlighting their ability to synchronize and adjust their movements during the mission. The figure explains the precise and accurate coordination required for the drones to maintain stability while lifting the payload. The tracking accuracy and smoothness of the trajectories explain the effectiveness of the control technique in ensuring reliable multi-UAV coordination and irregularly shaped payload transportation. Trajectory accuracy is directly influenced by thrust variations and real-time inter-UAV adjustments. This level of precise trajectory tracking is crucial for complex UAV applications such as medical supply delivery in remote areas. However, a key challenge is ensuring similar performance in real-world environments with unpredictable external factors.

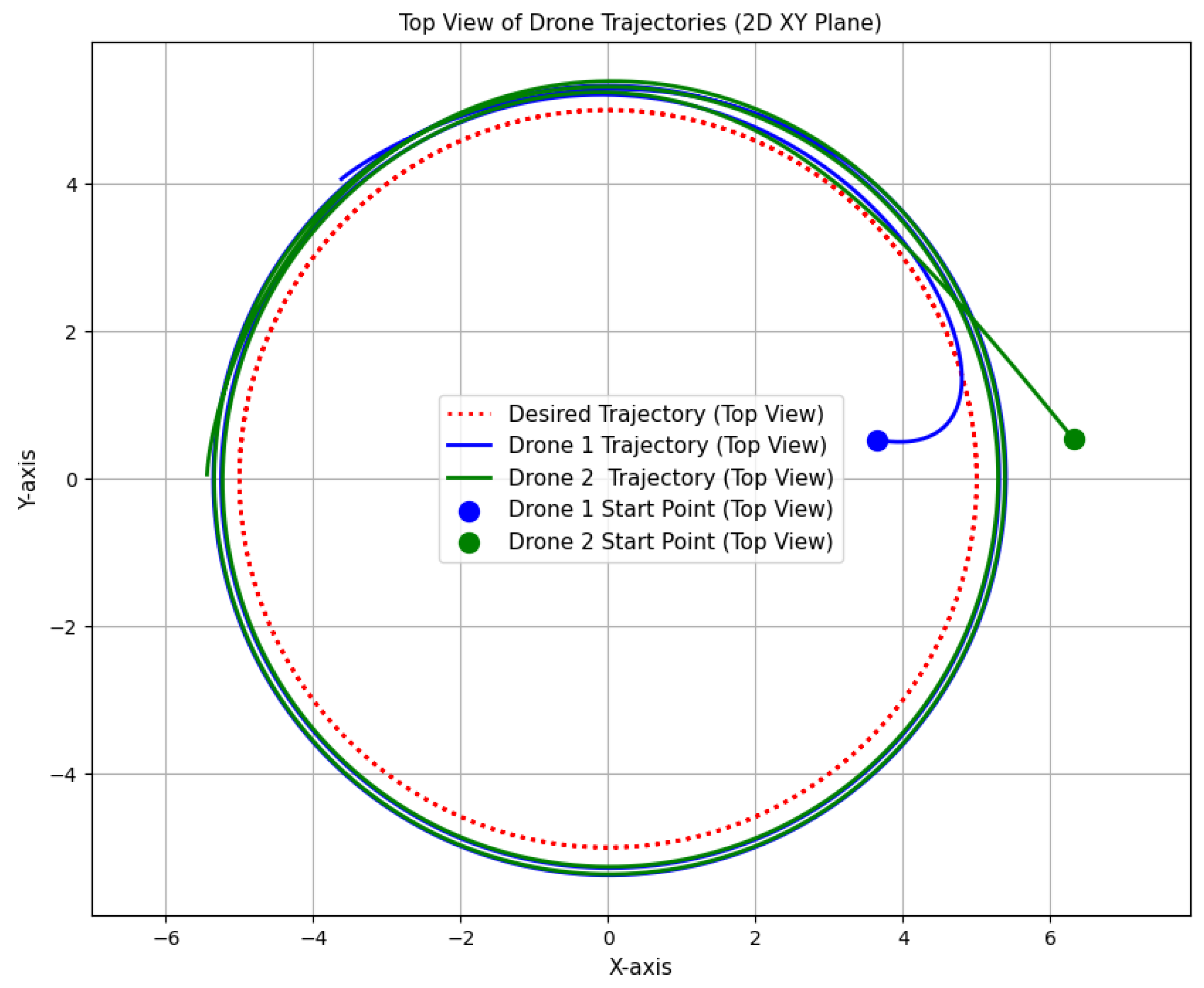
Figure 4 explains the 2D top view of the trajectory tracking of two heterogeneous UAVs. The dashed line represents the predefined reference helix trajectory, which is the path that both UAVs are supposed to follow. The solid lines represent the actual trajectories of both UAVs, as they attempt to follow the reference path. UAVs start from their initial positions marked with solid circles. As the UAVs move along their respective paths, both are able to closely follow the desired trajectory, showing the effectiveness of the coordination and control technique. The plot emphasizes the precision and accuracy with which the UAVs track the desired trajectory, ensuring that their movement remains synchronized in the plane. This highlights the ability of the heterogeneous UAVs to work together effectively in completing the operation, with slight deviations from the desired path that are corrected over time. The ability to maintain this trajectory in 2D ensures overall stability in the 3D tracking, confirming the robustness of the DSMC framework. This is particularly useful in search and rescue operations, where UAVs must navigate precise waypoints efficiently. A potential limitation is that this analysis assumes ideal sensor measurements, whereas real UAVs may suffer from GPS drift or sensor noise, which could impact accuracy.

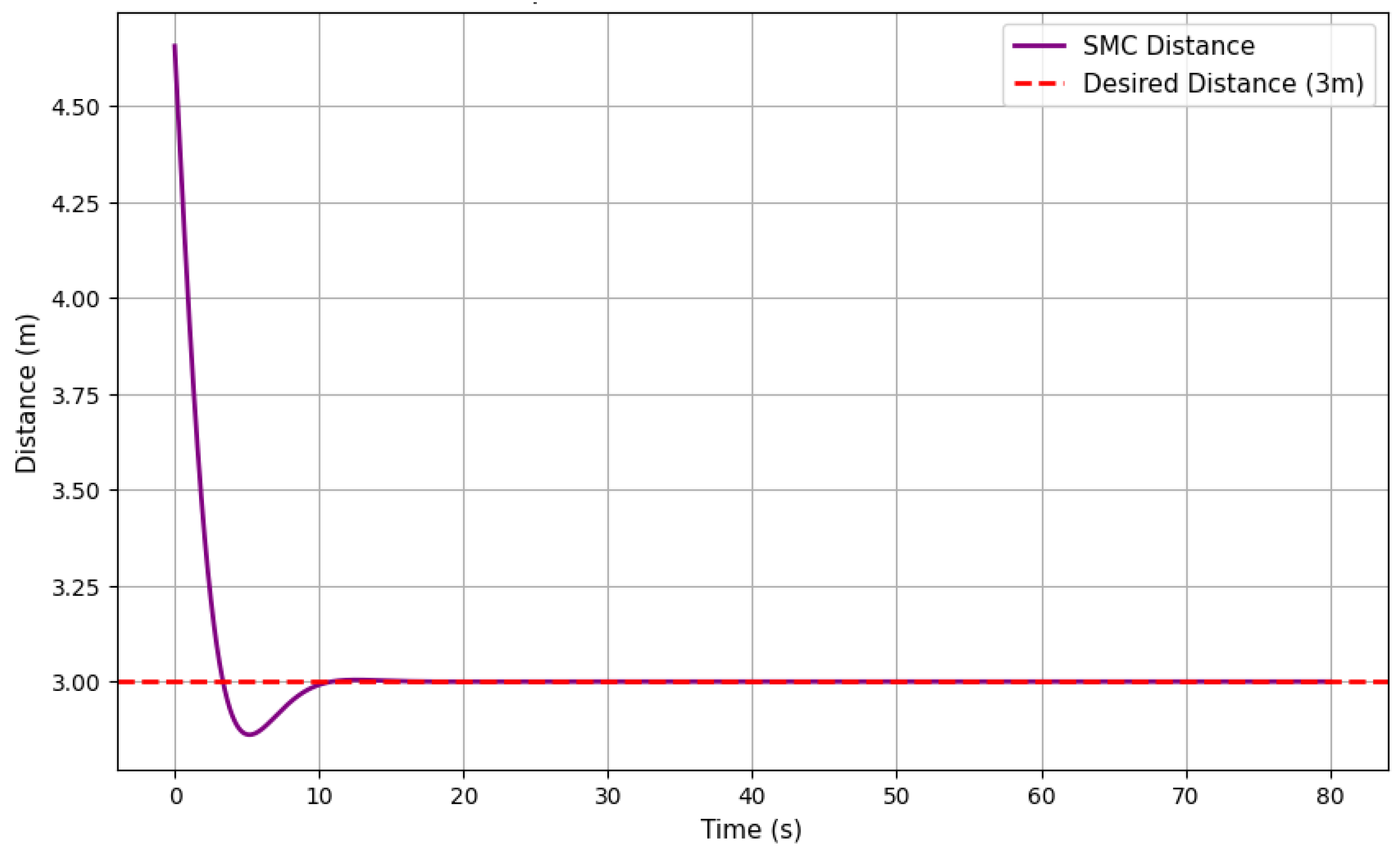
Figure 5 represents the safety distance between the two heterogeneous UAVs over time. The dashed line represents the reference safety distance between them. The initial distance between the UAVs is 5 m, because of the initial position of the UAVs. As the time increases, the distance rapidly decreases, stabilizing at the desired safety distance of 3 m. This behavior indicates that the UAVs are adjusting their positions to maintain a safe and consistent distance from each other, ensuring coordination during the operation. The sharp decline in the start of the plot indicates that UAVs are quickly aligning with the safety distance. It shows the efficient response of the control strategy in maintaining the safe inter-UAV distance, which is critical for ensuring stability and preventing collisions during irregularly shaped payload transportation. Maintaining this safety distance is crucial for preventing mid-air collisions, which could destabilize the payload and lead to mission failure. Additionally, inter-UAV spacing directly influences thrust variations, as closer UAVs must adjust their thrust to counteract aerodynamic interactions. One challenge in practical implementations is handling unexpected external disturbances, such as wind gusts, which may momentarily alter the relative distances between UAVs, requiring further robustness enhancements.

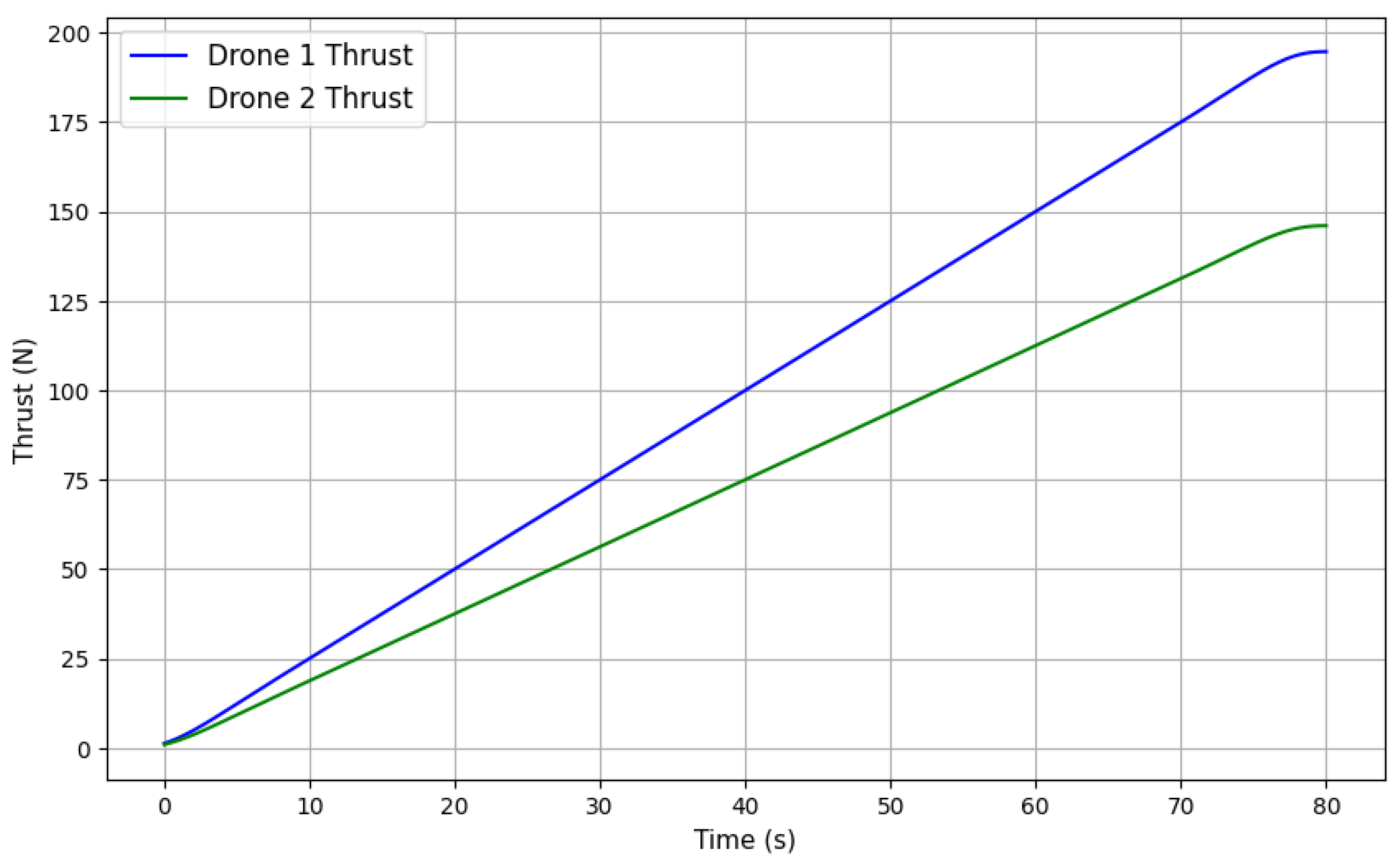
Thrust required by two heterogeneous UAVs as they move upward along a predefined helix trajectory while carrying an irregularly shaped payload with even mass distribution is represented in Figure 6. The thrust values of both UAVs increase over time because they are following the reference helix trajectory moving upward. The difference in the thrust is attributed to the varying capabilities of UAVs. The figure shows a linear increase in thrust, indicating a steady rise in the required power to lift and stabilize the payload during the upward motion. The consistency in the thrust profiles represents that the control technique is effectively managing the flight dynamics of both UAVs to maintain smooth operation throughout the mission. This increase in thrust is directly linked to trajectory tracking performance, as any imbalance in thrust can cause deviations in the flight path. In practical applications, such as precision agriculture and infrastructure inspection, maintaining smooth thrust transitions is necessary to avoid excessive energy consumption. However, one limitation is that the model assumes ideal motor responses, while real UAVs may experience actuator saturation or delays, affecting stability.

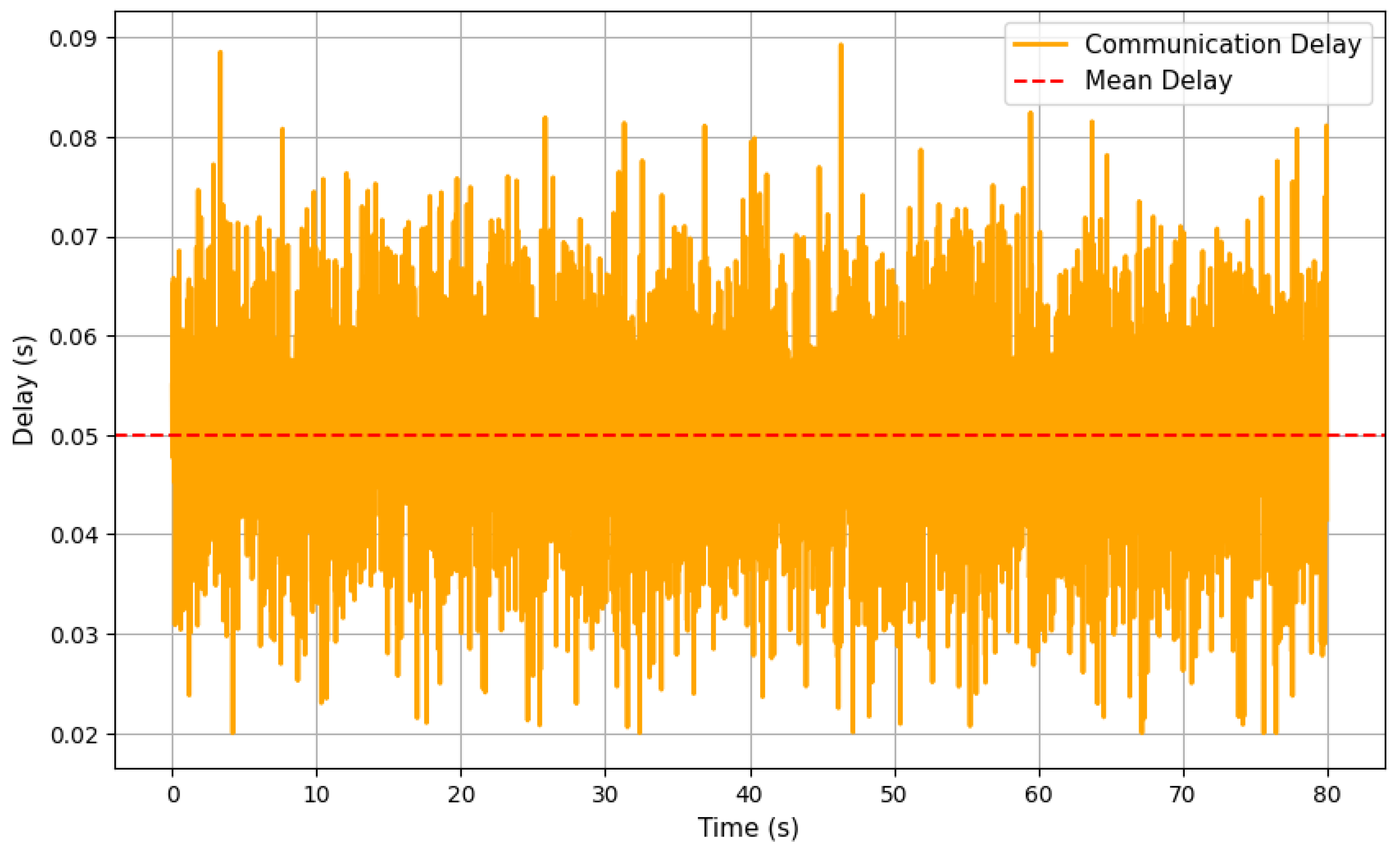
The communication delay between the drones is presented in Figure 7. The plot shows the delay variations, while the dashed line represents the mean delay. The delays remain within a reasonable range, indicating that the communication protocol effectively supports real-time coordination. This reliability is critical for maintaining synchronization in thrust adjustments, trajectory tracking, and safety distance. Effective communication is critical for UAV synchronization, as any delay in information exchange could result in de-synchronization and an increased trajectory tracking error. This is particularly relevant in real-world swarm UAV applications, where communication reliability affects overall mission success. Future work could explore adaptive control strategies to compensate for varying communication latencies.

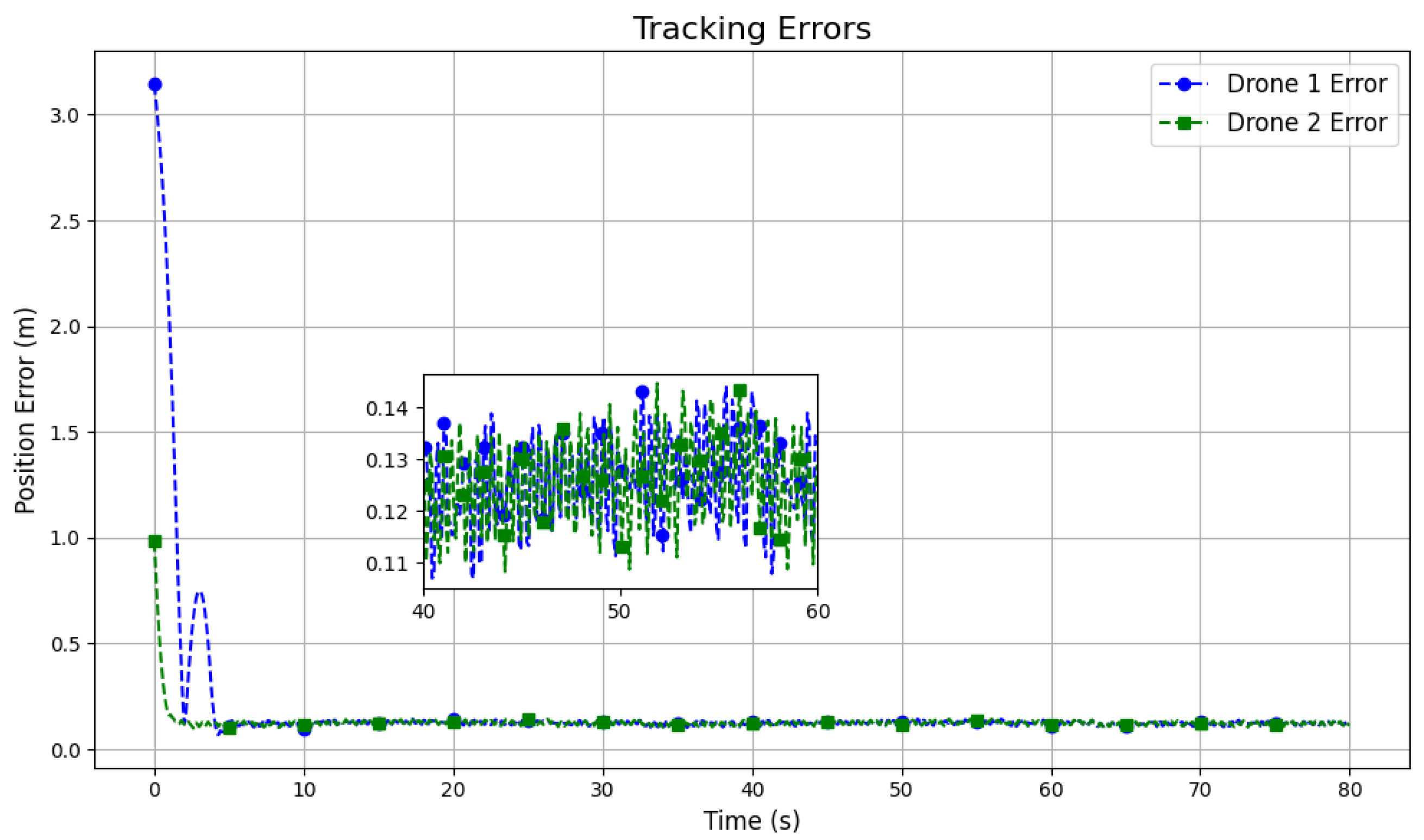
Trajectory tracking errors for both drones are shown in Figure 8. Initially, the drone exhibits a large error, whereas, relatively, Drone 2 shows a smaller initial error (due to the initial position of the drones). Both errors rapidly decrease, indicating effective trajectory tracking. After an initial transient phase, the errors stabilize at a low level. The zoom section shows small oscillations around 0.12–0.14 meters, suggesting the presence of minor steady-state fluctuation. The results confirm that both drones achieve accurate trajectory tracking with minimal error after stabilization. This result confirms the effectiveness of the DSMC in minimizing deviations, directly correlating with the accuracy of thrust control and safe distance maintenance. In real-world applications, such precise tracking is essential for missions such as aerial surveying and package delivery, where even minor deviations can lead to operational failures. One limitation is that external disturbances and model uncertainties could lead to increased steady-state errors, necessitating future improvements in disturbance rejection techniques.

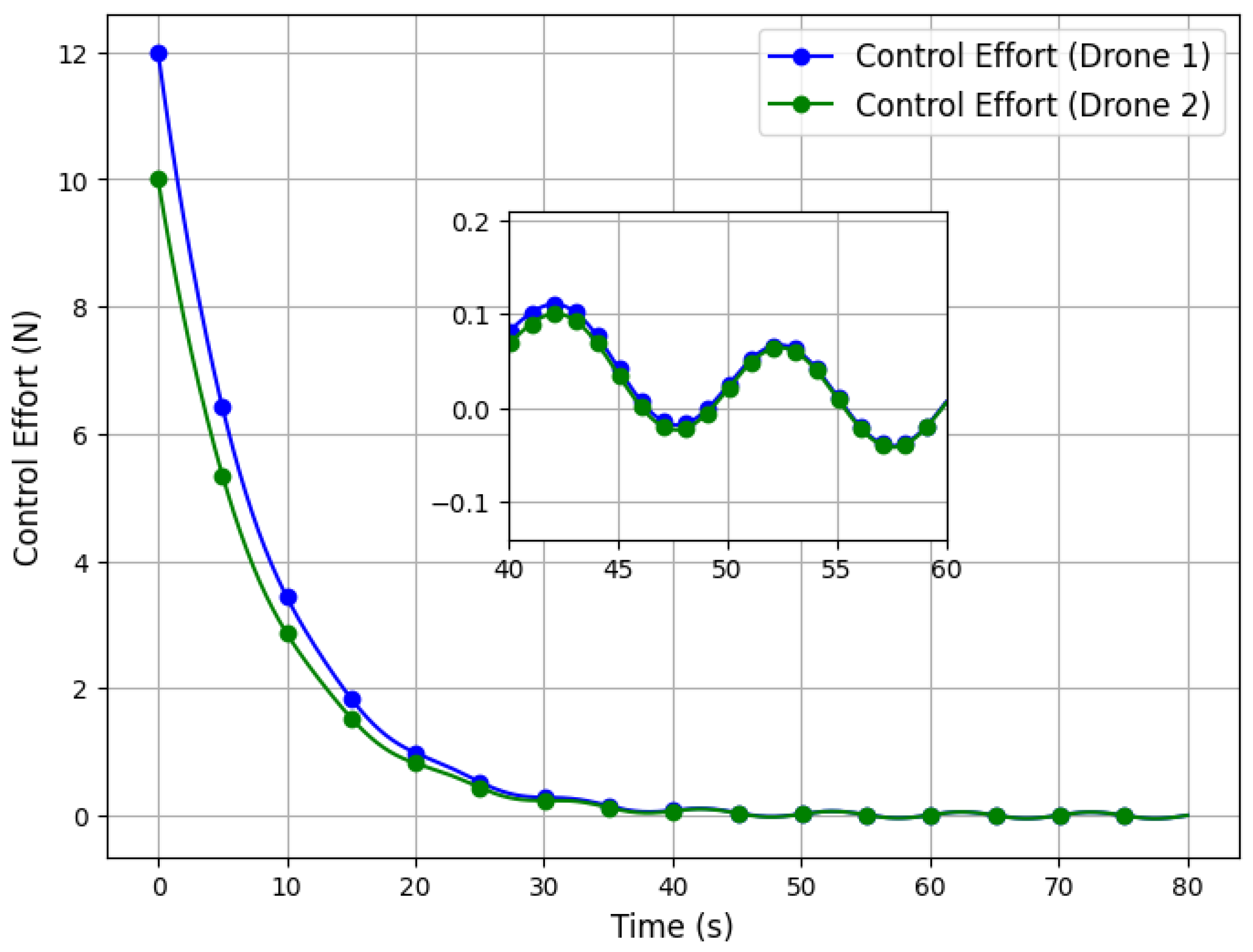
Figure 9 illustrates the control effort required by Drone 1 and Drone 2 during the operation. Initially, the control effort rises sharply as both drones stabilize and synchronize their trajectories to align with the desired path. After this transient phase, the control effort stabilizes and remains nearly constant over time, indicating that the drones have reached steady-state operation. The similar values for both drones highlight effective coordination and balance in their control strategies, ensuring the payload remains stable throughout the mission. The smooth and low control effort also reflects the efficiency of the applied sliding mode control algorithm.

Based on the above results in Figure 6 and Figure 7, the DSMC framework performs as a robust controller by ensuring stable UAV coordination despite uncertainties in terms of communication delay and different thrust capabilities. It effectively handles communication delays, preventing de-synchronization in trajectory tracking. DSMC compensates for thrust variation among heterogeneous UAVs, ensuring smooth flight, and adapts to irregular payloads, redistributing control efforts to maintain stability. These abilities validate its robustness in real-world UAV applications.

Comparative Analysis

To evaluate the effectiveness of the distributed sliding mode controller (DSMC), a comparative analysis is conducted using the proportional integral derivative (PID) controller. Parameters of the PID controller are tuned using the Ziegler–Nichols method, which is widely used for determining optimal gains based on the system’s critical oscillation response. This ensures that the PID controller operates with optimized parameters, allowing for a fair comparison between DSMC and PID controllers. The performance of both controllers is analyzed in terms of trajectory tracking accuracy, safety distance maintenance, trajectory tracking error, and control effort.

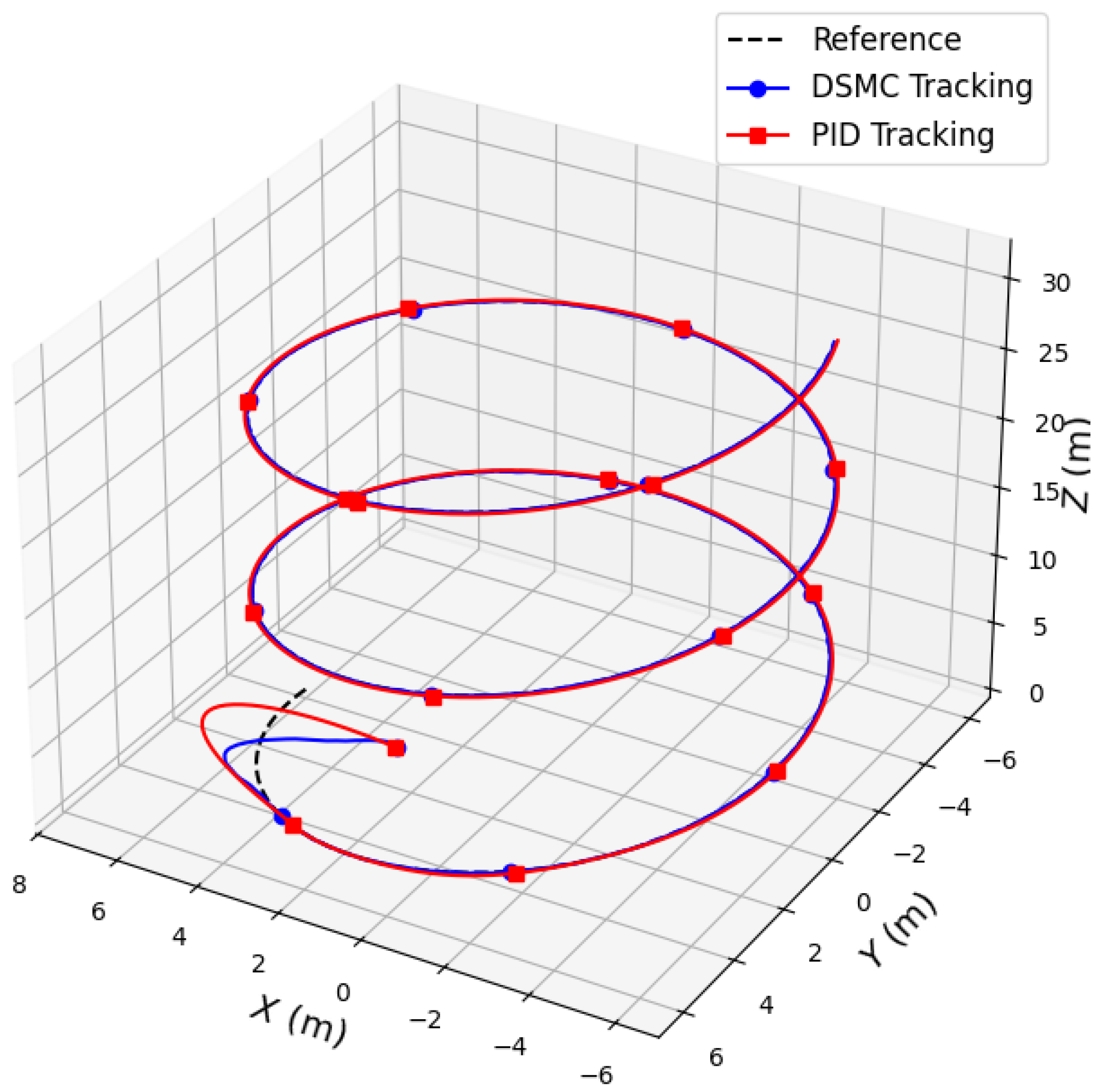
Figure 10 describes the 3D trajectory tracking of both DSMC and PID controller. DSMC shows a more precise and robust tracking performance, while PID exhibits more deviations. The comparison highlights that DSMC offers better convergence and adaptability, making it more suitable for dynamic environments.

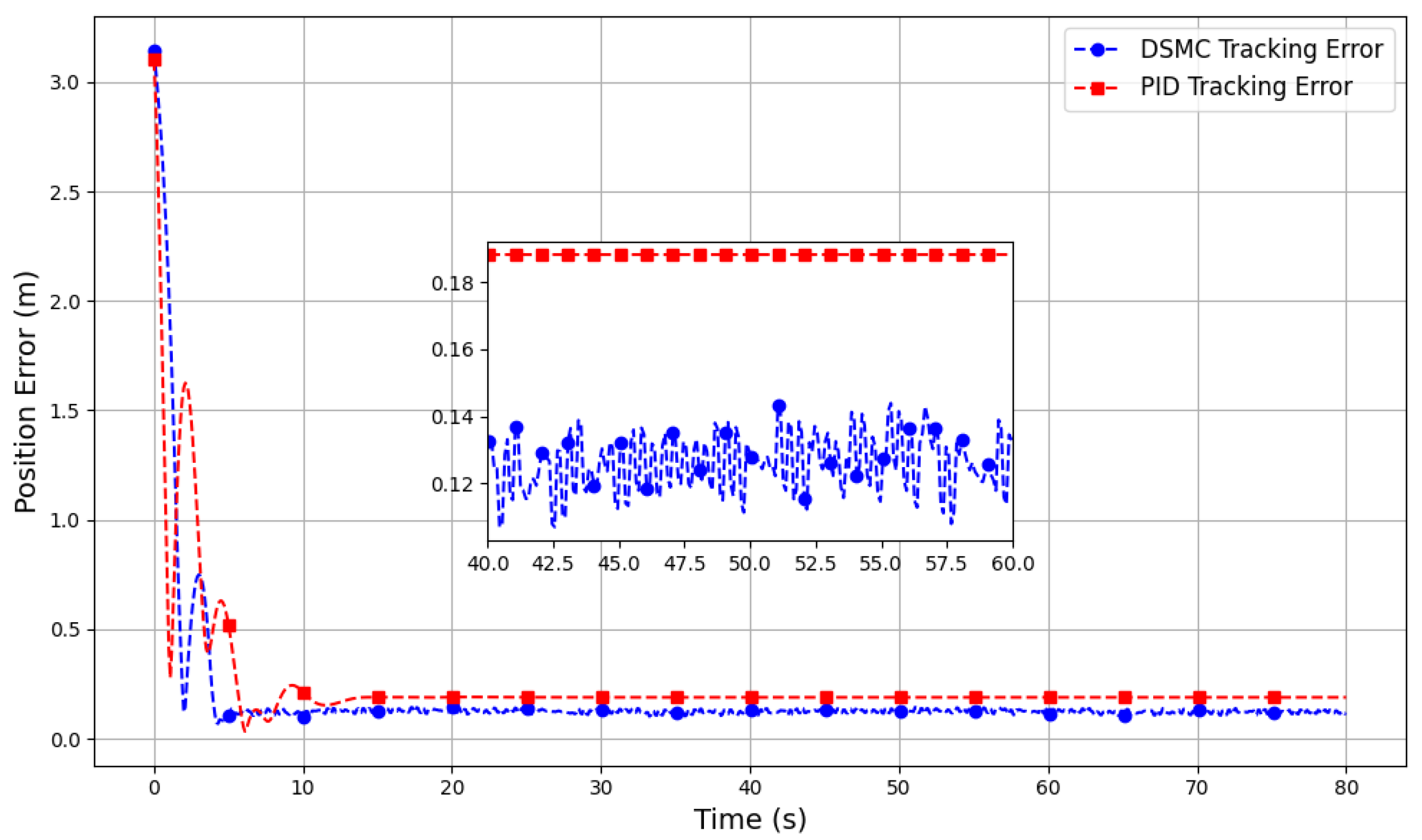
Trajectory tracking error over time is shown in Figure 11 for both controllers. Comparatively, DSMC shows a more stable and lower error compared to the PID controller, which exhibits fluctuations. This comparison gives crucial analysis in evaluating the precision of both controllers in handling sudden trajectory changes.

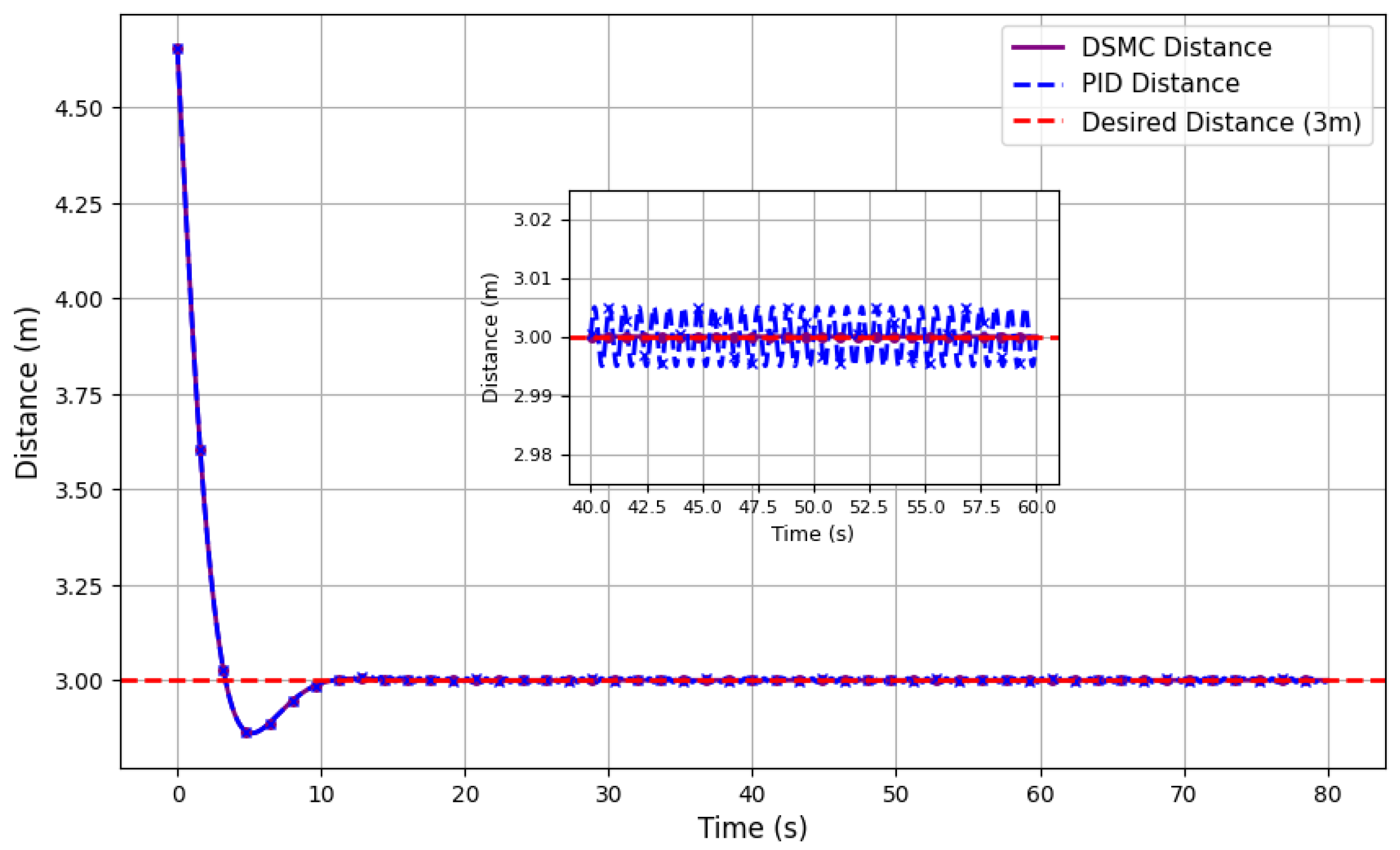
Comparative analysis of safety distance maintenance is shown in Figure 12. DSMC enforce more consistent distance, while the PID controller struggles with transient deviations, especially in dynamic maneuvers. The persistent oscillations in the PID controller indicate that PID requires additional adaptation mechanisms to match DSMC precision in inter-drone spacing.

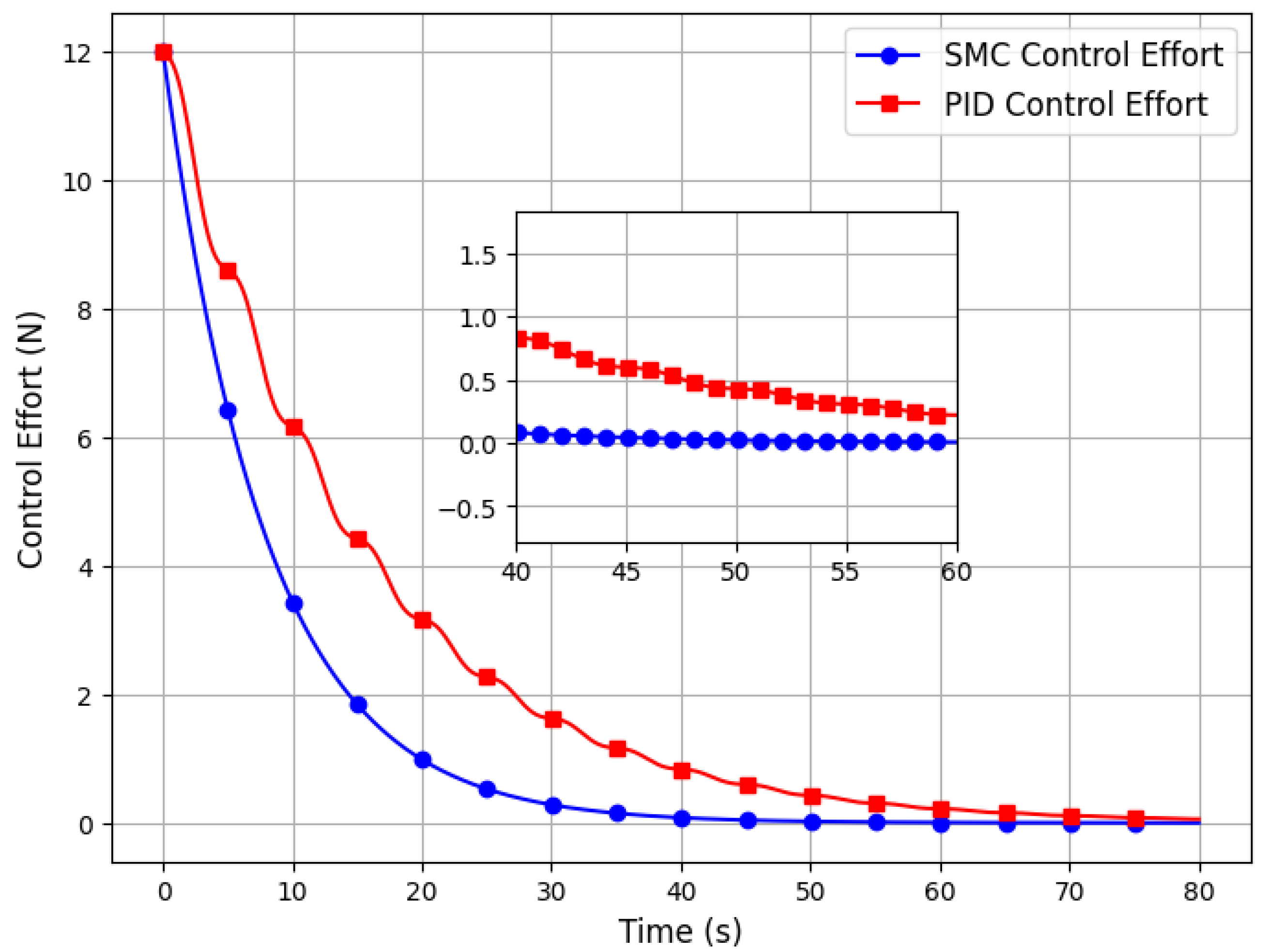
Figure 13 compares the control effort required by the DSMC and PID controllers. Control effort directly influences energy consumption and actuator stress. The DSMC might show slightly higher control effort due to its robustness but remains efficient in maintaining stability. The PID controller, on the other hand, may have larger fluctuations, indicating inefficient energy usage or excessive actuator demands.

6. Conclusions and Future Work

In this paper, a robust distributed sliding mode control (DSMC) strategy for coordinated trajectory tracking and irregularly shaped payload delivery by heterogeneous UAVs is presented. The proposed technique effectively shows the stable and synchronized operation of two heterogeneous UAVs while managing an irregularly shaped payload. The results show that DSMC ensures stable, synchronized, and disturbance-resistant UAV coordination, effectively managing trajectory tracking accuracy, adapting thrust allocation, and ensuring safe inter-UAV distance maintenance. However, one limitation is that DSMC assumes ideal sensor measurements, whereas real-world UAVs may experience sensor noise and actuator constraints, which could affect overall stability. Additionally, a comparative analysis between DSMC and PID control was conducted, demonstrating the superior performance of DSMC in terms of trajectory tracking accuracy, disturbance rejection, and payload stability. The results confirm that DSMC offers enhanced robustness and adaptability, making it a more suitable choice for complex UAV coordination tasks compared to PID. The results indicate that the DSMC is a promising approach for handling complex multi-UAV coordination challenges in dynamic and uncertain environments.

Future research of the proposed framework will extend to the physical implementation of dynamic payload adjustment scenarios, where the weight and center of mass of the payload may change during flight operations. Efforts will be focused on improving energy efficiency by integrating adaptive control and machine learning techniques to optimize the thrust and control effort in real time. Moreover, robust fault-tolerant mechanisms will be investigated to ensure UAV coordination even under sensor failures or actuator degradations. Advanced autonomous decision-making algorithms will be developed to enable UAVs to adapt trajectories and select lifting points autonomously, enabling their application in critical areas such as disaster response, logistics, and infrastructure inspections.