Adaptive Q-Learning Grey Wolf Optimizer for UAV Path Planning

Abstract

Path planning is crucial for safely and efficiently navigating unmanned aerial vehicles (UAVs) toward operational goals. Often, this is a complex, multi-constraint, and non-linear optimization problem, and metaheuristic algorithms are frequently used to solve it. Grey Wolf Optimization (GWO) is one of the most popular algorithms for solving such problems. However, standard GWO has several limitations, such as premature convergence, susceptibility to local minima, and unsuitability for dynamic environments due to its lack of adaptive learning. We propose a Q-learning-based GWO algorithm to address these issues in this study. QGWO introduces four key features: a Q-learning-based adaptive convergence factor, a segmented and parameterized position update strategy, a long-jump mechanism for population diversity preservation, and the replacement of non-dominant wolves for improved exploration. In addition, the Bayesian optimization algorithm is used to set parameters in QGWO for better performance. To evaluate the quality and robustness of QGWO, extensive numerical and simulation experiments were conducted on IEEE CEC 2022 benchmark functions, comparing it with standard GWO and some of its recent variants. In path planning simulation, QGWO lowers the path cost by 27.4%, improves the convergence speed by 19.06%, and reduces the area under the curve (AUC) by 23.8% over standard GWO, achieving optimal trajectory. Results show that QGWO is an efficient, reliable algorithm for UAV path planning in dynamic environments.

1. Introduction

The rapid advancements in UAV technology have revolutionized UAV use in high-risk and dangerous assignments, such as search and rescue operations, battlefield missions, critical and remote transportation, and surveillance [1]. Path planning stands out as a significant challenge among the critical areas of UAV research. Path planning refers to finding the best path for a specific UAV according to different mission objectives, environmental restrictions, and UAV dynamics [2]. A practical and reliable path-planning algorithm guarantees mission success, establishing it as a fundamental aspect of UAV technology.

Path planning comprises three components: motion planning, trajectory planning, and navigation [3]. Motion planning prioritizes the minimization of distance and the avoidance of sudden moves. Trajectory planning involves velocity, orientation, and other UAV parameters, whereas navigation guarantees the UAV complies to the specified route with precision. The process of path planning is intrinsically a multi-constraint and complex optimization problem. Traditional methods, such as grid-based and sampling-based algorithms, have limitations in scaling up because they require a lot of computing power [4]. Moreover, traditional approaches such as potential field methods can end up in local optima, generating sub-optimal paths [5].

Metaheuristic algorithms have been used to solve these challenges, namely, genetic algorithms (GA) [6], particle swarm optimization (PSO) [7], and ant colony optimization (ACO) [8], among others. Their flexibility to dynamic conditions makes them suitable for UAV path planning applications [9]. However, a recent study shows that the GWO proposed by Mirjalili et al. [10] performs better compared to the other three dominant algorithms, i.e., PSO, GA, and ACO, for UAV path planning [11].

However, GWO has some inherent limitations, such as an equal position update strategy during evolution, which can lead to premature convergence and low diversity in the solutions [12]. The issue becomes more significant in the case of multi-constraint optimization problems, where balancing exploration and exploitation plays an important role in generating optimal solutions [13]. In UAV path planning, GWO’s performance is further limited by its linearly decreasing convergence factor, which may not adapt effectively to dynamic mission requirements [5]. However, few studies have been conducted to modify GWO and address these challenges.

In this study, we propose a new GWO variant, named QGWO, to mitigate these drawbacks and improve the algorithm for UAV path planning. The key contributions of this study are summarized as follows:

• We propose a Q-learning-based adaptive GWO (QGWO) to address multi-constraint optimization problems such as UAV path planning.
• QGWO includes four novel features: an adaptive convergence factor based on Q-learning, a segmented and parameterized position update strategy, long jumps by random wolves to improve the exploration ability, and the replacement of non-dominant wolves by random wolves to increase diversity.
• A Bayesian optimization algorithm is used for parameter tuning to ensure optimal output by the algorithm.

The rest of the paper is organized as follows: Section 2 briefly overviews the GWO algorithm, its limitations, and the challenges in UAV path planning. Section 3 introduces existing works and the motivation behind this study. Section 4 describes the mathematical formulation of the UAV path planning problem and the mathematical model used to conduct the simulation work. In Section 5, we elaborate on the proposed QGWO algorithm and its convergence analysis. Numerical simulation results and a comparative analysis illustrating the algorithm’s effectiveness are presented in Section 6. Section 7 presents the conclusion.

2. Overview

This section provides an overview of the GWO algorithm and its limitations.

2.1. The GWO Algorithm

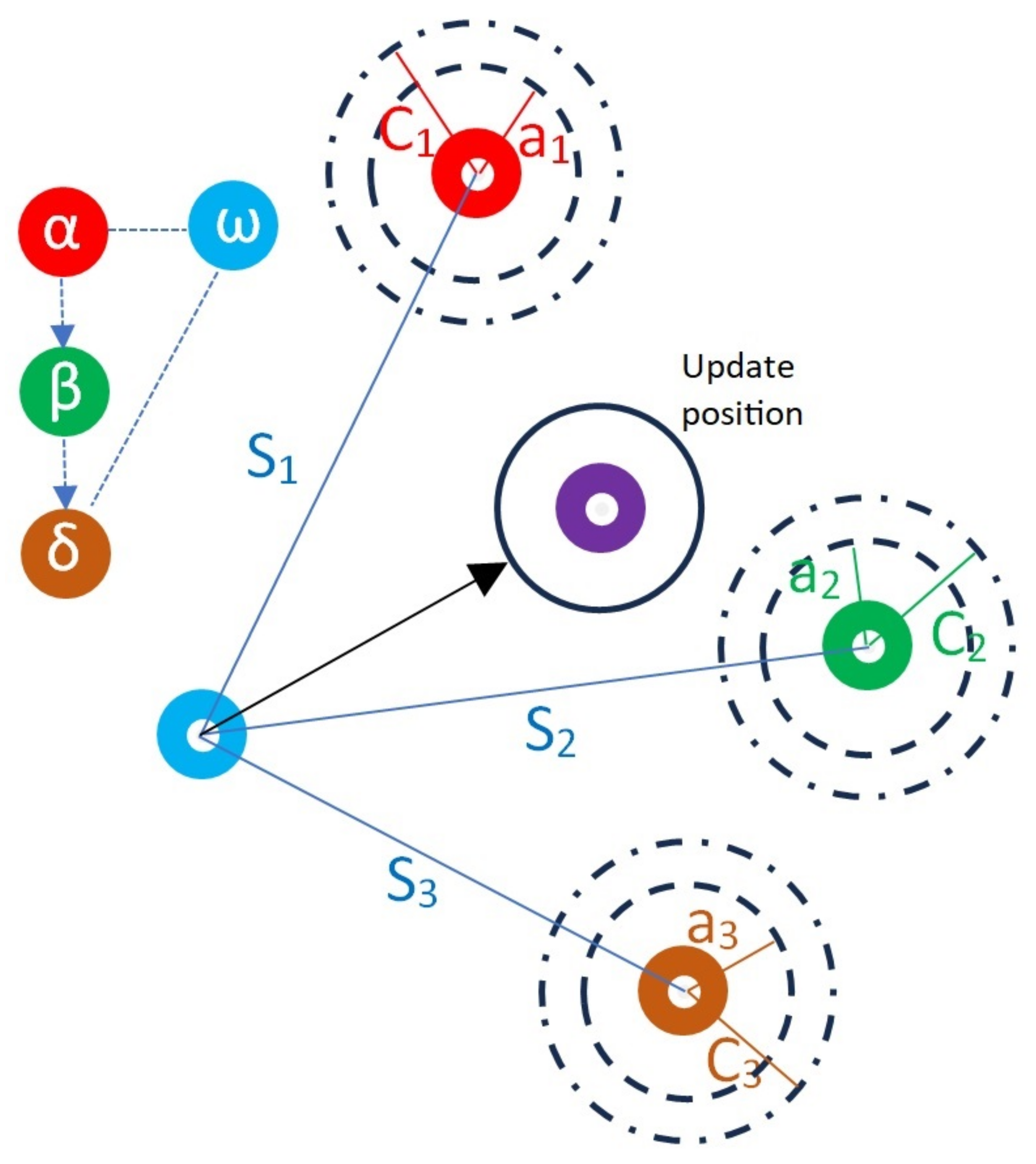
Inspired by grey wolf natural hunting and social interactions, the GWO is a metaheuristic algorithm that mimics three key characteristics seen in the wolves’ hunting approach: (a) searching and tracking prey, (b) encircling the prey to limit its movement, and (c) hunting the prey to capture it. The GWO algorithm also simulates the grey wolf pack’s hierarchical structure. The hierarchy consists of:

• Alpha wolf: The top-level decision-maker wolf.
• Beta wolf: The second-best wolf in the pack.
• Delta wolf: The third-ranking wolf.
• Omega wolves: The non-ranking wolves that assist in the evolution overall process.

One significant benefit of GWO is that it relies on group decision-making, which is governed by the social hierarchy, which enhances its problem-solving abilities. This allows the algorithm to adapt quickly to the nature of a given problem, making it highly effective for solving a broad range of MCOPs. Figure 1 shows a semantic representation of the algorithm.

2.1.1. Social Hierarchy

The GWO algorithm organizes possible solutions into a hierarchy, categorizing them as leader and general wolf. Leader wolves are responsible for hunting and encircling activities that lead to new solutions. The best three solutions are categorized as leader wolves and are known as alpha ($\alpha$), beta ($\beta$), and delta ($\delta$). The alpha denotes the optimal option, followed by the beta and delta, which are the second and third most effective solutions, respectively.

The remaining wolves in the pack, called omega ($\omega$) wolves, fulfill a crucial function in the evolutionary process. Rather than taking the lead, they assist the dominant wolves by adhering to their direction. This hierarchical framework reflects real-world dynamics, as certain members assume leadership roles while others adhere to their guidance, making the algorithm dynamic and adaptable.

2.1.2. Encircling

The mathematical operation of the algorithm starts with the encircling phase that aims to identify the prey. Based on this part’s alpha, beta, and delta positions, the algorithm tries to enclose or surround the best solution. The encircling operation is expressed by Equations (1) and (2):

$$S=\left|C·P_p-P_i\right|$$

(1)

$$P_i=P_p-A·S$$

(2)

where S denotes the absolute spatial distance between the prey`s position ($P_p$) (alpha, beta, and delta solutions are supposed to be at a close distance from the prey) and all wolves’ positions ($P_i$) at each iteration ($it$). C and A are two important coefficients used in the algorithm, which are formulated as follows:

$$A=2·a\left(it\right)·r{d}_1-a$$

(3)

$$C=2·r{d}_2$$

(4)

$$a\left(it\right)=2-{\displaystyle \frac{2·it}{MaxIter}}$$

(5)

Here, $r{d}_1$ and $r{d}_2$, two random numbers from [0, 1] were used to randomize the candidate solutions. One of the critical characteristics of metaheuristics algorithms is the randomness in the candidate solutions, often called diversity. It allows the algorithm to explore more possible solutions in the search space and mitigate the local minima problem of the algorithm [10]. The parameter a in Equation (3) is called the convergence factor of the GWO algorithm. The value of a ranges from [2, 0].

2.1.3. Hunting

In hunting, GWO uses the alpha, beta, and delta positions to generate the next solution round. The key idea is that the alpha, beta, and delta positions are considered the closest to the prey, i.e., global solution in the search space. These three best positions generate the next round of candidate solutions [10]. The algorithm can achieve the closest position to the prey through the hunting processes. The following equations can express the hunting operation:

$$\left\{\begin{array}{c}{S}_{\alpha }=|C_1·P_{\alpha }-P_i|\hfill \\ S_{\beta }=|C_2·P_{\beta }-P_i|\hfill \\ S_{\delta }=|C_3·P_{\delta }-P_i|\hfill \end{array}\right.$$

(6)

$$\left\{\begin{array}{c}{P}_1=P_{\alpha }-A_1·S_{\alpha }\hfill \\ P_2=P_{\beta }-A_2·S_{\beta }\hfill \\ P_3=P_{\delta }-A_3·S_{\delta }\hfill \end{array}\right.$$

(7)

$$P_i={\displaystyle \frac{P_1+P_2+P_3}{3}}$$

(8)

In the equation, $S_{\alpha /\beta /\delta }$ reflect the spatial separation between the present location of the wolf $\left(P_i\right)$ and $\alpha$, $\beta$, $\gamma$ wolves in each iteration ($it$). $C_1$, $C_2$, and $C_3$ are the three random coefficients defined by Equation (4) and $A_1$, $A_2$, and $A_3$ are calculated by using Equation (3)

2.1.4. Search and Attack

The algorithm’s best solution is discovered during the searching phase (also known as exploration), while the hunting phase aids in the algorithm’s convergence towards that solution (also known as exploitation).

The Grey Wolf Optimizer (GWO) employs a stochastic coefficient denoted as A to execute the search and attack operations. The wolves are driven to diverge or relocate from their current prey to seek more optimal solutions or prey when $\left|A\right|>1$. This behavior demonstrates the exploratory characteristics exhibited by the algorithm for finding global solutions. When $\left|A\right|<1$, the algorithm engages in convergence towards the prey. Hence, the variable A exerts a substantial influence on the algorithm. The value of parameter A is determined by a linearly decreasing function, commonly known as the convergence factor (Equation (5)).

Furthermore, the GWO method incorporates the coefficient C to enhance the level of randomness within the solutions. The subsequent solutions round is generated by randomizing the influence of the three most effective solutions: alpha, beta, and delta. Introducing more randomness in the generated solutions during a specific iteration enhances the randomness inside the search space, hence mitigating the risk of becoming trapped in local minima. The GWO algorithm is characterized by two governing parameters, A and C that effectively manage the balance between exploration and exploitation operations and the level of solution variety, which is reflected in the volatility of the results.

2.2. Limitations of GWO

The GWO proposed in [10] has shown promising results compared to other popular metaheuristics algorithms such as PSO, ACO, and GA [14]. Also, fewer parameters in the algorithm attract the researcher to apply the algorithm in various applications. However, it can easily fall for local minima in the case of MCOPs and complex problems. Also, the algorithm suffers from insufficient diversity among the candidate solutions, which results in premature convergence [15].

The linear adjustment of the control parameter A can also cause an imbalance between exploration (finding various answers) and exploitation (refining solutions), reducing GWO’s effectiveness in dynamic or vast search areas. The method initially performs well, but convergence slows as it approaches the optimal solution. This renders it unsuitable for time-sensitive applications. The initial settings of GWO, such as the number of wolves and the parameters A and C, significantly impact its performance and reduce its robustness across various problem domains [16]. One issue is its inefficiency in high-dimensional problems like UAV path planning [17]. Recent studies showed that there are two significant limitations in the algorithm, which are discussed below.

2.2.1. Linear Convergence Factor $\left(a\right)$

In GWO, the convergence factor a lowers linearly from 2 to 0 over iterations, regulating the balance between exploration and exploitation. On the other hand, a fixed linear reduction lacks the flexibility to fit various search environments. Intense exploration is required in early iterations to broaden the search space while exploitation is important in later iterations for refining the solution.

By dynamically changing the value of a, a non-linear convergence factor allows more flexible transition between exploration and exploitation. Unlike linear convergence, in which the decrease in search space exploration follows a fixed rate, a non-linear decay adjusts operation based on problem complexity, therefore preventing premature convergence and enhancing local search efficiency. This method guarantees that GWO gets enough exploration evolving towards solution accuracy in later iterations  [18]. Also, adaptive non-linear convergence strategies reduce stagnation and enable GWO to retain different search agents while enhancing convergence behavior in complicated and high-dimensional problem environments [19].

2.2.2. Equal Position Update Strategy

The alpha wolf is seen to be the closest to the prey or global solution in the GWO, the beta wolf is thought to be in the second-best position, and the delta wolf is thought to be in the third-best position from the prey. Social hierarchy is one of the algorithm’s fundamental properties. However, when updating positions (as described in Equation (8)), all three best solutions are given equal consideration in generating the subsequent batch of solutions. The phenomenon above contradicts the notion of a social leadership hierarchy inside the GWO, resulting in suboptimal and rigid position update efficiency.

Consequently, this approach can lower the efficiency of the position updates, restricting the algorithm’s convergence speed and solution quality. Recent research indicates that allocating different weights to the wolves depending on their hierarchy could enhance the optimization process, ensuring that the alpha wolf has a more dominant role in driving the search while preserving sufficient diversity to investigate other solutions properly.

3. Related Works

In recent years, numerous approaches have been introduced to address the limitations of the GWO. Based on the methods employed, these proposals can be categorized into four categories.

3.1. Non-Linear Convergence Factor (a)

In recent years, several solutions have emerged that aim to address the issue of balancing the exploration and exploitation behavior of the GWO by incorporating a non-linear convergence factor. These ideas outperformed the traditional GWO in terms of performance. An improved GWO method is described in [19]. It is based on a non-linear convergence factor, and the linear convergence factor is changed using a trigonometric formula. To make the convergence of GWO more accurate, Ref. [20] suggests using a non-linear increasing [0 to 2] convergence factor. A logarithmic non-linear convergence factor ranging from [2 to 1] was used in Ref. [21] to make GWO better at global search by focusing on exploration more. An idea for improving GWO’s exploration skills is put forward in [22]: a non-linear increasing convergence factor. Ref. [23] presented a non-linear decreasing and random convergence factor with a range [2 to 1]. The range of a in the proposed modification allowed the algorithm to emphasize global exploration more than exploitation. In [24], a non-linear convergence factor with a value that decreases exponentially is suggested as a way to make the GWO more accurate. Ref. [25] proposed a non-linear convergence factor using logarithmic and tangent formulas. A better GWO for a multi-objective optimization problem was shown in reference [26] by adding a non-linear convergence factor that goes down in an exponential way. The work of [27] suggests a non-linear adaptive convergence factor for GWO that is based on how quickly wolves’ spatial orientation changes. Newer research indicates that using deep reinforcement learning to help plan a UAV’s path when it is under threat is effective ([28]). Optimization can also be made more effective with adaptive convergence factor strategies that are based on reinforcement learning [11,29,30].

3.2. Modified Position Update Strategy

Adding a non-linear convergence factor to GWO made it more accurate at convergence, but it still has problems with local minima, especially for complex and multi-modal functions. Therefore, the position update strategy plays a significant role in the GWO algorithm. As a result, several proposals used a modified position update strategy along with their proposed GWO improvements. Most proposals alter both the position update strategy and the GWO convergence factor. In [19], a modified population update formula is proposed where a randomly selected wolf position is used along with the existing three best wolf positions. Ref. [23] proposed a modified position update formula based on alpha and beta wolf positions. A time-varying weighted position update formula is proposed to improve the local minima avoidance ability of GWO in [24]. Yan et al. [25] proposed adaptive weights for GWO based on the fitness values of alpha, beta, and delta wolves. In [31], a static variable weight for position update in GWO is proposed to improve the exploration ability of GWO. In [32], the author suggested a time-varying variable weight for a position update. Ref. [26] presented an adaptive position update strategy for GWO. An adaptive weight for a position update based on the spatial orientation of wolves is proposed in [27]. Ref. [33] introduced a disturbance factor from the lion optimizer algorithm into GWO for the position update strategy. Introducing the disturbance factor increases the randomness of the wolves’ position, thereby mitigating the fall for the local minima problem.

3.3. Modified Wolves Arrangement

In this category, the proposed models change the algorithm’s orientation of the wolves’ behavior. In [34], the GWO algorithm is modified by replacing the group hunting behavior with Archimedes’s spiral mathematical model. To enhance the exploratory capabilities of the GWO algorithm, a Cauchy random walk-based GWO named RW-GWO is proposed in [35]. A hill climbing-based local search strategy for hunting behavior is suggested in [36] to improve the accuracy of GWO convergence. In [32], an additional wolf position (top omega wolf) or the fourth-best position is used for hunting. Ref. [37] presented opposition-based learning (OBL) incorporating GWO, where the OBL approach is applied to improve the prediction ability of the solution. An additional position update strategy called tracking and seeking modes is proposed in [38]. Each wolf updates its position based on the best position ($\alpha$ wolf) at each iteration along with the hunting process, allowing the wolves to move towards a better position. In [39], the exploration and exploitation ability of GWO is increased by adapting the Gaussian walk and levy flight approach. Recently, deep reinforcement learning has been used to improve UAV navigation’s ability to avoid obstacles. This helps autonomous systems safely navigate complex environments [40,41]. These studies highlight the importance of adaptive behaviors in improving search diversity and solution robustness.

3.4. Hybridization of GWO

This approach involves merging two or more metaheuristic algorithms to mitigate their downsides. So far, there are two types of hybridization approaches, i.e., low-level and high-level co-evolutionary hybridization approaches [42]. Most of the suggested methods use a low-level co-evolutionary hybridization method, which combines the better parts of two algorithms to make the whole thing work better. Among different metaheuristic algorithms, PSO is one of the most widely used algorithms to hybridize the GWO. Proposals like [43,44,45] showed that the strong exploitation ability of PSO can be incorporated in GWO to improve its performance. In [46], a hybrid GWO algorithm is proposed based on the beetle antenna search algorithm. The algorithm also used a non-linear convergence factor based on the cosine function. The proposed algorithm adds a learning strategy for the alpha wolf in GWO that facilitates its superior exploration ability, resulting in a more accurate solution. This is because two additional new positions (left and right) are calculated to move the alpha position into better positions, which helps the algorithm to generate a better solution than standard GWO. Other hybridization methods, such as GWO with GA [47], GWO with DE [48], GWO with HS [49], and GWO with CSA [50], are proposed to improve the overall performance of GWO in high-dimensional and multi-objective problems. New research indicates that when planning a UAV path, using both geometric obstacle avoidance strategies and genetic algorithms works very well, [51]. Similarly, bi-level optimization methods based on deep reinforcement learning have shown promise in improving the efficiency of assigning tasks to multiple robots [52].

Although the hybridization approach has increased optimization performance, it introduces some significant limitations, like a higher computational cost and parameter tuning complexity [53,54,55]. Also, hybrid models might not always give better results because their use depends on the problem and how well the algorithms work together [56]. Some hybrid methods might give up GWO’s ability to explore in favor of exploitation, which could lead to early convergence in difficult search areas [44,45].

3.5. Motivation

These developments show how flexible GWO is in addressing certain optimization problems. While convergence, exploration, and exploitation have greatly improved GWO’s capabilities, several methods need more validation in practical settings to guarantee scalability and resilience. Literary assessments have, however, shown their shortcomings, especially in terms of balancing exploration and exploitation and their inclination to converge too soon to a local optimum. Attempts to address these flaws have distinguished two main strategies.

As covered in Section 2.2, the first category emphasizes adding modified position update techniques and non-linear convergence parameters. These techniques improve the performance of the GWO framework without appreciable computing overhead, thereby preserving its simplicity. The retention of this simplicity aligns with GWO’s primary appeal and motivates us to build upon it. To achieve performance increases, the second category consists of hybridizing GWO with different metaheuristics. Although efficient, these hybrid approaches sometimes result in higher processing costs and algorithmic complexity, which would reduce the attractiveness of GWO’s simple architecture. Thus, our analysis specifically refutes hybrid strategies in favor of improving the current GWO architecture.

We want to show that GWO can be much better at optimizing things if the right mix of non-linear convergence factors and position updating techniques are used. We keep the simplicity and computational efficiency of the method while enhancing its ability to explore the solution space and evade local optima. Detailed studies confirm the suggested changes by demonstrating better performance than current GWO versions.

4. Mathematical Framework for UAV Path Planning

This section presents the mathematical model for UAV path planning, environment setup, and the obstacle model. A brief description of the problem is provided. Additionally, a three-dimensional (3D) search space is considered in the simulation to better replicate real-world scenarios.

4.1. Environment

A 3D environment is considered in this work. Cylindrical shapes are used to represent the obstacles (Obs). Figure 2 shows a typical 3D environment scenario considered for this work. The 3D search space can be defined using the rectangular matrix $S\in {\mathbb{R}}^3$. The three dimensions are represented by three axes, i.e., $P·Q·R$, where P and Q represent the x-axis and y-axis, respectively, and R represents the height. Each cell is represented by $C=\{p_i,q_i,r_i\}$, $p_i\in P$, $q_i\in Q$, $r_i\in R$, for $i=1$ to N. The obstacles are represented by a rectangular matrix expressed as follows:

$$Obs=\left[\begin{array}{cccc}{p}_1& q_1& r_1& d_1\\ p_2& q_2& r_2& d_2\\ ⋮& ⋮& ⋮& ⋮\\ p_n& q_n& r_n& d_n\end{array}\right],$$

(9)

where $(p_i,q_i)$ represents the center, $r_i$ represents the height, and $d_i$ represents the diameter of the i-th cylindrical obstacle. To improve the complexity of the problem, a random obstacle with random start and end points is considered in this study.

4.2. UAV and UAV Path

A UAV is an autonomous robot capable of moving or steering in any direction in a 3D space [57]. The 3D axes can represent the position of a UAV. Let us consider a UAV $U\left(t\right)$ that has three movement axes, i.e.,

$$U\left(t\right)=(p^t,q^t,r^t)$$

(10)

where $p^t$, $q^t$, and $r^t$ represent the 3D axis position of the UAV at time t. A UAV path in a 3D space can be defined as a line passing through n number of points called waypoints. However, the path should avoid sharp turns, as rapid sharp turns may not be executable by UAV kinematics [58]. Therefore, an interpolation formula such as the Bezier curve [59] or B-spline curve [30] is used over the waypoints to generate an equal time-spaced UAV-followable contiguous path. In our proposed model, we used a B-spline cubic interpolation formula with a smoothing factor of 0.2, as proposed in [60]. Figure 3 shows a typical B-spline curve generated from the given waypoints.

4.3. Cost Function and Obstacle Avoiding Path Planning

Essentially, the path planning problem aims to find an optimal feasible trajectory [2]. There are three major criteria that define optimality: time, cost, and energy efficiency. Therefore, an optimal path should consider minimizing travel time, operational cost, and energy consumption. Path length, angle stability, and energy consumption are among several constraints that can govern the motion of a given UAV. This paper presents an optimization algorithm based on multiple constraints, such as the constraints of path length, energy consumption, yaw angle, and pitch angle, which directly affect the UAV’s maneuverability and efficiency. To avoid conflicting turns when approaching a maneuver, a cost on yaw is added to discourage sharp direction changes; similarly, to avoid large changes in altitude during waypoint transitions, a cost on pitch is introduced. An electrical cost function that minimizes the energy consumption further improves flight efficiency. The algorithm generates n waypoints that build a feasible trajectory from the source to the destination while attempting to be as close to the optimization function as possible. The ultimate goal is to investigate which combination of waypoints can minimize the cost function in aggregate while generating stable, low-cost, and viable UAV trajectories for real-world implementation.

The cost function is crucial to an optimization problem. It provides a methodical technique for selecting the optimal outcome or solution from the specified domain. In this study, multiple constraints related to UAV path planning are considered to define the cost function. The weighted multi-constraint cost function is represented as follows:

$$C_m={\lambda }_1·C_{\mathrm{path}}+{\lambda }_2·C_{\mathrm{energy}}+{\lambda }_3·C_{\mathrm{angle}}+{\lambda }_4·C_{\mathrm{obs}}$$

(11)

where ${\lambda }_1,{\lambda }_2,{\lambda }_3$, and ${\lambda }_4$ are weights used to tune the optimization function.

4.3.1. Path

The fundamental goal of UAV path planning is to generate an optimal trajectory that minimizes overall cost while ensuring operational feasibility [2]. In this study, the cost function considers multiple constraints, including the path length, energy consumption, yaw angle, and pitch angle. The optimization algorithm selects an optimal set of n waypoints from the source to the destination, forming a trajectory that minimizes the cost function.

A suboptimal path refers to a trajectory that does not efficiently minimize the cost function, resulting in increased travel distance, higher energy consumption, and excessive angular variations. These inefficiencies negatively impact UAV mission performance by increasing flight time, reducing energy efficiency, and affecting trajectory stability. To mitigate these issues, the proposed algorithm penalizes unnecessary path deviations, ensuring that the generated UAV paths are smooth, stable, and energy-efficient.

The path cost is calculated using the Euclidean distance formula:

$$C_{\mathrm{path}}=\sum _{i=1}^{n-1}\sqrt{{(p_{i+1}-p_i)}^2+{(q_{i+1}-q_i)}^2+{(r_{i+1}-r_i)}^2},$$

(12)

where $(p_i,q_i,r_i)$ are the coordinates of the i-th waypoint.

4.3.2. Energy Cost

The energy cost includes both kinetic and potential energy. For a constant velocity UAV, the kinetic energy is:

$$E_k={\displaystyle \frac{1}{2}}m{v}^2,$$

(13)

where m is mass and v is velocity. The potential energy due to altitude change is:

$$E_p=m·g·\Delta r,$$

(14)

where g is the gravitational acceleration. The total energy consumption is:

$$C_{\mathrm{energy}}=(N-1)·E_k+\sum _{i=1}^{N-1}m·g·(r_{i+1}-r_i).$$

(15)

4.3.3. Yaw and Pitch Angle Costs

The angle cost is calculated by considering the UAV’s yaw angle and pitch angle orientation while navigating the generated path. The yaw angle represents the UAV’s orientation to the horizontal plane, which is essential for its directional stability. The yaw angle is calculated from the positive x-axis in a 2D projection of a 3D path, and the yaw angle cost is calculated by successive absolute yaw angle differences at each step of the path. The yaw angle cost is calculated using:

$$C_{\mathrm{yaw}}=\sum _{i=1}^{N-1}|{\theta }_{\mathrm{yaw}}^{(i+1)}-{\theta }_{\mathrm{yaw}}^{\left(i\right)}|,$$

(16)

where ${\theta }_{\mathrm{yaw}}^{\left(i\right)}=arctan2(q_{i+1}-q_i,p_{i+1}-p_i)$. Similarly, the pitch angle cost is:

$$C_{\mathrm{pitch}}=\sum _{i=1}^{N-1}|{\theta }_{\mathrm{pitch}}^{(i+1)}-{\theta }_{\mathrm{pitch}}^{\left(i\right)}|,$$

(17)

where ${\theta }_{\mathrm{pitch}}^{\left(i\right)}=arctan2\left({\displaystyle \frac{r_{i+1}-r_i}{\sqrt{{(p_{i+1}-p_i)}^2+{(q_{i+1}-q_i)}^2}}}\right)$. The total angle cost is:

$$C_{\mathrm{angle}}=C_{\mathrm{yaw}}+C_{\mathrm{pitch}}.$$

(18)

By minimizing these angle costs, the algorithm ensures smoother UAV trajectories, reducing sharp directional changes and improving overall flight efficiency. This contributes to an energy-efficient and dynamically stable flight path, which is crucial for real-world UAV deployment.

4.3.4. Incorporating Obstacle Avoidance Models in Path Planning

When planning a robotic path, it is important to avoid obstacles. To make this possible, obstacle avoidance models must be added to the cost function so that the UAV can move around without running into them. The aim is to represent the real-world scenario by using a mathematical model that allows the algorithm to produce efficient and realizable paths for UAVs. Most existing works on obstacle avoidance models use no-fly penalty functions. This study integrates the repulsive-force method for obstacle avoidance with the no-fly zone penalty function.

When using only penalty function-based methods, metaheuristic algorithms can come up with solutions that are either not possible or are locally optimal. As a way to get from source to destination, the repulsive force method acts as a catalyst and tells the algorithm to make paths that naturally avoid the obstacle region. Repulsive methods have been shown to work well in robotic path planning recently [61,62].

Additionally, penalty functions for obstacle collision remain a well-established method for obstacle handling in metaheuristic algorithms. If a solution fails to avoid obstacles, resulting in constraint violations, the penalty function imposes a heavy cost on the optimization function [63].

The obstacle avoidance term penalizes paths based on the inverse distance to nearby obstacles, introducing a repulsive effect to discourage UAVs from approaching obstacles too closely. Let $d_{i,k}$ denote the distance between the i-th point on the path and the k-th obstacle, and let $\sigma$ be a weight parameter scaling the avoidance penalty. With N points in the path and n obstacles, the avoidance cost can be expressed as follows:

$$C_{\mathrm{avoid}}=\sigma \sum _{i=1}^N\sum _{k=1}^n{\displaystyle \frac{1}{d_{i,k}}}$$

(19)

On the other hand, the obstacle collision function is penalized heavily in the case of obstacle collision. Let $\rho$ represent the penalty weight applied for each intersection. This penalty function is expressed as follows:

$$C_{\mathrm{col}}=\rho \sum _{j=1}^N{I}_j$$

(20)

Here, $I_j$ is an indicator function that equals 1 if the j-th point lies within an obstacle area, and 0 otherwise. The total obstacle avoidance cost is then given by:

$$C_{\mathrm{obs}}=C_{\mathrm{avoid}}+C_{\mathrm{col}}$$

(21)

In summary, this study incorporates a comprehensive set of constraints into the objective function for UAV path planning, aiming to align the problem closely with real-world scenarios.

5. The QGWO Algorithm

The QGWO algorithm uses reinforcement learning to dynamically modify the exploration-exploitation balance of the standard GWO, enhancing its adaptability and convergence in complex search spaces. The algorithm is equipped with four key features:

• A Q-learning-based reinforcement learning approach to adaptively control the key parameter a, which affects the movement of the wolves and enhances the exploration-exploitation balance.
• Different position update rules in the exploration phase and exploitation phase.
• Replacing weaker wolves with random wolves to prevent premature convergence.
• A random jump mechanism based on the Red Fox Algorithm (RFA) [64] enables jumping randomly to a different position, which is helpful in avoiding local optima, especially in highly multimodal search spaces like UAV path planning.

In addition, we use Bayesian optimization ([65]) to adjust the parameters involved in this algorithm to achieve the best performance for various problem domains.

5.1. Adaptive Control of a Using Q-Learning

Adaptive adjustment of the parameter a allows the algorithm to search for new solutions during the initial stages and then focus on refining the search in regions that have been well explored. The integration of Q-learning [66] allows the algorithm to adaptively adjust a according to the search results to improve GWO’s performance and efficiency in complex or changing environments. Q-learning is a reinforcement learning technique in which an agent learns to take actions from the rewards it receives from the environment. The Q-learning algorithm reward function is given in Equation (22).

$$\begin{array}{c}\hfill Q(\mathrm{state},\mathrm{action})=Q(\mathrm{state},\mathrm{action})+{\alpha }_q\left(\mathrm{reward}+{\gamma }_q·\underset{a^{\prime }}{max}Q(\mathrm{next\_state},a^{\prime })-Q(\mathrm{state},\mathrm{action})\right).\end{array}$$

(22)

In the proposed QGWO, Q-learning is used to find the best changes to a by checking the search process after each round and balancing exploration and exploitation on the fly. Algorithm 1 provides the steps of the Q-learning algorithm for generating the value of a. The Q-learning-based approach makes sure that the parameter a changes as the search goes on. This makes it easier for the algorithm to find the right balance between exploration and exploitation. The proposed algorithm utilizes a reinforcement-learning strategy to dynamically update the control parameter a in GWO. The variable a lies in a range [0, 2], which is discretized in the states and has three types of actions: Increase, Maintain, and Decrease. These operations dynamically control the value they can take. An epsilon-greedy policy incorporates a balance between exploration (choosing actions randomly, irrespective of state-action value) and exploitation (choosing behaviors based on learned state-action pair values).

Algorithm 1 Q-learning for adaptive control of parameter a in GWO

1: Initialize:

Define range of a ($a_{\min },a_{\max }$), discretize states, and set actions {Increase, Maintain, Decrease}.

Set $Q(\mathrm{state},\mathrm{action})=0$, learning rate ${\alpha }_q$, discount factor ${\gamma }_q$, and exploration rate $ϵ$.

Randomly initialize wolves and evaluate fitness to identify $\alpha ,\beta ,\delta$.

2: for $t=1$ to MaxIt do

3:     Identify the current state of a.

4:     Action Selection:

With probability $ϵ$, select a random action (exploration).

Otherwise, select the action with the highest Q-value for the current state (exploitation).

5:     Update a: Adjust a based on the selected action:

If Increase: $a\leftarrow min(a+\mathrm{step},a_{\max })$.

If Maintain: a remains unchanged.

If Decrease: $a\leftarrow max(a-\mathrm{step},a_{\min })$.

6:     Update wolves’ positions using GWO equations with the updated a.

7:     Compute reward based on fitness improvement of the alpha wolf:

$\mathrm{reward}=\mathrm{old}\mathrm{fitness}-\mathrm{new}\mathrm{fitness}$.

8:     Q-table Update:

Identify the next state of a.

Update $Q(\mathrm{state},\mathrm{action})$ as Equation (22).

9:    Decay exploration rate: $ϵ\leftarrow ϵ·\mathrm{decay}\mathrm{factor}$.

10: end for

11: Output: Return the updated a for use in GWO updates.

In this case, the Q-table is used to store the state-action pairs. In every iteration, a and the wolves’ positions are updated using GWO equations. The Q-table is updated using the Q-learning update rule, with a reward obtained from the alpha wolf’s improvement in fitness. Over successive iterations, the exploration rate $ϵ$ decays, gradually shifting the algorithm’s focus from exploration to exploitation. This adaptive mechanism enhances convergence and solution quality in complex optimization landscapes.

5.2. Adaptive Position Update Strategy

Two critical features of any metaheuristic algorithm are exploration and exploitation. The proposed algorithm employs an adaptive position update strategy that dynamically adjusts the computation of new positions (${\overrightarrow{P}}_{\mathrm{new}},{\overrightarrow{Q}}_{\mathrm{new}},{\overrightarrow{R}}_{\mathrm{new}}$) based on the control parameter a and a predefined threshold $\beta$. This strategy ensures a balance between global exploration and local exploitation, enabling effective navigation through the solution space during various stages of the optimization process.

5.2.1. Exploration Phase ($a\ge \beta$)

If $a\ge \beta$, the algorithm attempts to explore. In this phase, the new position is represented as the mean of the positions of the four top wolves ($\alpha$, $\beta$, $\delta$, $\omega$), greatly increasing the area of exploration over the original GWO model. In this phase, the position update formula is given by:

$$X(t+1)={\displaystyle \frac{1}{4}}\left(X_{\alpha }\left(t\right)+X_{\beta }\left(t\right)+X_{\delta }\left(t\right)+X_{\omega }\left(t\right)\right)$$

(23)

This averaging method helps wolves converge at the centroid of the positions that are gated by four leaders. It allows the algorithm to search a larger area of the solution space by evenly distributing the impact. It works very well in the early stage, as diversity should be preserved to avoid premature convergence.

5.2.2. Exploitation Phase ($a<\beta$)

When a is below the threshold $\beta$, the algorithm concentrates on exploitation. In this phase, the new position is calculated as a linear combination of the positions of the three best wolves ($\alpha$, $\beta$, $\delta$), with the dominant wolves contributing more significantly. The update formula for the position is given by:

$${\overrightarrow{P}}_i^{\mathrm{new}}={\alpha }_1{\overrightarrow{P}}_1+{\alpha }_2{\overrightarrow{P}}_2+{\alpha }_3{\overrightarrow{P}}_3$$

(24)

where $({\alpha }_1,{\alpha }_2,{\alpha }_3)$ are assigned weights (with ${\alpha }_1>{\alpha }_2>{\alpha }_3$) so that the influence of the $\alpha$ wolf is the greatest. This leads to a narrowing of the search around promising regions by excluding the fourth wolf ($\omega$), which typically corresponds to poor solutions. This strategy is critical during later iterations as the algorithm converges towards the optimal solution.

5.3. Replacements for Non-Dominant Wolves

The QGWO has introduced some new wolves to help improve the diversity of the population by replacing the least-performing wolves. This mechanism allows the algorithm to strike a balance between exploration and exploitation, facilitating its ability to avoid premature convergence and navigate complex optimization landscapes. The formula to determine the number of non-dominant wolves to replace is given by:

$$\mathtt{num}\_\mathtt{replacements}=max\left(1,\lfloor r_1·n_{\mathrm{Wol}}\rfloor \right)$$

(25)

where $r_1$ is a randomly generated number in the interval $[0,1]$, and $n_{\mathrm{Wol}}$ is the population size. In every iteration, this guarantees that at least one wolf will be replaced because of the use of $max(1,\lfloor r_1·n_{\mathrm{Wol}}\rfloor )$.

During replacement, new wolves (denoted as rep_wolf) are created using the function initwolf, and they are randomly located within the problem bounds. These new wolves fill the role of those that are not performing well in the population (i.e., the ones in the bottom positions). This process both culls the poor performers and injects new individuals into the optimization process.

5.4. Random Jumping Mechanism

The proposed algorithm also enables the wolves to occasionally perform large random jumps to enhance exploration behavior. This mechanism allows the algorithm to avoid local minima, preserve population diversity, and explore new regions of the solution space.

Each wolf in the QGWO algorithm has a small chance, controlled by $r_2$ (e.g., $0.05$), of executing a random jump, as determined by a stochastic condition. Specifically, if a randomly generated value, rnd, satisfies

$$-r_2<\mathrm{rnd}<r_2,$$

then the wolf jumps to a new position. This probability allows for controlled exploration without excessive randomness.

When a jump occurs, the wolf’s new position, represented by $(p,q,r)$, is generated uniformly within the defined boundaries of the search space. The fitness of this new position is evaluated using the objective function $C_m(p,q,r)$. A greedy selection mechanism ensures that the wolf’s position is updated only if the new position improves its fitness (i.e., achieves a lower value in minimization problems). This strategy preserves solution quality while enhancing the algorithm’s exploration capability.

The complete QGWO algorithm steps are briefly presented in Algorithm 2.

Algorithm 2 The QGWO Algorithm

1: Initialize:

Define Q-learning parameters: ${\alpha }_q$,${\gamma }_q$, ${ϵ}_q$

Define search space boundaries and initialize wolves with random positions.

Set $a=a_{\max }$ and discretize a into n states.

Initialize Q-table $Q(\mathrm{state},\mathrm{action})=0$.

2: for $t=1$ to MaxIt do

3:     Sort wolves by fitness and identify $\alpha ,\beta ,\delta ,\omega$.

4:     Calculate the current state of a.

5:     Select an action using the $ϵ$-greedy policy.

6:     Update a based on (Algorithm 1)

7:     Save the current alpha wolf’s fitness as $\mathrm{old\_fitness}$.

8:     for each wolf i do

9:      Calculate $P_{\mathrm{new}},Q_{\mathrm{new}},R_{\mathrm{new}}$ based on:

10:      if $a\ge \beta$ then $$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{P}_{\mathrm{new}}={\displaystyle \frac{P_1+P_2+P_3+P_4}{4}},\mathrm{and}\mathrm{similarly}\mathrm{for}Q,R.$$

11:      else $$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{P}_{\mathrm{new}}={\alpha }_1{P}_1+{\alpha }_2{P}_2+{\alpha }_3{P}_3,\mathrm{and}\mathrm{similarly}\mathrm{for}Q,R.$$

12:      end if

13:      Perform boundary adjustment to keep the wolf within limits.

14:      Random Jump Feature: With probability $r_2$

15:      Compute new fitness and update the wolf’s position using greedy selection.

16:     end for

17:     Sort wolves and update $\alpha ,\beta ,\delta ,\omega$.

18:     Replace non-dominant wolves:

Generate random wolves to replace the weakest $\lfloor r_1·n_{\mathrm{Wol}}\rfloor$ wolves.

19:     Compute reward for Q-table

20:     Update Q-table

21:     Decay $ϵ$

22: end for

23: Output: Return the alpha wolf’s position as the best solution.

5.5. Convergence Analysis of QGWO

The QGWO algorithm, which learns from reinforcement learning, adaptively achieves a dynamic balance between exploration and exploitation to guarantee convergence. The parameter a, controlled through Q-learning, drives the trade-off between two different position update strategies used in the algorithm. In the event of exploration ($a\ge \beta$), the averaging mechanism encourages extensive exploration of the solution space, thereby increasing diversity. Conversely, when $a<\beta$, weighted contributions from leading wolves focus the search on optimal solutions. With this structured transition, characterized by a decay mechanism for a, the algorithm converges to a global optimum.

The replacement strategy and random jump mechanism are also crucial for preventing stagnation by introducing randomness into the population. The random jump mechanism enables the algorithm to break free from local optima and ensures a strong exploratory capability, which is particularly beneficial in highly multimodal problems such as UAV path planning.

Convergence Criteria

The convergence of QGWO can be mathematically expressed as follows:

$$\underset{t\to \infty }{lim}f({\overrightarrow{P}}_i\left(t\right))=f({\overrightarrow{P}}_{\mathrm{opt}}),$$

(26)

where $f\left({\overrightarrow{P}}_{\mathrm{opt}}\right)$ represents the global optimum of the objective function. The following conditions ensure convergence:

• Fitness Improvement: The Q-learning reward mechanism favors actions that enhance the fitness value.
• Exploitation Refinement: Weighted contributions (${\alpha }_1,{\alpha }_2,{\alpha }_3$) ensure precise convergence towards optimal solutions.
• Population Diversity: Strategies like random jumps and replacement of non-dominant wolves prevent premature convergence by maintaining a diverse population.

The algorithm’s convergence is further supported by the decaying exploration rate $ϵ$ and learning rate ${\alpha }_q$, which gradually reduce randomness over iterations and favor exploitation. The reinforcement learning framework dynamically optimizes the evolution of a, ensuring a flexible and robust exploration-exploitation trade-off across various optimization scenarios.

6. Result and Discussion

6.1. Simulation Setup and Benchmark Comparison

The simulations were conducted on a PC with a Core i7 processor and 16 GB RAM, using Python 3.7 and the PyCharm IDE. To evaluate the QGWO algorithm, four recent GWO variants were selected for comparison: adaptive arithmetic GWO (AAGWO) [23], beetle antenna GWO (BGWO) [46], random walk GWO (RWGWO) [35], and reinforcement learning GWO (RLGWO) [30]. This selection was based on their significant impact on GWO aspects like exploration, exploitation, and adaptability.

AAGWO introduces dynamic arithmetic mechanisms for enhanced performance of GWO. BGWO introduces the beetle antenna concept in GWO, suited for discrete tasks. RWGWO integrates random walk behavior to escape the local optima, and RLGWO introduces reinforcement learning for parameter control, closely aligning with our QGWO’s approach. These variants offer a solid foundation for assessing QGWO’s performance, particularly in complex situations such as UAV path planning.

The parameters introduced in the QGWO algorithm are determined using Bayesian Optimization (BO) [67]. The newly introduced parameters are threshold ($\beta$), position update weights (${\alpha }_1,{\alpha }_2,{\alpha }_3$), diversity replacement rate ($r_1$), and random jump probability ($r_2$). BO balances the algorithm in the parameter space, reducing function evaluations and ensuring robust parameter tuning. This systematic approach enhances QGWO’s adaptability and effectiveness across complex optimization landscapes. The final parameter values set in QGWO are listed in

Table 1. Bayesian Optimization fine-tuned parameter settings for the QGWO algorithm.

Parameter	Type	Value
Learning Rate (${\alpha }_q$)	Q-Learning	0.7
Discount Factor (${\gamma }_q$)	Q-Learning	0.9
Exploration Rate (${ϵ}_q$)	Q-Learning	0.9 (initial)
Threshold ($\beta$)	GWO (Bayesian Optimized)	0.5
Position Weights (${\alpha }_1,{\alpha }_2,{\alpha }_3$)	GWO (Bayesian Optimized)	0.37, 0.49, 0.28
Diversity Replacement ($r_1$)	GWO (Bayesian Optimized)	0.30
Random Jump Probability ($r_2$)	GWO (Bayesian Optimized)	0.01
State Discretization	Q-Learning	500 states
Number of Wolves ($n_{\mathrm{Wol}}$)	GWO	200
Max Iterations (MaxIt)	Algorithm	500

.

6.2. Simulation Outcome

The environment in which the simulation is performed consists of a search space with high dimensionality ($1500\times 1600\times 600$). To make the problem more complicated, we randomly place between 40 and 100 cylindrical obstacles in each run. Moreover, the positions, radii, and heights of the obstacles are randomized for every simulation, so the algorithm faces a new set of challenges on each run.

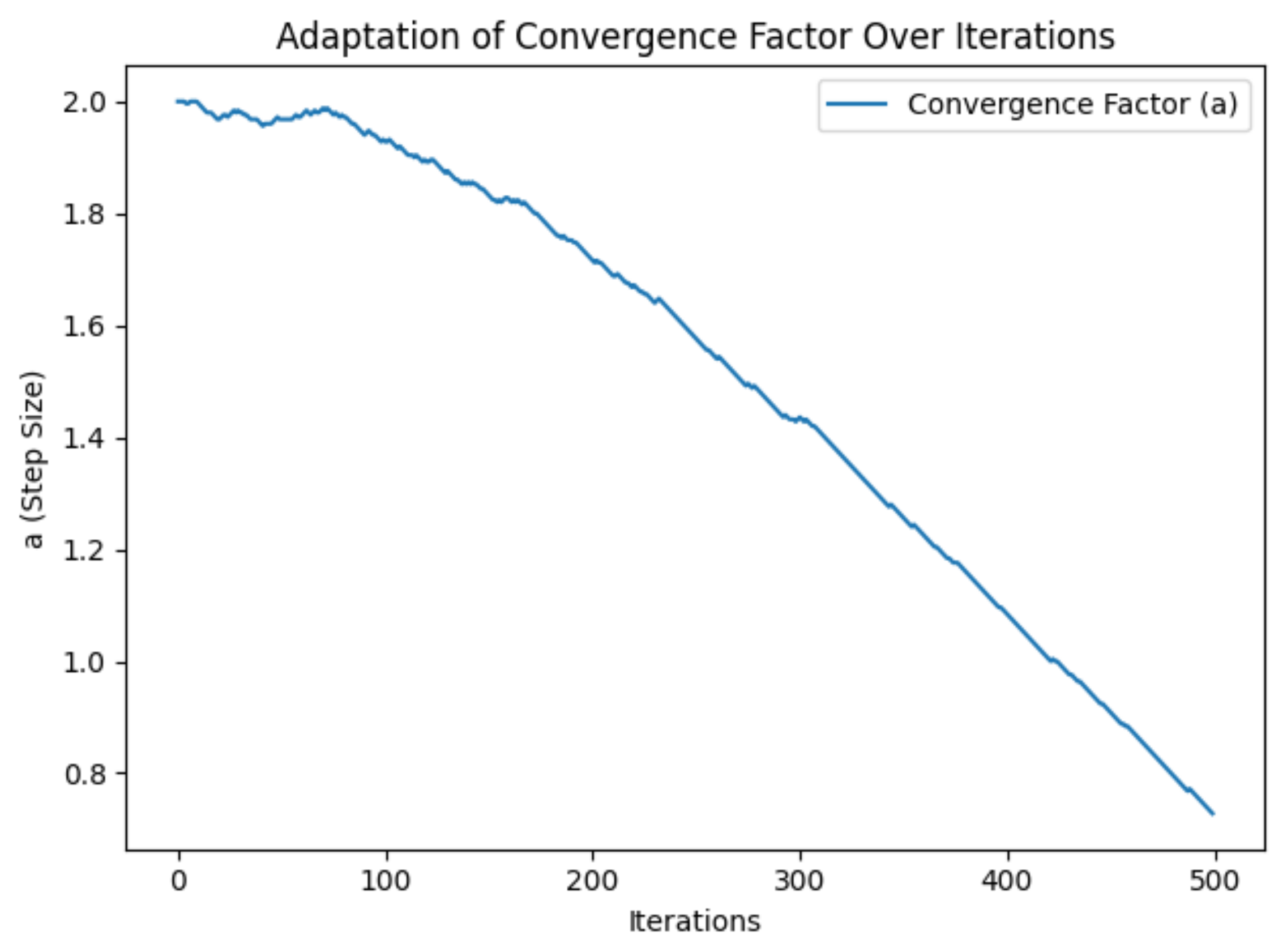
Figure 4, Figure 5, Figure 6 and Figure 7 show the simulation results, which demonstrate the strong performance of the Q-learning-based QGWO on complex optimization problems. As depicted in Figure 4, the dynamic adjustment mechanism for the convergence factor a enables the algorithm to transition smoothly from the exploration to the exploitation phase, allowing a to decrease gradually as iterations increase. 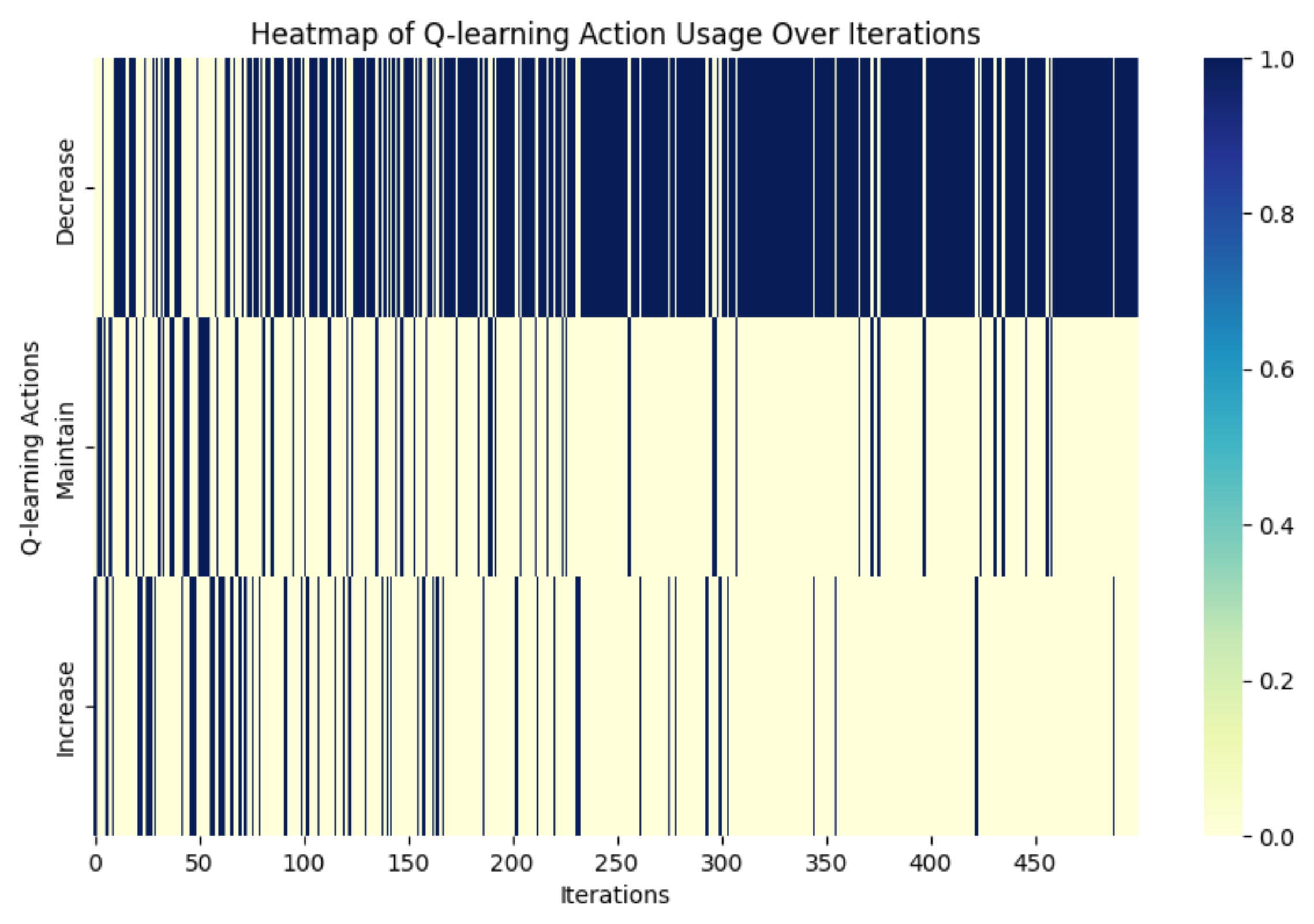Figure 5 provides insight into the exploration of the state actions “Increase”, “Maintain”, and “Decrease” at the initial state, and shows how fewer “Decrease” actions were reinforced in the final Q-learning state for improved solution refinement. 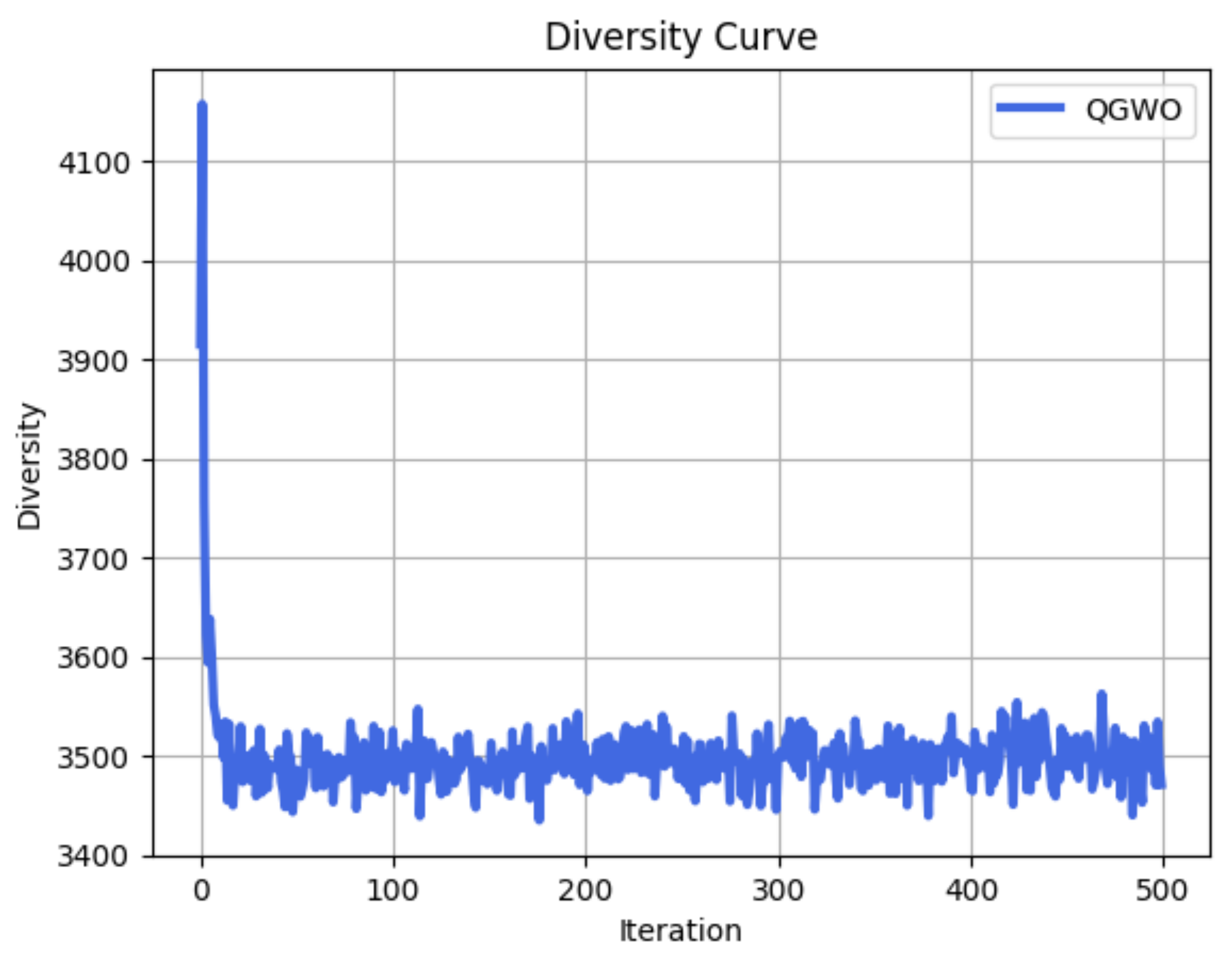Figure 6 illustrates the convergence curve by showing the algorithm’s cost dropping sharply in the first 50 iterations and then steadily decreasing, indicating that the algorithm efficiently converges to optimal solutions. Additionally, the diversity curve in Figure 7 clearly shows a rapid decay in the initial stage, followed by stabilization at a moderate level of diversity. This suggests that the QGWO can reduce diversity without risking premature convergence. The diversity curve is generated using the formula proposed in [68]. The visual results further illustrate the strengths of the proposed algorithm, including stability, adaptability, and superior performance in balancing exploration and exploitation, strongly suggesting that the proposed approach is well suited for multi-constraint UAV path planning and similar optimization tasks.

6.3. Numerical Analysis

Numerical experiments using the CEC 2022 benchmark functions (opfunu library [69]) were carried out to evaluate the performance of the proposed QGWO algorithm. These benchmark functions are commonly used in optimization studies that cover a wide range of challenges, such as unimodal, multimodal, and composition fitness landscapes, effectively simulating real-world problems such as UAV path planning.

The metrics that are used to evaluate the performance of the algorithm’s accuracy, robustness, and adaptability are the best value, average value, and standard deviation. The functions were grouped based on their domain on different optimization measures: F1–F3 measured exploitation in unimodal terrains; F4–F7 for exploration in multimodal landscapes; and F8–F10 represented more difficult, dynamic spaces. The numerical results in detail are shown in

Table 2. Performance analysis of various algorithms on CEC 2022 benchmark functions.

Function	Metric	GWO	AGGWO	BGWO	RWGWO	RLGWO	QGWO
F1	Best	3191.28	546.06	1622.22	1228.06	82,563.25	408.37
	Average	3191.28	2794.56	1622.22	1633.31	98,103.01	439.36
	STD	$4.55\times {10}^{-13}$	1428.65	$2.27\times {10}^{-13}$	401.23	8089.18	30.70
F2	Best	604.66	513.09	595.64	431.49	7409.92	421.49
	Average	604.66	572.91	595.64	522.73	12,228.92	536.71
	STD	0	57.01	$1.14\times {10}^{-13}$	51.99	2911.53	55.95
F3	Best	600.07	600.02	600.09	600.01	604.02	600.00
	Average	600.07	600.09	600.09	600.03	604.36	600.00
	STD	$1.14\times {10}^{-13}$	0.07	$1.14\times {10}^{-13}$	0.02	0.29	0.00
F4	Best	914.29	899.96	906.56	868.18	1349.19	902.03
	Average	914.29	946.63	906.56	910.96	1433.39	947.31
	STD	0	41.56	$1.14\times {10}^{-13}$	31.03	59.16	32.57
F5	Best	906.80	906.06	904.63	902.29	930.74	901.61
	Average	906.80	906.44	904.63	904.29	943.82	903.13
	STD	$1.14\times {10}^{-13}$	0.33	$1.14\times {10}^{-13}$	1.49	5.38	1.19
F6	Best	444,114.48	220,819.89	928,864.90	115,046.06	$5.44\times {10}^9$	63,546.22
	Average	444,114.48	1,732,777.92	928,864.90	602,610.10	$1.29\times {10}^{10}$	148,817.06
	STD	$5.82\times {10}^{-11}$	3,896,181.01	0	496,178.94	$3.52\times {10}^9$	61,186.04
F7	Best	2452.25	2202.05	2079.80	2479.86	15,578.99	2096.74
	Average	2452.25	2568.54	2079.80	2644.04	21,661.97	2214.70
	STD	$4.55\times {10}^{-13}$	226.06	0	144.06	4651.48	97.83
F8	Best	4987.22	2676.13	4102.48	2702.46	$1.12\times {10}^{13}$	2896.03
	Average	4987.22	3395.07	4102.48	3863.28	$3.96\times {10}^{15}$	3602.34
	STD	$9.09\times {10}^{-13}$	326.96	$9.09\times {10}^{-13}$	1283.17	$6.94\times {10}^{15}$	579.70
F9	Best	2697.76	2709.12	2648.81	2640.97	6142.76	2566.68
	Average	2697.76	2754.37	2648.81	2682.98	9003.42	2622.84
	STD	$4.55\times {10}^{-13}$	43.41	0	36.84	1521.63	66.30
F10	Best	5362.32	2869.99	4911.08	4041.53	7050.23	2817.44
	Average	5362.32	4495.92	4911.08	5037.42	7794.37	4022.68
	STD	$9.09\times {10}^{-13}$	982.10	0	728.83	477.63	1124.99

.

In the case of unimodal functions (F1–F3), which focus more on exploitation and accuracy, QGWO consistently outperformed the competition. In F1, it produced the best solution (408.37) with the least mean score (439.36), demonstrating its powerful capability on exploitation. For F2, QGWO had the best solution (421.49) and competitive average performance compared to the others, although the variability was low. Even for F3, where all algorithms performed at similar levels, the performance of QGWO was observed to be significantly higher, having a marginal STD (STD = 0.0007).

For multimodal functions (F4–F7), which are used to measure exploration and the ability to escape from local optima, QGWO continues to perform well. It always outperformed on the best solution, like F4 (best solution = 902.03) or F5 (best solution = 901.61), with low variability. In the cases of functions F6 and F7, QGWO exhibited its remarkable flexibility and stability, achieving much better fitness values and STDs than the other algorithms, thereby confirming its prowess in tackling different multimodal terrains.

In particular, the analysis of composition functions (F8–F10), which simulate complex real-world challenges, lastly emphasized the advantages of QGWO. It outperformed other algorithms in terms of a few problems (e.g., in F9: best solution = 2566.68; in F10: best solution = 2817.44) and is still competitive on various landscapes. Conversely, other competitive algorithms, especially RLGWO, performed poorly and with high variability, which demonstrates their incapacity to manipulate such complicated situations.

Therefore, the results confirm QGWO performance on all function types is outstanding (exploitation and exploration) without jeopardizing stability and flexibility. With low variability and the best solutions, it outperformed previous GWO variants and offers a reliable algorithm for solving complex optimization problems like UAV path planning.

6.4. Comparative Analysis

The proposed algorithm is evaluated in a UAV path planning simulation environment that mimics to some degree real-world conditions. As shown in Figure 8, each GWO-based algorithm consistently decreases its best cost throughout the iterations. Specifically, QGWO experiences a sharp decrease in cost over the first 50 iterations and remains below the other variants at the conclusion of the search. As opposed to this, RLGWO displays sudden increases in costs, which suggest that it sometimes explores low-performing sections of the search space and needs to backtrack to fetch back lower costs. The other methods BGWO, RWGWO, AGGWO, and the original GWO all fall behind, clustering at intermediate levels of performance, achieving reductions in cost but not as sharply as QGWO. This relative stability of QGWO indicates that adding Q-learning to GWO achieves a more balanced and consistent search and thus keeps the value of the overall cost of the algorithm from having wide fluctuations.

Figure 9 shows how each method explores the search space using different trajectories. Specifically, QGWO presents medium and stable diversity, which suggests it has a consistent balance between searching for new territories and exploiting the space of already discovered values. In comparison, RLGWO shows some instances of sudden spikes in diversity, causing abrupt and massive scale exploration, resulting in sharp fluctuations in cost. In contrast, BGWO, RWGWO, and AGGWO exhibit closer ranking diversity curves, indicating more conservatively controlled searching at the sacrifice of exploration adaptability. In general, a relatively wide but sufficiently stable diversity, such as that of QGWO, aids in preventing premature convergence and facilitates the convergence process toward better solutions.

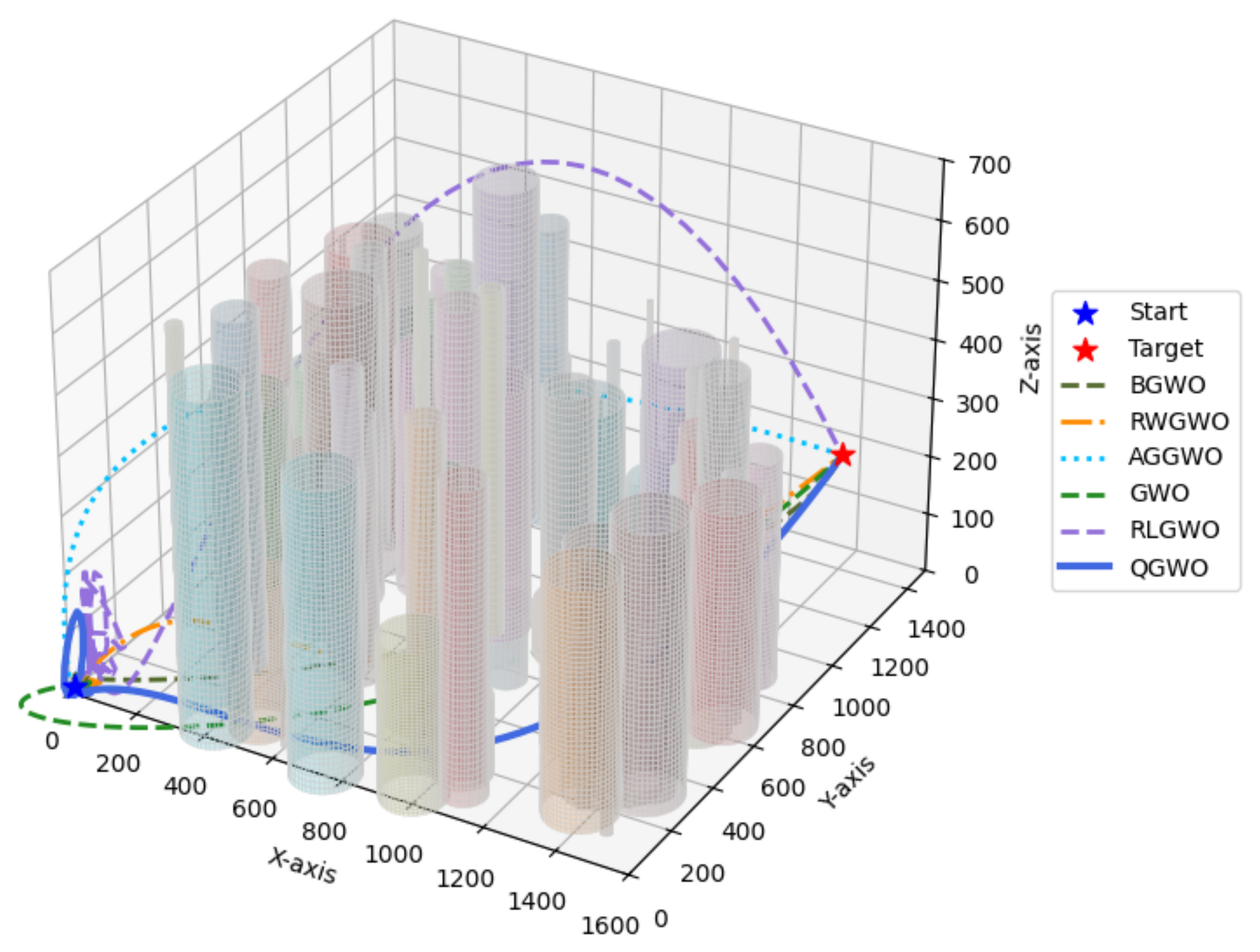
In the 3D example illustrated in Figure 10, we show how the different GWO-based methods move from the start (blue star) to target (red star) points while avoiding cylindrical obstacles of different sizes and heights. In particular, we observe that QGWO (solid blue) and GWO (green dashed line) exhibit relatively smooth arcs around dense obstacle clumps, while RLGWO (purple dashed line) results show frequent erratic maneuvers. While BGWO (olive dashed), RWGWO (orange dashed), and AGGWO (light blue dotted) also avoid collisions, their routes are for the most part only marginally less direct when compared with QGWO and GWO. Overall, all methods worked well, and the obstacles have been cleared, but QGWO outperforms others, showing a trade-off between detours versus safe clearance as well as the minimum deviation from the original course.

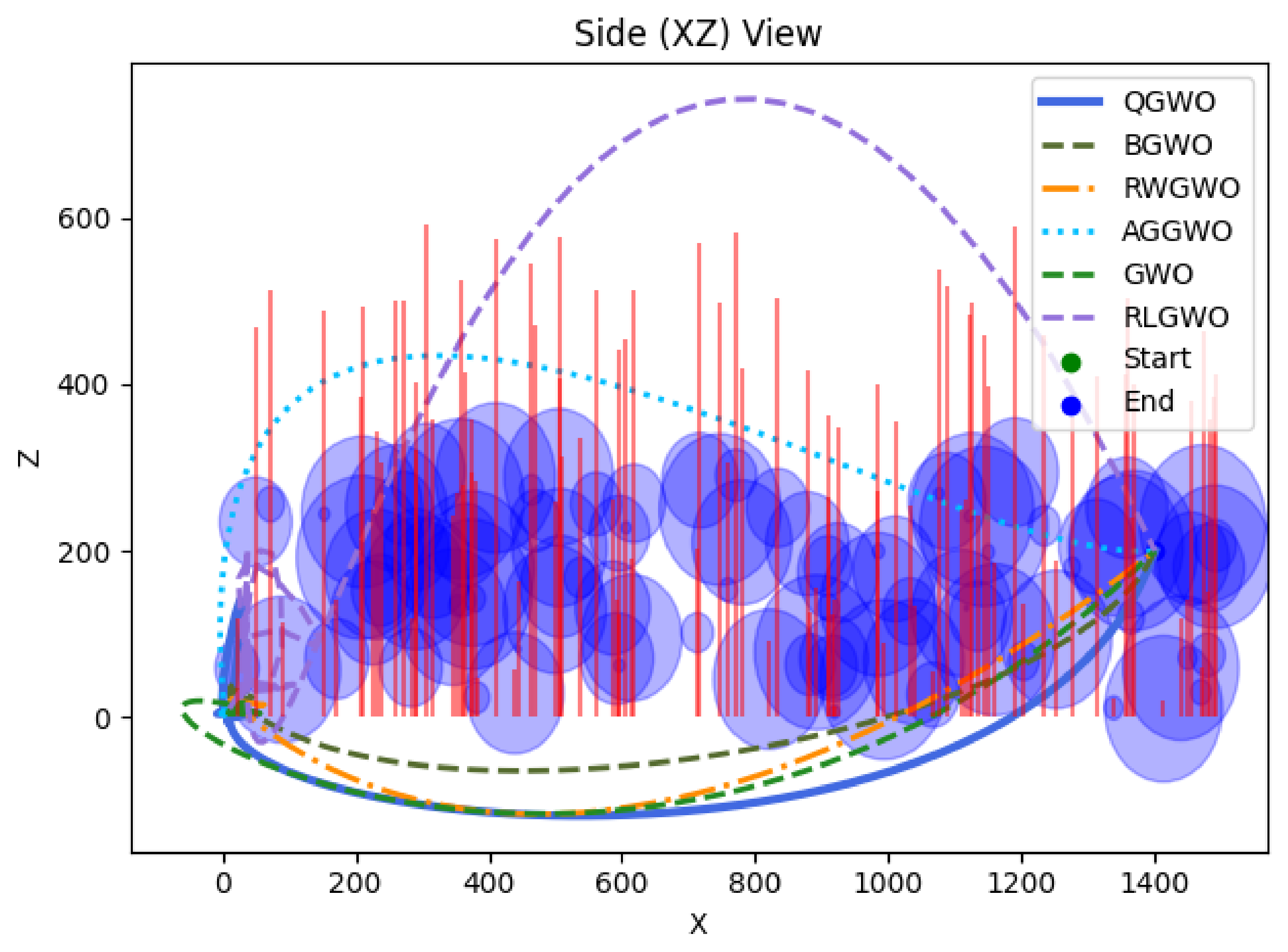
Figure 11 and Figure 12 display top-down (XY) and side (XZ) perspectives of each method’s path amid cylindrical obstacles (shown in blue). In the XY plane, QGWO, RWGWO, and GWO traverse smoothly around clusters, whereas RLGWO sometimes makes sharper detours, as highlighted in the XZ view. The tall red lines in the side view denote obstacle heights, illustrating that QGWO and BGWO maintain sufficient altitude. In contrast, RLGWO occasionally dips far below the zero plane, suggesting riskier maneuvers. Overall, these figures indicate that QGWO combines a feasible flight path with effective obstacle avoidance, resulting in a more efficient trajectory.

Based on the above observations, QGWO is evaluated on five test cases with different parameters (

Table 3. Simulation parameters for different cases.

Case	Maximum Iterations	Number of Wolves	Path Waypoints	Number of Obstacles
1	500	200	40	70
2	500	300	40	70
3	500	200	60	100
4	700	300	70	100
5	800	300	80	120

) in order to demonstrate its robustness and reliability. Each case became more complex, adding more iterations, wolves, waypoints, and finally, also including obstacles to closely represent real-world optimization problems.

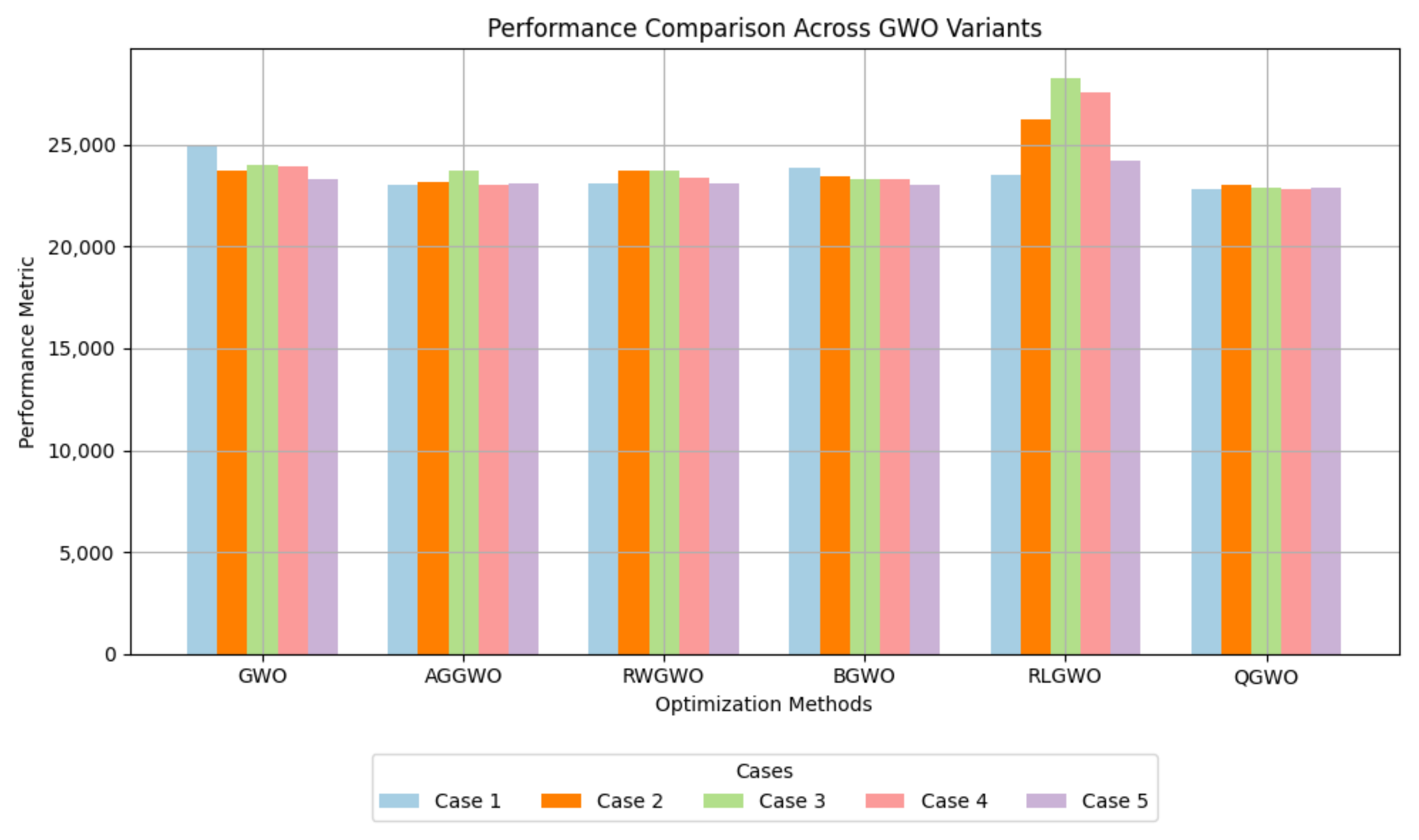
The performance comparison of QGWO against the other GWO variants is depicted in Figure 13, where it is observed that QGWO offered better path optimization than AGGWO, RWGWO, BGWO, and RLGWO. In simpler environments, such as Case 2, RLGWO delivered competitive results. However, as complexity increased, RLGWO struggled to maintain stability and efficiency. On the other hand, QGWO had steady adaptation and scalability, providing consistent and reliable performance over all the tested cases. The excellent performance of QGWO is due to the adaptive Q-learning-guided convergence factors and dynamic replacement strategy of non-dominant wolves, ensuring exploration, exploitation, and population diversity.

The AUC comparison between GWO and QGWO within various test cases is shown in Figure 14. As path planning is a minimization problem, a lower AUC means a more optimized trajectory that costs less in the path. This shows how QGWO consistently obtained a smaller AUC than GWO, which indicates that QGWO has a better ability to minimize the overall path cost. In the early test cases (from Case 1 to Case 3), QGWO shows small fluctuations because it uses the exploration mechanism of Q-learning. In contrast, as the optimization evolves (Case 4 to Case 5), QGWO attains stability and outperforms GWO, emitting a termination with a lower AUC in all the instances, thereby validating its strength in detecting the optimal paths.

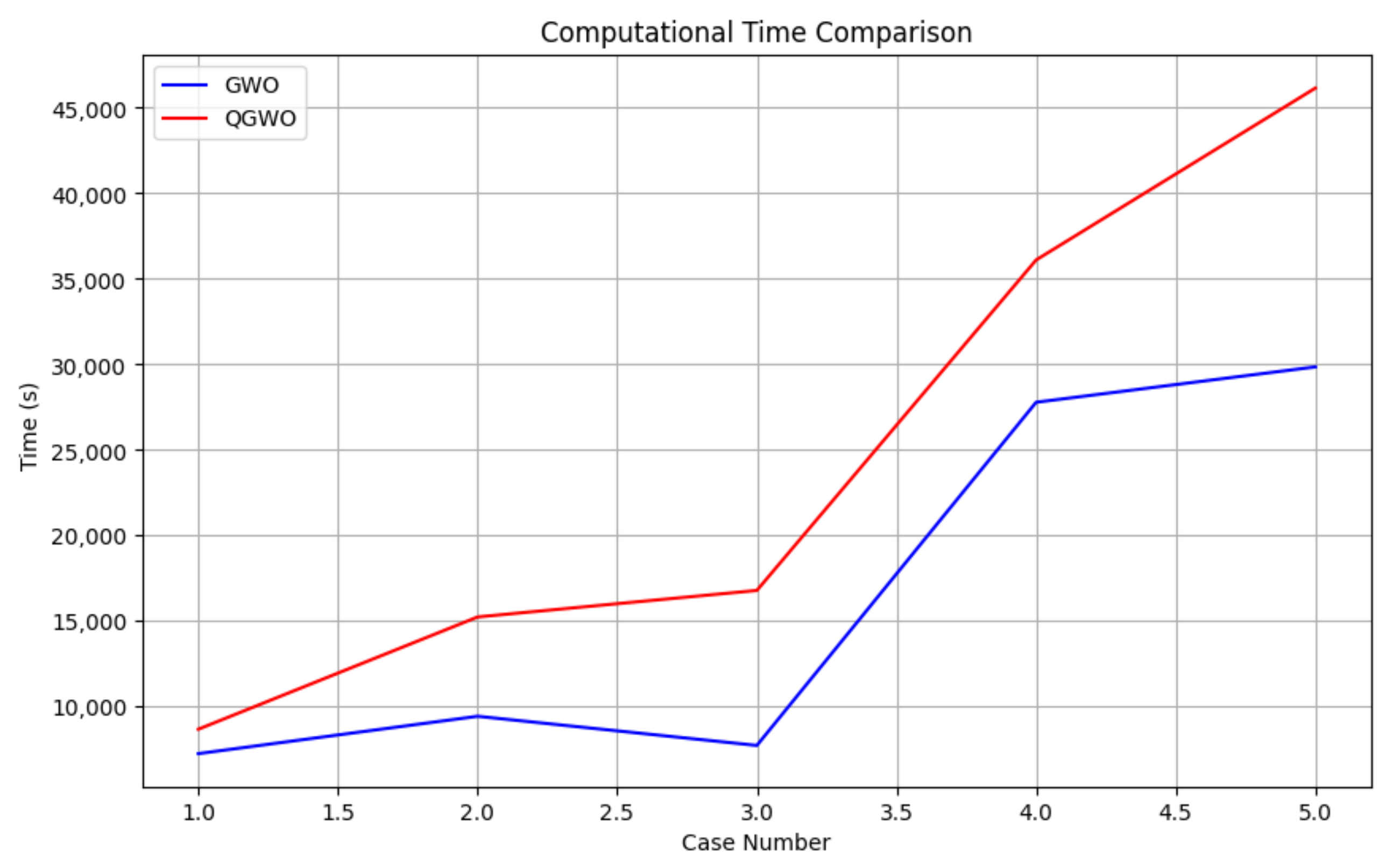
The comparison of computational time between QGWO and GWO is shown in Figure 15. The results show that QGWO requires higher execution time due to the integration of Q-learning for the adaptive parameter. While this increases convergence accuracy and improves path efficiency, it results in higher computational overhead. Future work will focus on optimizing QGWO’s computational efficiency to enhance its suitability for real-time UAV path planning.

Despite the increased computational complexity involved with QGWO, the enhanced trade-off between exploration and exploitation led to generating shorter and more efficient paths. This benefit is especially identified in intricate path finding conditions, and it establishes the potential of QGWO for sensible UAV usage requiring detailed as well as flexible trajectory preparation.

7. Future Research Work

Although the suggested model QGWO improves the path planning capability of UAVs, some limitations exist, leaving room for future research.

We first recognize that the existing obstacle modeling only considers cylinders as objects, while real-world urban or low-altitude environments tend to contain complex geometries. Extending the work to model obstacles with adaptive obstacle models to accommodate irregularly shaped obstacles like skyscrapers and rough terrains will improve the path feasibility and safety performance of the generated paths against dynamically moving barriers.

Second, this entire work is based on simulations and is not realistic. Although the simulation-based verification corroborates the potential of QGWO, on-field and real-world UAV experiments are necessary to assess uncertainties in the sensors, dynamics of the surroundings, and real-life computational restrictions.

Moreover, QGWO has a more complex algorithm structure to incorporate Q-learning for the dynamic adjustment of parameters, leading to greater computational cost. To further improve the efficiency of the method without sacrificing optimization accuracy, future work should be supplemented with computational optimizations to support real-time UAV path planning, including parallel processing, hardware acceleration, and lightweight deep reinforcement learning methods.

Finally, diversity retention improvements were observed via random jumps and non-dominant wolf replacement mechanisms under QGWO; the extent to which diversity increases over extended iterations requires further investigation. For a holistic perspective on the long-run stability and convergence, comparative studies with other general adaptive metaheuristics can also be carried out.

These adjustments would advance QGWO’s potential for practical implementation in autonomous UAV navigation and multi-agent optimization issues by making it more efficient, scalable, and adaptable.

8. Conclusions

Adaptive convergence factors, segmented position update strategies, and diversity enhancement mechanisms allow the proposed QGWO to outperform existing algorithms in terms of convergence speed, path efficiency, and robustness in obstacle avoidance. Extensive simulation experiments show that QGWO consistently excels over all state-of-the-art GWO variants on multiple benchmark cases, with both accuracy and efficiency. The proposed algorithm exhibits minimal path costs as well as displaying enhanced diversity retention among the solutions, which solidifies its ability to tackle complex high-dimensional, multi-constraint problems such as UAV navigation.

Though QGWO performed very well, it demands higher computational effort, which presents a trade-off between solution accuracy and real-time feasibility. Therefore, future studies should emphasize improving computational efficiency and extending QGWO scenarios to real UAV applications.

To briefly summarize, QGWO provides a practical and scalable optimization framework that can be further hybridized via advanced learning-based methods that can extend its applicability to several UAV path planning or complex optimization domains. This adaptability makes it a suitable candidate for future autonomous navigation systems in this particular context.