NOMA-Based Rate Optimization for Multi-UAV-Assisted D2D Communication Networks
Abstract
1. Introduction
1.1. Related Work
1.2. Motivation and Contribution
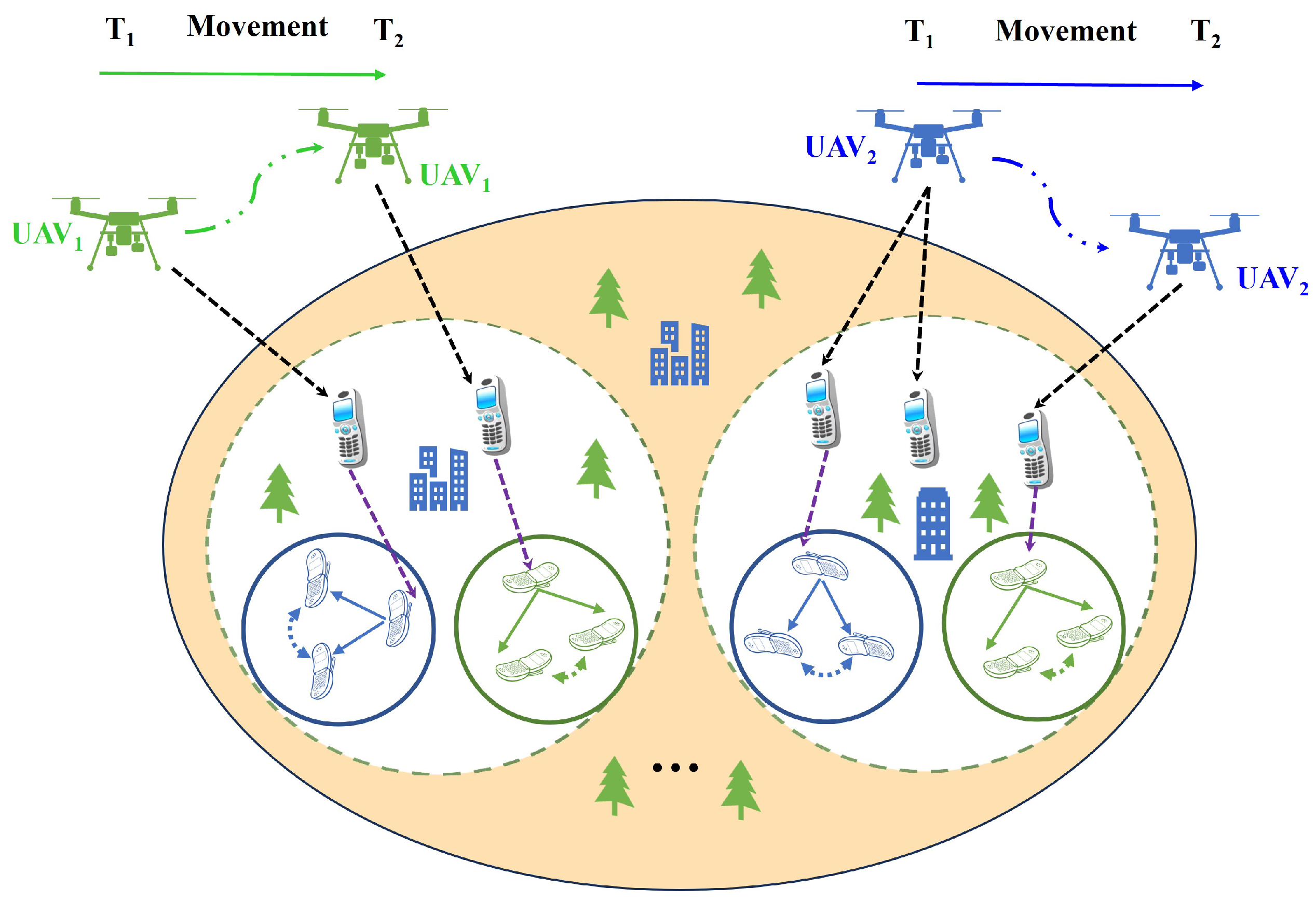
2. System Model
2.1. Network Model
2.2. Propagation Model
2.3. Communication Model
3. Problem Formation
4. Problem Solution
4.1. Subchannel Assignment Based on Dynamic Hypergraph Coloring
4.1.1. Construct the Dynamic Hypergraph
4.1.2. Dynamic Hypergraph Coloring
| Algorithm 1 Subchannel assignment based on dynamic hypergraph coloring. |
|
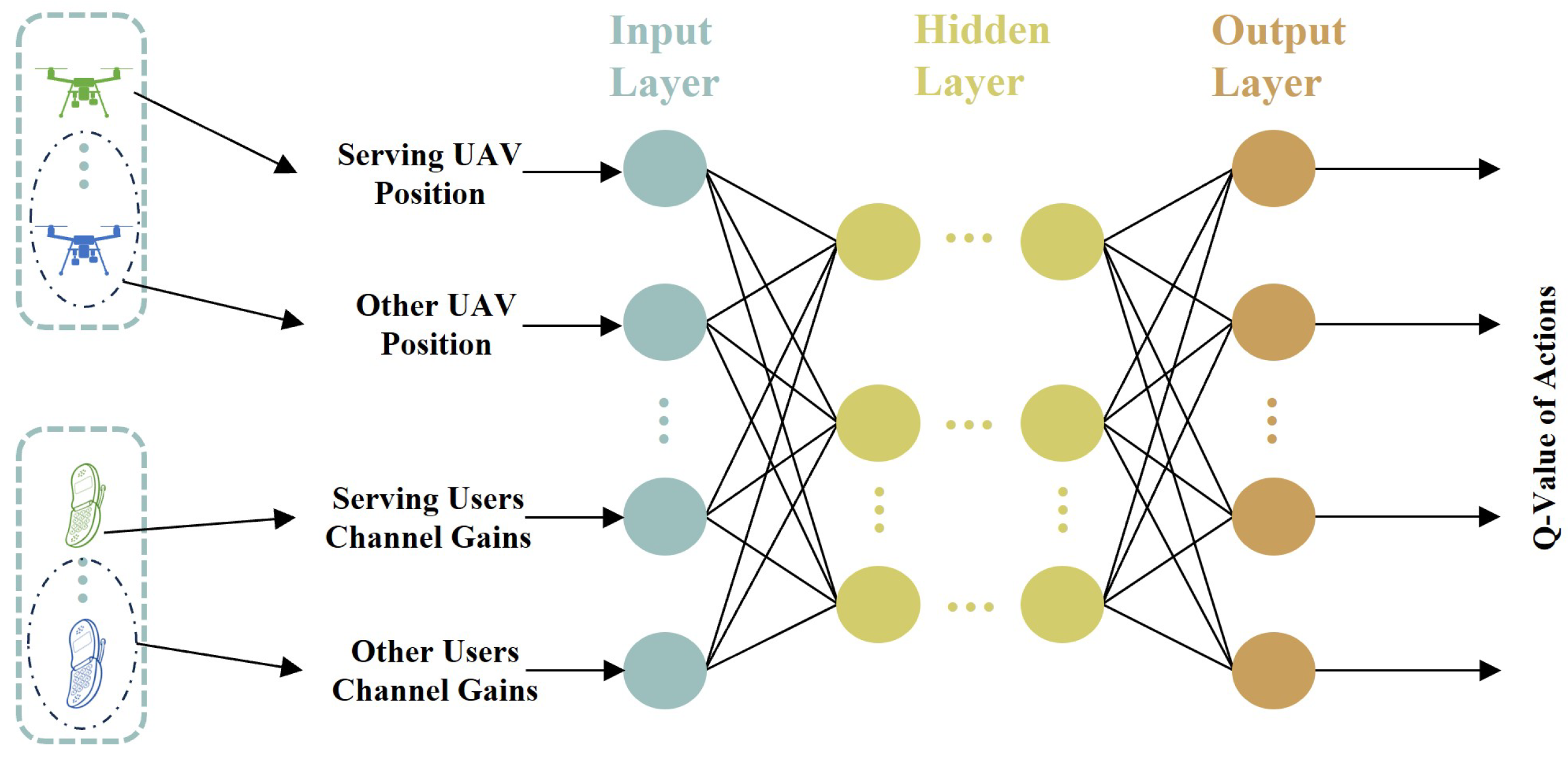
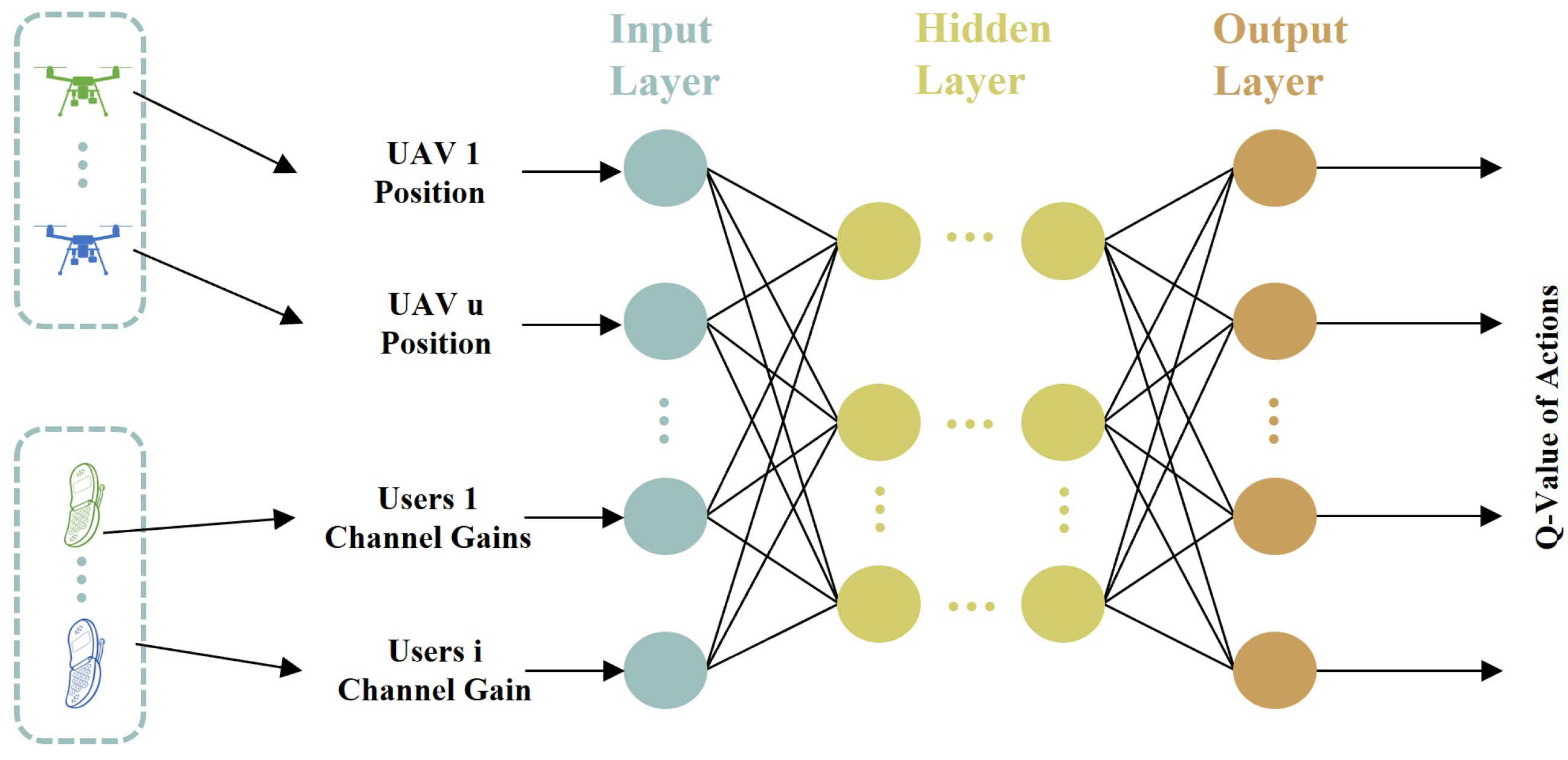
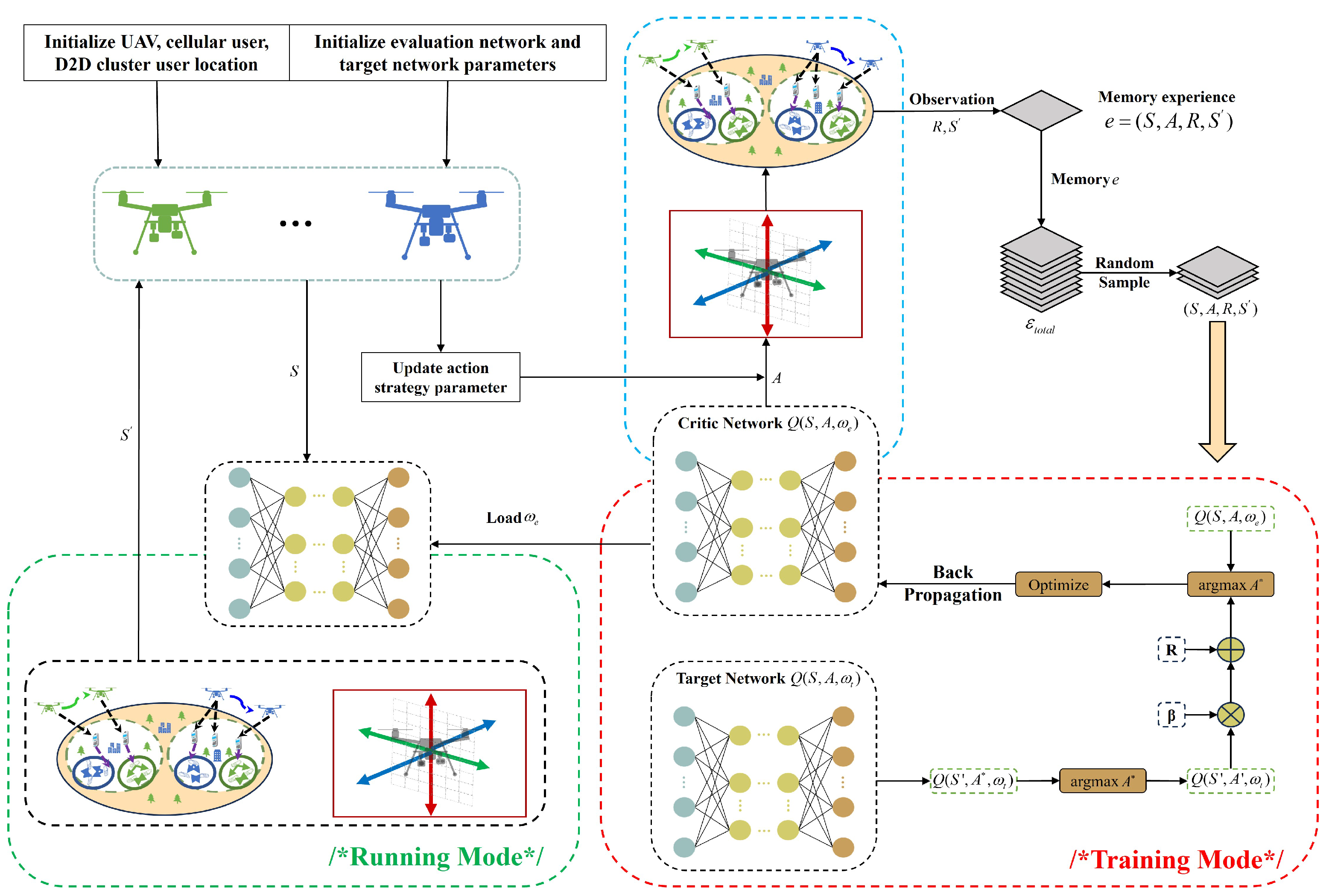
4.2. MDQN-Based Trajectory Design and Power Control
4.2.1. MDP Model
4.2.2. MDQN Algorithm
| Algorithm 2 MDQN-based trajectory design and power control algorithm. |
|
4.3. Joint Algorithm Design
| Algorithm 3 Joint dynamic hypergraph Multi-Agent Deep Q Network algorithm. |
|
5. Simulation Experiment and Result Analysis
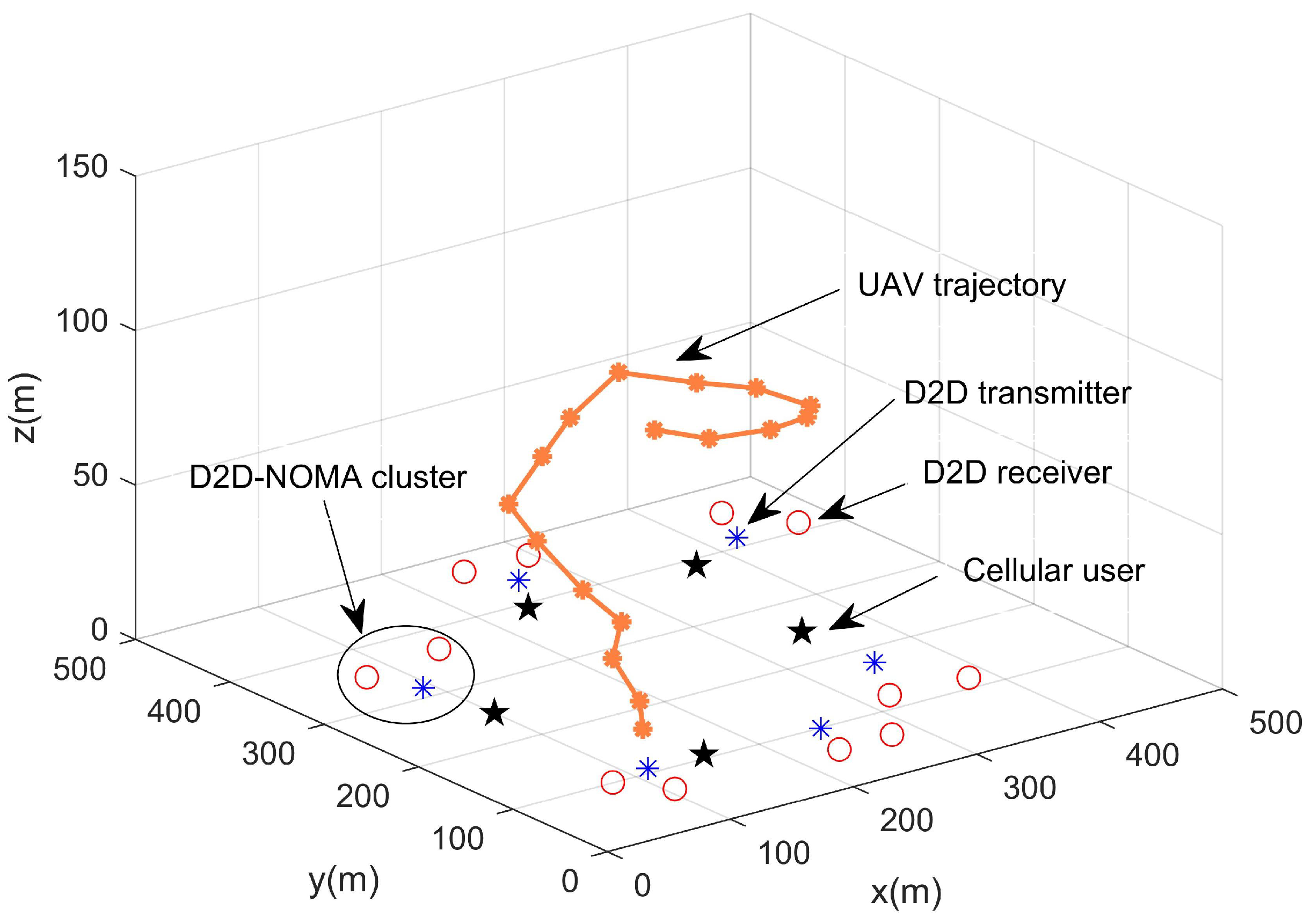
5.1. Simulation Experiment Parameter Setting
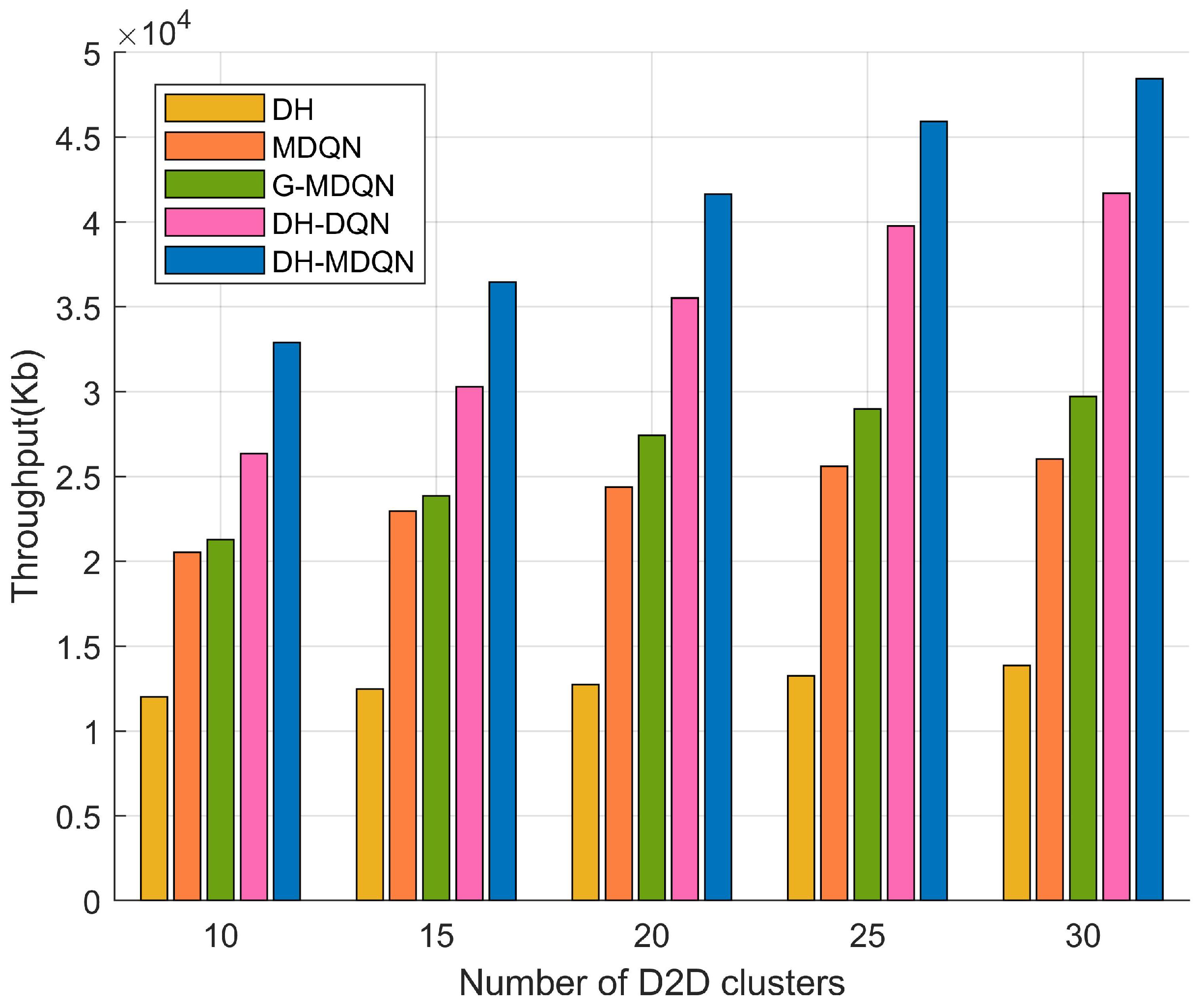
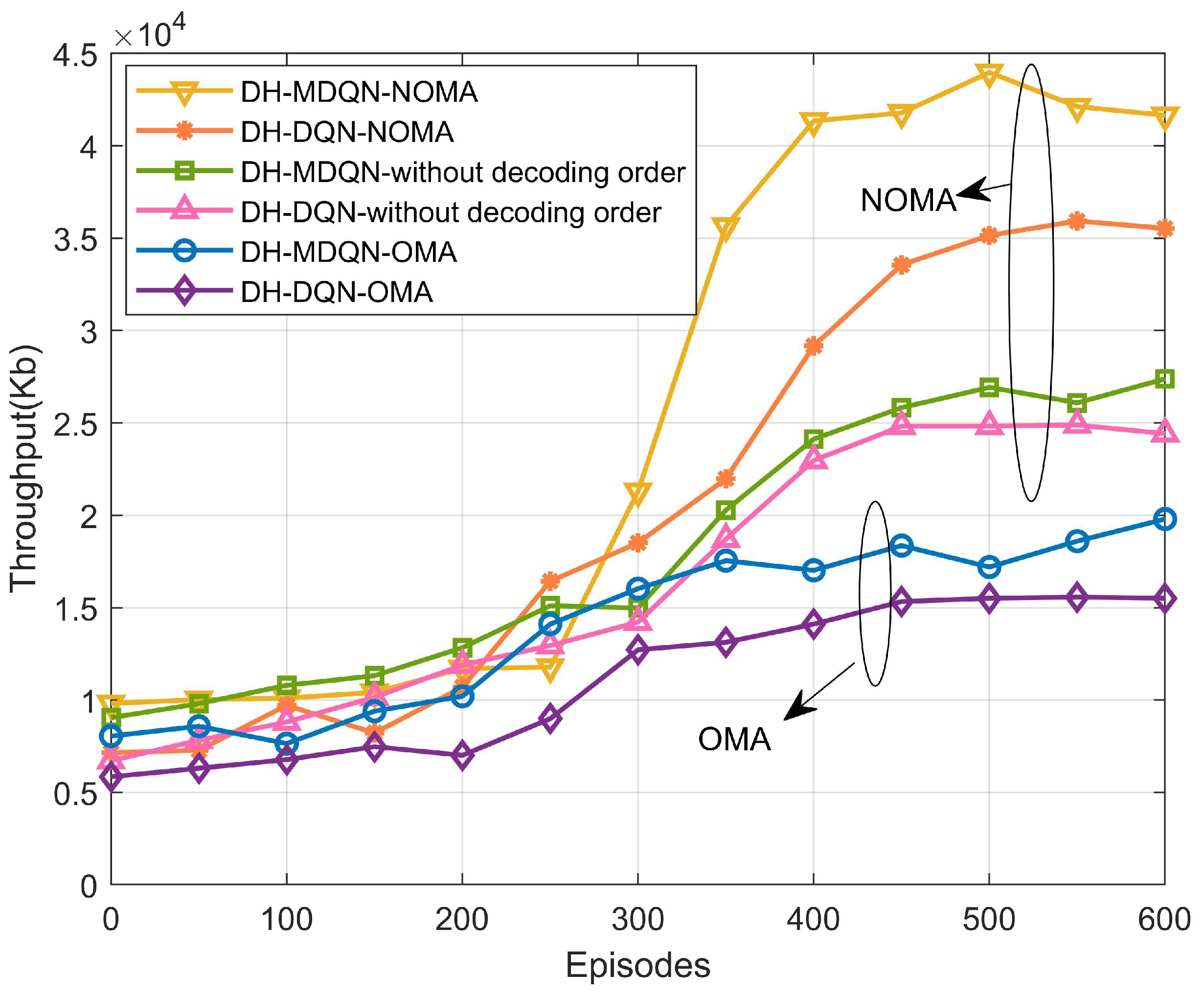
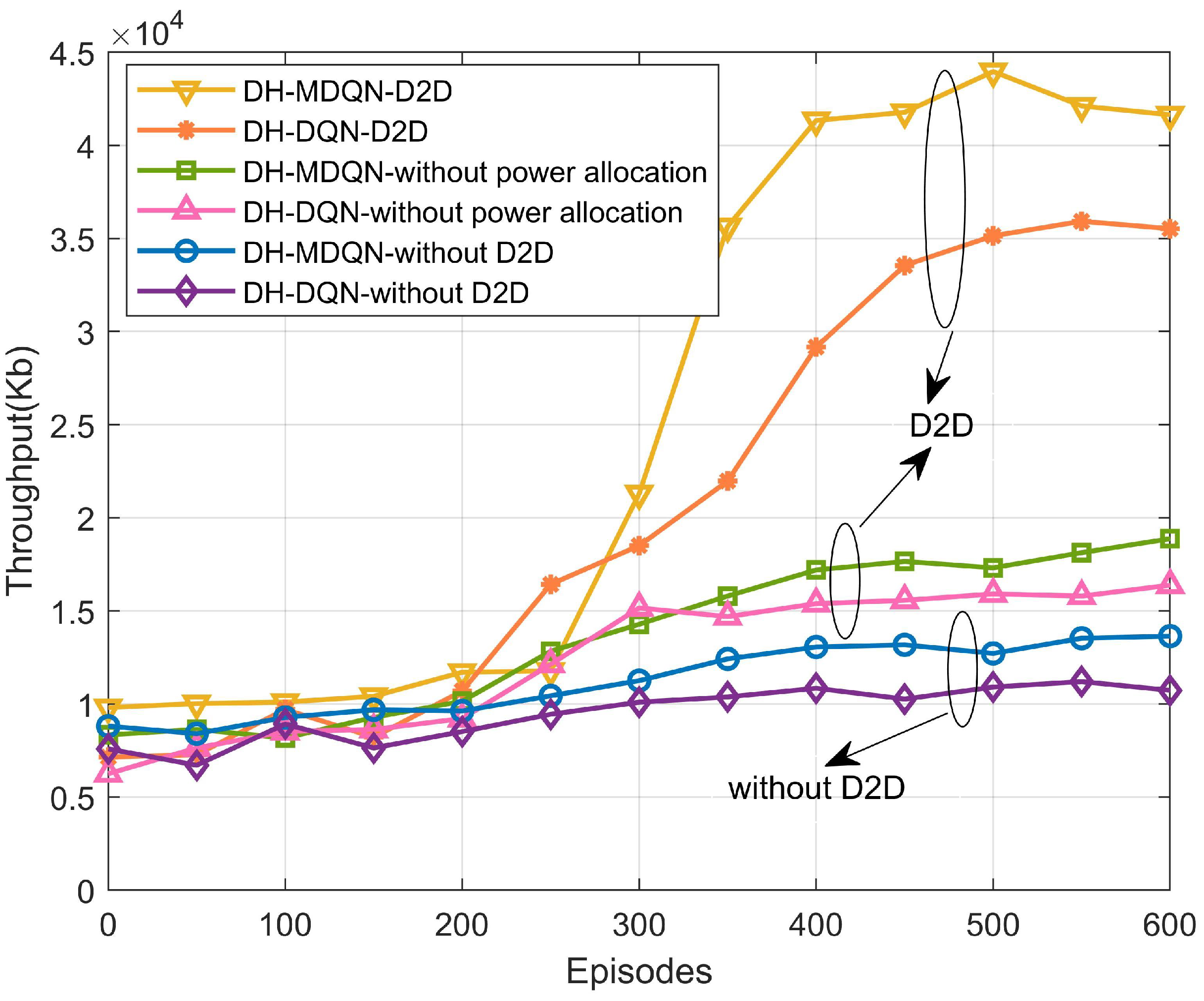
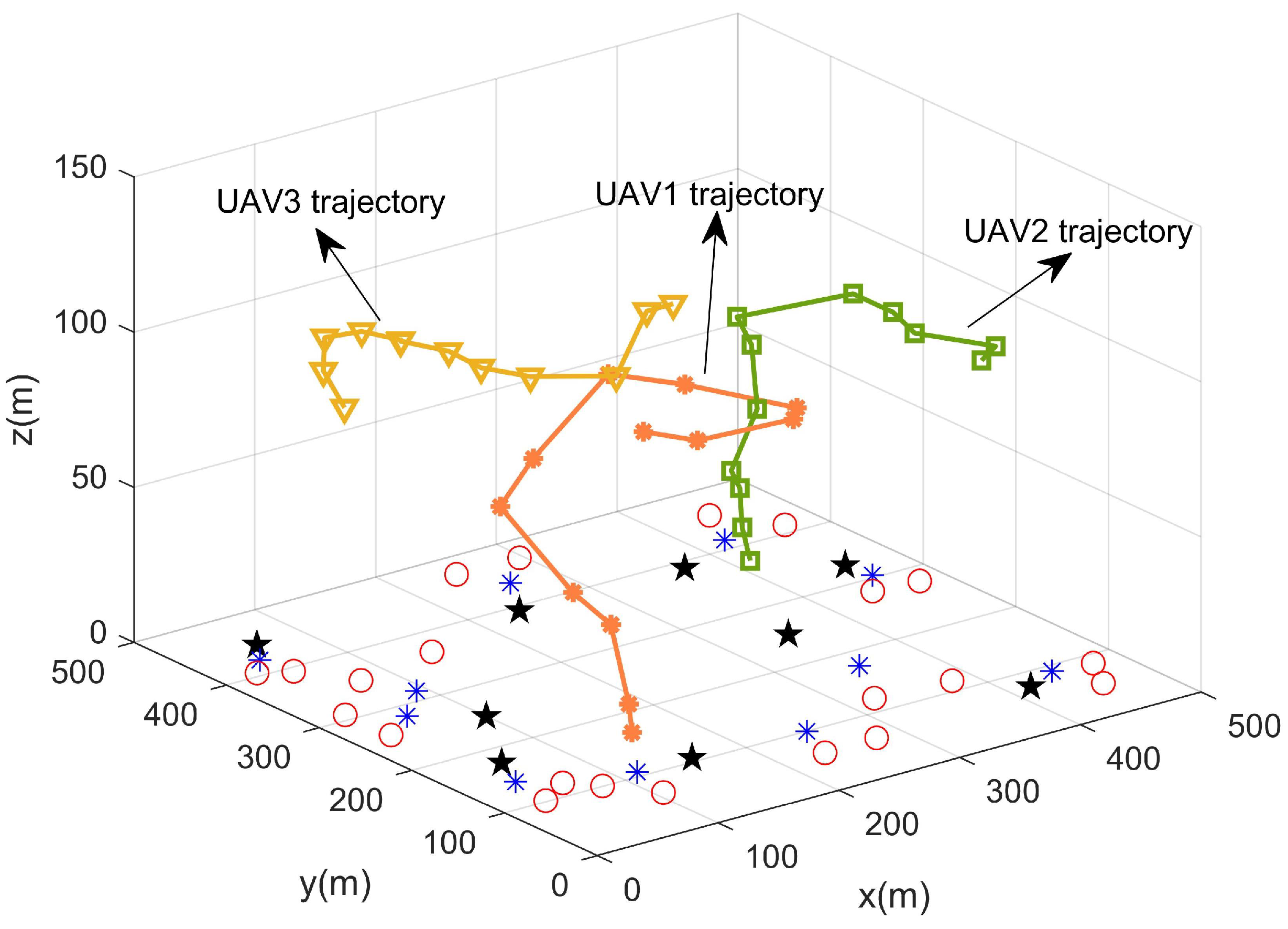
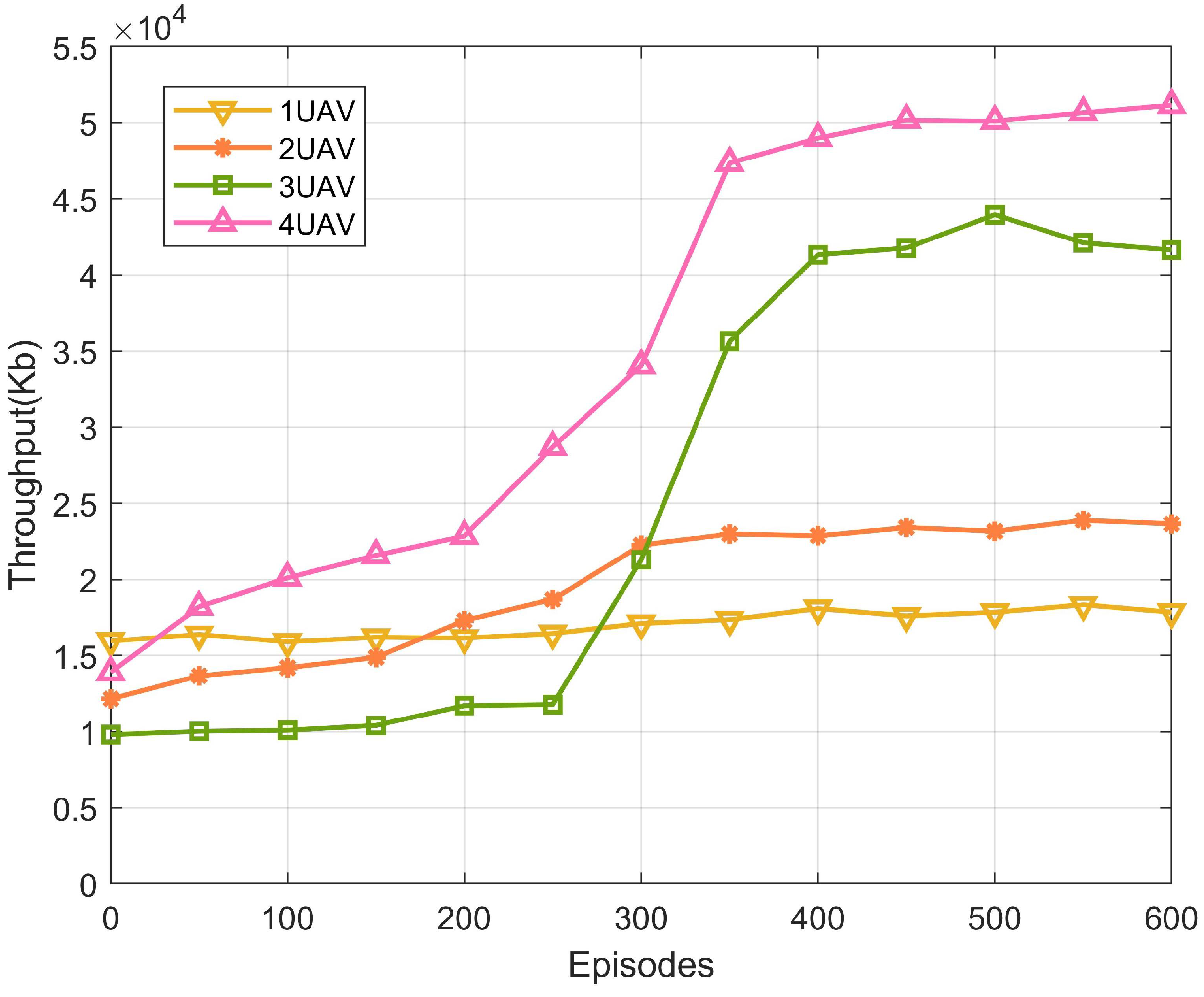
5.2. Analysis of Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of things: A survey on enabling technologies, protocols, and applications. IEEE Commun. Surv. Tutor. 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Islam, S.R.; Avazov, N.; Dobre, O.A.; Kwak, K.S. Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges. IEEE Commun. Surv. Tutor. 2016, 19, 721–742. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, Y.; Choi, J.; Sun, Q.; Elkashlan, M.; Chih-Lin, I.; Poor, H.V. Application of non-orthogonal multiple access in LTE and 5G networks. IEEE Commun. Mag. 2017, 55, 185–191. [Google Scholar] [CrossRef]
- Ding, Z.; Yang, Z.; Fan, P.; Poor, H.V. On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users. IEEE Signal Process. Lett. 2014, 21, 1501–1505. [Google Scholar] [CrossRef]
- Yadav, A.; Quan, C.; Varshney, P.K.; Poor, H.V. On performance comparison of multi-antenna HD-NOMA, SCMA, and PD-NOMA schemes. IEEE Wirel. Commun. Lett. 2020, 10, 715–719. [Google Scholar] [CrossRef]
- Liu, J.; Kato, N.; Ma, J.; Kadowaki, N. Device-to-device communication in LTE-advanced networks: A survey. IEEE Commun. Surv. Tutor. 2014, 17, 1923–1940. [Google Scholar] [CrossRef]
- Qiao, J.; Shen, X.S.; Mark, J.W.; Shen, Q.; He, Y.; Lei, L. Enabling device-to-device communications in millimeter-wave 5G cellular networks. IEEE Commun. Mag. 2015, 53, 209–215. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Chai, K.K.; Chen, Y.; Elkashlan, M. Joint subchannel and power allocation for NOMA enhanced D2D communications. IEEE Trans. Commun. 2017, 65, 5081–5094. [Google Scholar] [CrossRef]
- Wang, L.; He, Y.; Chen, B.; Hassan, A.; Wang, D.; Yang, L.; Huang, F. Joint Phase Shift Design and Resource Management for a Non-Orthogonal Multiple Access-Enhanced Internet of Vehicle Assisted by an Intelligent Reflecting Surface-Equipped Unmanned Aerial Vehicle. Drones 2024, 8, 188. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, Z.; Xiao, M.; Ding, Z.; Fan, P. Full-duplex device-to-device-aided cooperative nonorthogonal multiple access. IEEE Trans. Veh. Technol. 2016, 66, 4467–4471. [Google Scholar]
- Aggarwal, S.; Kumar, N.; Tanwar, S. Blockchain-envisioned UAV communication using 6G networks: Open issues, use cases, and future directions. IEEE Internet Things J. 2020, 8, 5416–5441. [Google Scholar] [CrossRef]
- Pan, G.; Lei, H.; An, J.; Zhang, S.; Alouini, M.S. On the secrecy of UAV systems with linear trajectory. IEEE Trans. Wirel. Commun. 2020, 19, 6277–6288. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, R.; Chen, C.; Cheng, X.; Yang, L.; Li, H.; Jin, Y. Graph-based file dispatching protocol with D2D-enhanced UAV-NOMA communications in large-scale networks. IEEE Internet Things J. 2020, 7, 8615–8630. [Google Scholar] [CrossRef]
- Liu, X.; Yang, B.; Liu, J.; Xian, L.; Jiang, X.; Taleb, T. Sum-Rate Maximization for D2D-Enabled UAV Networks with Seamless Coverage Constraint. IEEE Internet Things J. 2024. [Google Scholar] [CrossRef]
- Pan, H.; Liu, Y.; Sun, G.; Wang, P.; Yuen, C. Resource scheduling for UAVs-aided D2D networks: A multi-objective optimization approach. IEEE Trans. Wirel. Commun. 2023. [Google Scholar] [CrossRef]
- Zhang, Y.; Hou, X.; Du, H.; Zhang, L.; Du, J.; Men, W. Joint Trajectory and Resource Optimization for UAV and D2D-enabled Heterogeneous Edge Computing Networks. IEEE Trans. Veh. Technol. 2024. [Google Scholar] [CrossRef]
- Marani, M.R.; Mirrezaei, S.M.; Mirzavand, R. Joint throughput and coverage maximization for moving users by optimum UAV positioning in the presence of underlaid D2D communications. AEU-Int. J. Electron. Commun. 2023, 161, 154541. [Google Scholar] [CrossRef]
- Tang, R.; Wang, J.; Zhang, Y.; Jiang, F.; Zhang, X.; Du, J. Throughput Maximization in NOMA Enhanced RIS-Assisted Multi-UAV Networks: A Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2024. [Google Scholar] [CrossRef]
- Hosny, R.; Hashima, S.; Hatano, K.; Zaki, R.M.; El Halawany, B.M. UAV trajectory planning in NOMA-aided UAV-mounted RIS networks: A budgeted Multi-armed bandit approach. J. Phys. Conf. Ser. 2024, 2850, 012008. [Google Scholar] [CrossRef]
- Amhaz, A.; Elhattab, M.; Sharafeddine, S.; Assi, C. Uav-assisted cooperative downlink noma: Deployment and resource allocation. IEEE Trans. Veh. Technol. 2024. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Tran, M.H.; Tran, X.N. Joint Resource and Trajectory Optimization For Secure UAV-Based Two-way Relay System. Digit. Signal Process. 2024, 153, 104626. [Google Scholar] [CrossRef]
- Jabbari, A.; Khan, H.; Duraibi, S.; Budhiraja, I.; Gupta, S.; Omar, M. Energy Maximization for Wireless Powered Communication Enabled IoT Devices with NOMA Underlaying Solar Powered UAV Using Federated Reinforcement Learning for 6G Networks. IEEE Trans. Consum. Electron. 2024. [Google Scholar] [CrossRef]
- Yang, X.; Qin, D.; Liu, J.; Li, Y.; Zhu, Y.; Ma, L. Deep reinforcement learning in NOMA-assisted UAV networks for path selection and resource offloading. Ad Hoc Netw. 2023, 151, 103285. [Google Scholar] [CrossRef]
- Rezwan, S.; Chun, C.; Choi, W. Federated Deep Reinforcement Learning-Based Multi-UAV Navigation for Heterogeneous NOMA Systems. IEEE Sens. J. 2023. [Google Scholar] [CrossRef]
- Qin, P.; Fu, Y.; Zhang, J.; Geng, S.; Liu, J.; Zhao, X. DRL-Based Resource Allocation and Trajectory Planning for NOMA-Enabled Multi-UAV Collaborative Caching 6 G Network. IEEE Trans. Veh. Technol. 2024, 73, 8750–8764. [Google Scholar] [CrossRef]
- Docomo, N.T.T. 5G Channel Model for Bands up to 100 GHz; Technical Report; 2016; Available online: https://prepareforchange.net/wp-content/uploads/2018/12/5G_Channel_Model_for_bands_up_to100_GHz2015-12-6.pdf (accessed on 13 December 2024).
- Liang, L.; Li, G.Y.; Xu, W. Resource allocation for D2D-enabled vehicular communications. IEEE Trans. Commun. 2017, 65, 3186–3197. [Google Scholar] [CrossRef]
- Zhang, H.; Song, L.; Han, Z. Radio resource allocation for device-to-device underlay communication using hypergraph theory. IEEE Trans. Wirel. Commun. 2016, 15, 4852–4861. [Google Scholar] [CrossRef]
- Yuan, L.; Qin, L.; Lin, X.; Chang, L.; Zhang, W. Effective and efficient dynamic graph coloring. Proc. VLDB Endow. 2017, 11, 338–351. [Google Scholar] [CrossRef]
- Wang, B.; Sun, Y.; Sun, Z.; Nguyen, L.D.; Duong, T.Q. UAV-assisted emergency communications in social IoT: A dynamic hypergraph coloring approach. IEEE Internet Things J. 2020, 7, 7663–7677. [Google Scholar] [CrossRef]





| Simulation Parameters | Value |
|---|---|
| Plane area boundaries | m, m |
| UAV altitude range | m |
| Number of UAVs | |
| Maximum UAV flight speed | m/s |
| UAV maximum transmit power | dBm |
| Maximum cellular user transmit power | dBm |
| Number of cellular users | |
| D2D cluster maximum transmit power | dBm |
| Maximum spacing of D2D clusters | m |
| Number of D2D clusters | |
| Maximum number of D2D clusters associated with a UAV | |
| Carrier frequency | GHz |
| Bandwidth | kHz |
| AWGN power | dBm/Hz |
| Path loss coefficient | |
| Threshold | dBm |
| Learning rate | 0.001 |
| Discount factor | 1 |
| Experience replay pool | 10,000 samples |
| Batch size | 128 samples |
| Optimizer | Adam |
| Greed coefficient | 0–0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Chen, G.; Gu, X. NOMA-Based Rate Optimization for Multi-UAV-Assisted D2D Communication Networks. Drones 2025, 9, 62. https://doi.org/10.3390/drones9010062
Wu G, Chen G, Gu X. NOMA-Based Rate Optimization for Multi-UAV-Assisted D2D Communication Networks. Drones. 2025; 9(1):62. https://doi.org/10.3390/drones9010062
Chicago/Turabian StyleWu, Guowei, Guifen Chen, and Xinglong Gu. 2025. "NOMA-Based Rate Optimization for Multi-UAV-Assisted D2D Communication Networks" Drones 9, no. 1: 62. https://doi.org/10.3390/drones9010062
APA StyleWu, G., Chen, G., & Gu, X. (2025). NOMA-Based Rate Optimization for Multi-UAV-Assisted D2D Communication Networks. Drones, 9(1), 62. https://doi.org/10.3390/drones9010062






