Quadrotor Unmanned Aerial Vehicle-Mounted Launch Device Precision Analysis for Countering Intruding Drones
Abstract
1. Introduction
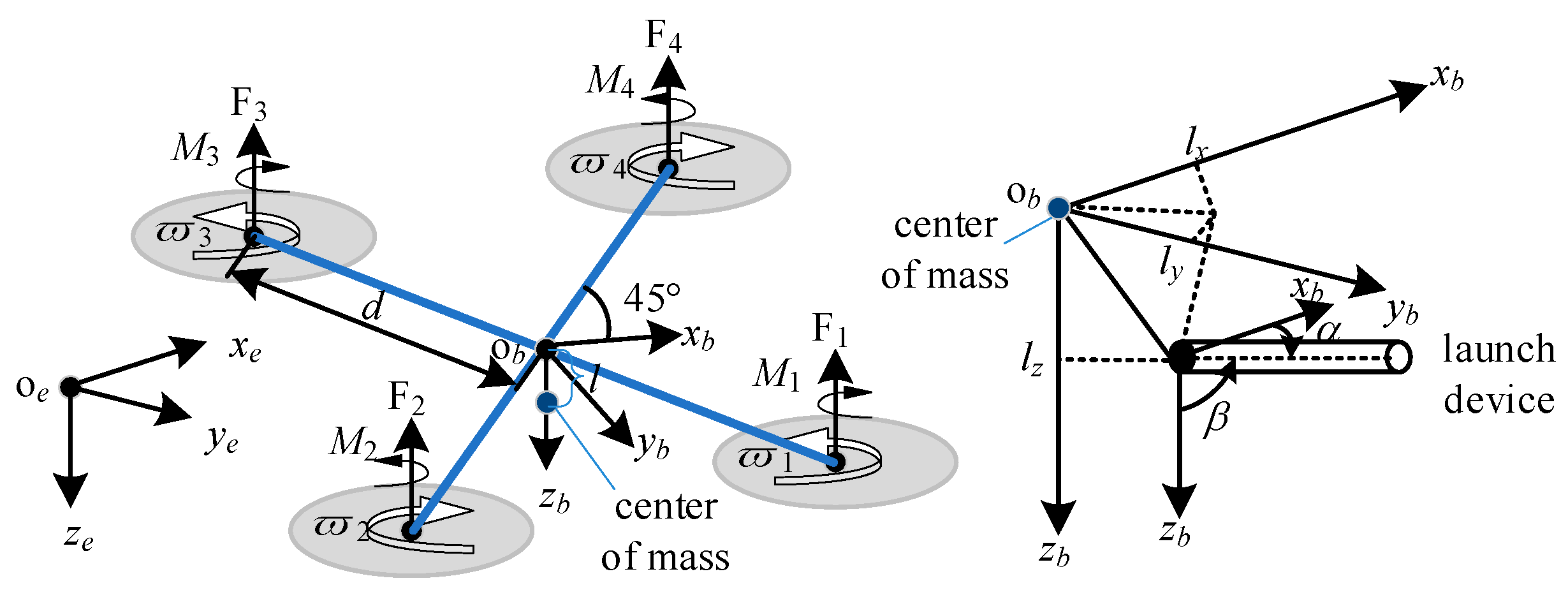
2. Establishment of a Quadrotor UAV Model with a Launch Device
2.1. Six-DOF Dynamics Equations of Multi-Rotor UAVs
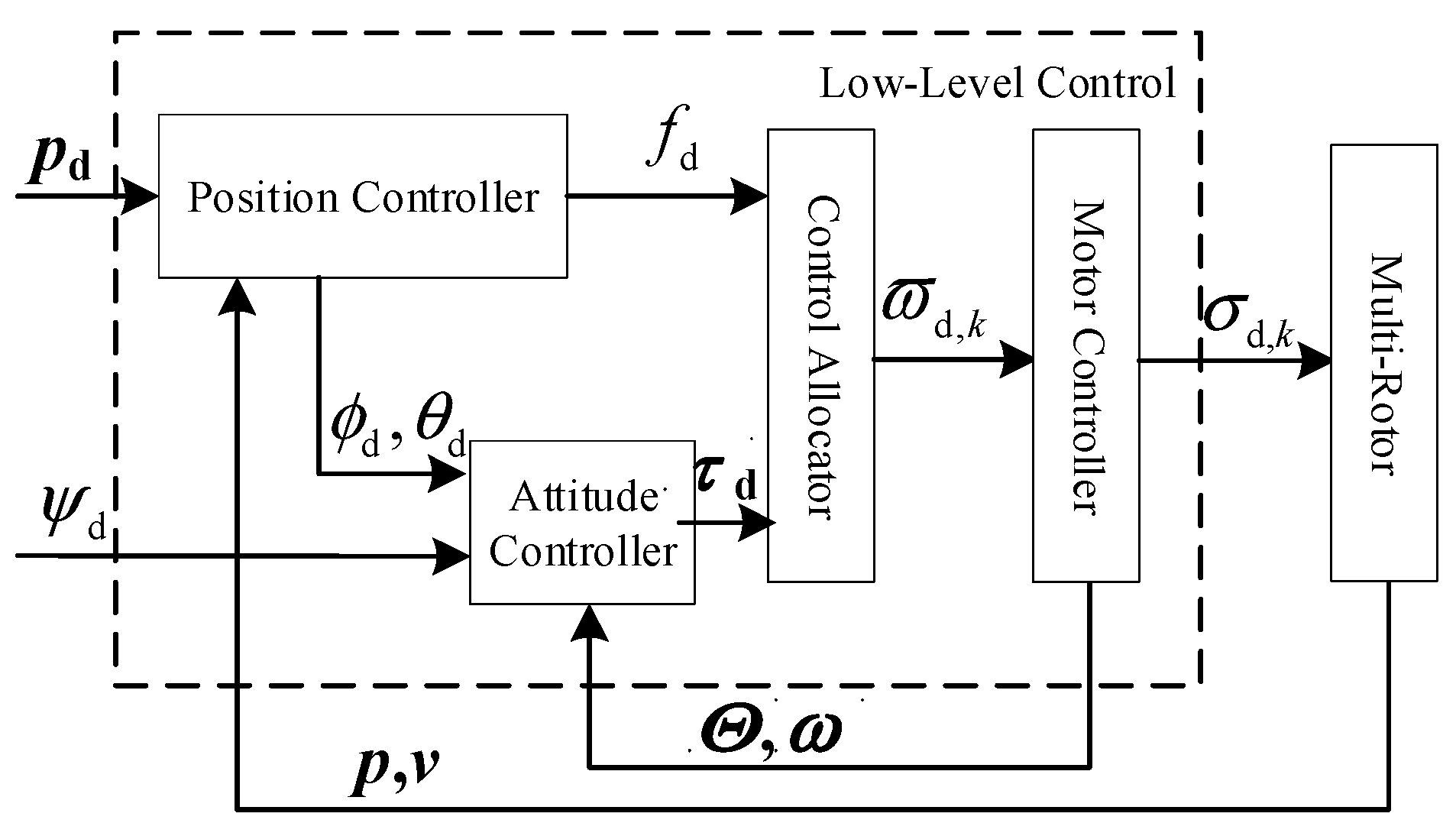
2.2. UAV Low-Level Control
2.3. Ballistic Equations of the Launch Device
2.4. Model Assumptions
- The weight of the UAV remains constant after firing;
- During firing, the entire UAV, gimbaled mount, and payload are considered as a single rigid body;
- The motion of the UAV is not affected by other disturbances;
- The effects of the Earth’s rotation and revolution are neglected;
- The safe range of UAV attitude angle changes is limited to between 0° and 55°;
- Within the safe range of UAV attitude angle changes, the effect of air resistance is ignored;
- Due to the short shooting distance, the projectile’s trajectory is assumed to be a straight line, and the projectile’s initial velocity direction is consistent with the aiming and firing direction, unaffected by the UAV body and gimbaled mount.
2.5. Input Parameter Settings
3. Analysis of UAV Single-Shot Firing with Heavy Payload
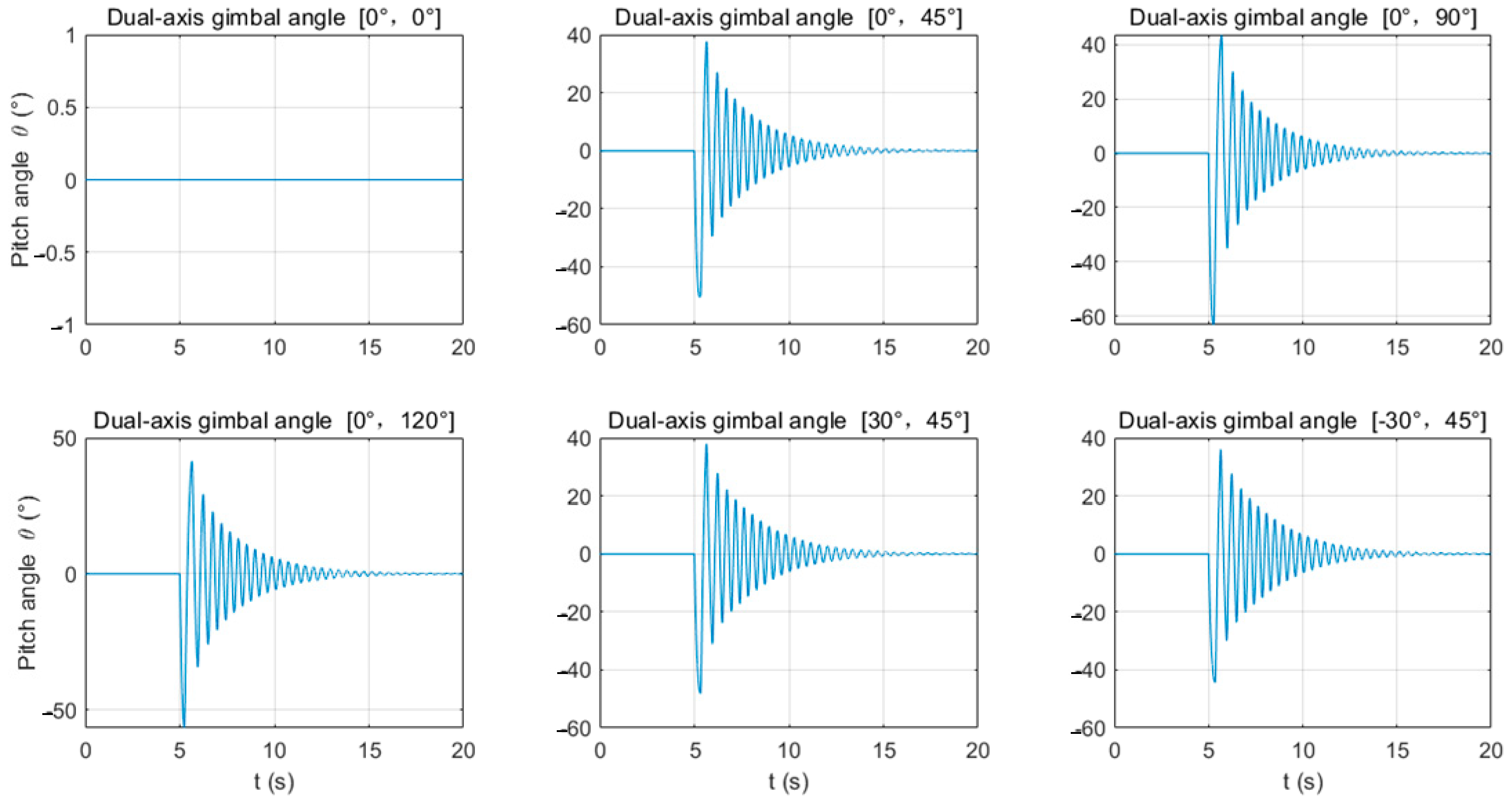
3.1. Patterns of UAV Attitude and Torque Changes During Single-Shot Firing
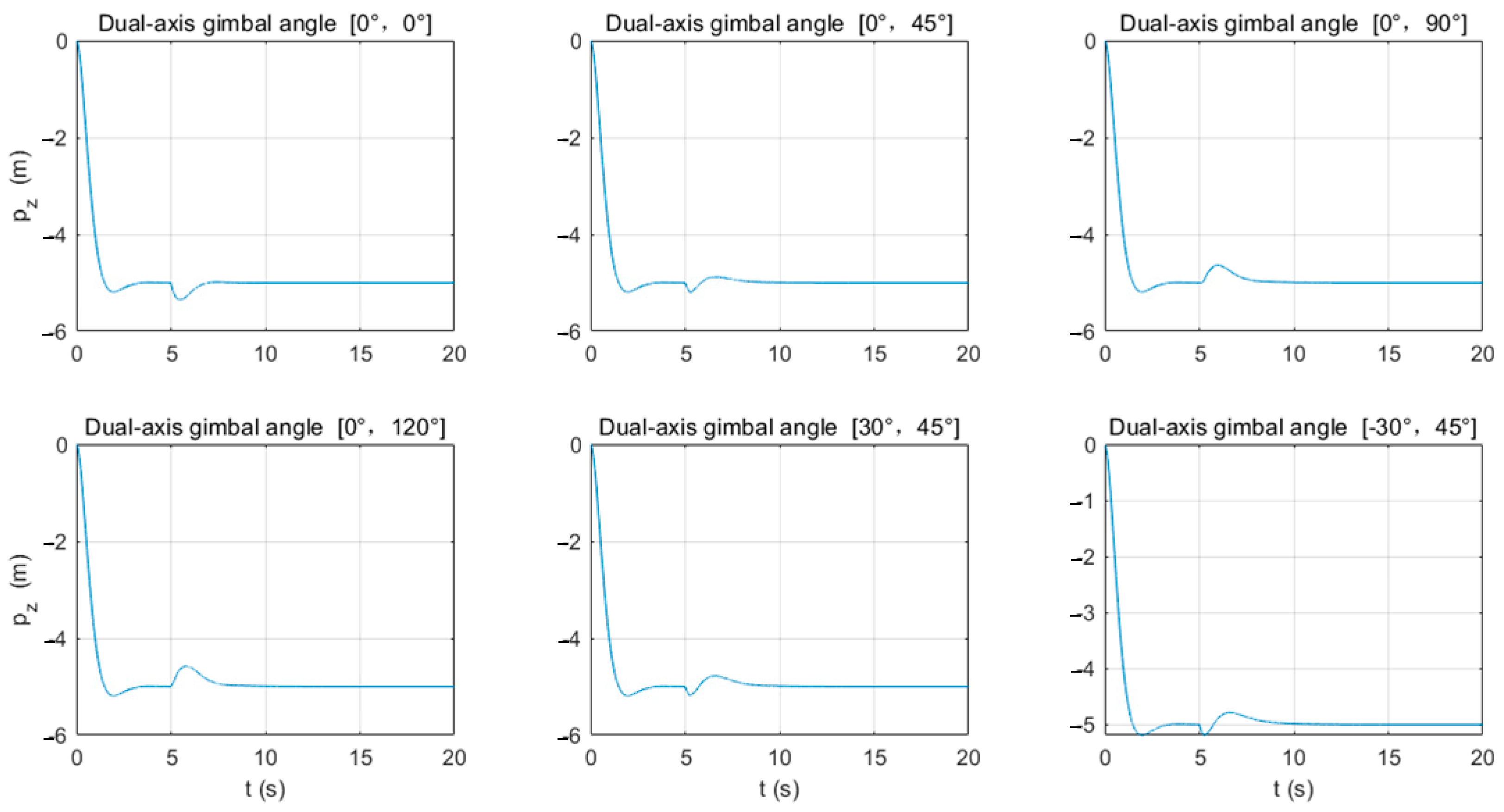
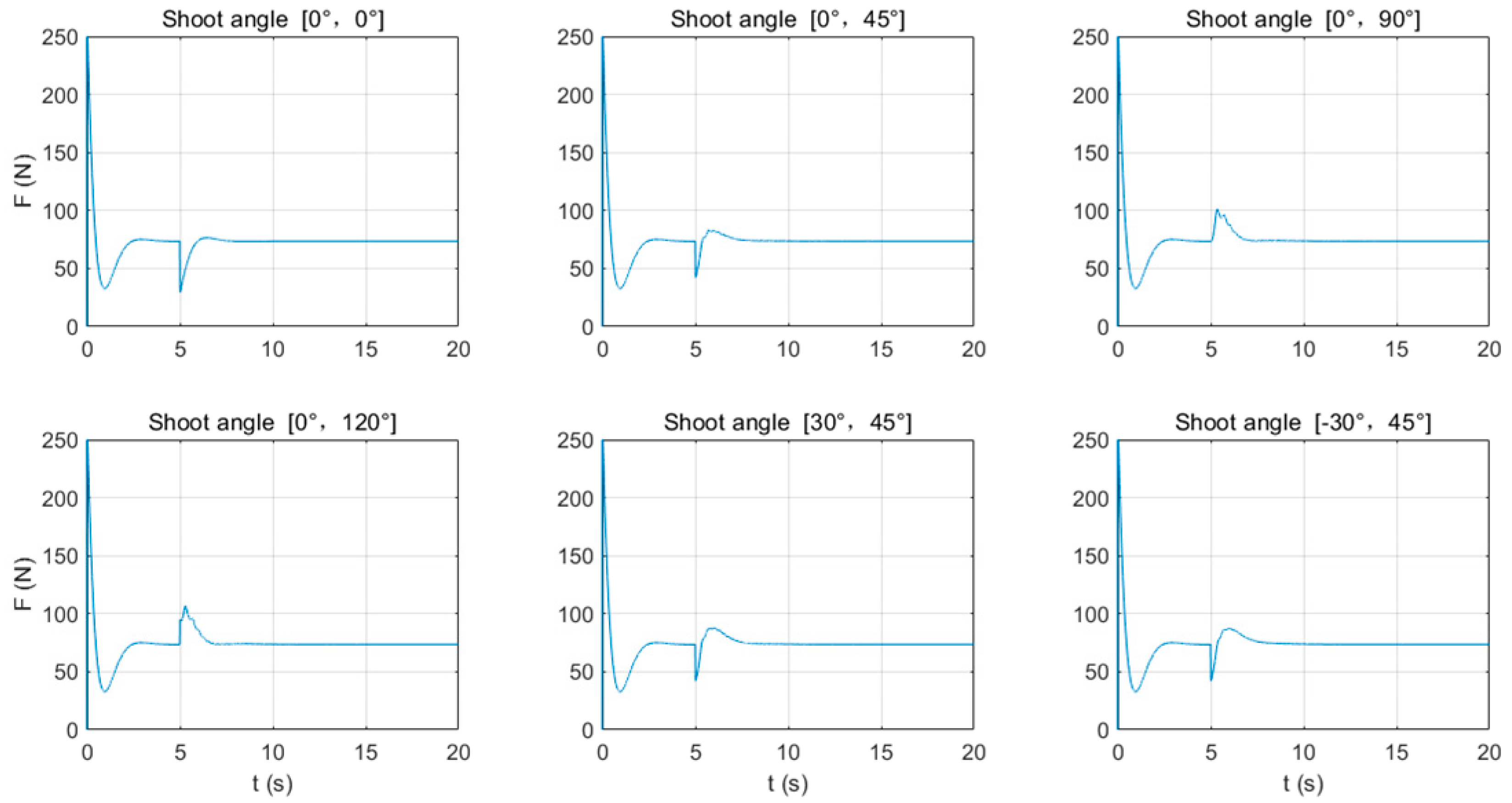
3.2. UAV Position and Lift Force Change Patterns
4. Analysis of UAV Burst Firing with Light Payload
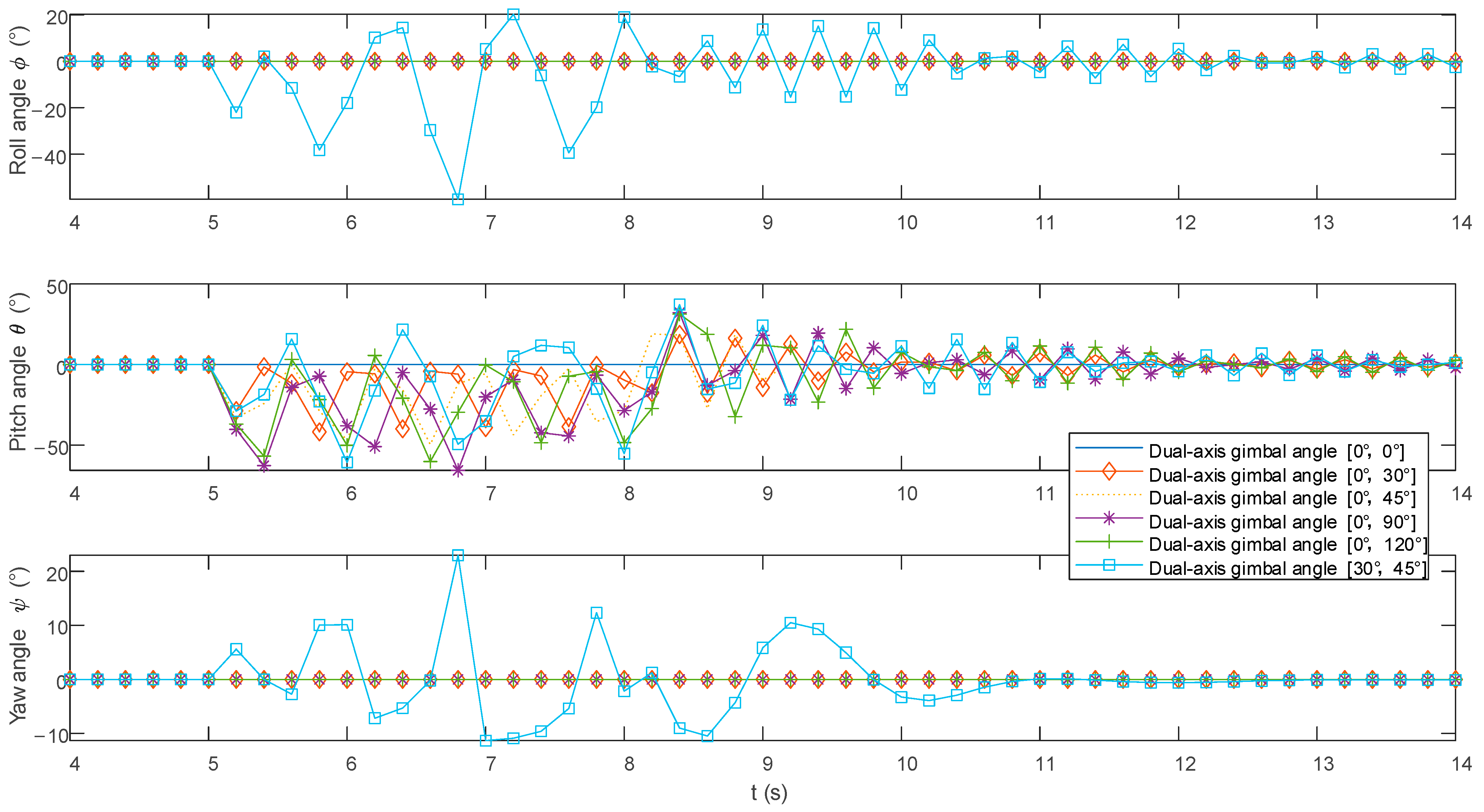
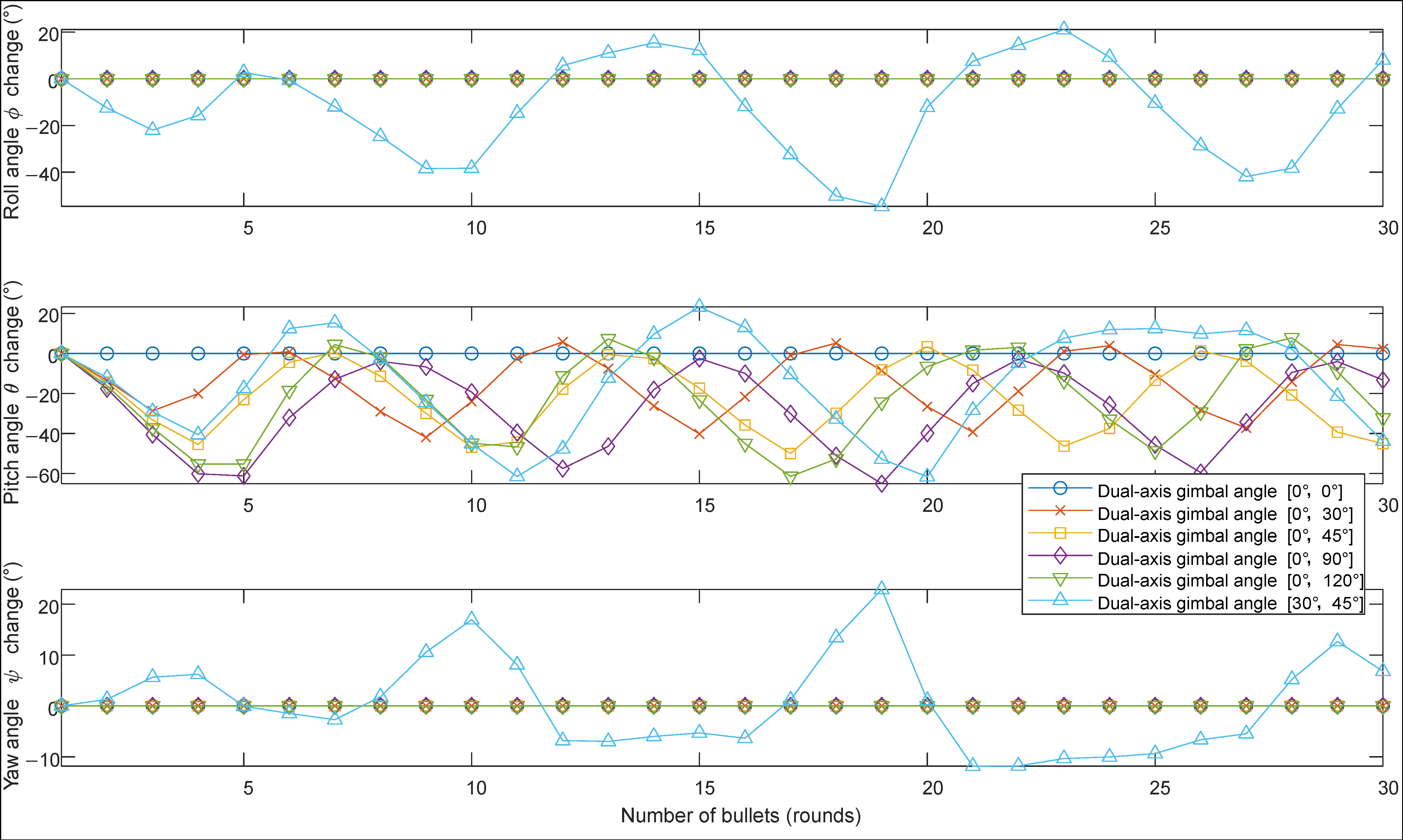
4.1. Patterns of UAV Attitude and Torque Changes During Burst Firing
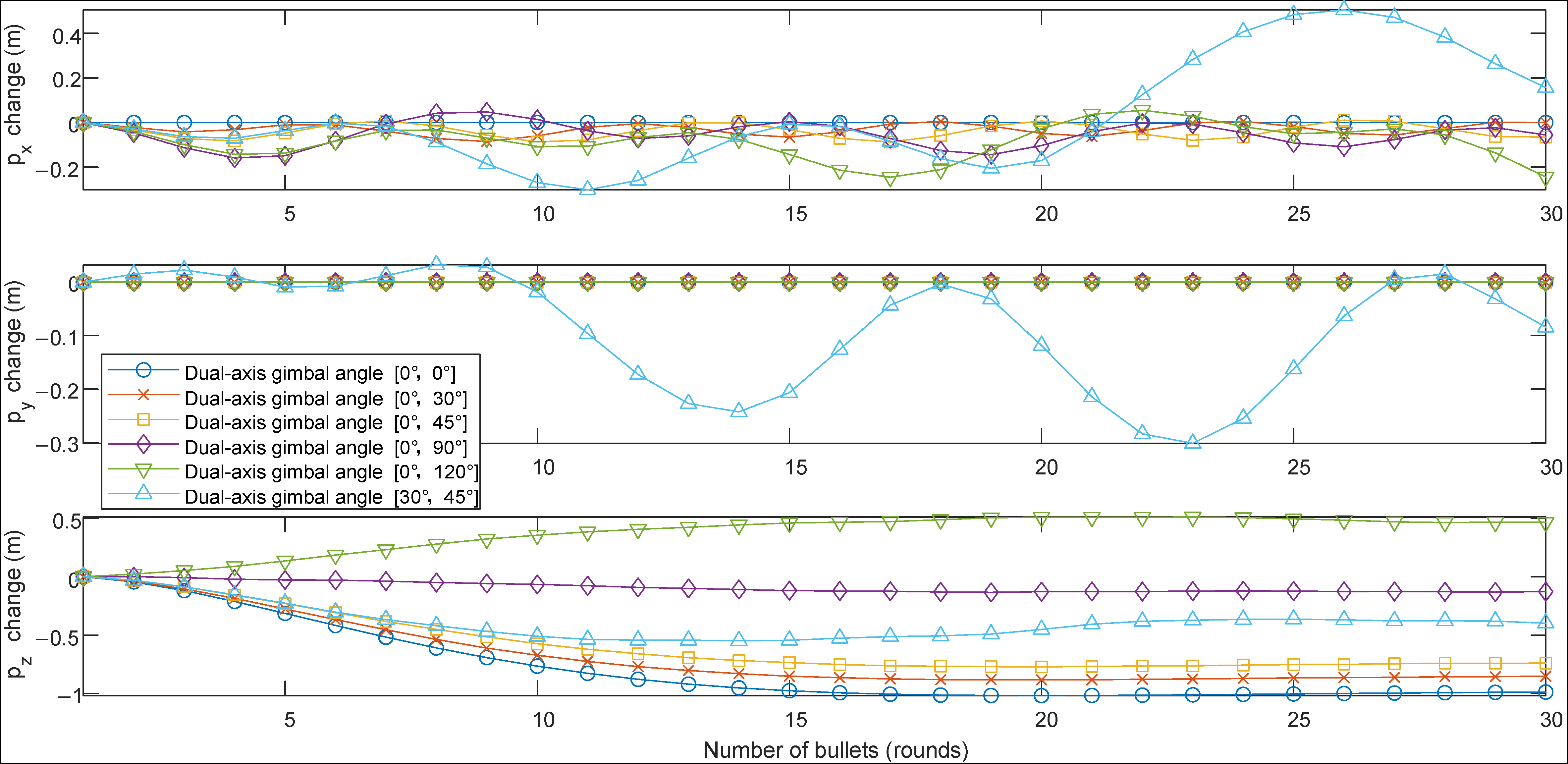
4.2. Patterns of UAV Position and Lift Force Changes
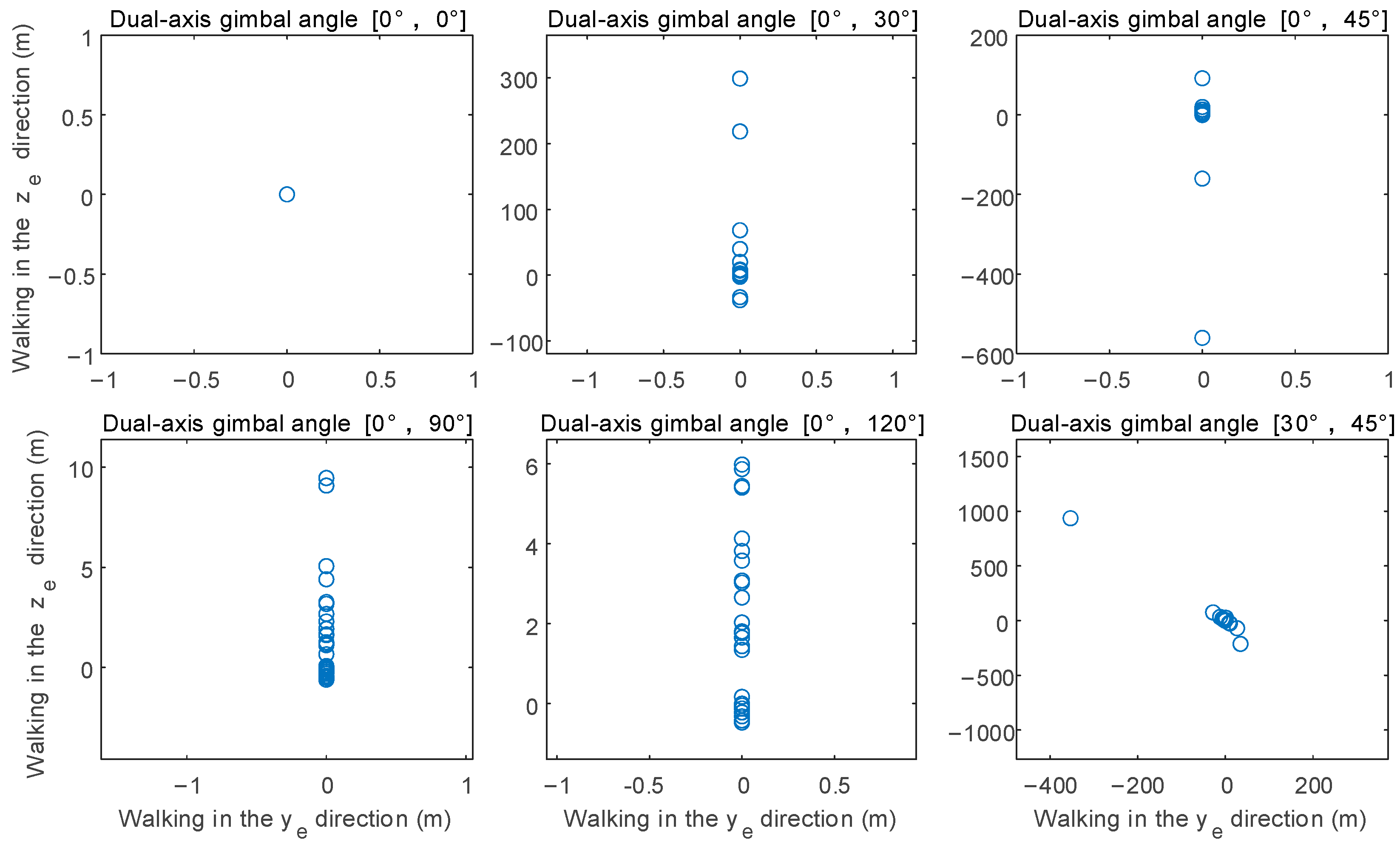
4.3. Strike Accuracy at a Fixed Distance
5. Conclusions
- Whether it is single-shot or continuous firing, the recoil torque after firing causes significant changes in the UAV’s pitch angle, which fluctuates during shooting. When firing horizontally, the firing torque is the greatest and may exceed the allowed angle of the UAV, leading to a crash. Therefore, this angle is suitable for smaller launch loads. For larger loads, it is recommended to fire downwards to reduce the amplitude of attitude changes. At the same time, changes in the UAV’s attitude angles during firing will cause changes in the direction of lift force, leading to greater vertical position changes than horizontal ones. Attention should be paid to the altitude direction after firing to avoid collisions with obstacles.
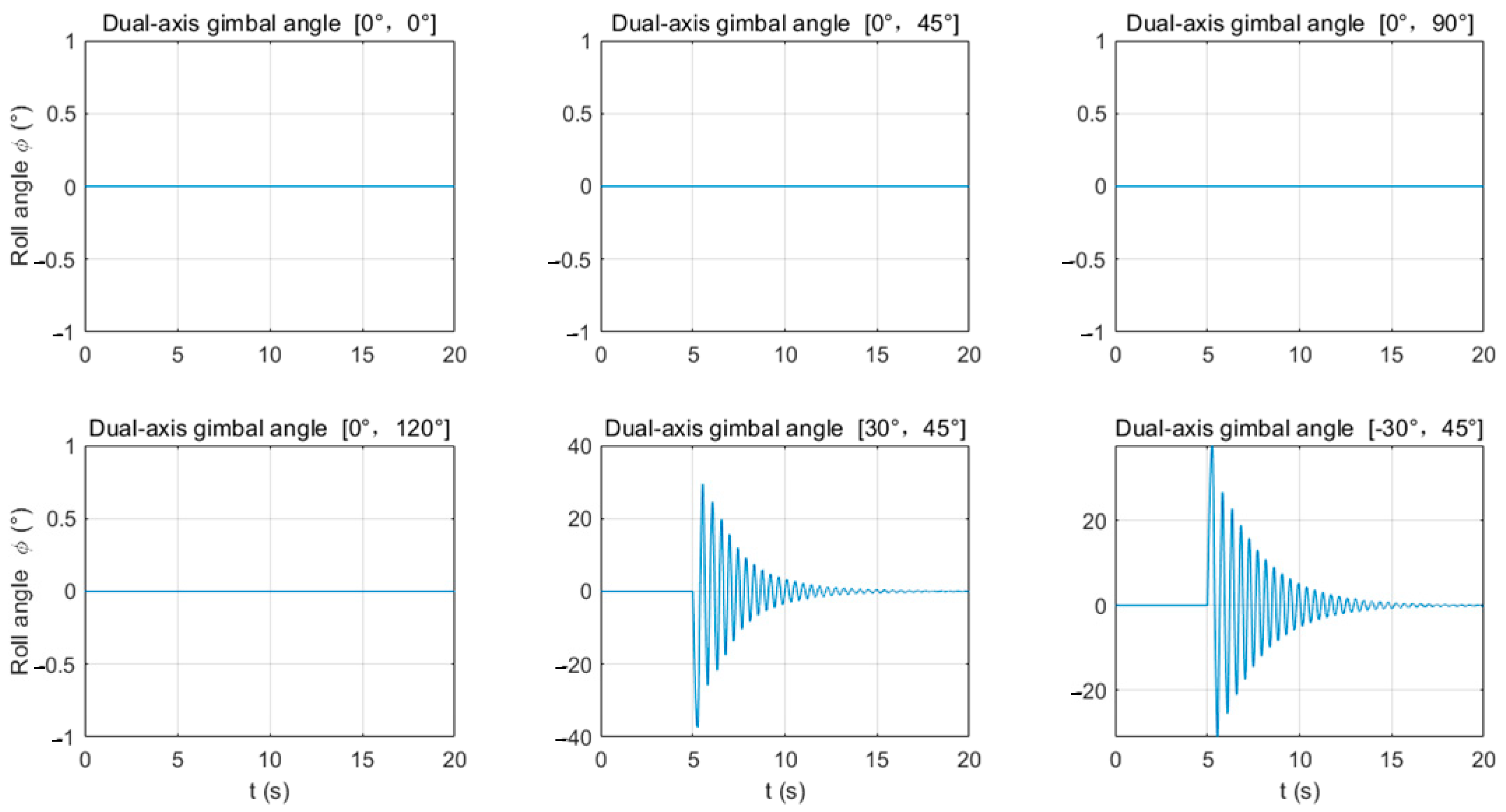
- When firing a large payload in a single shot, the analysis of six different launch angles revealed that the precision is highest when firing vertically downward (gimbal angles α = 0°, β = 0°), which can be used for counter-UAV purposes. Firing a capture net at a target UAV from above can effectively hit the target. When firing laterally downward (gimbal angles α = 30°, β = 45°), the torque is minimized, and the UAV’s attitude and position changes after firing can be effectively reduced.
- When the UAV fires a small payload in a burst, vertical downward firing also has the highest precision. In open areas, if the UAV’s maneuvering speed is fast, or the target is slow, a downward attack can be adopted. Unlike single-shot firing, the error in lateral firing during burst firing is larger, and it is not recommended. If the UAV needs to improve the precision of burst firing without a gimbaled mount, for targets ahead, the firing device can be installed at angles α = 0°, β = 90°; for targets in a narrow working area below, the firing device can be installed at angles α = 0°, β = 45°. Finally, controlling the burst interval is a key factor in controlling precision. When the interval between bursts is too short, precision is poor; if it is too long, firepower is weak. The optimal firing angles corresponding to different burst intervals are different and require specific calculations.
Author Contributions
Funding
Data Availability Statement
DURC Statement
Conflicts of Interest
References
- Quan, Q. Design and Control of Multi-Rotor Aircraft; Publishing House of Electronics Industry: Beijing, China, 2018; pp. 57–89. [Google Scholar]
- Kim, J.; Gadsden, S.A.; Wilkerson, S.A. A Comprehensive Survey of Control Strategies for Autonomous Quadrotors. Can. J. Electr. Comput. Eng. 2020, 43, 3–16. [Google Scholar] [CrossRef]
- Beard, R.W. Quadrotor Dynamics and Control. Brigh. Young Univ. J. 2008, 19, 46–56. [Google Scholar]
- Sabatino, F. Quadrotor Control: Modeling, Nonlinear Control Design, and Simulation. Master’s Thesis, KTH Electrical Engineering, Stockholm, Sweden, 2015; pp. 12–29. [Google Scholar]
- Roldán-Gómez, J.J.; González-Gironda, E.; Barrientos, A. A Survey on Robotic Technologies for Forest Firefighting: Applying Drone Swarms to Improve Firefighters’ Efficiency and Safety. Appl. Sci. 2021, 11, 363. [Google Scholar] [CrossRef]
- Yuan, C.; Liu, Z.; Zhang, Y. Fire Detection Using Infrared Images for UAV-Based Forest Fire Surveillance. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 567–572. [Google Scholar]
- Kunertova, D. The War in Ukraine Shows the Game-Changing Effect of Drones Depends on the Game. Bull. Atmos. Sci. 2023, 79, 95–102. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Song, H. Counter-unmanned aircraft systems (C-UAS): State of the art, challenges, and future trends. IEEE Aerosp. Electron. Syst. Mag. 2021, 36, 4–29. [Google Scholar] [CrossRef]
- Nichols, R.K.; Mumm, H.C.; Lonstein, W.D.; Ryan, J.J.; Carter, C.; Hood, J.P. Counter Unmanned Aircraft Systems Technologies and Operations; New Prairie Press: Manhattan, KS, USA, 2020. [Google Scholar]
- Valente, J.; Sari, B.; Kooistra, L.; Kramer, H.; Mücher, S. Automated Crop Plant Counting from Very High-Resolution Aerial Imagery. Precis. Agric. 2020, 21, 1366–1384. [Google Scholar] [CrossRef]
- Pang, J.Z. Research on Key Technologies of “Flying Gun” Fire Control System Based on Multi-Rotor Drones; Nanjing University of Science and Technology: Nanjing, China, 2023. [Google Scholar]
- Farinha, A.; Zufferey, R.; Zheng, P.; Armanini, S.F.; Kovac, M. Unmanned Aerial Sensor Placement for Cluttered Environments. IEEE Robot. Autom. Lett. 2020, 5, 6623–6630. [Google Scholar] [CrossRef]
- Zhu, C. Research on the Firing Characteristics of Miniature Unmanned Aerial Vehicles; North University of China: Taiyuan, China, 2021. [Google Scholar]
- Ye, B.S.; Liu, C.F.; Fang, T.; Zhou, N.M. A Micro Unmanned Aerial Vehicle Airborne Pneumatic Continuous Firing Device. Intelligent Comput. Appl. 2021, 11, 201–204. [Google Scholar]
- Fang, T. Dynamic Simulation and Analysis of a Micro Unmanned Aerial Vehicle Platform for Marching Firing; Shanghai University of Engineering Science: Shanghai, China, 2021. [Google Scholar]
- Chen, J. Research on Capture Net Counter-UAV Systems; Nanjing University of Science and Technology: Nanjing, China, 2018. [Google Scholar]
- Lu, S.H. Design and Analysis of Specialized Firearms for Small Rotorcraft Drones; Nanjing University of Science and Technology: Nanjing, China, 2017. [Google Scholar]
- Wang, L.T.; Wang, J. Four-rotor UAV Special Ammunition Hovering-launchMechanics Research. J. Ballistics. 2022, 34, 38–44. [Google Scholar] [CrossRef]
- Nan, F.; Sun, S.; Foehn, P.; Scaramuzza, D. Nonlinear MPC for Quadrotor Fault-Tolerant Control. IEEE Robot. Autom. Lett. 2022, 7, 5047–5054. [Google Scholar] [CrossRef]
- Lotufo, M.A.; Colangelo, L.; Perez-Montenegro, C.; Canuto, E.; Novara, C. UAV Quadrotor Attitude Control: An ADRC-EMC Combined Approach. Control Eng. Pract. 2019, 84, 13–22. [Google Scholar] [CrossRef]
- Mo, H.; Farid, G. Nonlinear and Adaptive Intelligent Control Techniques for Quadrotor UAV—A Survey. Asian J. Control 2019, 21, 989–1008. [Google Scholar] [CrossRef]
- Brahim, K.S.; Hajjaji, A.E.; Terki, N.; Alabazares, D.L. Finite Time Adaptive SMC for UAV Trajectory Tracking Under Unknown Disturbances and Actuators Constraints. IEEE Access 2023, 11, 66177–66193. [Google Scholar] [CrossRef]
- He, Y.; Xu, H.; Wang, L.; Di, L.; Liu, W.; Liu, L. Analysis of the Energy Storage Efficiency of a UAV-Mounted Sensor Launcher Built on Traditional Crossbow Launch Mechanisms. Drones 2024, 8, 712. [Google Scholar] [CrossRef]
- Wintyr Technology Co., Ltd. Drone Capture Net Gun/Pneumatic Net Gun/Robot Net Gun/DJI M300 M600. Available online: http://www.yjjycn.com/index.php?homepage=wintyr&file=sell&itemid=563 (accessed on 1 December 2024).
- MATHWORKS. PID Controller Tuning for a UAV Quadcopter [EB/OL]. Available online: https://www.mathworks.com/help/slcontrol/ug/pid-controller-tuning-for-a-uav-quadcopter.html (accessed on 28 November 2024).
- Yuan, D.W.; Sha, J.L.; Wang, X.J. Simulation Analysis Method of Single Shooting Accuracy of Air-Guided Rifle. J. Ballist. 2019, 31, 30–35. [Google Scholar]
- Li, Z.J. Calculation of Sniper Rifle Ballistic Trajectory and Research on Sniper Training Simulation; Jilin University: Changchun, China, 2016. [Google Scholar]
- MATHWORKS. Transition from Low- to High-Fidelity UAV Models in Three Stages. Available online: https://www.mathworks.com/help/uav/ug/transition-from-low-to-high-fidelity-uav-models.html (accessed on 11 November 2024).







| Category | Parameter | Value |
|---|---|---|
| Intrinsic physical parameters | The total mass of the UAV with the launch device, m (kg) | 7.5 |
| Gravity acceleration g (m/s2) | 9.8 | |
| Moments of inertia of the UAV with launch device () (kg·m2) | (0.1392, 0.1392, 0.28) | |
| Distance from the center of mass to the recoil force application point () (m) | (0, 0, 0.1) | |
| Initial state | Initial position () (m) | (0, 0, 0) |
| Initial velocity () (m/s) | (0, 0, 0) | |
| Initial Euler angles (ϕ, θ, ψ) (°) | (0, 0, 0) | |
| Initial angular velocities () (rad/s) | (0, 0, 0) | |
| Initial input parameter magnitude | Lift force F (N) | 0 |
| Torque () (N·m) | (0, 0, 0) | |
| Parameter output limit range | Output lift parameter range (min, max) | (0, 250) |
| Output torque parameter range (min, max) | (−50, 50) | |
| Parameter binding | Position proportional coefficients | (40, 40, 40) |
| Position differential coefficients | (0, 0, 0) | |
| Position integral coefficients | (25, 25, 25) | |
| Attitude proportional coefficients | (5, 5, 5) | |
| Attitude differential coefficients | (0, 0, 0) | |
| Attitude integral coefficients | (1, 1, 1) | |
| Desired position (m) | (0, 0, 5) |
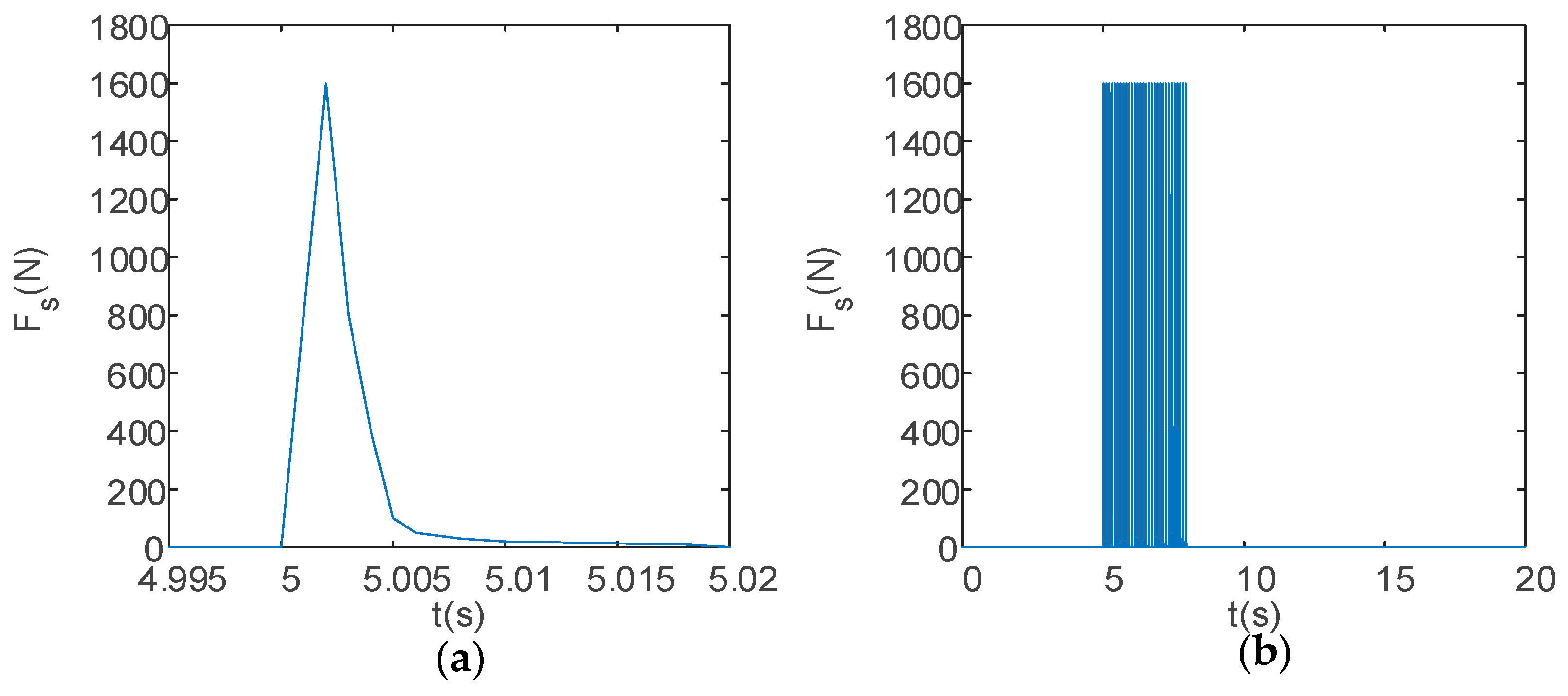
| Single-shot firing | Time (s) | 0.000 | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 |
| Recoil force (N) | 0 | 2500 | 3200 | 2500 | 1500 | 1000 | 500 | |
| Time (s) | 0.007 | 0.008 | 0.009 | 0.010 | 0.011 | 0.012 | 0.013 | |
| Recoil force (N) | 400 | 300 | 250 | 200 | 200 | 180 | 150 | |
| Time (s) | 0.014 | 0.015 | 0.016 | 0.017 | 0.018 | 0.0019 | 0.0020 | |
| Recoil force (N) | 140 | 130 | 120 | 110 | 100 | 50 | 0 | |
| Burst firing | Time (s) | 0.000 | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 |
| Recoil force (N) | 0 | 800 | 1600 | 800 | 400 | 100 | 50 | |
| Time (s) | 0.007 | 0.008 | 0.009 | 0.010 | 0.011 | 0.012 | 0.013 | |
| Recoil force (N) | 40 | 30 | 25 | 20 | 20 | 18 | 15 | |
| Time (s) | 0.014 | 0.015 | 0.016 | 0.017 | 0.018 | 0.0019 | 0.0020 | |
| Recoil force (N) | 14 | 13 | 12 | 11 | 10 | 5 | 0 |
| Parameter | Value | |||||
|---|---|---|---|---|---|---|
| Launch device gimbal angles [α, β] (°) | [0, 0] | [0, 45] | [0, 90] | [0, 120] | [30, 45] | [−30, 45] |
| Roll ϕ (min, max) (°) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−37.37, 29.52) | (−31.05, 37.7) |
| Pitch θ (min, max) (°) | (0, 0) | (−50.55, 37.65) | (−63.9, 43.61) | (−56.66, 41.48) | (−48.09, 37.94) | (−44.35, 35.96) |
| Yaw ψ (min, max) (°) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−5.28, 9.22) | (−10.17, 4.32) |
| Mx (min, max) (N·m) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−50, 15.5) | (−15.48, 50) |
| My (min, max) (N·m) | (0, 0) | (−50, 20.34) | (−50, 32.58) | (−50, 33.1) | (−50, 20.4) | (−50, 50) |
| Mz (min, max) (N·m) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−1.97, 2.53) | (−1.6, 2.09) |
| Launch Device Gimbal Angles [α, β] (°) | [0, 0] | [0, 45] | [0, 90] | [0, 120] | [30, 45] | [−30, 45] |
|---|---|---|---|---|---|---|
| (min, max) (m) | (−0.241, 0.009) | (−0.241, 0.009) | (−0.283, 0.09) | (−0.211, 0.129) | (−0.206, 0.009) | (−0.222, 0.009) |
| (min, max) (m) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−0.015, 0.105) | (−0.105, 0.013) |
| (min, max) + 5 (m) | (−0.353, 0.013) | (−0.189, 0.123) | (0, 0.364) | (0, 0.428) | (−0.182, 0.22) | (−0.187, 0.216) |
| F (min, max) (N) | (29.367, 76.452) | (41.997, 83.141) | (72.917, 101.359) | (73.48, 106.787) | (41.975, 87.744) | (42.026, 87.304) |
| Gimbal Angles [α, β] (°) | [0, 0] | [0, 30] | [0, 45] | [0, 90] | [0, 120] | [30, 45] | |
|---|---|---|---|---|---|---|---|
| Roll ϕ (min, max) | t = 0–20 s | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−62.01, 22.28) |
| t = 5–8 s * | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−67.25, 37.15) | |
| Pitch θ (min, max) | t = 0–20 s | (0, 0) | (−42.07, 19.9) | (−52.34, 33.54) | (−70.08, 33.02) | (−67.8, 42.71) | (−67.25, 37.15) |
| t = 5–8 s * | (0, 0) | (−41.98, 5.78) | (−50.06, 3.42) | (−65.15, 0) | (−61.49, 7.83) | (−61.64, 23.28) | |
| Yaw Ψ (min, max) | t = 0–20 s | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−12.44, 23.57) |
| t = 5–8 s * | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−11.86, 22.89) | |
| Gimbal Angles [α, β] (°) | [0, 0] | [0, 30] | [0, 45] | [0, 90] | [0, 120] | [30, 45] | |
|---|---|---|---|---|---|---|---|
| (min, max) (m) 1 | t = 0–20 s | (0, 0) | (−0.085, 0.007) | (−0.088, 0.103) | (−0.165, 0.048) | (−0.353, 0.05) | (−0.302, 0.505) |
| t = 5–8 s * | (0, 0) | (−0.085, 0.006) | (−0.087, 0.011) | (−0.159, 0.047) | (−0.245, 0.055) | (−0.302, 0.505) | |
| (min, max) (m) 2 | t = 0–20 s | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−0.302, 0.034) |
| t = 5–8 s * | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (0, 0) | (−0.301, 0.032) | |
(min, max) (m) 3 | t = 0–20 s | (−1.025, 0.037) | (−0.891, 0.067) | (−0.777, 0.103) | (−0.138, 0.112) | (0, 0.515) | (−0.551, 0.171) |
| t = 5–8 s * | (−1.019, 0.001) | (−0.884, 0.001) | (−0.773, 0.001) | (−0.133, 0.001) | (0.001, 0.513) | (−0.548, 0.001) | |
| Firing Interval (s) | Gimbal Angles [α, β] (°) | ||||||
|---|---|---|---|---|---|---|---|
| [0, 0] 1 | [0, 30] 1 | [0, 45] 1 | [0, 90] 1 | [0, 120] 1 | [30, 45] 1 | [30, 45] 2 | |
| 0.1 | 0 | 298.8 | −560.5 | 9.460 | 5.982 | 936.0 | −353.1 |
| 1.0 | 0 | 9.921 | 3.657 | −1.743 | −3.530 | 4.519 | −1.450 |
| 2.0 | 0 | 1.606 | 1.650 | −1.417 | 1.459 | 4.069 | −1.276 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Di, L.; Xu, H.; Zeng, W.; Li, W.; Cao, S. Quadrotor Unmanned Aerial Vehicle-Mounted Launch Device Precision Analysis for Countering Intruding Drones. Drones 2025, 9, 42. https://doi.org/10.3390/drones9010042
He Y, Di L, Xu H, Zeng W, Li W, Cao S. Quadrotor Unmanned Aerial Vehicle-Mounted Launch Device Precision Analysis for Countering Intruding Drones. Drones. 2025; 9(1):42. https://doi.org/10.3390/drones9010042
Chicago/Turabian StyleHe, Yanan, Lingsong Di, Huiqi Xu, Weigui Zeng, Wei Li, and Silei Cao. 2025. "Quadrotor Unmanned Aerial Vehicle-Mounted Launch Device Precision Analysis for Countering Intruding Drones" Drones 9, no. 1: 42. https://doi.org/10.3390/drones9010042
APA StyleHe, Y., Di, L., Xu, H., Zeng, W., Li, W., & Cao, S. (2025). Quadrotor Unmanned Aerial Vehicle-Mounted Launch Device Precision Analysis for Countering Intruding Drones. Drones, 9(1), 42. https://doi.org/10.3390/drones9010042






