Categorical-Parallel Adversarial Defense for Perception Models on Single-Board Embedded Unmanned Vehicles
Abstract
1. Introduction
- Identification of significant limitations: We identified substantial limitations in the adversarial training of unmanned vehicles perception models, including challenges associated with quantization for single-board computers and computational complexity arising from the large number of parameters in these models.
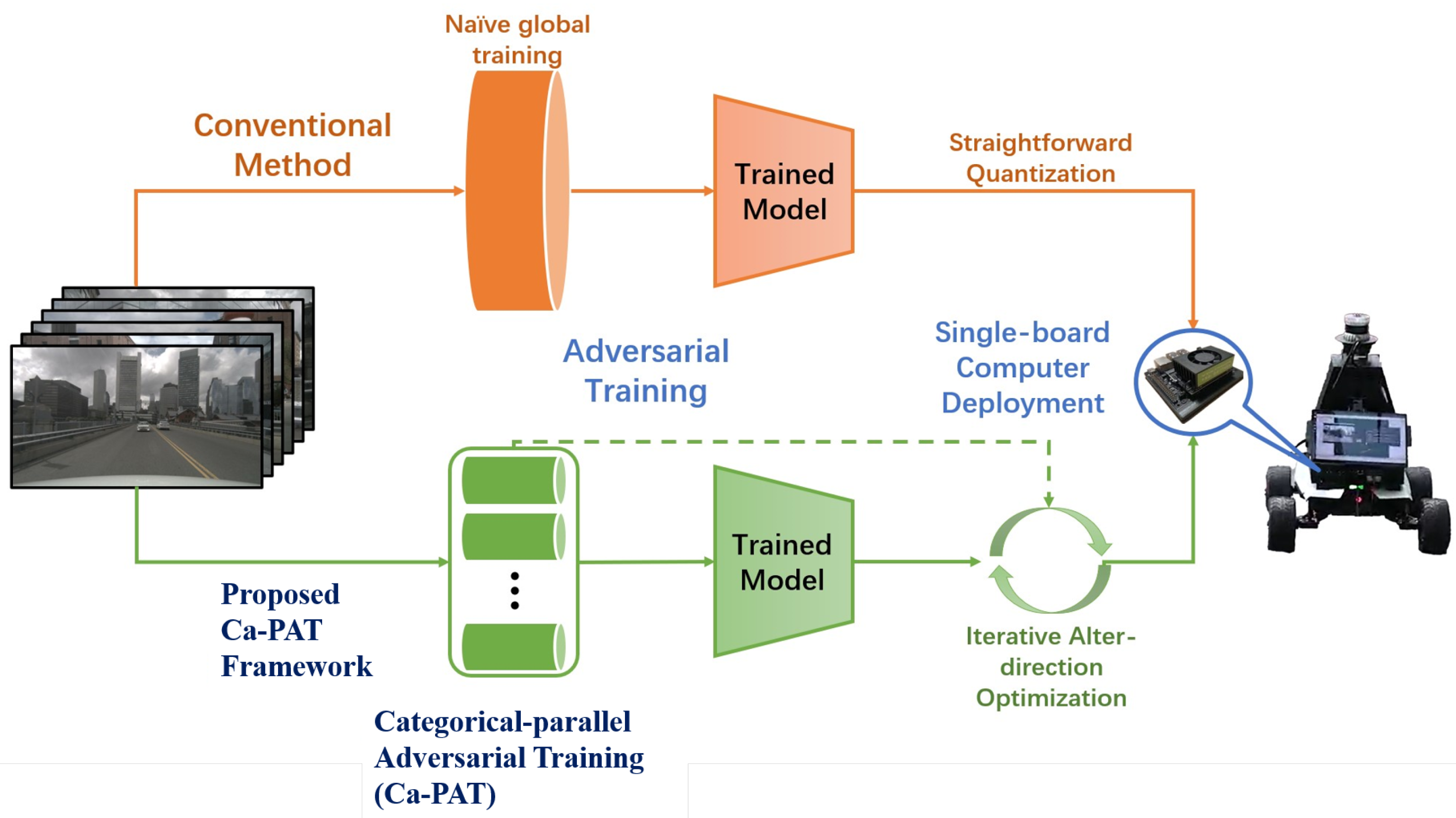
- Proposal of a comprehensive framework: To address these limitations, we introduce an adversarial training framework specifically tailored for perception models, termed Ca-PAT, designed for deployment on real-time single-board computing devices. This framework utilizes the alter-direction optimizer in combination with a novel categorical-parallel adversarial training method to simultaneously train and quantize the models.
- Rationale of the proposed Ca-PAT: We provide a rational proof of the effectiveness of Ca-PAT by deriving its theoretical upper bound during backward propagation.
2. Background and Definition
2.1. Overview of Unmanned Vehicles Perception Models
2.2. Adversarial Training to Enhance Network Robustness
2.3. Motivation of Ca-PAT
3. Categorical-Parallel Adversarial Training for Perception
3.1. Objective
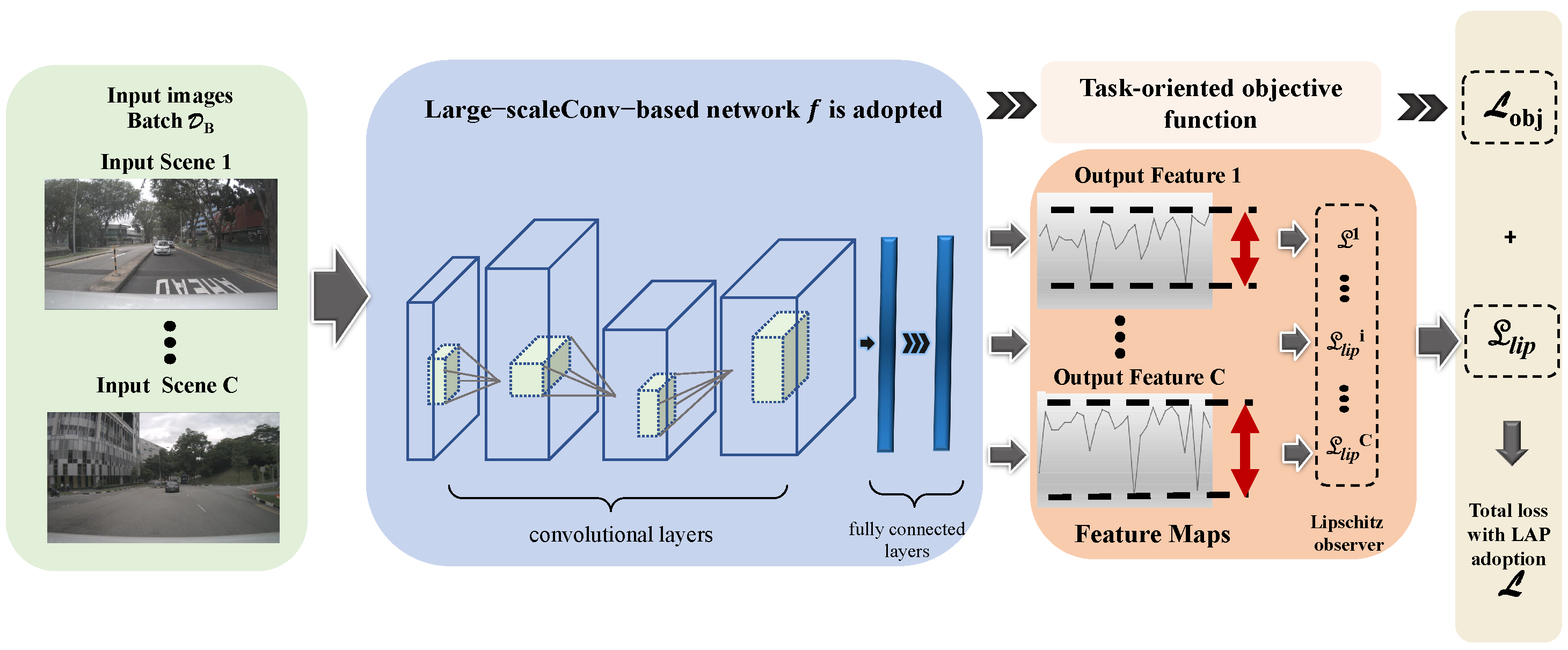
3.2. Categorical-Parallel Mechanism
3.3. Constraint on Categorical-Parallel Training
3.4. Categorical-Parallel Adversarial Training for Perception Module
3.5. Overall Optimization Process
4. Experimental Results
4.1. Datasets
4.2. Experimental Settings
- Baselines. For attack methods, we select five state-of-the-art methods, including Common Corruptions (CC) [28], Projected Gradient Descent (PGD) [29], and Ensemble Attack (Ens) that includes APGD, FAB, and Square Attack [8]. All attacks are conducted with a perturbation set to and a stride length of . Our adversarial images follow the above settings and are generated by iterative gradient ascent of the structural similarity loss, which is shown in (14). In this experiment, we compare the adversarial robustness of our strategy with five different baseline adversarial defense methods, configured in various ways, resulting in eight distinct adversarial defense approaches. The selected baseline defense methods include Robust Library [30], Salman [31], LLR [13], and TRADES [12]. Additionally, we include a baseline referred to as “Clean”, which represents the training without any adversarial examples (AEs). This provides a comparison point for the performance of models trained without adversarial perturbations.
- Implementation Details. All input images are cropped to a size of and processed using a WideResNet [32] for the task. The network architecture includes an initial convolution layer with a stride of 2, followed by three residual blocks with strides . This configuration is designed to demonstrate the effectiveness of our proposed Ca-PAT framework in enabling large-scale DNNs to achieve strong adversarial awareness. Following the established settings for LLR on ImageNet, we set the initial learning rate at 0.1, with a decay factor of 0.1 applied at epochs 35, 70, and 95. Our training regimen spans 100 epochs. For the proposed Ca-PET method, we specified as and as as the hyper-parameters. Additionally, we employed L2-regularization with a strength of 1e-4 and a batch size of 64 for the training process. The experiments are performed on an RTX 3090 GPU paired with an Intel(R) Xeon(R) Gold 5218R CPU, utilizing CUDA version 11.0. This setup provides the necessary computational power and efficiency to validate our approach.
- Evaluation Metrics. To ensure fair comparisons, we applied consistent hyperparameter configurations across all experimental groups. The methodologies evaluated include Robust Library [30], Salman [31], LLR [13], and TRADES [12]. These established approaches were rigorously assessed within the context of the proposed framework to confirm their compatibility and performance. This systematic evaluation allows for a thorough comparison and the identification of potential performance enhancements.
- −
- Robust Library. The Robust Library is a comprehensive toolkit designed for evaluating and improving the robustness of deep learning models against adversarial attacks. It provides a collection of pre-implemented adversarial attack methods and defense strategies, allowing researchers to systematically assess the resilience of their models. This library facilitates reproducible and consistent evaluations, enabling a standardized comparison of different approaches to adversarial robustness.
- −
- Salman. The Salman approach, named after the researchers Salman et al., focuses on adversarial training techniques to enhance model robustness. This methodology incorporates adversarial examples during the training process to improve the model’s ability to resist adversarial perturbations. By systematically exposing the model to challenging adversarial scenarios, the Salman method aims to strengthen the model’s defenses and improve its overall robustness against attacks.
- −
- Lipschitz Linear Regularization. LLR is a defense mechanism that aims to improve the robustness of neural networks by enforcing Lipschitz continuity. This approach introduces a regularization term that controls the Lipschitz constant of the network, ensuring that small changes in the input lead to proportionally small changes in the output. By doing so, LLR helps in mitigating the model’s sensitivity to adversarial perturbations, leading to enhanced stability and robustness against adversarial attacks.
- −
- TRADES. TRADES is an adversarial training framework designed to balance the trade-off between model accuracy and robustness. It introduces a surrogate loss function that explicitly quantifies and manages this trade-off. By optimizing this surrogate loss, TRADES aims to achieve a desirable balance where the model maintains high accuracy on clean data while also being robust against adversarial examples. This approach is particularly effective in scenarios where both accuracy and robustness are critical.
4.3. Learning Performance of Ca-PAT Framework
4.4. Time Complexity Analysis
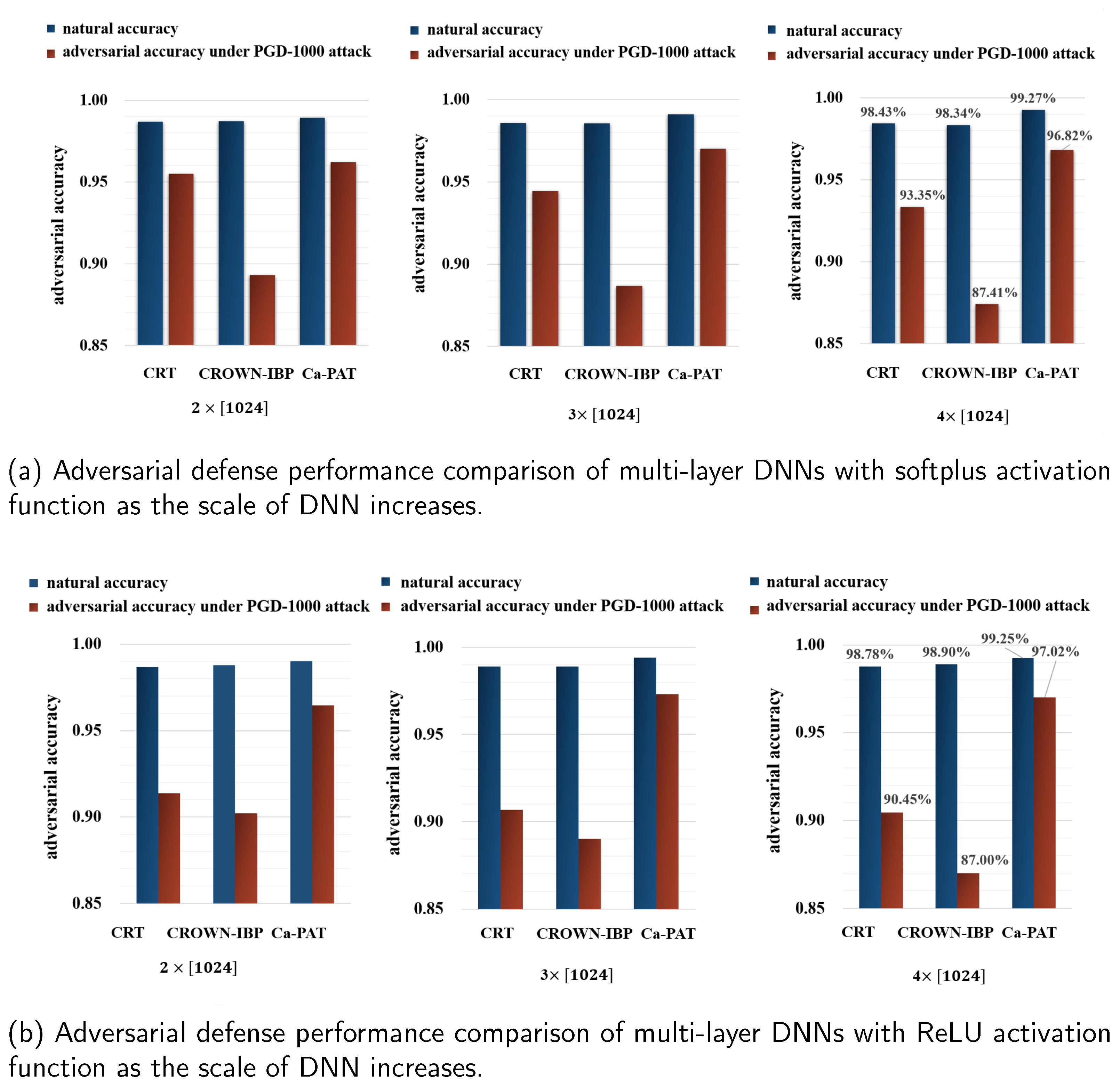
4.5. Effectiveness against Various DNN Sizes
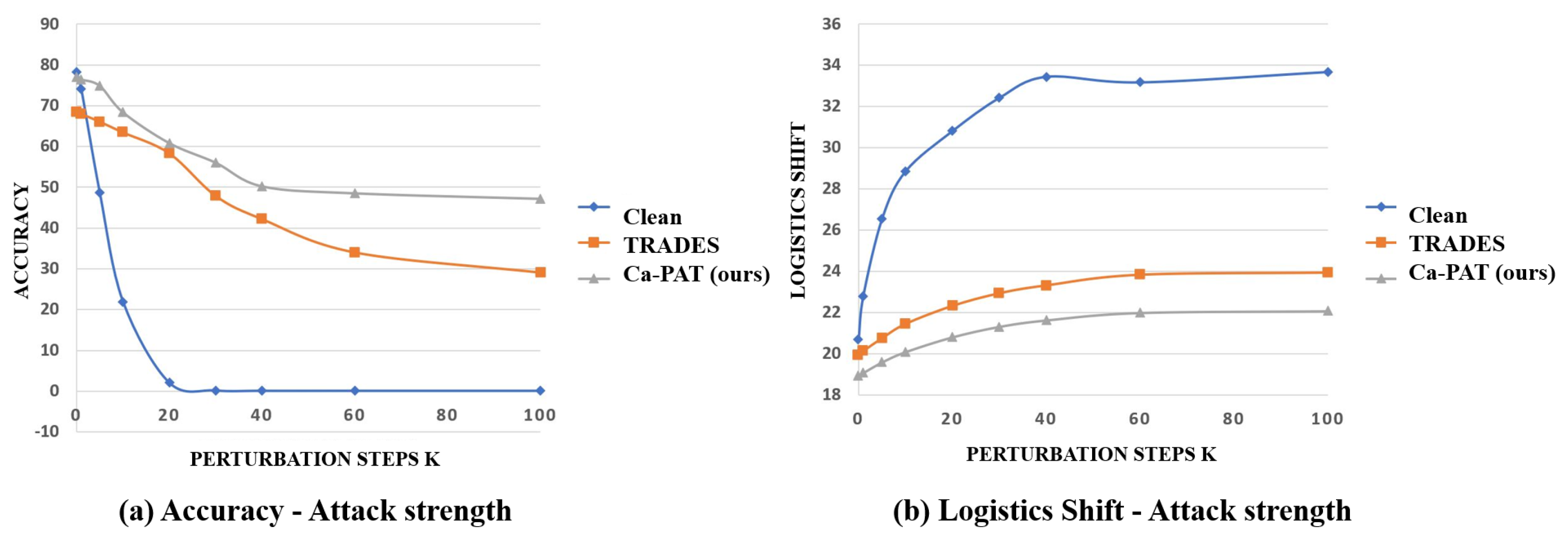
4.6. Effectiveness against Attack Strengths
4.7. End-to-End Evaluation
5. Discussion and Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Ca-PAT | categorical-parallel adversarial training |
| DNN | deep neural networks |
| SLAM | simultaneous localization and mapping |
| FLOPs | floating point operations |
References
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Papernot, N.; McDaniel, P.; Goodfellow, I.; Jha, S.; Celik, Z.B.; Swami, A. Practical black-box attacks against machine learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, Abu Dhabi, United Arab Emirates, 2–6 April 2017; pp. 506–519. [Google Scholar]
- Eykholt, K.; Evtimov, I.; Fernandes, E.; Li, B.; Rahmati, A.; Xiao, C.; Prakash, A.; Kohno, T.; Song, D. Robust physical-world attacks on deep learning visual classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1625–1634. [Google Scholar]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 99–112. [Google Scholar]
- Buckman, J.; Roy, A.; Raffel, C.; Goodfellow, I. Thermometer encoding: One hot way to resist adversarial examples. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April 30–3 May 2018. [Google Scholar]
- Huang, L.; Joseph, A.D.; Nelson, B.; Rubinstein, B.I.; Tygar, J.D. Adversarial machine learning. In Proceedings of the 4th ACM Workshop on Security and Artificial Intelligence, Chicago, IL, USA, 21 October 2011; pp. 43–58. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Croce, F.; Hein, M. Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 13–18 July 2020. [Google Scholar]
- Athalye, A.; Carlini, N.; Wagner, D. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. In Proceedings of the International Conference on Machine Learning, Stockholm Sweden, 10–15 July 2018; PMLR: Birmingham, UK, 2018; pp. 274–283. [Google Scholar]
- Shafahi, A.; Najibi, M.; Ghiasi, A.; Xu, Z.; Dickerson, J.; Studer, C.; Davis, L.S.; Taylor, G.; Goldstein, T. Adversarial training for free! arXiv 2019, arXiv:1904.12843. [Google Scholar]
- Tramèr, F.; Kurakin, A.; Papernot, N.; Goodfellow, I.; Boneh, D.; McDaniel, P. Ensemble adversarial training: Attacks and defenses. arXiv 2017, arXiv:1705.07204. [Google Scholar]
- Zhang, H.; Yu, Y.; Jiao, J.; Xing, E.; El Ghaoui, L.; Jordan, M. Theoretically principled trade-off between robustness and accuracy. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR: Birmingham, UK, 2019; pp. 7472–7482. [Google Scholar]
- Qin, C.; Martens, J.; Gowal, S.; Krishnan, D.; Dvijotham, K.; Fawzi, A.; De, S.; Stanforth, R.; Kohli, P. Adversarial robustness through local linearization. arXiv 2019, arXiv:1907.02610. [Google Scholar]
- Tsipras, D.; Santurkar, S.; Engstrom, L.; Turner, A.; Madry, A. Robustness may be at odds with accuracy. arXiv 2018, arXiv:1805.12152. [Google Scholar]
- Thrun, S. Simultaneous Localization and Mapping. In Robotics and Cognitive Approaches to Spatial Mapping; Jefferies, M.E., Yeap, W.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 13–41. [Google Scholar] [CrossRef]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the COMPSTAT’2010, Paris, France, 22–27 August 2010; pp. 177–186. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Dutta, S.; Jha, S.; Sankaranarayanan, S.; Tiwari, A. Output range analysis for deep feedforward neural networks. In Proceedings of the NASA Formal Methods Symposium, Newport News, VA, USA, 17–19 April 2018; Springer: Cham, Switzerland, 2018; pp. 121–138. [Google Scholar]
- Ehlers, R. Formal verification of piece-wise linear feed-forward neural networks. In Proceedings of the International Symposium on Automated Technology for Verification and Analysis, Pune, India, 3–6 October 2017; Springer: Cham, Switzerland, 2017; pp. 269–286. [Google Scholar]
- Ruan, W.; Huang, X.; Kwiatkowska, M. Reachability analysis of deep neural networks with provable guarantees. arXiv 2018, arXiv:1805.02242. [Google Scholar]
- Sun, S.; Zhang, Y.; Luo, X.; Vlantis, P.; Pajic, M.; Zavlanos, M.M. Formal Verification of Stochastic Systems with ReLU Neural Network Controllers. arXiv 2021, arXiv:2103.05142. [Google Scholar]
- Ghadimi, E.; Teixeira, A.; Shames, I.; Johansson, M. Optimal parameter selection for the alternating direction method of multipliers (ADMM): Quadratic problems. IEEE Trans. Autom. Control 2014, 60, 644–658. [Google Scholar] [CrossRef]
- Fazlyab, M.; Robey, A.; Hassani, H.; Morari, M.; Pappas, G.J. Efficient and accurate estimation of lipschitz constants for deep neural networks. arXiv 2019, arXiv:1906.04893. [Google Scholar]
- Latorre, F.; Rolland, P.; Cevher, V. Lipschitz constant estimation of neural networks via sparse polynomial optimization. arXiv 2020, arXiv:2004.08688. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuScenes: A multimodal dataset for autonomous driving. arXiv 2019, arXiv:1903.11027. [Google Scholar]
- Hendrycks, D.; Dietterich, T. Benchmarking Neural Network Robustness to Common Corruptions and Perturbations. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Engstrom, L.; Ilyas, A.; Salman, H.; Santurkar, S.; Tsipras, D. Robustness (Python Library). 2019, Volume 4, pp. 3–4. Available online: https://github.com/MadryLab/robustness (accessed on 21 July 2024).
- Salman, H.; Ilyas, A.; Engstrom, L.; Kapoor, A.; Madry, A. Do Adversarially Robust ImageNet Models Transfer Better? arXiv 2020, arXiv:2007.08489. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide residual networks. arXiv 2016, arXiv:1605.07146. [Google Scholar]
- Singla, S.; Feizi, S. Second-order provable defenses against adversarial attacks. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; PMLR: Birmingham, UK, 2020; pp. 8981–8991. [Google Scholar]
- Zhang, H.; Chen, H.; Xiao, C.; Gowal, S.; Stanforth, R.; Li, B.; Boning, D.; Hsieh, C.J. Towards stable and efficient training of verifiably robust neural networks. arXiv 2019, arXiv:1906.06316. [Google Scholar]
- Wong, E.; Kolter, Z. Provable defenses against adversarial examples via the convex outer adversarial polytope. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 5286–5295. [Google Scholar]
- Scout-2.0. Available online: https://www.iquotient-robotics.com/fuzhishouye.html (accessed on 22 May 2024).


| Parameter | Notation |
|---|---|
| input | |
| ground truth with respect to | |
| Dataset | |
| the objective function of the network | |
| DNN-based classifier | |
| adversarial perturbation | |
| maximum magnitude of | |
| Lipschitz Constant | |
| Lipschitz Constant over category i | |
| N dimensional space | |
| sup | supreme |
| p norm distance, | |
| , | the order of norm |
| the feature map from any conv layer |
| Nature b | CC-20 | CC-40 | CC-100 | |
| Clean a | ||||
| TRADES [12] | ||||
| LLR [13] | ||||
| RobustLib [30] | ||||
| Salman [31] | ||||
| Ca-PAT (ours) | ||||
| Nature b | PGD-20 | PGD-40 | PGD-100 | |
| Clean a | ||||
| TRADES [12] | ||||
| LLR [13] | ||||
| RobustLib [30] | ||||
| Salman [31] | ||||
| Ca-PAT (ours) | ||||
| Nature b | Ens-20 | Ens-40 | Ens-100 | |
| Clean a | ||||
| TRADES [12] | ||||
| LLR [13] | ||||
| RobustLib [30] | ||||
| Salman [31] | ||||
| Ca-PAT (ours) |
| Attacks | Def. Mtd. | Clean | Itr-20 | Itr-40 | Itr-100 |
|---|---|---|---|---|---|
| CC | Clean | 32.49 | 9.24 | 6.54 | 3.78 |
| TRADES [12] | 23.05 | 14.71 | 11.62 | 9.97 | |
| LLR [13] | 22.95 | 15.73 | 11.73 | 10.07 | |
| RobustLib [30] | 22.38 | 13.83 | 10.81 | 8.63 | |
| Salman [31] | 21.71 | 21.64 | 16.19 | 13.06 | |
| Ca-PAT (ours) | 22.33 | 20.62 | 19.71 | 18.13 | |
| PGD | Clean | - | 2.61 | 1.16 | 0.97 |
| TRADES [12] | - | 13.69 | 10.86 | 9.36 | |
| LLR [13] | - | 14.63 | 10.71 | 9.44 | |
| RobustLib [30] | - | 12.85 | 10.14 | 7.92 | |
| Salman [31] | - | 20.05 | 15.08 | 12.17 | |
| Ca-PAT (ours) | - | 19.07 | 17.97 | 17.12 | |
| Ens | Clean | - | 1.96 | 0.98 | 0.58 |
| TRADES [12] | - | 19.61 | 17.90 | 17.31 | |
| LLR [13] | - | 19.54 | 18.00 | 17.18 | |
| RobustLib [30] | - | 19.18 | 17.59 | 16.94 | |
| Salman [31] | - | 18.57 | 17.11 | 16.43 | |
| Ca-PAT (ours) | - | 19.02 | 17.44 | 16.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Fan, X.; Sun, S.; Lu, Y.; Liu, N. Categorical-Parallel Adversarial Defense for Perception Models on Single-Board Embedded Unmanned Vehicles. Drones 2024, 8, 438. https://doi.org/10.3390/drones8090438
Li Y, Fan X, Sun S, Lu Y, Liu N. Categorical-Parallel Adversarial Defense for Perception Models on Single-Board Embedded Unmanned Vehicles. Drones. 2024; 8(9):438. https://doi.org/10.3390/drones8090438
Chicago/Turabian StyleLi, Yilan, Xing Fan, Shiqi Sun, Yantao Lu, and Ning Liu. 2024. "Categorical-Parallel Adversarial Defense for Perception Models on Single-Board Embedded Unmanned Vehicles" Drones 8, no. 9: 438. https://doi.org/10.3390/drones8090438
APA StyleLi, Y., Fan, X., Sun, S., Lu, Y., & Liu, N. (2024). Categorical-Parallel Adversarial Defense for Perception Models on Single-Board Embedded Unmanned Vehicles. Drones, 8(9), 438. https://doi.org/10.3390/drones8090438






