A Minimal Solution Estimating the Position of Cameras with Unknown Focal Length with IMU Assistance
Abstract
1. Introduction
- We propose a minimal solution, using auxiliary information provided by the IMU, to determine the relative pose and focal lengths for cameras with unknown and variable focal lengths during random and planar motions.
- We propose a degenerated model designed to address the situation where cameras with unknown and fixed focal lengths undergo planar motion.
- We provide a degenerated model for estimating the relative pose and focal length between a fully calibrated camera and a camera with an unknown focal length.
2. Related Work
3. Minimal Solution Solver
3.1. Different and Unknown Focal Lengths
3.1.1. Random Motion Model
3.1.2. Planar Motion Model
3.2. Fixed and Unknown Focal Lengths for Planar Motion
3.3. Unknown Focal Length for One Side
4. Experiments
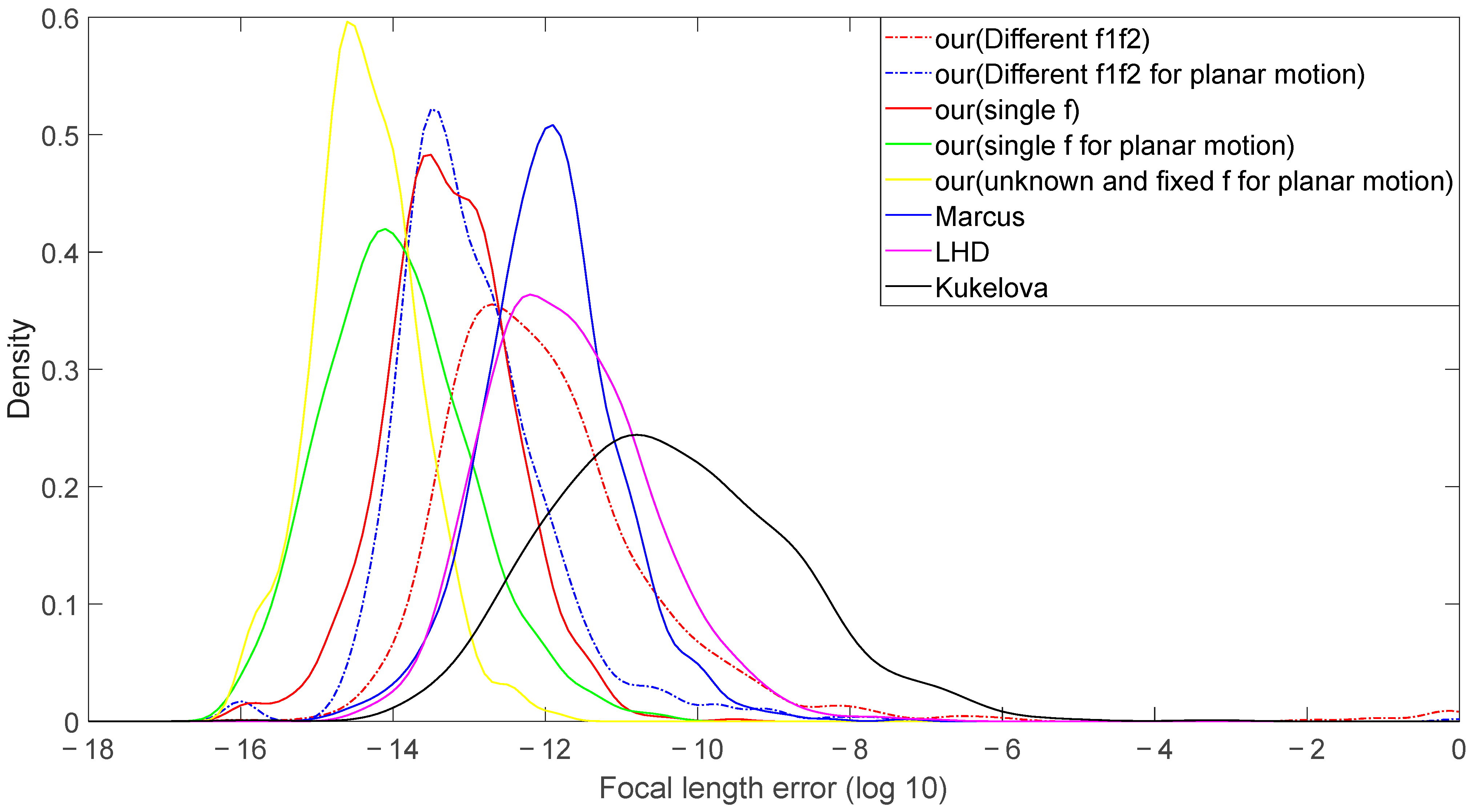
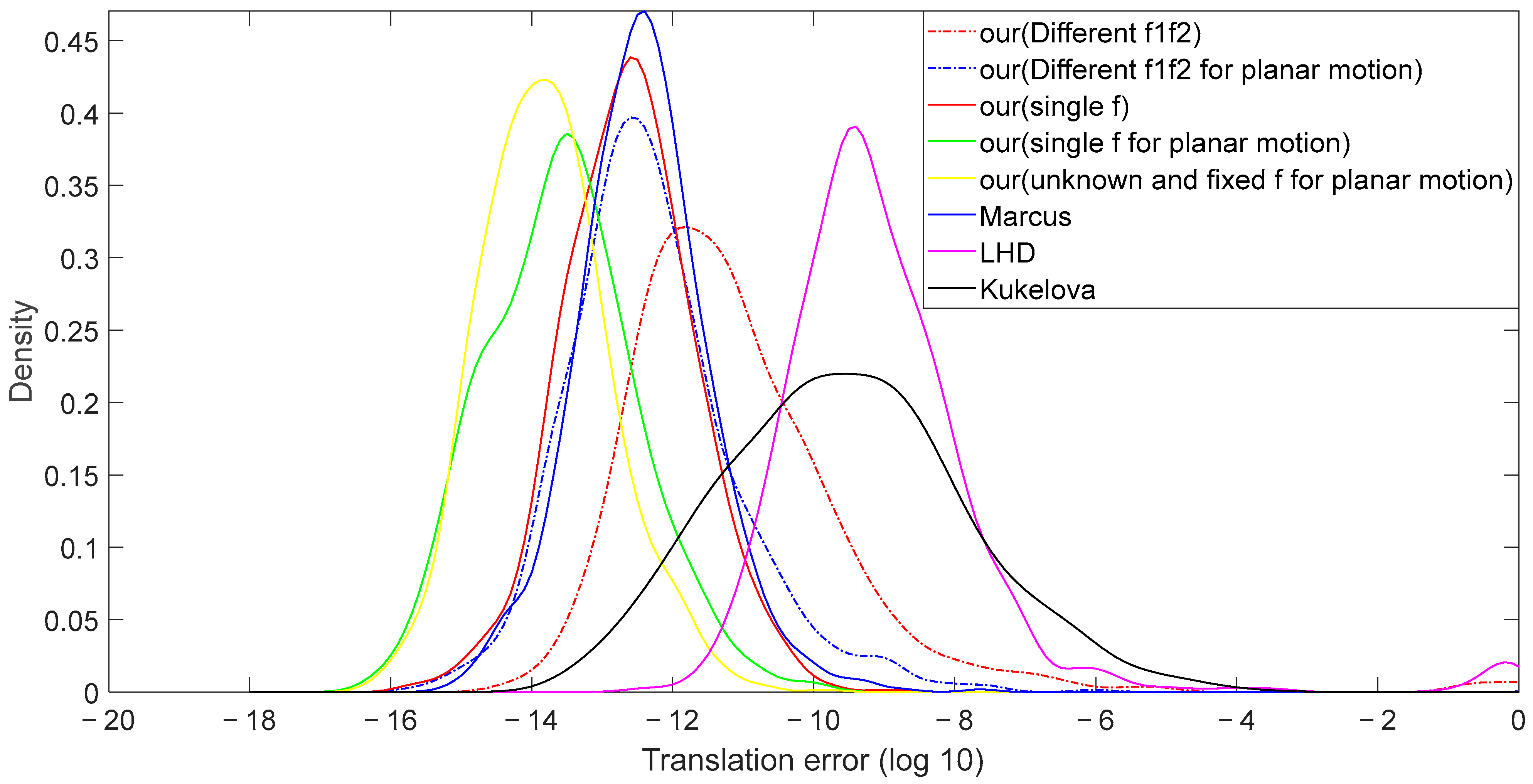
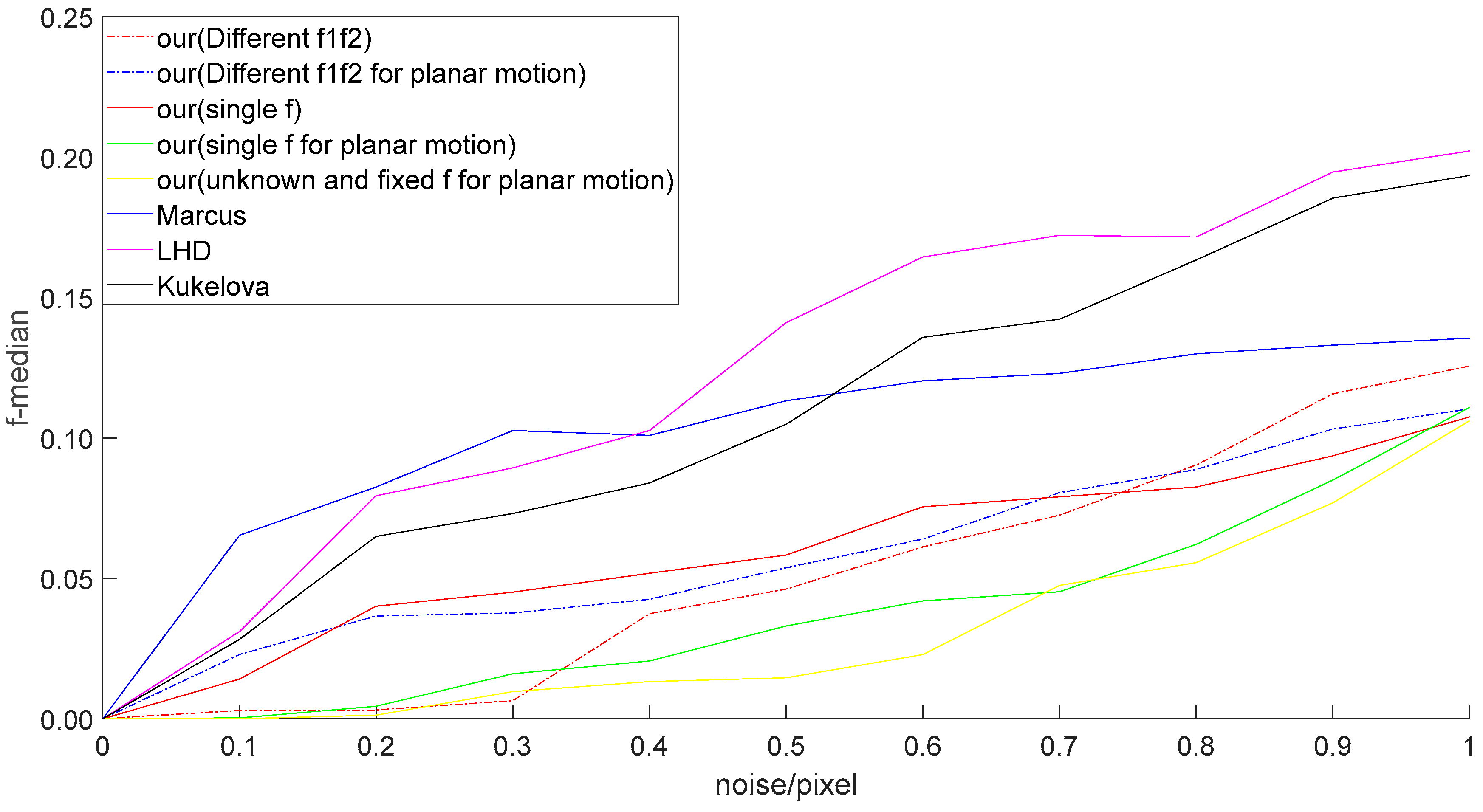
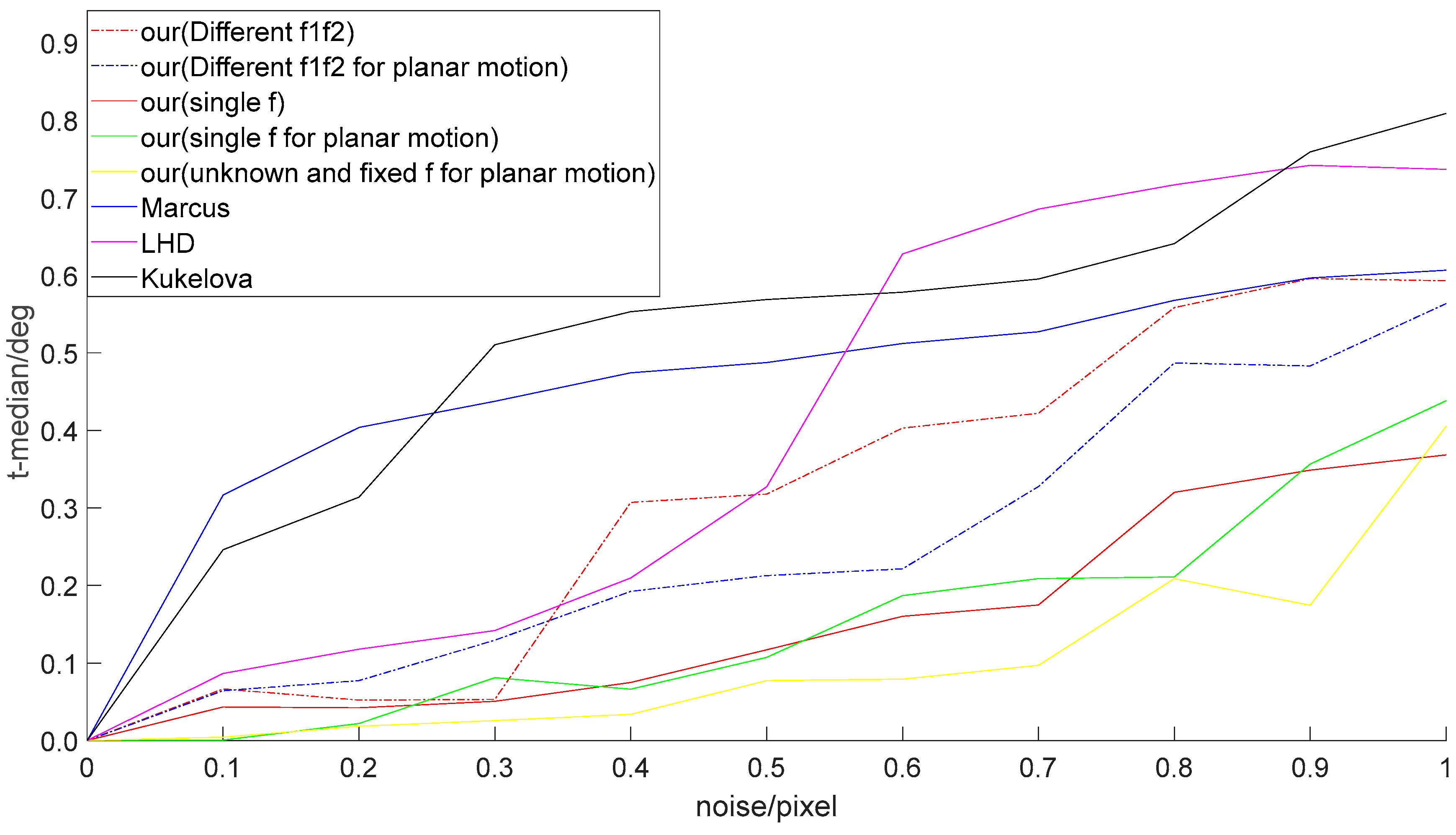
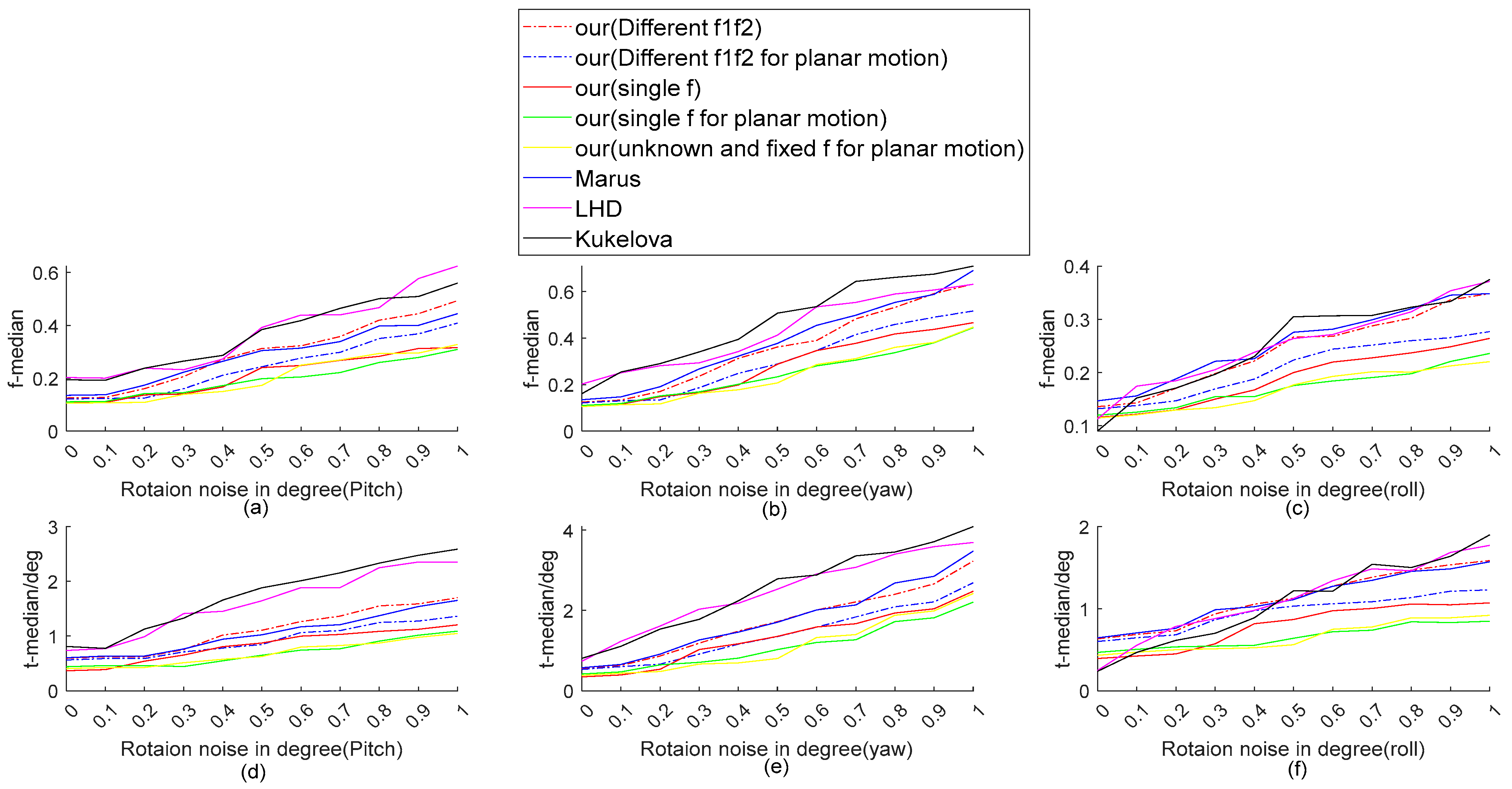
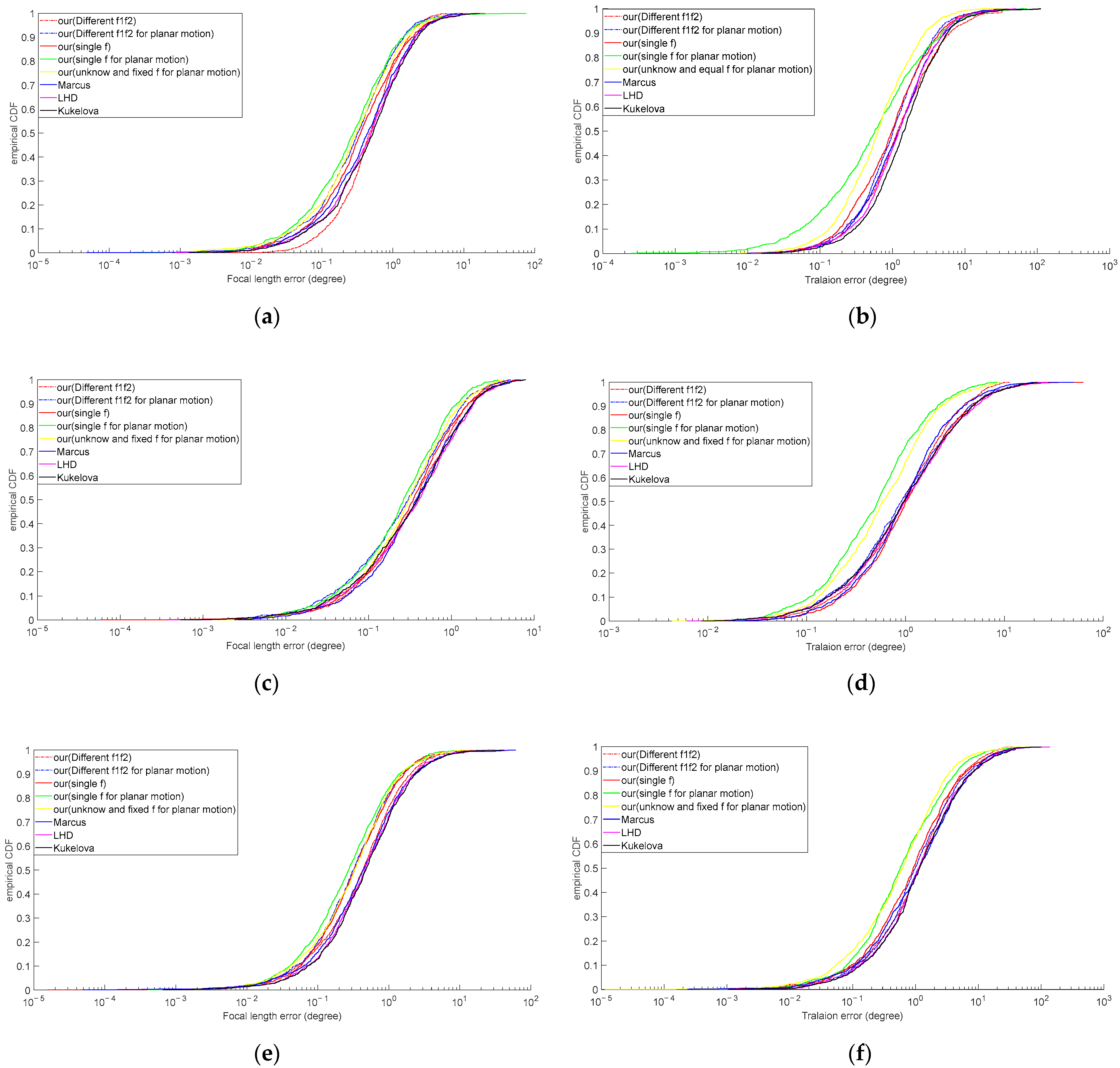
4.1. Synthetic Data
4.2. Real Data
4.2.1. Data Description
4.2.2. Relative Pose Analysis
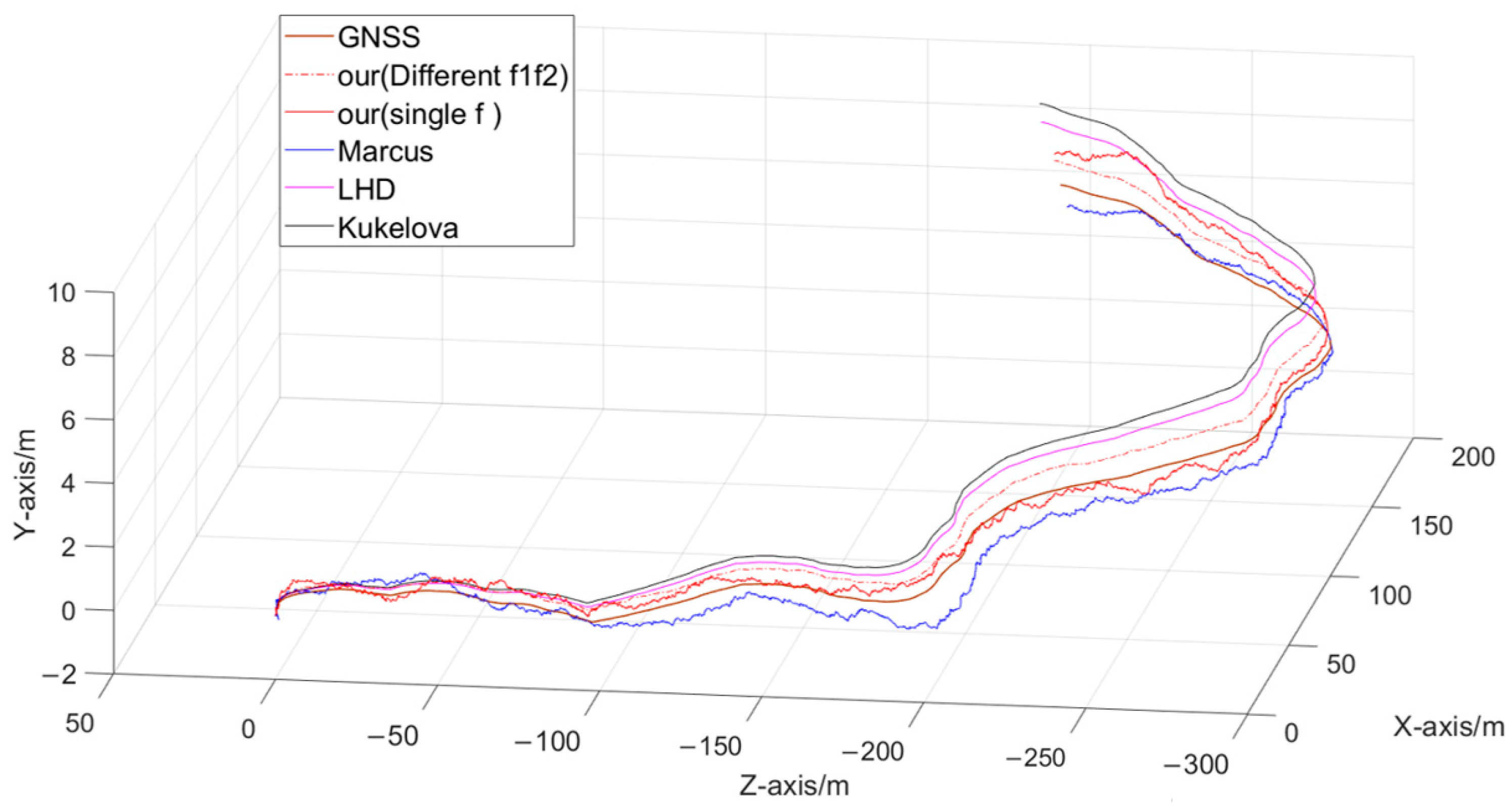
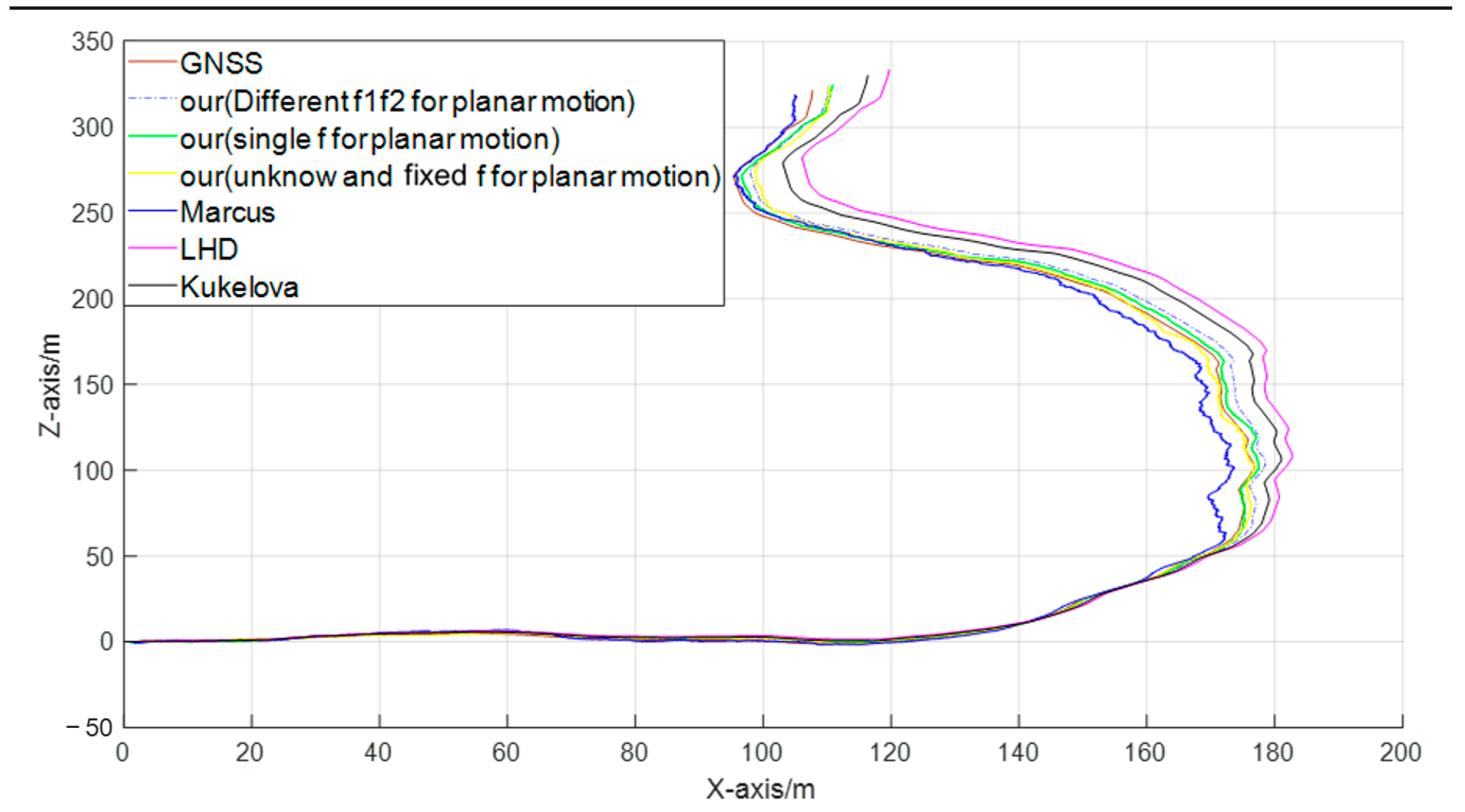
4.2.3. Position Estimation Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Ban, X.; Ding, F.; Xiao, Y.; Zhou, J. Monocular VO Based on Deep Siamese Convolutional Neural Network. Complexity 2020, 2020, 6367273. [Google Scholar] [CrossRef]
- Wang, K.; Ma, S.; Chen, J.L.; Ren, F.; Lu, J.B. Approaches, Challenges, and Applications for Deep Visual Odometry: Toward Complicated and Emerging Areas. IEEE Trans. Cogn. Dev. Syst. 2022, 14, 35–49. [Google Scholar] [CrossRef]
- Chen, J.; Xie, F.; Huang, L.; Yang, J.; Liu, X.; Shi, J. A Robot Pose Estimation Optimized Visual SLAM Algorithm Based on CO-HDC Instance Segmentation Network for Dynamic Scenes. Remote Sens. 2022, 14, 2114. [Google Scholar] [CrossRef]
- Hao, G.T.; Du, X.P.; Song, J.J. Relative Pose Estimation of Space Tumbling Non cooperative Target Based on Vision only SLAM. J. Astronaut. 2015, 36, 706–714. [Google Scholar]
- Yin, Z.; Wen, H.; Nie, W.; Zhou, M. Localization of Mobile Robots Based on Depth Camera. Remote Sens. 2023, 15, 4016. [Google Scholar] [CrossRef]
- Barath, D.; Mishkin, D.; Eichhardt, I.; Shipachev, I.; Matas, J. Efficient Initial Pose-graph Generation for Global SfM. In Proceedings of the Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Liang, Y.; Yang, Y.; Mu, Y.; Cui, T. Robust Fusion of Multi-Source Images for Accurate 3D Reconstruction of Complex Urban Scenes. Remote Sens. 2023, 15, 5302. [Google Scholar] [CrossRef]
- Kalantari, M.; Hashemi, A.; Jung, F.; Guedon, J.-P. A New Solution to the Relative Orientation Problem Using Only 3 Points and the Vertical Direction. J. Math. Imaging Vis. 2011, 39, 259–268. [Google Scholar] [CrossRef]
- Barath, D.; Toth, T.; Hajder, L. A Minimal Solution for Two-view Focal-length Estimation using Two Affine Correspondences. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Mach, C.A.C. Random Sample Consensus: A paradigm for model fitting with application to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar]
- Hajder, L.; Barath, D. Relative planar motion for vehicle-mounted cameras from a single affine correspondence. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Choi, S.-I.; Park, S.-Y. A new 2-point absolute pose estimation algorithm under planar motion. Adv. Robot. 2015, 29, 1005–1013. [Google Scholar] [CrossRef]
- Fraundorfer, F.; Tanskanen, P.; Pollefeys, M. A Minimal Case Solution to the Calibrated Relative Pose Problem for the Case of Two Known Orientation Angles. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Ding, Y.; Barath, D.; Yang, J.; Kong, H.; Kukelova, Z. Globally Optimal Relative Pose Estimation with Gravity Prior. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Ding, Y.; Yang, J.; Kong, H. An efficient solution to the relative pose estimation with a common direction. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Saurer, O.; Vasseur, P.; Boutteau, R.; Demonceaux, C.; Pollefeys, M.; Fraundorfer, F. Homography Based Egomotion Estimation with a Common Direction. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 327–341. [Google Scholar] [CrossRef] [PubMed]
- Sweeney, C.; Flynn, J.; Turk, M. Solving for Relative Pose with a Partially Known Rotation is a Quadratic Eigenvalue Problem. In Proceedings of the 2014 2nd International Conference on 3D Vision, Tokyo, Japan, 8–11 December 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Li, H. A simple solution to the six-point two-view focal-length problem. In Computer Vision-ECCV 2006, Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006, Proceedings, Part IV 9; Leonardis, A., Bischof, H., Pinz, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3954, pp. 200–213. [Google Scholar]
- Hartley, R.; Li, H. An Efficient Hidden Variable Approach to Minimal-Case Camera Motion Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2303–2314. [Google Scholar] [CrossRef] [PubMed]
- Stewenius, H.; Nister, D.; Kahl, F.; Schaffalitzky, F. A minimal solution for relative pose with unknown focal length. In Proceedings of the IEEE Computer Society Conference on Computer Vision & Pattern Recognition, San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Bujnak, M.; Kukelova, Z.; Pajdla, T. 3D reconstruction from image collections with a single known focal length. In Proceedings of the IEEE International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009. [Google Scholar]
- Torii, A.; Kukelova, Z.; Bujnak, M.; Pajdla, T. The Six Point Algorithm Revisited. In Proceedings of the Computer Vision–ACCV 2010 Workshops: ACCV 2010 International Workshops, Queenstown, New Zealand, 8–9 November 2010. [Google Scholar]
- Kukelova, Z.; Bujnak, M.; Pajdla, T. Polynomial Eigenvalue Solutions to Minimal Problems in Computer Vision. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1381–1393. [Google Scholar] [CrossRef] [PubMed]
- Hedborg, J.; Felsberg, M. Fast iterative five point relative pose estimation. In Proceedings of the 2013 IEEE Workshop on Robot Vision (WORV), Clearwater Beach, FL, USA, 15–17 January 2013. [Google Scholar]
- Kukelova, Z.; Kileel, J.; Sturmfels, B.; Pajdla, T. A clever elimination strategy for efficient minimal solvers. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Bougnoux, S. From projective to Euclidean space under any practical situation, a criticism of self-calibration. In Proceedings of the International Conference on Computer Vision, Bombay, India, 4–7 January 1998. [Google Scholar]
- Hartley, R.I. Estimation of Relative Camera Positions for Uncalibrated Cameras. In Computer Vision—ECCV’92: Second European Conference on Computer Vision Santa Margherita Ligure, Italy, May 19–22, 1992 Proceedings 2; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Li, H.; Hartley, R. A Non-Iterative Method for Correcting Lens Distortion from Nine Point Correspondences; OMNIVIS: South San Francisco, CA, USA, 2009. [Google Scholar]
- Jiang, F.; Kuang, Y.; Solem, J.E.; Åström, K. A Minimal Solution to Relative Pose with Unknown Focal Length and Radial Distortion; Springer International Publishing: Cham, Switzerland, 2015; pp. 443–456. [Google Scholar]
- Oskarsson, M. Fast Solvers for Minimal Radial Distortion Relative Pose Problems. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 3663–3672. [Google Scholar]
- Rnhag, M.V.; Persson, P.; Wadenbck, M.; Strm, K.; Heyden, A. Trust Your IMU: Consequences of Ignoring the IMU Drift. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Savage, P.G. Strapdown Analytics; Strapdown Associates: Maple Plain, MN, USA, 2000. [Google Scholar]
- Larsson, V.; Oskarsson, M.; Astrom, K.; Wallis, A.; Kukelova, Z. Beyond Grobner Bases: Basis Selection for Minimal Solvers. In Proceedings of the IEEE/CVF Conference on Computer Vision & Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Stewénius, H.; Engels, C.; Nistér, D. An Efficient Minimal Solution for Infinitesimal Camera Motion. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007. [Google Scholar]
- Byrod, M.; Josephson, K.; Astrom, K. Fast and Stable Polynomial Equation Solving and Its Application to Computer Vision. Int. J. Comput. Vis. 2009, 84, 237–256. [Google Scholar] [CrossRef]
- Cardano, G.; Witmer, T.R.; Ore, O. The Great Art or the Rules of Algebra; Dover Publications: New York, NY, USA, 1968. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Key-points. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]


| Methods | Minimum Points Required | Estimated Parameters | Motion Model |
|---|---|---|---|
| Different f1f2 | 4 | f1 f2 t | Random motion |
| Different f1f2 for planar motion | 3 | f1 f2 t | Planar motion |
| Single f | 3 | f t | Random motion |
| Single f for planar motion | 2 | f t | Planar motion |
| Unknown and fixed f for planar motion | 2 | f t | Planar motion |
| -Median/Pixel | -Median/Deg | |
|---|---|---|
| Marcus [32] | 1.1023 × 10−13 | 3.7090 × 10−13 |
| LHD [19] | 1.6473 × 10−12 | 5.3201 × 10−10 |
| Kukelova [24] | 3.1238 × 10−11 | 2.3635 × 10−10 |
| Different f1f2 | 1.3707 × 10−13 | 4.0739 × 10−13 |
| Different f1f2 for planar motion | 7.8180 × 10−15 | 9.6702 × 10−14 |
| Unknown and fixed f for planar motion | 1.3309 × 10−15 | 3.6772 × 10−15 |
| Single f | 9.8511 × 10−15 | 3.0763 × 10−14 |
| Single f for planar motion | 1.5763 × 10−15 | 3.5108 × 10−16 |
| Reprojection Error/Pixel | |
|---|---|
| Marcus [32] | 8.1885 × 10−13 |
| LHD [19] | 3.2519 × 10−12 |
| Kukelova [24] | 5.8134 × 10−11 |
| Different f1f2 | 7.8529 × 10−13 |
| Different f1f2 for planar motion | 5.2568 × 10−14 |
| Unknown and fixed f for planar motion | 7.7419 × 10−15 |
| Single f | 4.1573 × 10−14 |
| Single f for planar motion | 6.8135 × 10−15 |
| Parameter | Value | |
|---|---|---|
| Gyroscope | Range | ±300°/s |
| Angular random walk | 0.1 deg/√h | |
| In-run bias stability | 0.5 deg/h | |
| Bias repeatability | 0.5 deg/h | |
| Scale factor error | 300 ppm | |
| Accelerometer | Range | ±10 g |
| In-run bias stability | 0.3 mg | |
| Bias repeatability | 0.3 mg | |
| Scale factor error | 300 ppm |
| 1 | 2 | 3 | |||||
|---|---|---|---|---|---|---|---|
| Marcus [32] | Median | 0.4423 | 1.2126 | 0.3845 | 0.9842 | 0.4352 | 1.1189 |
| SD | 2.5118 | 4.6214 | 2.7978 | 4.3154 | 3.2684 | 4.9851 | |
| LHD [19] | Median | 0.4947 | 1.2342 | 0.4153 | 1.0059 | 0.4585 | 1.1216 |
| SD | 3.8273 | 5.1056 | 4.3158 | 6.6517 | 4.5627 | 8.6149 | |
| Kukelova [24] | Median | 0.5253 | 1.4352 | 0.3975 | 0.9818 | 0.4737 | 1.1587 |
| SD | 4.8628 | 7.5157 | 3.5159 | 8.3173 | 3.9791 | 5.9004 | |
| Different f1f2 | Median | 0.4707 | 1.1739 | 0.3809 | 0.9647 | 0.4336 | 1.1358 |
| SD | 2.4891 | 3.4239 | 2.3513 | 2.9058 | 2.6125 | 3.2268 | |
| Different f1f2 for planar motion | Median | 0.3173 | 1.0208 | 0.3047 | 0.9155 | 0.3159 | 0.9853 |
| SD | 2.1041 | 2.8518 | 2.2318 | 2.6517 | 2.3361 | 3.0156 | |
| Unknown and fixed f for planar motion | Median | 0.3058 | 0.6347 | 0.3114 | 0.5919 | 0.2931 | 0.6241 |
| SD | 1.9194 | 2.1273 | 2.0181 | 2.3158 | 1.9180 | 2.2368 | |
| Single f | Median | 0.3513 | 0.9766 | 0.3505 | 1.0183 | 0.3269 | 0.9186 |
| SD | 1.8108 | 2.2539 | 1.9173 | 2.1586 | 1.7689 | 1.9627 | |
| Single f for planar motion | Median | 0.2761 | 0.5706 | 0.2654 | 0.5286 | 0.2719 | 0.5697 |
| SD | 1.4931 | 1.6817 | 1.4168 | 1.8817 | 1.5217 | 1.8136 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, K.; Yu, Z.; Song, C.; Zhang, H.; Chen, D. A Minimal Solution Estimating the Position of Cameras with Unknown Focal Length with IMU Assistance. Drones 2024, 8, 423. https://doi.org/10.3390/drones8090423
Yan K, Yu Z, Song C, Zhang H, Chen D. A Minimal Solution Estimating the Position of Cameras with Unknown Focal Length with IMU Assistance. Drones. 2024; 8(9):423. https://doi.org/10.3390/drones8090423
Chicago/Turabian StyleYan, Kang, Zhenbao Yu, Chengfang Song, Hongping Zhang, and Dezhong Chen. 2024. "A Minimal Solution Estimating the Position of Cameras with Unknown Focal Length with IMU Assistance" Drones 8, no. 9: 423. https://doi.org/10.3390/drones8090423
APA StyleYan, K., Yu, Z., Song, C., Zhang, H., & Chen, D. (2024). A Minimal Solution Estimating the Position of Cameras with Unknown Focal Length with IMU Assistance. Drones, 8(9), 423. https://doi.org/10.3390/drones8090423






