Validation in X-Plane of Control Schemes for Taking off and Landing Manoeuvres of Quadrotors

Abstract

This paper shows the results obtained by using MATLAB/Simulink and X-Plane as co-simulation tools for the comparison of control schemes for takeoff and landing maneuvers of a quadrotor. Two control schemes based on nested saturations are compared to ensure the convergence of $\theta$ and $\varphi$ angles to the equilibrium point, each with its own specific characteristics in its design and tuning procedure. Furthermore, in both proposals, a Generalized Proportional Integral (GPI) control is used for the height part, while a feedforward PID control is used for the $\psi$ angle. The control schemes are proposed from a local geodetic coordinate system East, North, Up (ENU). Feedback data for the control schemes are obtained from X-Plane via User Datagram Protocol (UDP)-based interface; they are used in MATLAB/Simulink for the calculation of the control actions; the control actions are then entered into a transformation matrix that converts the actions into rotor angular velocities, which are sent to X-Plane. Several numerical simulations are presented to demonstrate the effectiveness and robustness of the proposed schemes, considering the presence of disturbances mainly due to wind speed. Finally, different performance indices are used to evaluate the schemes based on error; in this way, the use of X-Plane as a Model-in-Loop (MIL) environment is validated, which helps to identify errors or problems of the proposed controllers before their coding and physical implementation.

1. Introduction

Control schemes for quadrotor-type Unmanned Aerial Vehicles (UAV) have developed very rapidly in recent years and have been a pillar in the advancement of the science and technology of dynamic systems. Despite the above, there are still several problems related to the design of flight controllers, since there are no general laws applicable to these vehicles [1]. This problem is aggravated by several factors mainly due to the underacting property of this vehicle and its non-linear dynamics, as well as unmodeled dynamics and exogenous disturbances and poor estimation or measurement of moments of inertia and aerodynamic coefficients [2,3].

One of the main challenges for these vehicles is landing, which is affected by several factors, such as the presence of an air cushion during the maneuver; aerodynamic effects and environmental conditions [4,5]. Several studies have focused on the design of control algorithms at the simulation level, with MATLAB being the most used software [1,6]. Matlab offers complete freedom to define the dynamics of the UAV; however, the complexity of having to derive all flight dynamics often leads to oversimplifications or very basic PID flight controllers [7].

It is well known that the effectiveness of simulation depends on an accurate mathematical model, which is difficult to obtain. Flight simulators offer the advantage of taking advantage of the calculation of flight dynamics, as well as more complete results that would otherwise require too many hours of development, such as weather, 3D scenarios, elevation maps, advanced visualization functions, etc. [7]. Thus, the use of co-simulation tools with a high degree of precision such as a real flight contributes to verifying the control scheme and improving development efficiency [8]. The flight simulator X-Plane is widely used to develop and test flight control schemes [9].

X-Plane is one of the most realistic flight simulators in the world, it is used by different industries, such as the air force and aircraft manufacturers to predict the flight characteristics of fixed and rotary wing aircraft with high precision. X-Plane allows you to change existing airplane models, and even create custom airplane or helicopter designs with the Plane Maker software (version 10). Additionally, the X-Plane simulation environment supports programming languages such as C/C++, MATLAB/Simulink and Python [10,11].

X-Plane simulates aircraft flight responses with high accuracy; it uses blade element theory to produce the forces and moments acting on an element of the aircraft’s surfaces, then applies the processed results to the entire aircraft (it is not based on the mathematical model of the aircraft) [12].

Several research works have successfully utilized X-Plane to design and simulate control schemes for UAVs. For instance, [13] an attitude control law is used for small fixed-wing UAVs that are built considering two flight phases: stable flight and maneuvering flight, the experimental analysis and simulation was carried out in the software X-Plane. On the other hand, in [7] the behavior of a Vertical Take-Off and Landing (VTOL) type UAV is analyzed, which is conducted through Hardware-In-the-Loop (HIL) integration with all the functions of a commercial VTOL UAV, where the aircraft is modeled in X-Plane and the climatic conditions through real data.

In [14] an environment to simulate multiple UAVs simultaneously is described, as well as providing status data and control inputs for individual vehicles using X-Plane. In addition to this, X-plane and Matlab/Simulink are used to simulate a UAV with flapping wings [15], the flapping wing model is developed in aircraft manufacturing software and runs in the X-plane environment. Yu, Li, et al., provide an efficient method to verify the performance of hardware and software designs of a control scheme for a three-tilt-rotor UAV, using X-Plane-based HIL [8].

Cabecinhas et al. proposed a robust controller for landing maneuvers [4], in which the interaction of the UAV with the ground was considered. In [16], the mathematical developments to obtain a linear model for the quadrotor without perturbations are reported. This quadrotor linear model is used to design a control scheme that combines the backstepping procedure with saturation functions; moreover, in [1] a control architecture is presented, which results from the combination of a GPI controller with one based on nested saturations; it should be noted that the control scheme was designed to perform landing maneuvers despite external perturbations. It is important to mention that the physical implementation of this type of control scheme proposals is complicated to carry out, due to the higher cost of computational time required.

The background described highlights two important areas of opportunity: the use of co-simulation tools to validate control schemes without the need for a physical or experimental prototype [17] and the validation of robust control schemes for landing and takeoff maneuvers in the presence of external disturbances. In that sense, the use of a specialized Model-in-Loop (MIL) environment such as X-Plane is attractive.

Thus, this paper uses MATLAB/Simulink and X-Plane as co-simulation tools to visualize and analyze the behavior of three control schemes reported in the literature for takeoff and landing maneuvers in quadrotors. The three proposals are tested at wind speeds of 0, 25 and 50 kn. The simulation is carried out using User Datagram Protocol (UDP) communication between MATLAB/Simulink and X-Plane.

The first proposal consists of controlling the $z,\varphi ,\theta ,\psi$ axes using feedforward PID type control algorithms; the second focuses on the use of feedforward controllers in combination with a PD (for z axis), a PID (for $\psi$ axis) and a control law based on nested saturations to stabilize the roll ($\varphi$) and pitch $\theta$ axes [16]. The third proposal uses a feedforward Generalized Proportional Integral (GPI) controller for the z axis, while the $\psi$ axis is controlled by a feedforward PID controller, the $\varphi$ and $\theta$ axes are controlled by a feedforward control algorithm based on the use of nested saturations to control systems represented by a chain of integrators [1].

In particular, this work describes the use of the transformation matrix that allows mapping the control actions $u_i$, with $i=1,2,3,4$, to the angular velocities required in each motor; which is omitted in works that are only validated numerically [1,16]. Additionally, we show the use of X-Plane as a MIL environment, with which control schemes can be executed to identify errors and/or problems of the proposed controllers before their coding and physical implementation [18,19]; it allows to detect and know the logic of the signals and their relationship with the physical environment, in addition, the simulation speed can be modified (depending on the complexity of the proposed control schemes). Thus, the use of X-Plane allows us to verify or test the feasibility of implementing the developed control schemes or UAVs [20].

Regarding [1], they use a mathematical model based on a local geodetic coordinate system North, East, Down (NED), while in this paper we propose a local geodetic coordinate system East, North, Up (ENU), which has been reported in works such as [21,22,23]. In the above, although it does not modify the design steps of the controller, it does change the operating logic of the scheme.

The main contributions of this work are:

• The comparison between the control proposals to test the robustness of the controllers against different wind speeds.
• The flight analysis of the aircraft within the X-Plane software in a realistic environment.
• The communication between the software used MATLAB/Simulink and X-Plane.

The organization of this work is given as follows: Section 2 describes the dynamics of the quadrotor, its physical characteristics within Plane Maker and the configuration required for sending data between MATLAB/Simulink and X-Plane; Section 3 explains the controllers to be compared: Feedforward PID; feedforward PD in combination with nested saturations; GPI and nested saturations, both feedforward. Section 4 shows the results of the control schemes at different wind speeds, which are analyzed based on error-based performance indices. Finally, Section 5 presents the conclusions obtained.

2. System Description

Figure 1 shows a diagram of the reference frames of the forces acting on the quadrotor, the rotation of the motors and the reference frames that are usually used for analysis; fixed to the ground (I) and fixed to the vehicle (B) [1].

The main forces and moments acting on the quadrotor are produced by its rotors, of which two pairs of motors rotate in opposite directions to balance the total torque of the system.

Figure 1 also shows $f_1,f_2,f_3$ and $f_4$, which correspond to the thrust forces generated by each of the rotors. $u_1$ is the control action in the z-axis, which results from the combination of the thrust generated by each rotor. l corresponds to the length from the center of the quadrotor to the center of the rotor. ${\overrightarrow{x}}_L,{\overrightarrow{y}}_L,{\overrightarrow{z}}_L$ indicate the position of the quadrotor with respect to a reference frame fixed to it. $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$ corresponds to the position of the UAV with respect to the inertial frame of reference. $\varphi ,\theta ,\psi$ are the orientation angles of the roll, pitch and yaw, respectively.

The representation of the rotation movements of the quadrotor are shown in Figure 2, where, to maintain a constant lift, the four rotors must be kept at equal speeds as shown in Figure 2a. The roll motion ($\varphi$) is obtained by increasing the speed of rotor 4 and the speed of rotor 2 is reduced (See Figure 2b). For the pitch motion ($\theta$), the speed of rotor 1 is increased, while the speed of rotor 3 is reduced, as seen in Figure 2c. Finally, the yaw orientation motion ($\psi$) results from the increase in speed in rotors 1 and 3, while the speed of rotors 2 and 4 is decreased (See Figure 2d) [17,24].

Mathematical Model

The dynamics of the quadcopter can be obtained from the Euler–Lagrange methodology. The dynamic model can be deduced with respect to a reference frame fixed to it, or with respect to an inertial reference system [1]. In this work, we consider an inertial reference frame, represented as follows:

$$\begin{array}{ccc}\hfill m\ddot{x}& =& \left(cos\varphi sin\theta cos\psi +sin\varphi sin\psi \right)u_1+a_x\dot{x}\hfill \\ \hfill m\ddot{y}& =& \left(cos\varphi sin\theta sin\psi -sin\varphi cos\psi \right)u_1+a_y\dot{y}\hfill \\ \hfill m\ddot{z}& =& u_{1}cos\theta cos\varphi -mg+a_z\dot{z}\hfill \\ \hfill I_{xx}\ddot{\varphi }& =& (I_{yy}-I_{zz})\dot{\theta }\dot{\psi }-J_R{\Omega }_n\dot{\theta }+l{u}_2+b_{\varphi }\dot{\varphi }\hfill \\ \hfill I_{yy}\ddot{\theta }& =& (I_{zz}-I_{xx})\dot{\varphi }\dot{\psi }-J_R{\Omega }_n\dot{\varphi }+l{u}_3+b_{\theta }\dot{\theta }\hfill \\ \hfill I_{zz}\ddot{\psi }& =& (I_{xx}-I_{yy})\dot{\theta }\dot{\varphi }-u_4+b_{\psi }\dot{\psi }\hfill \end{array}$$

(1)

where m is the mass of the quadcopter, $a_x,a_y$ and $a_z$ represent aerodynamic forces acting on the quadcopter (on its respective axis), $J_R$ is the moment of inertia of the motor around its axis, $b_{\varphi }, b_{\theta }, b_{\psi }$ are the aerodynamic torques acting on the quadcopter, ${\Omega }_n$ is the angular velocity obtained by summing the velocities of the four motors, $I_{xx}, I_{yy}, I_{zz}$ are moments of inertia of the center of mass of the quadcopter, $u_i$ represents the control input, for $i=1,2,3,4$, l is the distance between the center of gravity of the quadrotor and the rotors; $\varphi , \theta , \psi , x, y, z$ are the rotation and translation positions with respect to an inertial frame, respectively.

It is required to control the rotors in terms of angular speeds in order to be able to manipulate the speed of said rotors, controlling the position and orientation axes of the quadrotor. In accordance with [25,26] the equations that relate the control inputs to the rotational speeds of the rotors are as follows:

$$\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\end{array}\right]=\left[\begin{array}{cccc}{k}_f& k_f& k_f& k_f\\ 0& k_{f}l& 0& k_{f}l\\ -k_{f}l& 0& k_{f}l& 0\\ k_m& -k_m& k_m& -k_m\end{array}\right]\left[\begin{array}{c}{{\omega }_1}^2\\ {{\omega }_2}^2\\ {{\omega }_3}^2\\ {{\omega }_4}^2\end{array}\right]$$

(2)

where: l is the distance from the rotor to the center of gravity of the quadrotor, $k_f$ is the lift coefficient and $k_m$ the drag coefficient. ${\omega }_i$ represents the angular velocities of each rotor, and can be obtained from (2).

3. Software Description and Communication for Sending and Receiving Data between MATLAB/Simulink and X-Plane

For the simulation and data analysis, the X-Plane (version 10) and MATLAB/Simulink (R2020a) software were used, where in MATLAB/Simulink the control and data analysis stage is carried out and in the X-Plane software the visualization of the behavior of the quadrotor is performed.

The use of X-Plane and MATLAB/Simulink is attractive for the validation of control schemes without the need for a physical prototype. Unlike traditional numerical simulations, where the mathematical model that describes the dynamic behavior of the UAV is used; the operating principle of X-Plane is based on the reading of the geometric shape of the aircraft, physical specifications (weight, engine power, wingspan, wing area, control surfaces and the center of gravity) [27]. This guarantees a better approximation to the real behavior of a UAV since the mathematical models that are usually used generally ignore aerodynamic properties and effects. Therefore, the results obtained with MATLAB/Simulink and X-Plane are closer to the real behavior of the UAV. Thus, X-Plane is a realistic flight simulator that has several aircraft models that can be simulated in different flight scenarios and environmental conditions, it even allows you to transmit and manipulate data from said aircraft. The X-Plane software integrates a platform called Plane Maker, which is used especially to design and modify aircraft according to your objectives [28].

The image shown in Figure 3 presents an example of X-Plane simulation scenarios.

3.1. Plane Maker

Plane Maker is a platform that includes X-Plane which allows users to design aircraft, accepting parameters such as weight, size, power and ratio of engines, and type and size of propellers, among many others. Within its workspace, Plane Maker makes it possible to use all its flight scenarios around the world, as well as having the aircraft that it includes as examples and communication between external software. For the simulation of the proposed control schemes, the quadrotor shown in Figure 1 was used, which was designed in Plane Maker.

The construction dimensions of the quadrotor designed in Plane Maker are presented in

Table 1. Quadrotor design dimensions.

Part	Parameter	Dimension
Cabin (fuselage)	Total length	$0.13$ m
	Total width	$0.10$ m
	Thickness	$0.05$ m
Arms	Total length	$0.30$ m
	Total width	$0.035$ m
	Thickness	$0.02$ m
Wheels	Longitudinal arm	$0.05$ m
	Diameter	$0.01$ m
	Thickness	$0.01$ m
Engines	Total length	$0.04$ m
	Total diameter	$0.03$ m
Propellers	Total length	$0.13$ m
	root rope	$0.02$ m
	point rope	$0.01$ m

.

The physical parameters of the quadrotor obtained from the design created in X-Plane/Plane maker are those shown in

Table 2. Physical parameters of the quadrotor.

Parameter	Simbol	Magnitude	Unit
Mass	m	1.133	kg
Distance from rotor to center of mass	l	0.1981	m
Moment of inertia about x	$I_{xx}$	0.1801	kg m2
Moment of inertia about y	$I_{yy}$	0.1801	kg m2
Moment of inertia about z	$I_{zz}$	0.3561	kg m2
Gravitational acceleration	g	9.81	m/s2

.

3.2. Communication between MATLAB/Simulink and X-Plane

In order to send and receive data between MATLAB/Simulink and X-Plane, the user datagram protocol (UDP) is used. This communication protocol consists of configuring an IP address, as well as the specific ports for sending and data reception.

MATLAB/Simulink provides a UDP communication library, which allows data exchange using the corresponding block programming. The UDP protocol is a relatively simple communication protocol for data transfer [29].

The standard protocol for sending and receiving data from X-Plane is UDP, and it is supported by Matlab/Simulink [30]. Its main advantage is the ability to communicate in near real-time with minimal delays; the only delays are caused by the Windows operating system (which is not considered a real-time operating system) [29].

To carry out the communication, an IP address and specific ports for sending/receiving data must be configured, for which it is important to take into account the following considerations:

• Within X-Plane, in the Settings → Network Connections → Data section, the IP address is indicated (see Figure 4).
• In the same section of X-Plane, the ports for sending and receiving data are indicated.

Once both the address and the communication ports are configured, it is possible to use the MATLAB/Simulink UDP blocks (see Figure 5) to send and receive data between MATLAB/Simulink and X-Plane.

The blocks used for sending and receiving data are located in the XPB X-Plane block set, which is designed for interaction between X-Plane and MATLAB/Simulink. These blocks can be downloaded at: https://la.mathworks.com/matlabcentral/fileexchange/76028-x-plane-blockset (accessed on 20 August 2024 ).

UDP communication supports both IPv4 (Internet Protocol version 4) and IPv6 (Internet Protocol version 6) addresses; IPv4 is frequently used in applications that require fast response times and tolerate some data loss, which is one of the reasons why X-Plane uses it [31]. A UDPv4 packet has a maximum length of 65,535 bytes, and Transmission Control Protocol (TCP) ports range from 0 to 65,535; of which 1024 to 49,151 are registered ports. Because these ports are reserved for specific applications, X-Plane uses them freely without affecting any other protocols.

To establish communication between MATLAB/Simulink and X-Plane, the IP address must first be configured, after this, set the UDP port to 49,001, which is provided by default to send data from X-Plane to MATLAB/Simulink.

4. Control Schemes

Since the system presented in (1) has highly nonlinear dynamics, it is difficult to control and stabilize it. Therefore, it is proposed to feedforward the system dynamics in combination with the control proposals raised in Section 4.1, Section 4.2, Section 4.3, Section 4.3.2 and Section 4.3.1. The aforementioned feedforward is obtained from (1) and its objective is to linearize the system in the coordinates $z,\varphi ,\theta ,\psi$.

For the feedforward, only the known dynamics of the quadrotor were considered, considering the rotor speed and friction coefficients as perturbations. Thus, the following feedforward control actions are proposed:

$$\begin{array}{ccc}\hfill u_1& =& \hfill {\displaystyle \frac{m(v_z+g)}{cos\varphi cos\theta }}\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill u_2& =& \hfill {\displaystyle \frac{I_{xx}{v}_{\varphi }-(I_{yy}-I_{zz})\dot{\theta }\dot{\psi }}{l}}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill u_3& =& \hfill {\displaystyle \frac{I_{yy}{v}_{\theta }-(I_{yy}-I_{zz})\dot{\varphi }\dot{\psi }}{l}}\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill u_4& =& \hfill I_{zz}{v}_{\psi }-(I_{xx}-I_{yy})\dot{\theta }\dot{\varphi }\hfill \end{array}$$

(6)

$v_z,v_{\varphi },v_{\theta }$ y $v_{\psi }$ are auxiliary controllers. To be clearer about the structure of the controllers applied in the system, it is worth mentioning that three proposals were carried out to analyze the behavior of the quadrotor.

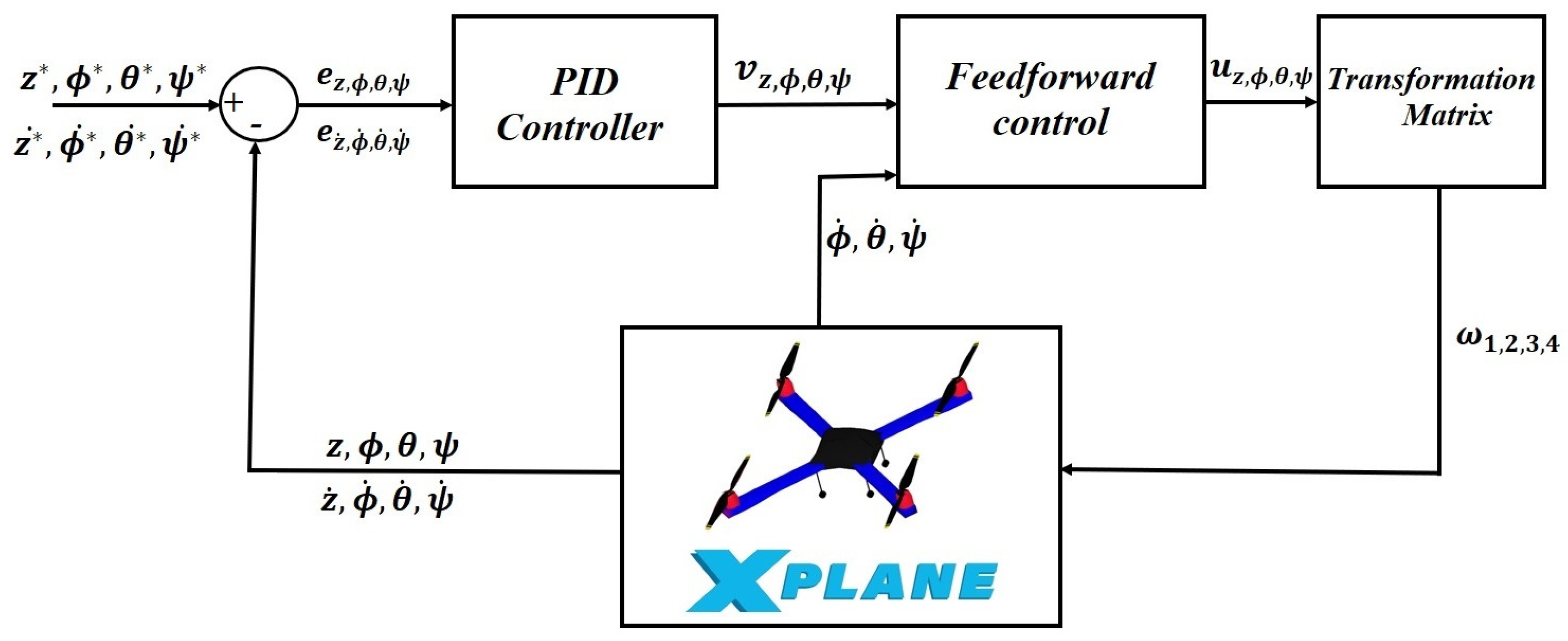
The control architecture is shown in Figure 6, which is applied to the flight control analysis of the quadrotor, presenting the interaction between MATLAB/Simulink and X-Plane for sending and receiving data between both software.

Figure 6 shows the control scheme used for the flight of the quadrotor, where the first block is the feedforward control block, which presents the dynamics shown in (3)–(6) combining the controllers mentioned in the following subsections with the objective of linearizing the system in the coordinates $z,\varphi ,\theta ,\psi$; the control inputs $u_z,u_{\varphi },u_{\theta },u_{\psi }$ are sent to a transformation matrix which converts the control force terms into terms of angular velocities ${\omega }_1,{\omega }_2,{\omega }_3,{\omega }_4$ which are sent to each rotor of the quadrotor in X-Plane through communication UDP, once this is conducted, by receiving data through UDP communication the coordinates $z,\varphi ,\theta ,\psi$ measured from X-Plane are obtained and with this feedback to the feedforward system with the desired coordinates $z^{*},{\varphi }^{*},{\theta }^{*},{\psi }^{*}$.

The compared control schemes are described below: Feedforward PID [17]; feedforward PD in combination with nested saturations [16]; GPI and nested saturations, both feedforward [1]. In the first proposal, PID-type controllers were used in the four axes to analyze the behavior of the quadrotor and achieve the desired values in the four axes satisfactorily. For the second proposal, a PD controller was used in the z-axis to reach the trajectory faster, in the $\varphi$ and $\theta$ axes, nested saturation controllers were used to stabilize the roll and pitch coordinates and in the $\psi$ a PID controller was used to reduce oscillations in the yaw angle. Finally, the third proposal was applied as follows: for the height axis z, a triple integrator GPI controller was used to better follow the trajectory tracking and reject disturbances; in the orientation part of the angles $\varphi$ and $\theta$ a control law for nested saturations was applied which consists of a chain of integrators design with a backtracking procedure to stabilize the system at these angles for open environments and as in the previous proposals; the angle $\psi$ is manipulated by a PID type controller.

4.1. Proposal 1: Feedforward PID

For this first control proposal, it was proposed that the auxiliary controllers $v_z,v_{\varphi },v_{\theta },v_{\psi }$ mentioned in Equations (3)–(6), were of PID type, which have the following structure:

$$v_i=k_{p_i}{e}_i\left(t\right)+k_{i_i}{\int }_0^t{e}_i\left(\tau \right)d\tau +k_{d_i}{\displaystyle \frac{d}{dt}}{e}_i\left(t\right)$$

(7)

with: $k_p$ the proportional gain, $k_i$ the integral gain and $k_d$ the derivative gain, $e_i\left(t\right)$ is the position error with respect to time, which is calculated as $desiredvalue-measuredvalue$.

Figure 7 presents a block structure which describes the PID controller.

4.2. Proposal 2: Feedforward PD, PID and Nested Saturations

A PD feedforward controller was used to manipulate the z axis and $\psi$ angle; while to stabilize the $\varphi$ and $\theta$ angles, a nested saturation controller was used [16].

The structure of the feedforward PD is the same as that presented in (7), omitting the integral part.

Nested Saturations Controller

The nested saturation controller used to stabilize the angles $\varphi$ and $\theta$ is the one proposed in [16], which has the following structure:

$$v_{\varphi }=-{\sigma }_{{\varphi }_1}\left(\dot{\varphi }+{\sigma }_{{\varphi }_2}\left(\varphi +\dot{\varphi }+{\sigma }_{{\varphi }_3}\left(2\varphi +\dot{\varphi }+{\displaystyle \frac{\dot{y}}{g}}+{\sigma }_{{\varphi }_4}\left(\dot{\varphi }+3\varphi +3{\displaystyle \frac{\dot{y}}{g}}+{\displaystyle \frac{y}{g}}\right)\right)\right)\right)$$

(8)

$$v_{\theta }=-{\sigma }_{{\theta }_1}\left(\dot{\theta }+{\sigma }_{{\theta }_2}\left(\theta +\dot{\theta }+{\sigma }_{{\theta }_3}\left(2\theta +\dot{\theta }-{\displaystyle \frac{\dot{x}}{g}}+{\sigma }_{{\theta }_4}\left(\dot{\theta }+3\theta -3{\displaystyle \frac{\dot{x}}{g}}-{\displaystyle \frac{x}{g}}\right)\right)\right)\right)$$

(9)

where ${\sigma }_{{\varphi }_i}$ and ${\sigma }_{{\theta }_i}$ are saturation functions, for $i=1,2,3,4$.

Based on the stability test performed in [16], the following conditions are proposed to keep the quadrotor in hover (at its equilibrium point):

$$M_{{\varphi }_1,{\theta }_1}\ge 2M_{{\varphi }_2,{\theta }_2},M_{{\varphi }_2,{\theta }_2}\ge 2M_{{\varphi }_3,{\theta }_3},M_{{\varphi }_3,{\theta }_3}\ge 2M_{{\varphi }_4,{\theta }_4}$$

(10)

$M_{{\varphi }_i}$ and $M_{{\theta }_i}$ for $i=1,2,3,4$ are the lower and upper bounds of the saturations.

The scheme that represents the dynamics of the control by nested saturations is shown in Figure 8.

4.3. Proposal 3: GPI Controller and Nested Saturations

In this section, a GPI controller with three integrators for height was considered; a nested saturation controller was proposed for open navigation environments to stabilize the angles $\varphi$ and $\theta$; while for the angle $\psi$ the same control law of Proposals 1 is used [1]. The proposed structures for the controllers used are presented below:

4.3.1. GPI Controller

The GPI controller structure was proposed as shown below [32]:

Be the system:

$$\ddot{z}=u_{GPI}+\xi$$

(11)

where: $\xi$ is an unknown constant disturbance signal.

We use the following integral reconstructor, which is designed to compensate for the lack of $\dot{z}$ measurement.

$$\widehat{\dot{z}}={\int }_0^t{u}_{GPI}\left(\tau \right)dt$$

(12)

Considering $z^{*}\left(t\right)$ as a smooth reference signal for z, $u_{GPI}$ is proposed as [1]:

$$v_{z_{GPI}}={\ddot{z}}^{*}+k_p{e}_z+k_d{\dot{e}}_z+k_{i_1}{\int }_0^t{e}_{z}d\tau +k_{i_2}{\int }_0^t{\int }_0^t{e}_{z}d{\tau }_{2}d{\tau }_1+k_{i_3}{\int }_0^t{\int }_0^t{\int }_0^t{e}_{z}d{\tau }_{3}d{\tau }_{2}d{\tau }_1$$

(13)

with ${\dot{e}}_z\left(t\right)=\widehat{\dot{z}}\left(t\right)-{\dot{z}}^{*}\left(t\right)$, $e_z\left(t\right)=z\left(t\right)-z{\left(t\right)}^{*}$.

If we substitute (11) into (13) and express the resulting dynamics in terms of the tracking error, we obtain the following dynamics:

$${e_z}^{\left(5\right)}+k_p{e_z}^{\left(4\right)}+k_d{e_z}^{\left(3\right)}+K_{i_1}{\ddot{e}}_z+K_{i_2}{\dot{e}}_z+K_{i_3}{e}_z=0$$

(14)

$k_i$, $i=0,1,2,3,4$ are chosen so that the roots of the characteristic polynomial $s^5+k_4{s}^4+k_3{s}^3+k_2{s}^2+k_{1}s+k_0$ lie on the left side of the complex (Hurwitz) plane. This makes the GPI controller robust to constant perturbations.

4.3.2. Nested Saturations Controller

A modification of the control scheme proposed in [1] is used, which uses a controller based on nested saturations to bring its equilibrium point to the $\varphi$ and $\theta$ angles. The technique has as its main requirement the representation of a non-linear system as chains of integrators with non-linear perturbations [33]. The design procedure consists of a backstepping procedure that results in a fixed-point equation at the control input [1,34].

The operating logic of this proposal considers the following steps: (1) the z axis and the $\psi$ angle are stabilized and (2) the coordinates $\theta ,x$ and $\varphi ,y$ are stabilized.

The nested saturation controller to stabilize the orientation angles $\varphi$ and $\theta$ has the following structure [1]:

For the control of the angle $\theta$, it is considered that controllers (3), (6) and (11) guarantee the convergence of the tracking error to the origin, in particular, ${\psi }^{*}=0$. Thus, the subsystem $x,\theta$ is represented as follows [1]

$$\begin{array}{ccc}\hfill {\dot{x}}_1& =& x_2\hfill \\ \hfill {\dot{x}}_2& =& gtan{\theta }_1+{\beta }_x{x}_2+{\dot{z}}_2^{*}tan{\theta }_1\hfill \\ \hfill {\dot{\theta }}_1& =& {\theta }_2\hfill \\ \hfill {\dot{\theta }}_2& =& v_{\theta }-{\eta }_{\theta }{\varphi }_2+{\beta }_{\theta }{\theta }_2\hfill \end{array}$$

(15)

where, ${\beta }_x={\displaystyle \frac{a_x}{m}}$, ${\beta }_{\theta }={\displaystyle \frac{b_{\theta }}{I_{yy}}}$, ${\eta }_{\theta }={\displaystyle \frac{J_R{\omega }_n}{I_{yy}}}$

The following transformation is defined, with which the system (15) can be expressed as a chain of integrators with non-linear perturbations.

$$\begin{array}{ccc}\hfill {\omega }_{1_{\theta }}& =& gtan{\theta }_1\hfill \\ \hfill {\omega }_{2_{\theta }}& =& {\dot{\omega }}_1=g{\theta }_{2}se{c}^2{\theta }_1\hfill \end{array}$$

(16)

getting

$$\begin{array}{ccc}\hfill q_{1_{\theta }}& =& \hfill x_1+3x_2+3{\omega }_{1_{\theta }}+{\omega }_{2_{\theta }}\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill q_{2_{\theta }}& =& x_2+2{\omega }_{1_{\theta }}+{\omega }_{2_{\theta }}\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill q_{3_{\theta }}& =& {\omega }_{1_{\theta }}+{\omega }_{2_{\theta }}\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill q_{4_{\theta }}& =& {\omega }_{2_{\theta }}\hfill \end{array}$$

(20)

Thus, the proposed controller has the following structure:

$$v_{\theta }=-q_{4_{\theta }}-{\sigma }_{{\alpha }_{\theta }}(q_{3_{\theta }}+{\sigma }_{{\beta }_{\theta }}(q_{2_{\theta }}+{\sigma }_{{\gamma }_{\theta }}\left(q_{1_{\theta }}\right)))$$

(21)

To control the angle $\varphi$; if ${\theta }_2$ and $x_2$ are very close to zero, the subsystem $y,\varphi$ is represented as follows:

$$\begin{array}{ccc}\hfill {\dot{y}}_1& =& y_2\hfill \\ \hfill {\dot{y}}_2& =& -gtan{\varphi }_1+{\beta }_y{y}_2-{\dot{z}}_2^{*}tan{\varphi }_1\hfill \\ \hfill {\dot{\varphi }}_1& =& {\varphi }_2\hfill \\ \hfill {\dot{\varphi }}_2& =& v_{\varphi }+{\beta }_{\varphi }{\varphi }_2\hfill \end{array}$$

(22)

The following transformation is applied:

$$\begin{array}{c}\hfill {\omega }_{1_{\varphi }}=gtan{\varphi }_1\\ \hfill {\omega }_{2_{\varphi }}=g{\varphi }_{2}se{c}^2{\varphi }_1\end{array}$$

(23)

As a result, the following chain of integrators is obtained:

$$q_{1_{\varphi }}=-y_1-3y_2+3{\omega }_{1_{\varphi }}+{\omega }_{2_{\varphi }}$$

(24)

$$q_{2_{\varphi }}=-y_2+2{\omega }_{1_{\varphi }}+{\omega }_{2_{\varphi }}$$

(25)

$$q_{3_{\varphi }}={\omega }_{1_{\varphi }}+{\omega }_{2_{\varphi }}$$

(26)

$$q_{4_{\varphi }}={\omega }_{2_{\varphi }}$$

(27)

Thus, the proposed controller is:

$$v_{\varphi }=-q_{4_{\varphi }}-{\sigma }_{{\alpha }_{\varphi }}(q_{3_{\varphi }}+{\sigma }_{{\beta }_{\varphi }}(q_{2_{\varphi }}+{\sigma }_{{\gamma }_{\varphi }}\left(q_{1_{\varphi }}\right)))$$

(28)

The control architecture that represents the routine performed by the nested saturation, GPI and PID controllers is shown in Figure 9.

5. Numerical Results and Comparison

This section shows the results obtained in the X-Plane software for the three proposals made; the implementation sequence for the quadrotor control analysis is shown in Figure 6. These proposals were made with different wind speeds that were selected between 0, 25 and 50 knots (kn).

Each case has the following purpose: in the z axis the aim is to track the trajectory of a Bezier polynomial of degree 9, reaching an initial value of 3 m and a final value of 40 m with initial and final times of 20 and 50 s, respectively. For the angles $\varphi$ and $\theta$, the equilibrium point of 0 rad must be reached and at angle $\psi$ we wish to achieve the tracking of a sine function of type $179+15sin\left(0.1t\right)$. The above is conducted with a fixed simulation step of 0.05 s.

The control parameters used in the simulations are shown in

Table 3. Gains used in auxiliary controllers.

Auxiliary Control	Proposal 1	Proposal 2	Proposal 3
$v_z$	$k_p$ = 27	$k_P=150$	$k_p=150$
	$k_i$ = 8.4	$k_d=5$	$k_d=5$
	$k_d$ = 36.6	$k_{i_1}=120$	$k_{i_1}=130$
		$k_{i_2}=15$	$k_{i_2}=15$
			$k_{i_3}=1$
$v_{\varphi }$	$k_p$ = 1425	${\sigma }_{{\varphi }_1}=0.5$	${\sigma }_{{\alpha }_{\varphi }}=1.5$
	$k_i$ = 170	${\sigma }_{{\varphi }_2}=0.25$	${\sigma }_{{\beta }_{\varphi }}=0.4285$
	$k_d$ = 97	${\sigma }_{{\varphi }_3}=0.125$	${\sigma }_{{\gamma }_{\varphi }}=0.09$
		${\sigma }_{{\varphi }_4}=0.0625$
$v_{\theta }$	$k_p$ = 4000	${\sigma }_{{\theta }_1}=1.5$	${\sigma }_{{\alpha }_{\theta }}=1$
	$k_i$ = 148	${\sigma }_{{\theta }_2}=0.75$	${\sigma }_{{\beta }_{\theta }}=0.5$
	$k_d$ = 90	${\sigma }_{{\theta }_3}=0.375$	${\sigma }_{{\gamma }_{\theta }}=0.25$
		${\sigma }_{{\theta }_4}=0.175$
$v_{\psi }$	$k_p$ = 15	$k_p=0.5$	$k_p=0.5$
	$k_i$ = 4	$k_i=0.1$	$k_d=0.8$
	$k_d$ = 8	$k_d=0.8$

.

The controller gains were obtained through trial and error estimation analysis, examining each selected value, following the procedure shown below: First, the gains of $v_z$ were calculated, then $v_{\varphi }$ was tuned, then $v_{\theta }$, finally obtaining the profits for $v_{\psi }$.

The tuning methodology used to find the values of the control gains was as follows: for the PID controller, first all the gains were set to zero, then the proportional constant $k_p$ was increased until a response was obtained that was most similar to the desired response. The integral gain $k_i$ was adjusted to correct the steady state error and finally $k_d$ was adjusted to reduce the overshoots.

The tuning to propose the values to the controller gains by nested saturations of proposal 2 was, starting from the stability test shown in [16], first ${\sigma }_{{\varphi }_1,{\theta }_1}$ was adjusted, then it was proposed ${\sigma }_{{\varphi }_2,{\theta }_2}={\displaystyle \frac{1}{2}}{\sigma }_{{\varphi }_1,{\theta }_1}$, ${\sigma }_{{\varphi }_3,{\theta }_3}={\displaystyle \frac{1}{2}}{\sigma }_{{\varphi }_2,{\theta }_2}$ and ${\sigma }_{{\varphi }_4,{\theta }_4}={\displaystyle \frac{1}{2}}{\sigma }_{{\varphi }_3,{\theta }_3}$, the above was proposed to maintain stability in the axes $\varphi$ and $\theta$. To tune the control gains by nested saturations of proposal 3, ${\sigma }_{{\varphi }_{\alpha ,\beta ,\gamma },{\theta }_{\alpha ,\beta ,\gamma }}$ were first placed at zero, then ${\sigma }_{{\varphi }_{\gamma },{\theta }_{\gamma }}$ was adjusted, then ${\sigma }_{{\varphi }_{\beta },{\theta }_{\beta }}$ was adjusted and finally ${\sigma }_{{\varphi }_{\alpha },{\theta }_{\alpha }}$ was estimated.

For the GPI controller gains, the values of $k_p$, $k_{i_1}$, $k_{i_2}$, $k_{i_3}$ and $k_d$ were initially proposed to ensure that the roots of the polynomial were Hurwitz (in numerical simulation). Subsequently, when linking MATLAB/Simulink with X-Plane, it was necessary to modify these (based on numerical results); first, the gain $k_p$ was increased, then $k_{i_1}$, subsequently $k_{i_2}$, then $k_{i_3}$ and finally $k_d$ to reduce the overshoot.

Figure 10 shows the results obtained in each of the quadrotor axes. It is observed that the applied controllers try to reach the desired value: in the z and $\psi$ axes it is observed that the desired trajectory is followed in the three proposals (see Figure 10a,d), for $\varphi$ and $\theta$ the controllers used aim to reach the equilibrium point (stabilize the quadrotor) (see Figure 10b,c). Thus, it is concluded that the proposed controllers 1 and 3 show better performance.

The responses shown in Figure 11, exhibit the behavior of the quadrotor for a wind speed of 25 kn, in this case, the trajectory tracking for the z and $\psi$ axes is observed with larger oscillations, where the controllers used in proposal 3 are the ones that present the best behavior towards trajectory following (see Figure 11a,d), at the angles $\varphi$ and $\theta$ the controllers of the three proposals carried out try to reach the intended value, so the controllers that have the best behavior are those of proposal 3 (see Figure 11b,c).

Figure 12 shows the results for the flight of the quadrotor at a wind speed of 50 knots, where large oscillations can be seen when trying to reach the desired value, as well as $\psi$ taking a longer time to achieve the control objective which is due to the fact that if the wind speed is higher, it will directly affect the angle $\psi$, on the other hand the controllers applied for proposal 3 continue to respond better than those applied in the proposals 1 and 2.

The control actions $u_1,u_2,u_3$ and $u_4$ shown in Figure 13, Figure 14 and Figure 15 present the behavior of the controllers at wind speeds of 0, 25 and 50 knots, it can be seen that if the wind speed is high, the force increases, which corresponds to the force required for the quadrotor to remain in stationary flight, while $u_1,u_2,u_3$ and $u_4$ They keep oscillating around zero, this to try to maintain the stability of the quadrotor. It is worth mentioning that the values of the controllers are limited to possible operating ranges.

Comparison of Control Schemes

To better observe the comparison of the behavior of the controllers applied in each proposal, the following error performance metrics were obtained: Integral Error (IE) = ${\int }_0^{T}e\left(t\right)dt$; Integral of the Absolute Error (IAE) = ${\int }_0^T\mid e\left(t\right)\mid dt$ and the Mean Square Error (MSE) = ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(e\right)}^2$.

Figure 16, Figure 17, Figure 18 and Figure 19 show the behavior of the error, IE, IAE and MSE, respectively, in the $z,\varphi ,\theta ,\psi$ axes for the three control proposals at a wind speed of 50 kn.

Figure 16 shows the comparison of the error in the $z,\varphi ,\theta ,\psi$ axes for the three mentioned proposals at a wind speed of 50 kn.

The Figure 17, Figure 18 and Figure 19 present the comparative behavior of the IE, IAE and the MSE, respectively, for the axes $z,\varphi ,\theta ,\psi$ at a wind speed of 50 kn.

Table 4. Error performance metrics.

Axis	Proposal and Wind Speed	Error	IE	IAE	MSE
z [m]	0 kn	0 kn	0 kn	0 kn	0 kn
	1	$0.85\times {10}^{-3}$	9.34	15.43	$7.147\times {10}^{-7}$
	2	0.27	23.08	44.17	0.0724
	3	0.035	0.75	15.17	0.001
	25 kn	25 kn	25 kn	25 kn	25 kn
	1	0.30	10.47	44.42	0.09
	2	0.17	24.38	45.99	0.03
	3	0.01	0.9	23.43	$0.37\times {10}^{-3}$
$\varphi$ [rad]	0 kn	0 kn	0 kn	0 kn	0 kn
	1	$0.4\times {10}^{-3}$	$7.4\times {10}^{-5}$	0.13	$1.1\times {10}^{-7}$
	2	0.01	0.2	2.09	$0.1\times {10}^{-3}$
	3	0.01	0.008	0.36	$0.14\times {10}^{-3}$
	25 kn	25 kn	25 kn	25 kn	25 kn
	1	$0.4\times {10}^{-3}$	0.004	0.74	$1.9\times {10}^{-7}$
	2	0.03	1.52	4.78	0.001
	3	0.005	0.56	0.9	$3.06\times {10}^{-5}$
$\theta$ [rad]	0 kn	0 kn	0 kn	0 kn	0 kn
	1	$7.47\times {10}^{-5}$	0.003	0.06	$9.9\times {10}^{-9}$
	2	0.02	0.52	2.3	$0.3\times {10}^{-3}$
	3	0.001	$0.8\times {10}^{-3}$	0.31	$2.85\times {10}^{-6}$
	25 kn	25 kn	25 kn	25 kn	25 kn
	1	$0.7\times {10}^{-3}$	0.01	0.56	$4.9\times {10}^{-7}$
	2	0.06	0.91	2.73	0.003
	3	0.003	0.06	0.46	$9.17\times {10}^{-6}$
$\psi$ [rad]	0 kn	0 kn	0 kn	0 kn	0 kn
	1	0.0012	0.03	0.02	$1.6\times {10}^{-6}$
	2	0.008	0.01	0.3	$6.47\times {10}^{-5}$
	3	$8.3\times {10}^{-6}$	0.01	0.12	$1.6\times {10}^{-9}$
	25 kn	25 kn	25 kn	25 kn	25 kn
	1	0.009	0.03	3.23	$9.8\times {10}^{-5}$
	2	0.005	0.001	0.83	$2.9\times {10}^{-5}$
	3	$0.2\times {10}^{-3}$	0.42	0.44	$4.2\times {10}^{-8}$

shows the results obtained for the error, IE, IAE and MSE, where the control performance is shown for each proposal applied.

The results seen in Table 4 are those obtained by exposing the Quadrotor to wind speeds of 0 kn and 25 kn.

From Table 4 and Figure 16, Figure 17, Figure 18 and Figure 19, it can be seen that control proposals 1 and 3 present good behavior in $z,\varphi ,\theta ,\psi$ at wind speeds of 0 kn and 25 kn, with proposal 3 being the one that shows the best control dynamics at a wind speed of 50 kn. Control proposal 2 can be seen to have acceptable behavior at a wind speed of 0 kn, since at higher wind speeds, this proposal fails to achieve the desired trajectory for the axes $z,\varphi ,\theta ,\psi$. From the above, proposal 3 exhibits better dynamics at wind speeds of 0, 25 and 50 kn.

To see in more detail the behavior of the quadrotor at different wind speeds with the proposals in this work, it is recommended to visit: https://www.youtube.com/watch?v=zbDBYA23-Dw (accessed on 20 August 2024 ).

The images shown in Figure 20, present the behavior of the quadrotor in the X-Plane, as well as its simulation environment.

6. Conclusions

The use of X-Plane and MATLAB/Simulink is attractive for the validation of control schemes without the need for a physical prototype. In this work, it was possible to integrate both tools and thus carry out the analysis of the behavior of the quadrotor in the face of environmental disturbances in a realistic simulation environment, validating the sending and receiving of data through the UDP communication protocol.

The advantages of using MATLAB/Simulink and X-Plane are as follows: being able to design your own aircraft and visualize its dynamics in different flight scenarios; in addition, meteorological variables that usually affect the aircraft in a real scenario can be added.

Regarding the control proposals, these allowed the tracking of the trajectories, even with the system exposed to different wind speeds. The application of the different control laws in the three proposals allowed us to know the robustness of each controller under different wind speeds; proposal 3 was the one that exhibited the best behavior under these environmental disturbances, allowing the desired values to be reached on the axes $z,\varphi ,\theta ,\psi$.

It is worth noting that the third controller differs from the controller reported in [1] in its operating logic; in this work, the z-axis is controlled first, then the $\psi$ angle, then $\theta$ and finally $\varphi$; while in [1]$\varphi$ is controlled before $\theta$. This is due to the mathematical model used, which in our case is based on a local geodetic coordinate system ENU. Thus, the design methodology proposed in [1] is validated for both ENU and NED-based models.

Using the transformation matrix, it was possible to determine the angular velocities of each motor based on the control actions, which allowed the analysis of the quadcopter flight control in the X-Plane software. Thus, it was possible to analyze the performance of the control schemes under different wind speeds.

It is essential to highlight that the quadrotor’s mathematical model was only used to design the control schemes, which, together with the transformation matrix, were programmed in MATLAB/Simulink. Thus, using X-Plane as a MIL environment is validated; this allows for identifying errors or problems of the proposed controllers, optimizing their performance, and evaluating different design/modification options before their coding and physical implementation [18]. The integration of MATLAB/Simulink and X-Plane results in a low-risk test environment, which allows testing and evaluating the control schemes without risking physical systems, saving time and money [35].

The proposed software integration presents opportunities for designing and validating new control schemes and innovative aircraft designs and inspires future work. Analyzing the flight behavior of large-scale aircraft stands out as a potential area for further research. The proposed co-simulation could also be expanded to include trajectory tracking, point-to-point route following, and quadrotor consensus or formation tasks. Additionally, the communication with external embedded control cards must be explored. These possibilities for future work highlight the potential for further innovation and research in this field.