A Distributed Task Allocation Method for Multi-UAV Systems in Communication-Constrained Environments

Abstract

This paper addresses task allocation to multi-UAV systems in time- and communication-constrained environments by presenting an extension to the novel heuristic performance impact (PI) algorithm. The presented algorithm, termed local reassignment performance impact (LR-PI), consists of an improved task inclusion phase, a novel communication and conflict resolution phase, and a systematic method of reassignment for unallocated tasks. Considering the cooperation in accomplishing tasks that may require multiple UAVs or an individual UAV, the task inclusion phase can build the ordered task list on each UAV with a greedy approach, and the significance value of tasks can be further decreased and conflict-free assignments can be reached eventually. Furthermore, the local reassignment for unallocated tasks focuses on maximizing the number of allocated tasks without conflicts. In particular, the non-ideal communication factors, such as bit error, time delay, and package loss, are integrated with task allocation in the conflict resolution phase, which inevitably exist and can degrade task allocation performance in realistic communication environments. Finally, we show the performance of the proposed algorithm under different communication parameters and verify the superiority in comparison with the PI-MaxAsses and the baseline PI algorithm.

1. Introduction

Teams of Unmanned Aerial Vehicles (UAV) have been proposed for use in applications that fall into the categories of the dull, dangerous, and dirty in military or civilian fields [1,2,3], such as search and rescue, surveillance and reconnaissance, pick-up and delivery, and intelligent transportation [4,5,6,7]. Ideally, the perfect communication factors between UAVs, such as low latency, high reliability, and so on are assumed, even though those ideal communication characteristics may be impossible irealistic communication environments [5,8]. The reason for this is that the realistic communication between UAVs on the battlefield naturally experiences bit error, multiple fading, and package loss. To develop and deploy the multi-UAV systems in communication-constrained environments, the task allocation problem that assigns the matching pairs between a finite number of UAVs and targets reasonably is a key challenge. For example, a team of UAVs is required to execute search and rescue tasks on a bounded terrain [4] where UAVs may suffer from unreliable, constrained, or degraded wireless communication. Thus, the aim is to rescue more survivors before special deadlines with respect to the communication constraints [2,9]. The challenge is then how to assign conflict-free matching pairs between the resource-constrained UAVs and the survivors with one or more system objectives optimized.

Multi-UAV task allocation problems have been shown to be NP-hard and considerable attention has been received in most recent research [10,11]. Generally, task allocation algorithms proposedin recent years fall broadly into either centralized or distributed categories. In centralized approaches for task allocation problems, the system objective can explicitly be optimized due to the full collection of information of all connected UAVs. However, several weaknesses inevitably exist, especially for large-scale task allocation problems. First, a heavy communication burden is placed on the master agent due to the conflict resolution communication between UAVs. Second, it is susceptible to a single point of failure, the reason being that many non-ideal communication factors, such as package loss and bandwidth limit, cannot be ignored in realistic communication environments. In contrast, robustness and flexibility advantages are offered by the distributed algorithms and the response to changes in situational awareness (SA) can be significantly faster than the centralized algorithms. The reason for this is that they can perform task allocation in an efficient and effective manner in terms of both communication and computation. In particular, it is noticeable, especially in the conflict-resolution phase where the information required to eliminate conflicts between UAVs is local with respect to the communication. Therefore, as a most representative market-based distributed approach, the PI algorithm inspired by the consensus-based bundle algorithm (CBBA) [12] is becoming increasingly attractive, since the positive properties of the auction and conflict resolution are combined to reach conflict-free assignments. In addition, with time constraints considered, the PI algorithm performs better in solving search and rescue problems in comparison with the baseline CBBA in terms of average rescuing time and the number of assigned survivors [4]. The reason for this is that the PI algorithm can directly optimize the system objective, and it is formulated under the problem of interest.

Based on the PI algorithm, numerous versions of the PI algorithm have been proposed to further optimize task allocation from different perspectives in most recent research. Whitbrook et al. [13] describe enhancements to the baseline PI algorithm and show how the presented work advances the task allocation of the time-critical multi-agent systems. In addition, additional action selection methods, such as soft max and $\epsilon$-greedy task selection, are introduced to escape from the local minima, and the average time can be reduced by up to 8%. Turner et al. [7] extend the distributed task allocation algorithms with a feasible time slot for unallocated tasks to maximize the number of allocated tasks, which comes at the expense of convergence time. The method proposed by Amanda Whitbrook et al. [14] is an essential extension to solve the dynamic task allocation with the SA altered rapidly. Moreover, numerical simulations demonstrate that the method that extends the PI algorithm in both task inclusion and consensus can reach conflict-free assignments. Jie et al. [15,16] proposed a prediction mechanism for conflicts to avoid the infinite cycles of changing the same task, and the advantages of the proposed algorithms over baseline PI are demonstrated through performing search and rescue tasks. Wang et al. [17] proposed a consensus-based timetable algorithm (CBTA) to minimize the average start time of all tasks indirectly. The extensive simulation results show the superiority of the CBTA in comparison with the CBBA and the consensus-based grouping algorithm. The method proposed by Wang et al. [18] improves the cost function and task release procedure in the PI algorithm to address the distributed task allocation problem with the number of allocated tasks maximized. Yang et al. [19] introduce a novel method termed RECPIA to support UAVs in starting to perform tasks simultaneously, and the dynamic task allocation can be resolved by coalition formation.

However, the recent progress is still not enough to address the multi-UAV task allocation problem in communication-constrained environments, where non-ideal communication factors are integrated with task allocation. First, there are numerous versions of the PI algorithm mentioned above, but in most cases, non-ideal communication factors are not considered, which naturally exist and inevitably affect the task allocation of multi-UAV systems in the real world. In addition, although some improvements have been made to maximize the number of assigned tasks, it is still a crucial problem, since much more communication and computation are required to reach conflict-free assignments. Finally, little analysis exists on the multi-UAV requirements of a single task, and it is defined as an ST-MR-TA task allocation problem [20] where multiple UAVs are required by an individual task. To this end, we make further developments to the PI algorithm in this paper to maximize task assignments with the deadlines and non-ideal communication factors (e.g., time delay, package loss, and bit error) considered. In the PI algorithm, once a task is included in the task inclusion phase, it may be released by one UAV and reassigned by another UAV. However, it will not be unassigned in the later iterations. In addition, due to the scoring strategies and the auction architecture, the PI algorithm cannot reassign tasks to UAVs although UAVs are capable of performing more tasks. On the battlefield, more reconnaissance tasks should be performed in time by UAVs, since the fuel capacity of each UAV is limited. Thus, the contributions of this paper are twofold. First, the paper presents a systematic method of reassignment for unallocated tasks to increase the total number of assigned tasks without conflicts. In detail, compared with the PI algorithm, a reassignment phase for unallocated tasks is proposed, where each UAV continuously checks if dropping a task or exchanging tasks with other UAVs can make more feasible time slots for unassigned tasks. Moreover, numerous simulations performed on multiple UAVs illustrate the performance of the LR-PI algorithm under different communication parameters and verify the superiority of LR-PI algorithm compared with PI-MaxAsses and the PI algorithm. Second, the PI algorithm is extended with an improved task inclusion phase and a novel communication and conflict resolution phase to deal with the task allocation problem with duo cooperation. In other words, a single matrix representing the removal performance impact (RPI) list matrix and UAV list is introduced based on the PI algorithm to redesign the task inclusion; thus, multiple UAVs can be assigned to a single task in the communication conflict resolution phase.

The remainder of the paper is organized as follows. The task allocation problem is first described in Section 2.1 while the process of the baseline PI algorithm is briefly introduced in Section 2.2. In Section 3, the proposed algorithm named LR-PI algorithm, and the non-ideal communication factors used in the paper are presented. The simulations performed with multiple UAVs are illustrated in Section 4. Finally, the conclusion is given in Section 5.

2. Problem Formulation and Baseline PI Algorithm

2.1. Problem Formulation

To formulate the problem mathematically, a bounded environment contains a network of $N_a$ heterogeneous UAVs (such as helicopters, large or small UAVs) and a set of $N_T$ reconnaissance tasks with known requirements and positions. The set of UAVs is denoted $U\stackrel{\Delta }{=}[U_1,U_2,U_3\cdots U_{N_a}]$ while the set of reconnaissance tasks is defined by $T\stackrel{\Delta }{=}[T_1,T_2,T_3\cdots T_{N_T}]$. The UAVs know their locations and the requirements of the tasks and can provide critical support for the reconnaissance tasks. For simplicity, $p_i$ is defined to store the scheduled task allocation result for the ith UAV. We will refer to it as the execution order of the ith UAV. In addition, the actual size of the $p_i$ may vary between UAVs from 0 to $min\{L_i,N_t\}$ because the number of tasks assigned to each UAV may be different. $L_i$ is the maximum number of tasks UAV i can perform. In actual battlefield conditions, distinguishing the different types of tasks is essential. With the deadlines and non-ideal communication factors considered, the paper presents two types of tasks. One is the task that requires a single UAV and the other that requires multiple UAVs to perform simultaneously due to higher importance. The optimization objective J of the task allocation presented in the paper is to minimize the average start time under the premise of allocating more tasks while respecting deadlines and communication constraints. The task allocation model can be stated as Equations (1) and (2).

$$J=min\left\{\sum _{i=1}^{N_a}\sum _{j=1}^{|p_i|}{\displaystyle \frac{1}{|p_i|}}·c_{ij}\left(p_i\right)·x_{ij}\right\}$$

(1)

subject to

$$\left\{\begin{array}{c}{\displaystyle \sum _{j=1}^{N_T}}{x}_{ij}\le L_i\hfill \\ {\displaystyle \sum _{i=1}^{N_a}}{x}_{ij}=nu{m}_j\hfill \\ c_{ij}\left(p_i\right)\le t_j^{start}\hfill \\ d_i\le D_i^{limit}\hfill \end{array}\right.$$

(2)

where $N_a$ is the number of heterogeneous UAVs, $N_T$ is the number of reconnaissance tasks, $\left|p_i\right|$ is the number of tasks that assigned to the UAV i. $x_{ij}=0$ symbolizes the task j will not be performed by the ith UAV, otherwise $x_{ij}=1$. $nu{m}_j$ represents the number of UAVs the task j required. $t_j^{start}$ is the deadline required by the task j. $d_i$ is the fight distance and can be calculated by the fifth-order Pythagorean hodograph [6]. $D_i^{limit}$ represents the maximum flight distance when the ith UAV performs the scheduled tasks. In addition, a symmetric communication matrix $G\left(t\right)$ is presented here to illustrate the communication between UAVs. For example, when the non-ideal communication factors mentioned in Section 3 are satisfied, an entry $g_{ik}\left(t\right)=1$ in the symmetric communication matrix $G\left(t\right)$ indicates that the direct communication exists between the ith UAV and kth UAV. Otherwise $g_{ik}\left(t\right)=0$.

2.2. Baseline PI Algorithm

As one of the most representative distributed task allocation algorithms, the PI algorithm can run separately on each UAV in the multi-UAV systems [4]. To reach conflict-free assignments, two phases are introduced in the PI algorithm [14]. Meanwhile, the basic framework of the CBBA is used. The first phase is the task inclusion phase, where a greedy strategy is introduced to insert tasks to the execution order of each UAV until the capacity is reached or no more tasks can be allocated. In the second phase, the local schedule of each UAV will be shared with neighboring UAVs. Then, based on the consensus method first introduced in [12], the allocation conflicts can be resolved one by one until the Equation (2) is satisfied. Unlike CBBA, the execution times of the later tasks will be delayed if a new task is included in the execution order $p_i$ in the task inclusion phase. Likewise, the performance times will be shifted forward when a task is removed in the communication and conflict resolution phase. In other words, the concept of the performance impact of a task is introduced to determine whether to add or remove the task to optimize the overall system objective.

In the PI algorithm, the reward of the multi-UAV systems and the impact of a task on other assignments are both considered. Among them, the RPI termed $w_k(p_i\ominus t_k)$ is measured as task $t_k$’s reward in $p_i$ plus the difference in reward of later tasks. It can illustrate the impact of the task $t_k$ on the ith UAV in the task allocation process. When a task is removed, it is worth pointing out that the start times of the tasks earlier than the task in $p_i$ are not affected while the start times of other tasks in $p_i$ will be advanced. The contribution of the task $t_k$ to the ith UAV can be expressed as Equation (3).

$$w_k(p_i\ominus t_k)=\sum _{w=b}^{|p_i|}{c}_{i,w}\left(p_i\right)-\sum _{w=b+1}^{|p_i|}{c}_{i,w}(p_i\ominus t_k)$$

(3)

where $p_i\ominus t_k$ symbolizes the task $t_k$ is removed from the $p_i$. b is the possible insert position of the task $t_k$ in the $p_i$. $c_{i,w}\left(p_i\right)$ is the performing reward of a task inserted at index w of the $p_i$. ${\displaystyle \sum _{w=b}^{|p_i|}}{c}_{i,w}\left(p_i\right)$ represents the reward for the ith UAV when the task $t_k$ is included in the $p_i$. ${\displaystyle \sum _{w=b+1}^{|p_i|}}{c}_{i,w}(p_i\ominus t_k)$ is the reward for the ith UAV without the task $t_k$ in the $p_i$. Moreover, an RPI list ${\gamma }_i=[w_1^{\ominus },w_2^{\ominus },w_3^{\ominus }\cdots w_{N_T}^{\ominus }]$ is thus complied for UAV i. To facilitate the consensus, a UAV list ${\beta }_i=[{\beta }_1,{\beta }_2\cdots {\beta }_{N_T}],i=1,2\cdots N_a$ is updated for each UAV. In addition, ${\gamma }_i$ records the matching pairs between UAVs and tasks from the local view of the ith UAV.

To measure the local inclusion performance of the task $t_k$, a newly added task in the $p_i$, the inclusion performance impact (IPI) is used in the section. Moreover, the IPI of the task $t_k$ for the ith UAV can be defined as the reward of task $t_k$ plus the maximum difference in reward when the tasks after the task $t_k$ are performed. The IPI of task k is computed as Equation (4), which can find the maximum IPI and record it as the task $t_k$’s IPI.

$$w_k(p_i\oplus t_k)=\underset{l=1}{\overset{|p_i|+1}{max}}\left\{\sum _{w=l}^{|p_i|+1}{c}_{i,w}\left(p_i{\oplus }_l{t}_k\right)-\sum _{w=l}^{|p_i|}{c}_{i,w}(p_i)\right\}$$

(4)

where $p_i{\oplus }_l{t}_k$ symbolizes the task $t_k$ is added to the $p_i$ at the position l. Likewise, to store the IPI of all tasks in the task inclusion phase, ${\gamma }_i^{\oplus }=[w_1^{\oplus },w_2^{\oplus }\cdots w_{N_T}^{\oplus }]$ is defined for the ith UAV. The main steps of the PI algorithm are presented in Algorithm 1.

Algorithm 1 Task allocation procedure for the baseline PI algorithm running on UAV i.

$1:\mathrm{Define}Tasks,UAVs,Networktopology$

$2:$Initilize$p_i,{\gamma }_i,\mathrm{maximum}\mathrm{number}\mathrm{of}\mathrm{iterations}{T}_{max}$

$3:Converged\leftarrow false$

$4:\mathrm{for}n=1:T_{max}$

$5:({\gamma }_i,p_i)=TaskInclusion(T,U,L_i)$

$6:({\gamma }_i,p_i)=CommunicationandConflictResolution$

$7:\mathrm{Check}\mathrm{convergence}$

$8:\mathrm{if}Convergenced$

$9:\mathrm{break}$

$10:\mathrm{end}\mathrm{if}$

$11:\mathrm{end}\mathrm{for}$

$12:\mathrm{return}{p}_i$

In line 1 of the Algorithm 1, the information of tasks and UAVs, such as location, velocity, total number, and deadlines, is generated randomly. Additionally, the communication offered to produce the communication links between UAVs is presented. What is more, the marginal significance of all tasks not assigned to UAV i are calculated to update the $p_i$ and the RPI list ${\gamma }_i$ [4] in line 5. To facilitate consensus, $p_i$, ${\gamma }_i$ and time stamps are exchanged with neighboring UAVs according to the conflict resolution method that is introduced in [12] at the first time to determine which UAV has the most up-to-date information in line 6.

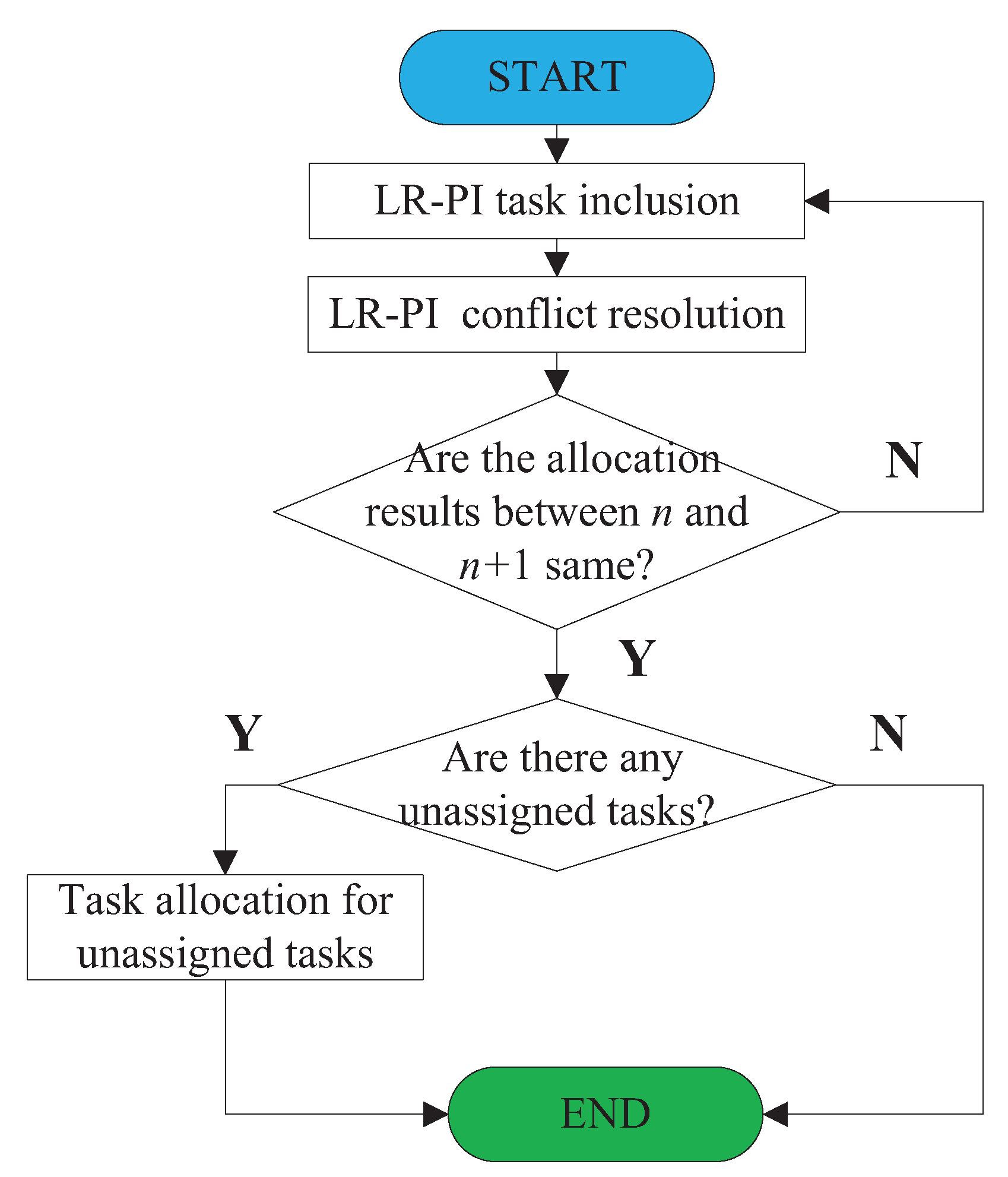
3. Local Reassignment PI Algorithm

In some simulated experiments, such as the simulated experiments in the references [4,7], the PI algorithm can fail to allocate all tasks to UAVs even though the UAVs are capable of accomplishing them. Due to the auction architecture, the PI algorithm can not reassign the unallocated tasks when it is possible to allocate more tasks for the multi-UAV systems. To this end, a systematic method of reassignment for unallocated tasks is provided in the section. This new version, which minimizes the average start time while respecting deadlines and communication constraints, is referred to as the LR-PI algorithm. To create more feasible spaces for the unallocated tasks in the task allocation process, the presented algorithm coupled with reassigning unallocated tasks focuses on maximizing the number of task assignments without conflicts. In addition, it builds upon the baseline PI algorithm, extending it with a novel method for collaborative task allocation with time and communication constraints. The process of the LR-PI algorithm is presented in Figure 1.

3.1. LR-PI Task Inclusion Phase

In some real-world applications, each task may require a varying number of UAVs to improve the efficiency of performing a task. With the PI algorithm, an RPI list ${\gamma }_i=[w_1^{\ominus },w_2^{\ominus },w_3^{\ominus }\cdots w_{N_T}^{\ominus }]$ and an UAV list ${\beta }_i=[{\beta }_1,{\beta }_2\cdots {\beta }_{N_T}],i=1,2\cdots N_a$ is stored on each UAV. In the communication and conflict resolution phase, the ${\gamma }_i$ together with the ${\beta }_i$ is transferred to the communicated UAV k where $g_{ik}\left(t\right)=1$ as shown in Section 2.1. However, the inconsistent problems may be caused between UAVs for tasks that require multiple UAVs. The reason for this is that the ${\gamma }_i$ and ${\beta }_i$ can not provide enough space to store the data for each assignment. Therefore, a single matrix $Z_i$ representing the RPI lists matrix is presented here to store the assignments between UAVs and tasks. To merge ${\gamma }_i$ and ${\beta }_i$ into a single matrix, the size of $Z_i$ is $N_a·N_T$. In addition, an entry $z_{kj}^i$ in $Z_i$ represents UAV i estimating the RPI value of the task $t_j$. The task inclusion phase of the LR-PI algorithm is illustrated in Algorithm 2.

If the number of UAVs required by task j is not satisfied in line 4 of Algorithm 2, task j will be inserted into the $p_i$ at the position l. Likewise, the task with a smaller PRI value than the maximum value in $\{k\in N_a|Z_{kj}^i\ne 0\}$ is added to the $p_i$ in lines 9–10. Furthermore, the single-UAV tasks are added to $p_i$ in the same way as the baseline PI algorithm in line 16. Finally, the $Z_i$ should be updated when the task inclusion phase ends in line 20.

Algorithm 2 LR-PI task inclusion phase for UAV.

$1:\mathrm{while}|p_i|<L_i$

$2:\mathrm{for}\forall j\in T$

$3:\mathrm{if}nu{m}_j>1$

$4:\mathrm{if}nu{m}_j>{\displaystyle \sum _{k=1}^{N_a}}(z_{kj}^i\ne 0)$

$5:\mathrm{compute}\mathrm{IPI}\mathrm{value}{\omega }_j^{\oplus }\mathrm{and}\mathrm{position}l\mathrm{according}\mathrm{to}\mathrm{the}\mathrm{Equation}\left(4\right)$

$6:\mathrm{add}\mathrm{task}j\mathrm{into}{p}_i\mathrm{at}\mathrm{position}l$

$7:\mathrm{else}$

$8:\mathrm{if}{z}_{ij}^i<max\left(z_{kj}^i\right)$

$9:\mathrm{compute}\mathrm{IPI}\mathrm{value}{\omega }_j^{\oplus }\mathrm{and}\mathrm{position}l\mathrm{according}\mathrm{to}\mathrm{the}\mathrm{Equation}\left(4\right)$

$10:\mathrm{add}\mathrm{task}j\mathrm{into}{p}_i\mathrm{at}\mathrm{position}l$

$11:\mathrm{else}$

$12:\mathrm{continue}$

$13:\mathrm{end}\mathrm{if}$

$14:\mathrm{end}\mathrm{if}$

$15:\mathrm{else}$

$16:\mathrm{task}\mathrm{inclusion}\mathrm{of}\mathrm{the}\mathrm{baseline}\mathrm{PI}\mathrm{algorithm}$

$17:\mathrm{end}\mathrm{if}$

$18:\mathrm{end}\mathrm{for}$

$19:\mathrm{end}\mathrm{while}$

$20:\mathrm{update}{Z}_i$

3.2. LR-PI Communication and Conflict Resolution Phase

The communication and conflict resolution phase is necessary and applied to eliminate conflicts, since the number of UAVs locally assigned to task j may be unequal to $nu{m}_j$. In the phase, the $Z_i$ and $s_i$ are exchanged with other UAVs if the non-ideal communication factors mentioned in Section 3.4 are satisfied. $s_i$ represents the timestamp of UVA i. In addition, $s_i$ records the least time for which UVA i communicates with other UAVs. Based on the timestamps, the most up-to-date UAV can be selected to update the scheduled task list. Additionally, a new consensus method is presented here to reach conflict-free assignments by enabling the maximum value in $Z_i$ to move downward. The conflict resolution of the LR-PI algorithm running on each UAV is summarized in Algorithm 3.

Algorithm 3 LR-PI conflict resolution phase for UAV.

$1:\mathrm{send}{Z}_i\mathrm{and}{s}_i\mathrm{to}\mathrm{UAV}k\mathrm{with}{g}_{ik}\left(t\right)=1$

$2:\mathrm{receive}{Z}_k\mathrm{and}{s}_k\mathrm{from}\mathrm{UAV}k\mathrm{with}{g}_{ki}\left(t\right)=1$

$3:\mathrm{for}\forall j\in T$

$4:\mathrm{for}\forall m\in N_a\&z_{mj}^i\ne 0$

$5:\mathrm{if}k=m\&s_{km}>s_{im}$

$6:z_{mj}^i=z_{mj}^k$

$7:\mathrm{end}\mathrm{if}$

$8:\mathrm{for}\forall m\in N_a\&z_{mj}^k\ne 0$

$9:\mathrm{if}i\ne m\&s_{km}>s_{im}$

$10:\mathrm{if}{\displaystyle \sum _{m=1}^{N_a}}(z_{mj}^i\ne 0)<nu{m}_j$

$11:z_{mj}^i=z_{mj}^k$

$12:\mathrm{else}$

$13:\mathrm{if}max(z_{nj}^i,\forall n\in N_a)>z_{mj}^k$

$14:z_{nj}^i=0,z_{mj}^i=z_{mj}^k$

$15:\mathrm{end}\mathrm{if}$

$16:\mathrm{end}\mathrm{if}$

$17:\mathrm{end}\mathrm{if}$

$18:\mathrm{end}\mathrm{for}$

$19:\mathrm{end}\mathrm{for}$

$20:\mathrm{end}\mathrm{for}$

$21:\mathrm{update}{p}_i\mathrm{according}\mathrm{to}{\mathrm{Z}}_{\mathrm{i}},s_i$

In the communication and conflict resolution phase of the LR-PI algorithm, the $Z_i$, and time stamps $s_i$ should be transmitted to the UAV k if $g_{ik}\left(t\right)=1$ (line 1 of the Algorithm 3) to notify it of eliminating conflicts and get the significance value further decreased. In lines 4–7, the UAV i updates the $Z_i$ by merging the $Z_k$ and $s_k$ with those of UAV i to produce consistent information. In addition, $s_{km}>s_{im}$ in line 9 represents that the information of UAV k is the most up-to-date and the date of UAV k can be more accurate than that of UAV i. In lines 10–12, the $z_{mj}^i$ is updated by $z_{mj}^k$, since the requirement of the task j is not satisfied. Otherwise, the maximum value in $\{k\in N_a|Z_{kj}^i\ne 0\}$ is set to 0 in line 14. In other words, the UAV with a higher performance impact releases the task j in line 14 as a lower RPI indicates a more optimal assignment [7]. Finally, the $p_i$ is updated according to the $Z_i$ in line 21.

3.3. Reassignment for Unallocated Tasks

To increase the total number of allocated tasks, the reassignment presented in the section is not just a case of rerunning the task allocation algorithm for all tasks. The reason for this is that some tasks may have been allocated in the task inclusion phase and conflict resolution of the LR-PI algorithm mentioned in Section 3. In addition, fewer reassignments can minimize the convergence time and preserve the advantages of the PI algorithm. Along this line, the reassignment can follow the auction architecture depicted in Algorithms 2 and 3. Instead of allocating all tasks, the candidate tasks in the reassignment process are those not already in $p_i$, and UAVs for a task are insufficient but compatible with the capability of UAV i according to $Z_i$. In other words, the candidate tasks T can be replaced by the unallocated tasks in line 2 of Algorithm 2 and line 3 of Algorithm 3. The candidate tasks can be defined formally as Formula (5).

$$T_u=[t_{u1},t_{u2}\cdots t_{\varsigma }]t_q\notin p_i\&\sum _{m=1}^{N_a}(z_{mq}^i\ne 0)<nu{m}_q$$

(5)

where $T_u$ is the unassigned tasks, the number of unallocated tasks is represented by $\varsigma$, $t_q$ is one of the unassigned tasks. To create more feasible spaces for the unallocated tasks, a task in the $p_i$ is dropped in the task inclusion phase if the release of the task can permit more unallocated tasks to be assigned to the UAV i. In the PI algorithm, the unallocated tasks cannot be reassigned to UAVs against time constraints due in part to the scoring strategies and the auction architecture, although it is possible to do so [7]. In the reassignment phase of the LR-PI algorithm, each UAV tries to include each unassigned task mentioned in the Formula (5) first, and then one allocated task is removed from the current task list of a UAV and reallocated to another UAV if more tasks can be allocated to all UAVs. Therefore, the UAV continuously checks if dropping a task can improve the number of allocated tasks and minimize the average start time. Moreover, dropping a portion of the allocated tasks for more allocations can avoid rebroadcasting and recalculating as frequently.

3.4. Communication Model

The communication model in the distributed task allocation algorithm is presented in the section. In this paper, the non-ideal communication channels are characterized by time delay, package loss, and bit error. Thus, the non-ideal communication factors can be integrated with task allocation to illustrate the flow of information in imperfect communication environments. As described in Section 2.1, the communication links exist when the non-ideal communication constraints are all satisfied.

3.4.1. Package Loss Model

Path loss is caused by the dissipation of the power radiated by the transmitter as well as by the effects of the propagation channel [21]. Shadowing is associated with signal attenuation due to obstacles between the transmitter and the receiver [8,21]. Moreover, a radio signal will encounter multiple objects in the environments, resulting in reflected, diffracted or scattered copies of the transmitted signal, and multiple replicas of the transmitted signal can arrive at the receiver, which is called multipath fading [21,22]. Considering the path loss and fading effects of the wireless signal, this paper adopts the Rayleigh fading model [8] for the received SNR in the transmission between neighboring UAVs as it comes closer to realistic environments compared to other models such as Bernoulli and Gilbert–Elliot [15,23]. The Rayleigh fading model [8] can be expressed as Formula (6).

$${\gamma }_{dB}=P_T+K_{dB}-P_{L_0}-10\delta lg(d/d_0)-N({\mu }_{dB},{\sigma }_{dB}^2)$$

(6)

where ${\gamma }_{dB}$ is the Signal-to-Noise Ratio (SNR), $P_T$ is the transmitted power, $P_{L_0}$ is the path loss at reference distance $d_0$, $\delta$ is the path loss exponent varying between 2 and 6. Generally, $\delta =2$ represents free space while $\delta =6$ represents environments congested with obstacles [24]. d is the distance between the receiver and transmitter, $K_{dB}$ is a gain based on equipment characteristics, $N({\mu }_{dB},{\sigma }_{dB}^2)$ is the noise term with a mean of ${\mu }_{dB}$ and a variance of ${\sigma }_{dB}^2$.

3.4.2. Bit Error Model

In this section, we are interested in task allocation by using the end-to-end bit error rate (BER) to characterize the probability that messages arrive in error between UAVs. BER and SNR are related fundamental parameters that characterize the performance channel and have been used extensively [9,24]. As a result, the instantaneous received SNR directly affects the BER and the reception quality. Let $Tu$ indicate a transmitting UAV that needs to send messages to other UAVs, which is referred to as receiving UAV $Ru$. In a fully connected network, the $Tu$ can directly send information to neighboring UAVs. Otherwise, the connected UAVs will act as routers by relating the information eventually to $Ru$. Then, the BER is defined as $P_b(message\_T_u\ne message\_R_u)$, where $message\_T_u$ and $message\_R_u$ represent the transmitted message and the received messages, respectively. Especially, it is worth pointing out that information must arrive at its destination with acceptable BER. In [9], a general approximation for the BER can be derived as the Equation (7).

$$P_b=0.2·exp\{-{\displaystyle \frac{1.5}{M-1}}·{\gamma }_{dB}\}$$

(7)

where M represents the modulation constellation.

3.4.3. Time Delay Model

When the UAV communication is performed over a huge distance or a ‘slow’ communication channel is used, a time delay appears in the information transmission between UAVs [25]. In this paper, UAVs exchange information with their neighbors, and then neighboring UAVs transmit the information to the next hop and update their information. The one-hop distance can be expressed as formula (8) [8,26].

$$d_{hop}=d_0·{10}^{{\displaystyle \frac{P_T+K_{dB}-P_{L_0}-{P_{ba}}_r-{\mu }_{dB}-{\sigma }_{dB}}{10\delta }}}$$

(8)

where ${P_{ba}}_r$ is the threshold, $d_{hop}$ is the distance that the received signal power equals to ${P_{ba}}_r$. The BER is approximately 1 if the distance between UAVs exceeds $d_{hop}$. In addition, information must be routed along links and arrive at neighboring UAVs with acceptable ${\tau }_{hop}$. In other words, the max bid wait time $t_{wait}$ is greater than the time delay ${\tau }_{hop}$. Otherwise, the communication fails.

3.5. Convergence Analysis

The convergence of the LR-PI algorithm is presented in this section. In the LR-PI algorithm, UAVs try to decrease the average start time as much as possible. This can illustrate the characteristics of convergence. In detail, the IPI and RPI are calculated by recursively adding tasks to the execution order until the capacity is reached or no more tasks can be allocated. Meanwhile, the average start time decreased locally. In the communication and conflict resolution phase, the performance impact of a task can be highly correlated with that in other UAVs. The maximum value in Z decreases by eliminating the conflict tasks with the Equation (2) satisfied. In the reassignment phase, more tasks can be allocated if there exist feasible time slots.

Preliminary experiments running the baseline PI algorithm showed that two or more UAVs occasionally get caught in an infinite cycle exchanging the same tasks [15,16]. To avoid infinite cycles and guarantee convergence, the solution in this paper is to limit the number of times a UAV can exclude the same tasks from its assignment before it no longer attempts to include the task. The number of times each task has been removed from $p_i$ is stored in a vector ${\varpi }_i$ and a maximum limit on removals $\eta \in Z_{+}$ can be set. In the task inclusion phase, a task $t_q$ is considered as a candidate when ${\varpi }_{iq}<\eta$ and ${\varpi }_{iq}={\varpi }_{iq}+1$ when a task $t_q$ is removed from $p_i$ in the conflict resolution phase. Then, the convergence of the LR-PI algorithm can be guaranteed when no changes can be made to the performance impact.

4. Simulations

In the section, the simulation results for the LR-PI algorithm in communication-constrained environments are presented to illustrate the outstanding performance. In addition, to further illustrate the effectiveness and the superiority of the LR-PI algorithm, the performance of the LR-PI algorithm is compared with those of the PI algorithm [4] and PI-MaxAsses [7] using a range of parameter settings. In this paper, the locations of UAVs and tasks are randomly generated within a 10 km × 10 km rectangular area at the beginning and the deadline for each task is placed in $[0,500]$ s in a random manner. It is worth pointing out that the parameter settings in the section are not necessary for the LR-PI algorithm to work.

All the simulations were ran in the Matlab2018 environment on a Hewlett-Packard (HP) computer with 8 GB RAM and an Intel Core i5-7500 processor (Intel Company, Santa Clara, USA), and the system is a Windows 7 Professional system.

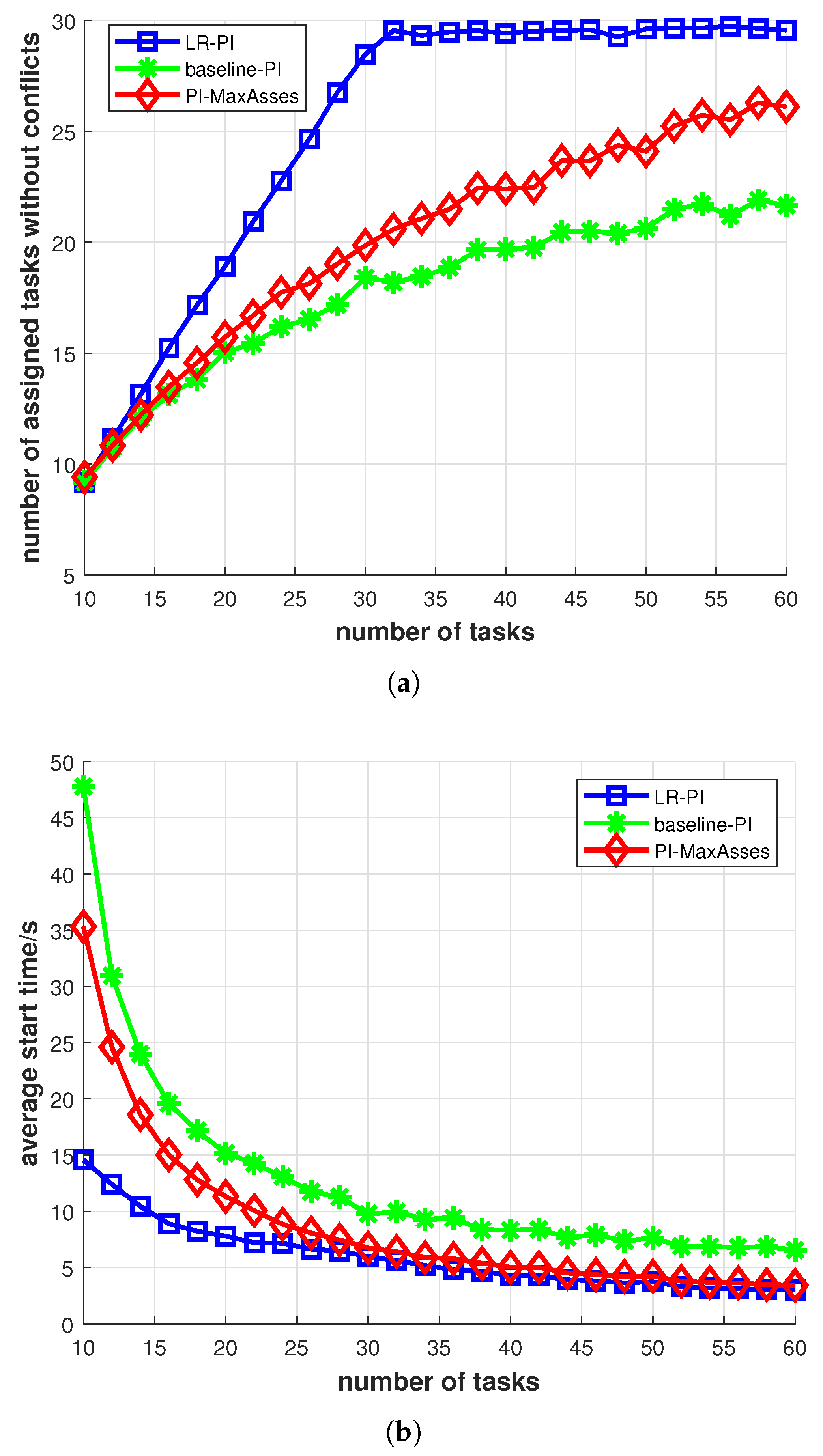
4.1. Feasibility of LR-PI Algorithm

In this section, $N_a=5$ UAVs marked $U_1-U_5$ are required to accomplish $N_T=5$ reconnaissance tasks marked $T_1-T_5$ and the number of UAVs required is from 1 to 5, respectively. The flight speed of the UAVs is 80–100 m/s and they are flying at an altitude of 200 m. The communication factors mentioned in Section 3.4 are shown as follows [8]: $P_{L_0}=80\mathrm{dB}$, $P_T=30\mathrm{dBm}$, $d_0=100\mathrm{m}$, $K_{\mathrm{dB}}=30\mathrm{dB}$, ${\mu }_{\mathrm{dB}}=-70\mathrm{dBm}$, ${\sigma }_{\mathrm{dB}}=7\mathrm{dBm}$, $\delta =2$, $p_b={10}^{-8}$, $t_{wait}=0.05$ s, ${\tau }_{hop}=0.03$ s. Moreover, fifth-order Pythagorean hodograph curves (PH curves) and the kinematic model of the UAV [6] are considered to obtain more flyable paths. Figure 2 shows the scheduled task allocation results of the LR-PI algorithm.

As shown in Figure 2a, the performing sequence of $U_1-U_5$ is represented by the blue line, green line, red line, black line, and cyan line, respectively, while the tasks and UAVs are represented by square and circle marks separately. As expected, the paths of UAVs are closer to flyable paths due to the fact that the fifth-order Pythagorean hodograph curves (PH curves) and the kinematic model of the UAVs are considered. In addition, the successful assignments are shown in Figure 2a, where each task requires a single UAV or multiple UAVs. In Figure 2b, horizontal colored lines are used here to denote the period for executing each task. Meanwhile, the lines with the same color but in the schedule of different UAVs represent those UAVs performing the task cooperatively. Furthermore, UAVs can arrive simultaneously for $T_2-T_5$ and the convergence time of the LR-PI algorithm is 0.22 s.

In the experiment, the task allocation results are obtained with Equation (2) being satisfied in mild communication conditions, this is due to the fact that the deadlines are considered when calculating the IPI in Algorithm 2 and the number of UAVs bidding for a task is limited in Algorithm 3. In other words, the UAV with a maximum PRI is removed from the execution order to eliminate conflicts if $\{k\in N_a|Z_{kj}^i\ne 0\}$ is greater than ${num}_j$. Additionally, the reassignment of the unallocated tasks can ensure that more tasks are included in the task schedule of a UAV. To solve the simultaneous task allocation problem, the real start time of a task depends on the arrival of the latest UAV. This can be guaranteed due to their different cruising speed. Therefore, the LR-PI algorithm can solve the cooperative task allocation problem in time- and communication-constrained environments.

4.2. Validation of LR-PI Algorithm

A case of the LR-PI algorithm is depicted above to present the detailed task allocation in non-ideal communication environments. In this section, the PI algorithm and PI-MaxAsses are conducted to compare with the LR-PI algorithm on the number of tasks, which is referred to as task-to-vehicle ratio in [4,14]. Given the nature of the distributed task allocation, a fully connected network with $N_a=6$ UAVs is presented to perform reconnaissance tasks. For simplicity, $L_i=5$ and the period for executing each task is not considered in the section. Each experiment is analyzed for each increasing number of reconnaissance tasks between 10 to 50 by running 100 times. Moreover, the same times are repeated with the PI algorithm and PI-MaxAsses in the same environments. Also, the communication parameters mentioned in Section 4.1 are adopted here. For each set of examples, the number of assigned reconnaissance tasks without conflicts, the average start time, and convergence time are compared and analyzed in Figure 3.

Figure 3a shows the number of assigned reconnaissance tasks without conflicts, the corresponding average start time and convergence time when the number of tasks is changed are presented in Figure 3b,c. The result shows that the LR-PI algorithm can improve the total number of allocated reconnaissance tasks significantly in comparison with the baseline PI algorithm and PI-MaxAsses, which is due to the fact that some unassigned tasks can be included in the reassignment phase. Moreover, the convergence time of PI-MaxAsses is the longest and the situation becomes even worse with a high task-to-UAV ratio. This is due to the fact that PI-MaxAsses makes few improvements on the baseline PI algorithm solution and accordingly the convergence time is unnecessarily increased [7]. As shown in Figure 3c, the convergence time of the LR-PI is lower compared with that of the PI-MaxAss, the reason for this being that the convergence time for a run of PI-MaxAss is the sum of the convergence time taken for the PI algorithm and the PI-MaxAss. In addition, the convergence time of the LR-PI algorithm is more than that of the PI algorithm; this is because the local reassignment requires more time to find feasible time slots for unallocated tasks. Furthermore, the average start time is reduced, which can be observed in Figure 3b. The reason for this is that the average start time J is inversely proportional to the $|p_i|$ in Equation (1).

4.3. The Influence of Package Loss

To analyze the influence of the package loss on the LR-PI algorithm more comprehensively and generally, $N_a=6$ UAVs with $L_i=5$ are assigned to perform $N_T=20$ tasks. It is noted that each setup with the same communication parameters as those in Section 4.1 but different path loss exponents $\delta$ varying from 2.0 to 5.0 to give a total of 16 communication levels run one hundred times to avoid contingency. Other parameters of UAVs and tasks presented in Section 4.2 are adopted here. The performances of the LR-PI algorithm with different package loss exponents are shown in Figure 4.

Figure 4 shows the mean and distribution of performance data separately. As $\delta$ increases, the number of tasks without conflicts decreases while the box plots increase in Figure 4a. The result is obvious that considering a larger $\delta$ when UAVs communicate with each other could increase the package loss significantly. Moreover, it can be seen that, with the increasing path loss exponent, the change in convergence time shown in Figure 4c is not significant. Conversely, a rise in the average start time is presented in Figure 4b, which results from the average start time being inversely proportional to the $|p_i|$. This is consistent with the analysis in Section 4.2. Meanwhile, the high interquartile ranges for the number of assigned tasks, average start time, and convergence time are due to the randomized UAV and task locations and noise term in the communication model.

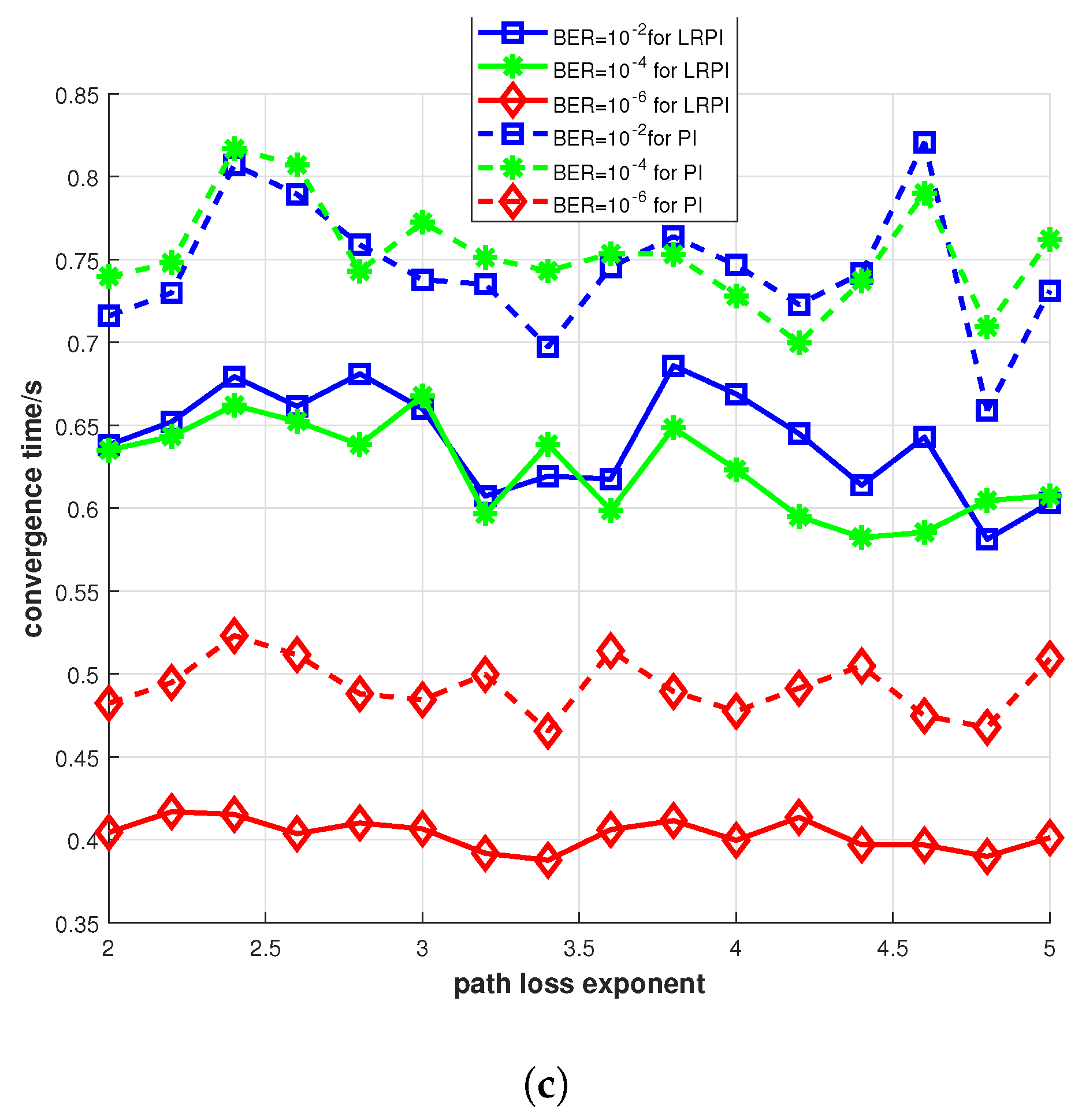
4.4. The Influence of Bit Error Rate

In the section, the simulation results of the LR-PI algorithm with different bit error rates are presented to illustrate the influence of BER. The analytical outcomes are validated by utilizing Monte Carlo simulations that use 100 samples. Due to the random initialization of parameters, such as task and UAV locations and deadlines, sometimes it is impossible to reach conflict-free assignments with the non-ideal communication and deadlines satisfied [4,8,17]. Moreover, it is worth pointing out that each setup with the same communication parameters as those in Section 4.3 have different bit error rates $p_b$${10}^{-2}$, ${10}^{-4}$, and ${10}^{-6}$. To further illustrate the superiority of the LR-PI, the PI algorithm is used to compare to the LR-PI algorithm. The performances of the LR-PI algorithm with different bit error rates are shown in Figure 5.

Figure 5 shows how average start time, convergence time, and number of allocated tasks change as bit error rate and package loss exponents increase while other parameters, such as the number of UAVs and tasks, stay the same. First, as shown in Figure 5a,b, when $\delta$ varies from 2.0 to 5.0, the number of allocated tasks without conflicts and average time decrease gradually; this is because that the average start time is inversely proportional to the $|p_i|$ in Equation (1). Especially, although $p_b$ is small enough in multi-UAV systems, the bit error probability to the entire multi-UAV systems cannot be negligible. The reason for this is that a large number of bits are required in the task allocation. It should be noted that a larger $p_b$ would degrade the algorithm’s optimality. Conflicts between UAVs exist eventually in Figure 5a and the decrease in efficiency in Figure 5c. This is due to the high value of $p_b$ in multi-UAV systems and $p_b$ can indicate the probability an information bit be dropped between UAVs. Thus, with a higher $p_b$, it is more difficult for an information bit to arrive at its destination. The proposed LR-PI algorithm shows improvements compared to the PI algorithm on task allocation, given the different bit error rates.

4.5. The Influence of Max Bid Wait Time

The effect of increasing the max bid wait time $t_{wait}$ is illustrated in this section. $N_T=20$ reconnaissance tasks are presented to be performed by $N_a=6$ UAVs with $L_i=5$. The time delay values ${\tau }_{hop}$ are randomly generated within [0.02, 0.06] s. Other parameters used in Section 4.4 are presented here. The performances of the LR-PI algorithm with different $t_{wait}$ are presented in Figure 6. In addition, it is worth pointing out that the number of assigned tasks and average start time are similar to Section 4.4, and thus omitted.

In Figure 6, an exponential rise in the convergence time to gain conflict-free assignments is presented with the increase in $t_{wait}$, which results from the fact that more time is required in the conflict resolution phase and reassignment phase. Moreover, the convergence time with varying $\delta$ does not change significantly. As expected, the result shown here is consistent with the analysis above.

5. Conclusions

This paper presents an extension of the state-of-art PI algorithm to solve the multi-UAV task allocation problems, which, coupled with reassigning unallocated tasks, focuses on maximizing the number of task assignments without conflicts. Thus, it is much applicable to real-world task allocation problems with time and communication constraints. Additionally, the non-ideal communication factors, such as bit error, time delay, and package loss, are integrated with task allocation in the conflict resolution phase, which inevitably exist and can degrade task allocation performance in realistic communication environments. Finally, we show the performance of the proposed algorithm under different communication parameters and verify its superiority in comparison with the PI-MaxAsses and the baseline PI algorithm. In future research, a suitable method will be designed to reduce the effect of non-ideal communication factors, and the dynamic task allocation of UAVs with some novel control methods considered will form an element of future work to be undertaken, as the characteristics of the tasks cannot be accurately predicted.