1. Introduction
With the great development of hypersonic-related technologies, High Supersonic Unmanned Vehicles (HSUAVs) have become a major threat in future wars. It will stimulate the continuous development and innovation of defending systems against HSUAVs. Correspondingly, the interception scenarios against HSUAVs are becoming complicated, and the capabilities of interceptors are upgrading dramatically. The traditional penetration strategies of HSUAVs are becoming increasingly inadequate for penetration tasks in complex interception scenarios. Consequently, the penetration strategy of high-speed aircraft is gradually being regarded as a significant and challenging research topic. Inspiringly, the Artificial-Intelligence-based penetration methods have become promising candidate solutions.
In early research, the penetration strategies with programmed maneuver prelaunch were designed, which had been extensively applied in engineering, such as the sinusoidal maneuver [
1], the spiral maneuver [
2,
3], the jump–dive maneuver [
4], the
S maneuver [
5], the weaving maneuver [
6,
7], etc., but their penetration efficiency was very limited. In order to improve the penetration effectiveness, the penetration guidance laws based on modern control theory have been widely studied. The authors in [
8] presented optimal-control-based evasion and pursuit strategies, which can effectively improve survival probability under maneuverability constraints in one-on-one scenarios. The differential game penetration guidance strategy was derived in [
9], and the neural networks were introduced in [
10] to optimize the strategy to solve the pursuit–evasion problem. The improved differential game guidance laws were derived in [
11,
12], and the desired simulation results were obtained. In [
13,
14], a guidance law in a more sophisticated target–missile–defender (TMD) scenario was derived with control saturation, which could ensure the missile escaped from the defender. These solutions are mainly performed based on the linearized models, resulting in a loss of accuracy.
The inadequacy of existing strategies’ capabilities and the significant superiority of Artificial Intelligence motivate us to solve the problem of penetration in complex scenarios by intelligent algorithms. As far as the authors are concerned, in most of the research on penetration strategies based on modern control theory, the interception scenario was simplified to a two-dimensional (2D) plane, wherein only one interceptor was considered. However, in practical situations, the opponent usually launches at least two interceptors to deal with high-speed targets. Therefore, the performance of these penetration strategies would degrade distinctly in practical applications. In recent years, intelligent algorithms have been widely developed due to their excellent adaptability and learning ability [
15]. Deep Reinforcement Learning (DRL) was proposed by DeepMind in 2013 [
16]. DRL combines the advantages of Deep Learning (DL) and Reinforcement Learning (RL), with powerful decision making and situational awareness capabilities [
17]. The designs of guidance laws based on DRL were proposed in [
18,
19,
20], and it has been proven that the new methods are superior to the traditional proportional navigation guidance (PNG). DRL has been applied in much research, such as collision avoidance methods for Urban Air Mobility (UAM) vehicles [
21] and Air-to-Air combat [
22]. In the field of high-speed aircraft penetration or interception, a pursuit–evasion game algorithm was designed by PID control and Deep Deterministic Policy Gradient (DDPG) algorithm in [
23], and it achieved better results than only PID control. Intelligent maneuver strategies using DRL algorithms have been proposed in [
24,
25] to solve the problem of one-to-one midcourse penetration of an aircraft, which can achieve higher penetration win rates than traditional methods. In [
26,
27], the traditional deep Q-network (DQN) was improved into a dueling double deep Q-network (D3Q) and a double deep Q-network (DDQN) to solve the problem of attack–defense games between aircraft, respectively. In [
28], the GAIL-PPO method that combined the Proximal Policy Optimization (PPO) and imitation learning was proposed. Compared with classic DRL, the improved algorithm provided new approaches for penetration methods.
Based on a deep understanding of the penetration process, high-speed UAVs can only make correct decisions by predicting the intention of interceptors. Therefore, algorithms are required to be able to process state information over a period of time, which is not available in the current DRL due to the sampling method of the replay buffer. To attack this problem, a Recurrent Neural Network (RNN) that specializes in processing time series data is incorporated into the classic DRL. The Long Short-Term Memory (LSTM) networks [
29] are mostly used as memory modules because of their stable and efficient performance and excellent memory capabilities. The classic DRL algorithms were extended by LSTM networks in [
30,
31], which demonstrated superior performance than classic DRL in the problems of Partially Observable MDPs (POMDPs). The conspicuous advantages of memory modules in POMDPs were demonstrated. The LSTM-DDPG (Deep Deterministic Policy Gradient) approach has been proposed to solve the problem of sensory data collection of UAVs in [
32], and the numerical results show that LSTM-DDPG could reduce packet loss more than classic DDPG.
The above research demonstrates the advantages of the DRL algorithm with memory modules, but it has not yet been applied to the penetration strategy of high-speed UAVs. The Soft Actor–Critic (SAC) algorithm [
33] was proposed in 2018 and has been applied with the advantages of wide exploration capabilities. Therefore, the LSTM networks are incorporated into the SAC to explore the application of LSTM-SAC in the penetration scenario of a high-speed UAV escaping from two interceptors. The main contributions in this paper can be summarized as follows:
- (a)
A more complex 3D space engagement scenario is constructed, where the UAV faces two interceptors with a surrounding case and its penetration difficulty dramatically increases.
- (b)
A penetration strategy based on DRL is proposed, in which a reward function is designed to enable high-speed aircraft to evade interceptors with low energy consumption and minimum deviation, resulting in a more stable effect than conventional strategies.
- (c)
A novel memory-based DRL approach, LSTM-SAC, is developed by combining the LSTM network with the SAC algorithm, which can effectively make optimal decisions on input temporal data and significantly improve training efficiency compared with classic SAC.
The rest of the paper is organized as follows: The engagement scenario and basic assumptions are described in
Section 2. The framework of LSTM-SAC is introduced in
Section 3, and the state space, action space, and reward function are designed based on MDP and engagement scenarios. In
Section 4, the algorithm is trained and validated. Finally, the simulation results are analyzed and summarized.
2. Engagement Scenario
The combat scenario modeling, kinematic, and dynamic analysis are formulated in this chapter. To simplify the scenario, some basic assumptions are made as follows:
Assumption 1: Both the high-speed aircraft and interceptors are described by point-mass models. The 3-DOF particle model is established in the ground coordinate system:
where
are the coordinates of the vehicle.
indicate the vehicle’s velocity, flight path angle, and flight path azimuth angle, and
represents gravitational acceleration.
denote the projection of the overload vector on each axis of the direction of velocity. Specifically, overload is the ratio of the force exerted on the aircraft to its own weight, which is a dimensionless variable used to describe the acceleration state and the maneuverability of the aircraft.
where
represents the projection of the external force on the
-axis in the direction of velocity, and
represents the gravity of the aircraft.
is tangential overload, which indicates the ability of the aircraft to change the magnitude of its velocity, and
are normal overloads, which represent the ability of the aircraft to change the direction of its flight in the plumb plane and the horizontal plane, respectively.
Assumption 2: The high-speed UAV cruises at a constant velocity toward the ultimate attack target when encountering two interceptors. The enemy is able to detect the high-speed UAV at a range of 400 km and launches two interceptors from two different launch positions against one target. The onboard radar of the aircraft starts to work at a range of 50 km relative to the interceptor and then detects the position information of the interceptor missile.
Assumption 3: The enemy is capable of recognizing the ultimate attack target of the high-speed aircraft. The guidance law of the interceptors does not switch during the entire interception procession. The interceptors adopt proportional navigation guidance (PNG) law with varying navigation gain:
where
denotes the acceleration command of the interceptor.
denote the relative distance and line of sight (LOS) between the interceptor and the high-speed aircraft, respectively.
The above assumptions are widely used in the design of maneuvering strategies of aircraft, which can simplify the calculation process while providing accurate approximations.
In 3D planar, it is difficult to directly obtain the analytical relationship between LOS and fight-path angle. The motion of an aircraft in three-dimensional space can be simplified as a combination of horizontal and plumb planes, which can help us analyze and understand the motion characteristics of the aircraft more easily. Therefore, for the convenience of engineering applications, the motion of the 3D planar is projected onto two 2D planes (horizontal and plumb). Due to the two interceptors surrounding the horizontal plane instead of the plumb plane to strike high-speed aircraft, it is more difficult to escape on the horizontal plane. Maneuvers on the horizontal plane should be primarily considered. In addition, limited by engine technology conditions, maneuvering is primarily conducted on the horizontal plane.
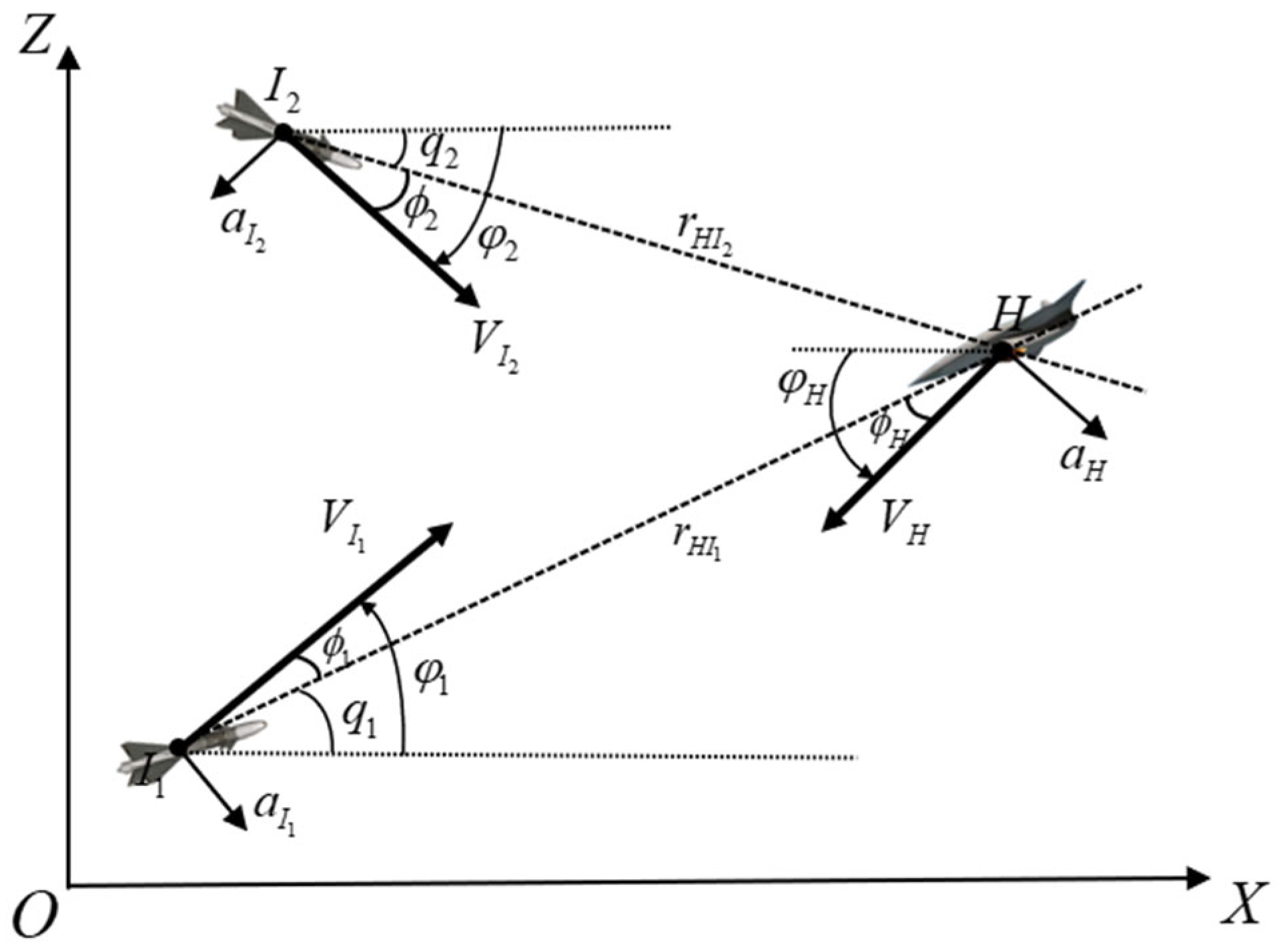
Taking the horizontal plane as an example, the engagement between two interceptors and one high-speed aircraft is considered. As in
Figure 1, X-O-Z is a Cartesian inertial reference frame. The notations
and
are two interceptors and an aircraft, respectively, and the variables with subscripts
and
represent the variables of the two interceptors and the high-speed aircraft. The velocity and acceleration are denoted by
, respectively. The notations of
are LOS angle, fight-path azimuth angle, and lead angle. The notation
is the relative distance between the interceptor and the high-speed aircraft.
Taking the interceptor-Ⅰ as an example, the relative motion equations of the interceptor-Ⅰ and the high-speed aircraft are:
To make the simulation model more realistic, the characteristics of an onboard autopilot for both interceptors and high-speed aircraft are incorporated. The first-order lateral maneuver dynamic is assumed as follows:
where
is the time constant of the target dynamics, and
denotes the overload command.
5. Conclusions
In this paper, the penetration strategy of a high-speed UAV is transformed into decision-making issues based on MDP. A memory-based SAC algorithm is applied in decision algorithms, in which LSTM networks are used to replace the fully connected networks in the SAC framework. The LSTM networks can learn from previous states, which enables the agent to deal with decision-making problems in complex scenarios. The architecture of the LSTM-SAC approach is described, and the effectiveness of the memory components is verified by mathematical simulations.
The reward function based on the motion states of both sides is designed to encourage the aircraft to intelligently escape from the interceptors under energy and range constraints. By the LSTM-SAC approach, the agent is able to continuously learn and improve its strategy. The simulation results demonstrate that the converged LSTM-SAC has similar penetration performance to the SAC, but the LSTM-SAC agent with three historical states has a training efficiency improvement with 75.56% training episodes reduction compared with the classical SAC algorithm. In the engagement scenarios wherein two interceptors with strong maneuverability and random initial flight states within a certain range are considered, the probability of successful evasion of the high-speed aircraft is higher than 90%. Compared with the conventional programmed maneuver strategies represented by the sinusoidal maneuver and the square maneuver, the LSTM-SAC maneuver strategy possesses a win rate of over 90% and more robust performance.
In the future, noise and unobservable measurements are about to be introduced to the engagement scenarios, and the effect of LSTM-SAC will be evaluated in more realistic engagement scenarios. Additionally, the 3-DOF dynamic model is based on simplified aerodynamic effects. Due to the complex aerodynamic effects in the real battlefield, there is no guarantee that the strategies trained on the point-mass model will perform as well in real scenarios as they do in the simulation environment. In subsequent research, the 6-DOF dynamics model, which can better simulate complex maneuvers, will be considered for implementing penetration strategy research. In summary, the LSTM-SAC can effectively improve the training efficiency of classic DRL algorithms, providing a new promising method for the penetration strategy of high-speed UAVs in complex scenarios.