Establishment and Verification of the UAV Coupled Rotor Airflow Backward Tilt Angle Controller
Abstract
1. Introduction
2. Materials and Methods
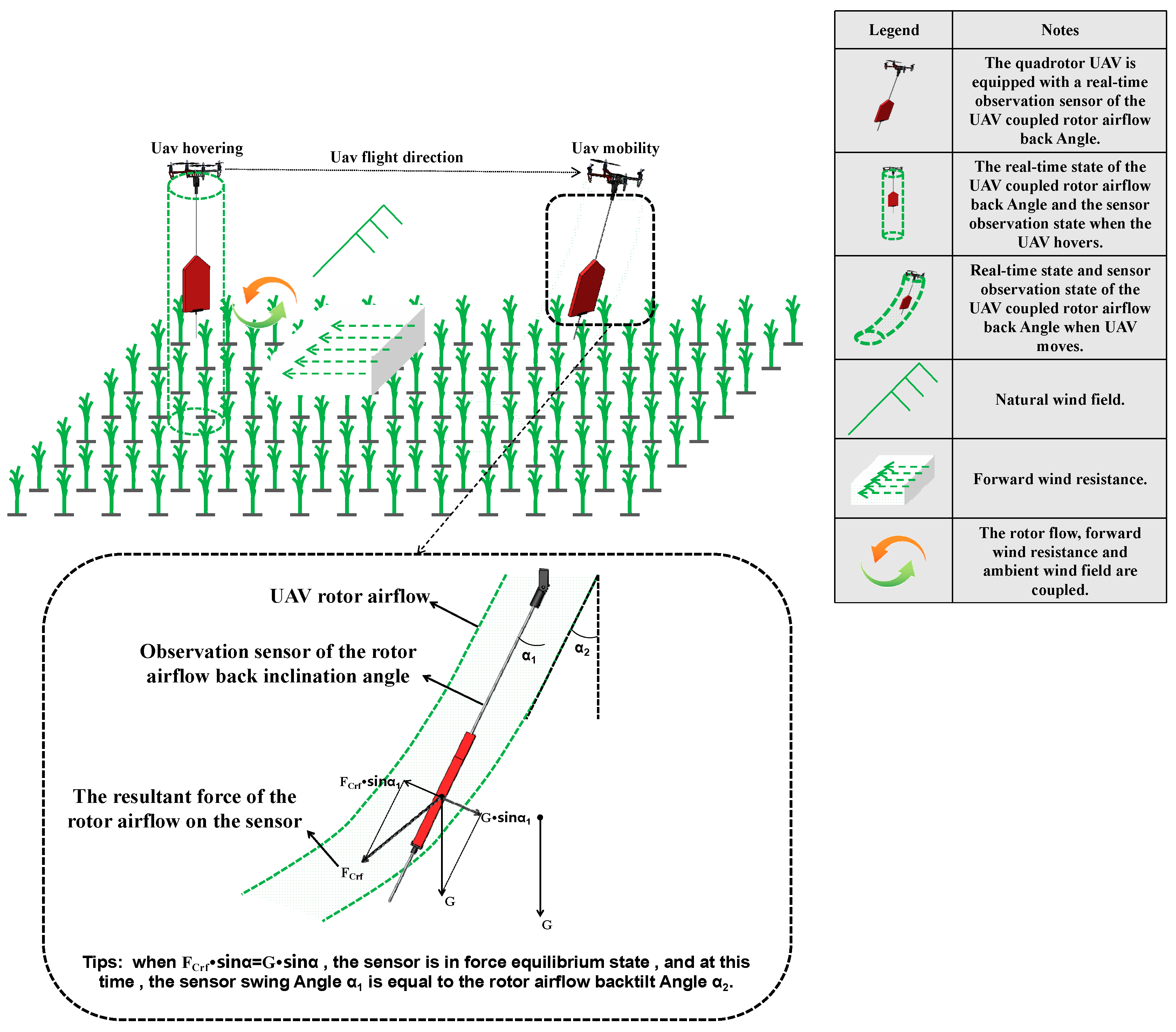
2.1. Design of the RABTA Sensor
2.1.1. Principle of RABTA Sensor
2.1.2. RABTA Sensor Structure
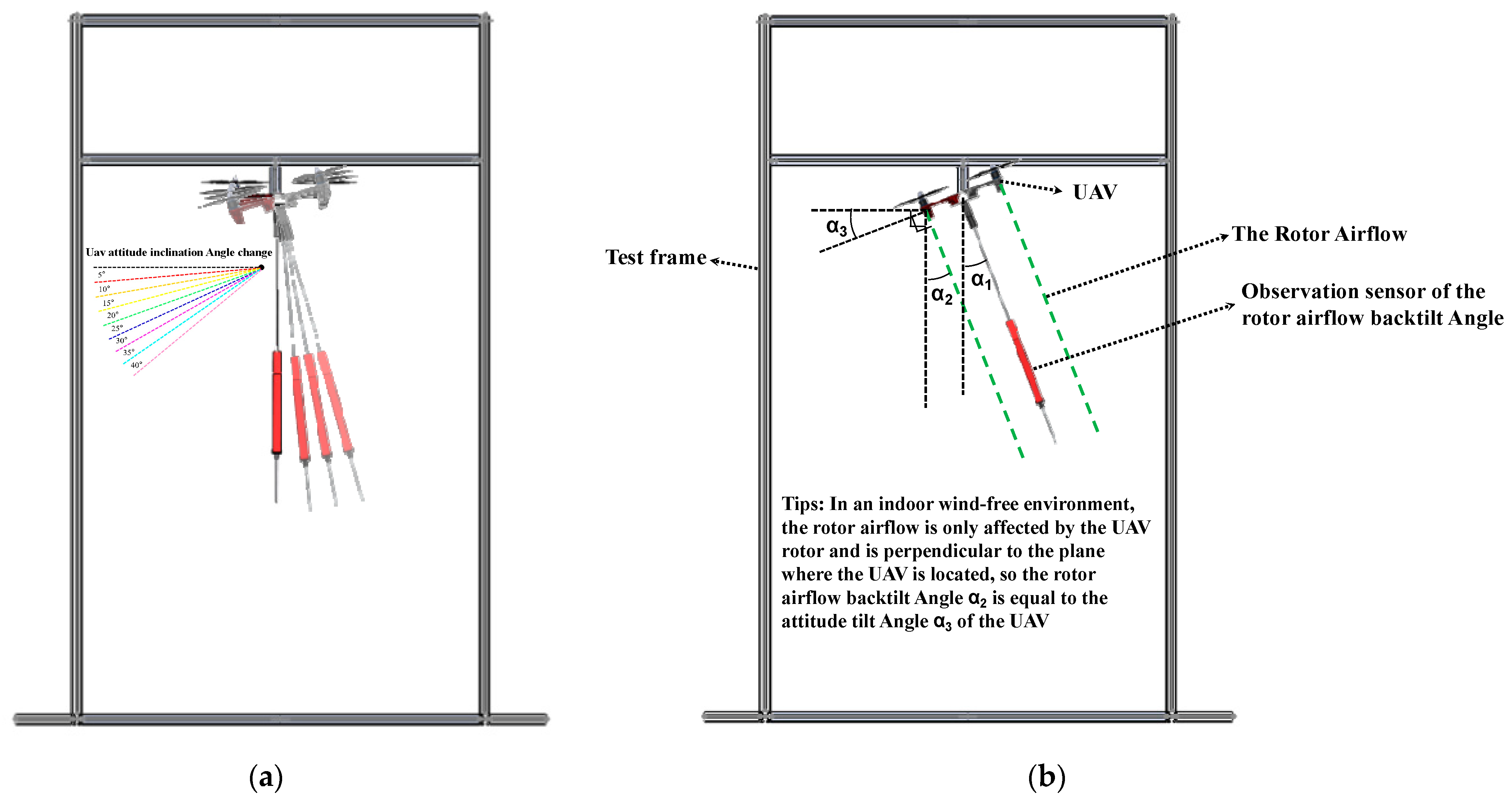
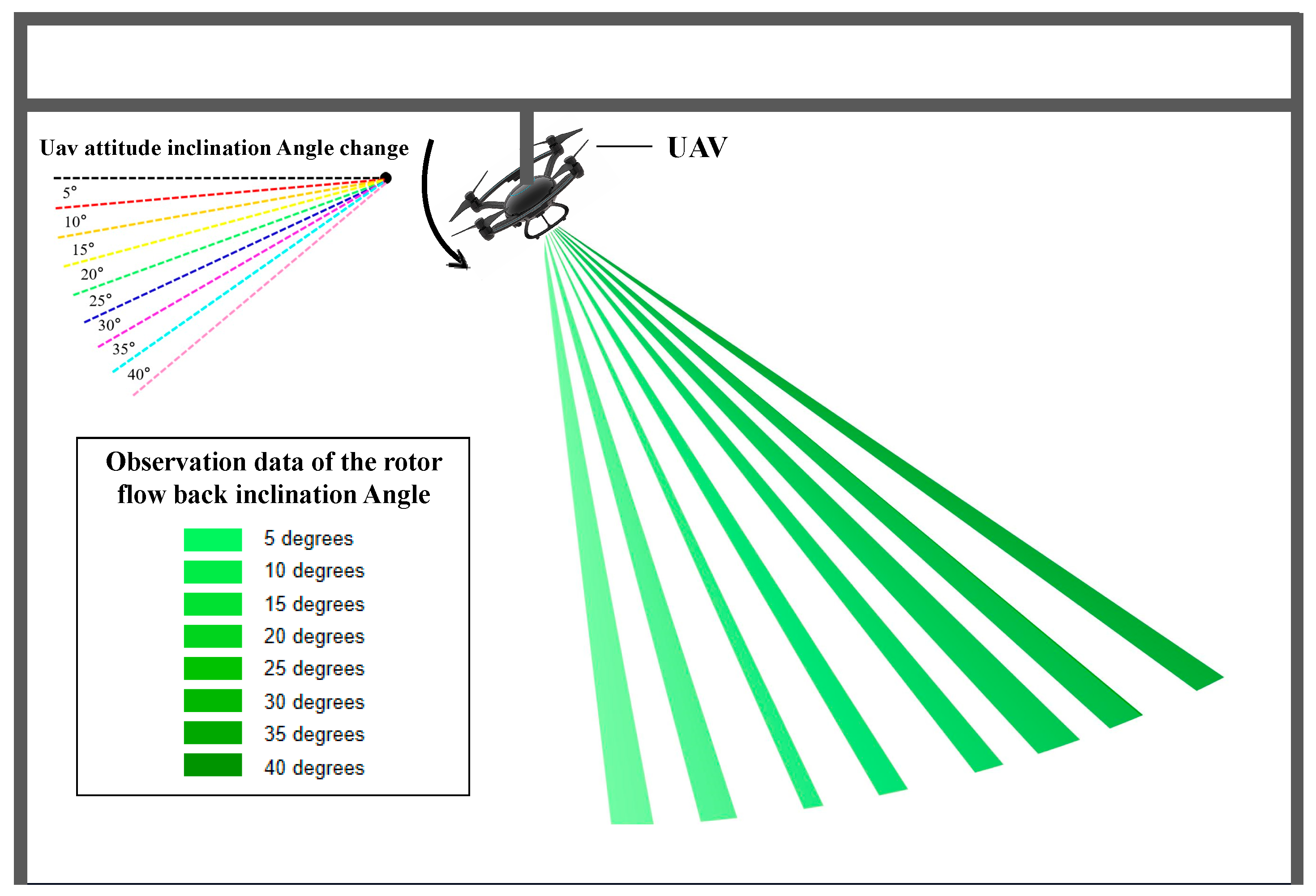
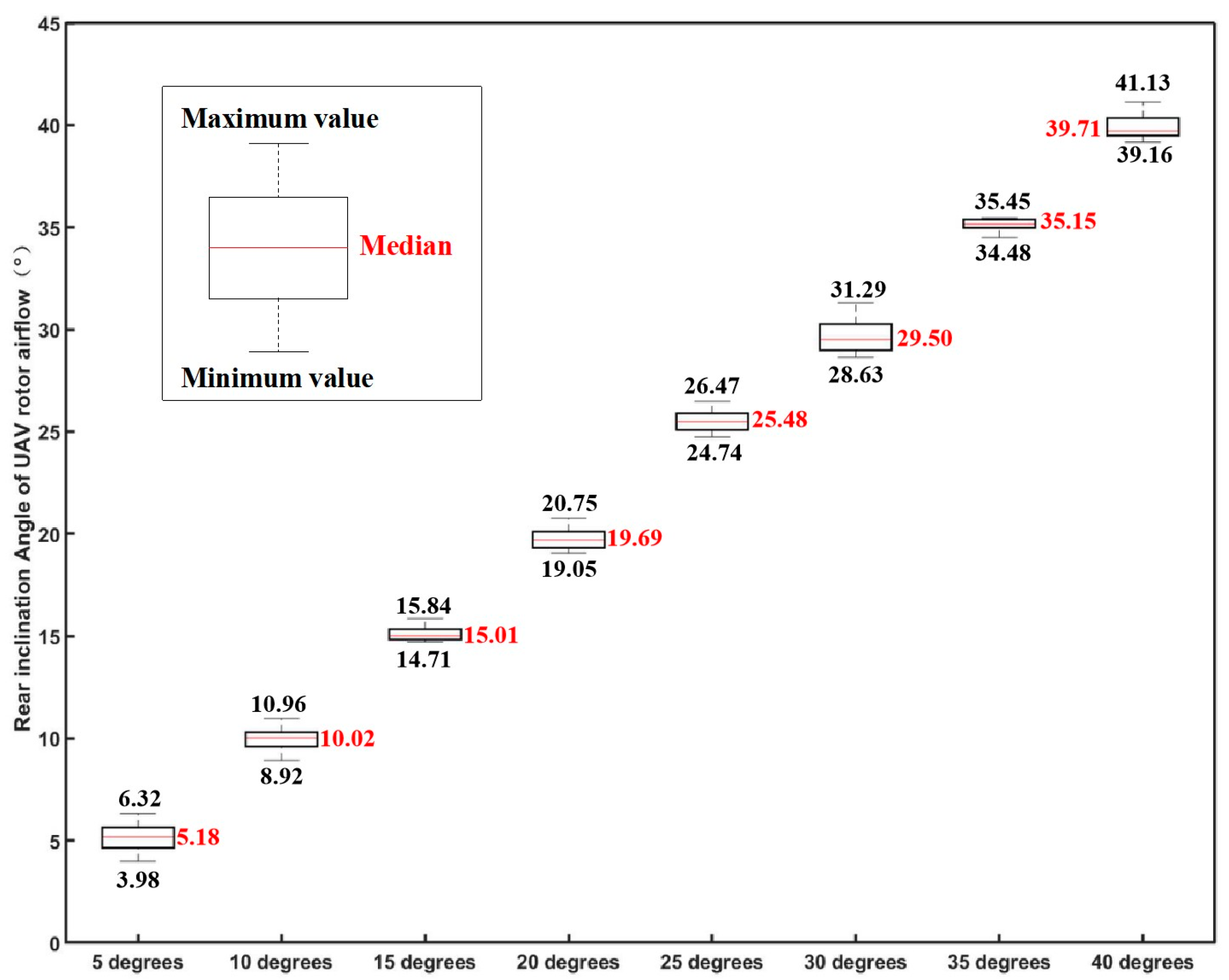
2.1.3. RABTA Sensor Observation Effect Verification Experiment
Test Site and Materials
Experimental Process and Result Analysis
2.2. Collection Experiment of the Backward Tilt Angle Observation State at Different Flight Speeds
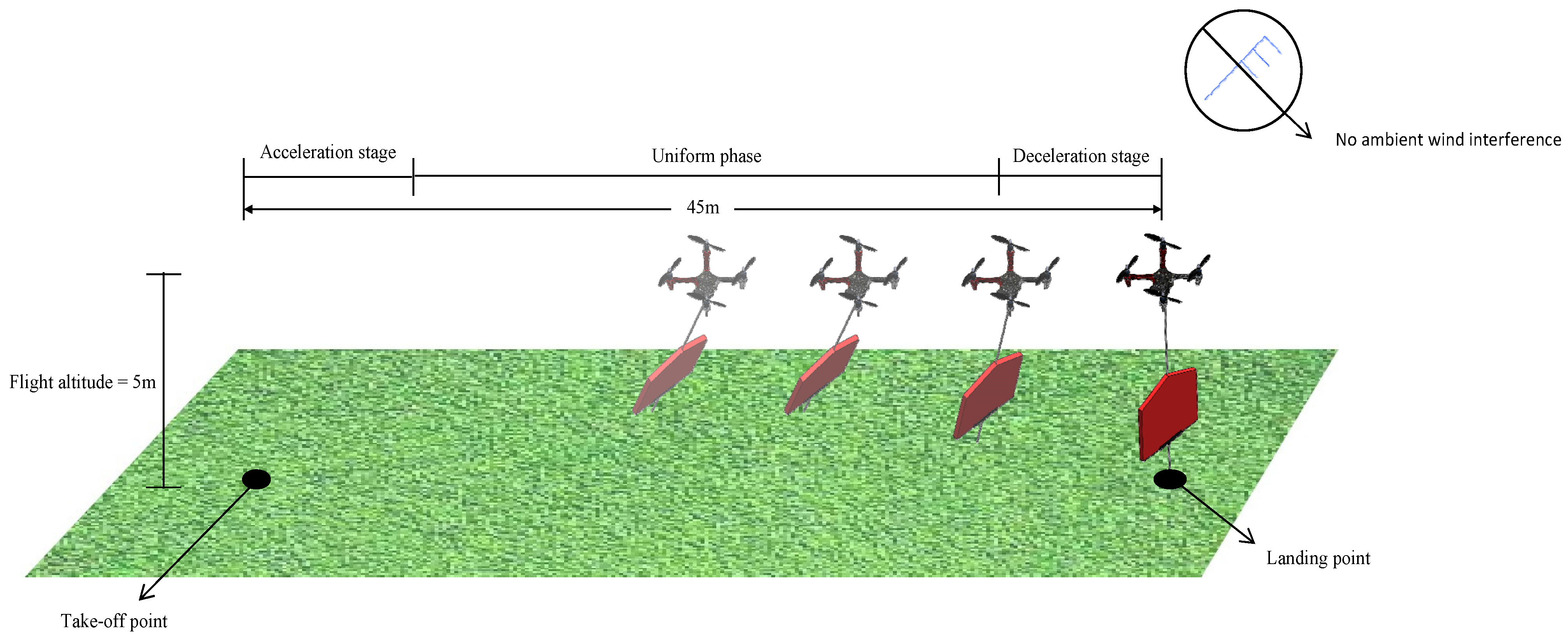
2.2.1. Test Site and Materials
2.2.2. Experimental Methods and Parameters
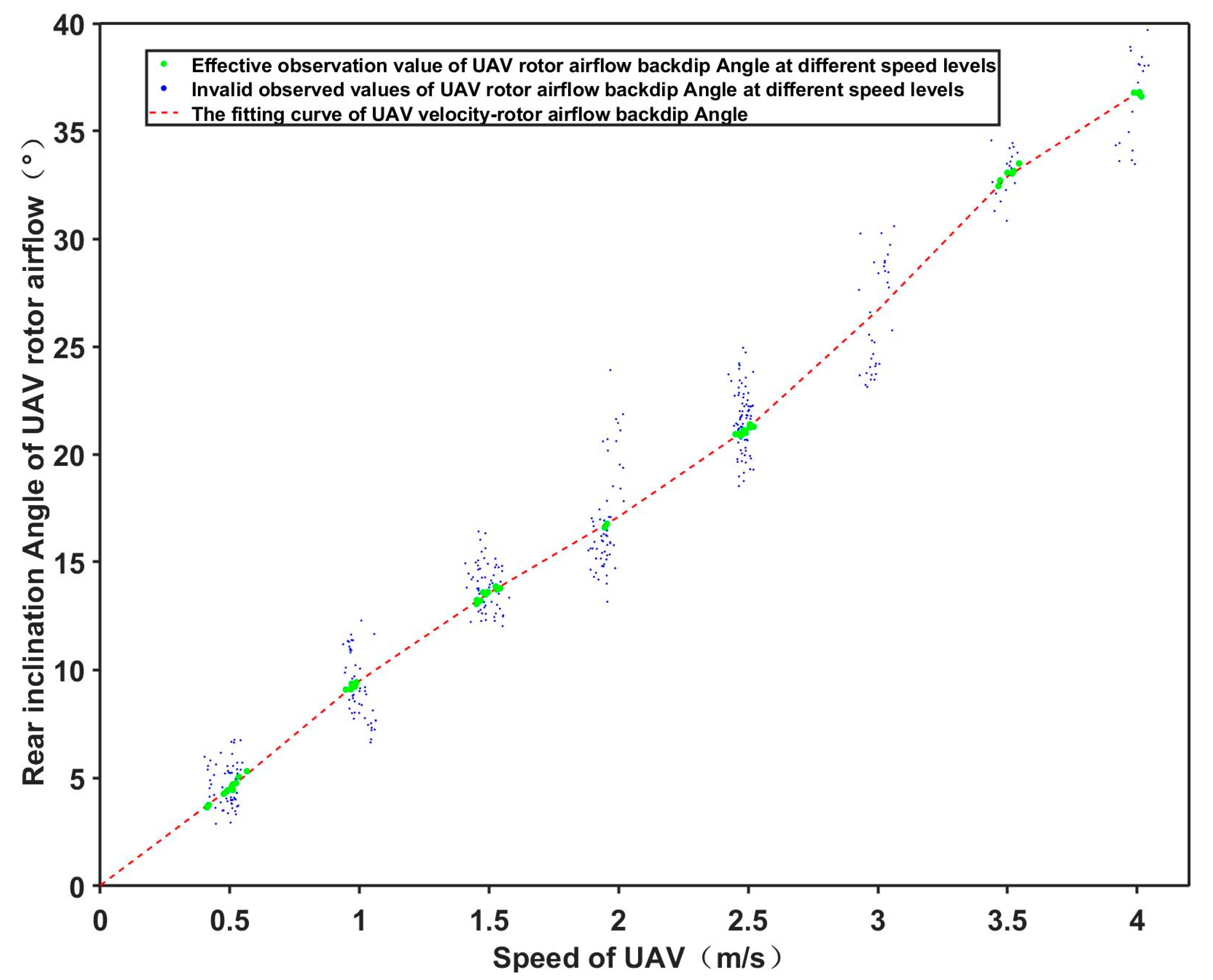
2.2.3. Experimental Results
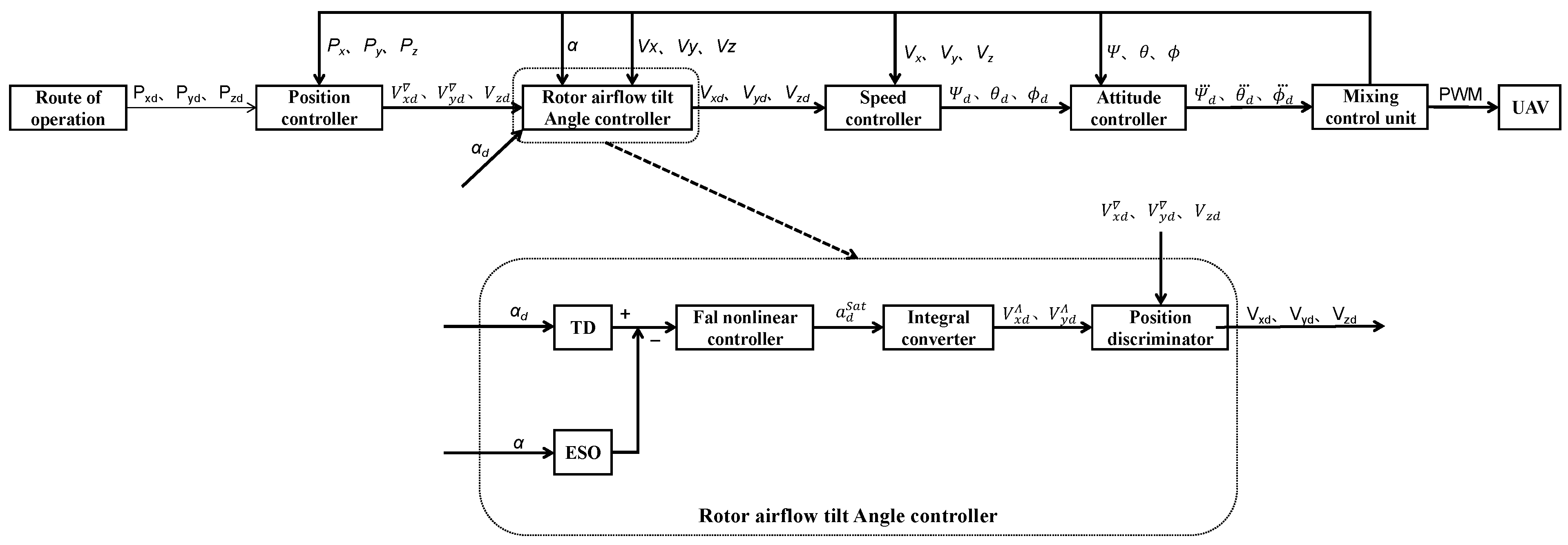
2.3. Establish RABTA Controller
2.3.1. The Differential Tracker
2.3.2. Expanded State Observer (ESO)
2.3.3. fal Nonlinear Controller
2.3.4. Integral Converter and Position Discriminator
3. Experimental Results and Discussion
3.1. Evaluation Metrics
3.2. Experimental Results
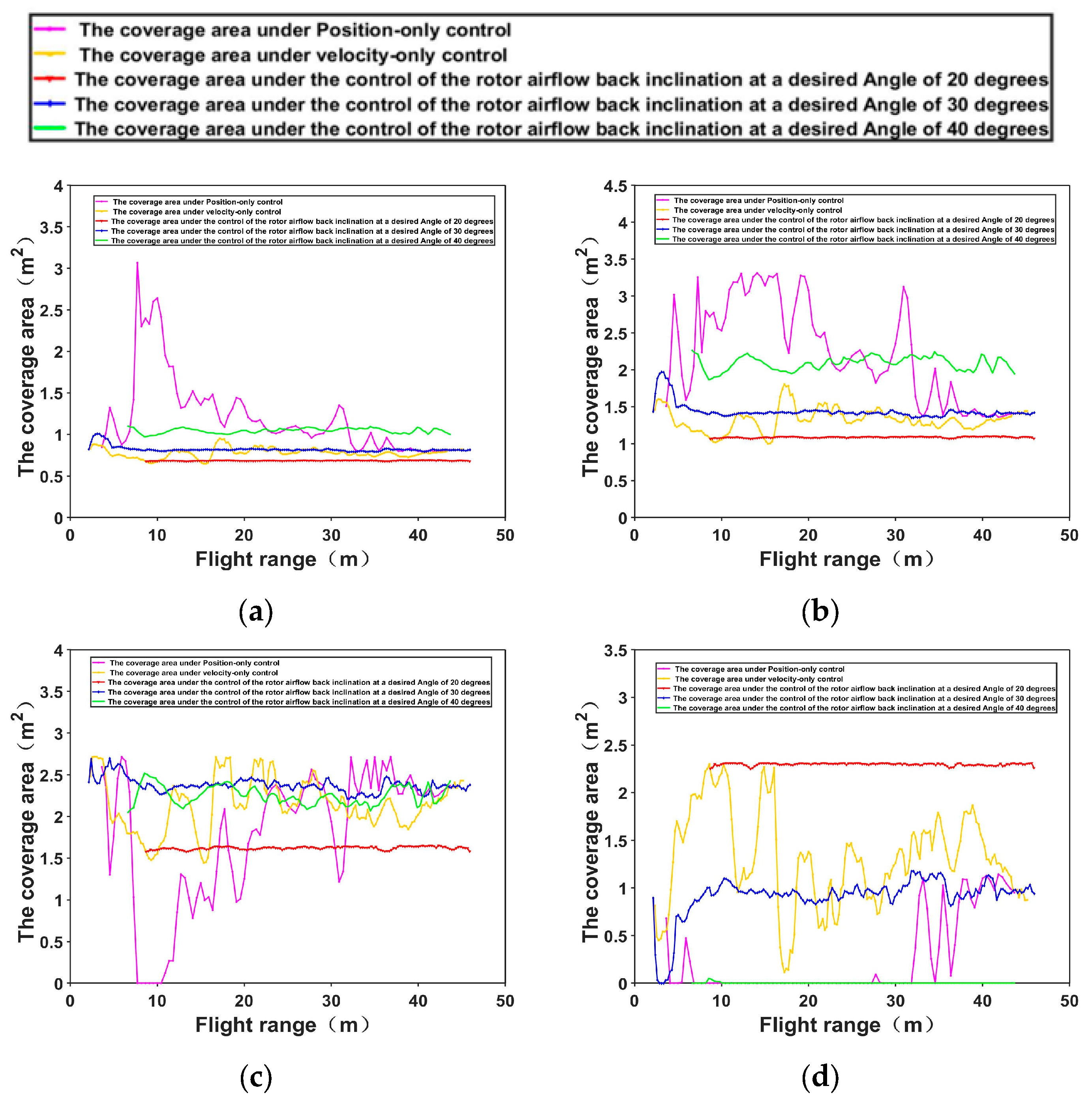
3.3. Comparison and Analysis of the Control Effect and Operation Effect between the Traditional Flight Controller and RABTA Controller
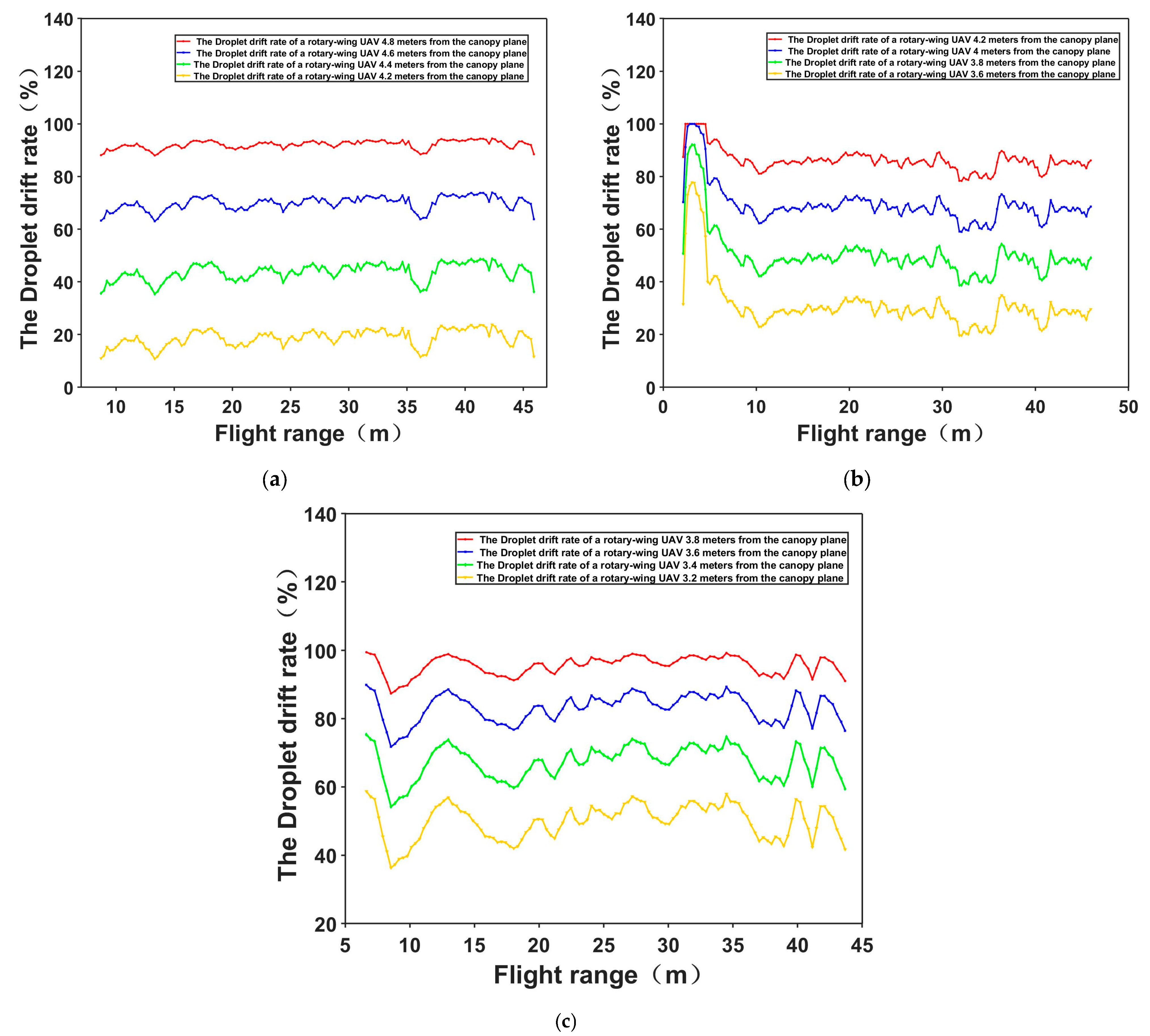
3.4. Comparison and Analysis of the Control Effects and Operation Effects of the RABTA Controller under Different Expected Angles
4. Conclusions
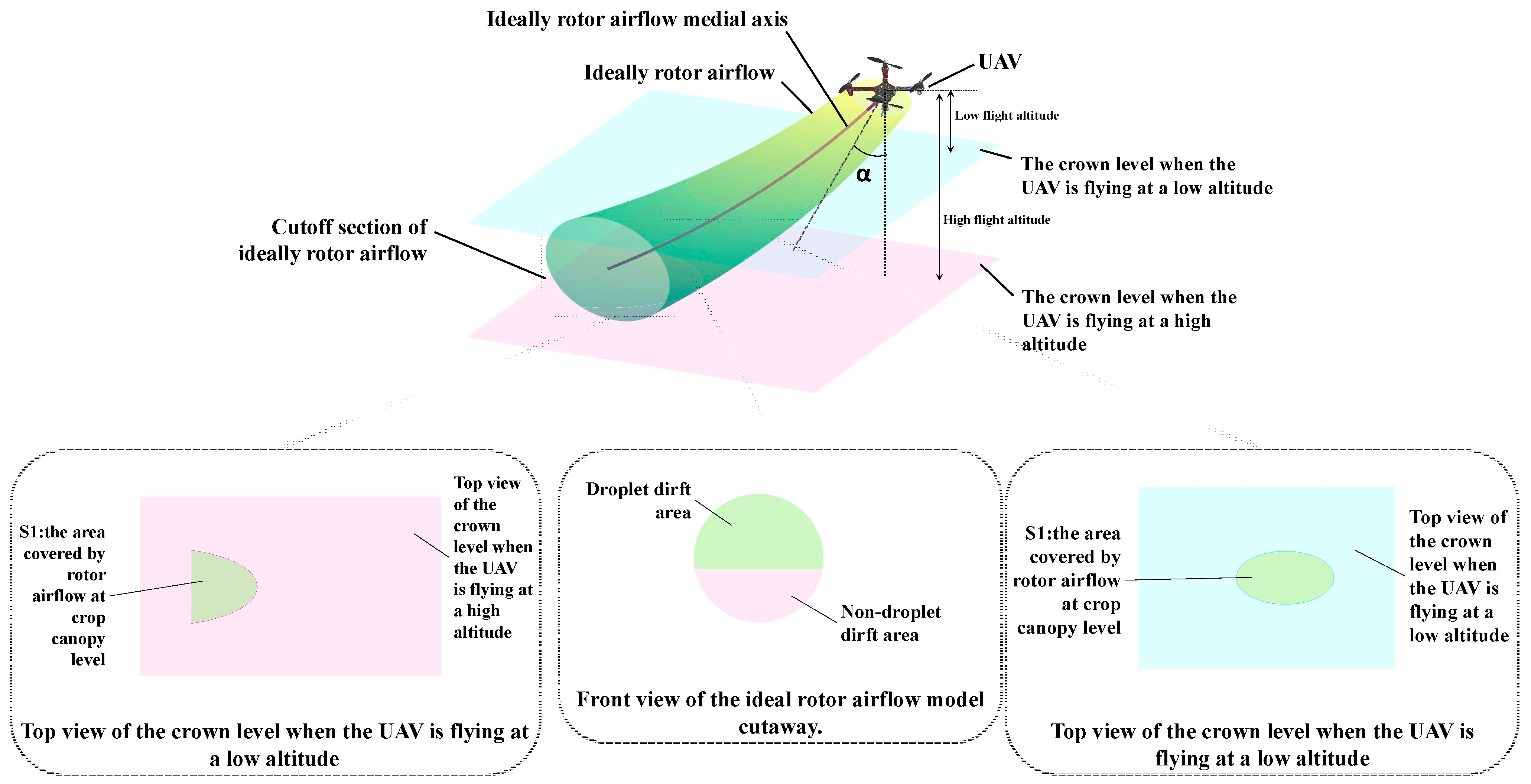
- In the field application process of the rotor UAV, the RABTA controller can replace the traditional UAV flight controller to control the backward tilt angle and maintain the control error below 1 degree, achieving a 48.3% improvement in the uniformity of the distribution of pesticides droplets across the crop canopy. This will provide a new operational control mode for agricultural UAV, which is a new direction for efficient and high-quality operations with field work effect factors as the control objects, achieving innovation in the control paradigm of agricultural UAV.
- In the actual field application process of the rotor UAV, the RABTA controller can accurately and quickly control the backward tilt angle in the range of 20 degrees to 40 degrees to maintain a better state to complete the work (the maximum steady-state error is 0.92 degrees, and the maximum adjustment time is 3.3 s), reducing the degree of the non-uniform distribution of droplets by 83.8% and the drift rate of droplets by 48.3%. On the basis of retaining the high efficiency of agricultural drone operations, it introduces new indicators for enhanced effectiveness, increases crop yield, and achieves economic benefits in agriculture.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiyu, L.; Lan, Y.; Jianwei, W.; Shengde, C.; Cong, H.; Qi, L.; Qiuping, L. Distribution law of rice pollen in the wind field of small UAV. Int. J. Agric. Biol. Eng. 2017, 10, 32–40. [Google Scholar] [CrossRef]
- Li, J.; Shi, Y.; Lan, Y.; Guo, S. Vertical distribution and vortex structure of rotor wind feld under the infuence of rice canopy. Comput. Electron. Agric. 2019, 159, 140–146. [Google Scholar] [CrossRef]
- Wang, L.; Xu, M.; Hou, Q.; Wang, Z.; Lan, Y.; Wang, S. Numerical verification on influence of multi-feature parameters to the downwash airflow field and operation effect of a six-rotor agricultural UAV in flight. Comput. Electron. Agric. 2021, 190, 106425. [Google Scholar] [CrossRef]
- Zhu, Y.; Guo, Q.; Tang, Y.; Zhu, X.; He, Y.; Huang, H.; Luo, S. CFD simulation and measurement of the downwash airflow of a quadrotor plant protection UAV during operation. Comput. Electron. Agric. 2022, 201, 107286. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, C.L.; Wang, S.W.; Wang, R.T.; Zhang, L.Y.; Lv, T. Longitudinal attitude control system design and simulation of agricultural UAV. Agric. Mech. Res. 2016, 10, 6–10. [Google Scholar]
- Orsag, M.; Poropat, M.; Bogdan, S. Hybrid fly-by-wire quadrotor controller. Automatica 2010, 51, 19–32. [Google Scholar]
- Benallegue, A.; Mokhtari, A.; Fridman, L. High-order sliding-mode observer for a quadrotor UAV. Int. J. Robust Nonlinear Control. 2008, 18, 427–440. [Google Scholar] [CrossRef]
- Cano, J.M.; López-Martínez, M.; Rubio, F.R. Asynchronous networked control of linear systems via L2-gain-based transformations: Analysis and synthesis. IET Control Theory Appl. 2011, 5, 647–654. [Google Scholar] [CrossRef]
- Efe, M.Ö. Neural network assisted computationally simple PID. IEEE Trans. Ind. Inform. 2011, 7, 354–361. [Google Scholar] [CrossRef]
- Fahimi, F.; Saffarian, M. The control point concept for nonlinear trajectory-tracking control of autonomous helicopters with fly-bar. Int. J. Control. 2011, 84, 242–252. [Google Scholar] [CrossRef]
- Zhang, R.; Quan, Q.; Cai, K.Y. Attitude control of a quadrotor aircraft subject to a class of time-varying disturbances. IET Control Theory Appl. 2011, 5, 1140–1146. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An integral predictive/nonlinear H∞ control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Shi, X.; Cheng, Y.; Yin, C.; Dadras, S.; Huang, X. Design of fractional-order backstepping sliding mode control for quadrotor UAV. Asian J. Control. 2019, 21, 156–171. [Google Scholar] [CrossRef]
- Fujimoto, K.; Yokoyama, M.; Tanabe, Y. I&I-Based Adaptive Control of a Four-Rotor Mini Helicopter. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 144–149. [Google Scholar]
- Yang, H.; Cheng, L.; Xia, Y.; Yuan, Y. Active disturbance rejection attitude control for a dual closed-loop quadrotor under gust wind. IEEE Trans. Control Syst. Technol. 2018, 26, 1400–1405. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, H.; Shao, X.; Huang, Y. The attitude control of UAV in carrier landing based on ADRC. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 832–837. [Google Scholar]
- Zhang, Y.; Chen, Z.; Zhang, X.; Sun, Q.; Sun, M. A novel control scheme for quadrotor UAV based upon active disturbance rejection control. Aerosp. Sci. Technol. 2018, 79, 601–609. [Google Scholar] [CrossRef]
- Qi, G.; Chen, Z.; Yuan, Z. Model-free control of affine chaotic systems. Phys. Lett. A 2005, 344, 189–202. [Google Scholar] [CrossRef]
- Qi, G.; Chen, Z.; Yuan, Z. Adaptive high order differential feedback control for affine nonlinear system. Chaos Solitons Fract. 2008, 37, 308–315. [Google Scholar] [CrossRef]
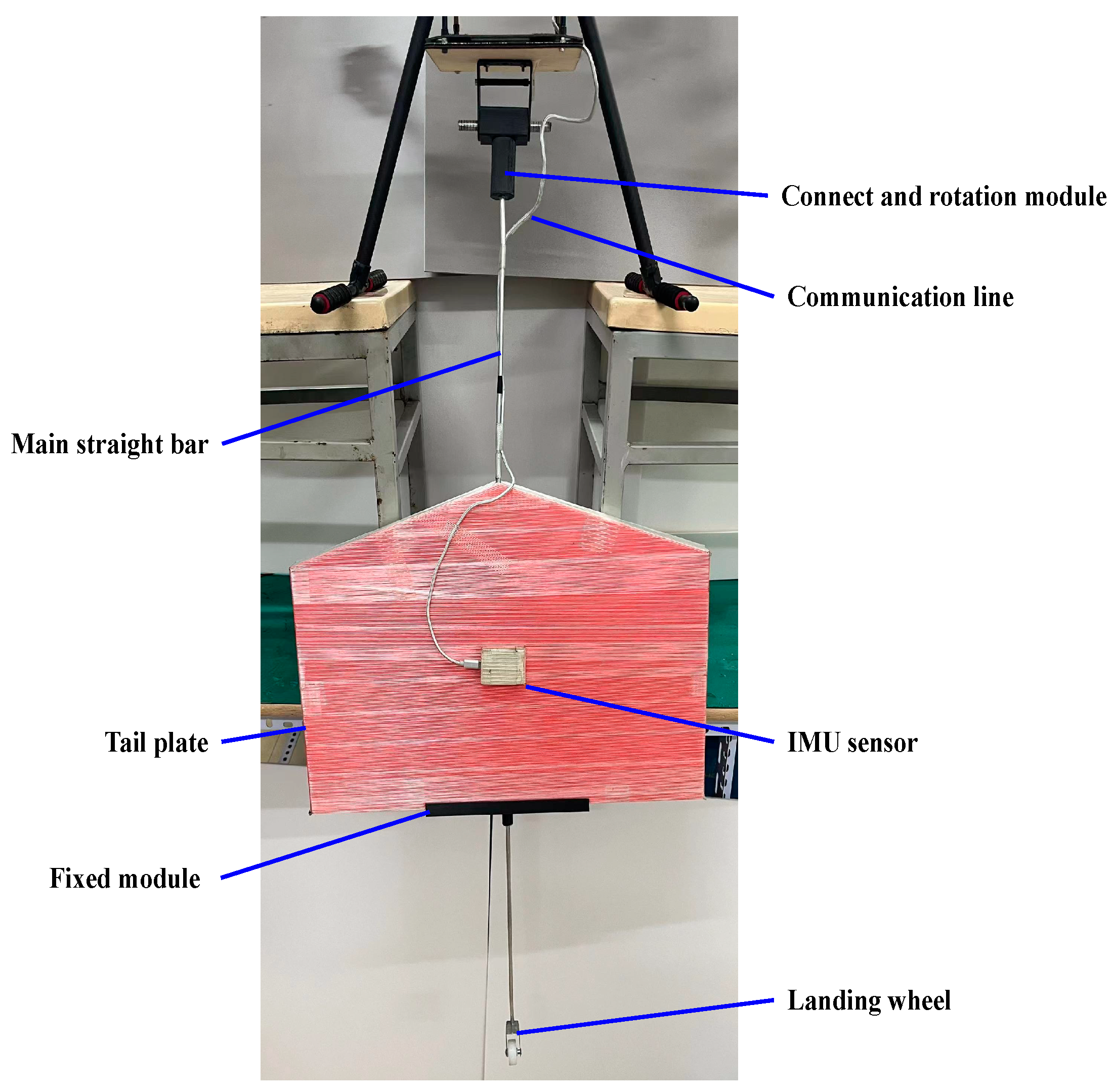



| Name | Material | Size (mm) | Weight (g) | Function |
|---|---|---|---|---|
| Connection and rotation module | PLA and aluminum | 114.5 × 56 × 25.5 | 31 | Used to connect UAVs and provide rotation function as a rotation axis |
| Communication line | Aluminum alloy and plastics | 1500 | 5 | Data communication |
| Main straight bar | Aluminum | Diameter: 5 Length: 100 | 11 | As the bearer of all modules |
| Tail plate | KT plate | 200 × 300 × 15 | 90.2 | Improve the wind sensing capability of the sensor |
| Fixed module | PLA | 25 × 250 × 30 | 3 | Fixed tail plate |
| IMU sensor | NA | 31.5 × 43.1 | 5.6 | Output the sensor swing Angle information |
| Landing wheel | Aluminum alloy and plastics | 40 × 18 × 36 | 4.2 | Enable the drone to land safely |
| Device Name | Model Number | Main Features | Purpose |
|---|---|---|---|
| Quadrotor UAV | BlueX450 | Wheelbase: 450 mm Type of motor: DJi 2216 Size of blade: 9 inches | Used to generate rotor airflow and its attitude is changed to simulate different backward tilt angle |
| Test frame | NA | 1.5 m × 1.5 m × 2.5 m | Fixed UAV |
| RABTA sensor | NA | As shown in Table 1 | It is used to realize the observation of backward tilt angle |
| Power supply | ANS 60V 300A Regulated voltage supply | 0.6 m × 0.6 m × 0.4 m | Powering drones |
| Remote control | RadioLink AT9S | NA | Controlling of the motor speed of the UAV |
| Laptop computer | Lenovo Savior Y520 | NA | Saving data |
| Pitch Angle of the Rotor UAV (Degree) | Backward Tilt Angle (Degree) | Sensor Output Data (Degree) | Error (Degree) | Range of Fluctuation (Degree) | |||
|---|---|---|---|---|---|---|---|
| Average Value | Maximum Value | Minimum Value | Average Error | Maximum Error | |||
| 5 | 5 | 5.17 | 6.32 | 3.98 | 0.17 | 1.32 | 2.34 |
| 10 | 10 | 9.97 | 10.96 | 8.92 | −0.03 | 1.08 | 2.04 |
| 15 | 15 | 15.09 | 15.84 | 14.71 | 0.09 | 0.84 | 1.13 |
| 20 | 20 | 19.73 | 20.75 | 19.05 | −0.27 | 0.95 | 1.70 |
| 25 | 25 | 25.52 | 26.47 | 24.74 | 0.52 | 1.47 | 1.73 |
| 30 | 30 | 29.65 | 31.29 | 28.63 | −0.35 | 1.37 | 2.66 |
| 35 | 35 | 35.14 | 35.45 | 34.48 | 0.14 | 0.52 | 0.96 |
| 40 | 40 | 39.93 | 41.13 | 39.16 | −0.07 | 1.13 | 1.98 |
| Material Name | Quantity | Main Features | Uses |
|---|---|---|---|
| ZD680 quadrotor UAV | 1 | Wheelbase: 680 mm Type of motor: SUNNYSKY X4110S Size of blade: 15 inches Type of battery: 6S 10,000 mAh Type of Flight control: Pixhawk cube black Rated load: Over 5 kg Endurance time: Over 20 min | It is used to carry out all the flights required for the experiment. |
| Beidou RTK positioning System | 1 | Accuracy of positioning: Centimeter level Type of output: NMEA Quality: 14 g | It is used to provide centimeter-level position data and speed data for UAVs. |
| RABTA sensor | 1 | Connecting rod length: 100 cm Wind plate shape: Tail airfoil type Size of air sensing plate: 48 cm × 36 cm Quality of sensor: 320 g | It is used to obtain the observed value of the backward tilt angle during the actual flight of the UAV. |
| Jetson TX2 airborne processor | 1 | Quality: 251 g | It is used to save the observed values of the UAV speed and backward tilt angle. |
| Flight Sorties | Flight Speed (m/s) | Height over Terrain (m) | Flight Range(m) | Collect Data | ||
|---|---|---|---|---|---|---|
| Accelerated Range | Constant Range | Retarded Range | ||||
| 1 | 0.5 | 5 | 0.6 | 43.6 | 0.8 | Flight speed and observation state of backward tilt angle at constant-velocity stage |
| 2 | 1 | 5 | 1.9 | 41.8 | 1.3 | |
| 3 | 1.5 | 5 | 2.0 | 40.8 | 2.1 | |
| 4 | 2 | 5 | 2.3 | 40.1 | 2.6 | |
| 5 | 2.5 | 5 | 3.4 | 38.2 | 3.3 | |
| 6 | 3 | 5 | 4.4 | 36.8 | 3.8 | |
| 7 | 3.5 | 5 | 5.2 | 34.4 | 5.4 | |
| 8 | 4 | 5 | 6.0 | 32.3 | 6.7 | |
(m/s) | (Degree) | (m/s) | (Degree) | (m/s) | (Degree) | (m/s) | (Degree) |
|---|---|---|---|---|---|---|---|
| 0.41 | 3.64 | 0.95 | 9.08 | 1.53 | 13.71 | 2.52 | 21.27 |
| 0.42 | 3.75 | 0.97 | 9.09 | 1.54 | 13.78 | 3.46 | 32.44 |
| 0.48 | 4.26 | 0.97 | 9.35 | 1.95 | 16.59 | 3.47 | 32.71 |
| 0.49 | 4.38 | 0.98 | 9.22 | 1.95 | 16.77 | 3.5 | 33.07 |
| 0.49 | 4.42 | 0.99 | 9.42 | 2.45 | 20.93 | 3.52 | 33.03 |
| 0.51 | 4.60 | 1.45 | 13.05 | 2.46 | 20.94 | 3.52 | 33.15 |
| 0.51 | 4.58 | 1.45 | 13.23 | 2.47 | 20.85 | 3.54 | 33.5 |
| 0.51 | 4.44 | 1.47 | 13.2 | 2.48 | 21.11 | 3.99 | 36.78 |
| 0.51 | 4.70 | 1.48 | 13.59 | 2.49 | 21.09 | 4.01 | 36.74 |
| 0.52 | 4.76 | 1.49 | 13.49 | 2.49 | 20.99 | 4.01 | 36.81 |
| 0.53 | 5.04 | 1.50 | 13.6 | 2.51 | 21.39 | 4.02 | 36.61 |
| 0.57 | 5.30 | 1.52 | 13.86 | 2.51 | 21.25 |
| Control Mode | Backward Tilt Angle (Degree) | One-Sample t-Test | Vertical Distance of the UAV from the Crop Canopy Level (m) | Coverage Area (m2) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Expected Value | Mean Value | Steady State Error | t Value | p-Value | Mean Value | Standard Deviation | Variable Coefficient | ||
| Position | 30 | 40.96 | 10.96 | 11.9076 | 4.8865 × 10−20 | 1 | 1.21 | 0.47 | 0.39 |
| 2 | 2.24 | 0.66 | 0.30 | ||||||
| 3 | 1.78 | 0.81 | 0.46 | ||||||
| 4 | 0.25 | 0.42 | 1.63 | ||||||
| Velocity | 30 | 27.84 | 7.84 | −9.3934 | 2.2761 × 10−17 | 1 | 0.78 | 0.08 | 0.10 |
| 2 | 1.32 | 0.20 | 0.15 | ||||||
| 3 | 2.12 | 0.40 | 0.19 | ||||||
| 4 | 1.35 | 0.65 | 0.48 | ||||||
| Rotor airflow back tilt angle | 30 | 30.92 | 0.92 | 1.7389 | 0.0837 | 1 | 0.83 | 0.05 | 0.06 |
| 2 | 1.47 | 0.14 | 0.10 | ||||||
| 3 | 2.41 | 0.09 | 0.04 | ||||||
| 4 | 0.82 | 0.28 | 0.34 | ||||||
| Expected Value (Degree) | Steady Rotor Flow Back Angle (Degree) | Adjust Time (s) | One-Sample t-Test | Vertical Distance of the UAV from the Crop Canopy Level (m) | Average Coverage Area (S1) (m2) | Vertical Distance of the UAV from the Crop Canopy Level (m) | Average Drift Rate () (%) | ||
|---|---|---|---|---|---|---|---|---|---|
| Mean Value | Error | t Value | p-Value | ||||||
| 20 | 20.27 | 0.27 | 3.3 | 1.1441 | 0.2545 | 1 | 0.68 | 4.8 | 91.77 |
| 2 | 1.08 | 4.6 | 69.27 | ||||||
| 3 | 1.62 | 4.4 | 42.98 | ||||||
| 4 | 2.30 | 4.2 | 17.98 | ||||||
| 30 | 30.92 | 0.92 | 2.7 | 1.7389 | 0.0837 | 1 | 0.83 | 4.2 | 88.19 |
| 2 | 1.47 | 4 | 72.47 | ||||||
| 3 | 2.41 | 3.8 | 54 | ||||||
| 4 | 0.82 | 3.6 | 35.02 | ||||||
| 40 | 40.05 | 0.05 | 2.9 | 0.6135 | 0.5408 | 1 | 1.05 | 3.8 | 95.73 |
| 2 | 2.09 | 3.6 | 83.32 | ||||||
| 3 | 2.25 | 3.4 | 67.44 | ||||||
| 4 | 0.002 | 3.2 | 50.12 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Liu, D.; Zhao, Y.; Liu, Z.; Liang, Y.; Liu, Z.; Huang, T.; Liang, K.; Xie, S.; Li, J. Establishment and Verification of the UAV Coupled Rotor Airflow Backward Tilt Angle Controller. Drones 2024, 8, 146. https://doi.org/10.3390/drones8040146
Wu H, Liu D, Zhao Y, Liu Z, Liang Y, Liu Z, Huang T, Liang K, Xie S, Li J. Establishment and Verification of the UAV Coupled Rotor Airflow Backward Tilt Angle Controller. Drones. 2024; 8(4):146. https://doi.org/10.3390/drones8040146
Chicago/Turabian StyleWu, Han, Dong Liu, Yinwei Zhao, Zongru Liu, Yunting Liang, Zhijie Liu, Taoran Huang, Ke Liang, Shaoqiang Xie, and Jiyu Li. 2024. "Establishment and Verification of the UAV Coupled Rotor Airflow Backward Tilt Angle Controller" Drones 8, no. 4: 146. https://doi.org/10.3390/drones8040146
APA StyleWu, H., Liu, D., Zhao, Y., Liu, Z., Liang, Y., Liu, Z., Huang, T., Liang, K., Xie, S., & Li, J. (2024). Establishment and Verification of the UAV Coupled Rotor Airflow Backward Tilt Angle Controller. Drones, 8(4), 146. https://doi.org/10.3390/drones8040146








