Multi-UAV Obstacle Avoidance and Formation Control in Unknown Environments
Abstract
1. Introduction
2. UAV Kinematic Modeling and Communication Topology
2.1. UAV Kinematic Modeling and Formation Modeling
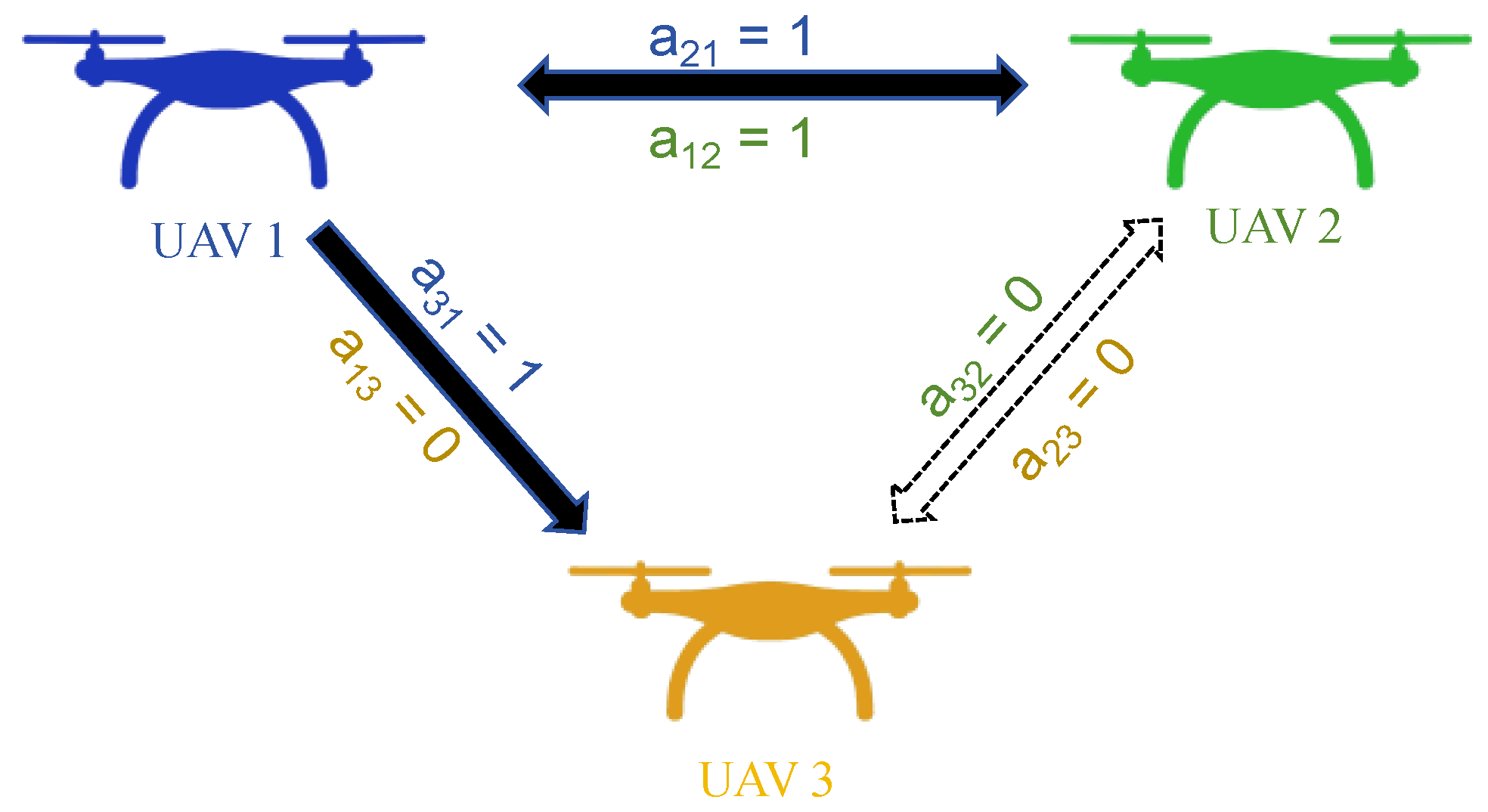
2.2. Graph Theory and Communication Topology
3. Design of Multi-UAV Formation Obstacle Avoidance Method Based on IAPF and Optimal Consensus
3.1. IAPF Based on an Improved Repulsive Potential Field Model
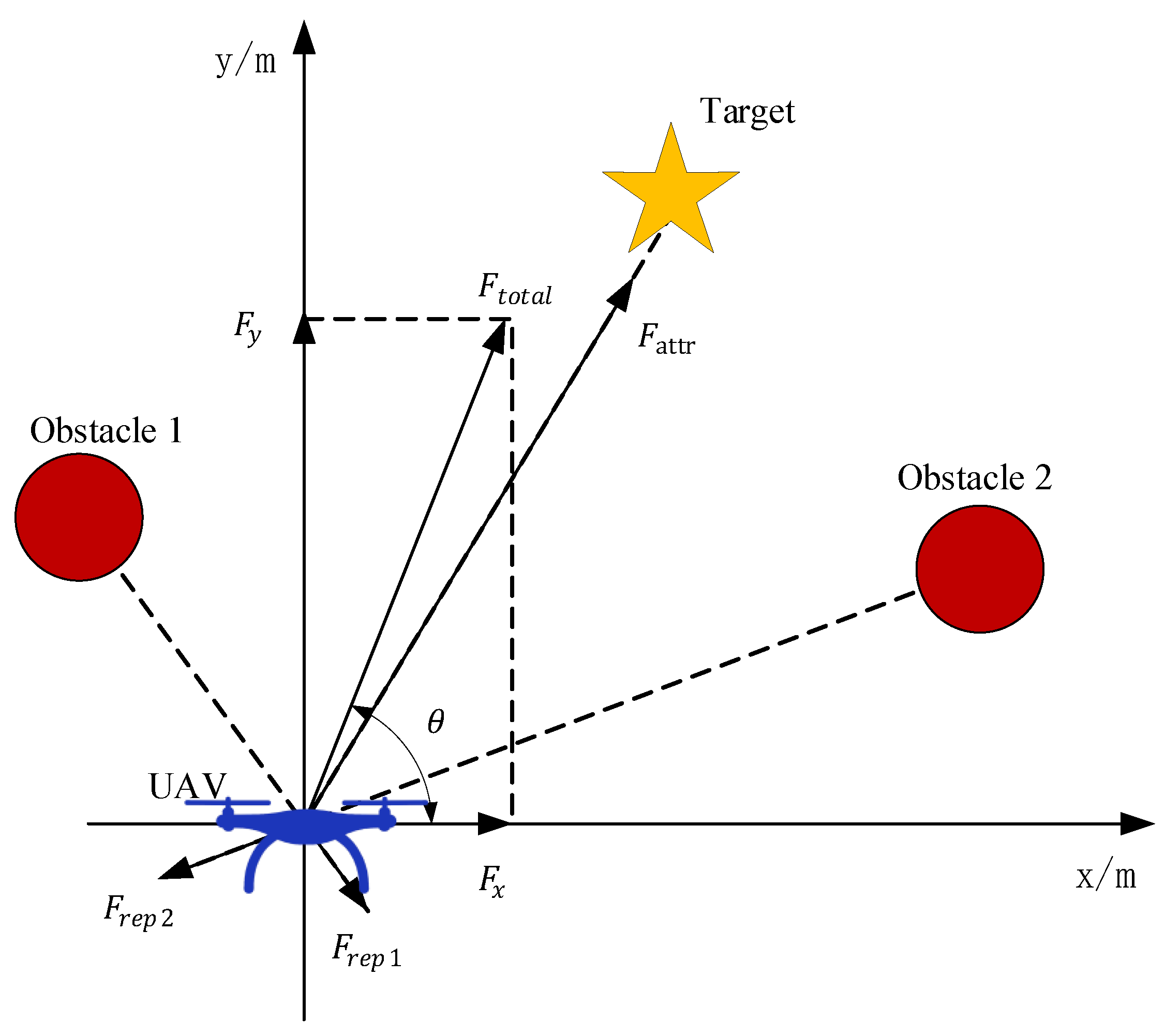
3.1.1. Overview of Traditional APF Principles
- Target unreachability: The closer the UAV is to the target point, the less gravitational force it receives; the closer the UAV is to the obstacle, the more repulsive force it receives; if there is an obstacle present in the vicinity of the target point, the UAV hovers around and is unable to reach the target point.
- Local minima: The moving direction of the UAV is determined by the combined force; when the combined force received by the UAV at a certain point is 0 or the direction of the combined force is co-linear with the gravitational force and repulsive force, the Local Minimal Value Problem occurs, as shown in Figure 3.
3.1.2. Improved Repulsive Potential Field Model Based on Power Functions
3.2. Optimal Consensus Formation Control Method
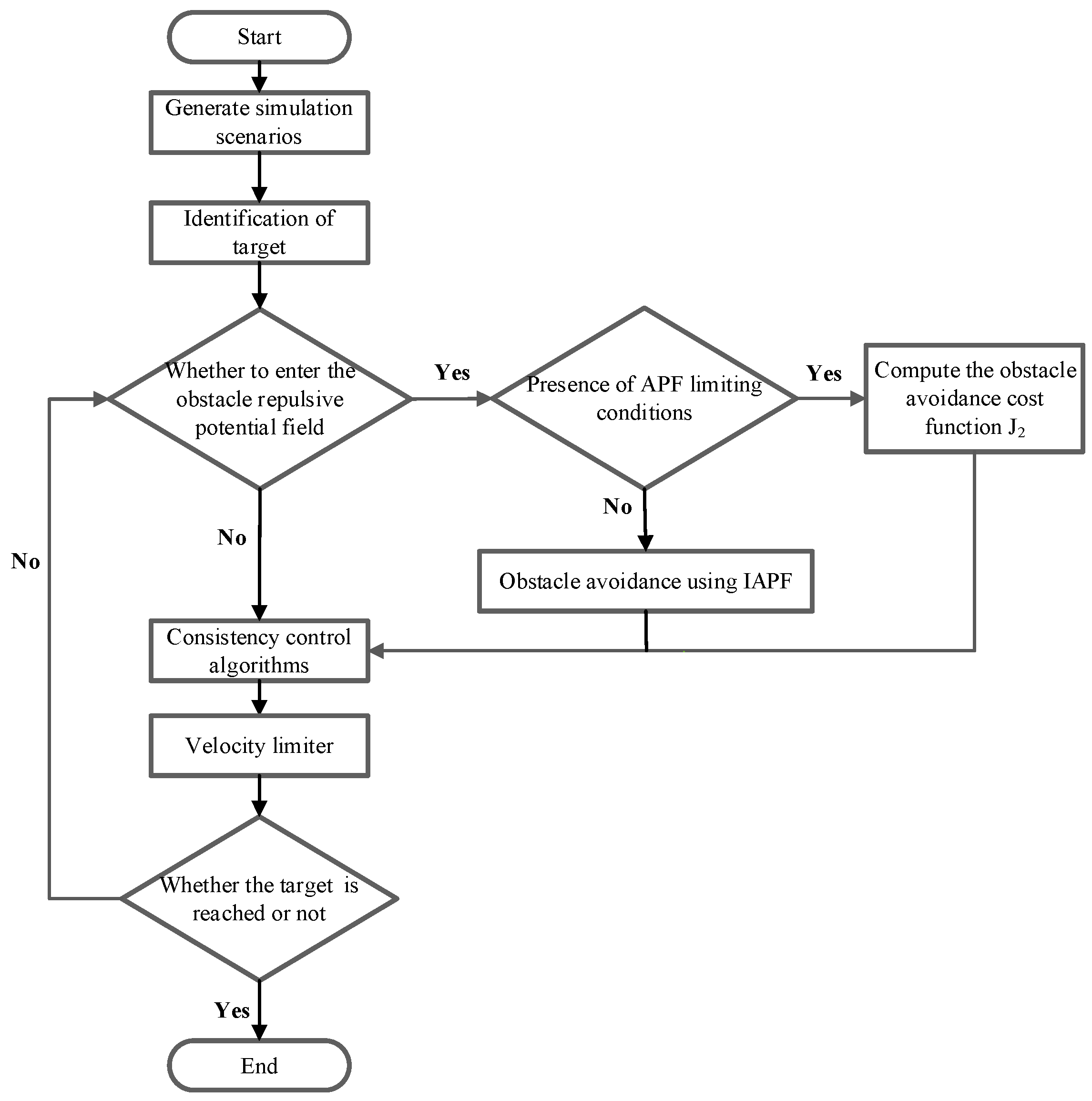
3.3. Design of Optimal Consensus Formation Control Algorithm Based on IAPF
3.4. Simulation Conditions and Analysis in Known Environments
3.4.1. Simulation Conditions in Known Environments
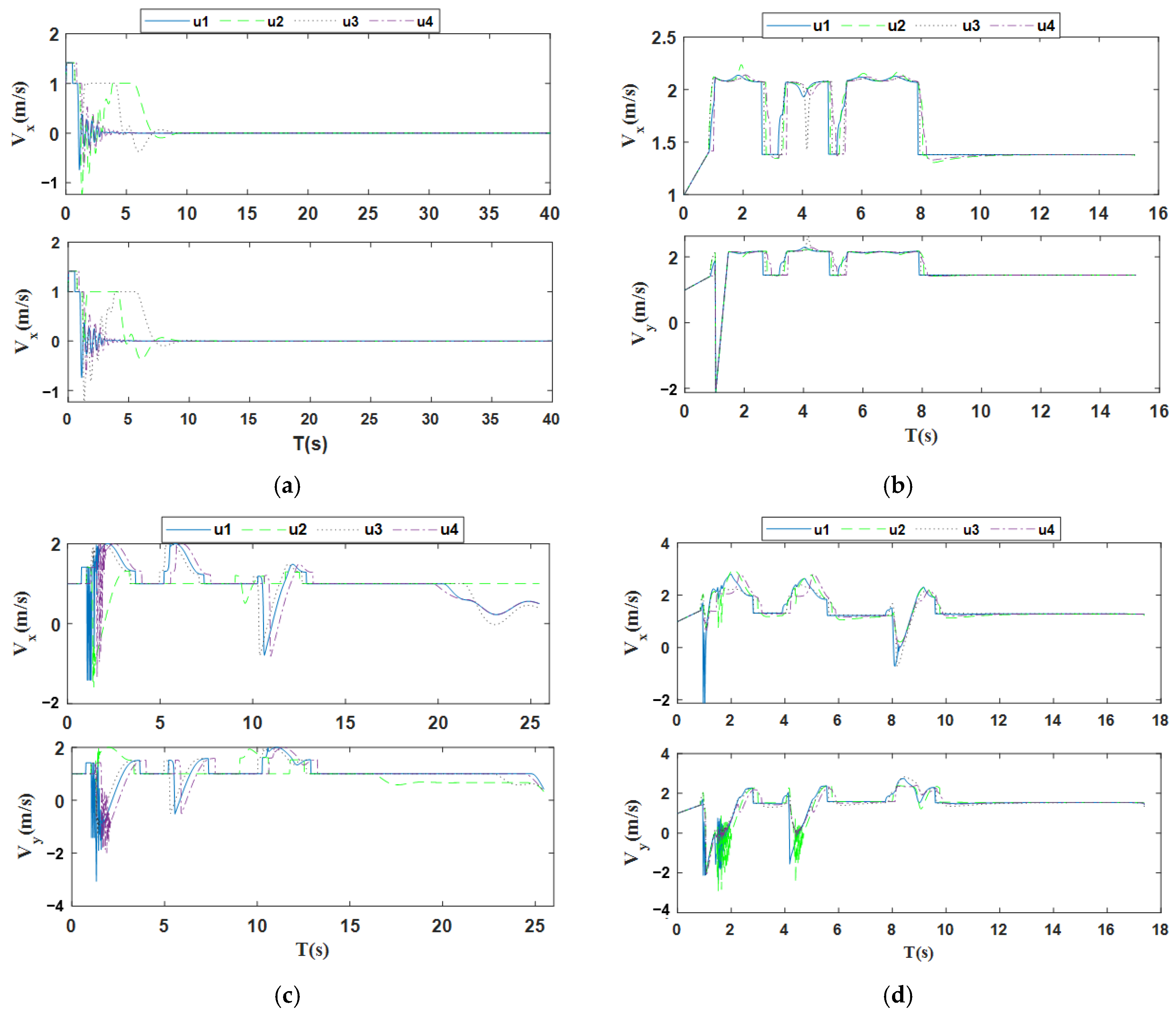
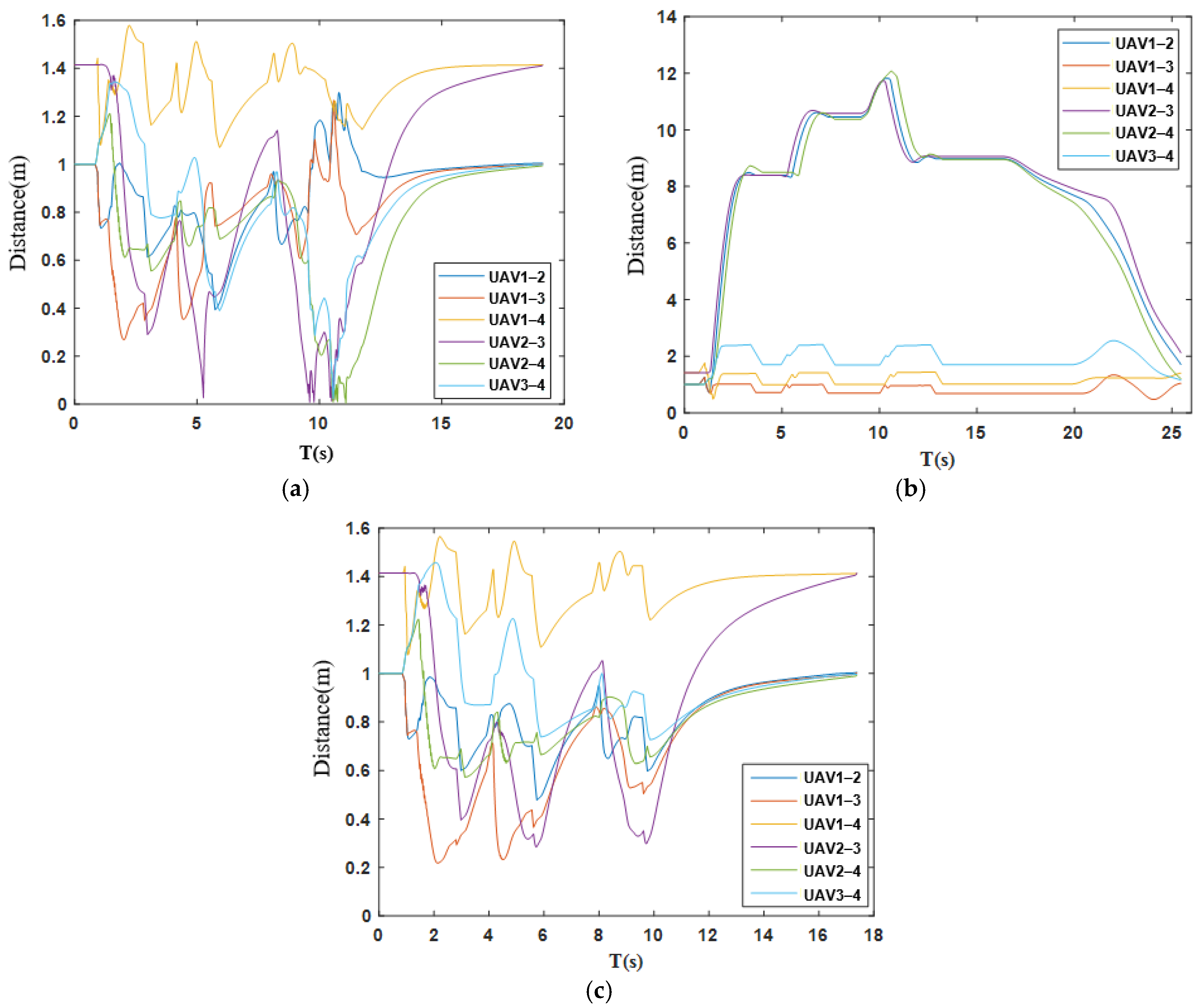
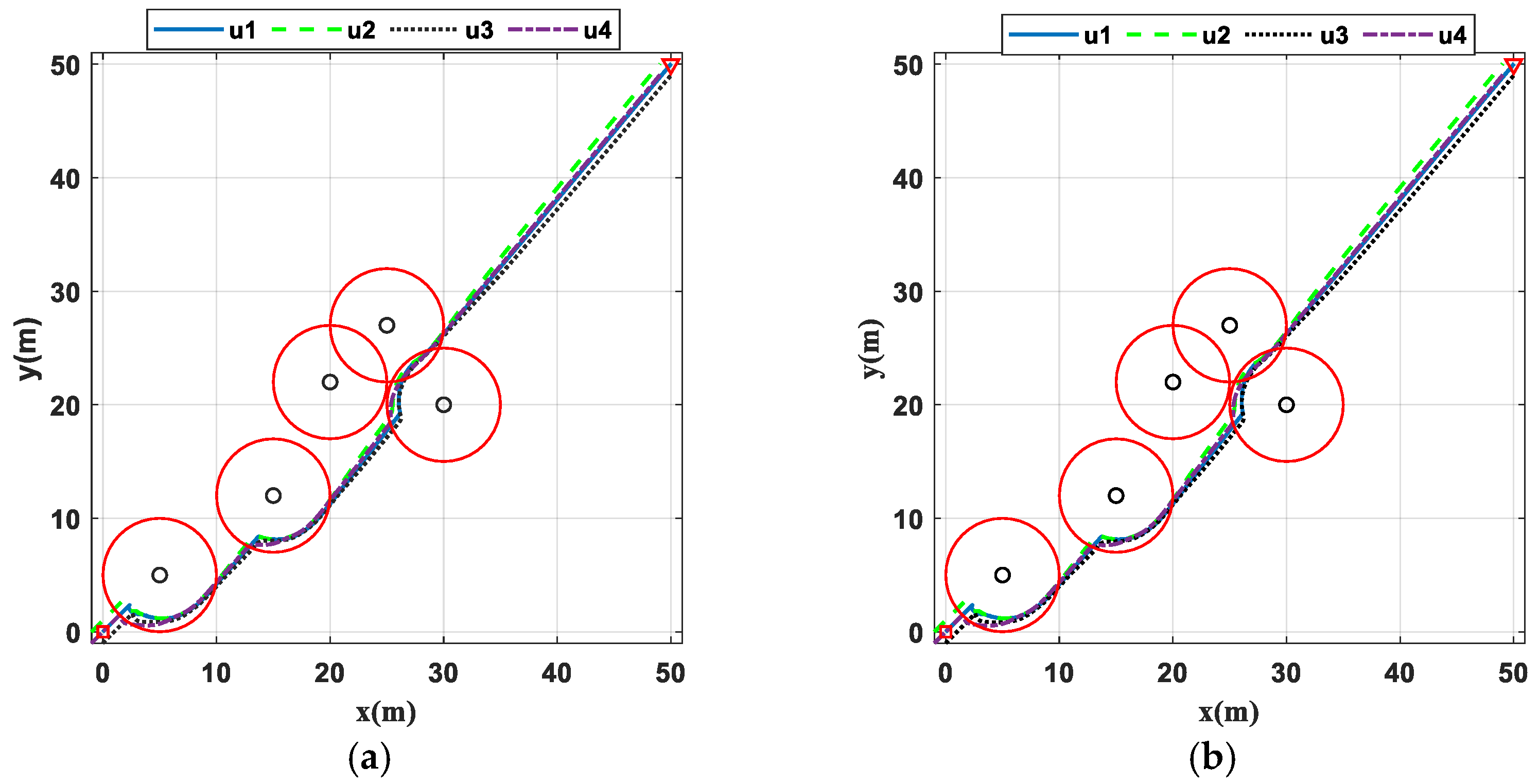
3.4.2. Analysis of Simulation Results in Known Environments
4. Design of the Multi-UAV Formation Obstacle Avoidance Method Based on RSHO in Unknown Environments
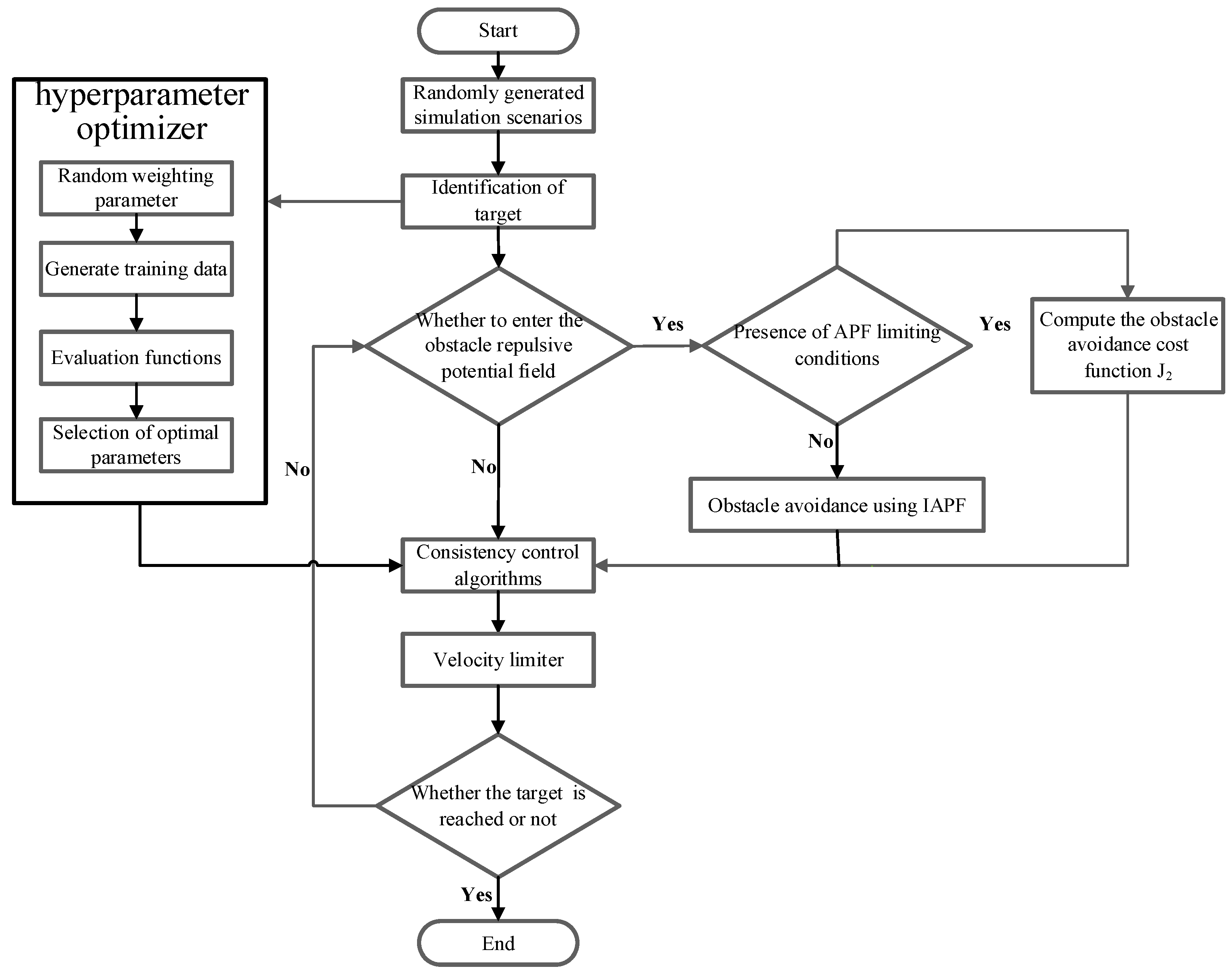
4.1. Hyperparametric Optimizer Model Design
4.2. Simulation Conditions and Analysis in Unknown Environments
4.2.1. Simulation Conditions in Unknown Environments
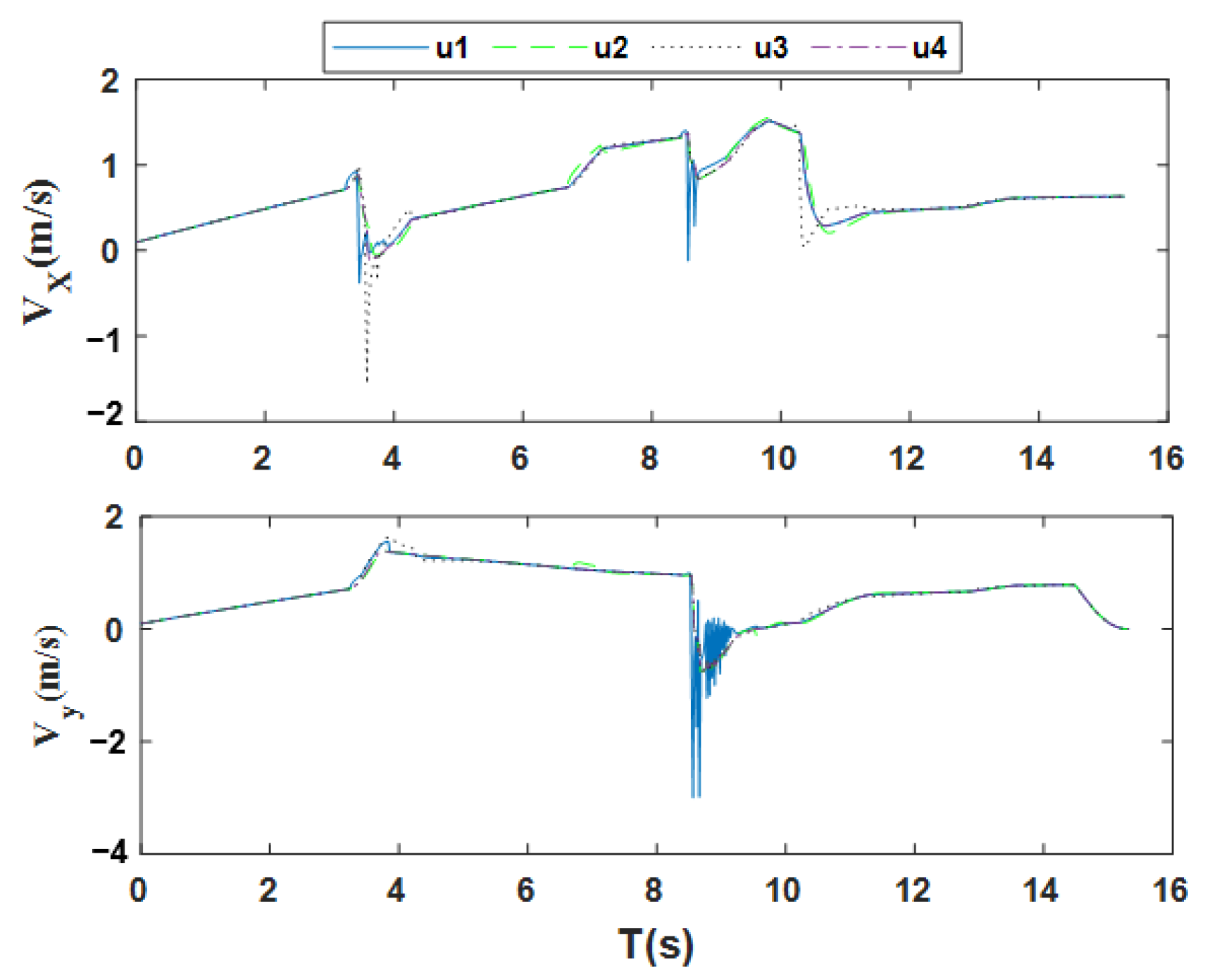
4.2.2. Analysis of Simulation Results in Unknown Environments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shakeri, R.; Al-Garadi, M.A.; Badawy, A.; Mohamed, A.; Khattab, T.; AI-Ali, A.K. Design challenges of multi-UAV systems in cyber-physical applications: A comprehensive survey and future directions. IEEE Commun. Surv. Tutor. 2019, 21, 3340–3385. [Google Scholar] [CrossRef]
- Tahir, A.; Böling, J.; Haghbayan, M.H.; Toivonen, H.T.; Plosila, J. Swarms of unmanned aerial vehicles—A survey. J. Ind. Inf. Integr. 2019, 16, 100106. [Google Scholar] [CrossRef]
- Xu, H.; Niu, Z.; Jiang, B.; Zhang, Y.; Chen, S.; Li, Z.; Gao, M.; Zhu, M. ERRT-GA: Expert Genetic Algorithm with Rapidly Exploring Random Tree Initialization for Multi-UAV Path Planning. Drones 2024, 8, 367. [Google Scholar] [CrossRef]
- Xu, D.; Chen, G. Autonomous and cooperative control of UAV cluster with multi-agent reinforcement learning. Aeronaut. J. 2022, 126, 932–951. [Google Scholar] [CrossRef]
- Suo, W.B.; Wang, M.Y.; Zhang, D.; Qu, Z.J.; Yu, L. Formation Control Technology of Fixed-Wing UAV Swarm Based on Distributed Ad Hoc Network. Appl. Sci. 2022, 12, 535. [Google Scholar] [CrossRef]
- Ouyang, Q.; Cong, Y.; Wang, Z. Formation Control of Unmanned Aerial Vehicle Swarms: A Comprehensive Review. Asian J. Control 2023, 25, 570–593. [Google Scholar] [CrossRef]
- Bu, Y.; Yan, Y.; Yang, Y. Advancement Challenges in UAV Swarm Formation Control: A Comprehensive Review. Drones 2024, 8, 320. [Google Scholar] [CrossRef]
- Seo, J.; Kim, Y.; Kim, S.; Tsourdos, A. Consensus-based reconfigurable controller design for unmanned aerial vehicle formation flight. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 817–829. [Google Scholar] [CrossRef]
- Amirkhani, A.; Barshooi, A.H. Consensus in multi-agent systems: A review. Artif. Intell. Rev. 2022, 55, 3897–3935. [Google Scholar] [CrossRef]
- Gao, C.; He, X.; Dong, H.; Liu, H.; Lyu, G. A survey on fault-tolerant consensus control of multi-agent systems: Trends, methodologies and prospects. Int. J. Syst. Sci. 2022, 53, 2800–2813. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.; Zhang, Z.; Luo, K.; Liu, J. Cooperative Control of UAV Cluster Formation Based on Distributed Consensus. In Proceedings of the 2019 IEEE 15th International Conference on Control and Automation (ICCA), Edinburgh, UK, 16–19 July 2019; pp. 788–793. [Google Scholar]
- Fu, X.; Pan, J.; Wang, H.; Gao, X. A formation maintenance and reconstruction method of UAV swarm based on distributed control. Aerosp. Sci. Technol. 2020, 104, 105981. [Google Scholar] [CrossRef]
- Wu, Y.; Gou, J.; Hu, X.; Huang, Y. A new consensus theory-based method for formation control and obstacle avoidance of UAVs. Aerosp. Sci. Technol. 2020, 107, 106332. [Google Scholar] [CrossRef]
- Yang, X.; Wang, W.; Huang, P. Distributed optimal consensus with obstacle avoidance algorithm of mixed-order UAVs–USVs–UUVs systems. ISA Trans. 2020, 107, 270–286. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Weng, P.; Tian, X.; Mai, Q.Q. Distributed adaptive fixed-time formation control for UAV-USV heterogeneous multi-agent systems. Ocean. Eng. 2022, 267, 113240. [Google Scholar] [CrossRef]
- Wang, W.; Chen, X.; Jia, J.B.; Wu, K.L.; Xie, M.Y. Optimal formation tracking control based on reinforcement learning for multi-UAV systems. Control Eng. Pract. 2023, 141, 105735. [Google Scholar] [CrossRef]
- Foead, D.; Ghifari, A.; Kusuma, M.B.; Hanafiah, N.; Gunawan, E. A systematic literature review of A* pathfinding. Procedia Comput. Sci. 2021, 179, 507–514. [Google Scholar] [CrossRef]
- He, W.J.; Qi, X.G.; Liu, L.F. A novel hybrid particle swarm optimization for multi-UAV cooperate path planning. Appl. Intell. 2021, 51, 7350–7364. [Google Scholar] [CrossRef]
- Xiong, T.; Liu, F.; Liu, H.; Ge, J.; Li, H.; Ding, K.; Li, Q. Multi-Drone Optimal Mission Assignment and 3D Path Planning for Disaster Rescue. Drones 2023, 7, 394. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, S.; Jiang, Z.; Liu, Z.; Cheng, H. Collision Avoidance of High-Speed Obstacles for Mobile Robots via Maximum-Speed Aware Velocity Obstacle Method. IEEE Access 2020, 8, 138493–138507. [Google Scholar] [CrossRef]
- Yang, S.; Bai, W.; Li, T.; Shi, Q.; Yang, Y.; Wu, Y.; Chen, C.P. Neural-network-based formation control with collision, obstacle avoidance and connectivity maintenance for a class of second-order nonlinear multi-agent systems. Neurocomputing 2021, 439, 243–255. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, H.; Zhang, H.; Lin, C.; Yu, D.; Li, C. AUV Obstacle Avoidance Planning Based on Deep Reinforcement Learning. J. Mar. Sci. Eng. 2021, 9, 1166. [Google Scholar] [CrossRef]
- Hu, J.; Wang, M.; Zhao, C.; Pan, Q.; Du, C. Formation control and collision avoidance for multi-UAV systems based on Voronoi partition. Sci. China Technol. Sci. 2020, 63, 65–72. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, C.; Xia, Y.; Xiong, H.; Shao, X. An improved artificial potential field method for path planning and formation control of the multi-UAV systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1129–1133. [Google Scholar] [CrossRef]
- Zhu, X.; Liang, Y.; Yan, M. A flexible collision avoidance strategy for the formation of multiple unmanned aerial vehicles. IEEE Access 2019, 7, 140743–140754. [Google Scholar] [CrossRef]
- Ma, C.; Li, J.; Shang, Y.; Zhang, S.; Yang, Q. A Dynamic Obstacle Avoidance Control Algorithm for Distributed Multi-UAV Formation System. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–10 August 2022; pp. 876–881. [Google Scholar]
- Ding, Q.; Xu, X.; Gui, W. Path planning based on reinforcement learning with improved APF model for synergistic multi-UAVs. In Proceedings of the 2023 26th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Rio de Janeiro, Brazil, 24–26 May 2023; pp. 432–437. [Google Scholar]
- Wu, G.; Wang, N.; Ying, J. Research on distributed real-time formation tracking control of high-order multi-UAV system. IEEE Access 2022, 10, 36286–36298. [Google Scholar] [CrossRef]
- Dewangan, V.; Kandath, H. MPC-Based Obstacle Aware Multi-UAV Formation Control Under Imperfect Communication. In Proceedings of the 2024 10th International Conference on Automation, Robotics and Applications (ICARA), Athens, Greece, 22–24 February 2024; pp. 273–277. [Google Scholar]






| Control Structure | Control Method | Advantages | Disadvantages |
|---|---|---|---|
| Centralized | Leader–Follower Method | Simple to implement and high formation accuracy. | High computational complexity, poor robustness and flexibility. |
| Virtual Structure Method | Has relatively high control accuracy and a certain degree of fault tolerance. | Rigid body motion restricts the flexibility and adaptability of the system. | |
| Distributed | Behavior Method | Better flexibility and communication capabilities. | Difficult to precisely control the overall accuracy of the cluster and perform stability analysis. |
| Consensus Method | Has good flexibility, robustness, and adaptability. | The algorithm design is relatively complex. | |
| Decentralized | Decentralized Model Predictive Method | Strong scalability and simple implementation. | High construction cost and poor robustness. |
| Parametric | Value | Unit |
|---|---|---|
| n | 4 | |
| k | 10 | |
| m | 40 | |
| d0 | 5 | m |
| 20 | ||
| p0 | 0.8 | m |
| 3 | m/s | |
| 0.11 | ||
| 2 | ||
| M | 50 | kg |
| UAV Number | Initial Position (m) | Initial Velocity (m/s) | Target Position (m) |
|---|---|---|---|
| UAV1 | (0,0) | (1,1) | (20,20) |
| UAV2 | (−1,0) | (1,1) | (19,20) |
| UAV3 | (0,−1) | (1,1) | (20,19) |
| UAV4 | (−1,−1) | (1,1) | (19,19) |
| Obstacle Number | Obstacle Coordinates (m) |
|---|---|
| 1 | (5,5) |
| 2 | (15,12) |
| 3 | (15,12) |
| 4 | (15,12) |
| 5 | (15,12) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, P.; Wang, Z.; Rong, D.; Niu, M.; Liu, C. Multi-UAV Obstacle Avoidance and Formation Control in Unknown Environments. Drones 2024, 8, 714. https://doi.org/10.3390/drones8120714
Li Y, Zhang P, Wang Z, Rong D, Niu M, Liu C. Multi-UAV Obstacle Avoidance and Formation Control in Unknown Environments. Drones. 2024; 8(12):714. https://doi.org/10.3390/drones8120714
Chicago/Turabian StyleLi, Yawen, Pengfei Zhang, Zhongliu Wang, Dian Rong, Muyang Niu, and Cong Liu. 2024. "Multi-UAV Obstacle Avoidance and Formation Control in Unknown Environments" Drones 8, no. 12: 714. https://doi.org/10.3390/drones8120714
APA StyleLi, Y., Zhang, P., Wang, Z., Rong, D., Niu, M., & Liu, C. (2024). Multi-UAV Obstacle Avoidance and Formation Control in Unknown Environments. Drones, 8(12), 714. https://doi.org/10.3390/drones8120714






