Abstract
With the continuous development of modern UAV technology and communication technology, UAV-to-ground communication relay has become a research hotspot. In this paper, a Multi-Agent Reinforcement Learning (MARL) method based on the ε-greedy strategy and multi-agent proximal policy optimization (MAPPO) algorithm is proposed to address the local optimization problem, improving the communication efficiency and task execution capability of UAV cluster control. This paper explores the path planning problem in multi-UAV-to-ground relay communication, with a special focus on the application of the proposed Mix-Greedy MAPPO algorithm. The state space, action space, communication model, training environment, and reward function are designed by comprehensively considering the actual tasks and entity characteristics such as safe distance, no-fly zones, survival in a threatened environment, and energy consumption. The results show that the Mix-Greedy MAPPO algorithm significantly improves communication probability, reduces energy consumption, avoids no-fly zones, and facilitates exploration compared to other algorithms in the multi-UAV ground communication relay path planning task. After training with the same number of steps, the Mix-Greedy MAPPO algorithm has an average reward score that is 45.9% higher than the MAPPO algorithm and several times higher than the multi-agent soft actor-critic (MASAC) and multi-agent deep deterministic policy gradient (MADDPG) algorithms. The experimental results verify the superiority and adaptability of the algorithm in complex environments.
1. Introduction
During the continuous evolution of modern UAV technology and communication technology, with the wide application of UAVs in both civil and military fields, UAV cluster-to-ground communication relay has become a research hotspot, i.e., to realize the optimal communication coverage through the efficient management and collaboration of UAV clusters. The current application of multi-agent reinforcement learning (MARL) in the field of UAV technology is constantly increasing, and it has become one of the key technologies to improve the control efficiency of UAV clusters [1]. As a communication relay platform, UAV clusters have unique advantages and the potential to significantly improve network robustness, extend communication distance, and achieve efficient mission execution capability through multi-agent collaborative optimization. The purpose of this paper is to explore the application of the MAPPO algorithm in multi-agent reinforcement learning in multi-UAV cluster-to-ground relay communication, and to analyze its importance and the challenges it faces in UAV cluster control in light of current research progress [2].
Enhancement of network robustness is a key objective in UAV communication relay systems. When UAVs are utilized as communication relay nodes, the robustness of the communication network and the communication distance between ground platforms can be significantly elevated, especially in the face of natural disasters, environmental occlusion, and other situations that result in the limited use of traditional ground-based communication infrastructures. In addition, UAVs are able to be rapidly deployed to provide emergency communication support [3]. The capability of UAVs to relay communications at different altitude layers helps to extend the communication range of ground platforms, enabling data transmission and reception over longer distances [4]. This flexibility and mobility makes UAVs ideal for applications in both emergency and long-range communications missions.
Multi-agent Reinforcement Learning (MARL) algorithms, especially the MAPPO (Multi-Agent Proximal Policy Optimization) algorithm, show promising potential in facilitating collaboration among units when used for UAV cluster control [5]. Through continuous learning and optimization, UAV cluster path planning based on the MAPPO algorithm can improve the overall communication efficiency of air-ground networks and the performance of UAV relay missions [6]. The MAPPO algorithm, through the coordination between and policy optimization among multiple agents, is able to adapt the communication policy in real time to dynamic environmental conditions, such as changes in terrain, weather conditions, and interference of wireless signals in a complex and changing environment, thus ensuring the stability and reliability of the communication [7].
As a multi-agent system, the UAV cluster demands an effective coordination mechanism to ensure the consistency of actions of individual UAVs and avoid conflicts and collisions. This coordination is a critical issue in the control of UAV clusters [8]. The MAPPO algorithm is able to realize the coherence of individual UAVs in the cluster through policy sharing and collaborative learning among multiple agents to ensure the successful execution of the mission [9]. In some application scenarios, such as emergency rescue or military operations, UAV communication relaying must meet the requirements of real-time and determinism. Reinforcement learning algorithms need to be capable of making decisions quickly and ensuring the stability and reliability of the decisions to meet the needs of efficient communication and mission execution [10].
However, UAVs have limited hardware performance and energy supply, which restricts the capability of the communication and computing devices mounted on them. Under such constraints, it is a technical challenge to achieve effective communication relaying [11]. The application of the MAPPO algorithm to UAV cluster control requires not only optimization in algorithm design but also in-depth exploration of communication technologies, computational capabilities, and energy management to overcome these limitations and achieve efficient communication relaying tasks [12].
In this paper, we conduct an exploration of the application of multi-agent reinforcement learning in multi-UAV ground-to-air relay communication by combining the characteristics of the MAPPO algorithm and ε-greedy strategy and introduce the Mix-Greedy MAPPO algorithm. The proposed algorithm strengthens the exploration capability of the MAPPO algorithm by introducing simulated annealing, which could prevent MAPPO algorithm from falling into local optimal solutions in complex environments. The improvements proposed in this paper also enhance the flexibility and adaptability of the MAPPO algorithm, so that UAVs can acquire not only higher reward scores in dynamic environments but also higher robustness to elements changes in the environment.
By reviewing and analyzing the existing research, this paper will further clarify the advantages and limitations of the MAPPO algorithm in UAV cluster control and propose future research directions and improvement suggestions. To this end, this paper designs a reinforcement learning training environment for multi-UAV ground communication relaying and proposes the Mix-Greedy MAPPO algorithm based on the MAPPO algorithm with ε-greedy strategy, which is more adapted to the realistic UAV ground relaying communication cluster path planning task. The environment design takes UAV safe distance, no-fly zones, and survival in a threatened environment into consideration, which have often been overlooked in previous studies. After training with the same number of steps, the Mix-Greedy MAPPO algorithm has the highest average reward score lead of 45.9% compared to the MAPPO algorithm and is much higher than the MASAC and MADDPG algorithms.
The key novelty and contribution of this paper is the introduction of the ε-greedy strategy into the MAPPO algorithm to enhance the exploratory behavior of the agents in order to avoid falling into local optimal solutions in complex environments and to improve the flexibility and adaptability of the strategy. This approach not only promotes the development of existing technologies, but also provides new research ideas and methods in the field of multi-UAV co-operation. Our experiment results verify the superiority and adaptability of the algorithm in complex simulation environments and provide a basis for improving the algorithm’s metrics such as time complexity and convergence speed in a wider range of practical applications in the future.
This paper can provide new perspectives and references for research in the field of UAV swarm control and promotes the development and application of this field. The next sections will detail the related work, the design and implementation of the Mix-Greedy MAPPO algorithm, and demonstrate its effectiveness in multi-UAV ground communication relay path planning tasks.
2. Related Work
2.1. State of the Art Research in UAV Communication Relaying
An unscented Kalman filter and hybrid particle swarm optimization (UKF-HPSO) algorithm is proposed by Li et al. [13] to optimize the relay communication throughput in multi-UAV wireless networks. By predicting UAV positions in real-time and considering obstacle avoidance, the algorithm effectively improves communication performance in dynamic environments. However, the study assumes a simplified channel model and fixed-altitude flight, which does not fully consider the complexity in real-world environments.
Liu et al. [14] explore the joint deployment strategy of multiple Unmanned Aerial Vehicles (UAVs) in UAV-assisted Air-Ground Integration Networks (AGINs), aiming to improve communication performance in disaster relief and network expansion. The study proposes various schemes, including static and mobile UAV base station deployment, UAV multi-hop relay deployment, and UAV formation relay deployment, to optimize coverage, transmission performance, and communication reliability. However, the study mainly focuses on theoretical modeling and simulation experiments, and the dynamic environment adaptability and security issues in practical applications have not been thoroughly explored.
Current research in the field of UAV-to-ground relay communication often assumes static environments; in highly dynamic environments, such as disaster rescue scenarios, UAVs must be able to quickly adapt to changing environments, but existing methods often struggle to converge when dealing with large amounts of interaction data.
2.2. Traditional Approaches to UAV Path Planning
Jiang et al. [15] propose a multi-UAV autonomous communication relay position planning method based on predictive modeling, aiming to solve the communication interruption problem between UAVs and ground stations in complex mountainous missions. By establishing a visibility model and a lightweight characterization of the terrain, the autonomous planning of relay UAV positions is realized to ensure the continuity of the communication link. However, the method may be limited by the adaptability to environmental changes and the computational complexity of the algorithm in practical applications.
IIker et al. [16] propose a multi-unmanned aerial vehicle (MUAV) mission planning heuristic algorithm for Flight Self-Organizing Networks (FANETs), aiming to minimize the total time to visit all target points while maintaining network connectivity. The study considers the heterogeneity of the UAVs, the temporal and spatial constraints of the mission, and the communication constraints and validates the effectiveness of the algorithm through a series of experiments. However, the approach assumes that the UAV has unlimited energy and perfect localization capabilities and is simulated on 2D terrain, which may not be directly applicable to 3D complex environments.
A multi-UAV path planning method based on a genetic algorithm is proposed by Li et al. [17] to solve the multi-traveler problem (MTSP) of UAVs in information-gathering missions. A multi-UAV path planning model is constructed by determining relay nodes through K-means clustering, and the path is optimized using a genetic algorithm to minimize the flight distance. The experimental results verified the effectiveness of the algorithm in different scenarios. However, the study did not consider the battery life and flight cost of UAVs, which have an important impact on path planning in practical applications.
Song et al. [18] propose a strategy to protect multi-UAV relay communications from the threat of ground eavesdroppers through joint trajectory design and power control. The non-convex optimization problem is solved using SCA and the S-procedure, and the algorithm performance is verified through simulation. However, the study assumes a static environment and does not consider the hardware limitations of UAVs such as battery life, power constraints of communication devices, and processing capabilities.
A multi-UAV path planning method based on cellular decomposition and task allocation algorithms is proposed by Wan et al. [19], which optimizes task allocation through simulated annealing and genetic algorithms to achieve efficient path planning in complex scenarios. However, the method has limitations in real-time, dynamic environment adaptation and generalization ability to unknown environments, and compared to the multi-intelligence deep reinforcement learning method, although it may be more efficient in terms of data dependency and computational resource requirements, it has disadvantages in terms of adaptability to complex and changing task.
An adaptive evolutionary multi-objective estimation distribution algorithm (AEMO-EDA) is proposed by Yuhang et al. [20] for solving the multi-UAV cooperative path planning problem. The algorithm improves population diversity and convergence through adaptive tuning and comprehensive evaluation strategies, but has limitations in high-dimensional optimization and dynamic environment adaptation. Compared with multi-intelligence deep reinforcement learning methods, AEMO-EDA may have limited ability to make on-the-fly decisions for dynamic changes in the environment.
Hardware limitations of UAVs, such as battery life and power limitations of communication devices, are often ignored in traditional approaches to UAV path planning studies. In real-world deployments, UAVs also need to consider no-fly zones and other environmental factors, which are usually under-considered in existing studies. To overcome these limitations, future research needs to consider the complexity of real-world applications more comprehensively and develop UAV communication systems that are more adaptable to dynamic environments and are both energy-efficient and safe.
2.3. Deep Reinforcement Learning in UAV Applications
According to Tamba et al. [21], an iterative learning algorithm based on Q-learning is proposed that uses a multi-intelligent body reinforcement learning framework to solve the area coverage problem of UAV networks through Markov game modeling. However, the study assumed a static environment and a simplified UAV motion model, and did not fully consider the dynamic changes in practical applications. Nie et al. [22] propose a resource management method for UAV-assisted MEC systems based on multi-intelligent body federated reinforcement learning, which effectively solves the problem of computational offloading and resource allocation while considering privacy protection. However, the study has limitations in scalability and security verification in real dynamic environments.
Karimata et al. [23] utilize multi-intelligent reinforcement learning to optimize the flight strategies of groups of UAVs to form functional ad hoc networks. The study demonstrates UAVs cooperating in flight, but does not consider radio interference and communication constraints in real-world environments. Chang et al. [24] propose a deep reinforcement learning-based trajectory design and resource allocation scheme for multi- UAVs communication systems. Joint user association, power allocation, and UAV trajectory design problems are investigated by maximizing the system utility. Centralized Deep Reinforcement Learning (CDRL) and Multi-Agent Deep Reinforcement Learning (MADRL) algorithms are proposed for distributed implementation and adaptive network dynamics. Although the algorithms show advantages in simulation studies, the paper does not fully explore the scalability and robustness of the algorithms in real complex environments.
In the field of UAV path planning based on deep reinforcement learning, although researchers have proposed a variety of algorithms and models to solve complex path planning problems, the robustness of the algorithms in the face of environmental noise and uncertainty is a pivotal issue, but many existing algorithms still leave much to be desired in this regard. In addition, the design of the reward function has an essential impact on the performance of the algorithms, and the reward function design in several of the above studies is still insufficient in terms of the reproduction of the actual dynamic scene. In this paper, we will introduce random factors into the environment and consider more practical elements in the reward function design to enhance the robustness of the algorithm proposed in this paper and allow it to be more adaptable to complex dynamic environments.
3. Problem Definition
3.1. Description of the Relaying Problem for UAV-to-Ground Communication
In response to the lack of real-world environment simulation and the inadequacy of UAV path planning in the above studies, this paper comprehensively considers a variety of factors when studying the multi-UAV to ground communication relay problem. In this paper, the design of state space and action space, communication modeling, the construction of the training environment, and the design of reward function are combined with the characteristics of actual tasks and real entities [25]. As it is shown in Figure 1, the core objective of a multi-UAV to ground communication relay is to maximize the communication coverage and reliability of the ground platform through the optimization of UAV trajectories and communication strategies, while minimizing energy consumption and avoiding dangerous areas [26].
Figure 1.
Schematic diagram of the effect of communication relay achieved by the UAV network.
3.2. System Modeling and Assumptions
The design of the state space and action space is crucial in the UAV ground communication relay task. The state space includes all environmental variables that can influence the UAV’s decision making. In this environment, the state space contains the following elements:
- : The position of the UAVs (2D coordinates) with a state dimension of 2 for each UAV.
- : The location of the ground platforms (2D coordinates), each with a state dimension of 2.
Other joint considerations include location and radius of the no-fly zone and the connection state of the ground platforms.
Therefore, the dimension of the state space is:
where is the number of UAV agents, is the number of ground platforms, denotes the number of no-fly zones, and is the connection state of ground platforms.
The action space includes the UAV’s motion and communication power decisions. Specifically, the actions of each UAV include:
- and : indicate the movement of the UAV in the horizontal direction, in the range [−0.1, 0.1].
- : Transmit power: range is [0, 50] in dBm.
- Thus, the action space of the UAV is a three-dimensional vector:
The advantage of this design is that it adequately captures the key parameters required by the UAV in the communication relay task, while simplifying the complexity of the problem and allowing the reinforcement learning algorithm to learn and optimize the strategy efficiently.
3.3. Calculation of Communication Probability and Energy Consumption
The modeling of communication between UAVs and ground platforms is based on the free-space path loss model, the lognormal fading model, and the Rayleigh fading model [27]. This modeling can reflect the communication characteristics in the actual environment more accurately. The received strength of the communication signal (RSSI) in dBm is calculated by the following equation:
where is the antenna gain, the (total path loss) is:
where Free Space Path Loss (FSPL) is modeled as [28]:
where is the distance between the UAV and the ground platform or between the UAV and another UAV, and is the communication frequency (in GHz).
Lognormal decay is modeled as:
where denotes the shadowing stand distribution, which is the standard deviation of the shadowing effect.
The Rayleigh fading model is crucial in accurately simulating the signal attenuation experienced in UAV-to-ground communication links, which accounts for the multipath fading that occurs when a signal travels from the transmitter (UAV) to the receiver (ground platform). In the multipath environment designed in this paper, the signal arrives at the receiver via several paths, each with different lengths and phases, leading to constructive and destructive interference patterns. The Rayleigh distribution is used to model the power of the envelope of the received signal, which is a key factor in determining the reliability of the communication link. As a result, Rayleigh’s decline is modeled as:
where the scale parameter represents the average power of the received signal. The impact of Rayleigh fading on the communication link is significant as it introduces variability in the received signal strength, which in turn affects the communication probability and the overall performance of the entire UAV relay network. By incorporating this model into the environment, it could be ensured that UAVs can adapt their communication strategies in real-time to the dynamic environmental conditions, thus enhancing the stability and reliability of the communication.
Communication probabilities are mapped to the range [0, 1] by RSSI values using an S-shaped function:
This function transforms the received signal strength into a probability value, where higher RSSI values correspond to higher communication probabilities. This mapping is essential for MARL algorithms to make informed decisions about the transmission power of each UAV, as it directly influences the communication strategies that maximize the communication coverage and reliability of the network.
This multi-model communication modeling can more comprehensively simulate the various influencing factors in the actual communication environment, thus improving the credibility of the simulation results.
The energy consumption for each UAV, indexed by , is calculated as a sum of three primary components: movement cost, hovering cost, and communication cost. The comprehensive energy cost can be expressed as follows:
represents the baseline energy consumption for maintaining a steady position and altitude. A fixed value is used to model this component, reflecting the continuous energy required to counteract gravitational forces and stabilize the UAV. is a constant representing the energy consumed per time unit during hovering.
cost is incurred when the UAV changes its position. It is a function of the distance moved, which is determined by the UAV’s speed and the magnitude of the positional action vector :
where is the Euclidean norm of the action vector (representing the movement direction and magnitude), is the maximum speed of the UAV, and is a scaling factor translating distance into energy cost.
encapsulates the energy used during signal transmission. It is directly proportional to the transmit power :
where is a conversion factor linking transmit power to energy consumption.
The total energy cost for a UAV executing a given action can be succinctly expressed as:
This formula incorporates both the operational dynamics of the UAV (movement and hovering) and its communication activities. It allows for the evaluation of different action policies within the Mix-Greedy MAPPO framework, ensuring that the chosen trajectories not only maximize communication efficiency but also adhere to energy constraints.
3.4. Reward Function Design
The reward function is designed to balance multiple objectives, including maximizing communication probability, minimizing energy consumption, avoiding no-fly zones, facilitating exploration, and maintaining reasonable UAV spacing. The specific reward function is as follows:
Specific bonus and penalty items include:
Average distance from the platform (the closer the distance the higher the reward) is calculated by:
where is the average distance between UAVs and ground platforms, is the safe distance limitation, and is the max communication distance between the UAV and the ground platforms.
Communication probability (the higher the communication probability the higher the reward) is calculated by:
where is the number of links.
Exploration bonus (covers new or less visited areas) is calculated by:
where is the number of girds explored by UAVs.
Energy depletion penalty (the lower the depletion, the higher the reward) is calculated by:
where is the max energy capacity of UAVs.
No-fly zone penalty (penalty for entering a no-fly zone) is calculated by:
Hover penalties (penalties for drone position changes less than a certain threshold) is calculated by:
where is distance that a UAV moved through.
Inter-UAV communication rewards and penalties (rewards when the distance is right, penalties when too close or too far) is calculated by:
where is the current distance between UAVs and is the max communication distance between UAVs.
This comprehensive multi-objective reward function design can effectively guide UAVs to realize optimal strategies in complex environments, balancing communication quality, energy consumption, and safety.
3.5. System State Transfer Probability Analysis
The state transfer of the whole system is based on the UAV’s maneuver selection and the dynamics of the environment. The specific state transfer is determined by the following factors:
- The motion of the UAV: determined by and in the action space.
- Communication behavior of the UAV: determined by the transmit power, which affects the connection state and communication probability of the ground platform.
- Motion of the ground platform: updates the position based on a set random direction and velocity.
- Energy consumption of the drone: determined by the distance traveled and the transmit power.
- Location of no-fly zones and obstacles in the environment: fixed.
The state transfer probabilities depend on the current state and action and contain uncertainties introduced by random variables (e.g., fading and shadowing effects in communication probabilities). By utilizing the MAPPO algorithm in deep reinforcement learning, the optimal UAV action strategy can be learned step-by-step. The specific state transfer formula is:
where is the current state, is the current action, denotes random noise (e.g., fading effects), and is the state transfer function. In this paper, it is assumed that the motions of the ground platform and the air platform are linear in each time slot .
Assume that the motion of the ground platform can be described in terms of position and velocity. Let the position of the ground platform in the time slot be , the velocity be , and the acceleration be .
The equation of movement of the ground platform can be expressed as:
Assume that the movement of the UAV can be described equally in terms of position and velocity. Let the position of the airborne platform in the time slot be , the velocity be , and the acceleration be .
where the is the interval of a time slot.
4. Algorithm and Experiment Design
4.1. Mix-Greedy MAPPO
The ε-greedy strategy is a simple but effective exploration strategy that introduces a probability factor ε into the decision-making process of an agent. The agent chooses the currently optimal action with a probability of 1 − ε (i.e., the greedy strategy), and randomly selects an action with a probability of ε. This strategy is a straightforward and effective exploration strategy that introduces a probability factor ε into the decision-making process of an agent. The advantage of this strategy is that it is simple to implement and is able to trade-off between exploration (trying new actions) and exploitation (choosing the best-known action). However, the ε-greedy strategy may not be flexible enough in the face of complex environments because it explores uniformly at random and may not prioritize the exploration of states that are more likely to lead to high payoffs.
MAPPO is a commonly used algorithm in the field of MARL, which is based on the extension of the single-agent PPO (Proximal Policy Optimization) algorithm. The fundamental idea of MAPPO is to use a centralized value function to coordinate the policy updates of multiple agents, while keeping the policy network decentralized so that each agent can make decisions based on local observations [29].
The MAPPO algorithm relies primarily on the policy gradient approach to learn the optimal policy directly by optimizing the policy network. The MAPPO algorithm enhances the exploratory nature of the agents specifically by means of stochastic policies with entropy regularization. In the policy network output, actions are sampled from the policy distribution instead of always selecting the optimal action, and the stochastic nature of this distribution naturally introduces exploratory behavior [30]. In terms of entropy regularization, the MAPPO algorithm encourages the strategies to maintain a certain degree of randomness by adding an entropy regularization term to the loss function, thus enhancing exploration. At each strategy update, the data collected are sampled according to the current strategy, which also incorporates the exploratory behavior of the strategy.
While the policy gradient approach in MAPPO already includes an exploration mechanism, in some complex environments, an additional exploration mechanism may further improve performance. ε-greedy policies are typically used in value-based reinforcement learning algorithms, such as Q-learning and DQN, where the agent selects random actions with probability ε (exploration) and optimal actions with probability 1-ε (exploitation). This strategy ensures that the agent continuously tries new actions during the training process, thus avoiding falling into a local optimum. In this paper, the mix-greedy MAPPO is proposed, where the ε-greedy strategy is introduced into the MAPPO algorithm to enhance the exploration efficiency of the agent, expand the state coverage, and improve the flexibility and adaptability of the strategy.
The ε-greedy strategy increases the diversity of the MAPPO algorithm’s explorations by randomly selecting actions, which contributes to the discovery of better collaborative strategies for multi-agent systems. Through randomized exploration, agents are more likely to access states that are not often accessed, which facilitates a more complete understanding of the environment. The execution process of Mix-Greedy MAPPO is shown in Algorithm 1. The introduction of the ε-greedy strategy improves the adaptability of the MAPPO algorithm in the face of changes in the environment because it allows agents to experiment with new combinations of actions while utilizing known strategies. The ε-greedy strategy can achieve a smooth transition from high exploration to high utilization by gradually decreasing the value of ε during the training process [31]. This dynamic adjustment enables the agents to fully explore the environment in the early stage and utilize the already learned knowledge more in the later stage, thus improving the overall training effect. Especially in a multi-intelligent body environment, the introduction of randomness can effectively avoid the strategies of multiple intelligences interfering with each other, which would lead to an unstable learning process [32].
| Algorithm 1: UAV Relay Communication using MAPPO with Epsilon-Greedy Strategy |
| 1: Initialize environment env, MAPPO agent mappo_agent |
| 2: Initialize ε, εdecay, εmin, Nepisodes, Smax |
| 3: for episode = 1 to Nepisodes do |
| 4: state, info ← env.reset() |
| 5: for t = 1 to Smax do |
| 6: for agent in env.agents do |
| 7: if random() < ε then |
| 8: action[agent] ← env.action_space[agent].sample() //Exploration |
| 9: else |
| 10: action[agent] ← mappo_agent.select_action(state[agent]) //Exploitation |
| 11: end if |
| 12: end for |
| 13: next_state, Rtotal, Fterminated, Ftruncated, info ← env.step(action) |
| 14: mappo_agent.update(state, action, rewards, next_state, Fterminated) |
| 15: state ← next_state |
| 16: if ε > εmin then |
| 17: ε ← ε× εdecay |
| 18: end if |
| 19: if all (Fterminated) or Ftruncated then |
| 20: break |
| 21: end if |
| 22: end for |
| 23: end for |
The execution and training process of the Mix-Greedy MAPPO algorithm is divided into three main phases: the initialization, the episode loop, and the time interval evolution, where the algorithm will continuously update the strategy until a termination condition is triggered. The following figure (Figure 2) illustrates the main execution steps of Mix-Greedy MAPPO. The algorithm adopts a centralized training with decentralized execution (CTDE) architecture, where each agent has its own independent Actor-Critic network. As a result, agents can effectively exploit the global information to achieve better and more stable training results, while only local information can be utilized when deploying on UAV, leading to a promising application potential of the Mix-Greedy MAPPO algorithm.
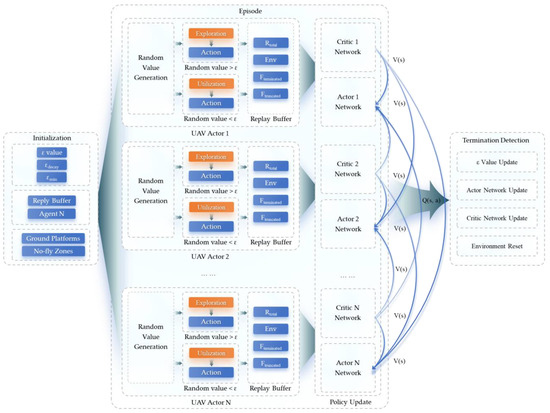
Figure 2.
Overview of Mix-Greedy MAPPO approach.
In the initialization phase, the agent employing the MAPPO algorithm is first initialized, which is able to share strategies and states with other agents in the training environment, thereby achieving collaboration among multiple agents as well as UAVs. In order to balance exploration and exploitation, Mix-Greedy MAPPO sets the exploration probability parameter ε and introduces εdecay to gradually reduce the exploration probability, thus reducing the exploration behavior and facilitating the algorithm to converge to the desired state. In addition, the algorithm introduces a minimum exploration probability εmin to ensure that the exploration probability does not fall below this value, thus avoiding the failure of the exploration strategy.
Next, in the episode loop phase, the algorithm conducts learning by executing multiple episodes. At the beginning of each episode, the environment is reset to its initial state. Subsequently, the algorithm enters the time interval evolution, in which for each agent in the environment, the algorithm generates a random number and compares it with the current ε value. According to the ε-greedy policy, if the random number is less than ε, the agent will perform exploration, i.e., randomly select an action to interact with the environment; otherwise, the agent will select an optimal action based on the acquired experience. After executing the selected action, the agent will acquire the next state, the reward score, the end-of-episode flag, and the training truncation flag in the environment. Then, the experience from the current interaction is passed to update the MAPPO agent’s policy and value function, and the current state is updated. At the end of each time interval, the algorithm decays the ε, while ensuring that it does not fall below εmin.
Finally, the algorithm will examine if the end-of-episode flag and the training truncation flag satisfy the termination condition of the training. If all agents have triggered the termination condition or reached the maximum episode number, the current episode and training process will be terminated. Through the above process, the proposed algorithm in this paper can effectively combine the ε-greedy policy with the MAPPO algorithm to improve the global exploration ability of multiple agents while avoiding falling into local optimality, thus allowing the multi-UAV system to achieve a higher communication relay performance than other algorithms. Main parameters involved in above process is shown in Table 1.

Table 1.
Exploration parameters in Mix-Greedy MAPPO algorithm.
The integration of the ε-greedy strategy with MAPPO is the major innovation of the proposed Mix-Greedy MAPPO algorithm, which improves the exploration efficiency of the algorithm as well as its adaptability to dynamic environments, so the probability of falling into a local optimum is significantly reduced. This combination provides a more adaptive and efficient exploration of the state space, which is crucial for UAV path planning in dynamic environments. By gradually decreasing the value of ε during the training process, the proposed algorithm can transition smoothly from high exploration to high exploitation. This adaptability enables the UAVs to fully explore the environment in the early stages and utilize learned knowledge more in later stages, improving overall training effectiveness.
The above innovations distinguish the Mix-Greedy MAPPO algorithm from other MARL-based methods and highlight its potential for practical applications in UAV path planning and communication optimization missions.
4.2. Experiement Design
In order to evaluate the performance of the Mix-Greedy MAPPO algorithm in multi-UAV air-to-ground relay communications, a series of experiments are designed and implemented in this paper. The Experiment environment was constructed using the Python 3.10 programming language to simulate a UAV relay scenario for ground-to-ground communication. The environment is intended to conduct UAV cluster motion trajectory planning through the MAPPO algorithm so that the UAVs can perform their tasks with the goals of maximizing communication probability and minimizing energy consumption. The following is a detailed description of the experimental environment (Table 2).

Table 2.
Experiment environment parameters.
The number of UAVs indicates the quantity of UAVs that relay the communication signal, the number of ground platforms indicates the quantity of vehicles or robots that needs to connect to UAVs and each other, and the number of no-fly zones indicates the quantity of zones that UAVs are not supposed to fly into; explore grid is the basic cell of the space of environment.
To make the experiment environment adapt to the actual UAV working scenario and to guarantee the generalization ability of the model, the environment is initialized with the following parameters at each reset:
- The initial positions of the UAV and the ground platform are randomly generated in the environment space.
- The speed and direction of movement of the ground platform are also randomly initialized.
- The energy level of the drone is set to an initial value of 4000 mAh.
- The no-fly zone is randomly generated with its location and radius.
In addition, a number of auxiliary variables and structures are initialized to record the trajectories of the drone and the ground platform, as well as an exploratory map of the environment. The setting of the above training environment can simulate the typical scenarios in the actual UAV missions, which ensures the practical applicability and robustness of the simulation results.
Among the well-regarded MARL algorithms are Multi-Agent Soft Actor-Critic (MASAC) and Multi-Agent Deep Deterministic Policy Gradient (MADDPG). These algorithms are deployed as baselines to be compared with the proposed algorithm, which extends the principles of single-agent reinforcement learning (RL) to multi-agent domains, enabling the training of multiple agents in a shared environment. In the context of multi-UAV path planning, these algorithms offer distinct advantages, including improved coordination, scalability, and adaptability to dynamic environments.
MASAC is an extension of the Soft Actor-Critic (SAC) algorithm to multi-agent settings. SAC is a state-of-the-art off-policy RL algorithm known for its stability and sample efficiency, which it achieves through entropy regularization. MASAC incorporates an entropy term into the reward function, encouraging exploration by preventing premature convergence to suboptimal policies. This is particularly beneficial in multi-agent settings where diverse strategies may be necessary for effective coordination [33].
MADDPG extends the Deep Deterministic Policy Gradient (DDPG) algorithm to multi-agent environments. DDPG is an actor-critic algorithm that combines the benefits of policy gradients and Q-learning. MADDPG employs deterministic policies for each agent, parameterized by neural networks. The deterministic nature of the policies enables efficient learning in continuous action spaces, which is essential for UAV path planning [34]. Similar to MASAC, MADDPG employs a centralized critic for each agent during training. The critic computes Q-values using the global state and the actions of all agents. This centralized approach helps in addressing the non-stationarity issue in multi-agent environments. The training results of MASAC and MADDPG are shown in the results chapter.
Other communication parameters are indicated in the following table (Table 3).

Table 3.
Communication parameters.
4.3. Step Function Design
Within each time step, the experiment environment updates its position and energy level based on the UAV’s movements. The specific process includes:
- Action scaling: mapping the normalized action value to the actual speed by multiplying the action value and the max UAV speed.
- Position update: update the position of the UAV based on the movement and check if it enters the no-fly zone.
- Energy consumption: update the energy level of the drone based on the movement distance.
- Trajectory logging: records the new position of each drone and ground platform.
- Ground Platform Update: updates the position of the ground platform based on its speed and direction, and may randomly change its direction of movement.
In each step, the position update function for each UAV is as follows:
where is the new position of UAVi.
In each step, the position update function for each ground platform is as follows:
where is the position of each ground platform.
5. Results
The figure below (Figure 3) shows the rewards of each algorithm obtained during the training progress, where the average reward of each algorithm of Mix-Greedy MAPPO (ε = 0.97), Mix-Greedy MAPPO (ε = 0.9), MAPPO, MASAC, and MADDPG are 43.42, 38.93, 29.76, 13.16, and 7.28, respectively. To improve the readability of the figure, the colored lines in the figure below (Figure 3) indicate the smoothed reward curve of different algorithms while the dotted lines stand for the original ones.
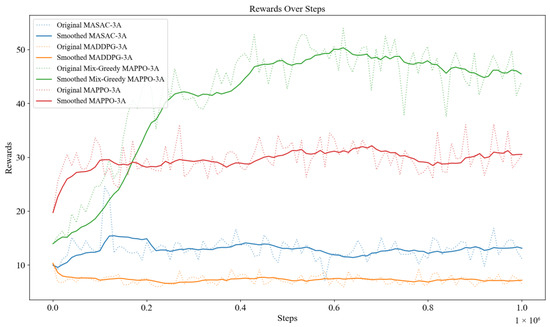
Figure 3.
Rewards of DRL algorithms through the training progress.
According to the training results, the MAPPO algorithm, which incorporates the ε-greedy strategy, is superior to other algorithms in the path planning task of multi-UAV ground communication relay. According to the training result based on the above setting, the Mix-greedy MAPPO algorithm proposed in this paper achieves highest reward and overcomes the local optimality problem. The basic MAPPO algorithm, which serves as the baseline for this paper, fails to obtain a higher score, although it scores above the MADDPG algorithm and the MASAC algorithm, as it falls into a local optimum shortly after starting training. The MASAC algorithm and the MADDPG algorithm were also evaluated against algorithms such as MAPPO, which achieved low scores in the same environment and could not be adapted to the multi-UAV path planning task in this paper.
To validate the superiority of proposed Mix-Greedy MAPPO algorithm, a comprehensive statistical analysis of the experimental results is conducted. According to the comparison between the performance of Mix-Greedy MAPPO with other algorithms using a two-tailed t-test, assuming equal variances, the p-values obtained from the above tests indicate that the performance differences between Mix-Greedy MAPPO and other algorithms are statistically significant. The confidence intervals provide a range within which we can be 95% confident that the true mean difference lies.
The Mix-Greedy MAPPO algorithm also has certain advantages in terms of individual scores such as , , and (Figure 4).
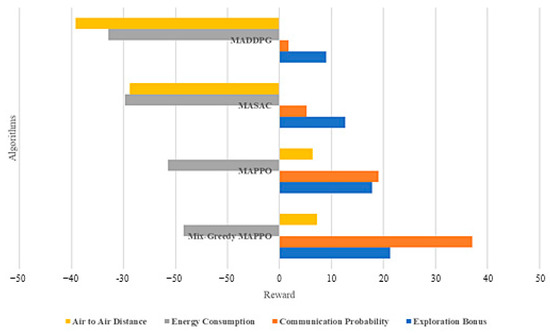
Figure 4.
Rewards of DRL algorithms through the training progress.
The training parameters are shown in the table below (Table 4).

Table 4.
Training parameters.
- Wider spatial exploration: in the path planning task, UAVs need to explore the optimal path in a complex environment. The introduction of the ε-greedy strategy allows the UAV to try more different paths in the initial stage, avoiding premature convergence to suboptimal paths, and thus finding a more optimal communication relay path.
- Enhance communication probability: since the UAV can explore different locations and paths in the initial phase, the combination of the ε-greedy strategy can help the UAV to find path combinations with higher communication probability and enhance the overall communication effect.
- Reduced energy consumption: by exploring more fully, UAVs can find path combinations with lower energy consumption. The ε-greedy strategy can help UAVs find ways to avoid energy-intensive paths during the exploration process, thus prolonging the endurance of UAVs.
- Enhanced collaboration: in a multi-UAV environment, each UAV needs to collaborate with each other UAV to accomplish tasks. With the introduction of the ε-greedy policy, the UAVs can better explore the possibility of collaboration at the initial stage, find better combinations of collaborative paths, and improve the overall mission accomplishment.
To the aspect of generalization, the Mix-Greedy MAPPO and MAPPO are tested in a different number of no-fly zones, which range from 1 to 19, as it might be an essential parameter during the application of the above algorithms in the real world. The figure below (Figure 5) shows the performance changes of the major algorithms while the number of no-fly zones increases. The blue line indicates the rewards of Mix-Greedy MAPPO while the orange line indicates the rewards obtained by MAPPO.
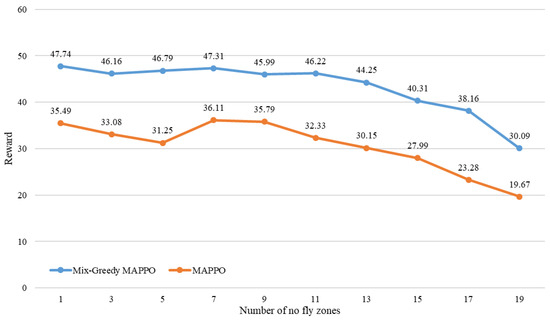
Figure 5.
Mean rewards of proposed algorithm and MAPPO with different number of no-fly zones.
By comparing the generalization performance of Mix-Greedy MAPPO and MAPPO, two algorithms with obvious performance advantages, in different numbers of no-fly zones, it can be found that the reward loss of Mix-Greedy MAPPO algorithm is lower than that of MAPPO as the number of no-fly zones increases. The Mix-Greedy MAPPO algorithm only begins to show significant attenuation when the number of no-fly zones reaches 13, while the performance of the MAPPO algorithm begins to decline significantly when the number of no-fly zones reaches 9.
To verify the robustness of the algorithm to the number of drones, this paper tested the training scores of Mix-Greedy MAPPO, MAPPO, MASAC, and MADDPG algorithms when controlling different numbers of UAVs to complete relay tasks in the training environment. The following figure (Figure 6) shows the highest reward results of various algorithms trained in environments with different numbers of UAVs. It can be seen from the figure that as the number of drones gradually decreases, the training reward of the Mix-Greedy MAPPO algorithm decays the least, and the reward of the Mix-Greedy MAPPO algorithm is higher than that of other algorithms in environments with different numbers of drones.
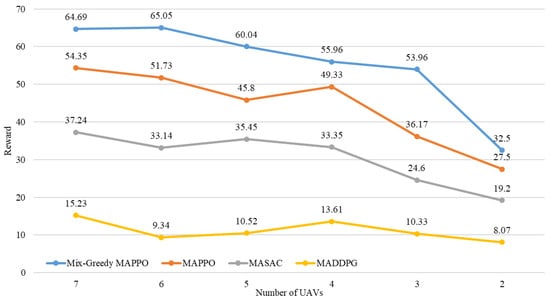
Figure 6.
Best rewards of each algorithm with different number of UAVs.
The higher the number of UAVs, the higher the score that each algorithm can achieve, but the improvement of the reward decreases, implying that simply increasing the number of UAVs is not the optimal solution for communication relaying, and optimization in cooperative path planning and communication power control is necessary. Therefore, Mix-Greedy MAPPO has a high potential for practical application due to its higher rewards than other algorithms for each number of UAVs.
To further validate the performance of each algorithm in a complex environment, the following figure (Figure 7) shows the rewards of each algorithm in a communication relay environment with five UAVs and seven ground platforms. The complexity of this environment is significantly higher compared to the original environment, but the Mix-Greedy MAPPO algorithm managed to achieve higher rewards compared to the other algorithms with the same number of training steps. Therefore, the Mix-Greedy MAPPO algorithm has a significant advantage in its ability to adapt to complex tasks and to maximize its efficiency in task execution.
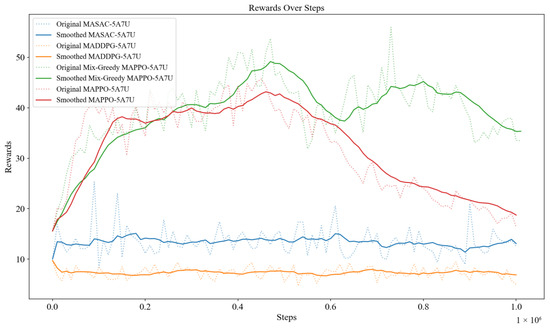
Figure 7.
Training results of each algorithm with five UAVs and seven ground platforms.
The following figure (Figure 8) shows the training curves of the Mix-Greedy MAPPO algorithm and the MAPPO algorithm for different numbers of drones, which indicates that the results tend to converge.
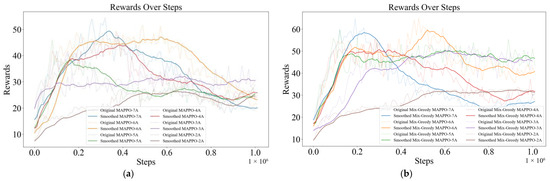
Figure 8.
Training curves of MAPPO and Mix-Greedy MAPPO: (a) the training results of 2~7 UAVs of MAPPO; (b) the training results of 2~7 UAVs of Mix-Greedy MAPPO.
The visualization of the UAV path planning results with the communication link allows for intuitive analysis of the results of each algorithm’s control of the path as well as the communication power. The following figure (Figure 9) shows the results of visualizing the state of the UAV and the ground platform, where the UAV movement is determined by the deep reinforcement learning algorithm. In the figure, the communication link between the UAV and the ground platform is represented by the purple dotted line, the communication link between the UAV and the UAVs is represented by the green dotted line, and the movements of the UAV and the ground platform are mapped into the three-dimensional space; a connecting line will be generated between the UAVs and the ground platform or the other UAVs when they establish a communication connection. For example, Figure 9a shows the planning result of the Mix-Greedy MAPPO algorithm at a certain point in time, in which three drones have established self-organized networks among themselves and covered four ground platforms through the ground-to-ground communication connection, and only one ground platform has not established a connection with the drone network due to its distance. Figure 9b shows the planning result of the MASAC algorithm at a certain point in time; although the three drones communication connection is also established between them, the network only covers three ground platforms, so the planning results of Mix-Greedy MAPPO can be analyzed in this way to have more practicality. This comparison visually demonstrates the superior coverage and connectivity achieved by the Mix-Greedy MAPPO algorithm.
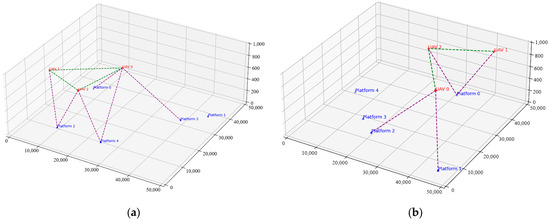
Figure 9.
Planning result of Mix-Greedy MAPPO and MASAC: (a) Mix-Greedy MAPPO UAV path plan result where three drones have established self-organized networks among themselves and covered four ground platforms through ground-to-ground communication connections. One ground platform remains unconnected due to distance, highlighting the algorithm’s ability to adapt to dynamic environments and establish efficient communication networks; (b) MASAC path plan result, where the network covers only three ground platforms.
The ε value determines the trade-off between exploring new strategies and utilizing known ones for the Mix-Greedy MAPPO algorithm. In this case the ε value has the most significant impact on the algorithm’s tendency to choose the exploration strategy. Different ε values were tested in the experiment, and the test results are shown in the figure below (Figure 10). The results show that when the ε value is small (purple curve), the algorithm is prone to achieve higher reward values faster at the initial stage, but it is not favorable for the algorithm to explore the global optimal strategy. On the contrary, with larger ε values (blue curve), the algorithm achieves a higher reward score in the end than the algorithms that choose other ε values, even though the initial reward score is lower. Due to the exploration, curves of Mix-Greedy MAPPO are generally higher than that of MAPPO (brown curve).
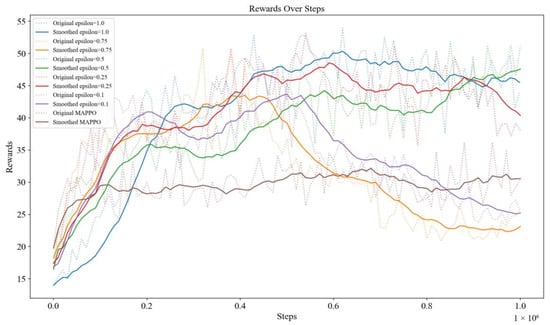
Figure 10.
Training results for Mix-Greedy MAPPO with different value of ε and MAPPO.
The εdecay determines the rate of decay of ε value over steps. A higher value of εdecay causes ε to decrease rapidly, resulting in the rapid shift of the algorithm from exploration to exploitation. In this case, the algorithm may fall into a local optimum solution prematurely. A lower value of εdecay causes ε to decay more slowly, increasing exploration time. Figure 11a below shows the training results for εdecay = 0.1, 0.5, and 0.9, where the maximum rewards are all higher than MAPPO and the algorithm has better performance for values of εdecay in the middle (orange curve).
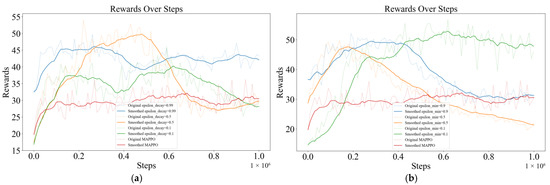
Figure 11.
(a) Training results for Mix-Greedy MAPPO with different values of εdecay and MAPPO. (b) Training results for Mix-Greedy MAPPO with different values of εmin and MAPPO.
The introduction of the εmin parameter ensures that the algorithm maintains a certain degree of exploratory behavior during the training process and avoids relying exclusively on known strategies. Higher values of εmin increase the exploratory behavior and help the algorithm to avoid falling into local optima but may reduce the stability of the algorithm. Lower values of εmin decrease exploration behavior and increase the stability of the algorithm but may cause the algorithm to stop exploring prematurely. Figure 11b below shows the training results for εmin = 0.1, 0.5, and 0.9, where the maximum scores are higher than MAPPO, indicating the effectiveness of the exploration strategy. The results in the figure suggest that εmin should not be too large, which will cause the algorithm to struggle to converge.
As a result, the Mix-Greedy MAPPO algorithm outperforms other algorithms by effectively adapting to changes in the environment. As shown in Figure 9a, Mix-Greedy MAPPO establishes communication with more ground platforms, indicating a higher adaptability to dynamic conditions. The Mix-Greedy MAPPO algorithm demonstrates higher communication efficiency by establishing more connections with ground platforms, as evidenced by the purple dotted lines in Figure 9a. This is in contrast to other algorithms, which connect with fewer platforms. The energy consumption of the Mix-Greedy MAPPO algorithm is lower than that of other algorithms, as it finds paths that minimize energy use while maintaining high communication probabilities, which is crucial for prolonging the endurance of UAVs in real-world applications. The Mix-Greedy MAPPO algorithm is more robust and generalizable than other algorithms for the number of no-fly zones, the number of UAVs, and the number of ground platforms, which are critical parameters in the given UAV-to-ground communication relay mission.
6. Conclusions
In this paper, the Mix-Greedy MAPPO algorithm is successfully applied to multi-unmanned aerial vehicle (UAV) path planning to optimize the communication efficiency and mission execution capability of UAV clusters in a complex environment with joint consideration on safe distance, no-fly zones, survival in a threatened environment, and energy consumption. Experimental results confirm that the Mix-Greedy MAPPO algorithm has significant advantages over MAPPO, MASAC, and MADDPG in improving communication probability, reducing energy consumption, avoiding no-fly zones, and facilitating exploration. The Mix-Greedy MAPPO algorithm proposed in this paper has an average reward score that is 45.9% higher than the MAPPO algorithm and several times higher than the MASAC and MADDPG algorithms. The algorithm effectively avoids falling into local optimal solutions by increasing the exploration behavior at the initial stage and improves the overall training effect by utilizing the learned strategies at the later stage. In addition, the flexibility and adaptability of the algorithm is verified in a dynamically changing environment, providing new research ideas and methods in the field of UAV cluster control. Future research can try to further optimize the time complexity and convergence speed and other indexes of this paper’s algorithm in a wider range of practical applications.
7. Future Work
The Mix-Greedy MAPPO algorithm proposed in this study has certain application potential in real-world UAV systems, and this paragraph will discuss in detail its implementation strategy and specific mission scenarios in real-world environments to provide a theoretical basis for future pilot tests. In terms of the implementation strategy, the Mix-Greedy MAPPO algorithm can be integrated into the existing UAV control system as a software module, achieving collaborative control of multiple UAVs by inquiring about environment situational information and outputting control commands. However, due to the complexity of real-world environments, some of the parameters in this algorithm (e.g., the value of ε in the ε-greedy strategy) may require tuning based on real-world tests in mission-specific environments, which can be conducted in well-controlled environments, such as UAV test ranges or simulated analog environments. The goal of the tests is to evaluate the performance of the algorithms when addressing real-world problems, including communication efficiency, task execution capability, and energy consumption. Through these tests, specific data can be collected after the algorithms are combined with the UAV direction, providing a basis for further optimization and improvement of the algorithms.
Since the Mix-Greedy MAPPO algorithm proposed in this paper is oriented to communication relay scenarios, its practical applications can include post-disaster emergency communication, communication assurance in environments with limited communication infrastructure, and so on. For example, after a natural disaster, legacy communication infrastructures may be damaged, in which case the Mix-Greedy MAPPO algorithm can be utilized to rapidly deploy UAVs to establish a temporary airborne communication network to provide critical communication support for rescue teams. In border patrol missions, where UAVs in heterogeneous unmanned clusters need to cover a wide area and maintain communications with specific units on the ground, unmanned clusters can be controlled collaboratively by applying the Mix-Greedy MAPPO algorithm to achieve multi-UAV control to optimize UAV flight paths and improve communication efficiency while reducing energy consumption. The above discussion of implementation strategies and specific use cases can demonstrate potential real-world applications of the Mix-Greedy MAPPO algorithm and provide guidance for future research and practice.
Author Contributions
Software, Y.Y.; Supervision, Y.C.; Validation, Z.L.; Writing—original draft, Y.W.; Writing—review and editing, X.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Huang, K.; Qiu, X.L.; Yin, J.; Yang, X.W. Adaptive Multi-Mode Routing Algorithm for FANET Based on Deep Reinforcement Learning. Comput. Eng. Appl. 2023, 59, 268–274. [Google Scholar] [CrossRef]
- Wang, R.; Xu, L. Application of Deep Reinforcement Learning in UAVs: A Review. In Proceedings of the 34th Chinese Control and Decision Conference, CCDC 2022, Hefei, China, 15–17 August 2022; pp. 4096–4103. [Google Scholar] [CrossRef]
- Guan, Y.; Zou, S.; Li, K.; Ni, W.; Wu, B. MAPPO-Based Cooperative UAV Trajectory Design with Long-Range Emergency Communications in Disaster Areas. In Proceedings of the 2023 IEEE 24th International Symposium on a World of Wireless, Mobile and Multimedia Networks, WoWMoM 2023, Boston, MA, USA, 12–15 June 2023; pp. 376–381. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, H.; Zhang, J.; Gong, G.; Pan, X.; Chen, H.; Wei, J. Topology Optimization Based on Adaptive Hummingbird Algorithm in Flying Ad Hoc Networks. Dianzi Yu Xinxi Xuebao/J. Electron. Inf. Technol. 2023, 45, 3685–3693. [Google Scholar] [CrossRef]
- Ndiaye, M.N.; Bergou, E.H.; El Hammouti, H. Muti-Agent Proximal Policy Optimization For Data Freshness in UAV-Assisted Networks. In Proceedings of the 2023 IEEE International Conference on Communications Workshops: Sustainable Communications for Renaissance, ICC Workshops 2023, Rome, Italy, 28 May–1 June 2023; pp. 1920–1925. [Google Scholar] [CrossRef]
- Guan, Y.; Zou, S.; Peng, H.; Ni, W.; Sun, Y.; Gao, H. Cooperative UAV Trajectory Design for Disaster Area Emergency Communications: A Multiagent PPO Method. IEEE Internet Things J. 2024, 11, 8848–8859. [Google Scholar] [CrossRef]
- Chen, C.; Guo, Z.; Luo, D.; Xu, Y.; Duan, H. UAV Cooperative Air Combat Maneuvering Decision-Making Using GRU-MAPPO. In Proceedings of the IEEE International Conference on Control and Automation, ICCA, Reykjavík, Iceland, 18–21 June 2024; pp. 647–652. [Google Scholar] [CrossRef]
- Liu, J.; Na, Z.; Lin, Y.; Chen, J.; Lin, B. Joint Relay Selection and Location Deployment for Multi-UAV Relaying Systems Based on Stackelberg Game. In Proceedings of the 2023 IEEE/CIC International Conference on Communications in China, ICCC 2023, Dalian, China, 10–12 August 2023; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023. [Google Scholar]
- Cheng, X.; Wang, Z. Multi-UAV Autonomous Collaborative Target Tracking in Dynamic Environment Based on Multi-Agent Reinforcement Learning. In Proceedings of the 2023 3rd International Conference on Electronic Information Engineering and Computer, EIECT 2023, Shenzhen, China, 17–19 November 2023; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023; pp. 123–128. [Google Scholar]
- Liu, D.; Wang, J.; Xu, K.; Xu, Y.; Yang, Y.; Xu, Y.; Wu, Q.; Anpalagan, A. Task-Driven Relay Assignment in Distributed UAV Communication Networks. IEEE Trans. Veh. Technol. 2019, 68, 11003–11017. [Google Scholar] [CrossRef]
- Sha, P.; Wang, Q. Autonomous Navigation of UAVs in Resource Limited Environment Using Deep Reinforcement Learning. In Proceedings of the—2022 37th Youth Academic Annual Conference of Chinese Association of Automation, YAC 2022, Beijing, China, 19–20 November 2022; pp. 36–41. [Google Scholar] [CrossRef]
- Yan, Y.Q.; Zhou, J.S.; Duan, X.T.; Tian, D.X. UAV-Assisted Aerial-Ground Cooperative Networking and Transmission Optimization Method. Unmanned Syst. Technol. 2022, 3, 97–105. [Google Scholar] [CrossRef]
- Li, Y.; Wu, R.; Gan, L.; He, P. Development of an Effective Relay Communication Technique for Multi-UAV Wireless Network. IEEE Access 2024, 12, 74087–74095. [Google Scholar] [CrossRef]
- Liu, X.; Durrani, T.S. Joint Multi-UAV Deployments for Air-Ground Integrated Networks. IEEE Aerosp. Electron. Syst. Mag. 2022, 37, 4–12. [Google Scholar] [CrossRef]
- Jiang, H.; Chang, Y.; Sun, X.; Liu, X.; Yang, L.; He, Y. Autonomous Communication Relay Position Planning Based on Predictive Model. In Proceedings of the 2022 IEEE International Conference on Unmanned Systems, ICUS 2022, Guangzhou, China, 28–30 October 2022; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2022; pp. 102–108. [Google Scholar]
- Bekmezci, I.; Ermis, M.; Kaplan, S. Connected Multi UAV Task Planning for Flying Ad Hoc Networks. In Proceedings of the 2014 IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Odessa, Ukraine, 27–30 May 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Li, M.; Sun, P.F.; Jeon, S.W.; Zhao, X.; Jin, H. Multi-UAV Path Planning with Genetic Algorithm. In Proceedings of the International Conference on ICT Convergence, Jeju Island, Republic of Korea, 11–13 October 2023; IEEE Computer Society: Piscataway, NJ, USA, 2023; pp. 918–920. [Google Scholar]
- Gao, S.; Ma, Y.; Duo, B. Safeguarding Multi-UAVs Relaying via Joint Trajectory Design and Power Control. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 21–23 October 2020; IEEE: Piscataway, NJ, USA, 2020. ISBN 9781728172361. [Google Scholar]
- Wan, F.; Yang, H.; Meng, Q. A Three-Dimensional Coverage Path Planning Method for Multi-UAV Collaboration. In Proceedings of the International Conference on Geoinformatics, London, UK, 19–21 July 2023; IEEE Computer Society: Piscataway, NJ, USA, 2023. [Google Scholar]
- Ren, Y.; Zhang, L. An Adaptive Evolutionary Multi-Objective Estimation of Distribution Algorithm and Its Application to Multi-UAV Path Planning. IEEE Access 2023, 11, 50038–50051. [Google Scholar] [CrossRef]
- Tamba, T.A. Optimizing the Area Coverage of Networked UAVs Using Multi-Agent Reinforcement Learning. In Proceedings of the Proceedings of the 2021 International Conference on Instrumentation, Control, and Automation, ICA 2021, Bandung, Indonesia, 25–27 August 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 197–201. [Google Scholar]
- Nie, Y.; Zhao, J.; Gao, F.; Yu, F.R. Semi-Distributed Resource Management in UAV-Aided MEC Systems: A Multi-Agent Federated Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2021, 70, 13162–13173. [Google Scholar] [CrossRef]
- Karimata, G.; Nakazato, J.; Tran, G.K.; Suto, K.; Tsukada, M.; Esaki, H. Multi-UAVs Strategies for Ad Hoc Network with Multi-Agent Reinforcement Learning. In Proceedings of the International Conference on Information Networking, Ho Chi Minh City, Vietnam, 17–19 January 2024; IEEE Computer Society: Piscataway, NJ, USA, 2024; pp. 726–729. [Google Scholar]
- Chang, Z.; Deng, H.; You, L.; Min, G.; Garg, S.; Kaddoum, G. Trajectory Design and Resource Allocation for Multi-UAV Networks: Deep Reinforcement Learning Approaches. IEEE Trans. Netw. Sci. Eng. 2023, 10, 2940–2951. [Google Scholar] [CrossRef]
- Pan, W.; Lv, N.; Chen, K.; Pan, Y.; Hong, X.; Zhang, X. Multi-UAV Relay Deployment Algorithm Based on Voronoi Diagram Division. In Proceedings of the 2023 6th International Conference on Electronics Technology, ICET 2023, Chengdu, China, 12–15 May 2023; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023; pp. 624–628. [Google Scholar]
- Yin, H.; Wei, J.; Zhao, H.; Zhang, J.; Wang, H.; Ren, B. Intelligent Communication and Networking Key Technologies for Manned/Unmanned Cooperation: States-of-the-Art and Trends. J. Commun. 2024, 45, 1–17. [Google Scholar] [CrossRef]
- Jie, Z.; Chen, Y.; Xue, L.; Zhong, T. A Design of UAV-Borne Communication System of Non-Line-of-Sight Networking. J. Telem. Track. Command. 2022, 43, 1–10. [Google Scholar] [CrossRef]
- Supramongkonset, J.; Duangsuwan, S.; Promwong, S. A Study of A2A Channel Modeling for Small UAV-Enabled Wireless Communication. In Proceedings of the 8th International Conference on Engineering, Applied Sciences, and Technology, ICEAST 2022—Proceedings, Chiang Mai, Thailand, 8–10 June 2022; pp. 93–96. [Google Scholar] [CrossRef]
- Lyu, G.; Li, M. Multi-Agent Cooperative Control in Neural MMO Environment Based on MAPPO Algorithm. In Proceedings of the AICAS 2023—IEEE International Conference on Artificial Intelligence Circuits and Systems, Proceeding, Hangzhou, China, 11–13 June 2023. [Google Scholar] [CrossRef]
- Park, Y.M.; Hassan, S.S.; Hong, C.S. Maximizing Throughput of Aerial Base Stations via Resources-Based Multi-Agent Proximal Policy Optimization: A Deep Reinforcement Learning Approach. In Proceedings of the APNOMS 2022—23rd Asia-Pacific Network Operations and Management Symposium: Data-Driven Intelligent Management in the Era of beyond 5G, Takamatsu, Japan, 28–30 September 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Bhandarkar, A.B.; Jayaweera, S.K. Optimal Trajectory Learning for UAV-Mounted Mobile Base Stations Using RL and Greedy Algorithms. In Proceedings of the International Conference on Wireless and Mobile Computing, Networking and Communications, Bologna, Italy, 11–13 October 2021; pp. 13–18. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, K. Multi-UAV Searching Trajectory Optimization Algorithm Based on Deep Reinforcement Learning. In Proceedings of the International Conference on Communication Technology Proceedings, ICCT, Wuxi, China, 20–22 October 2023; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023; pp. 640–644. [Google Scholar]
- Zhang, K.; Xu, Y.; Liu, C.; Zhai, Y. Intelligent Air Combat Maneuvering Decision Method of Multi-UAV System Based on TA-MASAC. In Proceedings of the 2023 5th International Conference on Robotics, Intelligent Control and Artificial Intelligence, RICAI 2023, Hangzhou, China, 1–3 December 2023; pp. 299–303. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, E. Design of MADDPG Capture Algorithm for Multiple UAV Cooperation. In Proceedings of the 2023 IEEE International Conference on Mechatronics and Automation, ICMA 2023, Harbin, China, 6–9 August 2023; pp. 2021–2026. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).