Predictive State Observer-Based Aircraft Distributed Formation Tracking Considering Input Delay and Saturations
Abstract
1. Introduction
2. Preliminaries and Problem Statement
2.1. Basic Concepts on Graph Theory
2.2. Definitions and Lemmas
3. Mathematical Model of Fixed-Wing Aircraft
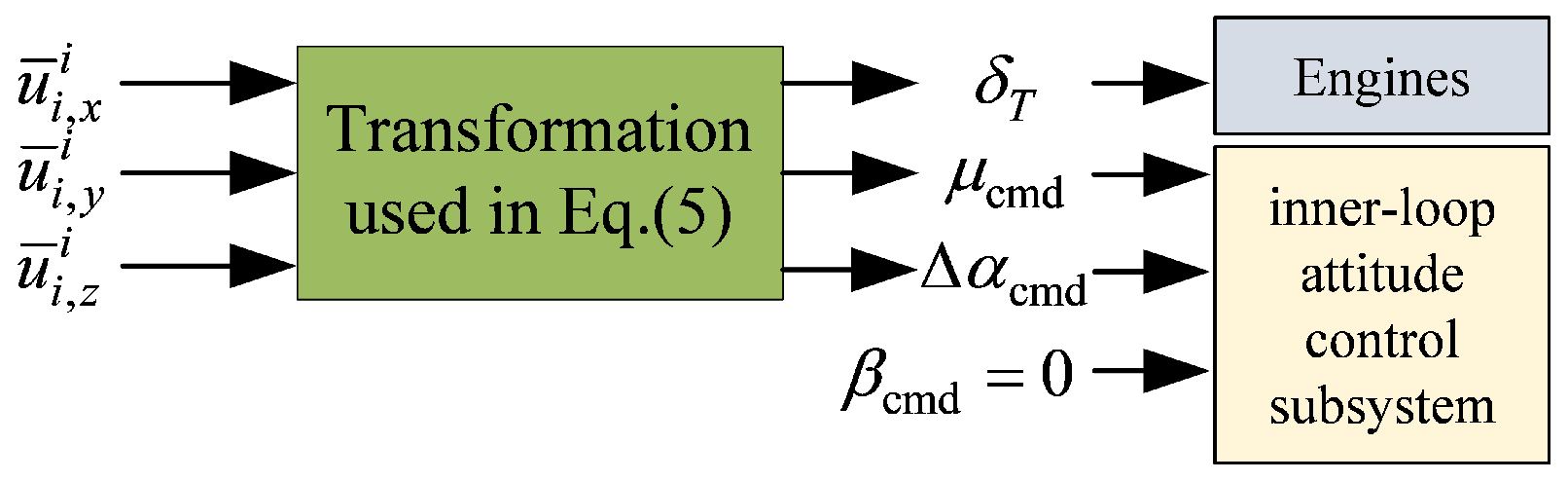
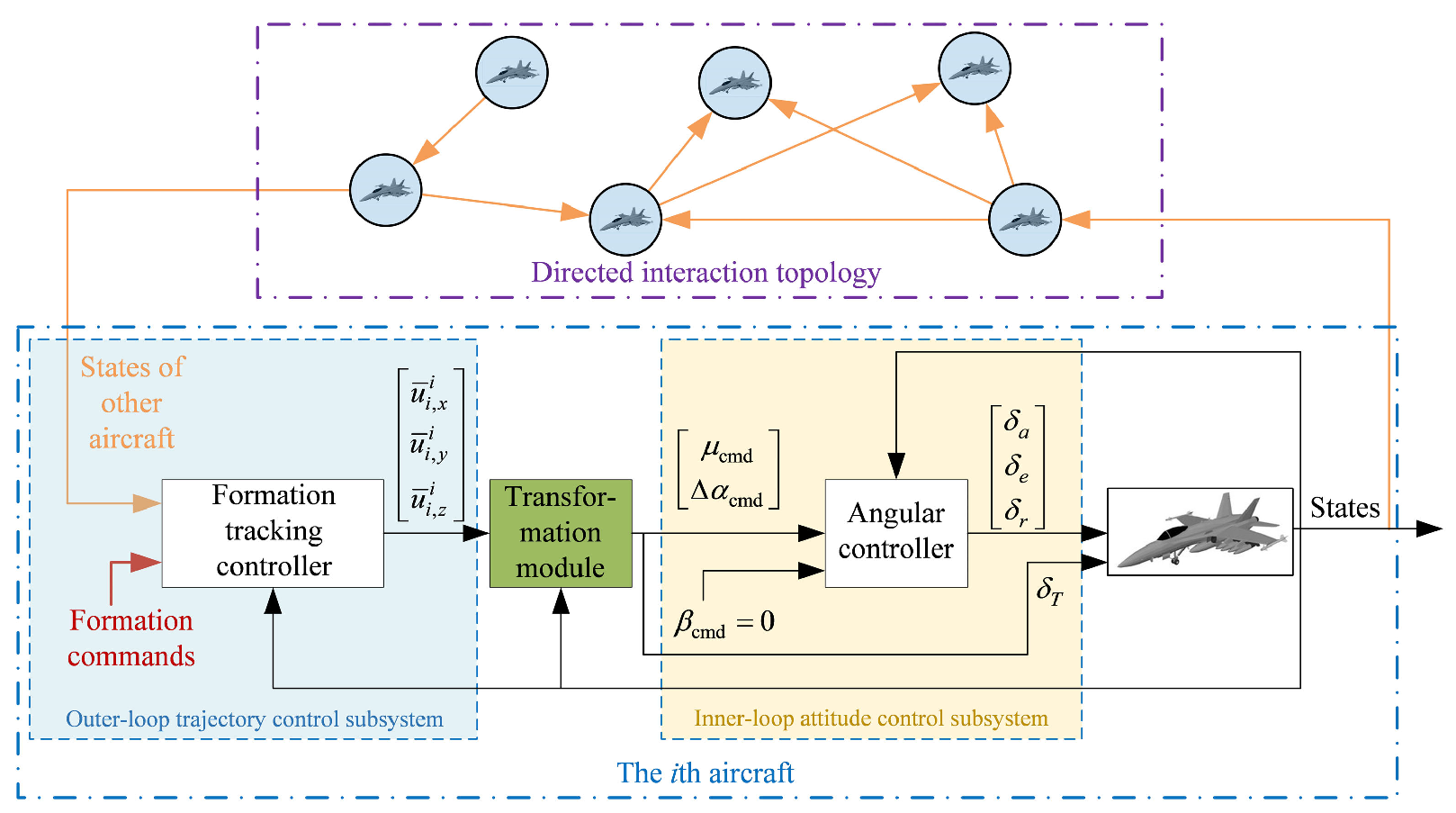
Problem Formulation
4. PESO-TVFTC Protocol Design and Analysis
4.1. PESO-TVFTC Protocol Design
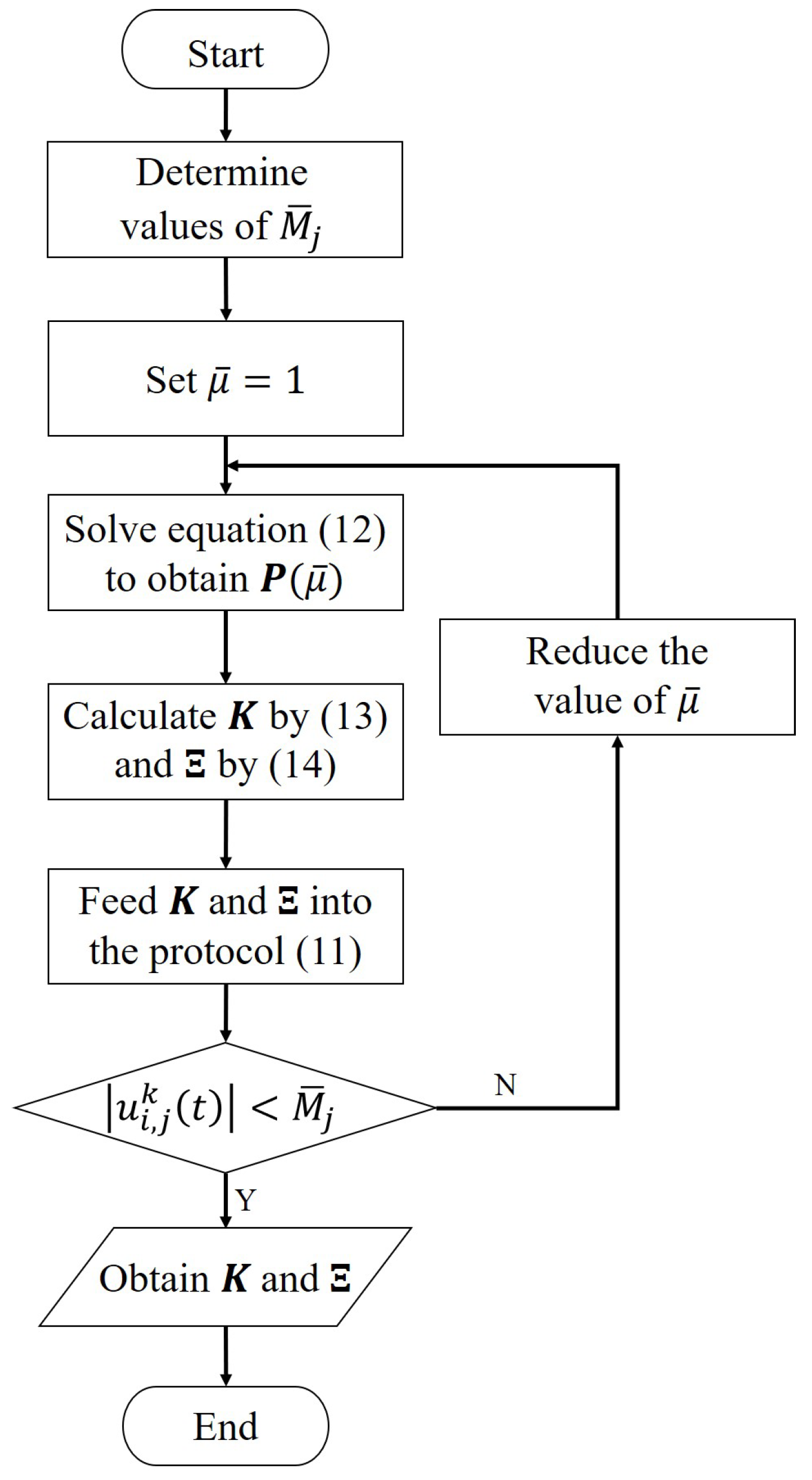
4.2. Low Gain Feedback Design Algorithm for Formation Tracking Control
| Algorithm 1 The parameters of protocol (11) can be specified in 4 steps: |
| Step 1. For systems (7) satisfying ANCBC, there exist a tuning parameter and a unique positive definite matrix satisfying the following algebraic Riccati equation: Step 2. The low gain feedback matrix can be specified by: Step 3. The gain matrix can be specified by: Step 4. The monotonically increasing function can be designed as |
4.3. Stability Analysis
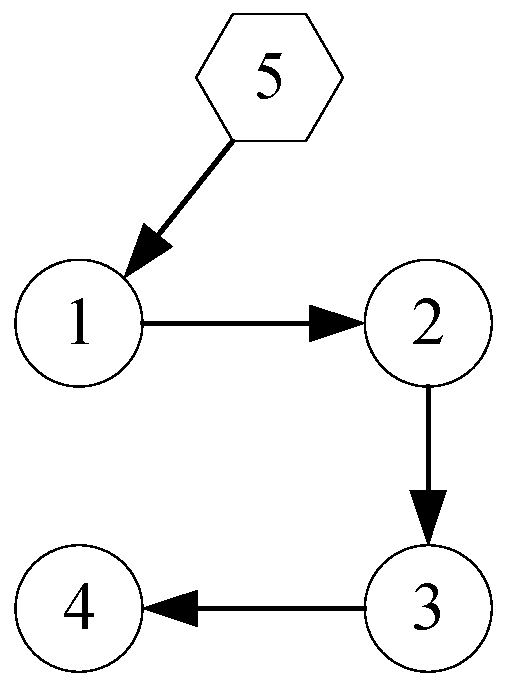
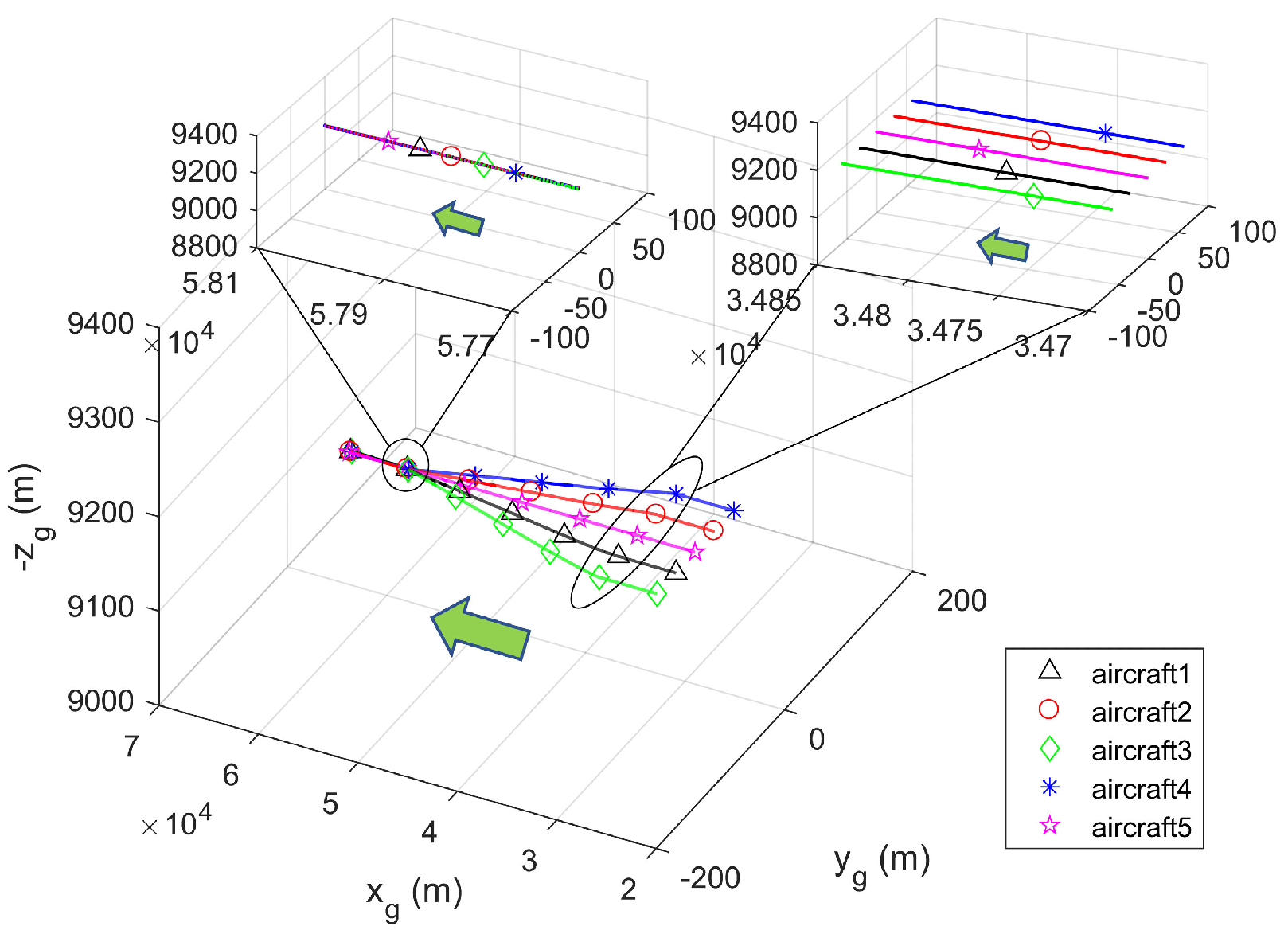
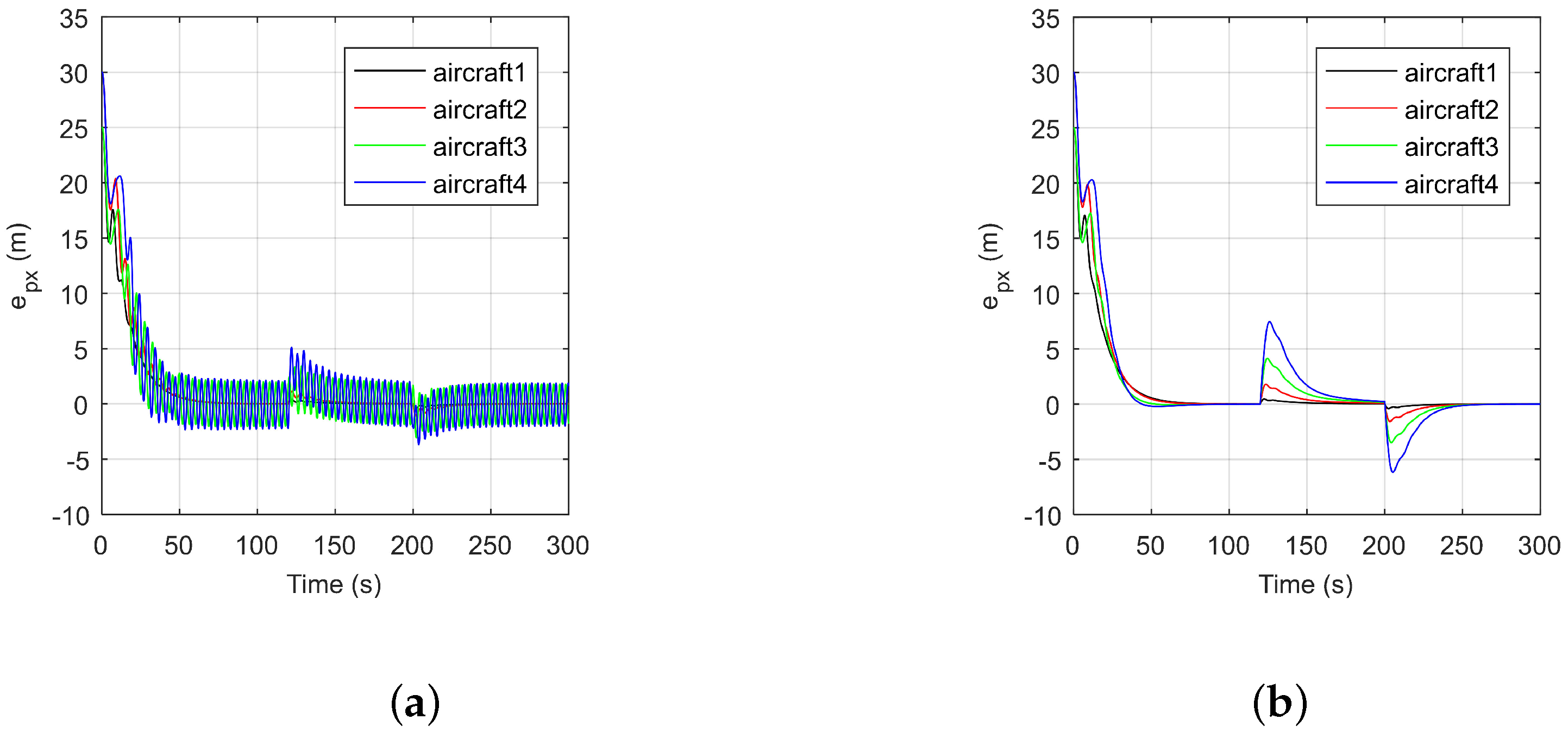
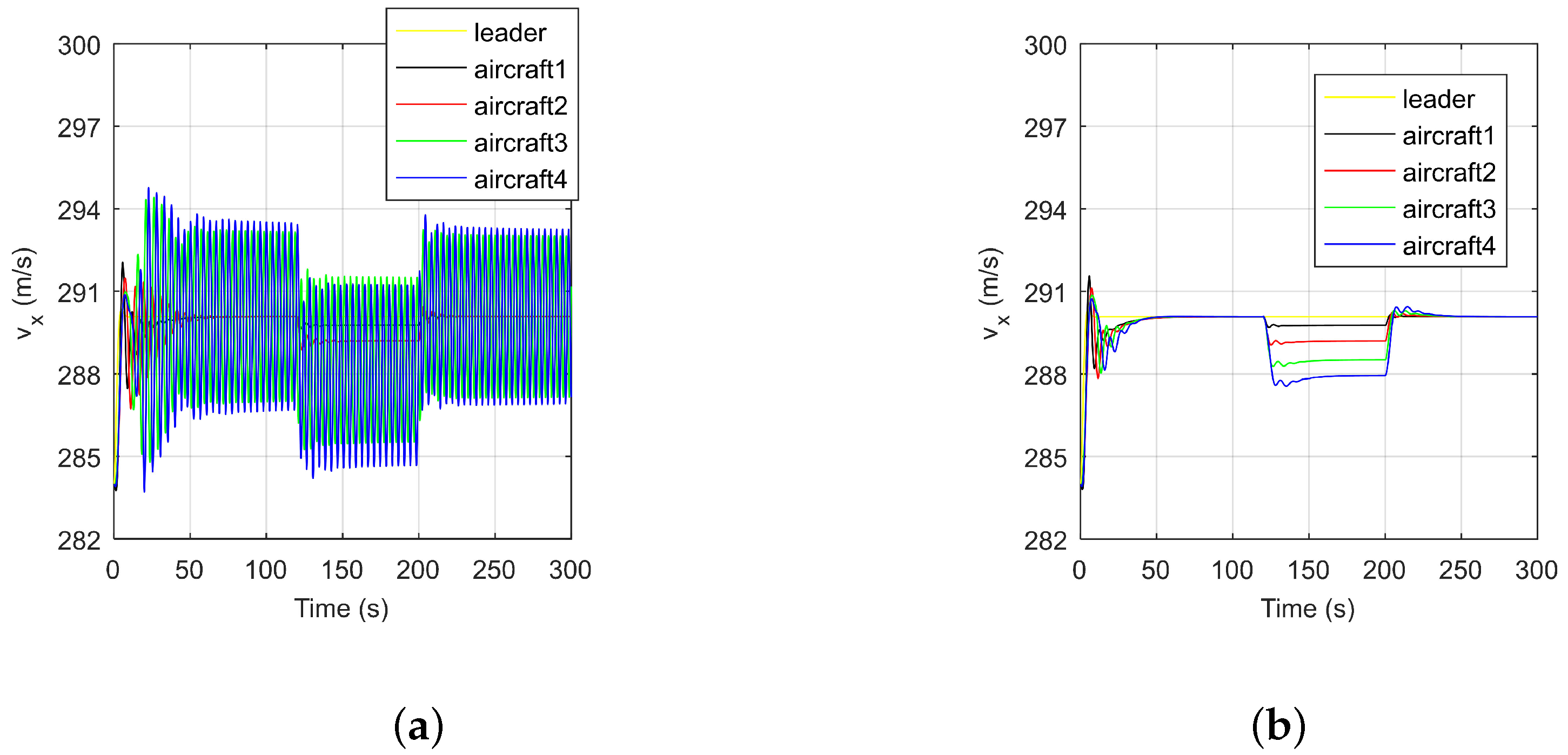
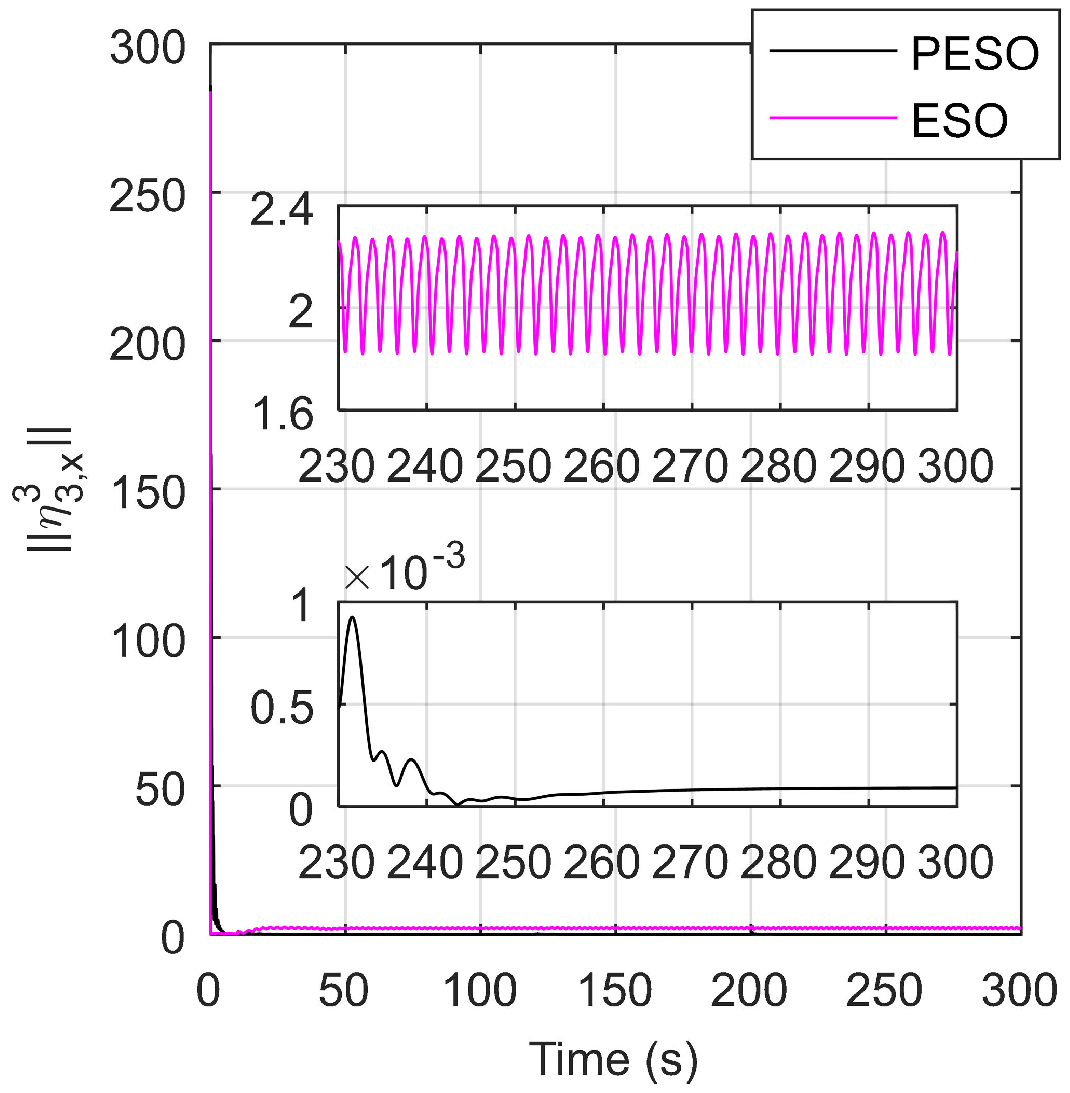
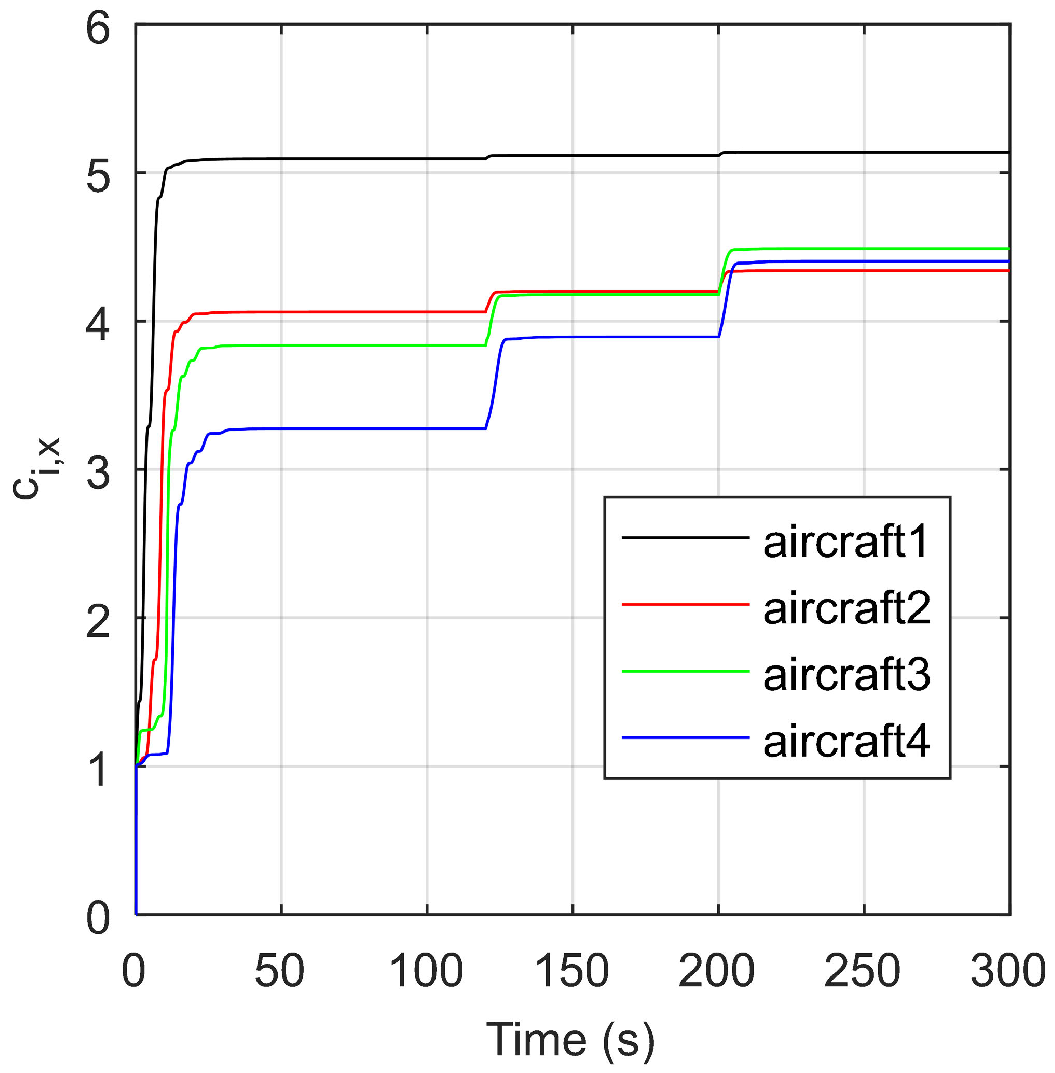
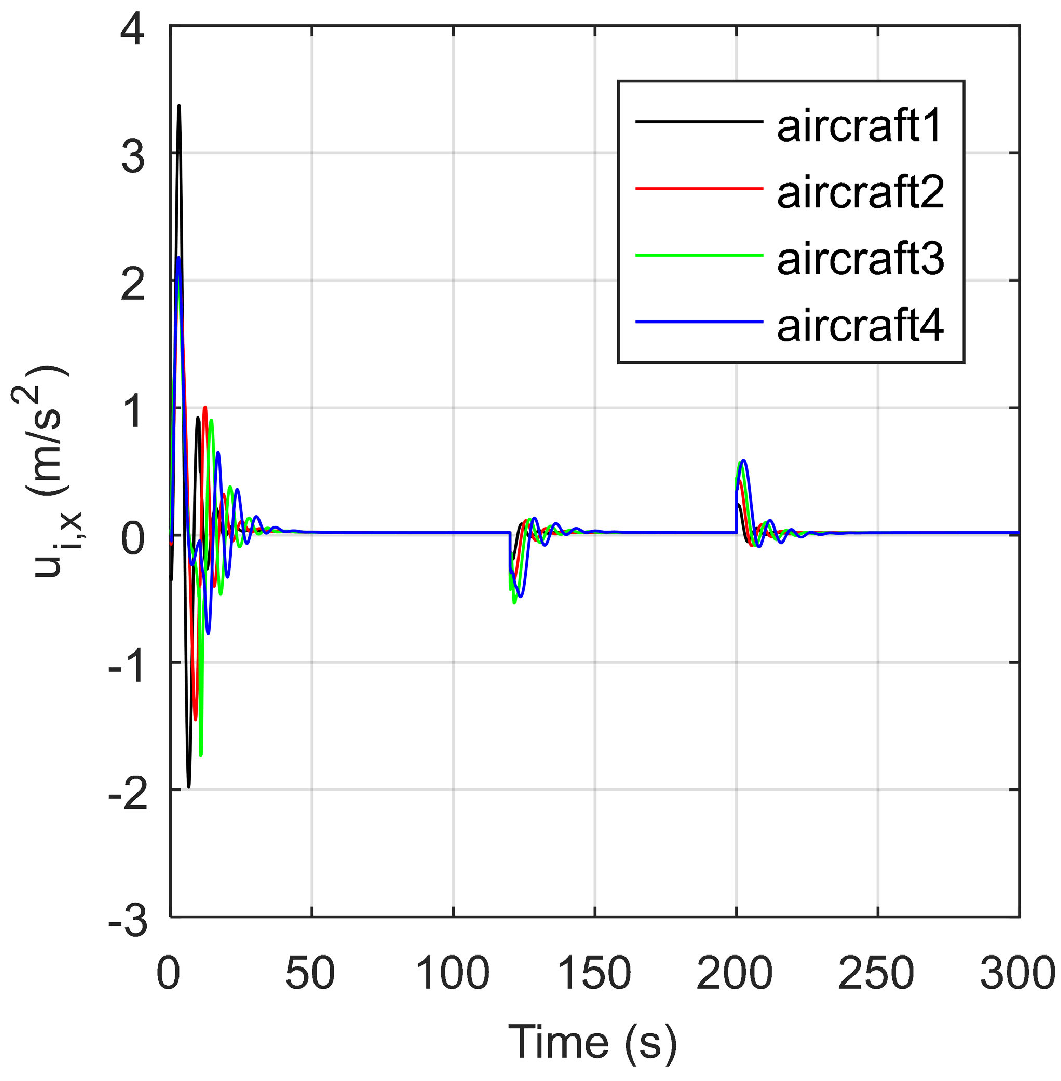
5. Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Lemma 6
References
- Challa, V.R.; Ratnoo, A. On maneuverability of fixed-Wing unmanned aerial vehicle formations. J. Guid. Control Dyn. 2021, 44, 142–149. [Google Scholar] [CrossRef]
- Monje, C.A.; Garrido, S.; Moreno, L.; Balaguer, C. UAVs formation approach using fast marching square methods. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 36–46. [Google Scholar] [CrossRef]
- Yasin, J.N.; Mohamed, S.A.S.; Haghbayan, M.; Heikkonen, J.; Tenhunen, H.; Plosila, J. Unmanned Aerial Vehicles (UAVs): Collision Avoidance Systems and Approaches. IEEE Access 2020, 8, 105139–105155. [Google Scholar] [CrossRef]
- Huang, S.; Teo, R.S.H.; Tan, K.K. Collision avoidance of multi unmanned aerial vehicles: A review. Annu. Rev. Control 2019, 48, 147–164. [Google Scholar] [CrossRef]
- Bolandi, H.; Pari, H.M.; Izadi, M.R. Multiple spacecraft formation and station-keeping control in presence of static attitude constraint via decentralized virtual structure approach. J. Aerosp. Eng. 2022, 35, 04021104. [Google Scholar] [CrossRef]
- Wu, Y.; Cao, X.; Zheng, P.; Zeng, Z. Variable structure-based decentralized relative attitude-coordinated control for satellite formation. IEEE Aerosp. Electron. Syst. Mag. 2012, 27, 18–25. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Monteiro, S.; Bicho, E. A dynamical systems approach to behavior-based formation control. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation, Washington DC, USA, 11–15 May 2002; Volume 14, pp. 2606–2611. [Google Scholar]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control. 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Ren, W. Consensus strategies for cooperative control of vehicle formations. IET Contr. Theory Appl. 2007, 1, 505–512. [Google Scholar] [CrossRef]
- Dong, X.; Zhou, Y.; Ren, Z.; Zhong, Y. Time-varying formation control for unmanned aerial vehicles with switching interaction topologies. Control Eng. Pract. 2016, 46, 26–36. [Google Scholar] [CrossRef]
- Dong, X.; Zhou, Y.; Ren, Z.; Zhong, Y. Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies With application to quadrotor formation flying. IEEE Trans. Ind. Electron. 2017, 64, 5014–5024. [Google Scholar] [CrossRef]
- Dong, X.; Hu, G. Time-varying formation tracking for linear multiagent systems with multiple leaders. IEEE Trans. Autom. Control 2017, 62, 3658–3664. [Google Scholar] [CrossRef]
- Wu, Y.; Gou, J.; Hu, X.; Huang, Y. A new consensus theory-based method for formation control and obstacle avoidance of UAVs. Aerosp. Sci. Technol. 2020, 107, 106332. [Google Scholar] [CrossRef]
- Li, Z.; Ren, W.; Liu, X.; Fu, M. Consensus of multi-agent systems with general linear and lipschitz nonlinear dynamics using distributed adaptive protocols. IEEE Trans. Autom. Control 2013, 58, 1786–1791. [Google Scholar] [CrossRef]
- Li, Z.; Wen, G.; Duan, Z.; Ren, W. Designing fully distributed consensus protocols for linear multi-agent systems with directed graphs. IEEE Trans. Autom. Control 2015, 60, 1152–1157. [Google Scholar] [CrossRef]
- Chen, C.; Xie, K.; Lewis, F.L.; Xie, S.; Davoudi, A. Fully distributed resilience for adaptive exponential synchronization of heterogeneous multiagent systems against actuator faults. IEEE Trans. Autom. Control 2019, 64, 3347–3354. [Google Scholar] [CrossRef]
- Jiang, W.; Wen, G.; Peng, Z.; Huang, T.; Rahmani, A. Fully distributed formation-containment control of heterogeneous linear multiagent systems. IEEE Trans. Autom. Control 2019, 64, 3889–3896. [Google Scholar] [CrossRef]
- Zhang, W.; Dong, C.; Ran, M.; Liu, Y. Fully distributed time-varying formation tracking control for multiple quadrotor vehicles via finite-time convergent extended state observer. Chin. J. Aeronaut. 2020, 33, 2907–2920. [Google Scholar] [CrossRef]
- Cheng, B.; Wu, Z.; Li, Z. Distributed edge-based event-triggered formation control. IEEE T. Cybern. 2021, 51, 1241–1252. [Google Scholar] [CrossRef]
- Nandiganahalli, J.S.; Kwon, C.; Huang, I. Delay-tolerant Adaptive Robust Control for Unmanned Aerial System. In Proceedings of the 2018 AIAA Information Systems-AIAA Infotech @ Aerospace, Kissimmee, FL, USA, 8–12 January 2018; p. 78. [Google Scholar]
- Muskardin, T.; Coelho, A.; Della-Noce, E.R.; Ollero, A.; Kondak, K. Energy-based cooperative control for landing fixed-wing uavs on mobile platforms under communication delays. IEEE Robot. Autom. Lett. 2020, 5, 5081–5088. [Google Scholar] [CrossRef]
- Muslimov, T.Z.; Munasypov, R.A. Consensus-based cooperative control of parallel fixed-wing UAV formations via adaptive backstepping. Aerosp. Sci. Technol. 2021, 109, 106416. [Google Scholar] [CrossRef]
- Zhen, Z.; Tao, G.; Xu, Y.; Song, G. Multivariable adaptive control based consensus flight control system for UAVs formation. Aerosp. Sci. Technol. 2019, 93, 105336. [Google Scholar] [CrossRef]
- Wang, X.; Saberi, A.; Stoorvogel, A.A.; Grip, F.H.; Yang, T. Consensus in the network with uniform constant communication delay. In Proceedings of the IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3252–3257. [Google Scholar]
- Zong, X.; Li, T.; Zhang, J.F. Consensus conditions of continuous-time multi-agent systems with time-delays and measurement noises. Automatica 2019, 99, 412–419. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, R.; Chen, G. Consensus control of second-order time-delayed multiagent systems in noisy environments using absolute velocity and relative position measurements. IEEE T. Cybern. 2021, 51, 5364–5374. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Ding, Z.; Cao, Z. Distributed output feedback consensus control of networked homogeneous systems with large unknown actuator and sensor delays. Automatica 2020, 122, 109249. [Google Scholar] [CrossRef]
- Artstein, Z. Linear systems with delayed controls: A reduction. IEEE Trans. Autom. Control 1982, 27, 869–879. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, C.; Meng, Y. Fully distributed time-varying formation tracking control of linear multi-agent systems with input delay and disturbances. Syst. Control Lett. 2020, 146, 104814. [Google Scholar] [CrossRef]
- Zhou, B.; Lin, Z. Consensus of high-order multi-agent systems with large input and communication delays. Automatica 2014, 50, 452–464. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Z.; Wang, C.; Ding, Z. Cascade structure predictive observer design for consensus control with applications to UAVs formation flying. Automatica 2020, 121, 109200. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Wang, C.; Zuo, Z.; Qi, Z.; Ding, Z. Predictor-based extended-state-observer design for consensus of mass with delays and disturbances. IEEE Trans. Cybern. 2019, 49, 1259–1269. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Peng, Z.; Rahmani, A.; Hu, W.; Wen, G. Distributed consensus of linear MASs with an unknown leader via a predictive extended state observer considering input delay and disturbances. Neurocomputing 2018, 315, 465–475. [Google Scholar] [CrossRef]
- Liu, L.; Cui, Y.; Liu, Y.; Tong, S. Observer-based adaptive neural output feedback constraint controller design for switched systems under average dwell time. IEEE Trans. Circuits Syst. I-Regul. Pap. 2021, 68, 3901–3912. [Google Scholar] [CrossRef]
- Kong, L.; He, W.; Liu, Z.; Yu, X.; Silvestre, C. Adaptive tracking control with global performance for output-constrained MIMO nonlinear systems. IEEE Trans. Autom. Control 2023, 68, 3760–3767. [Google Scholar] [CrossRef]
- Lin, Z. Low Gain Feedback, 1st ed.; Springer: London, UK, 1999; pp. 43–64. [Google Scholar]
- Su, H.; Chen, M.Z.; Lam, J.; Lin, Z. Semi-global leader-following consensus of linear multi-agent systems with input saturation via low gain feedback. IEEE Trans. Circuits Syst. I-Regul. Pap. 2013, 60, 1881–1889. [Google Scholar] [CrossRef]
- Chu, H.; Yuan, J.; Zhang, W. Observer-based adaptive consensus tracking for linear multi-agent systems with input saturation. IET Contr. Theory Appl. 2015, 9, 2124–2131. [Google Scholar] [CrossRef]
- Yang, T.; Stoorvogel, A.A.; Grip, H.F.; Saberi, A. Semi-global regulation of output synchronization for heterogeneous network of non-introspective, invertible agents subject to actuator saturation. Int. J. Robust Nonlinear Control 2014, 24, 548–566. [Google Scholar] [CrossRef]
- Su, H.; Ye, Y.; Qiu, Y.; Gao, Y.; Chen, M.Z. Semi-global output consensus for discrete-time switching networked systems subject to input saturation and external disturbances. IEEE Trans. Cybern. 2019, 49, 3934–3945. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Zhang, B. Semi-global robust tracking consensus for multi-agent uncertain systems with input saturation via metamorphic low-gain feedback. Automatica 2019, 103, 363–373. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Wang, J.; Zhang, B.; Shi, P. Semiglobal tracking cooperative control for multiagent systems with input saturation: A multiple saturation levels framework. IEEE Trans. Autom. Control 2021, 66, 1215–1222. [Google Scholar] [CrossRef]
- Ran, M.; Wang, Q.; Dong, C.; Xie, L. Active disturbance rejection control for uncertain time-delay nonlinear systems. Automatica 2020, 112, 108692. [Google Scholar] [CrossRef]
- Yu, J.; Dong, X.; Li, Q.; Ren, Z. Cooperative integrated practical time-varying formation tracking and control for multiple missiles system. Aerosp. Sci. Technol. 2019, 93, 105300. [Google Scholar] [CrossRef]
- Obuz, S.; Klotz, J.R.; Kamalapurkar, R.; Dixon, W. Unknown time-varying input delay compensation for uncertain nonlinear systems. Automatica 2017, 76, 222–229. [Google Scholar] [CrossRef]
- Ran, M.; Wang, Q.; Dong, C. Active disturbance rejection control for uncertain nonaffine-in-control nonlinear systems. IEEE Trans. Autom. Control 2017, 62, 5830–5836. [Google Scholar] [CrossRef]
- Chakraborty, A.; Seiler, P.; Balas, G. Applications of linear and nonlinear robustness analysis techniques to the F/A-18 flight control laws. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 5675. [Google Scholar]
- Acquatella, P.; van Kampen, E.J.; Chu, Q.P. Incremental backstepping for robust nonlinear flight control. In Proceedings of the 2nd CEAS Specialist Conference on Guidance, Navigation and Control, Delft, The Netherlands, 12–14 April 2013; pp. 1444–1463. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Liu, X.; Tan, W.; Deng, Y.; Jiao, J.; Zhao, M. Predictive State Observer-Based Aircraft Distributed Formation Tracking Considering Input Delay and Saturations. Drones 2024, 8, 23. https://doi.org/10.3390/drones8010023
Sun L, Liu X, Tan W, Deng Y, Jiao J, Zhao M. Predictive State Observer-Based Aircraft Distributed Formation Tracking Considering Input Delay and Saturations. Drones. 2024; 8(1):23. https://doi.org/10.3390/drones8010023
Chicago/Turabian StyleSun, Liguo, Xiaoyu Liu, Wenqian Tan, Yi Deng, Junkai Jiao, and Mengjie Zhao. 2024. "Predictive State Observer-Based Aircraft Distributed Formation Tracking Considering Input Delay and Saturations" Drones 8, no. 1: 23. https://doi.org/10.3390/drones8010023
APA StyleSun, L., Liu, X., Tan, W., Deng, Y., Jiao, J., & Zhao, M. (2024). Predictive State Observer-Based Aircraft Distributed Formation Tracking Considering Input Delay and Saturations. Drones, 8(1), 23. https://doi.org/10.3390/drones8010023





