Robust Multiple Unmanned Aerial Vehicle Network Design in a Dense Obstacle Environment
Abstract
1. Introduction
- Most methods focus on improving the robustness of the network in obstacle environments. The impact of link quantity is not considered. We propose a method that can reduce the number of links and ensure the robustness of the network.
- The traditional artificial potential field cannot be adapted to dense obstacle environments. To solve the problem, we propose an improved artificial potential field to make UAVs more compact.
- To realize distributed deployment, we design a reinforcement learning method base on centralized training and distributed execution. Well-trained reinforcement learning can be deployed to UAVs in a distributed manner.
- In multiple failure modes, we deeply study the robustness of networks under different proportions of node failures and analyze the impact of attack modes on networks.
2. Related Works
3. Problem Statement
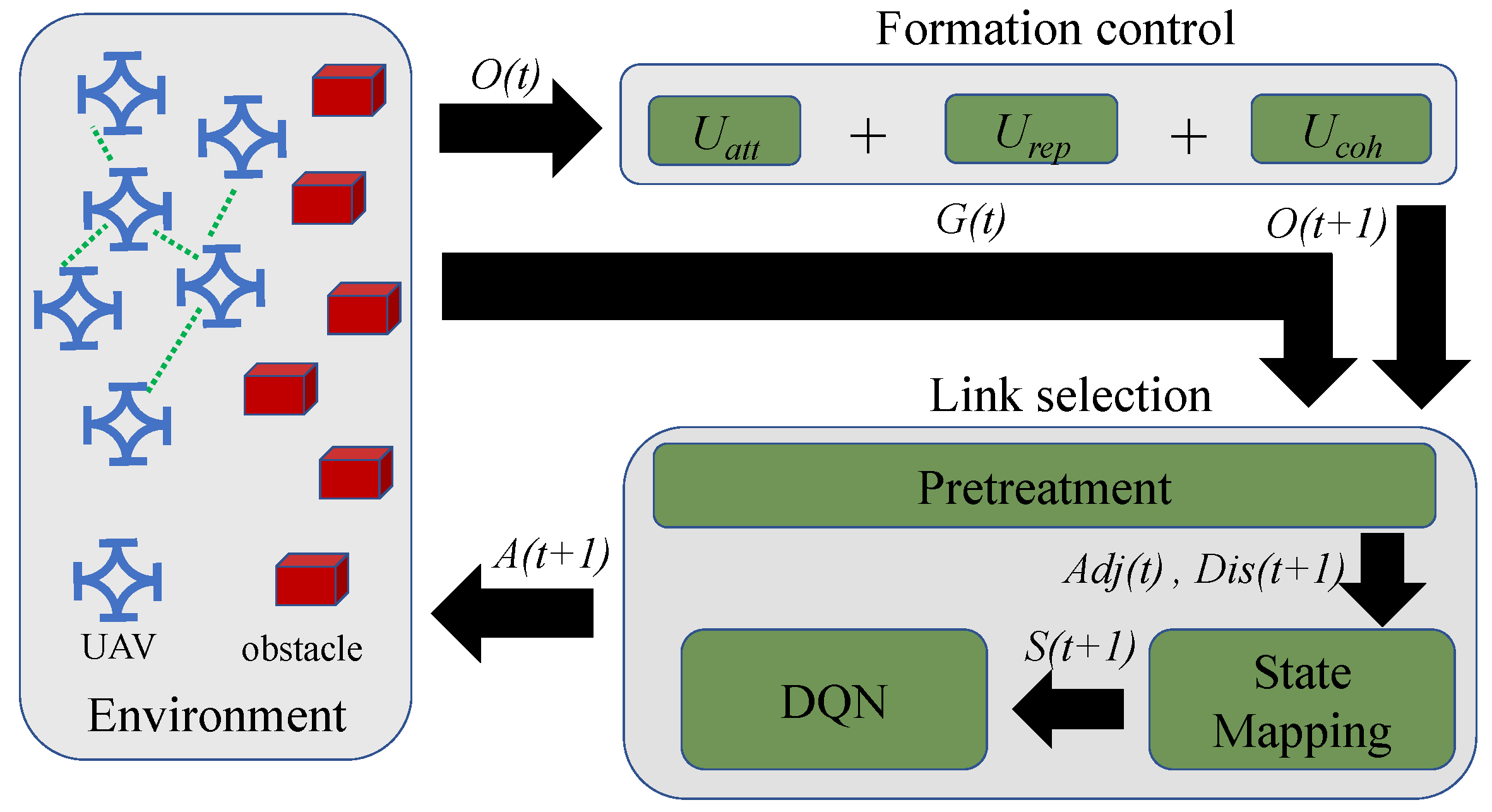
4. Proposed Method
4.1. Method Overview
4.2. Formation Control
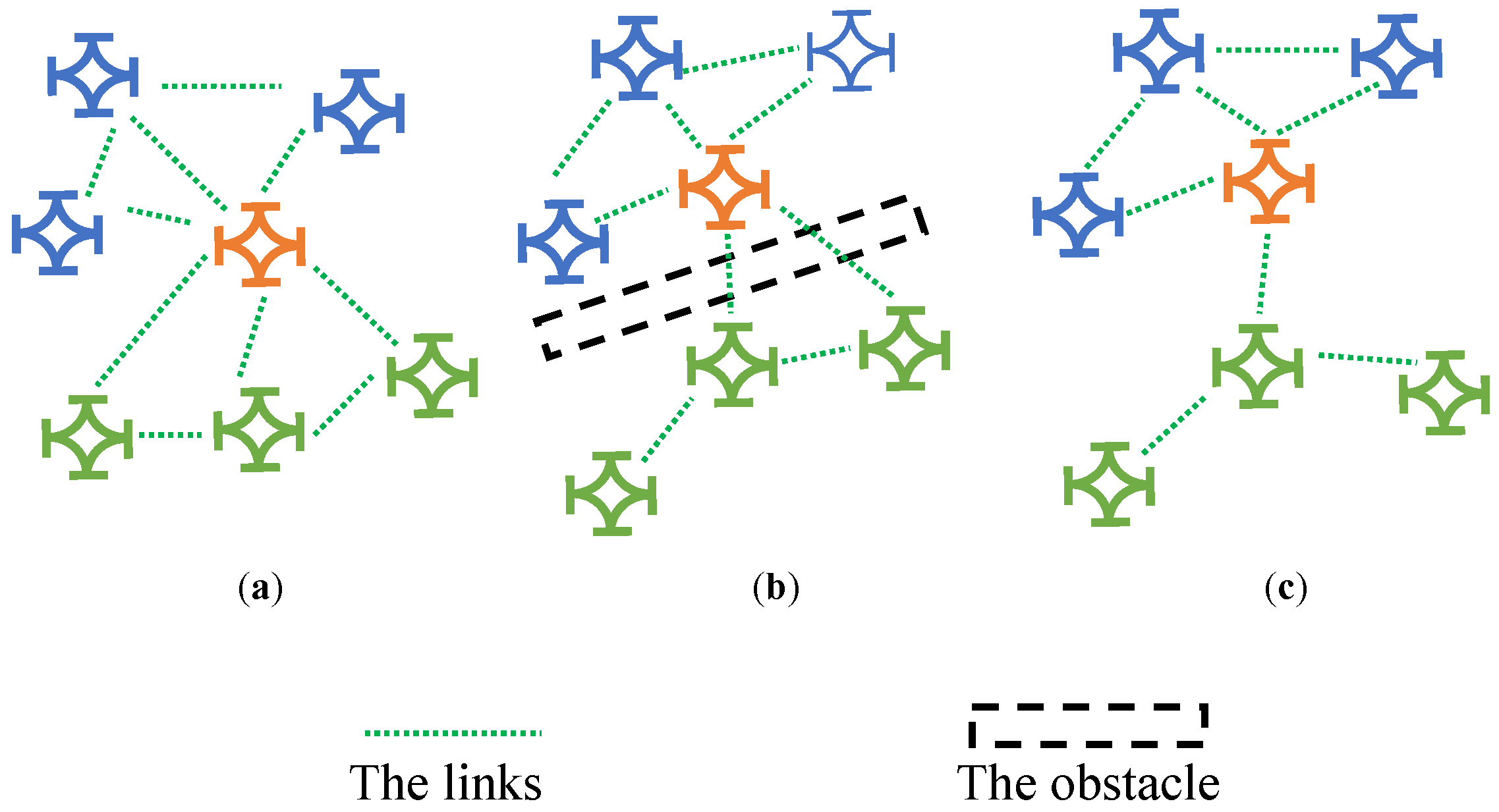
4.3. Link Selection
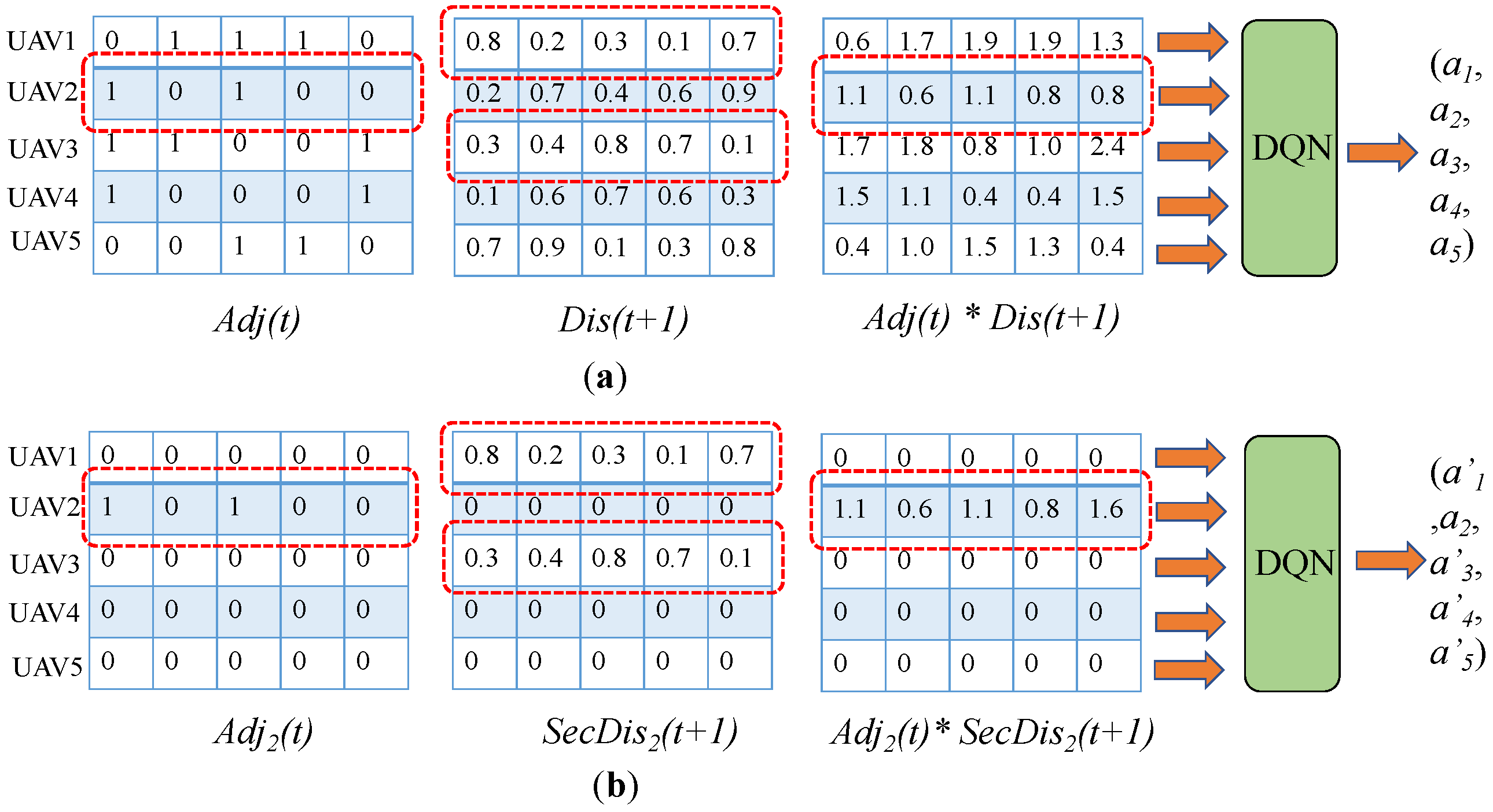
4.3.1. State Design
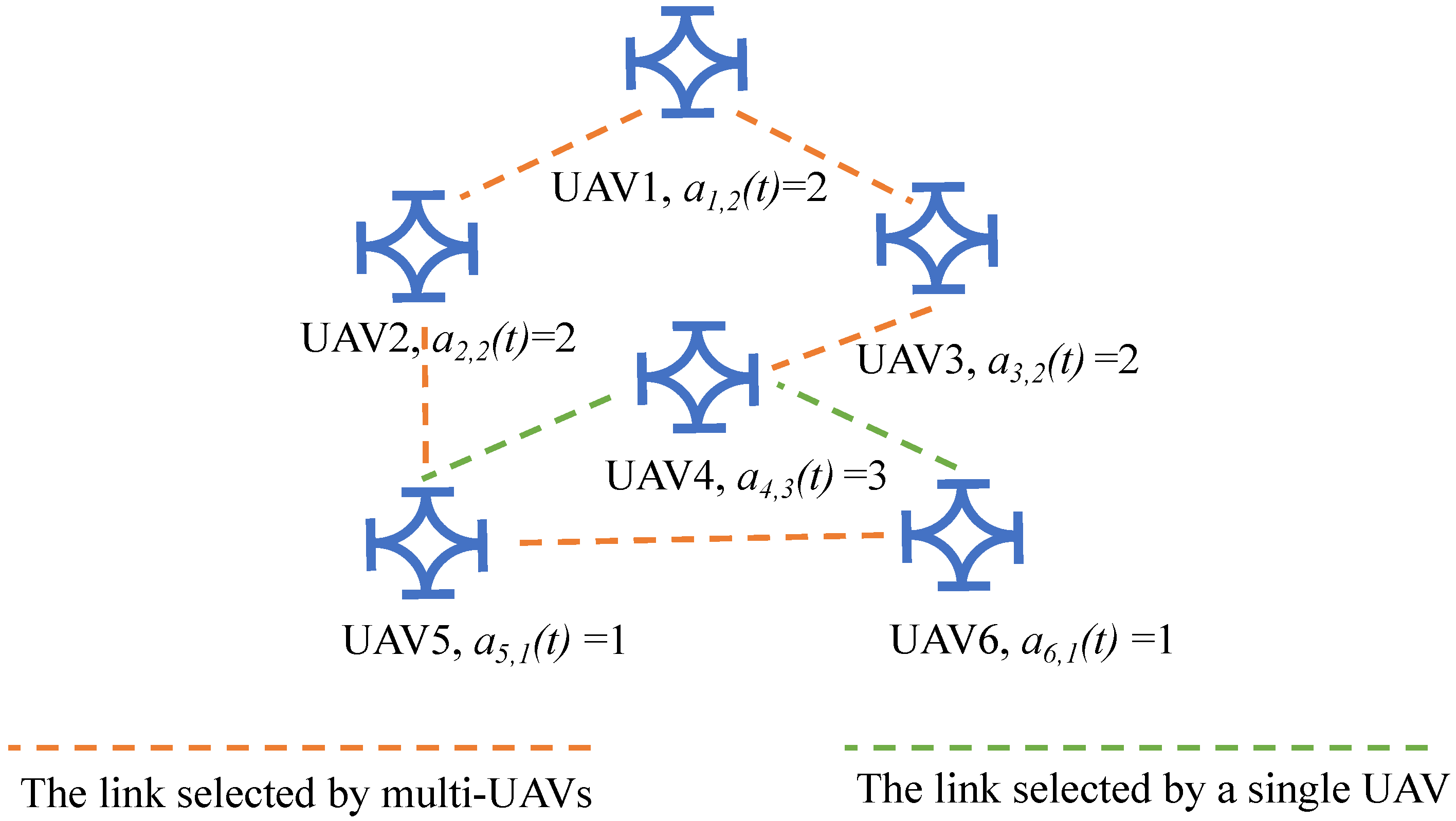
4.3.2. Action Design
4.3.3. Reward Design
5. Numerical Simulation
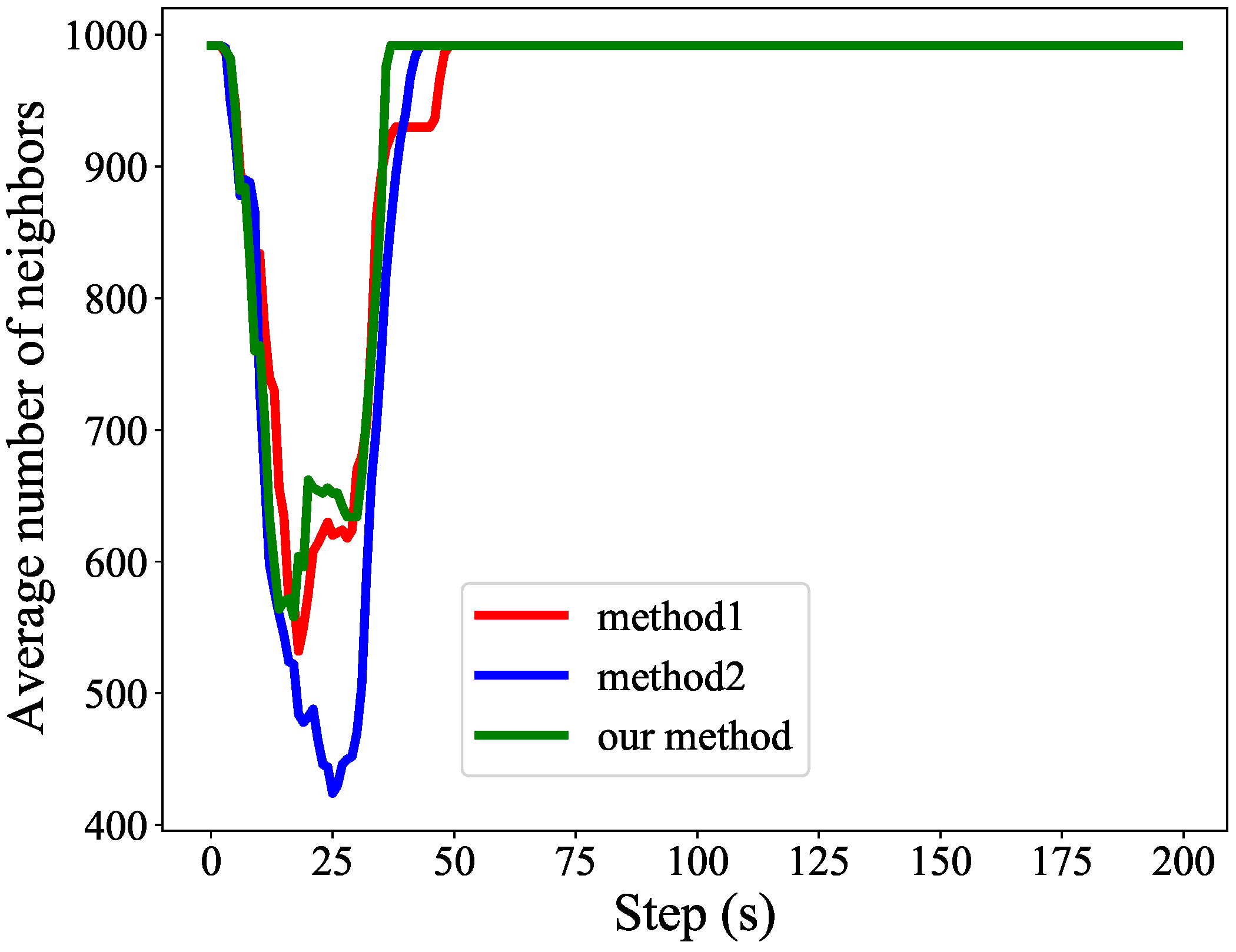
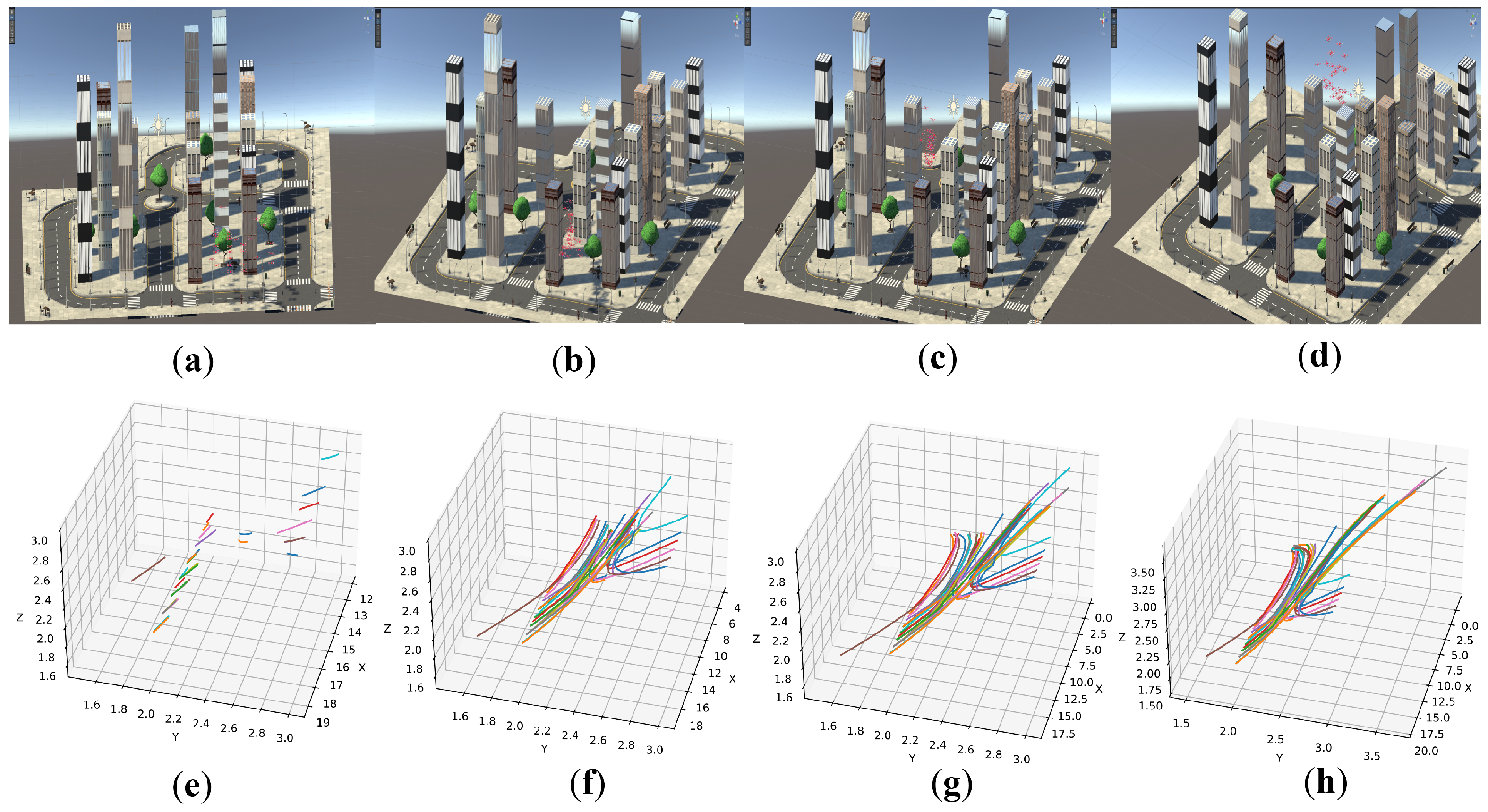
5.1. Verification of Flight Strategy
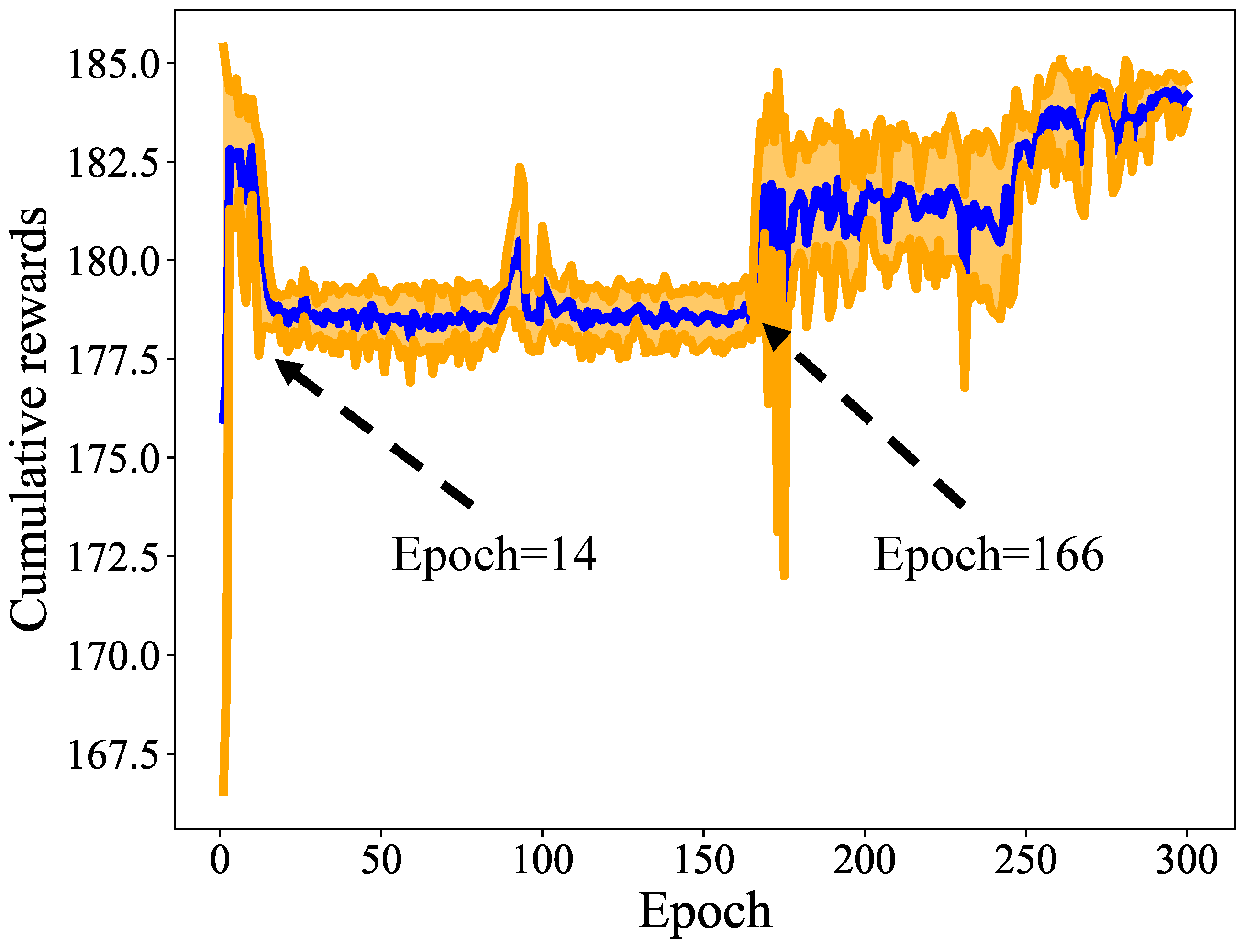
5.2. Verification of Convergence
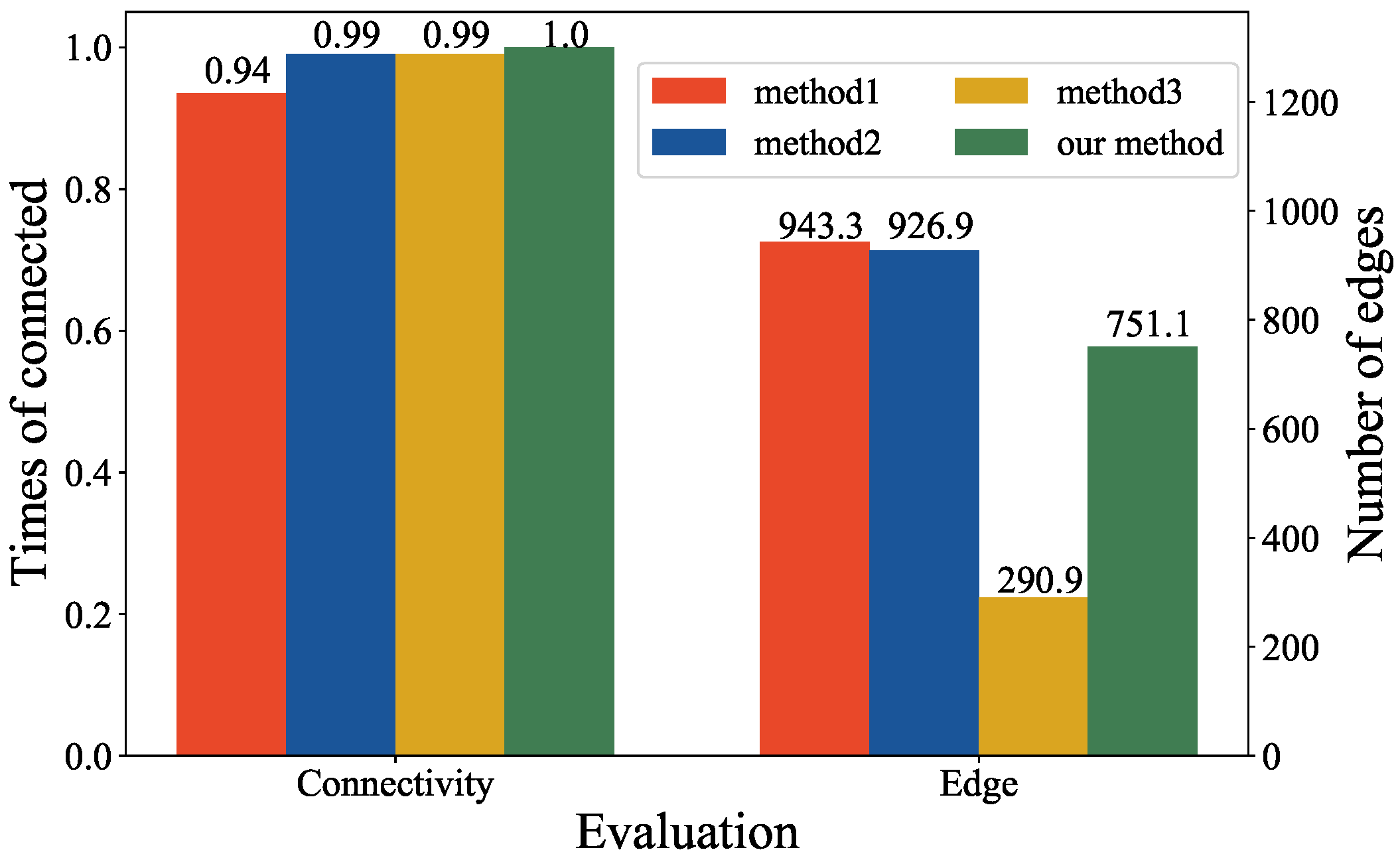
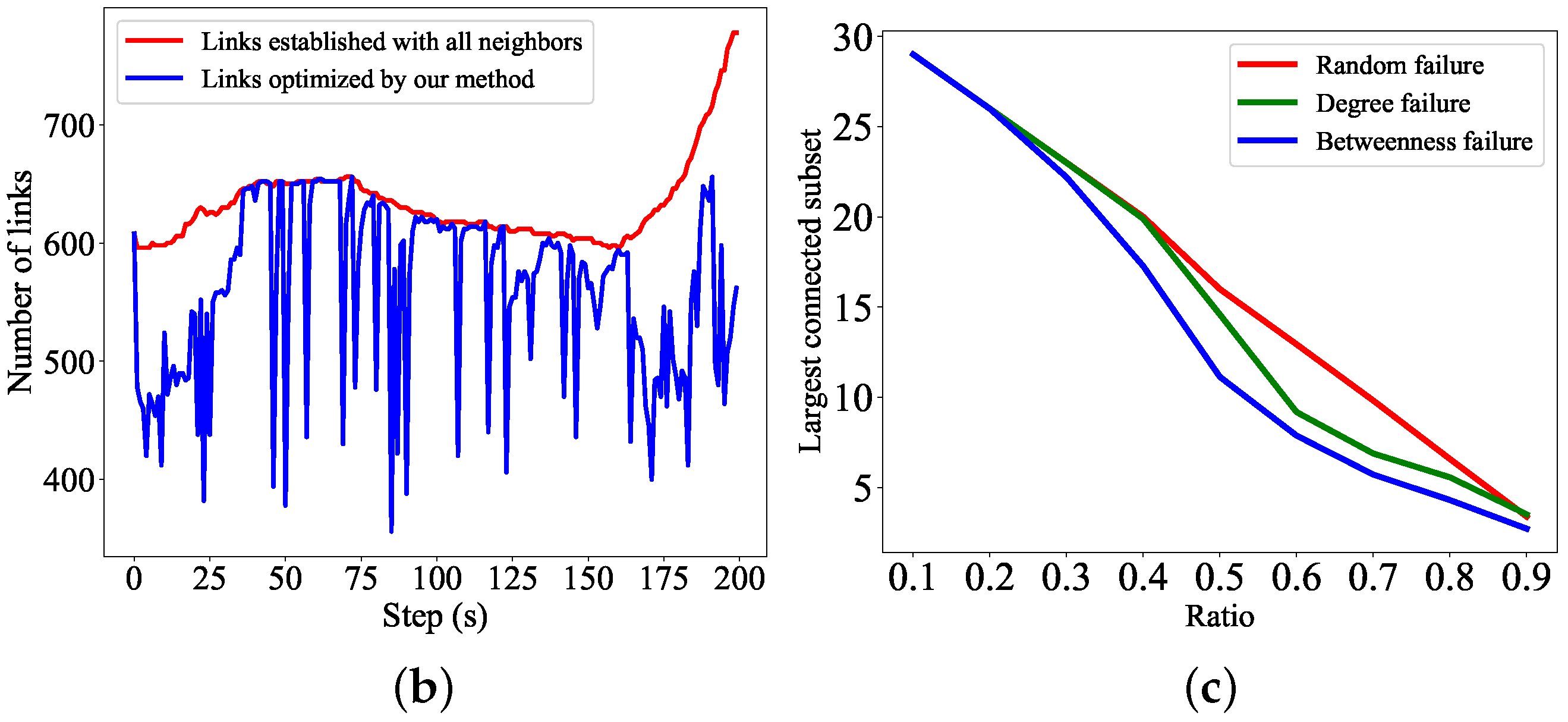
5.3. Verification of Connectivity
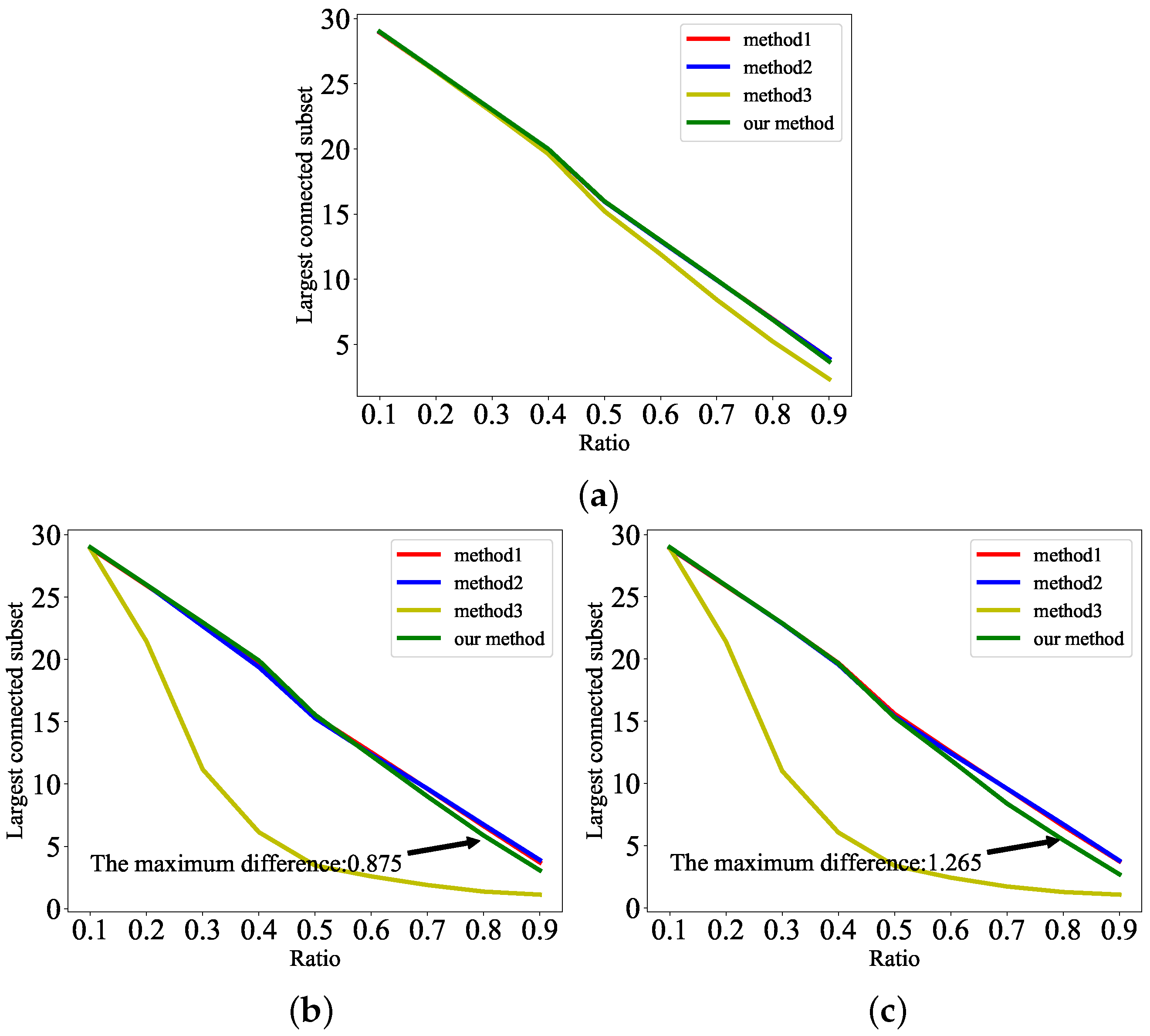
5.4. Verification of Robustness
5.5. Simulation in Unity 3D
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Zhao, H.; Zhang, J.; Ma, D.; Li, J.; Wei, J. Survey on unmanned aerial vehicle networks: A cyber physical system perspective. IEEE Commun. Surv. Tutor. 2019, 22, 1027–1070. [Google Scholar] [CrossRef]
- Lakew, D.S.; Sa’ad, U.; Dao, N.N.; Na, W.; Cho, S. Routing in flying ad hoc networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2020, 22, 1071–1120. [Google Scholar] [CrossRef]
- Khalil, H.; Rahman, S.U.; Ullah, I.; Khan, I.; Alghadhban, A.J.; Al-Adhaileh, M.H.; Ali, G.; ElAffendi, M. A UAV-Swarm-Communication Model Using a Machine-Learning Approach for Search-and-Rescue Applications. Drones 2022, 6, 372. [Google Scholar] [CrossRef]
- Nawaz, H.; Ali, H.M.; Laghari, A.A. UAV communication networks issues: A review. Arch. Comput. Methods Eng. 2021, 28, 1349–1369. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, M.; Wang, S.; Liu, P. A comparative study of network robustness measures. Front. Comput. Sci. 2017, 11, 568–584. [Google Scholar] [CrossRef]
- Lindqvist, B.; Haluska, J.; Kanellakis, C.; Nikolakopoulos, G. An Adaptive 3D Artificial Potential Field for Fail-safe UAV Navigation. In Proceedings of the 2022 30th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 28 June–1 July 2022; pp. 362–367. [Google Scholar]
- Pan, Z.; Zhang, C.; Xia, Y.; Xiong, H.; Shao, X. An Improved Artificial Potential Field Method for Path Planning and Formation Control of the Multi-UAV Systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1129–1133. [Google Scholar] [CrossRef]
- Maza, I.; Ollero, A.; Casado, E.; Scarlatti, D. Classification of multi-UAV architectures. In Handbook of Unmanned Aerial Vehicles; Springer: Dordrecht, The Netherlands, 2015; pp. 953–975. [Google Scholar]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Su, H.; Wang, X.; Lin, Z. Flocking of multi-agents with a virtual leader. IEEE Trans. Autom. Control 2009, 54, 293–307. [Google Scholar] [CrossRef]
- Consolini, L.; Morbidi, F.; Prattichizzo, D.; Tosques, M. Leader–follower formation control of nonholonomic mobile robots with input constraints. Automatica 2008, 44, 1343–1349. [Google Scholar] [CrossRef]
- Li, W.; Chen, Y.; Xiang, L. Cooperative Path Planning of UAV Formation Based on Improved Artificial Potential Field. In Proceedings of the 2022 IEEE 2nd International Conference on Electronic Technology, Communication and Information (ICETCI), Changchun, China, 27–29 May 2022; pp. 636–641. [Google Scholar]
- Xie, Y.; Wang, Y.; Wei, J.; Wang, J. Research on Radar Wave Avoidance for UAV Swarm Based on Improved Artificial Potential Field. In Proceedings of the 2022 10th International Conference on Intelligent Computing and Wireless Optical Communications (ICWOC), Chongqing, China, 10–12 June 2022; pp. 1–5. [Google Scholar]
- Koren, Y.; Borenstein, J. Potential field methods and their inherent limitations for mobile robot navigation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Sacramento, CA, USA, 7–12 April 1991; Volume 2, pp. 1398–1404. [Google Scholar]
- Damas, B.D.; Lima, P.U.; Custodio, L.M. A modified potential fields method for robot navigation applied to dribbling in robotic soccer. In Proceedings of the RoboCup 2002: Robot Soccer World Cup VI 6; Springer: Berlin/Heidelberg, Germany, 2003; pp. 65–77. [Google Scholar]
- Howard, A.; Matarić, M.J.; Sukhatme, G.S. Mobile sensor network deployment using potential fields: A distributed, scalable solution to the area coverage problem. In Distributed Autonomous Robotic Systems 5; Springer: Berlin/Heidelberg, Germany, 2002; pp. 299–308. [Google Scholar]
- Li, F.; Wang, Y.; Tan, Y.; Ge, G. Mobile robots path planning based on evolutionary artificial potential fields approach. In Proceedings of the Conference of the 2nd International Conference on Computer Science and Electronics Engineering (ICCSEE 2013), Hangzhou, China, 22–23 March 2013; Atlantis Press: Amsterdam, The Netherlands, 2013; pp. 1314–1317. [Google Scholar]
- Pateria, S.; Subagdja, B.; Tan, A.H.; Quek, C. Hierarchical reinforcement learning: A comprehensive survey. ACM Comput. Surv. 2021, 54, 109. [Google Scholar] [CrossRef]
- He, Y.; Wang, Y.; Lin, Q.; Li, J. Meta-Hierarchical Reinforcement Learning (MHRL)-based Dynamic Resource Allocation for Dynamic Vehicular Networks. IEEE Trans. Veh. Technol. 2022, 71, 3495–3506. [Google Scholar] [CrossRef]
- Wang, X.; Li, W.; Song, W.; Dong, W. Connectivity Controlling of Multi-robot by Combining Artificial Potential Field with a Virtual Leader. In Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics, Manchester, UK, 13–16 October 2013; pp. 374–377. [Google Scholar]
- Yi, S.; Luo, W.; Sycara, K. Distributed Topology Correction for Flexible Connectivity Maintenance in Multi-Robot Systems. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8874–8880. [Google Scholar]
- Capelli, B.; Fouad, H.; Beltrame, G.; Sabattini, L. Decentralized connectivity maintenance with time delays using control barrier functions. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 1586–1592. [Google Scholar]
- Siligardi, L.; Panerati, J.; Kaufmann, M.; Minelli, M.; Ghedini, C.; Beltrame, G.; Sabattini, L. Robust area coverage with connectivity maintenance. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 2202–2208. [Google Scholar]
- Dutta, A.; Ghosh, A.; Kreidl, O.P. Multi-robot informative path planning with continuous connectivity constraints. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3245–3251. [Google Scholar]
- Sun, C.; Hu, G.; Xie, L.; Egerstedt, M. Robust finite-time connectivity preserving consensus tracking and formation control for multi-agent systems. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1990–1995. [Google Scholar]
- Gu, N.; Wang, D.; Peng, Z.; Liu, L. Observer-based finite-time control for distributed path maneuvering of underactuated unmanned surface vehicles with collision avoidance and connectivity preservation. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 5105–5115. [Google Scholar] [CrossRef]
- Chen, B.; Ma, H.; Kang, H.; Liang, X. Multi-agent Distributed Formation Control Based on Improved Artificial Potential Field and Neural Network for Connectivity Preservation. In Proceedings of the 2021 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 15–17 October 2021; pp. 455–460. [Google Scholar]
- Peng, Z.; Wang, D.; Li, T.; Han, M. Output-feedback cooperative formation maneuvering of autonomous surface vehicles with connectivity preservation and collision avoidance. IEEE Trans. Cybern. 2019, 50, 2527–2535. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Yi, S.; Sycara, K. Behavior mixing with minimum global and subgroup connectivity maintenance for large-scale multi-robot systems. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 9845–9851. [Google Scholar]
- Capelli, B.; Sabattini, L. Connectivity maintenance: Global and optimized approach through control barrier functions. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 5590–5596. [Google Scholar]
- Panerati, J.; Gianoli, L.; Pinciroli, C.; Shabah, A.; Nicolescu, G.; Beltrame, G. From swarms to stars: Task coverage in robot swarms with connectivity constraints. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 7674–7681. [Google Scholar]
- Wu, S.; Pu, Z.; Liu, Z.; Qiu, T.; Yi, J.; Zhang, T. Multi-target coverage with connectivity maintenance using knowledge-incorporated policy framework. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8772–8778. [Google Scholar]
- Lin, C.; Luo, W.; Sycara, K. Online Connectivity-aware Dynamic Deployment for Heterogeneous Multi-Robot Systems. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8941–8947. [Google Scholar]
- Feng, J.; Dixon, W.E.; Shea, J.M. Positioning helper nodes to improve robustness of wireless mesh networks to jamming attacks. In Proceedings of the 2017 IEEE Global Communications Conference (GLOBECOM 2017), Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Hazra, K.; Shah, V.K.; Roy, S.; Deep, S.; Saha, S.; Nandi, S. Exploring Biological Robustness for Reliable Multi-UAV Networks. IEEE Trans. Netw. Serv. Manag. 2021, 18, 2776–2788. [Google Scholar] [CrossRef]
- Selvam, P.K.; Raja, G.; Rajagopal, V.; Dev, K.; Knorr, S. Collision-free Path Planning for UAVs using Efficient Artificial Potential Field Algorithm. In Proceedings of the 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Virtual, 25–28 April 2021; pp. 1–5. [Google Scholar]
- Wang, Y.; Sun, X. Formation control of multi-UAV with collision avoidance using artificial potential field. In Proceedings of the 2019 11th International Conference on Intelligent Human–Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 24–25 August 2019; Volume 1, pp. 296–300. [Google Scholar]
- Liang, Q.; Zhou, H.; Xiong, W.; Zhou, L. Improved artificial potential field method for UAV path planning. In Proceedings of the 2022 14th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Changsha, China, 15–16 January 2022; pp. 657–660. [Google Scholar]
- Yan, S.; Pan, F.; Xu, J.; Song, L. Research on UAV Path Planning Based on Improved Artificial Potential Field Method. In Proceedings of the 2022 2nd International Conference on Computer, Control and Robotics (ICCCR), Shanghai, China, 18–20 March 2022; pp. 1–5. [Google Scholar]
- Xie, H.; Qu, Y.; Fan, G.; Zhu, X. Three-Dimensional Path Planning of UAV Based on Improved Artificial Potential Field. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 7862–7867. [Google Scholar]
- Fernando, M. Online flocking control of UAVs with mean-field approximation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8977–8983. [Google Scholar]
- Luong, N.C.; Hoang, D.T.; Gong, S.; Niyato, D.; Wang, P.; Liang, Y.C.; Kim, D.I. Applications of deep reinforcement learning in communications and networking: A survey. IEEE Commun. Surv. Tutor. 2019, 21, 3133–3174. [Google Scholar] [CrossRef]
- Malli, I.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Robust Distributed Estimation of the Algebraic Connectivity for Networked Multi-robot Systems. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 9155–9160. [Google Scholar]
- Bulut, E.; Szymanski, B.K. Constructing limited scale-free topologies over peer-to-peer networks. IEEE Trans. Parallel Distrib. Syst. 2013, 25, 919–928. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| Maximum velocity of UAVs | m/s |
| Safe distance of UAVs | m |
| Communication range of UAVs | m |
| Coefficient of attraction | |
| Coefficient of repulsion | |
| Coefficient of cohesion | , |
| Coefficient of l | |
| Batch size of DQN | |
| Learning rate of DQN | |
| -greedy of DQN | |
| Discount factor of DQN | |
| Replay buffer of DQN | |
| Target update frequency of DQN |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Yao, W.; Zuo, Y.; Wang, H.; Zhang, C. Robust Multiple Unmanned Aerial Vehicle Network Design in a Dense Obstacle Environment. Drones 2023, 7, 506. https://doi.org/10.3390/drones7080506
Zhang C, Yao W, Zuo Y, Wang H, Zhang C. Robust Multiple Unmanned Aerial Vehicle Network Design in a Dense Obstacle Environment. Drones. 2023; 7(8):506. https://doi.org/10.3390/drones7080506
Chicago/Turabian StyleZhang, Chen, Wen Yao, Yuan Zuo, Hongliang Wang, and Chuanfu Zhang. 2023. "Robust Multiple Unmanned Aerial Vehicle Network Design in a Dense Obstacle Environment" Drones 7, no. 8: 506. https://doi.org/10.3390/drones7080506
APA StyleZhang, C., Yao, W., Zuo, Y., Wang, H., & Zhang, C. (2023). Robust Multiple Unmanned Aerial Vehicle Network Design in a Dense Obstacle Environment. Drones, 7(8), 506. https://doi.org/10.3390/drones7080506






