Abstract
To improve the autonomous flight capability of endo-atmospheric flight vehicles, such as cruise missiles, drones, and other small, low-cost unmanned aerial vehicles (UAVs), a novel minimum-effort waypoint-following differential geometric guidance law (MEWFDGGL) is proposed in this paper. Using the classical differential geometry curve theory, the optimal guidance problem of endo-atmospheric flight vehicles is transformed into an optimal space curve design problem, where the guidance command is the curvature. On the one hand, the change in speed of the flight vehicle is decoupled from the guidance problem. In this way, the widely adopted constant speed hypothesis in the process of designing the guidance law is eliminated, and, hence, the performance of the proposed MEWFDGGL is not influenced by the varying speed of the flight vehicle. On the other hand, considering the onboard computational burden, a suboptimal form of the MEWFDGGL is proposed to solve the problem, where both the complexity and the computational burden of the guidance law dramatically increase as the number of waypoints increases. The theoretical analysis demonstrates that both the original MEWFDGGL and its suboptimal form can be applied to general waypoint-following tasks with an arbitrary number of waypoints. Finally, the superiority and effectiveness of the proposed MEWFDGGL are verified by a numerical simulation and flight experiments.
1. Introduction
A key technology of endo-atmospheric flight vehicles, such as cruise missiles, drones, and other small, low-cost unmanned aerial vehicles (UAVs), is the ability to autonomously reach a destination via an expected path [1]. In terms of general multitarget missions, there are two mainstream methods for endo-atmospheric flight vehicles to realize waypoint-following guidance, by visiting multiple target points at a time. The first is to decompose the waypoint-following task into two parts: path planning and path tracking [2,3,4,5,6]. The second is to individually separate each waypoint on the desired path and transform the path-tracking problem into countless point-to-point guidance problems, using closed-circuit guidance. Missile guidance laws, which have been well-developed over the last few decades, can also be adopted to solve waypoint-following problems. Recent developments in advanced missile guidance laws resulted in many elegant solutions to problems related to waypoint following, such as pure pursuit guidance (PPG) [7], proportional navigation guidance (PNG) [8,9,10,11], and their variations [12,13,14,15].
Considering certain performance indexes, the first approach typically discovers the energy- or time-optimal path using complex numerical trajectory optimization methods [16,17,18,19,20]. However, numerical simulations require large onboard computing power, so they may not be suitable for the general growth of small endo-atmospheric flight vehicles, such as cruise missiles, drones, and other small, low-cost unmanned aerial vehicles (UAVs). The guidance instructions produced using the second method can be simple and concise, thus eliminating concerns about the capability of an onboard computer. However, under the boundary conditions of multiple waypoints, even the use of the minimum-effort point-to-point guidance law [21,22,23,24] between every two adjacent waypoints cannot guarantee the optimal total energy consumption for the duration of a task.
For such problems, inspired by the above two methods, an optimal error dynamics (OED) method for the design of guidance laws for UAVs that need to visit multiple waypoints was proposed in [25]. As mentioned in [25], the challenge of designing guidance laws is defined, firstly, as a finite-time tracking problem in cybernetics. Later, a global minimum-effort waypoint-following guidance law (MEWFGL) that can be applied to situations of arbitrary waypoint numbers was analytically derived in [26]. For the first time, the MEWFGL allowed for the development of a path-planning and tracking set in one single step, and it effectively reduced the complexity of the initial task’s analysis and design. However, the MEWFGL still assumed a constant speed and did not consider the influence of a change in a UAV’s speed on the performance of the guidance. Although a large number of numerical simulations and flight experiments showed that, under the assumption of a constant speed, the designed guidance laws still work in most practical varying speed guidance scenarios, their performances are degraded to some degree, since the speed of a UAV changes during the guidance process. In practical applications, real-time speeds can be obtained and utilized in guidance and control systems, as almost all endo-atmospheric flight vehicles are equipped with Doppler radars or accelerometers. Therefore, if guidance laws can be directly designed without the assumption of a constant speed, their performances must, hence, be assumed to be better.
In essence, the flight trajectory of an endo-atmospheric flight vehicle can be taken as a space curve, which is more suitably depicted with a Frenet–Serret frame, curvature, and torsion, using the classical differential geometry curve theory [27]. In addition to designing and analyzing guidance laws in the time domain, differential geometry theory can be used to design and derive a variety of guidance laws in the arc-length domain. In [28], the performance of a PNG and the capture region of a missile with time-varying speed that was directed at a stationary target were preliminarily explored in the arc-length domain. In [28], by introducing the differential of the arc length, the influence of the time-varying missile’s speed on the performance of the guidance law was eliminated for the first time. In addition, in [29], the PNG’s performance in the arc-length domain was further analyzed in detail, which revealed the essence of the guidance law design in theory, and this also showed that the differential geometry curve theory is beneficial for reducing the influence of time-varying speed on the performance of guidance law.
On the one hand, the computational capacities of small, low-cost endo-atmospheric flight vehicles are not powerful enough for the computational burden of the complex numerical calculations required to determine an optimal path. On the other hand, it is difficult to design guidance laws for time-varying speed endo-atmospheric flight vehicles because the remaining flying time cannot be estimated accurately, especially when the time-varying speed of an endo-atmospheric flight vehicle is considered. Motivated by the aforementioned observations, in this paper, a novel minimum-effort waypoint-following differential geometric guidance law (MEWFDGGL) is proposed for endo-atmospheric flight vehicles by combining the MEWFGL concept and the differential geometry curve theory, which can be used to improve the autonomous flight capabilities of small, low-cost flight vehicles. The nonlinear guidance model is presented in the arc-length domain. The MEWFDGGL is derived using the linearized dynamics of a zero-effort miss (ZEM) and adopting the optimal control theory. Next, numerical simulations of the MEWFDGGL with varying-speed endo-atmospheric flight vehicles are conducted, and the results are compared with the original MEWFGL to demonstrate the effectiveness and superiority of the guidance law. Finally, flight experiments based on a small quadrotor UAV are conducted to further verify the effectiveness of the proposed guidance law. For ease of presentation, we focus on small, low-cost UAVs in this paper, but it is worth emphasizing that the guidance law proposed in this paper is designed for numerous endo-atmospheric flight vehicles, including cruise missiles, drones, etc. The key contributions of the MEWFDGGL are threefold:
- The MEWFDGGL decouples the speed change in a UAV from the guidance problem in theory, rather than directly adopting the constant speed hypothesis. With the help of the classical differential geometry curve theory, the optimal guidance problem is transformed into an optimal space curve design problem, which makes the speed change in the UAV no longer a concern during the guidance law design process, and the optimality of the space curve is independent of the UAV’s speed in the process of the guidance law design.
- The MEWFDGGL is globally energy-optimal. By linearizing the ZEM dynamics and adopting the optimal control theory, the guidance curvature command of the MEWFDGGL can be obtained by solving the linear-quadratic optimal control problem, and then the energy consumption of a UAV throughout the whole guidance process can be minimized.
- The suboptimal MEWFDGGL can be applied to general waypoint-following tasks with arbitrary waypoint numbers. By adopting just two waypoints at one time to generate the guidance command, the formation of the original MEWFG becomes much simpler, and the computation burden is greatly reduced.
2. Materials and Methods
2.1. Preliminaries
2.1.1. Nonlinear Kinematics
We begin by taking into account that the UAV needs to visit N-many waypoints. The planar engagement geometry is shown in Figure 1, where XOY is the inertial coordinate system. The UAV is expressed as the symbol U, and the i-th waypoint is represented as Wi. The variables γ and signify the UAV’s flight path angle and LOS (Line-of-Sight) angle, respectively. For the sake of simplicity, the UAV is assumed to be a particle model, that is, the time delay of the autopilot is not considered. The variable , which cannot be zero, denotes the relative range between the UAV and the i-th waypoint. The symbol z represents the zero-effort miss (ZEM), which refers to the nearest distance during the process that the UAV moves to the i-th target waypoint at the current speed without any control input, namely, , as shown in Figure 1. Based on the principles of dynamics, as shown in Figure 1, the differential equations to describe the planar engagement geometry in the arc-length domain can be formulated as
where a and V represent the speed and acceleration of the UAV, respectively; κ is the guidance curvature; and the prime symbol (′) indicates the derivative of the variables with respect to s, the arc length of the UAV’s flight trajectory, such as how γ′ denotes the derivative of γ with respect to s. In this paper, κ is used as the guidance input command to design the guidance law, which can improve the performance of the guidance, to some extent, by avoiding using the speed value of the UAV during the process of the guidance law design, especially when the speed is time-varying.
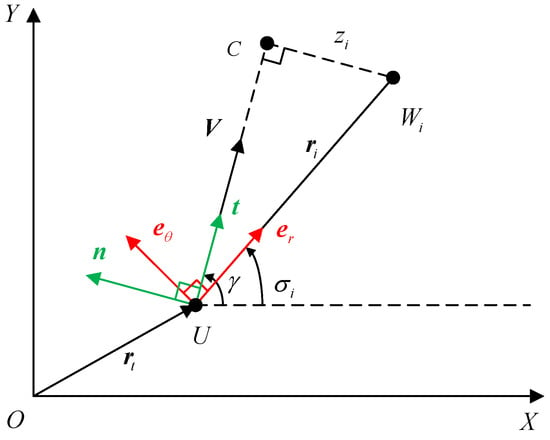
Figure 1.
Planar engagement geometry.
Omitting the derivation process, the dynamic equation of the varying-speed missile is directly given as follows [30]:
Decomposing the above formula in the LOS frame (er, eθ), we have
As mentioned before, the guidance command in the arc-length domain is κ. The transformational relation between the curvature command and the lateral acceleration command can be given directly as
2.1.2. Problem Formulation
Without losing generality, we can suppose that the order of the waypoints is numbered according to the corresponding path length as . The corresponding path length of the ith waypoint can be written directly as
where stands for the corresponding remaining path length to visit the ith waypoint.
Since it is difficult to exactly calculate the value of the remaining path length, it is generally replaced by its estimated value, . As shown in Figure 2, since the purpose of guidance design is to minimize the ZEM, that is, to make the leading angle tend to zero, the next flight trajectory of the UAV is generally within ΔUCWi, which means that the path to travel is larger than . If is the estimated value of , the remaining path length is expressed by
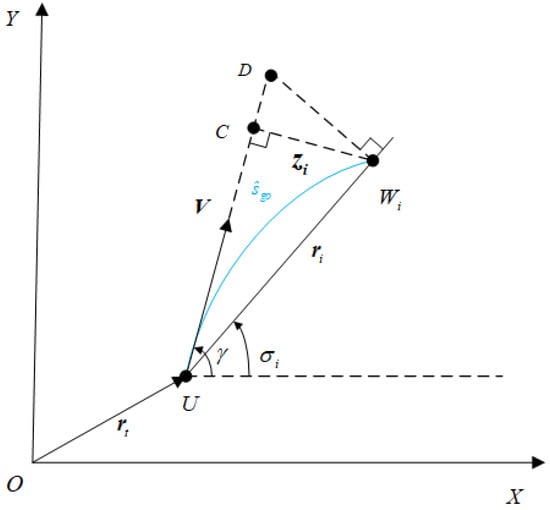
Figure 2.
ZEM geometric model.
As a matter of fact, energy consumption is extremely important for UAVs because it determines the endurance of a UAV, that is, it determines how long a vehicle can fly. For this reason, the performance index is taken into consideration as follows:
Similarly, minimizing the performance index is a valuable goal for the multi-objective optimization problem. It is worth noting that the performance index is a sum of the energy functions computed in each path length. Hence, finding an analytical solution for this problem is the main purpose of this paper, that is, we are adopting the given nonlinear dynamics model and finding the guidance curvature k, which ensures an optimal performance index and perfect ZEM constraints, as follows:
2.2. Guidance Law Design
2.2.1. Derivation
This section derives the energy-optimal differential geometric guidance law to solve the generalized optimal waypoint-following problem. As can be seen from Figure 2, the ZEM can be expressed as
Substituting the second Equation of (1) into (9), the ZEM is obtained as
Taking the arc length derivative of (10) results in
Substituting the second Equation of (3) into (11) provides
Then, by combining (12) and (6), the nonlinear ZEM dynamics can be acquired as follows:
Taking the assumption of a small leading angle into consideration, i.e., is small, we have the approximation as
The linear ZEM dynamics can be obtained by substituting (14) into (13), as follows:
Further, the system in (15) can be written as follows:
Introducing the terminal constraint terminal constraints in (8) and substituting them into (16) provides
According to [27], if the guidance curvature command k is optimal in the energy consumption, then there are N Lagrange multipliers (), so the guidance curvature k can be expressed as follows:
By substituting (18) into (17) and solving the corresponding equation, the Lagrange multiplier can be obtained. It is worth mentioning that this method can be regarded as an extension of the Schwartz inequality method for any number of terminal constraints. Hence, we consider only the case of in the following derivation, without the loss of generality. Therefore, substituting (17) into (18) provides
Defining the Lagrange multiplier vector as and the ZEM vector as , (19) can be given as a compact matrix format, as follows:
where the symmetric matrix can be obtained as
Then, the Lagrange multiplier vector is given by inverting both sides of (20), as follows:
Substituting (22) into (18), the guidance curvature command k in the case of can be written as
Remark 1.
Following a similar procedure, it is easy to obtain the solution in the case of . For instance, when , the ZEM vector will be reduced by one dimension and become , and then the matrix will reduce to
Hence, the guidance curvature k in the case of can be written as
Remark 2.
In order to effectively eliminate the deviation caused by the linearization process, the ZEM is written in a nonlinear form in practice, as follows:
By substituting (26) into (23), the guidance curvature command k, composed of the measured signals , , and , is obtained. It is worth noticing that (23) converts the linear terms of the substitution of (26) into the nonlinear expressions, which provides support for the engineering application of the guidance mentioned above.
2.2.2. Particular Cases
N = 1
When the UAV is only required to visit one waypoint, the problem is transformed into an energy-optimal interception problem. For such special cases, the guidance curvature (23) can be expressed as
The matrix G can reduce to a scalar form when N = 1, as follows:
and the Lagrange multiplier can easily be expressed as
Then, the clear guidance curvature command can be obtained by substituting (29) into (27), as follows:
In order to more conveniently analyze the MEWFDGGL, the guidance acceleration command can be given by substituting (4) into (30), as follows:
In the time domain, the ZEM could be signified as the following form:
Combining (32) and (31) results in
This is consistent with the classical energy optimal PNG. According to the statement in [31,32], the energy consumption of the PNG with a navigation gain of three is minimal when there is only a single waypoint to be visited. However, it is also clear from the previous derivation that when the number of waypoints is greater than two, merely adopting the PNG to visit each waypoint in turn cannot ensure that the energy consumption is optimal in the whole process of the guidance.
N = 2
Similarly, when a UAV is required to visit two waypoints, the guidance curvature command k, in the case of , can be expressed as follows:
The matrix G can be written as
and the corresponding Lagrange multiplier can be easily given from (22), as follows:
Then, substituting (36) into (34), the clear guidance curvature command can be obtained as follows:
From (32), the ZEM can be denoted in the arc-length domain as
Then, substituting (38) into (30) and (37), the clear guidance curvature command, in the case of N = 2, can be obtained as follows:
where
In other words, when , the MEWFDGGL can be regarded as a biased proportional guidance (BPN) that has a time-varying navigation gain. As mentioned earlier in (39), the first term represents the proportional guidance term for the first waypoint, and the second term represents the influence term of the second waypoint on the first one.
Remark 3.
Following a similar procedure, it is easy to obtain the solution, in the case of N > 2. For instance, when N = 3, the clear guidance curvature command is given as
According to Equation (41), the final form of the MEWFDGGL is a piecewise BNG law based on the waypoints segment, and its proportional navigation gain changes with time. This also shows that the MEWFDGGL is generic because it reduces to the classical PNG when there is only one waypoint to be visited.
2.2.3. Improvement
For a waypoint-following task with N waypoints, it follows from Equation (21) that implementing the MEWFDGG requires the calculation of the inverse of the matrix G. We notice that the size of matrix G is proportional to the number of waypoints to be traveled. Therefore, a large number of waypoints poses a great challenge to the computing power of an airborne computer. Hence, an algorithm based on finite waypoint information is proposed to improve the applicable scope of the guidance law and make it more suitable for the general situation of an arbitrary number of waypoints.
Without losing generality, we can assume that the UAV has visited the previous i-1th waypoint at the current moment and is required to visit the i-th waypoint to the nth waypoint sequentially. After several simulation analyses, it is found that the energy consumption is not significantly different from that of the MEWFDGG when adopting only two waypoints at one time to generate the guidance command. Therefore, the method proposed in this paper can be improved to design a suboptimal minimum-effort waypoint-following differential geometric guidance law (SMEWFDGGL), by considering only two waypoints.
Therefore, when , the guidance command of SMEWFG considers only two waypoints, and it can be expressed as follows:
where
In order to effectively eliminate the deviation caused by the linearization process, the ZEM is written in a nonlinear form in practice, as follows:
or
The algorithm can be expressed as follows:
| Algorithm 1: The suboptimal minimum-effort waypoint-following differential geometric guidance |
| Input: The relative range and LOS angle between the UAV and all waypoints, and , and the UAV speed . Require: . Denote: . Step 1: Compute the remaining path length . If , proceed to Step 2; otherwise, proceed to Step 3. Step 2: , . Return to Step 1. Step 3: If , proceed to Step 4; otherwise, proceed to Step 5. Step 4: Compute the remaining path length using Equation (6) (). Return to Step 1. Step 5: , Step 6: Determine the UAV’s current position. If , proceed to Step 7; otherwise, proceed to Step 8. Step 7: Compute the acceleration command k using Equation (42) and proceed to Step 9. Step 8: Step 9: Return k |
According to Step 7 in Algorithm 1, when the UAV passes a waypoint, the guidance command is updated, the information of this waypoint is discarded, and, hence, the guidance command may experience an abrupt change at the very moment of passing. However, this does not cause any unacceptably bad influence on the guidance law, because the classical PN could also be used as a waypoint-following guidance law in contrast, and it would only use the information of one waypoint each time (as its target). The guidance command of PN definitely greatly changes when the UAV passes this waypoint. This is seen in the simulation cases in Section 3.
3. Numerical Simulation Results
The MEWFDGGL designed in Section 2 is analyzed and demonstrated using numerical simulations in this section. The numerical simulations are conducted for two different scenarios: when the speed of the UAV changes periodically and when it is influenced by randomly varying wind. In all the following simulations, the UAV’s initial flight path angle is 30°, and there are eight waypoints to be visited. The UAV’s initial location is at the origin of the reference frame. The inertial positions of the eight waypoints to be visited are listed in Table 1.

Table 1.
Inertial positions of the eight waypoints.
3.1. Performance of the UAV under Varying Speeds
This subsection primarily verifies the performance of the MEWFDGGL and the SMEWFDGGL when the speed of the UAV periodically changes. As is known, due to the effect of actuator delay or resistance, the speed of a UAV does not always remain constant during flight. In practice, the actual speed of a UAV typically fluctuates around the expected speed during the implementation of speed control. Hence, in the considered scenario in this subsection, the UAV’s speed periodically changes, as shown in Figure 3.
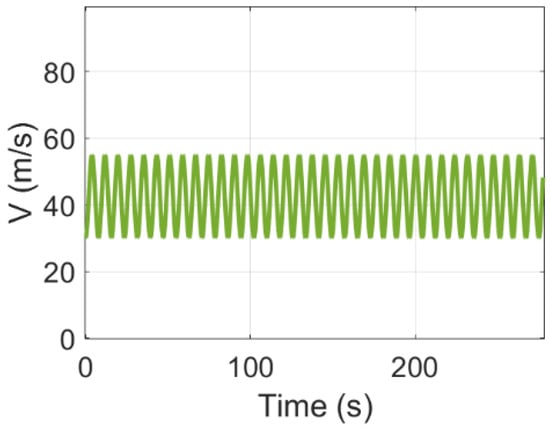
Figure 3.
The real-time speed of the UAV.
3.1.1. MEWFDGGL
Figure 4a compares the flight trajectories of the UAV guided by both the MEWFDGGL and the MEWFG. It can be clearly seen in Figure 4a that the UAV can follow the desired waypoints when guided by these two guidance laws. Although the flight trajectories largely coincided, it can still be seen that the MEWFDGGL is better than the MEWFG law, especially near the fifth waypoint. The UAV’s flight path angle is presented in Figure 4b, which clearly shows that the UAV guided by the MEWFG takes small, sharp turns, while the flight guided by the MEWFDGGL has a smooth path. For comparison purposes, the guidance curvature command in the arc-length domain is converted into the guidance acceleration command in the time domain. A comparison of the acceleration commands between the MEWFG and the MEWFDGGL is presented in Figure 4c. As exhibited in the diagram, when the UAV guided by the MEWFG passes the waypoint, an acceleration command occurs, which suddenly grows larger, whereas the variation in the command obtained from the MEWFDGGL is quite gentle. The reason for this phenomenon can be found in the comparison shown in Figure 4g,h. The periodic variation in the UAV’s speed leads to the oscillation in the remaining flight time, while the linear variation in the remaining path length ensures the stability of the calculation.
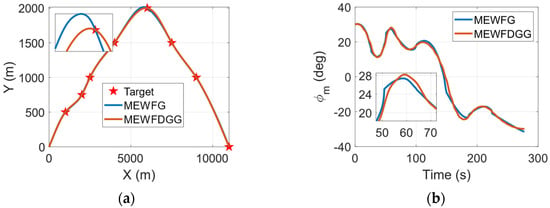
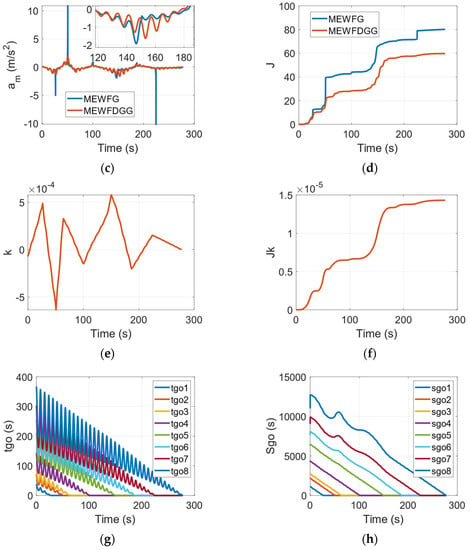
Figure 4.
Compared results of the MEWFDGGL and the MEWFG when the UAV’s speed changes periodically. (a) Flight trajectory. (b) Flight path angle. (c) Guidance acceleration command. (d) Performance index of a. (e) Guidance curvature command. (f) Performance index of k. (g) Remaining flight time. (h) Remaining path length.
The guidance curvature command and its quantitative energy consumption obtained from the MEWFDGGL are exhibited in Figure 4e,f. By comparing it to Figure 4c,e, we can observe that the derivation that is completely independent of the UAV’s speed ensures the smoothness of the guidance curvature command. The corresponding quantitative energy consumption of the guidance acceleration commands obtained from the MEWFDGGL and the MEWFG are compared in Figure 4d. As shown in Figure 4d, we can clearly observe that the UAV guided by the MEWFDGGL requires less energy consumption than the flight guided by the MEWFG. Therefore, the UAV guided by the MEWFDGGL can be reasonably considered to have better endurance in scenarios where its speed changes. The comparison results of the performance of the proposed guidance laws are shown in Table 2.

Table 2.
Performance comparison of the MEWFDGGL and the MEWFG under the varying speeds of UAVs.
3.1.2. SMEWFDGGL
In order to better prove the effectiveness of the improved guidance law, the MEWFDGGL and the optimal guidance law (OGL) of a single point are used as the control group for comparative analysis. The OGL can be expressed as follows:
which is essentially the optimal proportional guidance law in the arc-length domain.
In this scenario, the flight trajectories of UAVs under the three guidance laws are shown in Figure 5a. The UAVs guided by the different guidance laws can successively visit the target waypoints, with small error, and they have largely coincident trajectories, which indicates that the velocity variations along the velocity directions have little effect on the performances of all the guidance laws in the arc-length domain. A comparison of the flight path angles is shown in Figure 5b. As shown in Figure 5b, the UAV guided by the OGL makes a sharp turn when passing through the current waypoint, while the UAVs guided by the SMEWFDGGL and the MEWFDGGL show good performances, and all of them can ensure smooth flight trajectories.
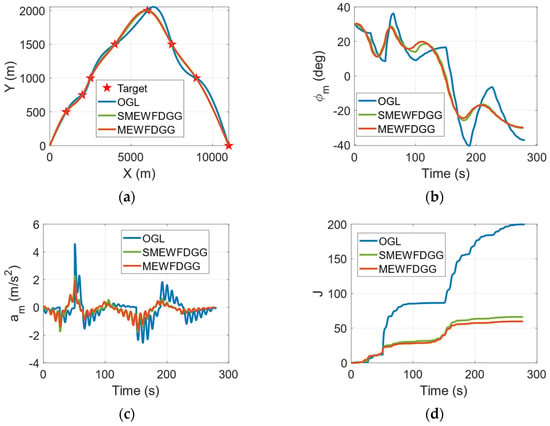
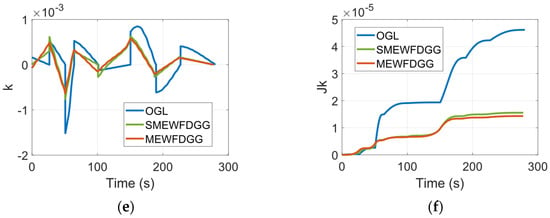
Figure 5.
The performance of the SMEWFDGGL under the varying speeds of the UAV. (a) Flight trajectory. (b) Flight path angle. (c) Guidance acceleration command. (d) Performance index of a. (e) Guidance curvature command. (f) Performance index of k.
A comparison of the acceleration command and the curvature command between the three guidance laws is presented in Figure 5c,e. As can be seen in Figure 5c,e, the curvature command under the OGL shows discontinuity when passing through the waypoint. Although the UAV guided by the SMEWFDGGL cannot produce a continuous curvature command compared with the UAV guided by the MEWFDGGL, the amplitude of discontinuity is obviously smaller than that of the UAV guided by the OGL, which has little influence on the implementation of the guidance. The quantitative energy consumption levels of the three guidance laws are compared in Figure 5d,f. In Figure 5d,f, the UAV guided by the OGL consumes the most energy—approximately three times as much as the UAVs guided by the MEWFDGGL and the SMEWFDGGL. The energy consumption levels under the MEWFDGGL and the SMEWFDGGL are not much different, with the consumption under the SMEWFDGGL being slightly more (approximately 10%) than that under the MEWFDGGL. The comparison results of the performances of the proposed guidance laws are shown in Table 3.

Table 3.
Performance comparison of the SMEWFDGGL under the varying speeds of UAVs.
3.2. Performance under the Influence of the Wind
This subsection primarily verifies the performance of the MEWFDGGL when the speed of the UAV is influenced by randomly varying wind. As is known, for aerial vehicles, a major factor that can affect their speed is wind. In this subsection, we simulate the direction of the wind with a uniformly generated random number, i.e., east, south, west, and north, and the size of the wind is simulated by a normally distributed random number with a standard deviation of 5 and a variance of 1. The UAV’s speed, as influenced by randomly varying wind, is shown in Figure 6.
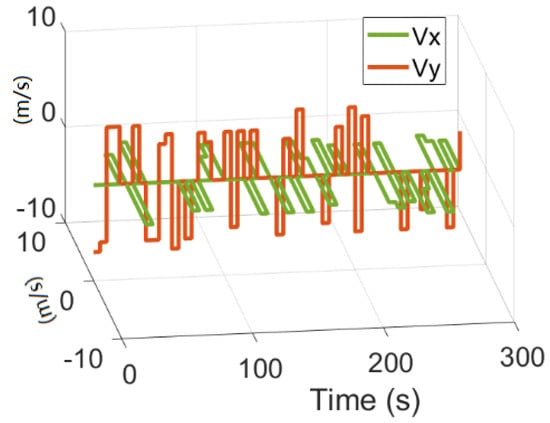
Figure 6.
The real-time speed of the UAV, as influenced by randomly varying wind.
3.2.1. MEWFDGGL
Figure 7a compares the flight trajectories of the UAVs guided by the MEWFDGGL and the MEWFG when the UAVs’ speeds are influenced by randomly varying wind. It can be clearly seen in Figure 7a that, although both of the UAVs can follow the desired waypoints guided by the two guidance laws, the flight trajectory obtained from the MEWFDGGL is closer to an ideal approaching course, especially near the fifth and sixth waypoints. This UAV’s flight path angle is presented in Figure 7b. Due to the influence of randomly varying wind, both of the curves obtained from the MEWFDGGL and the MEWFG are not smooth, which is inevitable. For comparison purposes, the guidance curvature command in the arc-length domain is converted into the guidance acceleration command in the time domain. A comparison of the acceleration commands between the MEWFG and the MEWFDGGL is presented in Figure 7c. As can be seen in the chart, when the UAV guided by the MEWFG passes the waypoint, an acceleration command occurs, which suddenly grows larger, whereas the variation in the command obtained from the MEWFDGGL is quite gentle. The reason for this phenomenon is similar to that in the previous section.
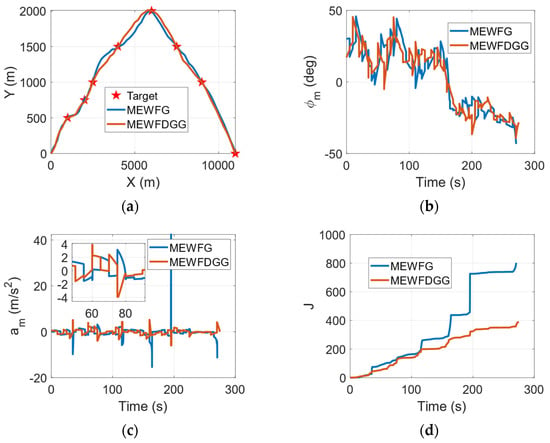
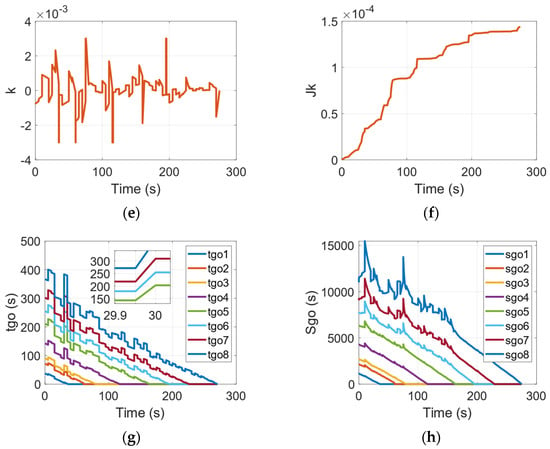
Figure 7.
Comparison of the results of the MEWFDGGL and the MEWFG when the UAVs’ speeds are influenced by randomly varying wind. (a) Flight trajectory. (b) Flight path angle. (c) Guidance acceleration command. (d) Performance index of a. (e) Guidance curvature command. (f) Performance index of k. (g) Remaining flight time. (h) Remaining path length.
The guidance curvature command and its quantitative energy consumption obtained from the MEWFDGGL when the UAV’s speed is influenced by randomly varying wind are shown in Figure 7e,f, respectively. By comparing Figure 4e and Figure 7e, it can be observed that the guidance curvature commands show random sharp turns, because the directions of the UAVs’ speeds are affected by randomly varying wind. The guidance curvature command may require adjustments at any time to ensure that an optimal trajectory is generated. The quantitative energy consumption levels of the guidance acceleration commands obtained from the MEWFDGGL and the MEWFG are compared in Figure 7d. As exhibited in Figure 7d, we can clearly observe that the UAV guided by the MEWFDGGL consumes approximately 50% less energy than the UAV guided by the MEWFG in the considered scenarios. Hence, it is reasonable to consider that the UAV guided by the MEWFDGGL is good at overcoming the effects of randomly varying wind and has a better endurance in the considered scenario. The comparison results of the performances of the proposed guidance laws are shown in Table 4.

Table 4.
Performance comparison of the MEWFDGGL and the MEWFG when the UAVs’ speeds are influenced by randomly varying wind.
3.2.2. SMEWFDGGL
When a UAV’s speed is influenced by randomly varying wind, the variation in the UAV’s velocity is no longer limited to the direction of that UAV’s velocity. As shown in Figure 8b, under the influence of randomly varying wind, the velocity direction of the UAV constantly changes, and the flight path angles of the UAVs under the three guidance laws are in discontinuous fluctuation. As can be seen in Figure 8a, compared with the ideal situation, the flight trajectory when a UAV’s speed is influenced by randomly varying wind has obvious jitter and a small turning point, while the flight trajectories under the guidance of the MEWFDGGL and the SMEWFDGGL are relatively smoother.
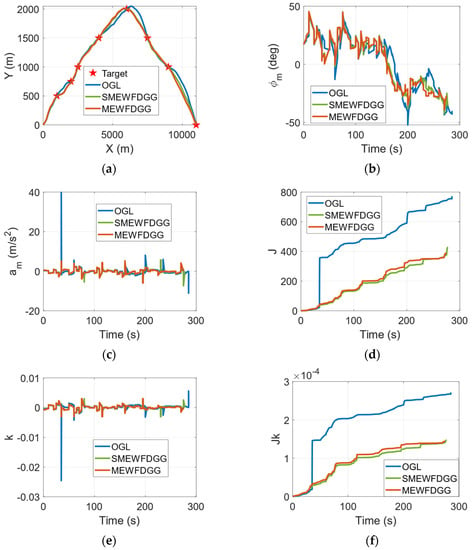
Figure 8.
The performance of the UAV guided by the SMEWFDGGL under the influence of randomly varying wind. (a) Flight trajectory. (b) Flight path angle. (c) Guidance acceleration command. (d) Performance index of a. (e) Guidance curvature command. (f) Performance index of k.
The guidance curvature command and its quantitative energy consumption obtained from the MEWFDGGL are shown in Figure 8e,f, respectively. When a UAV’s speed is influenced by randomly varying wind, the curvature instruction of that UAV’s guidance also shows discontinuity. If the sudden change value generated during the ill-conditioned solution of the guidance command is ignored, then the guidance energy consumption levels under the three guidance laws have little difference, which is consistent with the theoretical conclusion that the MEWFDGGL’s guidance energy consumption level is the lowest and that the SMEWFDGGL’s guidance energy consumption level is the second-lowest, although both of them are far lower than the guidance energy consumption level of the OGL. The comparison results of the performances of the proposed guidance laws are shown in Table 5.

Table 5.
Performance comparison of the SMEWFDGGL under the influence of randomly varying wind.
4. Experiment Verification
Using a small quadrotor UAV, the experimental verification of the proposed guidance laws is presented in this section. The outdoor experimental field is shown in Figure 9.

Figure 9.
The small quadrotor UAV and outdoor experimental field.
Considering the UAV’s performance and the limitations of the experimental site, the UAV starts from the take-off point and successively visits three target waypoints. The coordinates of the take-off point are (0,0), the initial flight path angle of the UAV is 60°, and the UAV’s initial velocity is 2 m/s. The specific position coordinates of all waypoints are shown in Table 6.

Table 6.
Inertial positions of the three waypoints in the experimental scenario.
4.1. MEWFDGGL
As can be seen in Figure 10a, the small quadrotor UAV guided by the two guidance laws can successfully visit the waypoints in the actual flight scenario, but the trajectory of the UAV guided by the MEWFDGG is significantly smoother, and its ZEM is smaller. A comparison of the acceleration commands between the MEWFG and the MEWFDGGL is presented in Figure 10b. Theoretically, the guidance acceleration instructions obtained by the two guidance laws are continuous. However, in the actual flight process, the UAV cannot visit the target waypoint along the completely ideal trajectory, which makes the UAV’s acceleration command discontinuous. It is worth emphasizing that both of the guidance laws are applicable to small quadrotor UAvs, but the latter has a more stable performance.
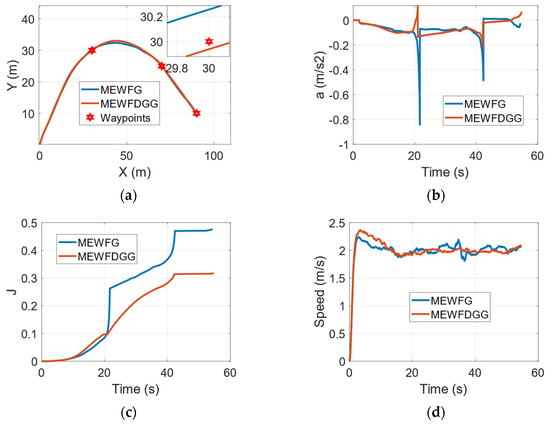
Figure 10.
The performance of the MEWFDGGL in the experimental scenario. (a) Flight trajectory. (b) Guidance acceleration command. (c) Performance index of a. (d) The real-time speed of the UAV.
The quantitative energy consumption levels of the two guidance laws are compared in Figure 10c. As shown in Figure 10c, the energy consumption level of the UAV guided by the MEWFDGGL is reduced by approximately 40% compared to that of the UAV guided by the MEWFGL. The comparison results of the performances of the proposed guidance laws are shown in Table 7.

Table 7.
Performance comparison of the MEWFDGGL and the MEWFG in the experimental scenario.
4.2. SMEWFDGGL
In this scenario, the flight trajectories of the UAVs under the three guidance laws are shown in Figure 11a. From the flight trajectories, we can see that the UAV guided by the MEWFDGG has a smoother flight trajectory than that of the UAV guided by the SMEWFDGGL, which obviously consumes less energy than the UAV guided by the OGL. The experimental results show that the energy consumption levels of the UAVs guided by the MEWFDGG and the SMEWFDGG are similar, and they are much lower than that of the UAV guided by the OGL. The experimental results are consistent with both the simulation results and the theoretical conclusions.
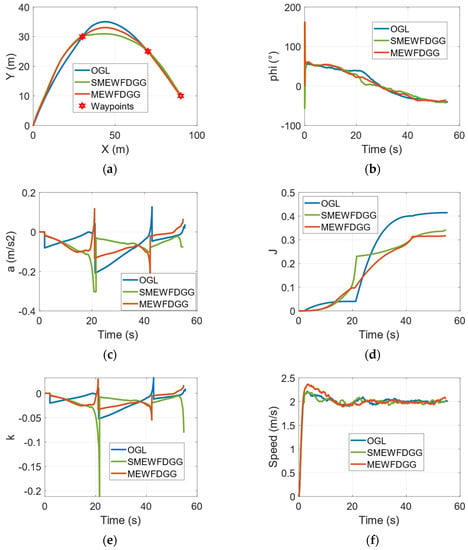
Figure 11.
The performance of the SMEWFDGGL in the experimental scenario. (a) Flight trajectory. (b) Flight path angle. (c) Guidance acceleration command. (d) Performance index of a. (e) Guidance curvature command. (f) The real-time speed of the UAV.
When carefully observing Figure 11d, it is not difficult to see that the guidance energy consumption level and the track angle of the UAV under the guidance of the MEWFDGGL remain in an approximately straight line for the last 20 s, while the guidance energy consumption levels nearly stay the same and do not increase. This is because the MEWFDGGL takes into account the influence of all waypoint constraints during the guidance process. When the UAV reaches the second waypoint, the speed direction of the UAV is adjusted to the direction of the last waypoint. However, the OGL cannot be used to adjust the flight angle of the UAV between every two waypoints, which is the reason why the MEWFDGGL can achieve global energy optimization. The performance comparison results of three guidance laws are shown in Table 8.

Table 8.
Performance comparison of the SMEWFDGGL in the experimental scenario.
5. Conclusions
A minimum-effort waypoint-following differential geometric guidance law (MEWFDGGL) and its suboptimal form for varying-speed endo-atmospheric flight vehicles were proposed in this paper. The optimal guidance problem was transformed into an optimal space curve design problem using the differential geometric guidance model. The speed changes in endo-atmospheric flight vehicles were theoretically decoupled from the guidance problem, rather than the constant speed hypothesis being directly adopted. It was theoretically proven that the proposed MEWFDGGL is a globally energy-optimal guidance law; the suboptimal MEWFDGGL was proposed in order to solve the problems of complexity and high computation burden, and it is advantageous for improving the autonomous flight capability of small, low-cost endo-atmospheric flight vehicles. Finally, in comparison with the original MEWFG law, the nonlinear numerical simulations and experimental verifications show that the MEWFDDGGL is more efficient for eliminating the adverse influences on the guidance performance caused by a UAV’s speed changes. It is worth noting that the MEWFDDGGL proposed in this paper does not break through some of the limitations faced by the MEWFG. For example, the optimality of the MEWFDDGGL is affected by the estimation accuracy of the remaining path length. However, for theoretical research, the proposed guidance law may also be extended to maneuvering target interception scenarios and salvo attack scenarios.
Author Contributions
Conceptualization, K.L.; Methodology, X.Q., K.L., Y.L. (Yangang Liang) and Y.L. (Yuanhe Liu); Software, X.Q.; Formal analysis, X.Q.; Investigation, X.Q.; Resources, X.Q.; Data curation, X.Q.; Writing—original draft, X.Q.; Writing—review & editing, X.Q., K.L., Y.L. (Yangang Liang) and Y.L. (Yuanhe Liu); Visualization, X.Q.; Supervision, K.L., Y.L. (Yangang Liang) and Y.L. (Yuanhe Liu); Project administration, X.Q., K.L. and Y.L. (Yangang Liang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [The National Natural Science Foundation of China] grant number [No. 12002370] and the APC was funded by [The National Natural Science Foundation of China] grant number [No. 12002370].
Data Availability Statement
The authors don’t create a link to the research data for this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- He, S.; Lee, C.-H.; Shin, H.-S.; Tsourdos, A. Optimal Guidance and Its Applications in Missiles and UAVs, 1st ed.; Springer: Cham, Switzerland, 2020; pp. 151–173. [Google Scholar]
- Beard, R.W.; Ferrin, J.; Humpherys, J. Fixed Wing UAV Path Following in Wind With Input Constraints. IEEE Trans. Control. Syst. Technol. 2014, 22, 2103–2117. [Google Scholar] [CrossRef]
- Ullah, N.; Mehmood, Y.; Aslam, J.; Shaoping, W.A.N.G.; Phoungthong, K. Fractional order adaptive robust formation control of multiple quad-rotor UAVs with parametric un-certainties and wind disturbances. Chin. J. Aeronaut. 2022, 35, 204–220. [Google Scholar] [CrossRef]
- Piprek, P.; Hong, H.; Holzapfel, F. Optimal trajectory design accounting for the stabilization of linear time-varying error dynamics. Chin. J. Aeronaut. 2022, 35, 55–66. [Google Scholar] [CrossRef]
- Pang, B.; Dai, W.; Hu, X.; Dai, F.; Low, K.H. Multiple air route crossing waypoints optimization via artificial potential field method. Chin. J. Aeronaut. 2020, 34, 279–292. [Google Scholar] [CrossRef]
- Medagoda, E.D.B.; Gibbens, P.W. Synthetic-Waypoint Guidance Algorithm for Following a Desired Flight Trajectory. J. Guid. Control. Dyn. 2015, 33, 601–606. [Google Scholar] [CrossRef]
- Wang, X.; Tan, G.; Dai, Y.; Lu, F.; Zhao, J. An Optimal Guidance Strategy for Moving-Target Interception by a Multirotor Unmanned Aerial Vehicle Swarm. IEEE Access 2020, 8, 121650–121664. [Google Scholar] [CrossRef]
- Sun, G.; Wen, Q.; Xu, Z.; Xia, Q. Impact time control using biased proportional navigation for missiles with varying velocity. Chin. J. Aeronaut. 2020, 33, 956–964. [Google Scholar] [CrossRef]
- Li, K.-B.; Shin, H.-S.; Tsourdos, A.; Tahk, M.-J. Performance of 3-D PPN Against Arbitrarily Maneuvering Target for Homing Phase. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3878–3891. [Google Scholar] [CrossRef]
- Li, K.-B.; Shin, H.-S.; Tsourdos, A.; Tahk, M.-J. Capturability of 3D PPN Against Lower-Speed Maneuvering Target for Homing Phase. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 711–722. [Google Scholar] [CrossRef]
- Kebo, L.I.; Zhihui, B.A.I.; Hyo-Sang, S.H.I.N.; Tsourdos, A.; Min-Jea, T.A.H.K. Capturability of 3D RTPN guidance law against true-arbitrarily ma-neuvering target with maneuverability limitation. Chin. J. Aeronaut. 2022, 35, 75–90. [Google Scholar]
- Zhao, Y.; Sheng, Y.; Liu, X. Trajectory reshaping based guidance with impact time and angle constraints. Chin. J. Aeronaut. 2016, 29, 984–994. [Google Scholar] [CrossRef]
- Kim, Y.-W.; Kim, B.; Lee, C.-H.; He, S. A unified formulation of optimal guidance-to-collision law for accelerating and decelerating targets. Chin. J. Aeronaut. 2022, 35, 40–54. [Google Scholar] [CrossRef]
- Qi, N.; Sun, Q.; Zhao, J. Evasion and pursuit guidance law against defended target. Chin. J. Aeronaut. 2017, 30, 1958–1973. [Google Scholar] [CrossRef]
- He, S.; Lee, C.-H.; Shin, H.-S.; Tsourdos, A. Optimal three-dimensional impact time guidance with seeker’s field-of-view constraint. Chin. J. Aeronaut. 2021, 34, 240–251. [Google Scholar] [CrossRef]
- Kyaw, P.T.; Le, A.V.; Veerajagadheswar, P.; Elara, M.R.; Thu, T.T.; Nhan, N.H.K.; Van Duc, P.; Vu, M.B. Energy-Efficient Path Planning of Reconfigurable Robots in Complex Environments. IEEE Trans. Robot. 2022, 38, 2481–2494. [Google Scholar] [CrossRef]
- Yin, Q.; Chen, Q.; Wang, Z. Energy-Optimal Waypoint-Following Guidance for Gliding-Guided Projectiles. In Proceedings of the 21st International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 12–15 October 2021; IEEE: New York, NY, USA, 2021; Volume 34, pp. 1477–1482. [Google Scholar]
- Chen, Y.; Yu, J.; Mei, Y.; Zhang, S.; Ai, X.; Jia, Z. Trajectory optimization of multiple quad-rotor UAVs in collaborative assembling task. Chin. J. Aeronaut. 2016, 29, 184–201. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Y.; Wang, D.; Zhang, Z. Mission-oriented cooperative 3D path planning for modular solar-powered aircraft with energy optimization. Chin. J. Aeronaut. 2022, 35, 98–109. [Google Scholar] [CrossRef]
- Zhou, Y.; Su, Y.; Xie, A.; Kong, L. A newly bio-inspired path planning algorithm for autonomous obstacle avoidance of UAV. Chin. J. Aeronaut. 2021, 34, 199–209. [Google Scholar] [CrossRef]
- Jeon, I.-S.; Lee, J.-I. Optimality of Proportional Navigation Based on Nonlinear Formulation. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 2051–2055. [Google Scholar] [CrossRef]
- Kim, T.-H.; Park, B.-G. Rapid Homing Guidance Using Jerk Command and Time-Delay Estimation Method. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 729–742. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Linear Quadratic Guidance Laws for Imposing a Terminal Intercept Angle. J. Guid. Control. Dyn. 2008, 31, 1400–1412. [Google Scholar] [CrossRef]
- Palumbo, N.F.; Blauwkamp, R.A.; Lloyd, J.M. Modern homing missile guidance theory and techniques. Johns Hopkins APL Tech. Dig. 2010, 29, 42–59. [Google Scholar]
- He, S.; Lee, C.-H. Optimality of Error Dynamics in Missile Guidance Problems. J. Guid. Control. Dyn. 2018, 41, 1620–1629. [Google Scholar] [CrossRef]
- He, S.; Lee, C.-H.; Shin, H.-S.; Tsourdos, A. Minimum-Effort Waypoint-Following Guidance Law. J. Guid. Control. Dyn. 2019, 32, 151–173. [Google Scholar] [CrossRef]
- Kobayashi, S. Differential Geometry of Curves and Surfaces, 1st ed.; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Lu, P. Intercept of Nonmoving Targets at Arbitrary Time-Varying Velocity. J. Guid. Control. Dyn. 1998, 21, 176–178. [Google Scholar] [CrossRef]
- Li, K.; Liang, Y.; Su, W.; Chen, L. Performance of 3D TPN against true-arbitrarily maneuvering target for exoat-mospheric interception. Sci. China Technol. Sci. 2018, 61, 1161–1174. [Google Scholar] [CrossRef]
- Li, K.B.; Su, W.S.; Chen, L. Performance analysis of differential geometric guidance law against high-speed target with arbitrarily maneuvering acceleration. Proc. Inst. Mech. Eng. Part G-J. Aerosp. Eng. 2019, 233, 3547–3563. [Google Scholar] [CrossRef]
- Li, K.B.; Su, W.S.; Chen, L. Performance analysis of realistic true proportional navigation against maneuvering targets using Lyapunov-like approach. Aerosp. Sci. Technol. 2017, 69, 333–341. [Google Scholar] [CrossRef]
- Shin, H.S.; Li, K.B. An Improvement in Three-Dimensional Pure Proportional Navigation Guidance. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3004–3014. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).