JO-TADP: Learning-Based Cooperative Dynamic Resource Allocation for MEC–UAV-Enabled Wireless Network
Abstract
:1. Introduction
1.1. Motivations and Objectives
- Inefficient Resource Allocation: Many existing works performed resource allocation, either through optimizing the trajectory of the UAV, position of the UAV, or association between users and UAV. However, none of them jointly consider all the constraints, which leads to inefficient resource allocation. Furthermore, the resource allocation was made only using limited parameters, which also reduced the efficiency of resource allocation.
- High Energy Consumption: The existing approaches mainly rely on independent resource allocation because UAVs independently perform resource allocation rather than cooperation with other UAVs, which leads to high energy consumption. Furthermore, every MU in the environment sends direct requests to the UAVs continuously, leading to increased energy consumption.
- Service Discontinuity: Most existing methods did not consider user mobility and its characteristics. Generally, the MUs are highly dynamic; thus, it is important to consider their dynamicity, otherwise, it may lead to service discontinuity and disruption.
- Random UAV Deployment: The existing works perform 3D UAV deployment, altitude optimization, and position optimization, which are not efficient for random UAV deployment and lead to unwanted energy consumption and poor connectivity.
- To reduce poor connectivity and energy consumption by performing optimum allocation of UAVs in the environment based on the density of MUs.
- The clustering of MUs is performed, which captures the mobility of MUs to reduce unnecessary energy consumption and make the UAV more reliable.
- To reduce the hovering energy consumption and achieve better coverage by autonomous trajectory planning, deep learning (DL) is employed to optimize the UAV altitude.
- To ensure optimal and dynamic resource allocation by performing request classification, an FL-based cooperated auction mechanism using DRL is used.
1.2. Paper Contribution
- The unwanted energy consumption and poor connectivity are reduced by optimally allocating the edge-assisted UAVs in the environment based on the MU’s request using the Beluga Whale Optimization (BLWO) algorithm.
- The energy consumption is minimized, and the mobility of users is captured by clustering the MUs using the triple-mode density peak clustering (TM-DPC) algorithm. This algorithm considers several parameters, such as mobility, density, acceleration, trajectory, and speed. The algorithm also selects cluster heads (CHs) based on high stability and less mobility.
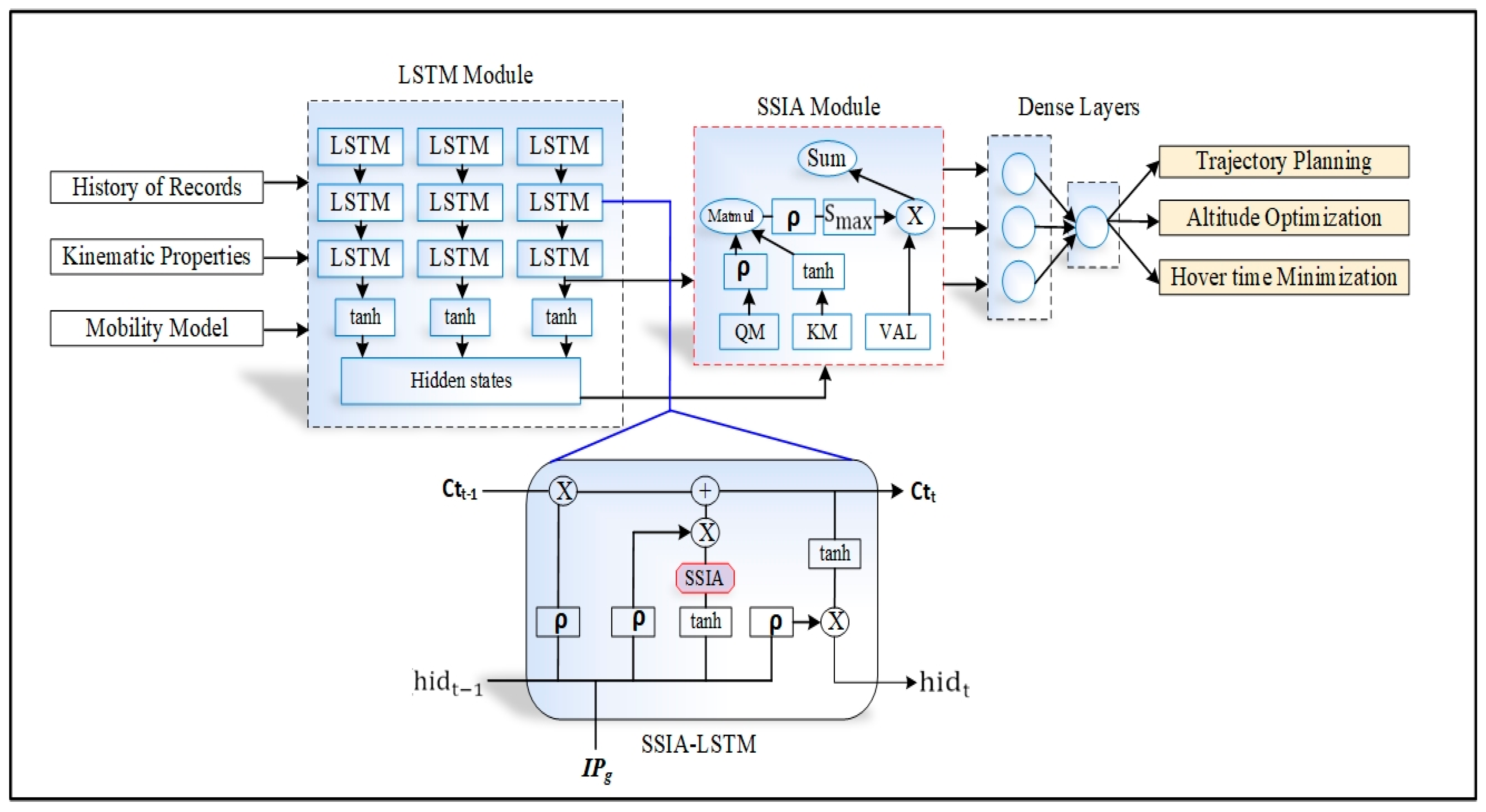
- Self-simulated inner attention long short-term memory (SSIA-LSTM) is used to optimize the hovering duration and reduce the energy consumption of MEC–UAVs during flight intervals. The autonomous trajectory planning and altitude optimization using SSIA-LSTM to enhance the coverage rate by optimally adjusting the altitude of UAVs.
- The robust resource allocation is achieved by applying an AFL-based cooperative dynamic E-UAV, which classifies the user request and performs auction-based dynamic resource allocation to MUs with less latency and optimized power consumption.
1.3. Novelty Highlights
1.4. Paper Organization
2. Literature Survey
2.1. UAV-Assisted Resource Allocation
2.2. MEC–UAV-Assisted Resource Allocation
3. Problem Formulation
4. System Model
4.1. Network Model
- A1: It is assumed that the MUs maintain a local database for executing fewer local computations.
- A2: It is considered that the MEC–UAVs have a higher capability and capacity to handle AI algorithms and execute computationally intensive tasks locally. Only in rare cases are the tasks from the UAVs offloaded to the GBSs.
- A3: The MEC–UAVs know the locations of other MEC–UAVs and MUs in the environment.
- A4: It is assumed that the MEC–UAVs generate local and shared global models for resource allocation using an AFL.
- A5: It is assumed that the multiple MEC–UAVs in the proposed environment do not collide with each other.
4.2. Modeling of Delay
4.3. Modeling of MU Association and Resource Allocation
4.4. Modeling of Energy Consumption
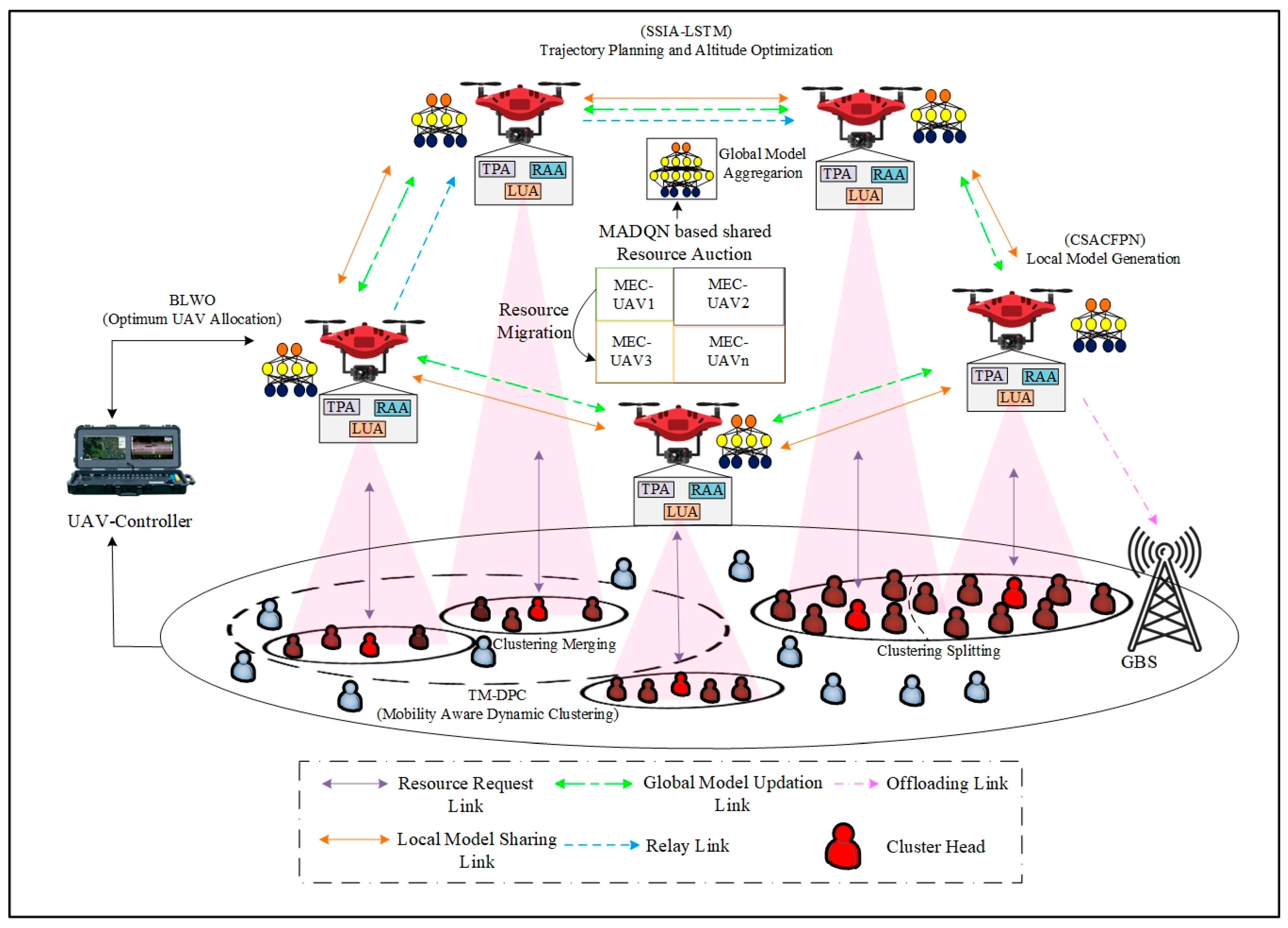
5. Proposed JO-TADP Model
- Optimum UAV allocation
- Mobility-aware dynamic MU clustering
- DL-based autonomous trajectory planning and altitude optimization
- AFL-based cooperative dynamic UAV resource allocation
5.1. Optimum UAV Allocation
5.1.1. Global Search Phase
5.1.2. Local Search Phase
5.1.3. Optimum Allocation Phase
5.2. Mobility-Aware Dynamic Clustering
- Cluster centers of MUs have increased local density
- Increased distance from the other cluster center
| Algorithm 1 Optimum MEC–UAV Allocation |
| Input: , |
| Output: Optimum MEC–UAV Allocation |
| Start |
| Population initialization and fitness evaluation using Equations (20) and (21) |
| While |
| Determine harmonization factor using Equation (22) |
| For every do |
| If then |
| ‘Global Search Phase’ |
| Update the position of MEC–UAVs using Equation (23) |
| Else If |
| ‘Local Search Phase’ |
| Computing levy flight and apprise the intensity factor |
| Update the position of MEC–UAVs using Equation (24) |
| End If |
| End For |
| For every do |
| ‘Optimum MEC–UAVs Allocation Phase’ |
| If then |
| Intensity factor updating |
| Compute the using Equation (26) |
| Update the position |
| Determine the using Equation (27) |
| End If |
| End For |
| iter = iter + 1 |
| End While |
| Return Optimum MEC–UAV Allocation |
| End |
5.3. DL-Based Autonomous Trajectory Planning and Altitude Optimization
| Algorithm 2 DL-based Trajectory Planning and Altitude Optimization |
| Input: Trajectory and Altitude Optimization Metrics |
| Output: |
| Start |
| Initialize |
| For all the MEC–UAVs do |
| Compute according to Equations (37) and (38) |
| For do |
| Initialize the gates according to Equation (39) |
| Determine the forget gate according to Equation (40) |
| Determine the Input gate according to Equation (41) |
| Determine according to Equation (42) |
| \* Self-Stimulated Inner Attention (SSIA)\* |
| Represent in the form of a matrix according to Equation (43) |
| Compute QM and KM according to Equations (44) and (45) |
| Compute ASM according to Equation (46) |
| Compute according to Equation (47) |
| Determine according to Equation (48) |
| Determine and according to Equations (49) and (50) |
| End For |
| Perform |
| Perform |
| Perform |
| End For |
| End |
5.4. AFL-Based Cooperative Dynamic MEC–UAV Resource Allocation
5.4.1. Local Model Generation
5.4.2. Shared Global Model Generation
- : It denotes the current state of MEC–UAVs, i.e., availability of resources, amount of CPU cycles, and current cost.
- : It denotes the actions taken by the MEC–UAVs in the environment, i.e., shared dynamic resource allocation based on the MU constraints.
- : Maximizing the utility function and satisfying the QoS of MUs.
| Algorithm 3 AFL-Based Shared Dynamic Resource Allocation |
| Input: Non-Familiar Resource Request from MUs |
| Output: Shared Dynamic Resource Allocation |
| Start |
| While all the non-familiar requests do |
| For all the MUs do |
| Perform local model generation according to Equations (55)–(61) |
| Provide the local model to MEC–UAVs |
| End For |
| For do |
| For all the MEC–UAVs do |
| Perform shared dynamic global model generation using Equations (62)–(64) |
| AFL-based shared global model, according to Equation (65) |
| End For |
| End For |
| End While |
| End |
6. Experimental Results
6.1. Simulation Setup
6.2. Comparative Analysis
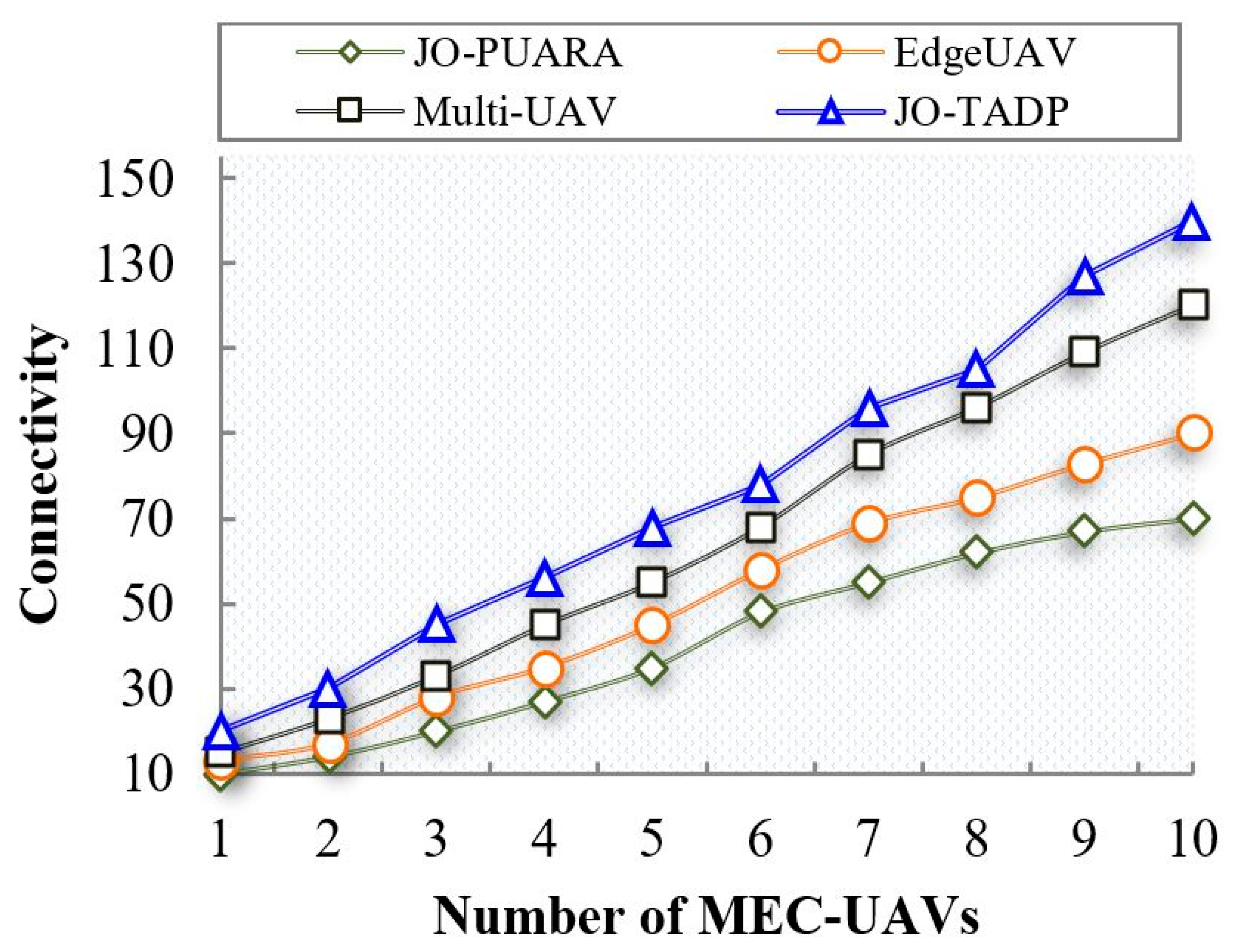
6.2.1. Analysis of Connectivity
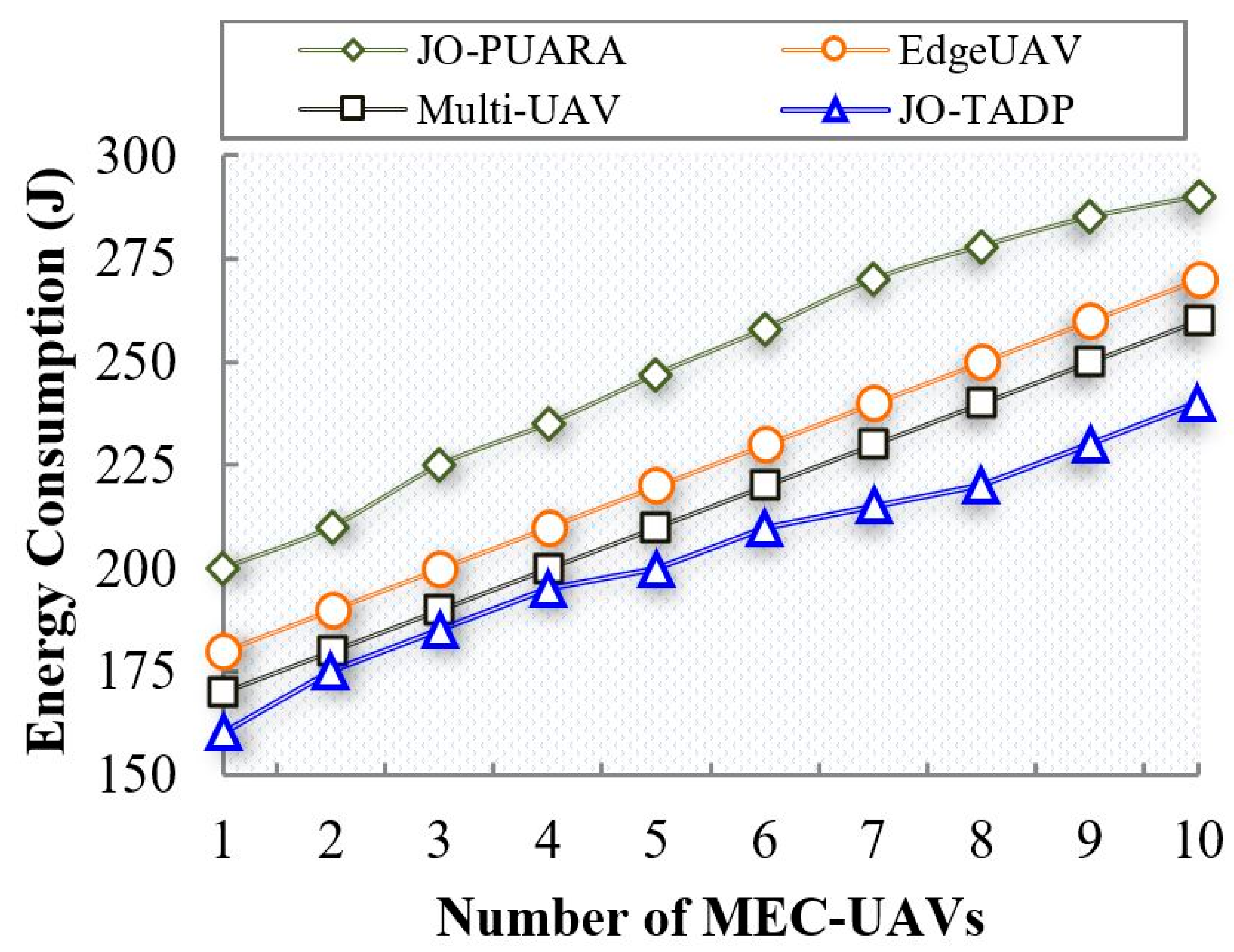
6.2.2. Analysis of Energy Consumption
6.2.3. Analysis of Utility Rate
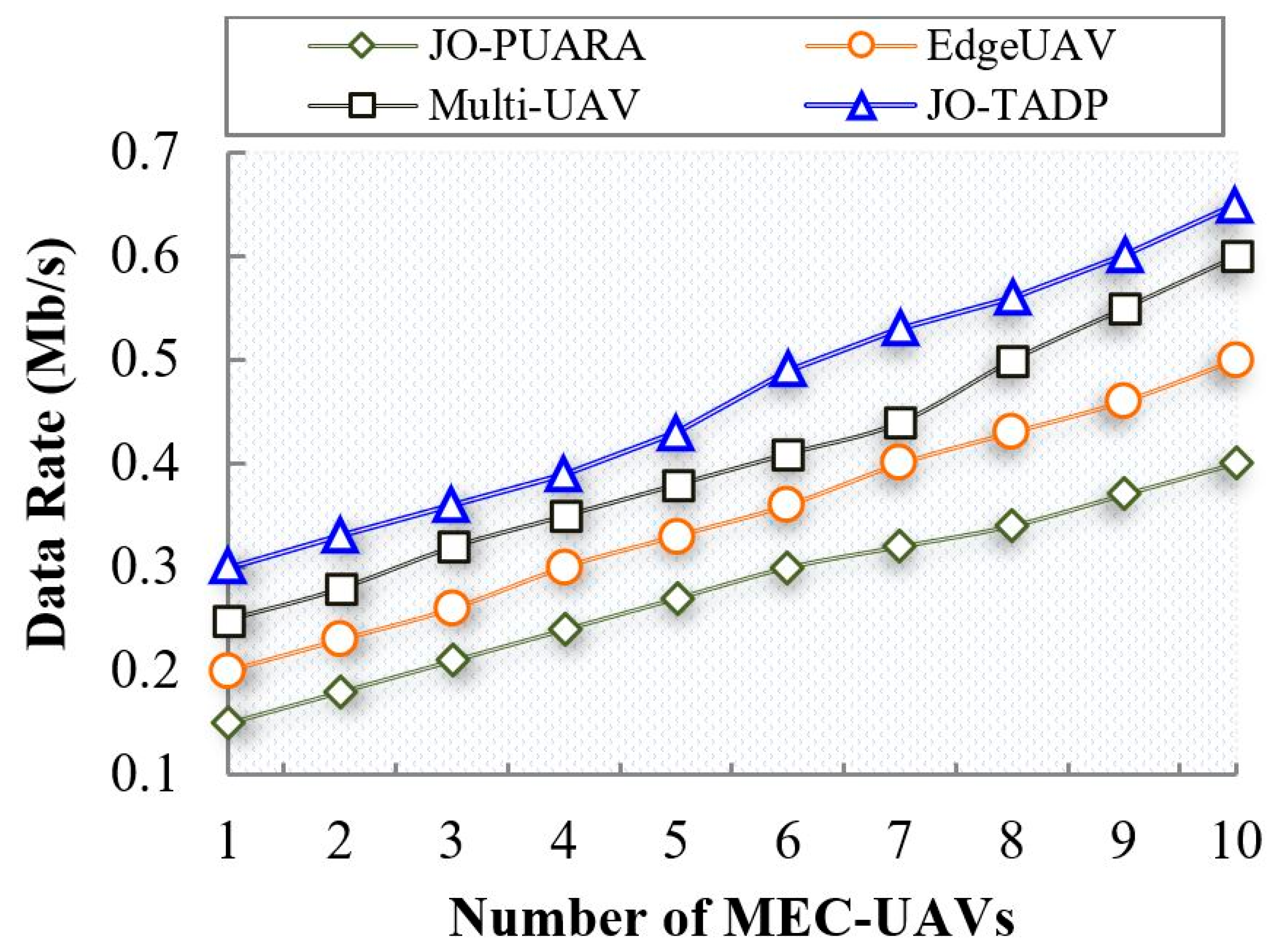
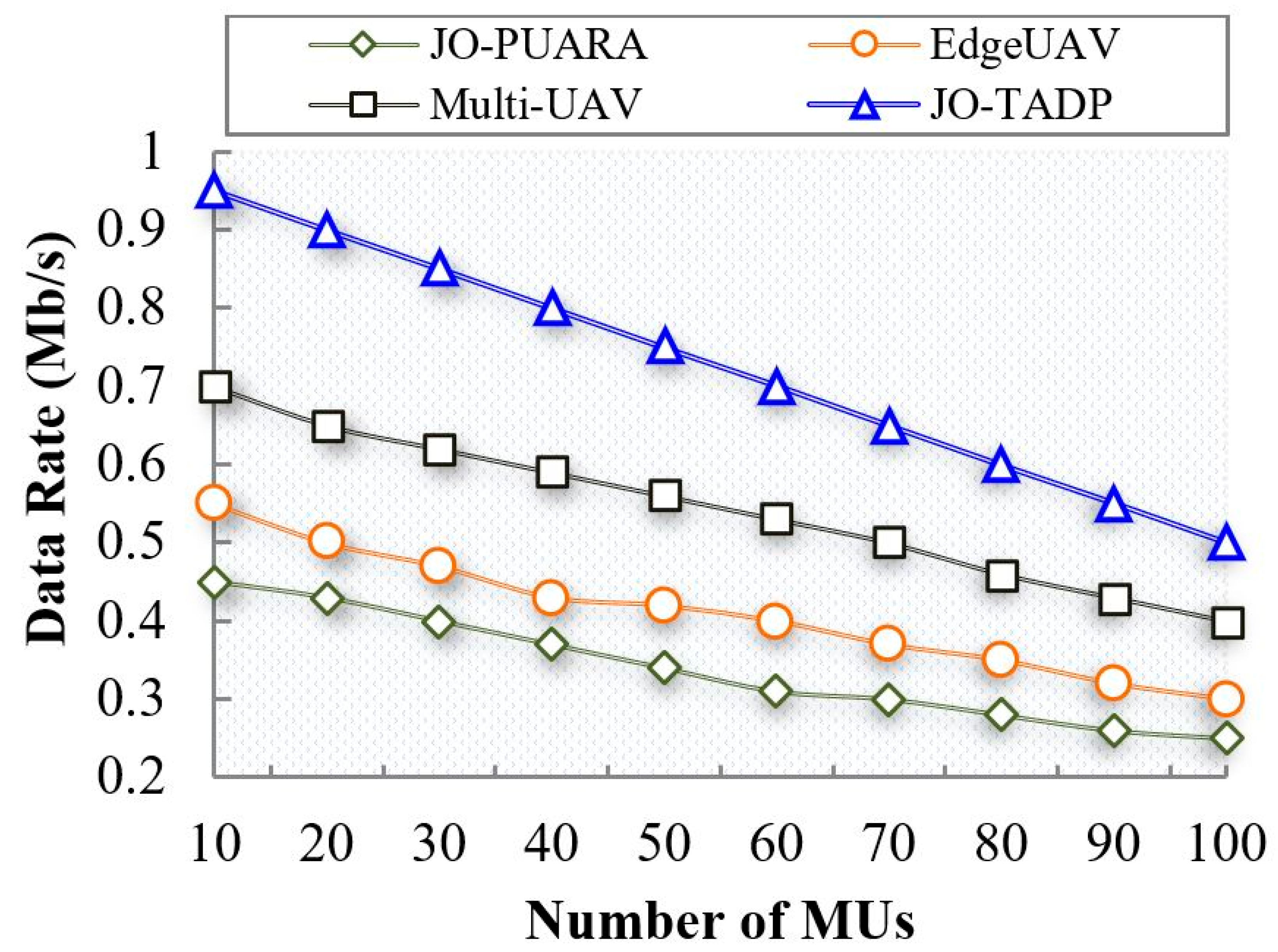
6.2.4. Analysis of Data Rate
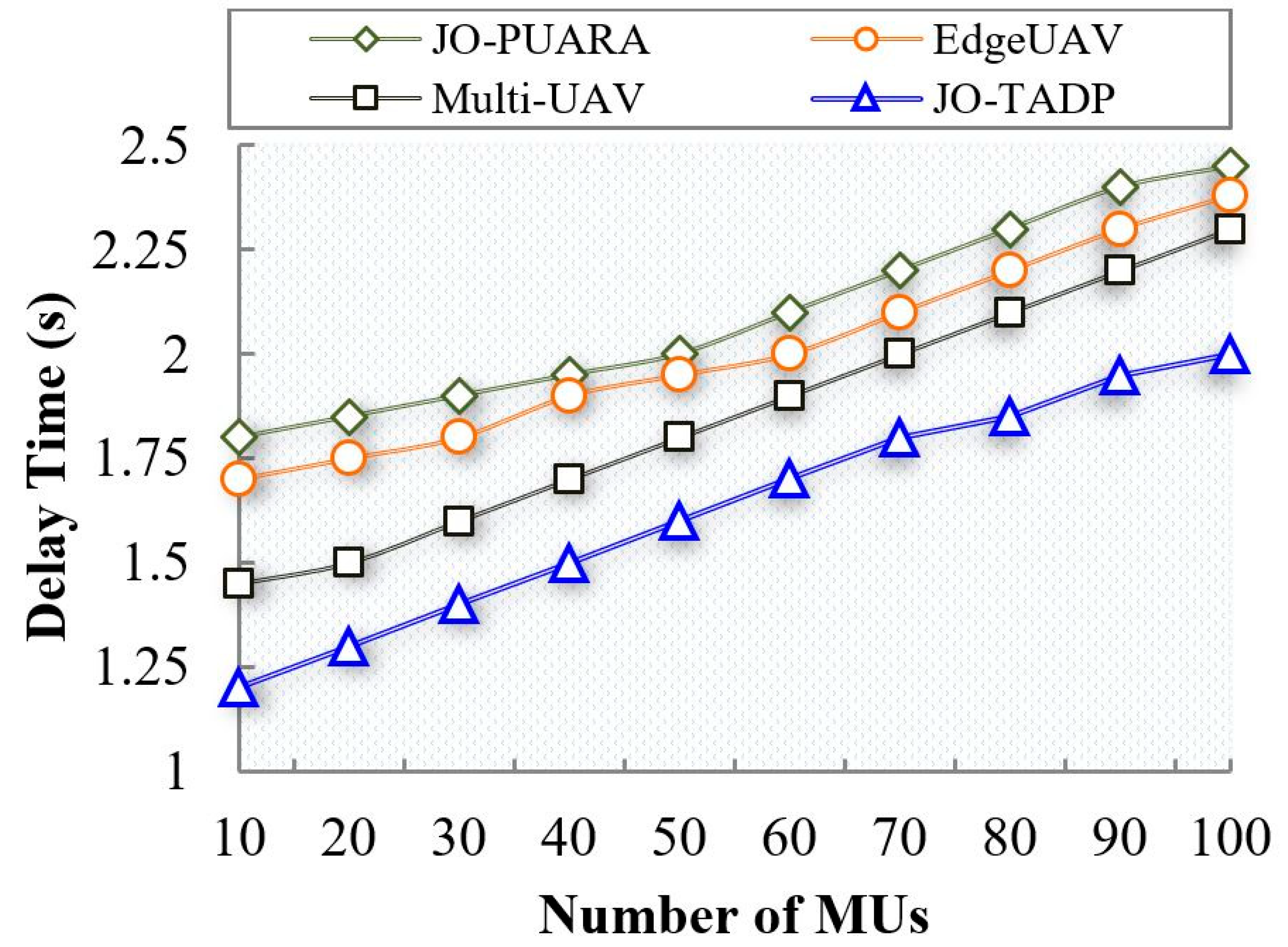
6.2.5. Analysis of Delay Time
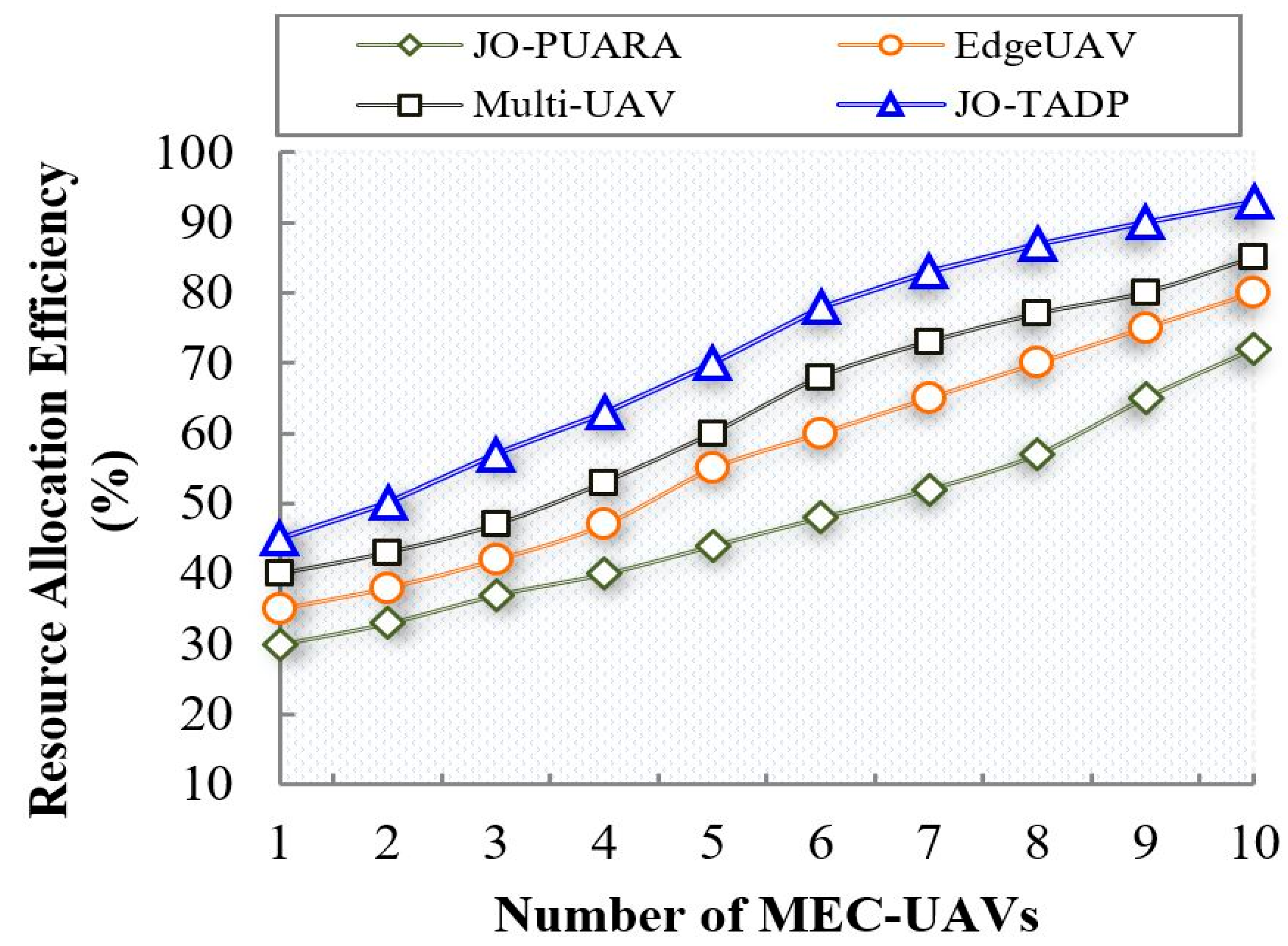
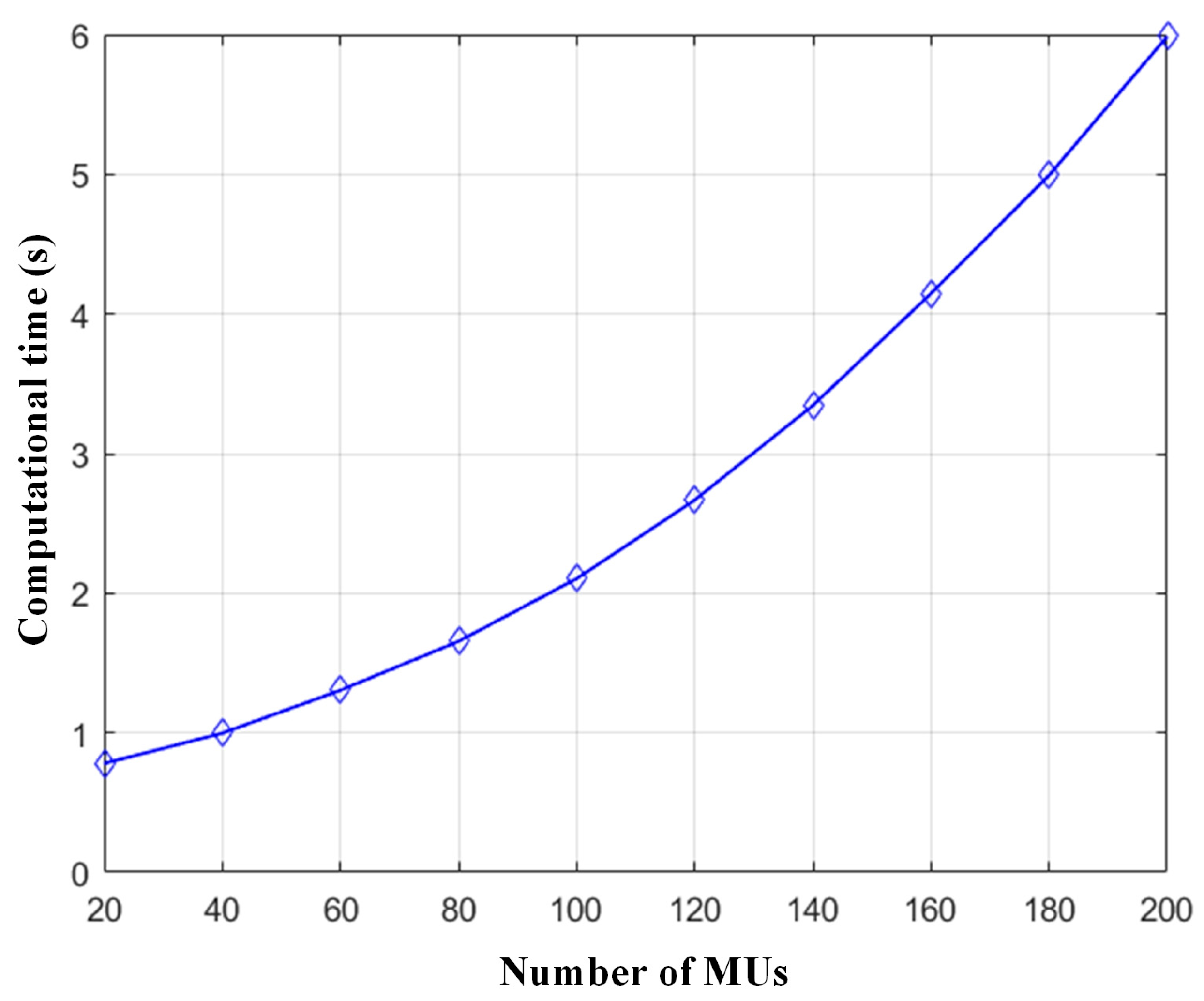
6.2.6. Analysis of Resource Allocation Efficiency
6.3. Summary
7. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dujuan, H. Mobile Communication Technology of Sports Events in 5G era. Microprocess. Microsyst. 2020, 80, 103331. [Google Scholar] [CrossRef]
- Ahmed, S.; Ameen, S.Y.; Zeebaree, S.R. 5G Mobile Communication System Performance Improvement with Caching: A Review. In Proceedings of the International Conference of Modern Trends in Information and Communication Technology Industry (MTICTI), Sana’a, Yemen, 4–6 December 2021; pp. 1–8. [Google Scholar]
- Zhang, J.A.; Rahman, M.L.; Wu, K.; Huang, X.; Guo, Y.J.; Chen, S.; Yuan, J. Enabling Joint Communication and Radar Sensing in Mobile Networks—A Survey. IEEE Commun. Surv. Tutor. 2020, 24, 306–345. [Google Scholar] [CrossRef]
- Khan, A.; Zhang, J.; Ahmad, S.; Memon, S.; Qureshi, H.A.; Ishfaq, M. Dynamic Positioning and Energy-Efficient Path Planning for Disaster Scenarios in 5G-Assisted Multi-UAV Environments. Electronics 2022, 11, 2197. [Google Scholar] [CrossRef]
- Kurniawan, I.F.; Asyhari, A.T.; He, F.; Liu, Y. Mobile Computing and Communications-Driven Fog-Assisted Disaster Evacuation Techniques for Context-Aware Guidance Support: A survey. Comput. Commun 2021, 179, 195–216. [Google Scholar] [CrossRef]
- Jung, S.; Yun, W.J.; Kim, J.; Kim, J. Coordinated Multi-Agent Deep Reinforcement Learning for Energy-Aware UAV-Based Big-Data Platforms. Electronics 2021, 10, 543. [Google Scholar] [CrossRef]
- Taleb, T.; Ksentini, A.; Hellaoui, H.; Bekkouche, O. On Supporting UAV Based Services in 5G and Beyond Mobile Systems. IEEE Netw. 2021, 35, 220–227. [Google Scholar] [CrossRef]
- Singhal, C.; Chandana, B.N. Aerial-SON: UAV-based Self-Organizing Network for Video Streaming in Dense Urban Scenario. In Proceedings of the International Conference on Communication Systems & NetworkS (COMSNETS), Bangalore, India, 5–9 January 2021; pp. 7–12. [Google Scholar]
- Kim, S.; Kim, Y. An Energy Efficient UAV-Based Edge Computing System with Reliability Guarantee for Mobile Ground Nodes. Sensors 2021, 21, 8264. [Google Scholar] [CrossRef]
- Islam, N.; Rashid, M.M.; Pasandideh, F.; Ray, B.R.; Moore, S.T.; Kadel, R. A Review of Applications and Communication Technologies for Internet of Things (IoT) and Unmanned Aerial Vehicle (UAV) Based Sustainable Smart Farming. Sustainability 2021, 13, 1821. [Google Scholar] [CrossRef]
- McEnroe, P.; Wang, S.; Liyanage, M. A Survey on the Convergence of Edge Computing and AI for UAVs: Opportunities and Challenges. IEEE Internet Things J. 2022, 9, 15435–15459. [Google Scholar] [CrossRef]
- Ren, J.; Yu, G.; He, Y.; Li, G.Y. Collaborative cloud and edge computing for latency minimization. IEEE Trans. Veh. Technol. 2019, 68, 5031–5044. [Google Scholar] [CrossRef]
- Khan, A.; Zhang, J.; Ahmad, S.; Memon, S.; Hayat, B.; Rafiq, A. Dqn-based Proactive Trajectory Planning of UAVs in Multi-access edge computing. Comput. Mater. Contin. 2023, 74, 4685–4702. [Google Scholar] [CrossRef]
- Wang, J.; Ma, Y.; Lu, R.; Wang, J.; Lin, M.; Cheng, J. Hovering UAV-Based FSO Communications: Channel Modelling, Performance Analysis, and Parameter Optimization. IEEE J. Sel. Areas Commun. 2021, 39, 2946–2959. [Google Scholar] [CrossRef]
- Qian, Y. Unmanned aerial vehicles and multi-access edge computing. IEEE Wirel. Commun. 2021, 28, 2–3. [Google Scholar] [CrossRef]
- Liu, Z.; Cao, Y.; Gao, P.; Hua, X.; Zhang, D.; Jiang, T. Multi-UAV network assisted intelligent edge computing: Challenges and opportunities. China Commun. 2022, 19, 258–278. [Google Scholar] [CrossRef]
- Niculescu, V.; Palossi, D.; Magno, M.; Benini, L. Fly, Wake-up, Find: UAV-based Energy-efficient Localization for Distributed Sensor Nodes. Sustain. Comput. Inform. Syst. 2022, 34, 100666. [Google Scholar] [CrossRef]
- He, X.; Jin, R.; Dai, H. Joint Service Placement and Resource Allocation for Multi-UAV Collaborative Edge Computing. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- He, X.; Li, X.; Ji, H.; Zhang, H. Resource Allocation for Secrecy Rate Optimization in UAV-assisted Cognitive Radio Network. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Li, K.; Ni, W.; Kurunathan, H.; Dressler, F. Data-driven Deep Reinforcement Learning for Online Flight Resource Allocation in UAV-aided Wireless Powered Sensor Networks. In Proceedings of the ICC—IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 1–6. [Google Scholar]
- Nie, Y.; Zhao, J.; Gao, F.; Yu, F.R. Semi-Distributed Resource Management in UAV-Aided MEC Systems: A Multi-Agent Federated Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2021, 70, 13162–13173. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, Y.; Zhang, H. Deep Reinforcement Learning based Path Planning for UAV-assisted Edge Computing Networks. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Tun, Y.K.; Dang, T.N.; Kim, K.; Alsenwi, M.; Saad, W.; Hong, C.S. Collaboration in the Sky: A Distributed Framework for Task Offloading and Resource Allocation in Multi-Access Edge Computing. IEEE Internet Things J. 2021, 9, 24221–24235. [Google Scholar] [CrossRef]
- Zhai, D.; Li, H.; Tang, X.; Zhang, R.; Cao, H. Joint Position Optimization, User Association, and Resource Allocation for load Balancing in UAV-assisted Wireless Networks. Digit. Commun. Netw. 2022. [Google Scholar] [CrossRef]
- Cheng, Z.; Liwang, M.; Chen, N.; Huang, L.; Guizani, N.; Du, X. Learning-based User Association and Dynamic Resource Allocation in Multi-Connectivity Enabled Unmanned Aerial Vehicle Networks. Digit. Commun. Netw. 2022. [Google Scholar] [CrossRef]
- Yang, H.; Zhao, J.; Xiong, Z.; Lam, K.; Sun, S.; Xiao, L. Privacy-Preserving Federated Learning for UAV-Enabled Networks: Learning-Based Joint Scheduling and Resource Management. IEEE J. Sel. Areas Commun. 2020, 39, 3144–3159. [Google Scholar] [CrossRef]
- Tran, D.; Nguyen, V.; Gautam, S.; Chatzinotas, S.; Vu, T.X.; Ottersten, B.E. UAV Relay-Assisted Emergency Communications in IoT Networks: Resource Allocation and Trajectory Optimization. IEEE Trans. Wirel. Commun. 2020, 21, 1621–1637. [Google Scholar] [CrossRef]
- Chen, X.; Liu, X.; Chen, Y.; Jiao, L.; Min, G. Deep Q-Network based Resource Allocation for UAV-assisted Ultra-Dense Networks. Comput. Networks 2021, 196, 108249. [Google Scholar] [CrossRef]
- Wang, Z.; Wen, M.; Dang, S.; Yu, L.; Wang, Y. Trajectory Design and Resource Allocation for UAV Energy Minimization in a Rotary-wing UAV-enabled WPCN. Alex. Eng. J. 2021, 60, 1787–1796. [Google Scholar] [CrossRef]
- Manzoor, A.; Kim, K.; Pandey, S.R.; Kazmi, S.M.; Tran, N.H.; Saad, W.; Hong, C.S. Ruin Theory for Energy-Efficient Resource Allocation in UAV-Assisted Cellular Networks. IEEE Trans. Commun. 2021, 69, 3943–3956. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Long, K.; Jiang, C.; Guizani, M. Joint Resource Allocation and Trajectory Optimization with QoS in UAV-Based NOMA Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 6343–6355. [Google Scholar] [CrossRef]
- Do-Duy, T.; Nguyen, L.D.; Duong, T.Q.; Khosravirad, S.R.; Claussen, H. Joint Optimisation of Real-Time Deployment and Resource Allocation for UAV-Aided Disaster Emergency Communications. IEEE J. Sel. Areas Commun. 2021, 39, 3411–3424. [Google Scholar] [CrossRef]
- Luong, P.; Gagnon, F.; Tran, L.; Labeau, F. Deep Reinforcement Learning-Based Resource Allocation in Cooperative UAV-Assisted Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 7610–7625. [Google Scholar] [CrossRef]
- Seid, A.M.; Boateng, G.O.; Anokye, S.; Kwantwi, T.; Sun, G.; Liu, G. Collaborative Computation Offloading and Resource Allocation in Multi-UAV-Assisted IoT Networks: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2021, 8, 12203–12218. [Google Scholar] [CrossRef]
- Cao, H.; Hu, Y.; Yang, L. Towards intelligent virtual resource allocation in UAVs-assisted 5G networks. Comput. Netw. 2020, 185, 107660. [Google Scholar] [CrossRef]
- Niu, H.; Zhao, X.; Li, J. 3D Location and Resource Allocation Optimization for UAV-Enabled Emergency Networks Under Statistical QoS Constraint. IEEE Access 2021, 9, 41566–41576. [Google Scholar] [CrossRef]
- Chang, Z.; Deng, H.; You, L.; Min, G.; Garg, S.; Kaddoum, G. Trajectory Design and Resource Allocation for Multi-UAV Networks: Deep Reinforcement Learning Approaches. IEEE Trans. Netw. Sci. Eng. 2022, 1. [Google Scholar] [CrossRef]
- Ji, J.; Zhu, K.; Yi, C.; Niyato, D.T. Energy Consumption Minimization in UAV-Assisted Mobile-Edge Computing Systems: Joint Resource Allocation and Trajectory Design. IEEE Internet Things J. 2021, 8, 8570–8584. [Google Scholar] [CrossRef]
- Huang, J.; Xu, S.; Zhang, J.; Wu, Y. Resource Allocation and 3D Deployment of UAVs-Assisted MEC Network with Air-Ground Cooperation. Sensors 2022, 22, 2590. [Google Scholar] [CrossRef] [PubMed]
- Ei, N.N.; Alsenwi, M.; Tun, Y.K.; Han, Z.; Hong, C.S. Energy-Efficient Resource Allocation in Multi-UAV-Assisted Two-Stage Edge Computing for Beyond 5G Networks. IEEE Trans. Intell. Transp. Syst. 2020, 23, 16421–16432. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, T.; Liu, Y.; Yang, D.; Xiao, L.; Tao, M. UAV-Assisted MEC Networks with Aerial and Ground Cooperation. IEEE Trans. Wirel. Commun. 2021, 20, 7712–7727. [Google Scholar] [CrossRef]
- Tan, T.; Zhao, M.; Zeng, Z. Joint Offloading and Resource Allocation Based on UAV-Assisted Mobile Edge Computing. ACM Trans. Sens. Netw. 2022, 18, 1–21. [Google Scholar] [CrossRef]
- Cao, P.; Liu, Y.; Yang, C. Robust Resource Allocation and Trajectory Planning of UAV-Aided Mobile Edge Computing in Post-Disaster Areas. Appl. Sci. 2022, 12, 2226. [Google Scholar] [CrossRef]
- Correll, N.; Hayes, B.; Heckman, C.; Roncone, A. Introduction to Autonomous Robots: Mechanisms, Sensors, Actuators, and Algorithms; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Yang, H.; Zhang, X.; Khanduri, P.; Liu, J. Anarchic Federated Learning. Int. Conf. Mach. Learn. 2022, 162, 25331–25363. [Google Scholar]



| Existing Methods | Proposed Novelties |
|---|---|
| The existing works deploy UAVs in the environment in a random manner for resource allocation, which leads to unwanted energy consumption and leads to poor connectivity issues. Even though they use 3D model deployment, this issue affects the performance of UAVs. | The proposed work mitigates that issue by deploying optimum MEC–UAVs based on the MU density. To increase the scalability and speed during optimum UAV allocation, we adopt a heuristics algorithm named BLWO algorithm. |
| Most existing works did not consider MU constraints regarding their mobility for resource allocation in UAV-based wireless networks. The MUs are not static, which leads to service discontinuity. | We reduce the service discontinuity rate by performing MU clustering using a novel clustering algorithm named TW-DPC for mobility control and user association. In addition, the clusters are optimally managed by clustering, splitting, and merging, respectively. |
| The existing approaches provide resource allocation using only limited strategies. Specifically, they either optimize trajectory and resource allocation or user association and resource allocation, affecting resource allocation efficiency. | In this paper, we jointly optimize the trajectory, delay, altitude, and power of the MEC–UAVs. Furthermore, we have proposed a cooperative dynamic resource allocation method using an AFL algorithm. |
| Notation | Definition |
|---|---|
| MEC–UAVs | |
| MUs | |
| Channel sets of MEC–UAVs | |
| , | Bandwidth of familiar and non-familiar resources |
| Resource request | |
| E, D, P, C | Energy, delay, power, and computation optimization |
| TR, AL | Trajectory and altitude optimization |
| Optimization constant | |
| User association | |
| Hovering energy consumption | |
| Hovering power consumption | |
| Harmonization factor | |
| Local density | |
| Euclidean distance among two MUs | |
| Positive cluster region | |
| Evidence theory co-efficient | |
| Jerk of MEC–UAVs | |
| Val | Value |
| MTNP-SVM hyperplane constant | |
| L2 regularization function |
| Existing Methods | Reference | Objective | Algorithms/ Methods | Resource Allocation Strategies | Limitations | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| UAV-Alloc | TR | AL | DM | PO | UA | CO | |||||
| UAV-assisted Resource Allocation | [24] | To increase the sum rate of all the MUs in UAV-based wireless networks | Branch and Bound Method | 🗶 | 🗶 | 🗶 | 🗶 | ✔ | ✔ | 🗶 | Resource Disruption, High Energy Consumption |
| [25] | To achieve optimal resource allocation in multi-connectivity UAV networks | DRL | ✔ | 🗶 | 🗶 | 🗶 | 🗶 | ✔ | 🗶 | Deprived user connectivity, Inefficient resource allocation | |
| [26] | To preserve the privacy of the UAV-enabled MUs during resource allocation | FL, A3C algorithm | ✔ | 🗶 | 🗶 | 🗶 | 🗶 | ✔ | 🗶 | Less network lifetime, Delayed service provisioning | |
| [27] | To enable a conjoined resource allocation for UAV-based IoT networks | Iterative Algorithm | 🗶 | ✔ | 🗶 | 🗶 | 🗶 | 🗶 | 🗶 | Inefficient service provisioning | |
| [28] | To achieve energy-efficient resource allocation for ultra-dense UAV networks | MDP-based DQN | 🗶 | 🗶 | 🗶 | 🗶 | ✔ | ✔ | 🗶 | Less Stability | |
| [29] | To achieve the joint optimal resource allocation for UAV-enabled WPCN | Iterative Algorithm | 🗶 | ✔ | 🗶 | ✔ | ✔ | ✔ | 🗶 | Experiences unwanted energy consumption | |
| [30] | To achieve energy-constrained resource allocation for cellular-based UAV | Water-filling algorithm and ruin theory | 🗶 | 🗶 | 🗶 | ✔ | ✔ | ✔ | 🗶 | Unable to handle more user density | |
| [31] | To increase the QoS and resource allocation efficiency by NOMA-based UAV networks | Heuristic Algorithm | 🗶 | ✔ | 🗶 | 🗶 | ✔ | 🗶 | 🗶 | Easily trapped with local minima and convergence problems | |
| [32] | To enhance the communication capability of UAVs by combined solutions | K-means Clustering Algorithm | ✔ | ✔ | 🗶 | 🗶 | ✔ | 🗶 | 🗶 | Increased complexity | |
| [33] | To increase the sum rate by enabling collaborative resource allocation using UAV | DQN and Convex Algorithm | ✔ | 🗶 | 🗶 | 🗶 | ✔ | ✔ | 🗶 | Unwanted energy consumption and poor connectivity | |
| [34] | To achieve collaborative resource allocation by multiple UAV-based IoT networks | Clustering and DDPG algorithm | 🗶 | 🗶 | 🗶 | ✔ | 🗶 | 🗶 | ✔ | Poor service provisioning | |
| [35] | To enable resource allocation in a virtual manner using 5G-based UAV networks | Two-stage resource allocation method | 🗶 | 🗶 | 🗶 | 🗶 | ✔ | ✔ | 🗶 | Ineffective resource allocation | |
| [36] | To improve the message efficiency by enabling 3D-based UAV resource allocation | Iterative Algorithm | ✔ | 🗶 | 🗶 | ✔ | ✔ | 🗶 | 🗶 | High collision rate and unwanted hovering | |
| [37] | To improve the coverage by enabling multiple UAV-based resource allocation | DQN algorithm | 🗶 | ✔ | 🗶 | ✔ | 🗶 | 🗶 | 🗶 | Poor coverage rate | |
| MEC–UAV-Assisted Resource Allocation | [38] | To reduce the resource allocation rate by MEC-based UAV resource allocation methods | Combined Resource Allocation Method | 🗶 | ✔ | 🗶 | 🗶 | ✔ | 🗶 | ✔ | Ineffective resource allocation and service provisioning, Poor trajectory optimization |
| [39] | To improve the resource allocation efficiency by 3D deployment in MEC-based UAV networks | Iterative Algorithm | ✔ | 🗶 | ✔ | ✔ | 🗶 | ✔ | 🗶 | Service discontinuity, Unwanted energy consumption | |
| [40] | To enhance the resource allocation efficiency by multiple UAV-based 5G MEC networks | Two-stage method and block successive upper bound minimization algorithm | 🗶 | 🗶 | 🗶 | ✔ | 🗶 | 🗶 | ✔ | Increased energy consumption | |
| [41] | To improve the connectivity among MUs and UAVs using MEC | Convex and Lagrange-based Methods | 🗶 | ✔ | 🗶 | ✔ | ✔ | ✔ | 🗶 | Experiencing poor coverage | |
| [42] | To enhance reliability by enabling combined offloading in MEC-based UAV networks | Power rate semi-qualitative relaxation method and Position optimization algorithm | ✔ | 🗶 | 🗶 | 🗶 | 🗶 | ✔ | ✔ | Lack of considering optimal user metrics | |
| [43] | To improve the connectivity in disaster areas by MEC-based UAVs | Iterative Algorithm and Lagrange Method | 🗶 | ✔ | 🗶 | 🗶 | ✔ | 🗶 | 🗶 | Lack of resilient coverage affects the connectivity | |
| Proposed Work JO-TADP | To improve the fairness and energy efficiency of MEC-assisted UAV networks | Optimization algorithm, Clustering algorithm, Deep learning algorithm, and DRL algorithm | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | Less energy consumption, High connectivity, Less delay, Increased reliability | |
| Entities in AFL | Properties |
|---|---|
| Global Server (Global model generator) |
|
| Clients (Local model generator) |
|
| Simulation and Network Parameters | Values |
|---|---|
| No. of MUs | 100 |
| No. of MEC–UAVs | 10 |
| No. of 5G GBS | 1 |
| No. of UAV controllers | 1 |
| Bandwidth | 2 MHz |
| Radius of the cell | [250, 350, 550, 850, 1050] |
| Average sensing radius of MEC–UAVs | 300 m |
| Minimum and Maximum height of MEC–UAVs | 40–140m |
| Carrier frequency | 3 GHz |
| Mobility model | Random waypoint |
| Area of simulation | 1500 m × 1500 m |
| Transmission power of MEC–UAVs | 30 dBm |
| Velocity of MEC–UAVs | ≈30 km/h |
| Velocity of MUs | 7 km/h |
| Slot for resource allocation | 25 ms |
| Interval of updation | 1.5 s |
| Size of the data | 50 MB |
| Noise of the MEC–UAVs | 10 dB |
| Path loss exponent and constant [24,38] | 3 and 1.54 × 10−5 |
| Loss due to air propagation | 0 dB |
| Loss in the free space | 33 dB |
| Validation Metrics | JO-PUARA | EdgeUAVs | Multi-UAV | JO-TADP | |
|---|---|---|---|---|---|
| Number of MEC–UAVs | Connectivity | 40.8 | 51.3 | 64.9 | 76.5 |
| Energy Consumption (J) | 249.8 | 225 | 215 | 203 | |
| Utility Rate | 176.5 | 216.5 | 257 | 323.2 | |
| Data Rate (Mb/s) | 0.278 | 0.347 | 0.408 | 0.464 | |
| Resource Allocation Efficiency (%) | 47.8 | 56.7 | 62.6 | 71.6 | |
| Number of MUs | Data rate (Mb/s) | 0.339 | 0.411 | 0.544 | 0.725 |
| Delay Time (s) | 2.095 | 2.008 | 1.855 | 1.63 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, S.; Zhang, J.; Khan, A.; Khan, U.A.; Hayat, B. JO-TADP: Learning-Based Cooperative Dynamic Resource Allocation for MEC–UAV-Enabled Wireless Network. Drones 2023, 7, 303. https://doi.org/10.3390/drones7050303
Ahmad S, Zhang J, Khan A, Khan UA, Hayat B. JO-TADP: Learning-Based Cooperative Dynamic Resource Allocation for MEC–UAV-Enabled Wireless Network. Drones. 2023; 7(5):303. https://doi.org/10.3390/drones7050303
Chicago/Turabian StyleAhmad, Shabeer, Jinling Zhang, Adil Khan, Umar Ajaib Khan, and Babar Hayat. 2023. "JO-TADP: Learning-Based Cooperative Dynamic Resource Allocation for MEC–UAV-Enabled Wireless Network" Drones 7, no. 5: 303. https://doi.org/10.3390/drones7050303
APA StyleAhmad, S., Zhang, J., Khan, A., Khan, U. A., & Hayat, B. (2023). JO-TADP: Learning-Based Cooperative Dynamic Resource Allocation for MEC–UAV-Enabled Wireless Network. Drones, 7(5), 303. https://doi.org/10.3390/drones7050303











