Abstract
This paper focuses on reducing execution delays of dynamic computing tasks in UAV-assisted fault-prone mobile edge computing (FP-MEC) systems, which combine mobile edge computing (MEC) and network function virtualization (NFV) technologies. FP-MEC is suited to meet Industrial Internet (IIN) requirements such as data privacy, low latency, and low-cost industrial scalability in specific scenarios. However, the reliability of virtual network functions (VNFs) deployed on UAVs could impact system performance. Thus, this paper proposes the dynamic task scheduling optimization algorithm (DTSOA) based on deep reinforcement learning (DRL) for resource allocation design. The formulated execution delay optimization problem is described as an integer linear programming problem and it is an NP-hard problem. To overcome the intractable problem, this paper discretizes it into a series of single-time slot optimization problems. Furthermore, the experimental rigor is improved by constructing a real-time server state update system to calculate the real-time server load situation and crash probability. Theoretical analysis and experiments show that the DTSOA has better application prospects than Q-learning and the recent search method (RSM), and it is closer to the traversal search method (TSM).
1. Introduction
IIN refers to the network that unites industrial production equipment with digital information technology, and it is a digital, informational and intelligent transformation carried out by industries. Taking industry as an example, it realizes real-time monitoring of the production processes through the use of Internet technology. It includes the overall improvement of the labor production safety and efficiency, breaking information barriers, optimizing energy consumption, reducing production costs, and improving the competitiveness of enterprises, etc. Unlike the consumer Internet, the IIN is more concerned with real-time data transmission, processing and data protection, rather than just the transmission of information. This means that the network and equipment of the IIN needs higher reliability and security to ensure the fast processing of the computing tasks while safeguarding data privacy. Computing tasks generated within the IIN system are mainly non-independent and identically distributed tasks with high variability in data size, type, and demand, which require execution equipment with the functions required to perform the tasks. The MEC technology makes up for the lack of computing resources in the terminal. At the edge of the network, the MEC technology allows the terminal to perform tasks with the help of computing resources. Furthermore, it reduces the risk of data leakage by keeping the data in the system. However, the computing resources provided by MEC are still limited. Thus, efficient algorithms need to be designed to optimize the computing resources allocation to overcome the rapidly growing number of terminals and data tasks.
Adopting computationally capable UAVs as MEC servers has the following two benefits. First and foremost, UAVs fully satisfy the data privacy requirements of IIN, and the UAV-assisted MEC combined with IIN (UAVs-MEC-IIN) system. It is more efficient than mobile edge computing combined with the Industrial Internet (MEC-IIN), which is directly connected to the Internet. UAVs-MEC-IIN systems build edge computing power and terminals in a local area network (LAN). The data could be isolated within the local area network, preventing data leakage from the root, and guaranteeing the special needs of some scenarios of IIN. Additionally, UAVs exist in the IIN system as auxiliary communication nodes for emergency scenarios. If there is an unexpected scenario of a sudden increase in data volume or a communication network failure, UAVs are quickly adopted to provide arithmetic power and build emergency communication networks based on its dynamic characteristics. In the case of difficult deployment of ground communication equipment such as earthquake relief, UAVs play the advantage of building communication networks in the air to ensure the smooth implementation of rescue and other operations.
NFV separates network functions from proprietary hardware and allows network service providers to implement network functions as software running on physical nodes [1], which has the advantage that service providers could provide a dynamic and adaptive service function chain (SFC) embedding solutions to handle the large amount of data in IIN networks [2,3], and then with the help of machine learning tools, the data can be used rationally, which effectively improves the carrying capacity of the system and optimizes the network performance.
In recent years, Pei et al. [4] studied the VNF placement problem in software defined networking (SDN) /NFV networks using DRL to schedule dynamic network loads. Suzuki et al. [5] used an efficient coordination algorithm based on reinforcement learning (RL) to assign VNFs to the physical network. Sun et al. [6] presented a study on the VNF placement problem, taking into account randomized data traffic. The goal is to identify optimal VNF deployment locations while minimizing overall end-to-end delay. Two metaheuristic approaches, greedy and simulated annealing, are proposed to find near-optimal placement solutions. As the field of NFV has been intensively studied, the problem of VNF/SFC configuration with reliability has attracted the attention of many scholars. Pham et al. [7] propose novel models and algorithms for fault tolerance in NFV. Their optimization models and algorithm efficiently protect an NFV service demand from network failures without controller intervention, and enable the recovery of affected bandwidth under multiple network failures. Deploying redundant backup VNFs near VNFs is a way to enhance the reliability of task execution [8,9,10]. Fan et al. [11] assumed that servers with static failure probability operate in an alternating normal and failure environment, and adopted an approximation algorithm to reduce the deployment cost of backup VNFs. Li et al. [12] aimed to maximize the number of requests received with reliability requirements over a period of time. Yang et al. [13] guaranteed the reliability of VNFs by converting static failure probability to k-1 backup VNFs deployed in the underlying network. Yu et al. [14] transformed the static failure probability into a dynamic crash probability that simultaneously changes with the number of tasks executing.
The above studies are all about the VNF tasks problem. The computing power of IIN terminals is significantly insufficient in processing various types of VNF computing tasks, which increases the probability of crashes of VNFs with a higher likelihood of failure and has an adverse impact on the system operation and task execution [15]. Fortunately, MEC technology could transfer computing tasks from terminals to edge computing servers with stronger computing capabilities. As mentioned earlier, UAV-assisted MEC has particular advantages in IIN. Therefore, the following mainly introduces the research work related to UAV-assisted MEC. Hu et al. [16] addressed the processing delay problem among terminals in UAV-assisted MEC systems, proposing an algorithm based on a penalty pairwise decomposition optimization framework to optimize computational offloading. Diao et al. [17] studied the problem of fair-aware task data allocation and trajectory optimization in UAV-assisted MEC systems. Pourghasemian et al. [18] investigated dynamic resource allocation, UAV trajectory design, VNF placement and scheduling framework for UAV-assisted networks to support heterogeneous services with different QoS requirements.
Current work related to UAV-assisted MEC systems focuses on studying the offload scheduling of computational tasks, and a few works introduce the study of the deployment location of VNFs, but do not consider the problem of dynamic crash probability of edge servers deployed with VNFs. UAVs are affected by factors such as size, and the service reliability is limited by deploying VNFs to UAVs. In order to achieve the goal of reducing the crash probability of each server and ultimately meet the low-latency and high-reliability service requirements of the IIN, it is necessary to optimize the offloading computation locations of the scheduled tasks. However, there is currently no relevant research in this field. Therefore, the work in this paper introduces failure-prone MEC systems to weigh the crash probability of MEC servers to optimize resource allocation and increase the reliability of deployed with VNFs UAV-assisted MEC servers.
The dynamic and unpredictable nature of task arrivals leads to dynamic changes in the reliability of the edge servers where VNFs are deployed [19,20]. A series of studies have shown that the problem of deploying VNF tasks is an NP-hard problem [21,22,23], and furthermore, the deployment of VNF tasks should be dynamically adjusted with device load and time [24]. Sun et al. [25] thoroughly examine the VNF placement problem, providing a comprehensive analysis of the latest research results and identifying open challenges in the field. They propose a general definition and fine-grained classification of VNF placement works, covering emerging scenarios such as backbone networks, mobile networks, and the Internet of Things. In summary, these problems within resource-limited FP-MEC systems pose three challenges for the reliable execution of SFCs under dynamic conditions: (1) how to dynamically select the execution locations of VNFs in each SFC to meet the task requirements; (2) how to deploy redundant backup VNF locations in each latency-sensitive SFC; and (3) how to obtain the maximum benefit in the face of computational resources that cannot meet all computational task requirements.
Most of the mentioned solutions to the VNF layout problem require complex mathematical models to solve the abstract problem. These complex mathematical models can only be used when the network size is small, and heuristic algorithms are preferred in large-scale networks. However, due to the lack of rigorous theoretical proofs, heuristic algorithms are not guaranteed to obtain near-optimal results. Unlike the above methods, the DTSOA algorithm proposed in this paper is based on the DRL technique, which has the advantages of being more robust to network size and scalability and is a feasible technique to solve NP-hard problems [5,25,26,27,28,29,30,31].
In this paper, we first describe the system time delay optimization problem as an integer linear programming problem, which is discretized into a series of single time slot optimization problems. In addition, in order to make the time delay model more accurate, this paper constructs a real-time server state update system to enhance the experimental rigor, which accurately feed and update the real-time state of each server at each time slot. Finally, this paper proposes an online scheme to solve this latency optimization problem. The limited intra-system resources are adopted to solve the computational tasks generated in the system, which achieve the purpose of reducing the total latency. The proposed scheme selects execution layer UAVs capable of performing the corresponding task type for each VNF computation task in each SFC, and also provides redundant backup VNFs for each VNF task in latency-sensitive SFCs to increase the reliability. Therefore, we use DRL in this paper, based on the characteristics of dynamicity, continuity and real-time data processing for task generation in the FP-MEC-IIN scenario. The intelligent processing of DRL is used to propose a DTSOA algorithm for dynamic task scheduling location optimization based on DRL, which schedules the offloading location of computational tasks and computational resource allocation in the system to optimize the total computational delay. The simulation experiments based on python were conducted to consider the impact of different parameters on the cost and give the algorithm performance simulation results. The main contributions of this paper are as follows:
- (1)
- In this paper, we study the problem of MEC-IIN scenario from a new perspective. According to the characteristics of the IIN scenario, dynamic UAVs are introduced as edge arithmetic to assist resource-limited IIN end devices to perform computational tasks.
- (2)
- For latency-sensitive tasks, the dynamic crash probability of MEC server is introduced, and the backup synchronous execution is used to increase the reliability. By jointly optimizing task execution device selection and computing resource allocation, an effective strategy to reduce system latency under this model is investigated.
- (3)
- In this paper, a real-time equipment status update system is constructed to make the equipment working status data in the system real-time and accurate. The introduction of this system makes the dynamic update of crash probability coefficients more accurate and provides more real-time valid information to assist decision making for the dynamic deployment of VNFs by algorithms.
- (4)
- To capture and handle the time-varying failure probabilities of VNFs, the long-term resource provisioning problem is discretized into a series of single-slot optimization problems, which are shown to be NP-hard.
2. Materials and Methods
2.1. System Model
2.1.1. Network Model
As shown in Figure 1, this paper studies the task scheduling and resource allocation problems in the cluster of UAVs, with the executing UAVs as edge servers to assist in computing. The UAVs keep the task data in the system and compensate for the lack of computing power and the need for long endurance of the IIN terminals. In this paper, we assume that UAVs have continuous input energy and meet the energy demand for any activity. Thus, the energy consumption of UAVs is ignored in this paper [14]. The system model uses a three-layer UAV cluster structure, and each of the three layers of UAVs has different functions. Each UAV’s position is represented by a three-dimensional coordinate (x, y, z).
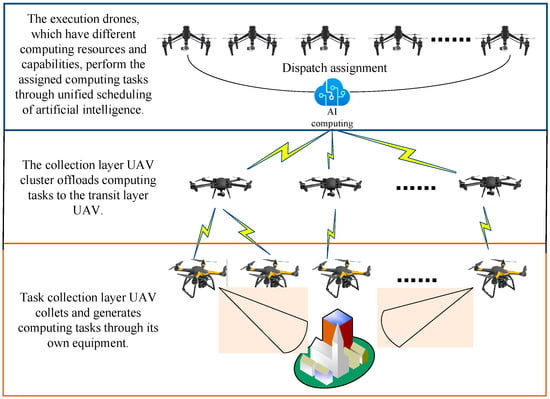
Figure 1.
Three-tier UAV non-independently and homogeneously distributed computational task execution system with the introduction of crash probability.
The lowermost UAVs serve as task collectors and are not responsible for computing tasks. They only generate computing tasks with specific task requirements through their own collection devices and transfer the task data to the transmission layer UAVs. The task data generated by different collection UAVs are independent of each other, and the transmission layer UAVs arrange the tasks transmitted by the collection UAVs within their reception range into one line according to the reception time SFC computation tasks. We assume that there are different kinds of VNFs deployed in the execution layer UAVs, by indicates a collection of virtual network features. Each execution layer UAV deploys one of these VNFs. The information transmitted to the transport layer UAV: VNF i = []. Where denotes the task generation time, denotes the VNF type required for the task, denotes the computational data size of the task, and is the delay-sensitive case marker.
The transport layer UAVs are located in the middle layer of the three-layer UAV system. This layer receives the computational tasks offloaded by the collection layer UAVs and synthesizes the computational task SFCs to send to the execution layer UAVs according to the rules, where each transport layer UAV receives only the computational tasks offloaded by the collection layer UAVs within its receiving range. Let Γ be an SFC task request sent by a transport layer UAV, it can then be defined as a . Where represents the set of demanded VNF categories, represents the SFC task sending time, represents the task reliability demand probability of request , which ranges from , is the set of computed data sizes, and is the delay-sensitive case marker.
2.1.2. Crash Probability Model
In this paper, we introduce system crash probability and dynamic crash probability for the execution layer UAVs. The crash probability values are positively correlated with the number of tasks executed simultaneously by the devices. In order to accurately discover the state of each device at each moment, this paper innovatively builds a real-time server state update system in the UAV-assisted MEC server. The technical principle is shown in Figure 2.
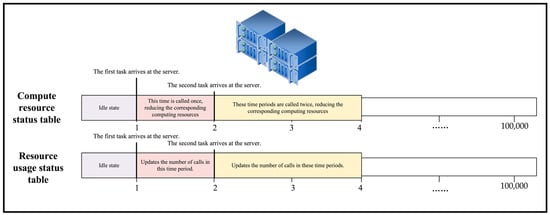
Figure 2.
The working principle of server status real-time update system.
When building a real-time server status update system, to begin with, two separate lists are created for each execution layer UAV: (1) a list of calculated resource states; (2) a list of the number of simultaneous resource invocation tasks. Second, the construction of the functionality is completed by writing functions that could read and update the above two lists in real time. On the one hand, the system introduced in this paper provides more information for the algorithm to dynamically deploy task execution location decision. On the other hand, the proposed system makes the dynamic crash probability of each device accurately updated in real time, so that the simulation experiment results are scientific and rigorous.
The crash probability of each executing UAV is dynamically updated with its own load; let UAV k have a base crash probability , and since the crash probability increases proportionally with the number of tasks executed simultaneously, let the crash probability increase by for each additional task. Thus, the final crash probability is expressed as follows:
where n denotes the number of simultaneous tasks performed by that UAV. It is assumed that the crash of any one UAV does not affect other UAVs, so the reliability of an SFC is the product of the reliability of the UAVs it uses:
where denotes the reliability rate of UAV k in the execution layer UAVs that SFC needs to use. The reliability rate of UAV k is denoted as follows:
2.1.3. Backup Parallel Execution Model
As shown in Figure 3: The SFCs in the system are divided into latency-sensitive and non-latency-sensitive, which are marked by location-specific values in the code. Latency-sensitive SFCs are assigned more computational resources and backup VNFs to ensure the speed and stability of task execution, and to guarantee the time efficiency of latency-sensitive SFCs to complete tasks. Take a backup SFC as an example, when executing a task, the latency-sensitive SFC first selects the best execution layer UAVs to execute the task according to the algorithm policy, while the backup SFC selects the second best execution layer UAVs to execute the task at the same time according to the algorithm policy. The benefit of the same SFC being executed by multiple different device chains in parallel has the following advantages: the crash of a single link device does not affect the execution stability of other links and improves the task execution reliability.
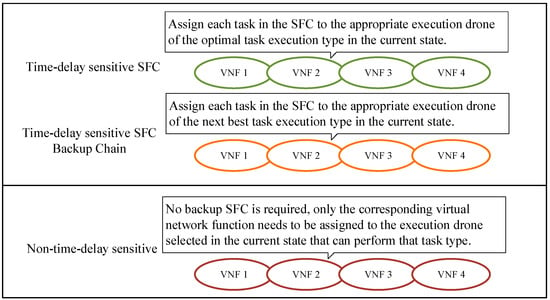
Figure 3.
Schematic diagram of the way delay-sensitive SFCs and non-delay-sensitive SFCs perform their tasks.
2.1.4. Communication Model
The execution layer UAVs are located at the uppermost layer of the three-tier UAV system. The task execution position of SFCs transmitted by the transport layer UAVs is planned and scheduled by the artificial intelligence system. The execution layer UAVs of the received tasks need to perform two parts of the operations: firstly, the task data belonging to that part are executed for calculation operations; secondly, the task calculation results and the original data of other tasks are forwarded to the execution UAVs of the subsequent received tasks, as shown in Figure 4.
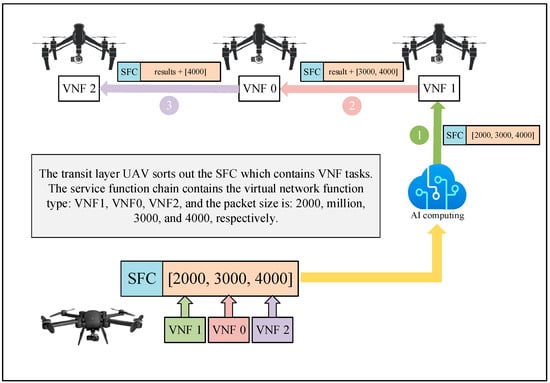
Figure 4.
The relationship between the packet transfer between UAVs and the execution of the SFC with 3 virtual network functions as an example.
According to the literature [32] the channel gain of the line-of-sight link between UAVs can be expressed as follows:
where is the channel gain at the reference distance d = 1 m, and is the Euclidean distance between the receiving UAV k and the transmitting UAV l, where k and l are the two UAVs involved in carrying out the transmission and reception of task i. Due to obstacle occlusion, the wireless transmission rate can be expressed as:
where B denotes the communication bandwidth, denotes the transmission power of the UAVs sending computational task data over the upload link, and denotes the noise power.
2.1.5. Computational Model
In the proposed system, the total system latency consists of the following three components: (1) the transmission latency for the collection layer UAVs to transmit the computational tasks to the transmission layer UAVs; (2) the transmission latency for the transmission layer UAVs to transmit all the data to the execution layer UAVs that perform the first subtask in the SFC, and the transmission latency for the execution layer UAVs to transmit the remaining computational data sequentially backward; (3) the time spent by the execution layer UAVs to process the computational tasks.
The computation task can be expressed as , where , are arrays of the length of the number of subtasks contained in , and according to the indices represent the computation task type and computation data size of the corresponding subtasks, respectively. Then, the transmission delay of receiving UAV k and sending UAV l for subtask i of can be expressed as:
where is the size of the data transmitted by the receiving UAV k and the sending UAV l for this round of communication.
The time delay resulting from the execution of the UAV m execution calculation can be expressed as follows:
where is the size of computational task data that UAV m needs to execute, is the computational resource allocated by UAV m according to the task demand of computational task .
2.2. Problem Description
Based on the above models and analysis, the optimization problem of the UAV-assisted FP-MEC-IIN system is presented. This study aims to minimize the overall task execution latency within the system by jointly optimizing the allocation of execution UAVs (k, v) and backup execution UAVs (b, l) for the execution of various tasks, as well as the computational resource allocation. This approach ensures efficient resource scheduling and enhanced reliability while making the best use of the limited resources within the system. Specifically, the optimization problem can be expressed as follows:
Subject to:
where represents the number of execution layer UAVs, represents the number of transport layer UAVs, and represents the task number. In (9), indicates that task i is on the transmission layer UAV l and is offloaded to the execution layer UAV k. If not, . In (10), indicates that task i is on the execution layer UAV k and is offloaded to the execution layer UAV v. Conversely . In (11), indicates that task i is on the execution layer UAV k and is not offloaded to any execution layer UAV v, in other words, the task is executed by the execution layer UAV k itself. In contrast, . In (12), indicates that task i is located on the transmission layer UAV l, and is offloaded to the execution layer UAV b, with the condition that UAV b and UAV k are not the same UAV. Otherwise stated, . In (13), indicates that task i is on the execution layer UAV b and is offloaded to the execution layer UAV h, with the condition that UAV h and UAV v are not the same UAV. Alternatively, . In (14), indicates that task i is on the execution layer UAV b and is not offloaded to any execution layer UAV h, in other words, the task is executed by the execution layer UAV b itself. If not, . In (15), represents that for any given execution UAV m and any VNF task i, the computing resources allocated to task i are integers. In (16), for any execution UAV m, the total computing resources allocated to all the received tasks at any given time slot cannot exceed the UAV m’s total available computing resources . Equations (17)–(19) indicate that the number of UAVs in each layer is a non-negative integer. Equation (20) implies that the reliability of any individual sub-task should meet the reliability requirements of SFC j when executing SFC j. In this case, v and b represent the executing UAV and the backup executing UAV for each VNF task, respectively.
2.3. Dynamic Task Scheduling Location Optimization Algorithm
This section first demonstrates that the problem studied in this paper is NP-hard by a well-known NP-hard problem, the lowest cost generalized assignment problem (LGAP) [33]. The LGAP problem is defined as follows: there is a set of elements, , where element consists of cost and size: , and there are some boxes, , where the capacity of each box is . The objective of the LGAP problem is to put as many elements into the boxes as possible at the lowest cost, where the sum of all the elements’ sizes put into each box cannot exceed the capacity of that box. The dynamic task scheduling location optimization problem studied in this paper can be transformed into an LGAP problem when the dynamic crash probability is reduced to zero. Specifically, the execution UAV i has total computational resources of , and each computational task needs to occupy part of the computational resources of the execution UAVs. Ultimately, the objective of the dynamic task scheduling location optimization problem is to complete all computational tasks with the lowest possible latency using the limited computational resources in the system.
Since the special case of the problem studied in this paper can be reduced to the LGAP problem, and the LGAP problem is NP-hard, it is obvious that the problem studied in this paper is also NP-hard. The difficulty and value of this class for the problem lies in the fact that their solutions are widely applicable and practical for solving practical problems and provide strong support for practical application scenarios. DRL is considered as an efficient method for solving NP-hard problems [3,5,25,27,28,34,35]. In this section, the paper firstly gives a brief introduction to the Markov decision process and defines in detail the setting of Markov decision process parameters in this paper, followed by the effect of empirical replay on the learning effect, then the Q-learning algorithm, and finally the DTSOA algorithm based on the dueling deep Q-network (DQN) proposed in this paper.
2.3.1. Markov Decision Process
A standard Markov decision process can be defined as [36,37], where S is the set of states generated by the environment; A is the action space, P is the state transfer probability, and R is the reward function. At each time slot t, tasks belonging to different service types are generated, i.e., a state is generated at time slot t. Then, an action is selected according to the current state. After executing a, the system enters the next state and receives a scalar reward according to the reward function. The parameters of the Markov decision process in this paper are defined in detail below.
- (1)
- State Space: The state of the system contains three layers of the UAVs state and task execution, namely: the location of each collection layer UAV and information about the computational tasks it generates; the location of each transmission layer UAV and information about SFC tasks after collating data; the location of each execution layer UAV, the contained VNF and resource usage information; and the current execution state of all tasks generated within the system. Among them, the locations of the UAVs are represented by a three-dimensional Cartesian coordinate system, and each generated task contains task generation time, task type, task data size, and task delay-sensitive composition.
- (2)
- Action Space: The action a of the system contains both the execution layer UAVs assigned for each task and the allocated computational resources. The task execution positions of the n tasks generated by the n collection layer UAVs can be denoted as , and the allocation of computational resources is denoted by f = [f1, f2, …, fN]. Thus, the action a is the combination of the elements in and f.
- (3)
- Reward Functions: For each step, after executing each action a, the intelligence will calculate the reward obtained according to the reward and punishment function R. The goal of the optimization problem in this paper is to obtain the minimum total system execution delay, while DRL pursues the actions that obtain the maximum reward sum. Therefore, in this paper, the delay derived from the i-th step operation is taken as its opposite, −, as the reward for the i-th step action, i.e., = −, so that the DRL algorithm tends to the direction of the reduction of the total system execution delay.
2.3.2. Experience Storage
During the training process, each interaction between the intelligence and the environment generates a set of data: the current state , the action ai selected according to the current state, the reward obtained, the next state after performing the selected action, and whether the state is terminated . The set of data ( generated during each training step is put into the memory bank M. When a certain amount of data is available in the memory bank M, a small batch_size set of data is randomly selected from the memory bank. After a certain amount of data is stored in the memory M, a small batch_size set of data is randomly selected from the memory and put into the neural network for training. In the actual training, it is necessary to adjust the value of the hyperparameter batch_size in the algorithm, although too large batch_size reduces the number of iterations required for convergence, it also leads to an increase in the time of each iteration, and the total time spent is more than that of small batch_size training. Therefore, when the value of batch_size is within a certain range, it achieves the purpose of making the network converge faster. If the value of batch_size is too small, the iteration convergence time increases and the gradient oscillation is severe, which is not conducive to convergence.
In general, taking a small batch_size for training can achieve the benefits of reusing data, avoiding overfitting problems due to local experience, and reducing memory pressure.
2.3.3. Q-Learning Algorithm
In Q-learning, it is necessary to use Q-table to record the Q-value of each action in each state. The role of Q-table is to return the action A that obtains the maximum Q-value by looking up the table when the state S is input, execute A, reach , input into Q-table, find the action a with the maximum Q-value at Q-value, multiply it by the discount rate plus the sum of the obtained rewards R as the update target of , calculate the loss function, and update the Q-network by the loss function.
The flow chart of Algorithm 1 is as follows:
| Algorithm 1: Q-learning algorithm |
| 1: Initialize Q form |
| 2: for episode 1→E do: |
| 3: Initialize the state of UAVs at each execution level |
| 4: Get the initial state of the environment s |
| 5: for episode 1→T do: |
| 6: Use the epsilon-greedy strategy to select the action a in the current state s based on Q-value |
| 7: Execute action a; get environment feedback of |
| 8: |
| 9: |
| 10: end for |
| 11: end for |
2.3.4. DTSOA Algorithm
Dueling DQN is another improvement algorithm of the DQN. Dueling DQN makes only minor changes to the traditional DQN, but it improves the performance of the DQN significantly. In reinforcement learning, the result of subtracting the state action value function from the state value function is usually defined as the dominance function, i.e., . The sum of the dominance values of all actions in the same state is 0, because the expectation of the action value of all actions is the state value of this state. Therefore, in Dueling DQN, the Q-network is modeled as:
where is the state value function, representing how much reward can be obtained from state s, and is the dominance function for taking different actions in that state, indicating the superiority of taking action a in state s compared with other actions; η is the network parameter shared by the state value function and the dominance function, which is generally used in neural networks to extract the first few layers of features; and α and β are the parameters of the state value function and the dominance function, respectively. The Dueling DQN model divides the last layer of the neural network into two parts, the state value function and the dominance function, and no longer lets the neural network output the Q-value directly, the state value function and the dominance function sum up to obtain the Q-value. The network structure of Dueling DQN is shown in Figure 5.
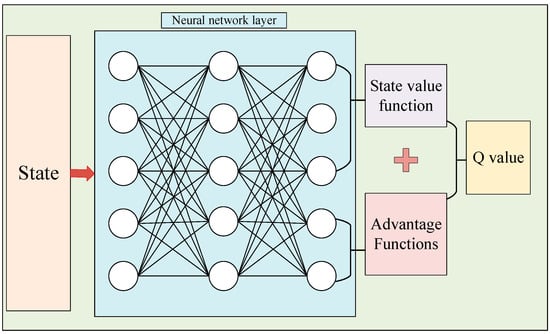
Figure 5.
Network structure of Dueling DQN.
The advantage of modeling the state value function and the dominance function separately is that in some contexts the intelligence will only be concerned with the value of the state and not with the differences caused by the different actions, and modeling them separately will enable the intelligence to better handle states that are less associated with actions.
In , the uncertainty of the dominance function and the state value function leads to a solution that is not unique and affects the training of the neural network. To solve this problem, Dueling DQN forces the Q-value of the optimal action to be equal to the V-value, so that the optimal action value in the dominance function is zero and all other values are negative, and since determining the V-value ensures the uniqueness of the value modeling, the neural network is trained as follows:
In the implementation, the literature [38] suggests that the maximum value can be replaced by the average value, i.e.:
Part of the reason for better Dueling DQN than DQN is that Dueling DQN learns the state value function more efficiently. Each time Dueling DQN updates the state value function, including Q-values of all the actions in the current state, unlike traditional DQN which updates only the Q-values of the action selected in the current state. Therefore, Dueling DQN learns the state value function more frequently and accurately (Algorithm 2).
| Algorithm 2: DTSOA algorithm |
| 1: Initialize neural network Q(s, a) parameters with random parameters |
| 2: Initialize experience replay pool M |
| 3:for episode 1→E do: |
| 4: Initialize the state of UAVs at each execution level |
| 5: Get the initial state of the environment s1 |
| 6: Initialization done = False |
| 7: while not done: |
| 8: Select action a1 according to the current network Q(s, a) with epsilon-greedy. strategy |
| 9: Execute action a1; get return r1; determine whether to enter the stop state, if yes, d1 = True, else d1 = False; and enter the new state s2 |
| 10: Store (s1, a1, r1, d1, s2) into the experience replay pool M |
| 11: if the data in M is enough then sampling n data from the {(si, ai, ri, di, si+1)}i=1, ……, n |
| 12: Put the data batch into the output dominance function and state value function through the neural network, and calculate the Q-value. |
| 13: Minimize target loss as a way to update the current network |
| 14: Update the target network |
| 15: end for |
| 16: end for |
2.3.5. Algorithm Complexity Analysis
The reinforcement learning algorithms have been trained to the convergence state, their computational complexity is usually taken as the number of nonlinear transformations propagated once in the forward direction. Therefore, the computational complexity of the algorithm can be expressed as , where L is the number of layers of the algorithm’s strategic neural network, and is the number of neurons in the lth hidden layer.
3. Results and Discussion
In this section, this paper evaluates the performance of the proposed algorithm based on the experimental results by forming an FP-MEC-IIN system at three layers of UAVs and conducting simulation experiments with the main parameters shown in Table 1.

Table 1.
Simulation parameters.
In this paper, the proposed algorithm is compared with three other baseline algorithms in the following simulation scenarios: “RSM” means that the edge server device performing the SFCs task always selects the execution layer UAVs that contain the corresponding VNFs type and have the shortest communication link; “Q-learning” (Algorithm 1) uses the Q-values recorded by the Q-network to assign the execution layer UAVs to the SFCs task; and “TSM” means that all possible solutions under the model are traversed and the best value is selected. The DTSOA algorithm proposed in this paper is presented as Algorithm 2.
Figure 6 shows the reward convergence trend of the randomized experiment, which verifies that the DTSOA algorithm proposed in this paper has good convergence.
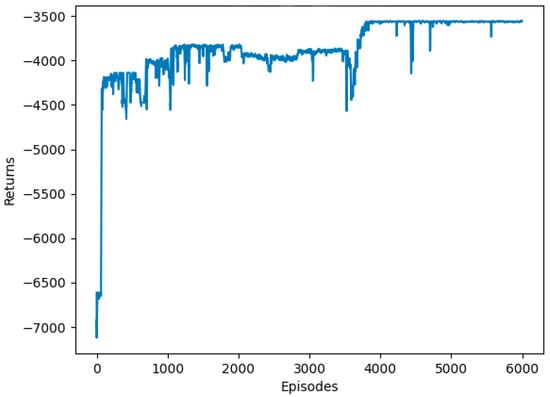
Figure 6.
Trend of DTSOA algorithm reward convergence based on Dueling DQN.
Figure 7 shows the performance simulation of the impact of the number of collection layer UAVs on the total system delay. As can be seen from the figure, compared with Q-leaning and RSM, the DTSOA proposed in this paper has optimal performance as the link length of the SFCs changes (i.e., during the change in the number of VNF subtasks contained in each SFC) and the achieved results are closer to the TSM curve. Furthermore, fewer computational tasks are generated in the corresponding system when the number of collection layer UAVs is smaller, where the gap between these four algorithms is the smallest since more computational resources are left for each execution layer UAVs at this time. The DTSOA algorithm analyzes the generated computational tasks and the server resource usage to efficiently schedule the system resources and obtain better results. Q-learning also uses computational tasks and server state as input of the algorithm. However, the Q-value of one state action pair can only be updated in each training iteration, and there is a problem of overestimation of the Q-value due to the internal design defect of the algorithm, which affects the algorithm results. Therefore, compared with Q-learning, DTSOA learns the state value function more frequently and accurately to select better actions and reduce the system latency.
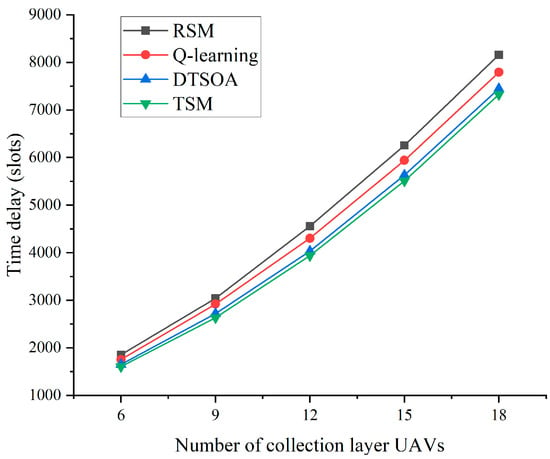
Figure 7.
Relationship between the number of collection layer UAVs and time delay.
Figure 8 shows the effect of increasing the crash probability factor on the total system delay. The simulation parameters are set as: . From the figure, it can be seen that RSM has the highest system latency affected by the crash probability coefficient, because only the nearest execution layer UAVs are selected for task offloading execution. Q-learning, DTSOA and TSM schedule the computation of task execution positions based on the working status of all execution layer UAVs in the system, which reduces the impact of the crash probability coefficient on the total system latency. DTSOA has better performance through the advantage of the algorithm design; the growth curve is closer to TSM compared to other baseline algorithms.
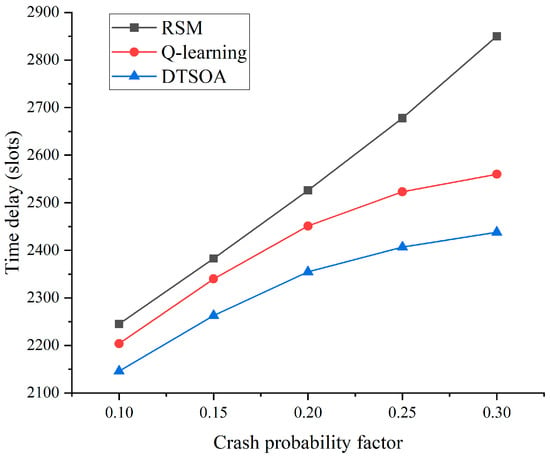
Figure 8.
Crash probability coefficient and time delay relationship graph.
Figure 9 investigates the relationship between the amount of task data and the time delay. The simulation parameters are set as: . The simulation results show that, compared with the results in Figure 8, all these four algorithms more fully utilize the system resources, and reduce the total latency in the system to a certain extent by increasing the number of SFC tasks with the same total task data volume. RSM is less efficient in utilizing the overall resources in the system than the other algorithms in the case of multiple tasks and large data volume. The DTSOA proposed in this paper, however, is still closer to the results of TSM than Q-learning and RSM in the face of multiple tasks counts and large data volumes, and is able to obtain a lower total system latency. Therefore, in the complex work scenario facing multiple SFC tasks, the performance of the DTSOA algorithm proposed in this paper is more advantageous in providing resource scheduling services to users.
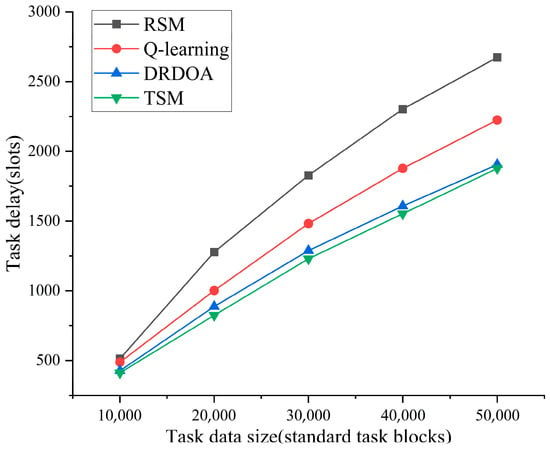
Figure 9.
Task data volume and latency relationship graph.
Figure 10 shows the relationship between the computational power and the latency of the executed UAVs. The simulation parameters are set as: . The simulation results show that the system latency under all four algorithms decreases as the computational power of the device increases. The reason for the gradual slowdown of the reduction is that too many computational resources are wasted in the face of a fixed computational task. In addition, compared with Q-learning and RSM, the proposed DTSOA algorithm is closer to TSM in terms of reduction magnitude and has lower latency. The advantages of the algorithm proposed in this paper are more obvious, especially when the resources in the system are insufficient. This reflects the algorithm’s ability to make good use of resources.
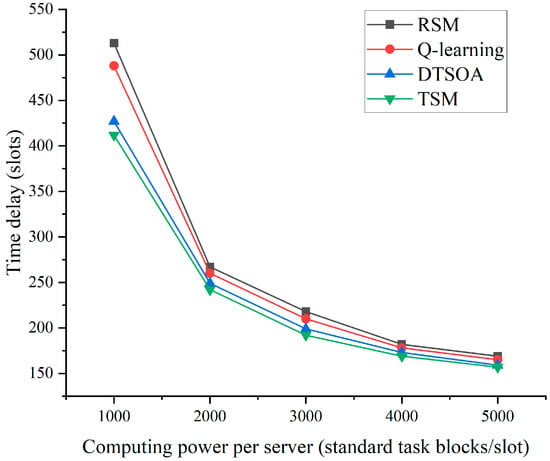
Figure 10.
Execution of UAVs computational power and latency relationship.
Figure 11 investigates the relationship between the number of delay-sensitive SFCs and the time delay. The simulation parameters are set as: . In this simulation, the reject task mechanism is introduced, if the selected execution device integrated reliability rate meets the task’s demand for the reliability rate. Then the task is accepted, and vice versa the task is rejected. The formula for calculating the latency in the simulation diagram is as follows: latency of the execution task + (number of rejected tasks × 200). Setting reject tasks leads to higher latency compared to the normal execution of the task. Let the algorithm meet the reliability rate demand of the computational tasks by coordinating the scheduling of the computing power in the system, reducing the number of reject tasks, and reducing the number of backup executions that do not meet the task requirements. Moreover, Figure 11 shows that the system latency under all four algorithms increases as the proportion of latency-sensitive tasks increases, and RSM increases the number of rejected tasks with the intensity of computational tasks due to the underutilization of computational resources in the system, leading to an increase in the integrated latency. In contrast, the DTSOA proposed in this paper utilizes system resources more efficiently than Q-learning and obtains lower latency, and the DTSOA algorithm is closer to TSM with lower latency, which verifies the superior performance of the algorithm.
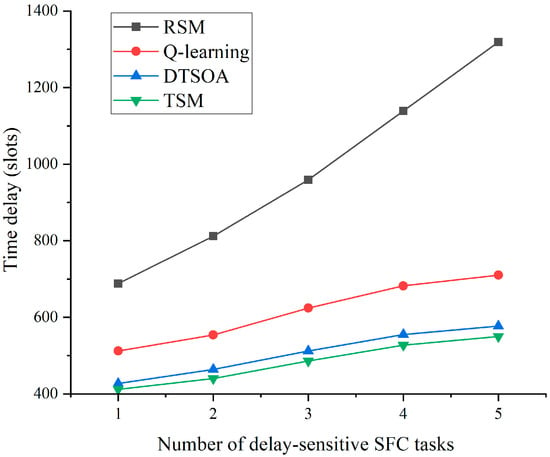
Figure 11.
Relationship between number of delay-sensitive SFCs and delay.
4. Conclusions
This paper presents the development of the FP-MEC-IIN framework to address the demand for low latency in intra-system communication networks, which involves diverse task types. The framework utilizes flexibly deployable (UAVs) as computational resources. A simulation study is conducted to investigate task offloading decisions and (MEC) computational resource allocation problems. This study compares the performance of the proposed DTSOA algorithm, which is based on Dueling DQN, with existing offloading schemes, including the RSM, Q-learning algorithm, and TSM. The simulation results demonstrate that the proposed algorithm is more effective in reducing system latency than the other algorithms. Compared with the complexity of state-action pairs limited Q-learning, the DTSOA algorithm improves the learning efficiency by separately modeling the state value function and the dominance function. The Dueling DQN algorithm updates the state value function more frequently and accurately than Q-learning, resulting in the improvement of the convergence speed and accuracy. The DTSOA algorithm has the potential to reduce the system delay and to facilitate the rapid construction of MEC networks in emergency scenarios, as well as to reduce industrial production costs and promote the development of green energy economies. In this study, the mobility of terminals and UAVs configured with the VNF during the transmission process has not been considered. In the IIN scenario, some terminals send computational tasks while moving, and IIN terminals also have requirements for extended endurance. In future work, we will build upon the foundation laid by this paper by introducing the characteristics of terminal mobility and long endurance.
Author Contributions
All authors contributed equally to the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by Beijing Natural Science Foundation L222004; Beijing Natural Science Foundation Haidian Original Innovation Joint Fund (No. L212026); R&D Program of Beijing Municipal Education Commission (KM202211232011).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, Y.; Yu, F.R.; Chen, J.; Kuo, Y. Resource Allocation for Information-Centric Virtualized Heterogeneous Networks with In-Network Caching and Mobile Edge Computing. IEEE Trans. Veh. Technol. 2017, 66, 11339–11351. [Google Scholar] [CrossRef]
- Pham, C.; Tran, N.H.; Ren, S.; Saad, W.; Hong, C.S. Traffic-Aware and Energy-Efficient VNF Placement for Service Chaining: Joint Sampling and Matching Approach. IEEE Trans. Serv. Comput. 2020, 13, 172–185. [Google Scholar] [CrossRef]
- Fu, X.; Yu, F.R.; Wang, J.; Qi, Q.; Liao, J. Service Function Chain Embedding for NFV-Enabled IoT Based on Deep Reinforcement Learning. IEEE Commun. Mag. 2019, 57, 102–108. [Google Scholar] [CrossRef]
- Pei, J.; Hong, P.; Pan, M.; Liu, J.; Zhou, J. Optimal VNF Placement via Deep Reinforcement Learning in SDN/NFV-Enabled Networks. IEEE J. Sel. Areas Commun. 2020, 38, 263–278. [Google Scholar] [CrossRef]
- Suzuki, A.; Kobayashi, M.; Takahashi, Y.; Harada, S.; Ishibashi, K.; Kawahara, R. Extendable NFV-Integrated Control Method Using Reinforcement Learning. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–7. [Google Scholar]
- Sun, J.; Liu, F.; Wang, H.; Ahmed, M.; Li, Y.; Zhang, L.; Zeng, H. Network Function Placement Under Randomly Arrived Networking Traffic. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 1382–1398. [Google Scholar] [CrossRef]
- Pham, T.-M.; Fdida, S.; Nguyen, T.-T.-L.; Chu, H.-N. Modeling and Analysis of Robust Service Composition for Network Functions Virtualization. Comput. Netw. 2020, 166, 106989. [Google Scholar] [CrossRef]
- Wang, M.; Cheng, B.; Chen, J. Joint Availability Guarantee and Resource Optimization of Virtual Network Function Placement in Data Center Networks. IEEE Trans. Netw. Serv. Manag. 2020, 17, 821–834. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, J. Latency-Efficient VNF Deployment and Path Routing for Reliable Service Chain. IEEE Trans. Netw. Sci. Eng. 2021, 8, 651–661. [Google Scholar] [CrossRef]
- Kang, R.; He, F.; Oki, E. Virtual Network Function Allocation in Service Function Chains Using Backups with Availability Schedule. IEEE Trans. Netw. Serv. Manag. 2021, 18, 4294–4310. [Google Scholar] [CrossRef]
- Fan, J.; Jiang, M.; Rottenstreich, O.; Zhao, Y.; Guan, T.; Ramesh, R.; Das, S.; Qiao, C. A Framework for Provisioning Availability of NFV in Data Center Networks. IEEE J. Sel. Areas Commun. 2018, 36, 2246–2259. [Google Scholar] [CrossRef]
- Li, J.; Liang, W.; Huang, M.; Jia, X. Reliability-Aware Network Service Provisioning in Mobile Edge-Cloud Networks. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 1545–1558. [Google Scholar] [CrossRef]
- Yang, S.; Li, F.; Yahyapour, R.; Fu, X. Delay-Sensitive and Availability-Aware Virtual Network Function Scheduling for NFV. IEEE Trans. Serv. Comput. 2022, 15, 188–201. [Google Scholar] [CrossRef]
- Qiu, Y.; Liang, J.; Leung, V.C.M.; Wu, X.; Deng, X. Online Reliability-Enhanced Virtual Network Services Provisioning in Fault-Prone Mobile Edge Cloud. IEEE Trans. Wirel. Commun. 2022, 21, 7299–7313. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Zhang, J.; Sun, W.; Kato, N. Mobile-Edge Computation Offloading for Ultradense IoT Networks. IEEE Internet Things J. 2018, 5, 4977–4988. [Google Scholar] [CrossRef]
- Hu, Q.; Cai, Y.; Yu, G.; Qin, Z.; Zhao, M.; Li, G.Y. Joint Offloading and Trajectory Design for UAV-Enabled Mobile Edge Computing Systems. IEEE Internet Things J. 2019, 6, 1879–1892. [Google Scholar] [CrossRef]
- Diao, X.; Zheng, J.; Cai, Y.; Wu, Y.; Anpalagan, A. Fair Data Allocation and Trajectory Optimization for UAV-Assisted Mobile Edge Computing. IEEE Commun. Lett. 2019, 23, 2357–2361. [Google Scholar] [CrossRef]
- Pourghasemian, M.; Abedi, M.R.; Hosseini, S.S.; Mokari, N.; Javan, M.R.; Jorswieck, E.A. AI-Based Mobility-Aware Energy Efficient Resource Allocation and Trajectory Design for NFV Enabled Aerial Networks. IEEE Trans. Green Commun. Netw. 2023, 7, 281–297. [Google Scholar] [CrossRef]
- Baumgartner, A.; Bauschert, T.; D’Andreagiovanni, F.; Reddy, V.S. Towards Robust Network Slice Design under Correlated Demand Uncertainties. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–7. [Google Scholar]
- Lin, T.; Zhou, Z. Robust Virtual Network Function Provisioning Under Random Failures on Network Function Enabled Nodes. In Proceedings of the 2018 10th International Workshop on Resilient Networks Design and Modeling (RNDM), Longyearbyen, Norway, 27–29 August 2018; pp. 1–7. [Google Scholar]
- Kuo, T.-W.; Liou, B.-H.; Lin, K.C.-J.; Tsai, M.-J. Deploying Chains of Virtual Network Functions: On the Relation Between Link and Server Usage. IEEEACM Trans. Netw. 2018, 26, 1562–1576. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Zhang, Y.; Su, L.; Jin, D. Improve Service Chaining Performance with Optimized Middlebox Placement. IEEE Trans. Serv. Comput. 2017, 10, 560–573. [Google Scholar] [CrossRef]
- Bari, F.; Chowdhury, S.R.; Ahmed, R.; Boutaba, R.; Duarte, O.C.M.B. Orchestrating Virtualized Network Functions. IEEE Trans. Netw. Serv. Manag. 2016, 13, 725–739. [Google Scholar] [CrossRef]
- Pei, J.; Hong, P.; Xue, K.; Li, D. Efficiently Embedding Service Function Chains with Dynamic Virtual Network Function Placement in Geo-Distributed Cloud System. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 2179–2192. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Y.; Liu, F.; Wang, H.; Xu, X.; Li, Y. A Survey on the Placement of Virtual Network Functions. J. Netw. Comput. Appl. 2022, 202, 103361. [Google Scholar] [CrossRef]
- Akbari, M.; Abedi, M.R.; Joda, R.; Pourghasemian, M.; Mokari, N.; Erol-Kantarci, M. Age of Information Aware VNF Scheduling in Industrial IoT Using Deep Reinforcement Learning. IEEE J. Sel. Areas Commun. 2021, 39, 2487–2500. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, W.; Ding, Y.; Xiong, N. Computation Offloading Optimization for UAV-Assisted Mobile Edge Computing: A Deep Deterministic Policy Gradient Approach. Wirel. Netw. 2021, 27, 2991–3006. [Google Scholar] [CrossRef]
- Du, J.; Joseph, Y.-T. Leung Minimizing Total Tardiness on One Machine Is NP-Hard. Math. Oper. Res. 1990, 15, 483–495. [Google Scholar] [CrossRef]
- Murty, K.G.; Kabadi, S.N. Some NP-Complete Problems in Quadratic and Nonlinear Programming. Math. Program. 1987, 39, 117–129. [Google Scholar] [CrossRef]
- Ye, H.; Li, G.Y.; Juang, B.-H.F. Deep Reinforcement Learning Based Resource Allocation for V2V Communications. IEEE Trans. Veh. Technol. 2019, 68, 3163–3173. [Google Scholar] [CrossRef]
- Fu, X.; Yu, F.R.; Wang, J.; Qi, Q.; Liao, J. Dynamic Service Function Chain Embedding for NFV-Enabled IoT: A Deep Reinforcement Learning Approach. IEEE Trans. Wirel. Commun. 2020, 19, 507–519. [Google Scholar] [CrossRef]
- Xiong, J.; Guo, H.; Liu, J. Task Offloading in UAV-Aided Edge Computing: Bit Allocation and Trajectory Optimization. IEEE Commun. Lett. 2019, 23, 538–541. [Google Scholar] [CrossRef]
- Nauss, R.M. Solving the Generalized Assignment Problem: An Optimizing and Heuristic Approach. Inf. J. Comput. 2003, 15, 249–266. [Google Scholar] [CrossRef]
- Sun, Y.; Ochiai, H.; Esaki, H. Decentralized Deep Learning for Multi-Access Edge Computing: A Survey on Communication Efficiency and Trustworthiness. IEEE Trans. Artif. Intell. 2022, 3, 963–972. [Google Scholar] [CrossRef]
- Solozabal, R.; Ceberio, J.; Sanchoyerto, A.; Zabala, L.; Blanco, B.; Liberal, F. Virtual Network Function Placement Optimization with Deep Reinforcement Learning. IEEE J. Sel. Areas Commun. 2020, 38, 292–303. [Google Scholar] [CrossRef]
- Wang, Z.; Schaul, T.; Hessel, M.; van Hasselt, H.; Lanctot, M.; de Freitas, N. Dueling Network Architectures for Deep Reinforcement Learning. arXiv 2016, arXiv:1511.06581v3. [Google Scholar]
- Hui, H.; Chen, W.; Wang, L. Caching with Finite Buffer and Request Delay Information: A Markov Decision Process Approach. IEEE Trans. Wirel. Commun. 2020, 19, 5148–5161. [Google Scholar] [CrossRef]
- Choi, M.; No, A.; Ji, M.; Kim, J. Markov Decision Policies for Dynamic Video Delivery in Wireless Caching Networks. IEEE Trans. Wirel. Commun. 2019, 18, 5705–5718. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).