Improved Crop Biomass Algorithm with Piecewise Function (iCBA-PF) for Maize Using Multi-Source UAV Data
Abstract
1. Introduction
2. Materials and Methods
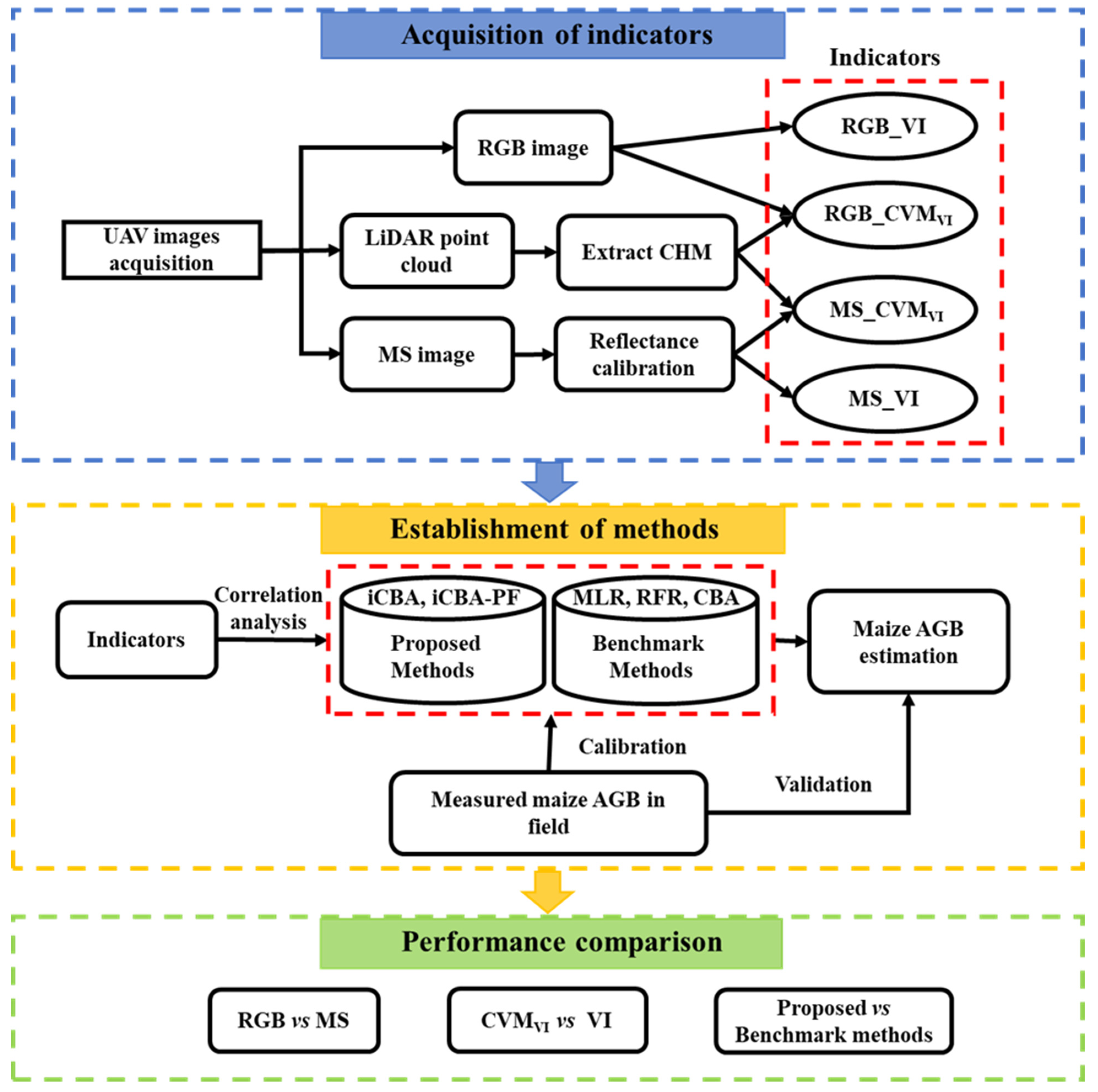
2.1. The Framework of the Article
2.2. Study Sites and Experimental Design
2.3. Data Acquisition and Pre-Processing
2.4. UAV Data Processing
2.4.1. Sample Plant Mask Extraction
2.4.2. Spectral Indices
2.4.3. VI-Weighted CVM (CVMVI)
2.4.4. Indicator Selection
2.5. Maize AGB Estimation
2.5.1. Benchmark Method 1: MLR
2.5.2. Benchmark Method 2: RFR
2.5.3. Benchmark Method 3: CBA
2.5.4. Development of New AGB Estimation Methods
2.6. Accuracy Assessment
3. Results
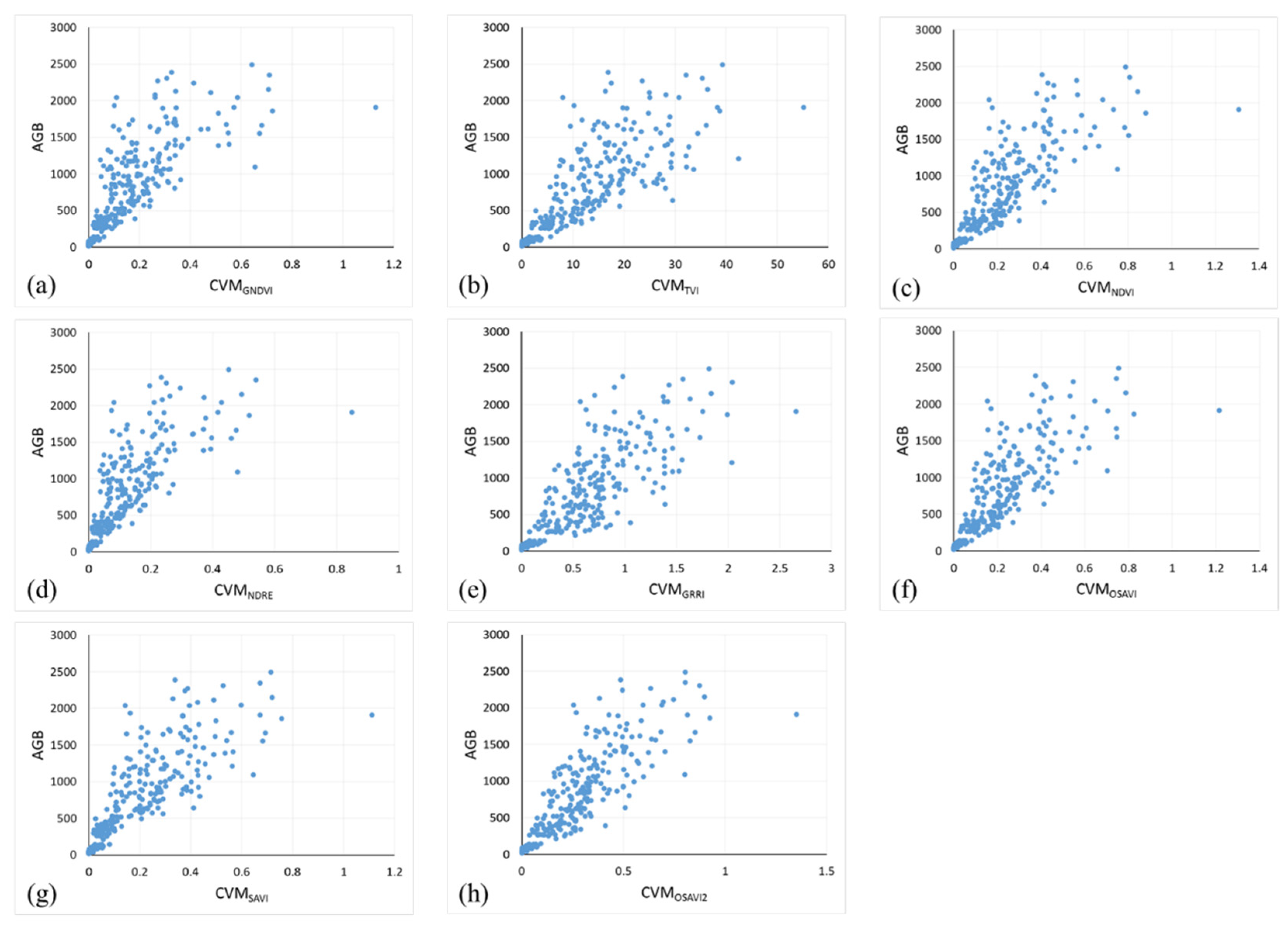
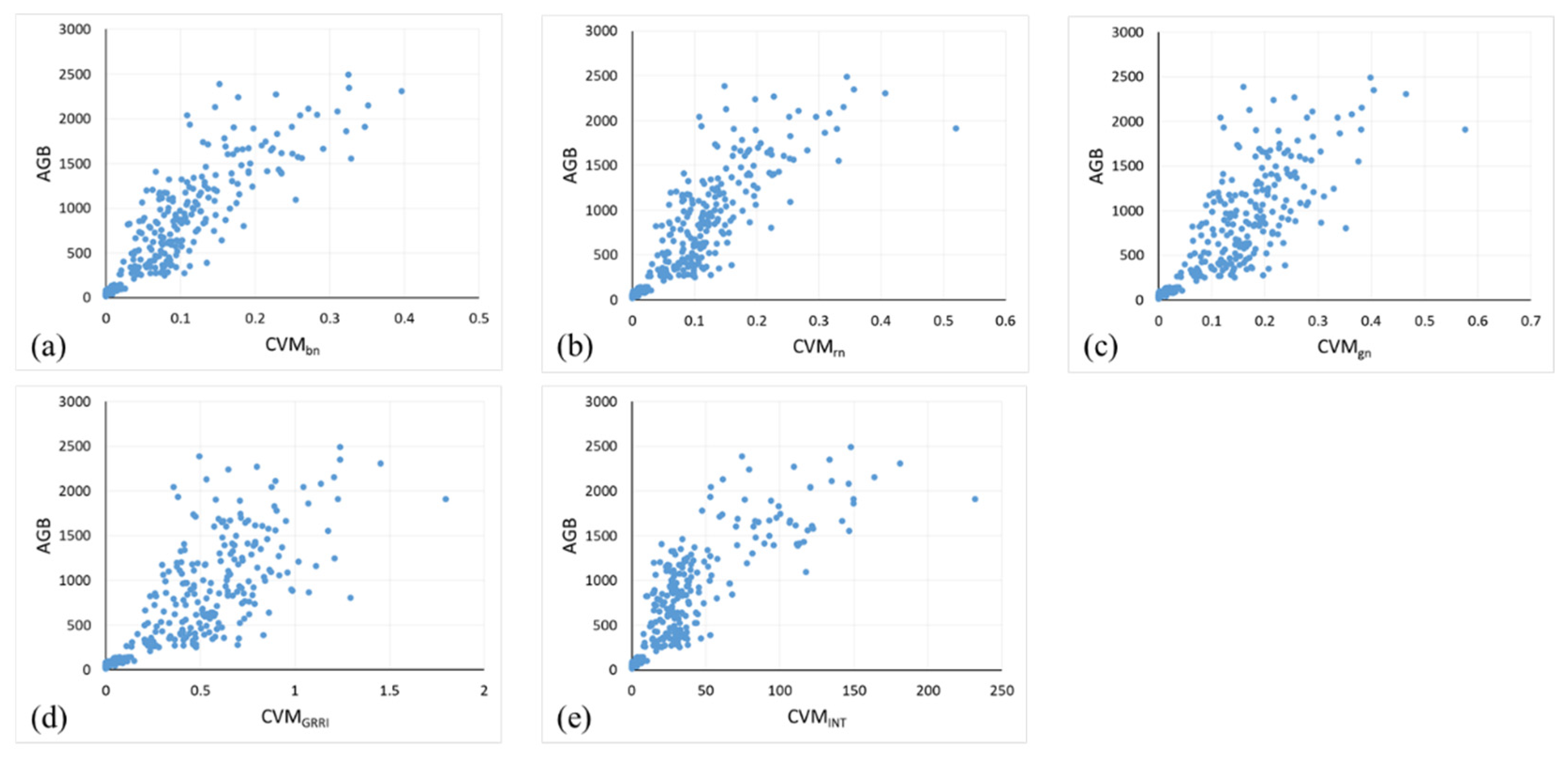
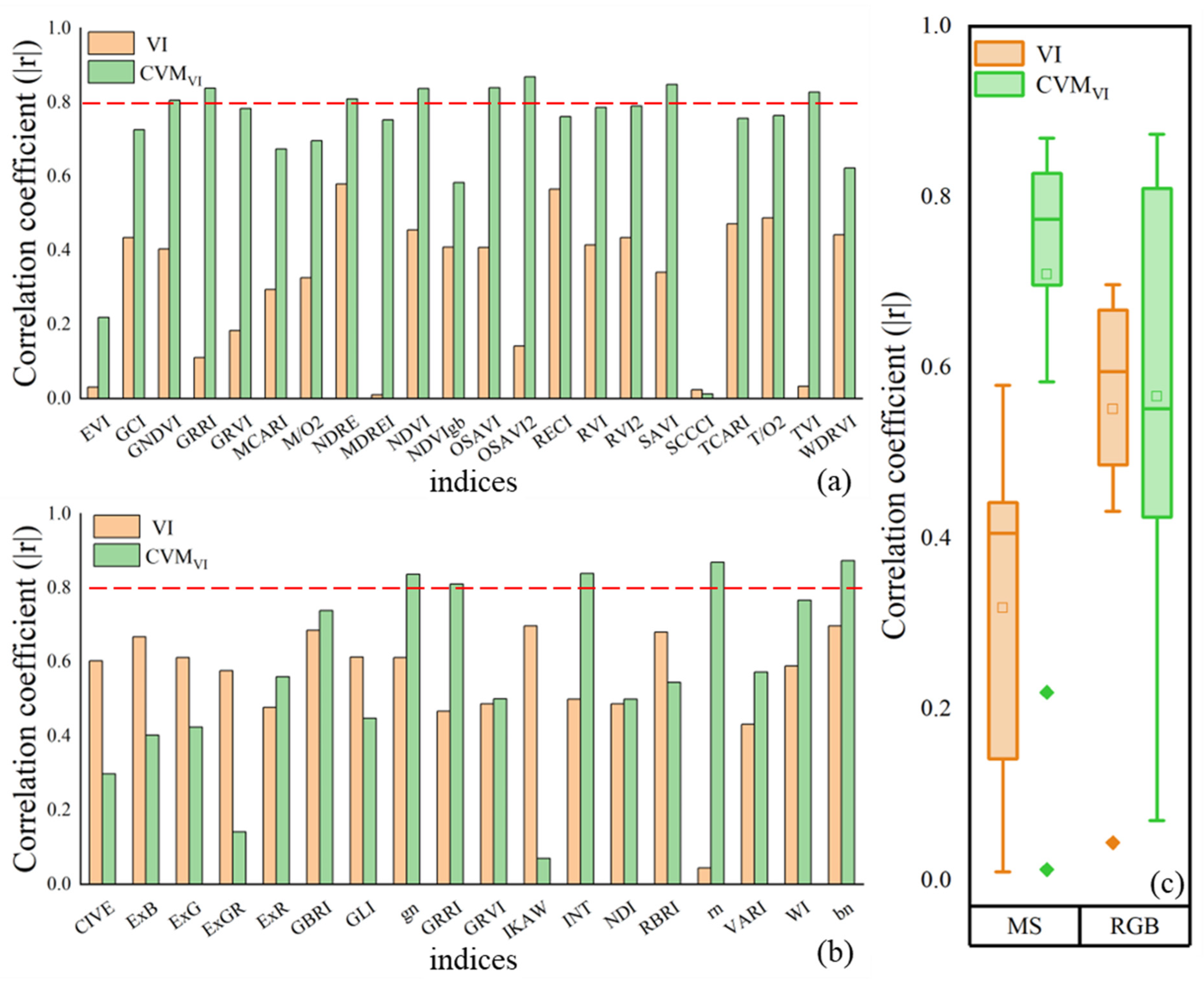
3.1. Correlation Analysis between VI, CVMVI, and AGB
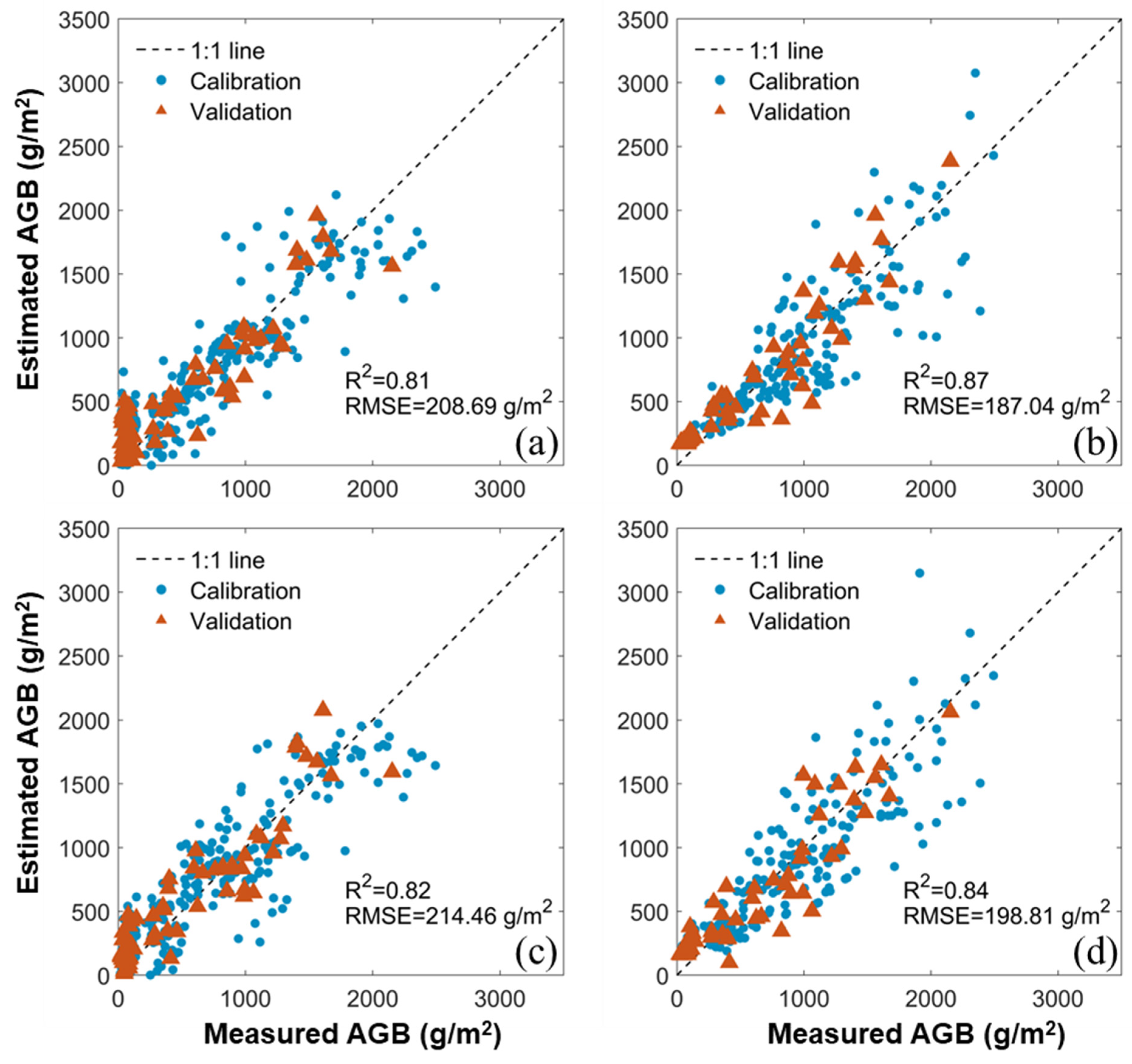
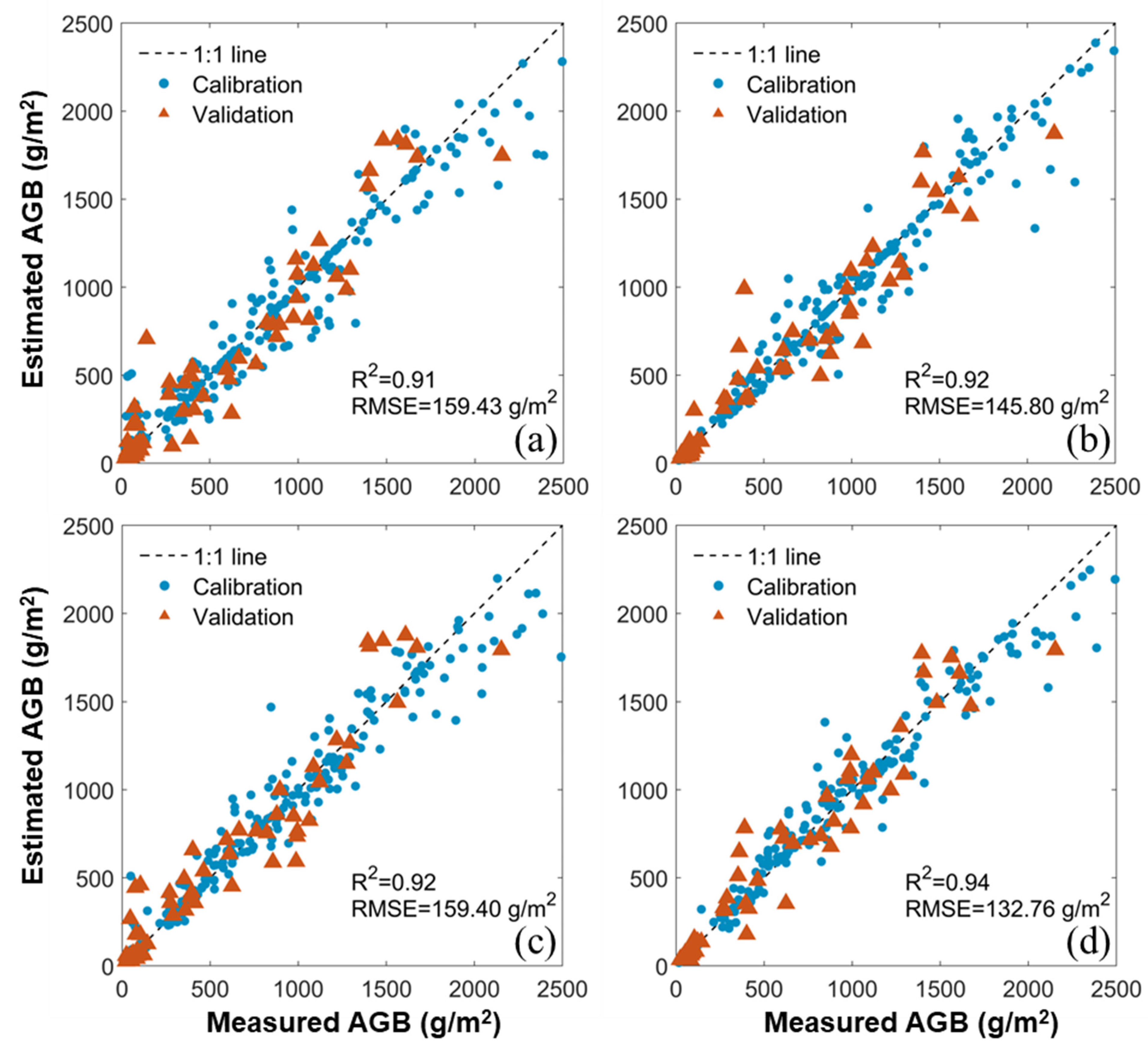
3.2. Estimation of AGB with Benchmark Methods
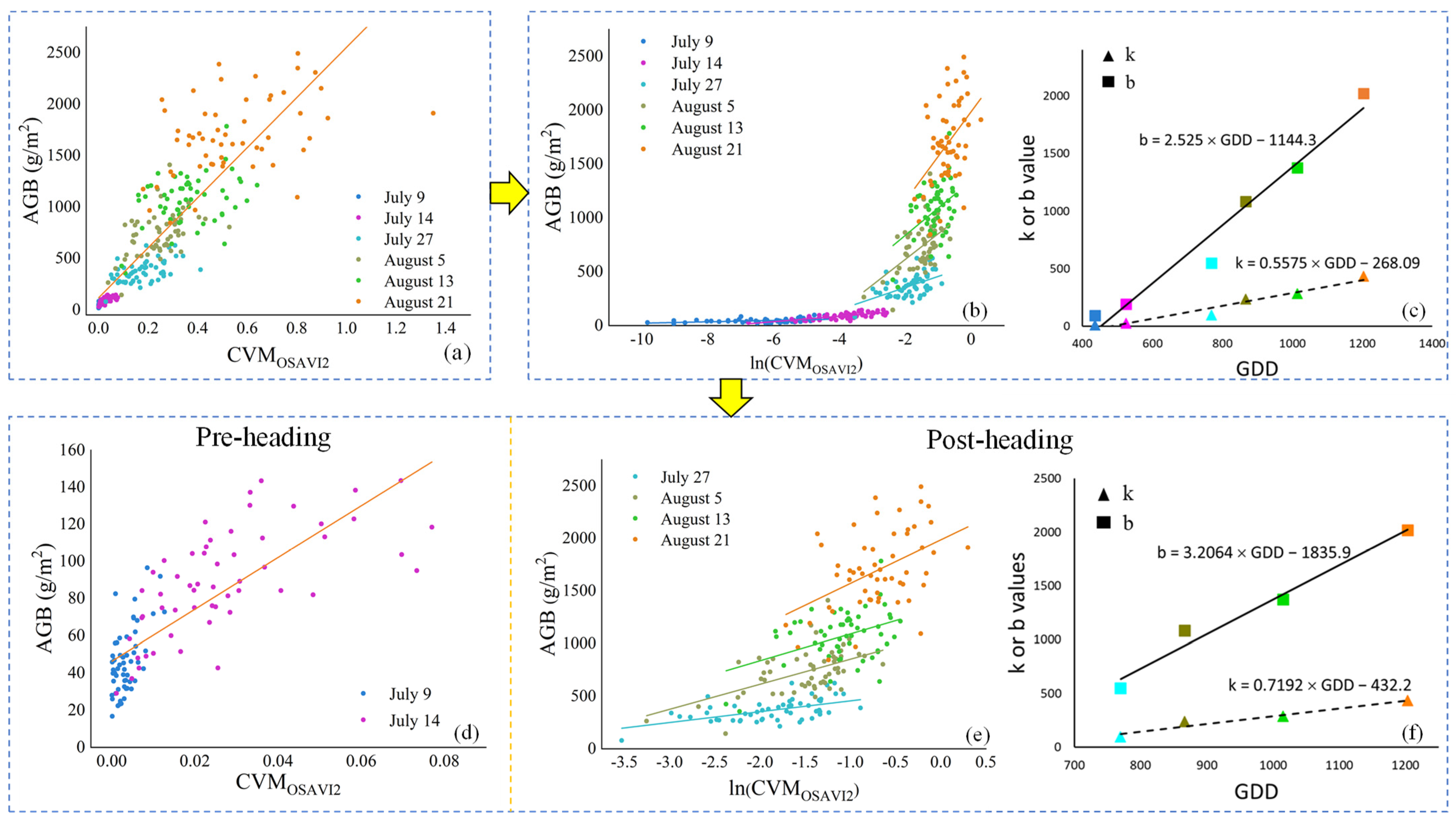
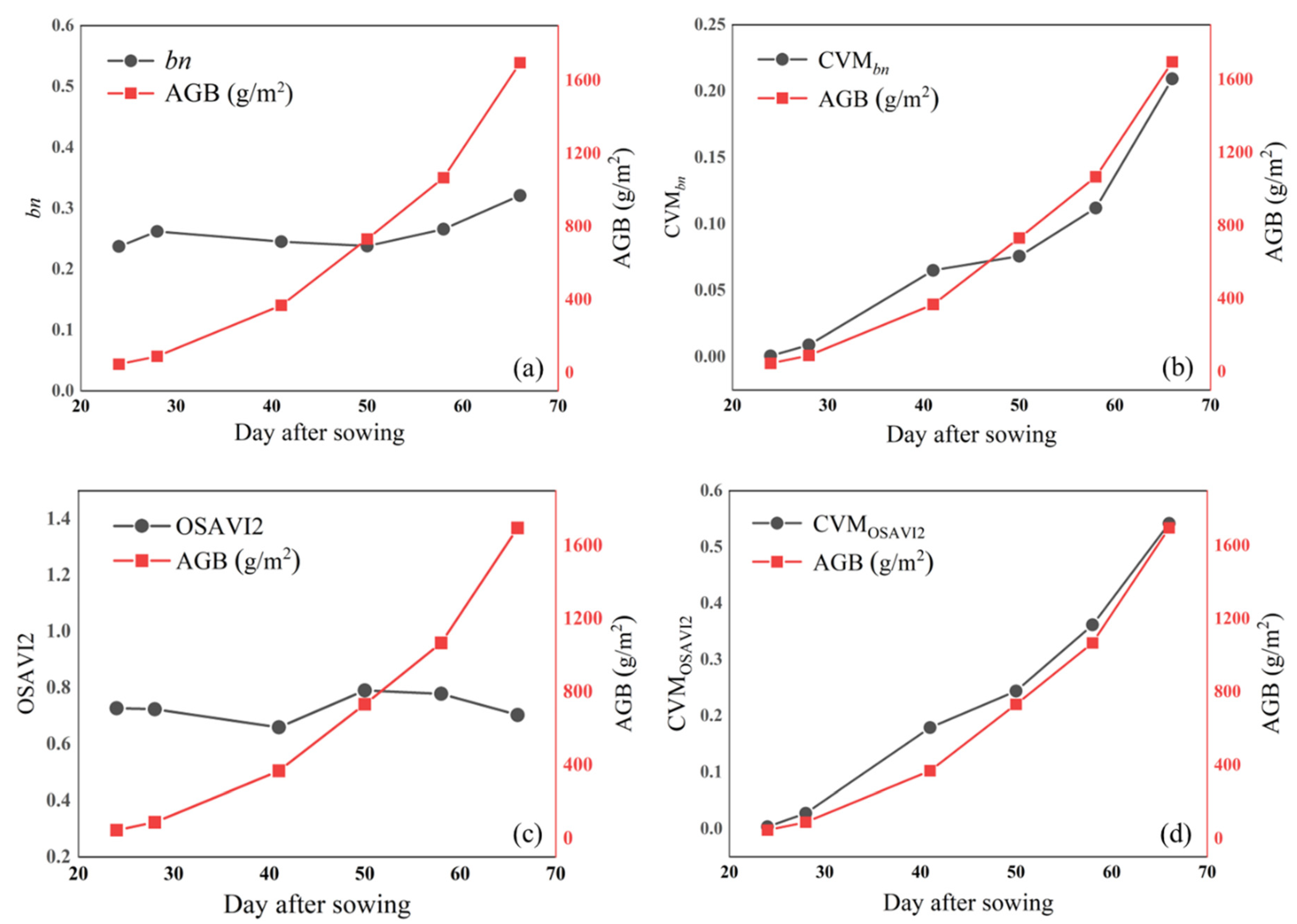
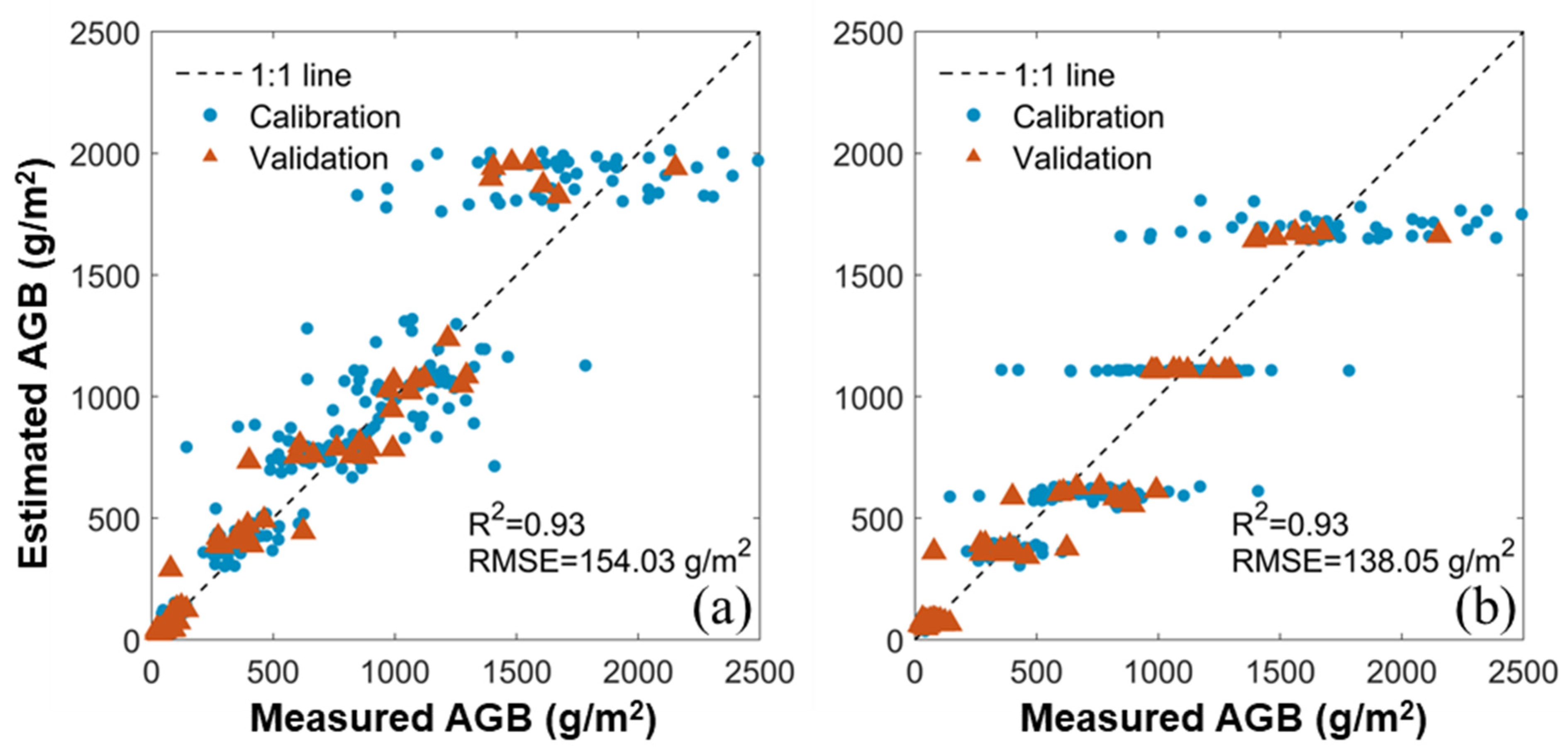
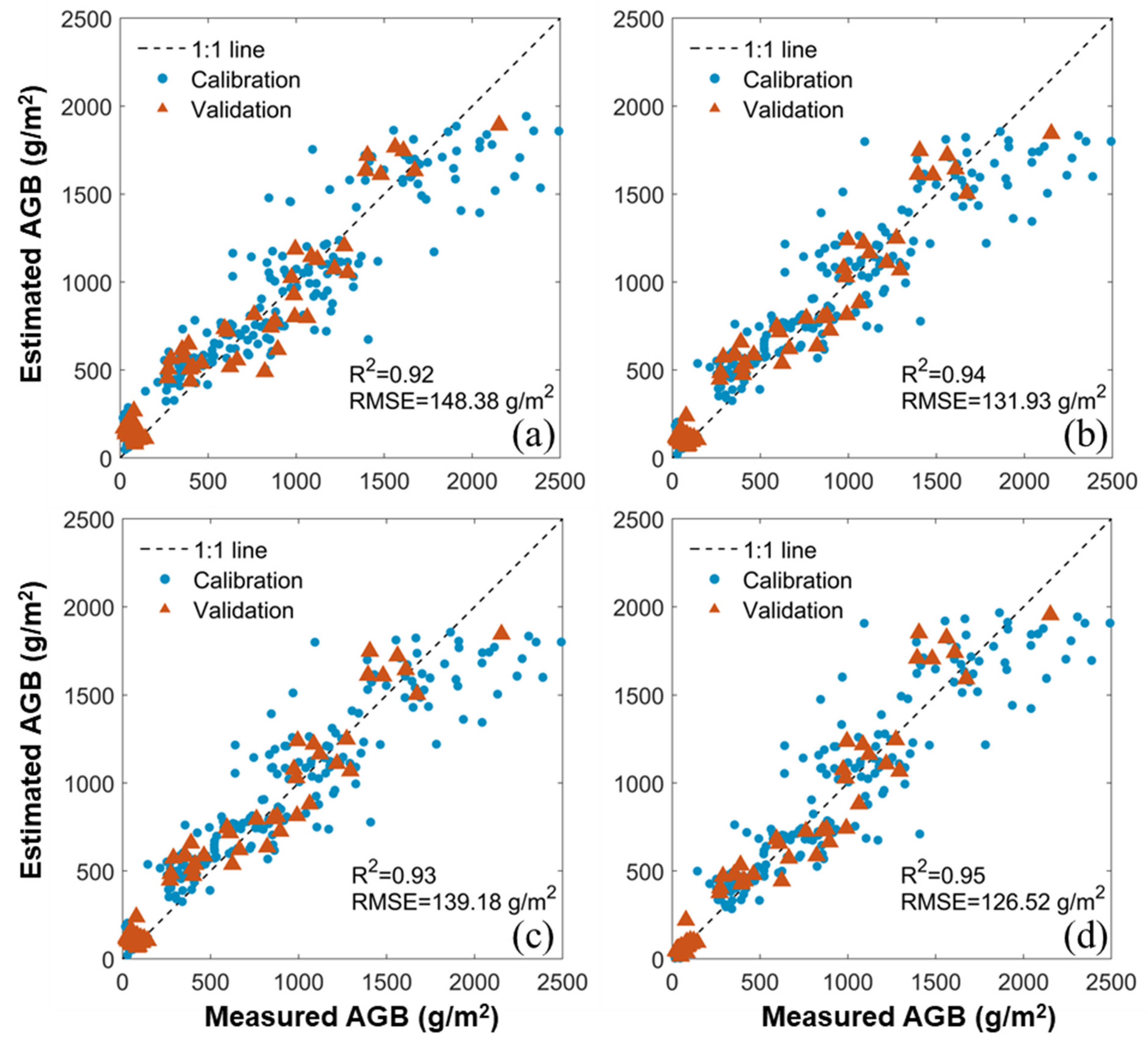
3.3. Estimation of AGB by iCBA and iCBA-PF
3.4. Comparison between the Benchmark and New Methods
4. Discussion
4.1. Comparison of MS and RGB Data in Different Methods
4.2. Performance Comparison between VI and CVMVI of Two Sensors
4.3. Performance Comparison between New Methods and Benchmark Methods
4.4. Limitation and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Shiferaw, B.; Prasanna, B.M.; Hellin, J.; Bänziger, M. Crops that feed the world 6. Past successes and future challenges to the role played by maize in global food security. Food Secur. 2011, 3, 307–327. [Google Scholar] [CrossRef]
- Jin, X.; Ma, J.; Wen, Z.; Song, K. Estimation of Maize Residue Cover Using Landsat-8 OLI Image Spectral Information and Textural Features. Remote Sens. 2015, 7, 14559–14575. [Google Scholar] [CrossRef]
- Cen, H.; Wan, L.; Zhu, J.; Li, Y.; Li, X.; Zhu, Y.; Weng, H.; Wu, W.; Yin, W.; Xu, C.; et al. Dynamic monitoring of biomass of rice under different nitrogen treatments using a lightweight UAV with dual image-frame snapshot cameras. Plant Methods 2019, 15, 32. [Google Scholar] [CrossRef]
- Niu, Y.; Zhang, L.; Zhang, H.; Han, W.; Peng, X. Estimating Above-Ground Biomass of Maize Using Features Derived from UAV-Based RGB Imagery. Remote Sens. 2019, 11, 1261. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Tian, Q.; Feng, H.; Xu, K.; Zhou, C. Estimate of winter-wheat above-ground biomass based on UAV ultrahigh-ground-resolution image textures and vegetation indices. ISPRS J. Photogramm. Remote Sens. 2019, 150, 226–244. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Ghulam, A.; Sidike, P.; Hartling, S.; Maimaitiyiming, M.; Peterson, K.; Shavers, E.; Fishman, J.; Peterson, J.; Kadam, S.; et al. Unmanned Aerial System (UAS)-based phenotyping of soybean using multi-sensor data fusion and extreme learning machine. ISPRS J. Photogramm. Remote Sens. 2017, 134, 43–58. [Google Scholar] [CrossRef]
- Han, L.; Yang, G.; Dai, H.; Xu, B.; Yang, H.; Feng, H.; Li, Z.; Yang, X. Modeling maize above-ground biomass based on machine learning approaches using UAV remote-sensing data. Plant Methods 2019, 15, 10. [Google Scholar] [CrossRef]
- Moeckel, T.; Dayananda, S.; Nidamanuri, R.; Nautiyal, S.; Hanumaiah, N.; Buerkert, A.; Wachendorf, M. Estimation of Vegetable Crop Parameter by Multi-temporal UAV-Borne Images. Remote Sens. 2018, 10, 805. [Google Scholar] [CrossRef]
- Chen, Q. Modeling aboveground tree woody biomass using national-scale allometric methods and airborne lidar. ISPRS J. Photogramm. Remote Sens. 2015, 106, 95–106. [Google Scholar] [CrossRef]
- Wang, G.; Liu, S.; Liu, T.; Fu, Z.; Yu, J.; Xue, B. Modelling above-ground biomass based on vegetation indexes: A modified approach for biomass estimation in semi-arid grasslands. Int. J. Remote Sens. 2018, 40, 3835–3854. [Google Scholar] [CrossRef]
- Roth, L.; Streit, B. Predicting cover crop biomass by lightweight UAS-based RGB and NIR photography: An applied photogrammetric approach. Precis. Agric. 2017, 19, 93–114. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, S.; Li, X.; Cunha, M.; Jayavelu, S.; Cammarano, D.; Fu, Y. Machine learning-based approaches for predicting SPAD values of maize using multi-spectral images. Remote Sens. 2022, 14, 1337. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X.; Wang, W.; Zheng, H.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W.; Chen, Q.; Cheng, T. Estimating aboveground and organ biomass of plant canopies across the entire season of rice growth with terrestrial laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102132. [Google Scholar] [CrossRef]
- Yue, J.; Feng, H.; Jin, X.; Yuan, H.; Li, Z.; Zhou, C.; Yang, G.; Tian, Q. A Comparison of Crop Parameters Estimation Using Images from UAV-Mounted Snapshot Hyperspectral Sensor and High-Definition Digital Camera. Remote Sens. 2018, 10, 1138. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Maimaitiyiming, M.; Hartling, S.; Peterson, K.T.; Maw, M.J.W.; Shakoor, N.; Mockler, T.; Fritschi, F.B. Vegetation Index Weighted Canopy Volume Model (CVMVI) for soybean biomass estimation from Unmanned Aerial System-based RGB imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 27–41. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Chen, H.; Li, D.; Wu, M.; Zhao, W. Remote estimation of canopy height and aboveground biomass of maize using high-resolution stereo images from a low-cost unmanned aerial vehicle system. Ecol. Indic. 2016, 67, 637–648. [Google Scholar] [CrossRef]
- Xu, L.; Zhou, L.; Meng, R.; Zhao, F.; Lv, Z.; Xu, B.; Zeng, L.; Yu, X.; Peng, S. An improved approach to estimate ratoon rice aboveground biomass by integrating UAV-based spectral, textural and structural features. Precis. Agric. 2022, 23, 1276–1301. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Li, J.; Guo, X.; Wang, S.; Lu, J. Estimating biomass of winter oilseed rape using vegetation indices and texture metrics derived from UAV multispectral images. Comput. Electron. Agric. 2019, 166, 105026. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Zhou, M.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Improved estimation of rice aboveground biomass combining textural and spectral analysis of UAV imagery. Precis. Agric. 2018, 20, 611–629. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Y.; Taylor, J.; Gaulton, R.; Jin, X.; Song, X.; Li, Z.; Meng, Y.; Chen, P.; Feng, H.; et al. Comparison and transferability of thermal, temporal and phenological-based in-season predictions of above-ground biomass in wheat crops from proximal crop reflectance data. Remote Sens. Environ. 2022, 273, 112967. [Google Scholar] [CrossRef]
- Liu, Y.; Nie, C.; Zhang, Z.; Wang, Z.; Ming, B.; Xue, J.; Yang, H.; Xu, H.; Meng, L.; Cui, N.; et al. Evaluating how lodging affects maize yield estimation based on UAV observations. Front. Plant Sci. 2022, 13, 979103. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS; NASA: Washington, DC, USA, 1974; Volume 1.
- Wang, F.M.; Huang, J.F.; Tang, Y.L.; Wang, X.Z. New Vegetation Index and Its Application in Estimating Leaf Area Index of Rice. Rice Sci. 2007, 14, 195–203. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Xue, L.; Cao, W.; Luo, W.; Dai, T.; Yan, Z.J. Monitoring Leaf Nitrogen Status in Rice with Canopy Spectral Reflectance. Agron. J. 2004, 96, 135–142. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Gitelson, A.; Vina, A.; Ciganda, V. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Verrelst, J.; Schaepman, M.E.; Koetz, B.; Environment, M. Angular sensitivity analysis of vegetation indices derived from CHRIS/PROBA data. Remote Sens. Environ. 2008, 112, 2341–2353. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Muhammad, H.; Yang, M.; Awais, R.; Jin, X.; Xia, X.; Xiao, Y.; He, Z. Time-series multispectral indices from unmanned aerial vehicle imagery reveal senescence rate in bread wheat. Remote Sens. 2018, 10, 809. [Google Scholar]
- Raper, T.B.; Varco, J.J. Canopy-scale wavelength and vegetative index sensitivities to cotton growth parameters and nitrogen status. Precis. Agric. 2015, 16, 62–76. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Daughtry, C.; Walthall, C.L.; Kim, M.S.; Colstoun, E.; McMurtrey Iii, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Gamon, J.; Surfus, J. Assessing leaf pigment content with a reflectometer. New Phytol. 1999, 143, 105–117. [Google Scholar] [CrossRef]
- Kawashima, S.; Nakatani, M. An Algorithm for Estimating Chlorophyll Content in Leaves Using a Video Camera. Ann. Bot. 1998, 81, 49–54. [Google Scholar] [CrossRef]
- Ahmad, I.S.; Reid, J.F. Evaluation of Colour Representations for Maize Images. J. Agric. Eng. Res. 1996, 63, 185–195. [Google Scholar] [CrossRef]
- Woebbecke, D.M.; Meyer, G.E.; Bargen, K.V.; Mortensen, D.A. Plant species identification, size, and enumeration using machine vision techniques on near-binary images. SPIE Proc. Ser. 1993, 1836, 208–219. [Google Scholar]
- Woebbecke, D.M.; Meyer, G.E.; Bargen, K.V.; Mortensen, D.A. Color Indices for Weed Identification Under Various Soil, Residue, and Lighting Conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
- Louhaichi, M.; Borman, M.M.; Johnson, D.E. Spatially Located Platform and Aerial Photography for Documentation of Grazing Impacts on Wheat. Geocarto Int. 2008, 16, 65–70. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Mao, W.; Wang, Y.; Wang, Y. Real-time Detection of Between-row Weeds Using Machine Vision. In Proceedings of the 2003 ASAE Annual Meeting, Las Vegas, NV, USA, 27–30 July 2003. [Google Scholar]
- Guijarro, M.; Pajares, G.; Riomoros, I.; Herrera, P.J.; Burgos-Artizzu, X.P.; Ribeiro, A. Automatic segmentation of relevant textures in agricultural images. Comput. Electron. Agric. 2011, 75, 75–83. [Google Scholar] [CrossRef]
- Duncanson, L.I.; Cook, B.D.; Hurtt, G.C.; Dubayah, R.O. An efficient, multi-layered crown delineation algorithm for mapping individual tree structure across multiple ecosystems. Remote Sens. Environ. 2014, 154, 378–386. [Google Scholar] [CrossRef]
- Hickey, S.; Callow, N.; Phinn, S.; Lovelock, C.; Duarte, C.M. Spatial complexities in aboveground carbon stocks of a semi-arid mangrove community: A remote sensing height-biomass-carbon approach. Estuar. Coast. Shelf Sci. 2018, 200, 194–201. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. Individual mangrove tree measurement using UAV-based LiDAR data: Possibilities and challenges. Remote Sens. Environ. 2019, 223, 34–49. [Google Scholar] [CrossRef]
- Ahmad, A.; Gilani, H.; Ahmad, S.R. Forest Aboveground Biomass Estimation and Mapping through High-Resolution Optical Satellite Imagery—A Literature Review. Forests 2021, 12, 914. [Google Scholar] [CrossRef]
- Jayathunga, S.; Owari, T.; Tsuyuki, S. Digital Aerial Photogrammetry for Uneven-Aged Forest Management: Assessing the Potential to Reconstruct Canopy Structure and Estimate Living Biomass. Remote Sens. 2019, 11, 338. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, M.; Yin, X.; Zhang, H.; Chu, Q.; Wen, X.; Chen, F. Spatiotemporal characteristics of heat and rainfall changes in summer maize season under climate change in the North China Plain. Chin. J. Eco-Agric. 2015, 23, 473–481. [Google Scholar]
- Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Deep neural network algorithm for estimating maize biomass based on simulated Sentinel 2A vegetation indices and leaf area index. Crop J. 2020, 8, 87–97. [Google Scholar] [CrossRef]
- Ross, A.; Willson, V.L. Paired Samples T-Test. In Basic and Advanced Statistical Tests: Writing Results Sections and Creating Tables and Figures; SensePublishers: Rotterdam, The Netherlands, 2017; pp. 17–19. [Google Scholar]
- Li, Z.; Lu, D.; Gao, X. Analysis of correlation between hydration heat release and compressive strength for blended cement pastes. Constr. Build. Mater. 2020, 260, 120436. [Google Scholar] [CrossRef]
- Jin, X.; Yang, G.; Li, Z.; Xu, X.; Wang, J.; Lan, Y. Estimation of water productivity in winter wheat using the AquaCrop model with field hyperspectral data. Precis. Agric. 2016, 19, 1–17. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Jin, X.; Liu, S.; Baret, F.; Hemerlé, M.; Comar, A. Estimates of plant density of wheat crops at emergence from very low altitude UAV imagery. Remote Sens. Environ. 2017, 198, 105–114. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, C.; Zhang, X.; Cheng, X.; Feng, G.; Wang, Y.; Gao, Q. Estimating the maize biomass by crop height and narrowband vegetation indices derived from UAV-based hyperspectral images. Ecol. Indic. 2021, 129, 107985. [Google Scholar] [CrossRef]

| Date of Data Acquisition | RGB | MS | LiDAR | |||
|---|---|---|---|---|---|---|
| FA (m) | SR (m) | FA (m) | SR (m) | FA (m) | SR (m) | |
| 9 July 2021 | 20 | 0.00279 | 20 | 0.018 | 30 | 0.016 |
| 12 July 2021 | 20 | 0.00219 | 20 | 0.018 | 30 | 0.014 |
| 26 July 2021 | 20 | 0.00218 | 20 | 0.018 | 30 | 0.017 |
| 31 July 2021 | 20 | 0.00346 | 20 | 0.018 | 30 | 0.025 |
| 8 August 2021 | 70 | 0.00792 | 70 | 0.050 | 30 | 0.019 |
| 18 August 2021 | 30 | 0.01140 | 100 | 0.078 | 30 | 0.019 |
| Sensor | Spectral Indices | Definition | Reference |
|---|---|---|---|
| MS | Normalized difference vegetation index (NDVI) | NDVI = (NIR − R)/(NIR + R) | [22] |
| Green-normalized difference vegetation index (GNDVI) | GNDVI = (NIR − G)/(NIR + G) | [23] | |
| Triangular vegetation index (TVI) | TVI = 60 × (NIR − G) − 100 × (R − G) | [24] | |
| Optimized soil adjusted vegetation index (OSAVI) | OSAVI = 1.16 × (NIR − R)/(NIR + R + 0.16) | [25] | |
| Soil-adjusted vegetation index (SAVI) | SAVI = 1.5 × (NIR − R)/(NIR + R + 0.5) | [26] | |
| Ratio vegetation index (RVI) | RVI = NIR/R | [27] | |
| Ratio vegetation index 2 (RVI2) | RVI2 = NIR/G | [28] | |
| Enhanced vegetation index (EVI) | EVI = 2.5 × (NIR − R)/(NIR + 6 × R − 7.5 × B + 1) | [29] | |
| Green chlorophyll index (GCI) | GCI = (NIR/G) − 1 | [30] | |
| Red-edge chlorophyll index (RECI) | RECI = (NIR/RE) − 1 | [30] | |
| Green–red vegetation index (GRVI) | GRVI = (G − R)/(G + R) | [31] | |
| Normalized difference vegetation index 2 (NDVIgb) | NDVIgb = (G − B)/(G + B) | [32] | |
| Normalized difference red-edge (NDRE) | NDRE = (NIR − RE)/(NIR + RE) | [33] | |
| Normalized difference red-edge index (NDREI) | NDREI = (RE − G)/(RE + G) | [34] | |
| Simplified canopy chlorophyll content index (SCCCI) | SCCCI = NDRE/NDVI | [35] | |
| Optimized soil adjusted vegetation index 2 (OSAVI2) | OSAVI2 = (NIR − R)/(NIR − R + 0.16) | [25] | |
| Modified chlorophyll absorption in reflectance index (MCARI) | MCARI = [(RE − R) − 0.2 × (RE − G)] × (RE/R) | [36] | |
| Transformed chlorophyll absorption in reflectance index (TCARI) | TCARI = 3 × [(RE − R) − 0.2 × (RE − G) × (RE/R)] | [36] | |
| MCARI/OSAVI2 (M/O2) | MCARI/OSAVI2 | [37] | |
| TCARI/OSAVI2 (T/O2) | TCARI/OSAVI2 | ||
| Wide dynamic range vegetation index (WDRVI) | WDRVI = (0.12 × NIR − R)/(0.12 × NIR + R) | [36] | |
| Green red ratio index (GRRI) | GRRI = G/R | [38] | |
| RGB | Nomalized Red (rn), Green (gn), Blue (bn) | rn = R/(R + G + B) gn = G/(R + G + B) bn = B/(R + G + B) | [39] |
| Green red ratio index (GRRI) | GRRI = G/R | [38] | |
| Green blue ratio index (GBRI) | GBRI = G/B | [15] | |
| Red blue ratio index (RBRI) | RBRI = R/B | [15] | |
| Color intensity index (INT) | INT = (R + G + B)/3 | [40] | |
| Green–red vegetation index (GRVI) | GRVI = (G − R)/(G + R) | [31] | |
| Normalized difference index (NDI) | NDI = (rn − gn)/(rn + gn + 0.01) | [41] | |
| Woebbecke index (WI) | WI = (G − B)/(R − G) | [42] | |
| Kawashima index (IKAW) | IKAW = (R − B)/(R + B) | [39] | |
| Green leaf index (GLI) | GLI = (2 × G − R − B)/(2 × G + R + B) | [43] | |
| Visible atmospherically resistance index (VARI) | VARI = (G − R)/(G + R − B) | [44] | |
| Excess red vegetation index (ExR) | ExR = 1.4 × rn − gn | [45] | |
| Excess green vegetation index (ExG) | ExG = 2 × gn − rn − bn | [45] | |
| Excess blue vegetation index (ExB) | ExB = 1.4 × bn − gn | [45] | |
| Excess green minus excess red index (ExGR) | ExGR = ExG − ExR | [45] | |
| Color index of vegetation (CIVE) | CIVE = 0.441 × R − 0.881 × G + 0.385 × B + 18.787 | [46] |
| Data Source | Coefficient | Model | R2 |
|---|---|---|---|
| MS_NDRE | k | −0.0047 × GDD2 + 8.3097 × GDD − 2589.5 | 0.75 |
| b | 2 × 10−11 × GDD4.5221 | 0.98 | |
| RGB_bn | k | −0.0265 × GDD2 + 39.614 × GDD − 13021 | 0.65 |
| b | 5.1096 × e0.005 GDD | 0.94 |
| Method | Data Source | Coefficient | Model | R2 |
|---|---|---|---|---|
| iCBA | MS_CVMOSAVI2 | k | 0.56 × GDD − 268.09 | 0.95 |
| b | 2.53 × GDD − 1144.3 | 0.96 | ||
| RGB_CVMbn | k | 0.5904 × GDD − 285.44 | 0.95 | |
| b | 3.1185 × GDD − 1416.2 | 0.97 | ||
| iCBA-PF | MS_CVMOSAVI2 | k | 0.72 × GDD − 432.2 | 0.95 |
| b | 3.2 × GDD − 1835.9 | 0.97 | ||
| RGB_CVMbn | k | 0.778 × GDD − 476.08 | 0.96 | |
| b | 3.8954 × GDD − 2205.2 | 0.97 |
| MLR | RFR | CBA | iCBA | iCBA-PF | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| VI | CVMVI | VI | CVMVI | VI | CVMVI | VI | CVMVI | VI | CVMVI | ||
| R2 | MS | 0.82 | 0.84 | 0.92 | 0.94 | 0.93 | - | - | 0.93 | - | 0.95 |
| RGB | 0.81 | 0.87 | 0.91 | 0.92 | 0.93 | - | - | 0.92 | - | 0.94 | |
| RMSE (g/m2) | MS | 214.46 | 198.81 | 159.40 | 132.76 | 154.03 | - | - | 139.18 | - | 126.52 |
| RGB | 208.69 | 187.04 | 159.43 | 145.80 | 138.05 | - | - | 148.38 | - | 131.93 | |
| Method | Independent Variables | R2 | RMSE | ||
|---|---|---|---|---|---|
| Mean | SD | Mean | SD | ||
| MLR | all RGB_CVMVI | 0.77 | 0.07 | 278.89 | 64.58 |
| RFR | all MS_CVMVI | 0.88 | 0.03 | 212.54 | 33.74 |
| CBA | bn | 0.84 | 0.05 | 231.94 | 37.89 |
| iCBA | MS_CVMOSAVI2 | 0.89 | 0.02 | 195.85 | 22.86 |
| iCBA-PF | MS_CVMOSAVI2 | 0.90 | 0.02 | 190.02 | 22.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, L.; Yin, D.; Cheng, M.; Liu, S.; Bai, Y.; Liu, Y.; Liu, Y.; Jia, X.; Nan, F.; Song, Y.; et al. Improved Crop Biomass Algorithm with Piecewise Function (iCBA-PF) for Maize Using Multi-Source UAV Data. Drones 2023, 7, 254. https://doi.org/10.3390/drones7040254
Meng L, Yin D, Cheng M, Liu S, Bai Y, Liu Y, Liu Y, Jia X, Nan F, Song Y, et al. Improved Crop Biomass Algorithm with Piecewise Function (iCBA-PF) for Maize Using Multi-Source UAV Data. Drones. 2023; 7(4):254. https://doi.org/10.3390/drones7040254
Chicago/Turabian StyleMeng, Lin, Dameng Yin, Minghan Cheng, Shuaibing Liu, Yi Bai, Yuan Liu, Yadong Liu, Xiao Jia, Fei Nan, Yang Song, and et al. 2023. "Improved Crop Biomass Algorithm with Piecewise Function (iCBA-PF) for Maize Using Multi-Source UAV Data" Drones 7, no. 4: 254. https://doi.org/10.3390/drones7040254
APA StyleMeng, L., Yin, D., Cheng, M., Liu, S., Bai, Y., Liu, Y., Liu, Y., Jia, X., Nan, F., Song, Y., Liu, H., & Jin, X. (2023). Improved Crop Biomass Algorithm with Piecewise Function (iCBA-PF) for Maize Using Multi-Source UAV Data. Drones, 7(4), 254. https://doi.org/10.3390/drones7040254








