Medium-Sized Lake Water Quality Parameters Retrieval Using Multispectral UAV Image and Machine Learning Algorithms: A Case Study of the Yuandang Lake, China
Abstract
1. Introduction
2. Materials and Methods
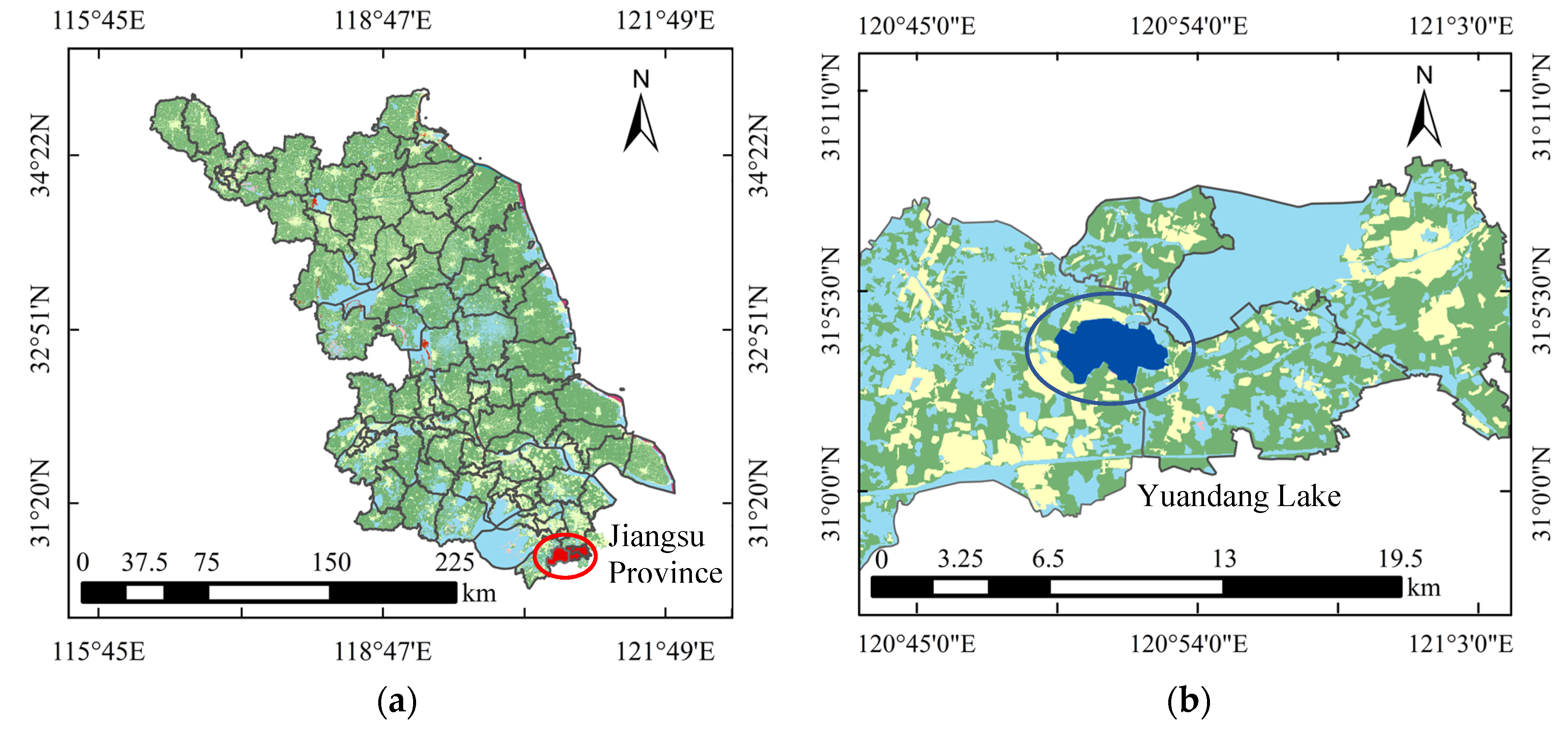
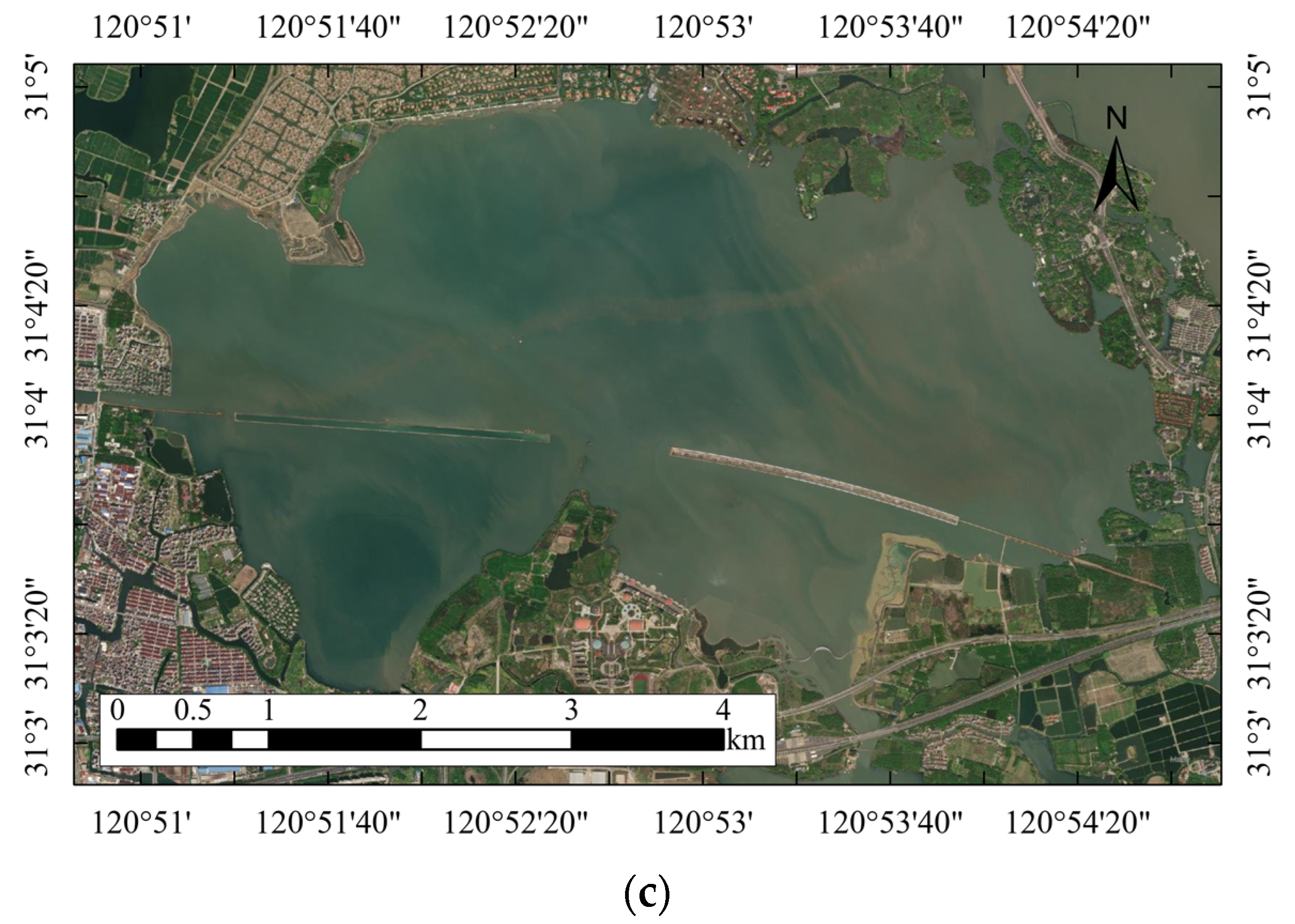
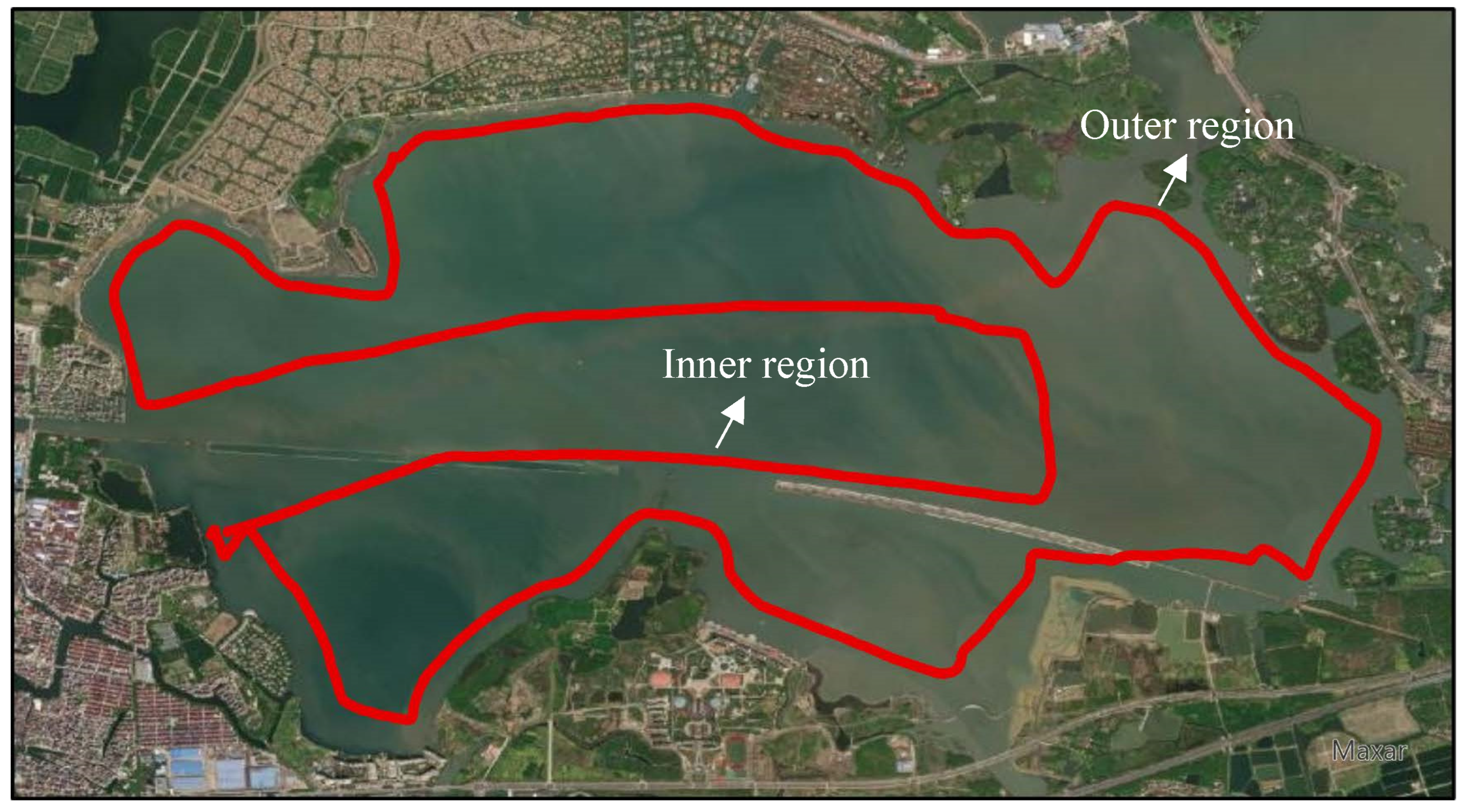
2.1. Study Area
2.2. Data Collection
2.2.1. UAV Multispectral Image Collection
2.2.2. In Situ Water Data Collection
2.3. Data Processing
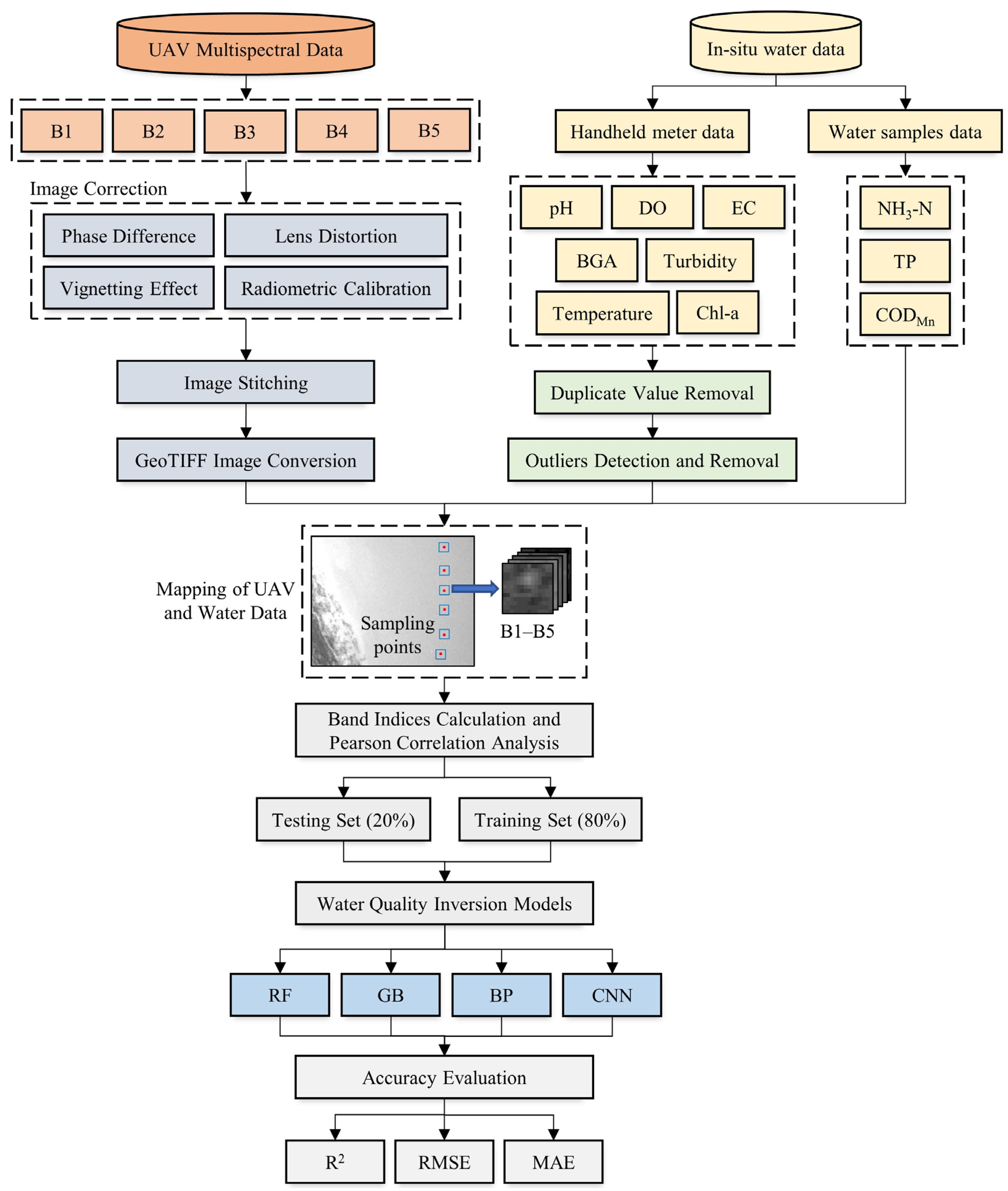
2.3.1. UAV Multispectral Image Data Processing
2.3.2. In Situ Water Data Processing
2.3.3. Mapping of UAV and Water Data
2.3.4. Calculation of Band Indices
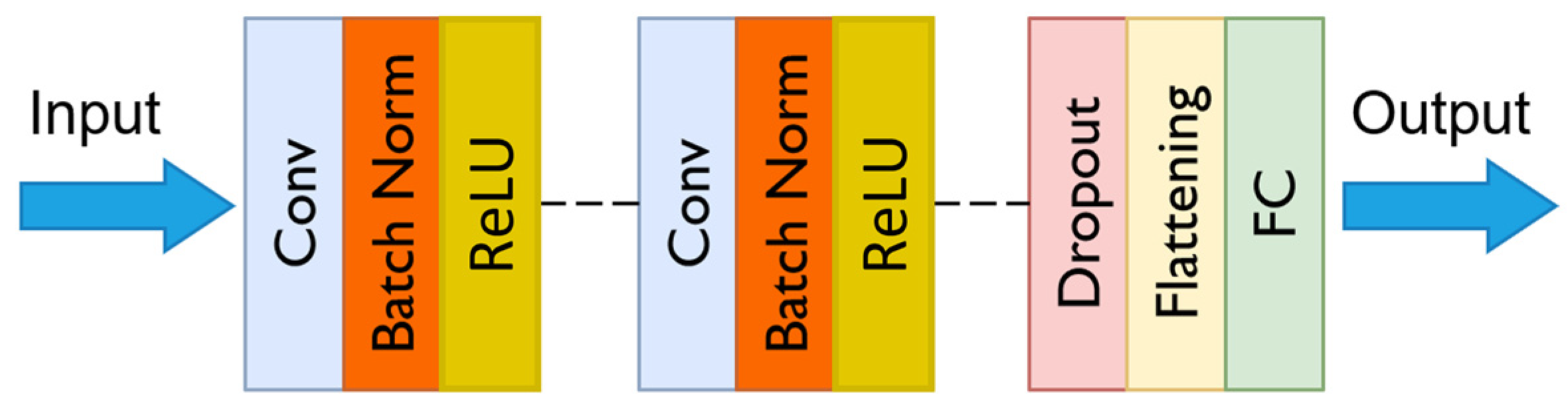
2.3.5. Machine Learning Models
2.3.6. Accuracy Evaluation
3. Results
3.1. Data Analysis
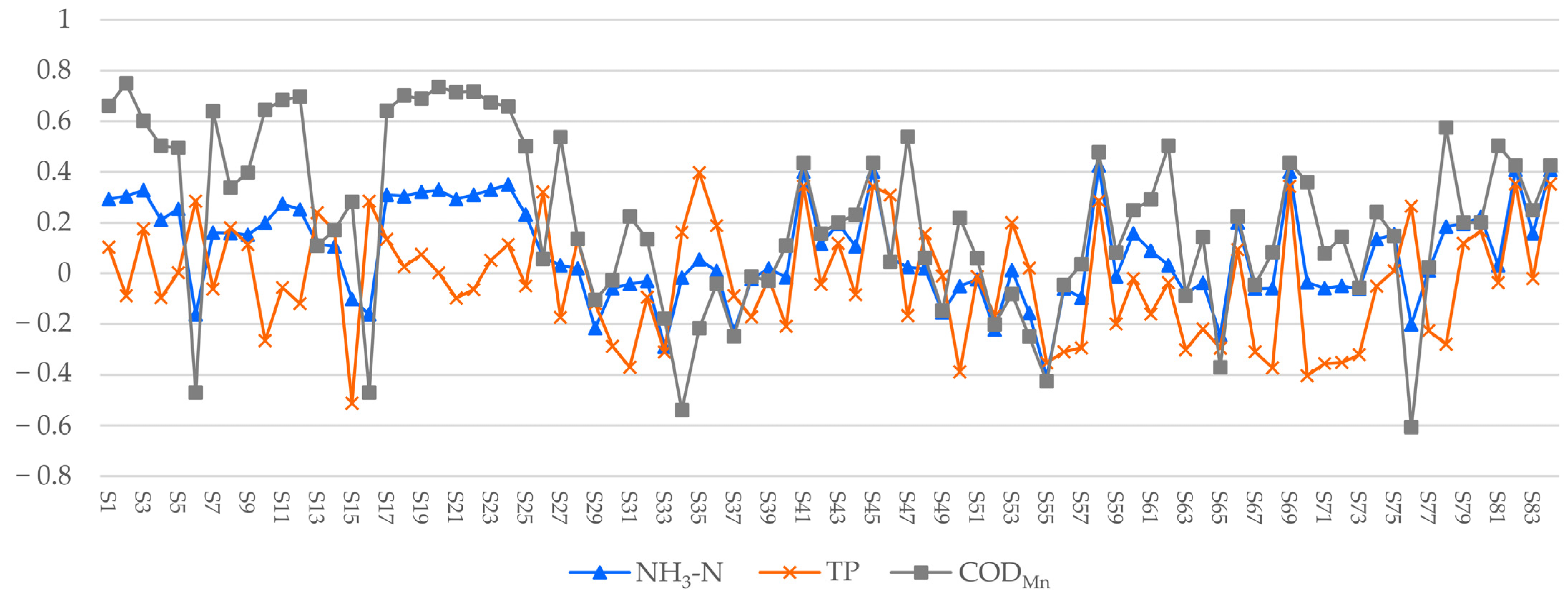
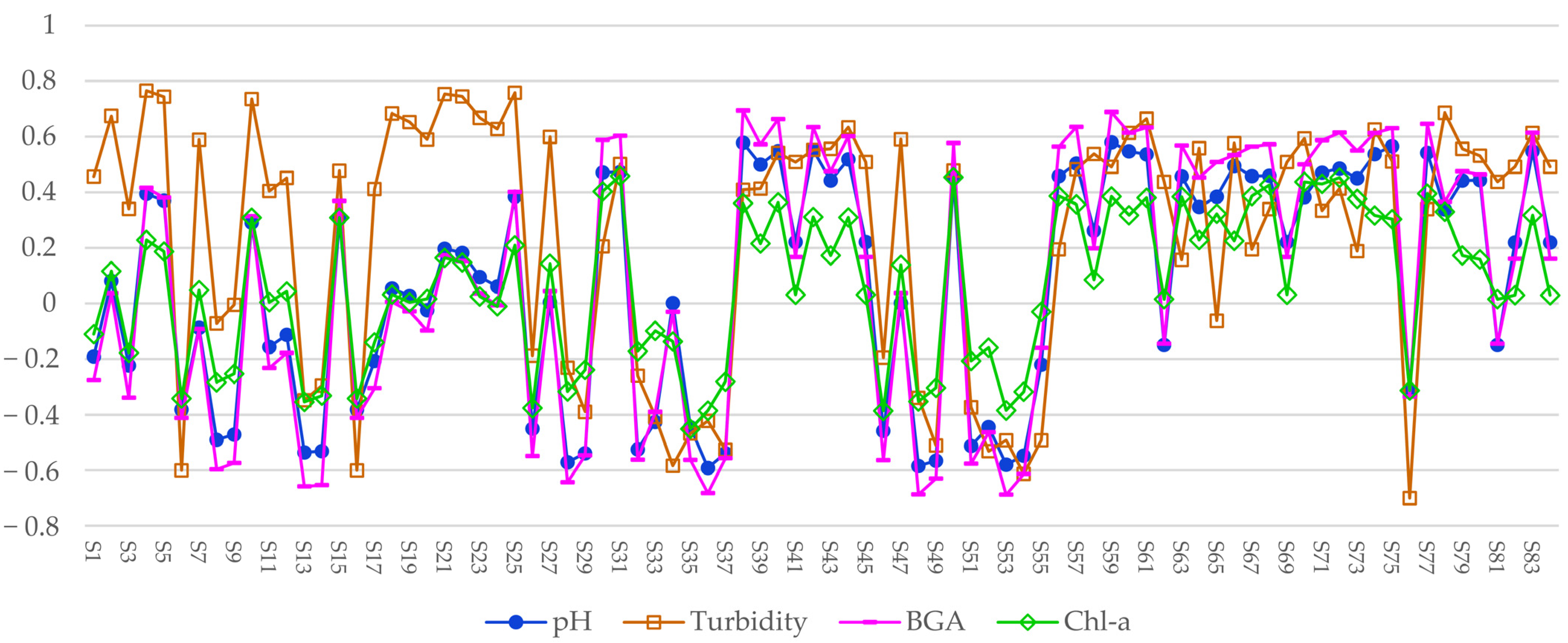
3.2. Spectral Index and Water Quality Parameters Correlation Analysis
3.3. Results of Multivariate Regression Models
4. Discussion
4.1. Correlated Features of Different Water Quality Parameters
4.2. Performance of ML Models in Water Quality Monitoring
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GB 3838–2002; Environmental Quality Standards for Surface Water. China, Ministry of Environmental Protection of the People’s Republic of China: Beijing, China, 2002.
- Thiemann, S.; Kaufmann, H. Determination of chlorophyll content and trophic state of lakes using field spectrometer and IRS-1C satellite data in the Mecklenburg Lake District, Germany. Remote Sens. Environ. 2000, 73, 227–235. [Google Scholar] [CrossRef]
- Seegers, B.N.; Werdell, P.J.; Vandermeulen, R.A.; Salls, W.; Stumpf, R.P.; Schaeffer, B.A.; Owens, T.J.; Bailey, S.W.; Scott, J.P.; Loftin, K.A. Satellites for long-term monitoring of inland US lakes: The MERIS time series and application for chlorophyll-a. Remote Sens. Environ. 2021, 266, 112685. [Google Scholar] [CrossRef]
- Coelho, C.; Heim, B.; Foerster, S.; Brosinsky, A.; De Araújo, J.C. In Situ and satellite observation of CDOM and chlorophyll-a dynamics in small water surface reservoirs in the brazilian semiarid region. Water 2017, 9, 913. [Google Scholar] [CrossRef]
- Warren, M.A.; Simis, S.G.; Selmes, N. Complementary water quality observations from high and medium resolution Sentinel sensors by aligning chlorophyll-a and turbidity algorithms. Remote Sens. Environ. 2021, 265, 112651. [Google Scholar] [CrossRef] [PubMed]
- Papenfus, M.; Schaeffer, B.; Pollard, A.I.; Loftin, K. Exploring the potential value of satellite remote sensing to monitor chlorophyll-a for US lakes and reservoirs. Environ. Monit. Assess. 2020, 192, 808. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Noor, K.; Herbert, K. Modelling reservoir chlorophyll-a, TSS, and turbidity using Sentinel-2A MSI and Landsat-8 OLI satellite sensors with empirical multivariate regression. J. Sens. 2020, 2020, 8858408. [Google Scholar] [CrossRef]
- Ferral, A.; Solis, V.; Frery, A.; Aleksinko, A.; Bernasconi, I.; Marcelo Scavuzzo, C. In-Situ and satellite monitoring of the water quality of a eutrophic lake intervened with a system of artificial aireation. IEEE Lat. Am. Trans. 2018, 16, 627–633. [Google Scholar] [CrossRef]
- Mohsen, A.; Elshemy, M.; Zeidan, B. Water quality monitoring of Lake Burullus (Egypt) using Landsat satellite imageries. Environ. Sci. Pollut. Res. 2021, 28, 15687–15700. [Google Scholar] [CrossRef]
- Tian, S.; Guo, H.; Xu, W.; Zhu, X.; Wang, B.; Zeng, Q.; Mai, Y.; Huang, J.J. Remote sensing retrieval of inland water quality parameters using Sentinel-2 and multiple machine learning algorithms. Environ. Sci. Pollut. Res. 2022, 30, 18617–18630. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Du, Y.; Zhao, H.; Chen, F. Water quality Chl-a inversion based on spatio-temporal fusion and convolutional neural network. Remote Sens. 2022, 14, 1267. [Google Scholar] [CrossRef]
- Aptoula, E.; Ariman, S. Chlorophyll-a retrieval from sentinel-2 images using convolutional neural network regression. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Torres-Bejarano, F.; Arteaga-Hernández, F.; Rodríguez-Ibarra, D.; Mejía-Ávila, D.; González-Márquez, L. Water quality assessment in a wetland complex using Sentinel 2 satellite images. Int. J. Environ. Sci. Technol. 2021, 18, 2345–2356. [Google Scholar] [CrossRef]
- Peterson, K.T.; Sagan, V.; Sloan, J.J. Deep learning-based water quality estimation and anomaly detection using Landsat-8/Sentinel-2 virtual constellation and cloud computing. GISci. Remote Sens. 2020, 57, 510–525. [Google Scholar] [CrossRef]
- Li, N.; Ning, Z.; Chen, M.; Wu, D.; Hao, C.; Zhang, D.; Bai, R.; Liu, H.; Chen, X.; Li, W. Satellite and Machine Learning Monitoring of Optically Inactive Water Quality Variability in a Tropical River. Remote Sens. 2022, 14, 5466. [Google Scholar] [CrossRef]
- Wu, C.; Wu, J.; Qi, J.; Zhang, L.; Huang, H.; Lou, L.; Chen, Y. Empirical estimation of total phosphorus concentration in the mainstream of the Qiantang River in China using Landsat TM data. Int. J. Remote Sens. 2010, 31, 2309–2324. [Google Scholar] [CrossRef]
- Dong, G.; Hu, Z.; Liu, X.; Fu, Y.; Zhang, W. Spatio-temporal variation of total nitrogen and ammonia nitrogen in the water source of the middle route of the South-to-North Water Diversion Project. Water 2020, 12, 2615. [Google Scholar] [CrossRef]
- Izadi, M.; Sultan, M.; Kadiri, R.E.; Ghannadi, A.; Abdelmohsen, K. A remote sensing and machine learning-based approach to forecast the onset of harmful algal bloom. Remote Sens. 2021, 13, 3863. [Google Scholar] [CrossRef]
- Yang, H.; Kong, J.; Hu, H.; Du, Y.; Gao, M.; Chen, F. A review of remote sensing for Water Quality Retrieval: Progress and challenges. Remote Sens. 2022, 14, 1770. [Google Scholar] [CrossRef]
- Mishra, V.; Avtar, R.; Prathiba, A.; Mishra, P.K.; Tiwari, A.; Sharma, S.K.; Singh, C.H.; Chandra Yadav, B.; Jain, K. Uncrewed Aerial Systems in Water Resource Management and Monitoring: A Review of Sensors, Applications, Software, and Issues. Adv. Civ. Eng. 2023, 2023, 3544724. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Chimonyo, V.G.; Clulow, A.D.; Shoko, C.; Mazvimavi, D.; Dube, T.; Mabhaudhi, T. Application of drone technologies in surface water resources monitoring and assessment: A systematic review of progress, challenges, and opportunities in the global south. Drones 2021, 5, 84. [Google Scholar] [CrossRef]
- Su, T.-C.; Chou, H.-T. Application of multispectral sensors carried on unmanned aerial vehicle (UAV) to trophic state mapping of small reservoirs: A case study of Tain-Pu reservoir in Kinmen, Taiwan. Remote Sens. 2015, 7, 10078–10097. [Google Scholar] [CrossRef]
- Flynn, K.F.; Chapra, S.C. Remote sensing of submerged aquatic vegetation in a shallow non-turbid river using an unmanned aerial vehicle. Remote Sens. 2014, 6, 12815–12836. [Google Scholar] [CrossRef]
- Su, T.-C. A study of a matching pixel by pixel (MPP) algorithm to establish an empirical model of water quality mapping, as based on unmanned aerial vehicle (UAV) images. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 213–224. [Google Scholar] [CrossRef]
- Chen, B.; Mu, X.; Chen, P.; Wang, B.; Choi, J.; Park, H.; Xu, S.; Wu, Y.; Yang, H. Machine learning-based inversion of water quality parameters in typical reach of the urban river by UAV multispectral data. Ecol. Indic. 2021, 133, 108434. [Google Scholar] [CrossRef]
- Xiao, Y.; Guo, Y.; Yin, G.; Zhang, X.; Shi, Y.; Hao, F.; Fu, Y. UAV Multispectral Image-Based Urban River Water Quality Monitoring Using Stacked Ensemble Machine Learning Algorithms—A Case Study of the Zhanghe River, China. Remote Sens. 2022, 14, 3272. [Google Scholar] [CrossRef]
- Wu, D.; Jiang, J.; Wang, F.; Luo, Y.; Lei, X.; Lai, C.; Wu, X.; Xu, M. Retrieving Eutrophic Water in Highly Urbanized Area Coupling UAV Multispectral Data and Machine Learning Algorithms. Water 2023, 15, 354. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Y.; Chen, Y.; Qiao, X.; Qian, W. Water Chlorophyll a Estimation Using UAV-Based Multispectral Data and Machine Learning. Drones 2023, 7, 2. [Google Scholar] [CrossRef]
- Ying, H.; Xia, K.; Huang, X.; Feng, H.; Yang, Y.; Du, X.; Huang, L. Evaluation of water quality based on UAV images and the IMP-MPP algorithm. Ecol. Inform. 2021, 61, 101239. [Google Scholar] [CrossRef]
- Wang, F.; Hu, H.; Luo, Y.; Lei, X.; Wu, D.; Jiang, J. Monitoring of Urban Black-Odor Water Using UAV Multispectral Data Based on Extreme Gradient Boosting. Water 2022, 14, 3354. [Google Scholar] [CrossRef]
- Cillero Castro, C.; Domínguez Gómez, J.A.; Delgado Martín, J.; Hinojo Sánchez, B.A.; Cereijo Arango, J.L.; Cheda Tuya, F.A.; Díaz-Varela, R. An UAV and satellite multispectral data approach to monitor water quality in small reservoirs. Remote Sens. 2020, 12, 1514. [Google Scholar] [CrossRef]
- Ma, R.; Yang, G.; Duan, H.; Jiang, J.; Wang, S.; Feng, X.; Li, A.; Kong, F.; Xue, B.; Wu, J.; et al. China’s lakes at present: Number, area and spatial distribution. Sci. China Earth Sci. 2011, 41, 394–401. [Google Scholar] [CrossRef]
- P4 Multispectral Image Processing Guide. Available online: https://dl.djicdn.com/downloads/p4-multispectral/20200717/P4_Multispectral_Image_Processing_Guide_EN.pdf (accessed on 18 February 2023).
- Guo, Y.; Senthilnath, J.; Wu, W.; Zhang, X.; Zeng, Z.; Huang, H. Radiometric calibration for multispectral camera of different imaging conditions mounted on a UAV platform. Sustainability 2019, 11, 978. [Google Scholar] [CrossRef]
- ArcGis Pro 2.8. Available online: https://pro.arcgis.com/ (accessed on 5 January 2023).
- Pu, F.; Ding, C.; Chao, Z.; Yu, Y.; Xu, X. Water-quality classification of inland lakes using Landsat8 images by convolutional neural networks. Remote Sens. 2019, 11, 1674. [Google Scholar] [CrossRef]
- Wang, L.; Yue, X.; Wang, H.; Ling, K.; Liu, Y.; Wang, J.; Hong, J.; Pen, W.; Song, H. Dynamic inversion of inland aquaculture water quality based on UAVs-WSN spectral analysis. Remote Sens. 2020, 12, 402. [Google Scholar] [CrossRef]
- Lu, Q.; Si, W.; Wei, L.; Li, Z.; Xia, Z.; Ye, S.; Xia, Y. Retrieval of water quality from UAV-borne hyperspectral imagery: A comparative study of machine learning algorithms. Remote Sens. 2021, 13, 3928. [Google Scholar] [CrossRef]
- He, Y.; Gong, Z.; Zheng, Y.; Zhang, Y. Inland reservoir water quality inversion and eutrophication evaluation using BP neural network and remote sensing imagery: A case study of Dashahe reservoir. Water 2021, 13, 2844. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [PubMed]
- Niu, C.; Tan, K.; Jia, X.; Wang, X. Deep learning based regression for optically inactive inland water quality parameter estimation using airborne hyperspectral imagery. Environ. Pollut. 2021, 286, 117534. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.; Mumtaz, R.; Anwar, Z.; Shaukat, A.; Arif, O.; Shafait, F. A multi–step approach for optically active and inactive water quality parameter estimation using deep learning and remote sensing. Water 2022, 14, 2112. [Google Scholar] [CrossRef]
- Chu, H.-J.; He, Y.-C.; Chusnah, W.N.U.; Jaelani, L.M.; Chang, C.-H. Multi-reservoir water quality mapping from remote sensing using spatial regression. Sustainability 2021, 13, 6416. [Google Scholar] [CrossRef]
- Petus, C.; Chust, G.; Gohin, F.; Doxaran, D.; Froidefond, J.-M.; Sagarminaga, Y. Estimating turbidity and total suspended matter in the Adour River plume (South Bay of Biscay) using MODIS 250-m imagery. Cont. Shelf Res. 2010, 30, 379–392. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Alikas, K.; Anstee, J.; Barbosa, C.; Binding, C.; Bresciani, M.; Cremella, B.; Giardino, C.; Gurlin, D. Simultaneous retrieval of selected optical water quality indicators from Landsat-8, Sentinel-2, and Sentinel-3. Remote Sens. Environ. 2022, 270, 112860. [Google Scholar] [CrossRef]





| Band | Wavelength Range (nm) |
|---|---|
| Blue (B1) | 450 ± 16 |
| Green (B2) | 560 ± 16 |
| Red (B3) | 650 ± 16 |
| Red Edge (B4) | 730 ± 16 |
| Near Infrared (B5) | 840 ± 16 |
| Index | Formula | Index | Formula | Index | Formula |
|---|---|---|---|---|---|
| S1 | B1 | S30 | S59 | ||
| S2 | B2 | S31 | S60 | ||
| S3 | B3 | S32 | S61 | ||
| S4 | B4 | S33 | S62 | ||
| S5 | B5 | S34 | S63 | ||
| S6 | S35 | S64 | |||
| S7 | S36 | S65 | |||
| S8 | S37 | S66 | |||
| S9 | S38 | S67 | |||
| S10 | S39 | S68 | |||
| S11 | S40 | S69 | |||
| S12 | S41 | S70 | |||
| S13 | S42 | S71 | |||
| S14 | S43 | S72 | |||
| S15 | S44 | S73 | |||
| S16 | S45 | S74 | |||
| S17 | S46 | S75 | |||
| S18 | S47 | S76 | |||
| S19 | S48 | S77 | |||
| S20 | S49 | S78 | |||
| S21 | S50 | S79 | |||
| S22 | S51 | S80 | |||
| S23 | S52 | S81 | |||
| S24 | S53 | S82 | |||
| S25 | S54 | S83 | |||
| S26 | S55 | S84 | |||
| S27 | S56 | ||||
| S28 | S57 | ||||
| S29 | S58 |
| Date | NH3-N (mg/L) | TP (mg/L) | CODMn (mg/L) | |
|---|---|---|---|---|
| 5 August 2022 (N = 20) | Max | 1.1499 | 0.1694 | 7.5345 |
| Min | 0.5809 | 0.0815 | 6.8058 | |
| Mean | 0.7967 | 0.1227 | 7.1573 | |
| SD | 0.1512 | 0.0250 | 0.2098 | |
| 8 August 2022 (N = 20) | Max | 1.0833 | 0.1632 | 5.9810 |
| Min | 0.4037 | 0.0676 | 3.4296 | |
| Mean | 0.7128 | 0.1201 | 5.3174 | |
| SD | 0.1758 | 0.0298 | 0.5582 | |
| 10 August 2022 (N = 20) | Max | 0.7209 | 0.1986 | 6.3950 |
| Min | 0.2658 | 0.1016 | 5.3114 | |
| Mean | 0.4148 | 0.14998 | 6.0241 | |
| SD | 0.1211 | 0.03413 | 0.3031 | |
| All data | Max | 1.1499 | 0.1986 | 7.5345 |
| Min | 0.2658 | 0.0676 | 3.4296 | |
| Mean | 0.6394 | 0.1308 | 6.1657 | |
| SD | 0.2235 | 0.0333 | 0.8656 |
| Date | Chl-a (ug/L) | BGA (ug/L) | Turbidity (NTU) | pH | NC (uS/cm) | DO (mg/L) | Temperature (°C) | |
|---|---|---|---|---|---|---|---|---|
| 5 August 2022 (N = 1519) | Max | 64.080 | 89.330 | 412.000 | 9.980 | 738.000 | 9.040 | 39.061 |
| Min | 0.480 | 0.270 | 4.850 | 7.930 | 12.000 | 5.930 | 32.654 | |
| Mean | 13.753 | 12.286 | 140.631 | 9.004 | 591.214 | 7.687 | 35.504 | |
| SD | 10.055 | 12.919 | 98.038 | 0.317 | 65.726 | 0.683 | 1.522 | |
| 8 August 2022 (N = 1767) | Max | 38.300 | 21.630 | 65.550 | 9.140 | 678.000 | 12.880 | 33.497 |
| Min | 1.840 | 2.560 | 16.990 | 7.890 | 6.200 | 5.280 | 31.473 | |
| Mean | 8.769 | 7.224 | 33.889 | 8.738 | 609.149 | 9.239 | 32.611 | |
| SD | 3.948 | 2.852 | 8.608 | 0.238 | 65.002 | 1.410 | 0.441 | |
| 10 August 2022 (N = 1546) | Max | 88.330 | 78.710 | 119.260 | 9.610 | 707.000 | 19.070 | 34.925 |
| Min | 1.280 | 1.000 | 11.890 | 8.130 | 6.300 | 5.030 | 30.839 | |
| Mean | 14.908 | 12.239 | 37.503 | 8.923 | 630.293 | 9.305 | 33.197 | |
| SD | 11.410 | 11.481 | 16.659 | 0.294 | 52.032 | 1.867 | 0.939 | |
| All data | Max | 88.330 | 89.330 | 412.000 | 9.980 | 738.000 | 19.070 | 39.061 |
| Min | 0.480 | 0.270 | 4.850 | 7.890 | 6.200 | 5.030 | 30.839 | |
| Mean | 12.300 | 10.420 | 68.600 | 8.881 | 610.276 | 8.772 | 33.708 | |
| SD | 9.300 | 10.172 | 74.279 | 0.304 | 63.331 | 1.590 | 1.618 |
| NH3-N (mg/L) | TP (mg/L) | CODMn (mg/L) | Chl-a (ug/L) | BGA (ug/L) | |||
|---|---|---|---|---|---|---|---|
| RF | Training | R2 | 0.8798 | 0.8852 | 0.9526 | 0.9047 | 0.9271 |
| RMSE | 0.0545 | 0.0078 | 0.1605 | 0.8272 | 0.6244 | ||
| Testing | R2 | 0.5104 | 0.4454 * | 0.7777 * | 0.3330 * | 0.4312 | |
| RMSE | 0.1211 | 0.0158 * | 0.3038 * | 2.2747 * | 1.7475 | ||
| MAE | 0.0962 | 0.0123 * | 0.2478 * | 1.6845 * | 1.2739 | ||
| GB | Training | R2 | 0.8421 | 0.7908 | 0.9454 | 0.6463 | 0.7322 |
| RMSE | 0.0637 | 0.0105 | 0.1605 | 1.6011 | 1.2086 | ||
| Testing | R2 | 0.5460 * | 0.3205 | 0.7351 | 0.3193 | 0.4468 | |
| RMSE | 0.1204 * | 0.0162 | 0.4192 | 2.1301 | 1.6738 | ||
| MAE | 0.0904 * | 0.0110 | 0.3641 | 1.5929 | 1.2613 | ||
| BP | Training | R2 | 0.2768 | 0.3598 | 0.6510 | 0.2517 | 0.5772 |
| RMSE | 0.1329 | 0.0191 | 0.4350 | 3.6743 | 2.5188 | ||
| Testing | R2 | 0.1474 | 0.2871 | 0.7607 | 0.2060 | 0.5160 * | |
| RMSE | 0.1481 | 0.0154 | 0.3295 | 3.9491 | 2.5766 * | ||
| MAE | 0.1141 | 0.0132 | 0.2550 | 2.8076 | 1.8558 * | ||
| CNN | Training | R2 | 0.2768 | 0.2953 | 0.6662 | 0.2029 | 0.4984 |
| RMSE | 0.1329 | 0.0196 | 0.4227 | 3.9036 | 2.6807 | ||
| Testing | R2 | 0.1475 | 0.2841 | 0.6397 | 0.1932 | 0.4331 | |
| RMSE | 0.1481 | 0.0177 | 0.3862 | 3.6436 | 2.9746 | ||
| MAE | 0.1142 | 0.0141 | 0.3066 | 2.6692 | 2.0371 |
| Turbidity (NTU) | pH | NC (uS/cm) | DO (mg/L) | Temperature (°C) | |||
|---|---|---|---|---|---|---|---|
| RF | Training | R2 | 0.9090 | 0.9596 | 0.9426 | 0.9572 | 0.9592 |
| RMSE | 19.5934 | 0.0382 | 4.5606 | 0.2195 | 0.2096 | ||
| Testing | R2 | 0.3403 | 0.7262 * | 0.6449 * | 0.6728 * | 0.7071 | |
| RMSE | 55.8828 | 0.0997 * | 11.1834 * | 0.6157 * | 0.5648 | ||
| MAE | 27.3925 | 0.0670 * | 7.6322 * | 0.4104 * | 0.3430 | ||
| GB | Training | R2 | 0.8014 | 0.8347 | 0.7744 | 0.8334 | 0.9061 |
| RMSE | 28.7807 | 0.0758 | 9.0432 | 0.4425 | 0.4625 | ||
| Testing | R2 | 0.3040 | 0.6706 | 0.5864 | 0.6161 | 0.7547 * | |
| RMSE | 58.7329 | 0.1111 | 12.0692 | 0.6745 | 0.7402 * | ||
| MAE | 30.6318 | 0.0808 | 8.6639 | 0.4847 | 0.4783 * | ||
| BP | Training | R2 | 0.3609 | 0.6819 | 0.4924 | 0.5877 | 0.6807 |
| RMSE | 52.1333 | 0.1073 | 24.6138 | 0.9955 | 0.8015 | ||
| Testing | R2 | 0.3127 | 0.6383 | 0.4469 | 0.5434 | 0.6359 | |
| RMSE | 55.5892 | 0.1140 | 28.0632 | 1.0763 | 0.8228 | ||
| MAE | 31.2054 | 0.0831 | 18.1743 | 0.7440 | 0.5692 | ||
| CNN | Training | R2 | 0.3925 | 0.3157 | 0.4141 | 0.4196 | 0.4397 |
| RMSE | 48.4631 | 0.1570 | 27.7655 | 1.1796 | 1.0511 | ||
| Testing | R2 | 0.3433 * | 0.3547 | 0.4033 | 0.3758 | 0.3792 | |
| RMSE | 50.3219 * | 0.1529 | 28.3178 | 1.2641 | 1.1083 | ||
| MAE | 27.2034 * | 0.1203 | 17.6918 | 0.9437 | 0.7495 |
| Parameters | Models | Source | R2 | RMSE |
|---|---|---|---|---|
| CODMn | RF | Our study | 0.778 * | 0.304 * |
| BP-RF | [26] | 0.270 | 0.770 | |
| TP | RF | Our study | 0.445 | 0.016 |
| BP | [26] | 0.430 | 0.053 | |
| GA_XGBoost | [25] | 0.699 * | 0.034 * | |
| NH3-N | GB | Our study | 0.546 | 0.120 |
| GA_XGBoost | [25] | 0.694 * | 0.163 * | |
| Turbidity | GB | Our study | 0.343 | 50.322 |
| GA_XGBoost | [25] | 0.597 * | 10.127 * | |
| Chl-a | RF | Our study | 0.333 | 2.274 |
| RF-XGB | [26] | 0.500 | 1.770 | |
| GA_XGBoost | [25] | 0.855 * | 0.046 * | |
| CNN | [28] | 0.790 | 8.770 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lo, Y.; Fu, L.; Lu, T.; Huang, H.; Kong, L.; Xu, Y.; Zhang, C. Medium-Sized Lake Water Quality Parameters Retrieval Using Multispectral UAV Image and Machine Learning Algorithms: A Case Study of the Yuandang Lake, China. Drones 2023, 7, 244. https://doi.org/10.3390/drones7040244
Lo Y, Fu L, Lu T, Huang H, Kong L, Xu Y, Zhang C. Medium-Sized Lake Water Quality Parameters Retrieval Using Multispectral UAV Image and Machine Learning Algorithms: A Case Study of the Yuandang Lake, China. Drones. 2023; 7(4):244. https://doi.org/10.3390/drones7040244
Chicago/Turabian StyleLo, Ying, Lang Fu, Tiancheng Lu, Hong Huang, Lingrong Kong, Yunqing Xu, and Cheng Zhang. 2023. "Medium-Sized Lake Water Quality Parameters Retrieval Using Multispectral UAV Image and Machine Learning Algorithms: A Case Study of the Yuandang Lake, China" Drones 7, no. 4: 244. https://doi.org/10.3390/drones7040244
APA StyleLo, Y., Fu, L., Lu, T., Huang, H., Kong, L., Xu, Y., & Zhang, C. (2023). Medium-Sized Lake Water Quality Parameters Retrieval Using Multispectral UAV Image and Machine Learning Algorithms: A Case Study of the Yuandang Lake, China. Drones, 7(4), 244. https://doi.org/10.3390/drones7040244








