Lane Level Positioning Method for Unmanned Driving Based on Inertial System and Vector Map Information Fusion Applicable to GNSS Denied Environments
Abstract
1. Introduction
- (1)
- An integrated positioning method based on inertial technology and vector map information fusion is proposed, which is applicable for GNSS denied environments such as underground parking lots and large logistics complex areas;
- (2)
- The matching strategies are established, and the inertial positioning error model is used as a basis to select candidate road segments;
- (3)
- Validation experiments have been conducted out in an underground parking lot, and the results show that the positioning error for driving 5 km has been reduced from the meter level to within 30 cm.
2. Definition of the Coordinate System
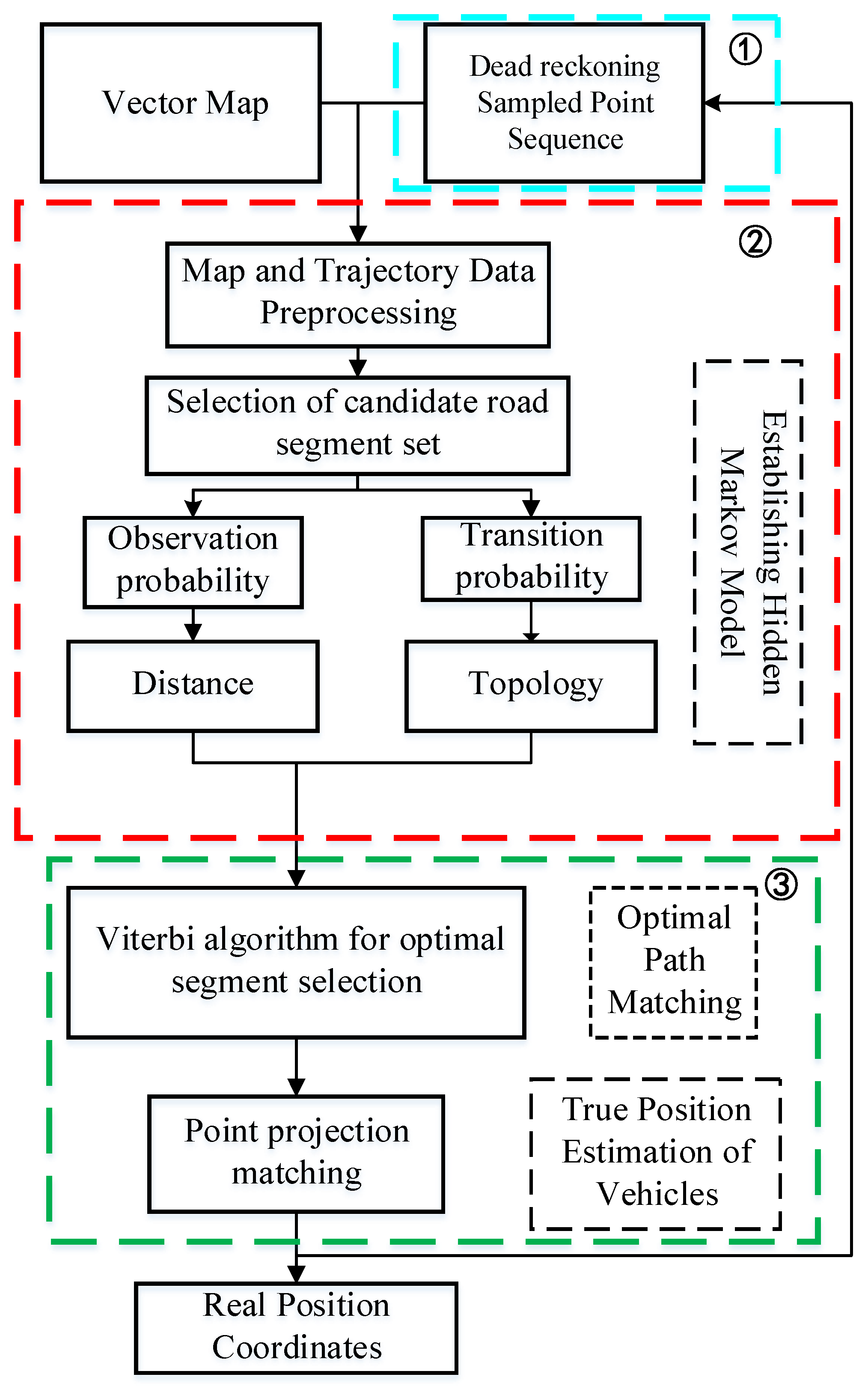
3. Overall Design of the Lane Level Positioning Method
4. Dead Reckoning Principle Based on Optical Fiber IMU/Odometer
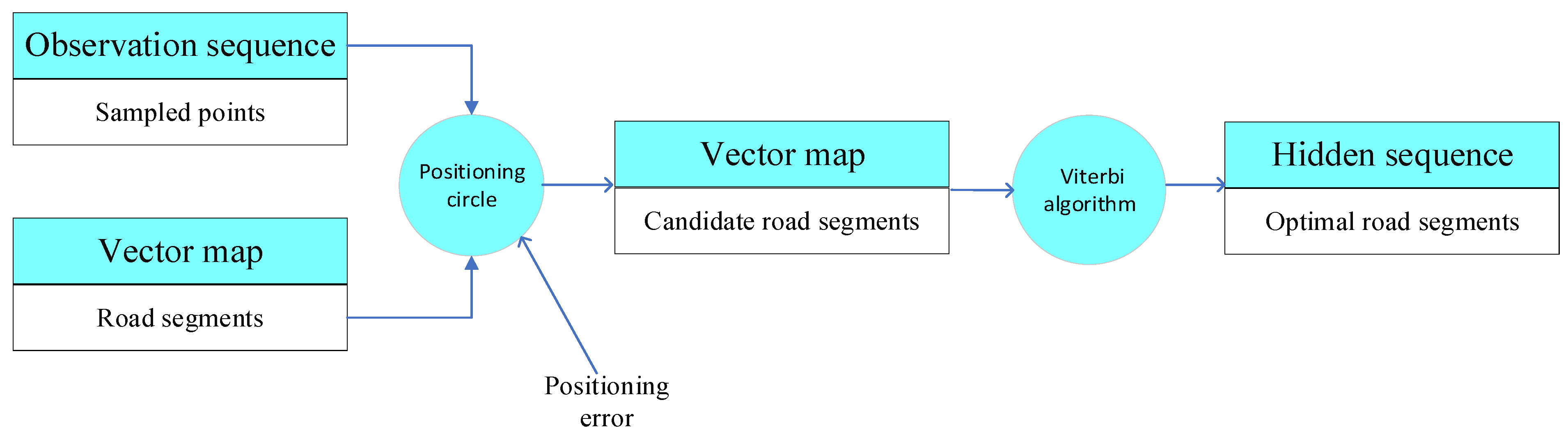
5. Map Matching Model Based on HMM
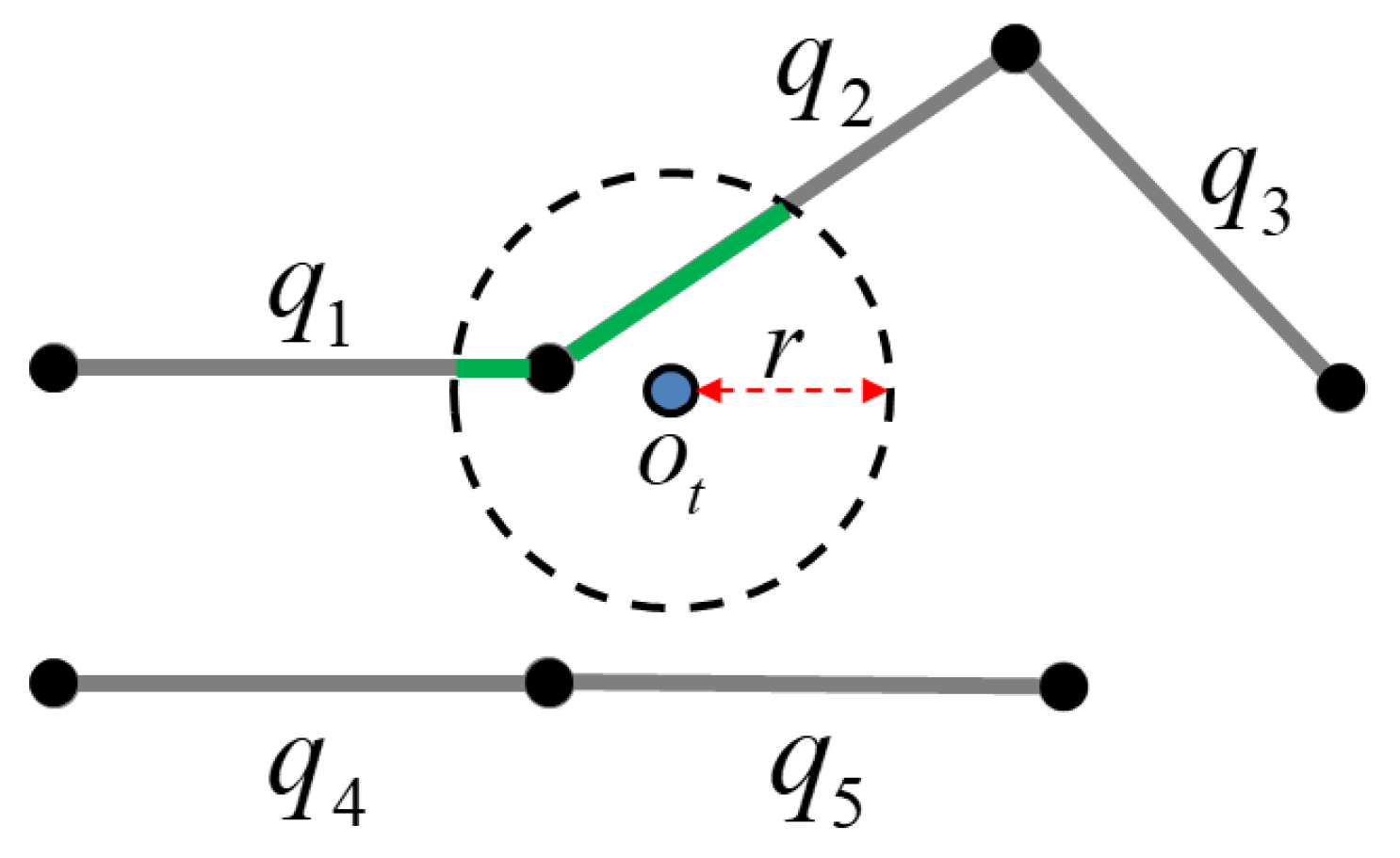
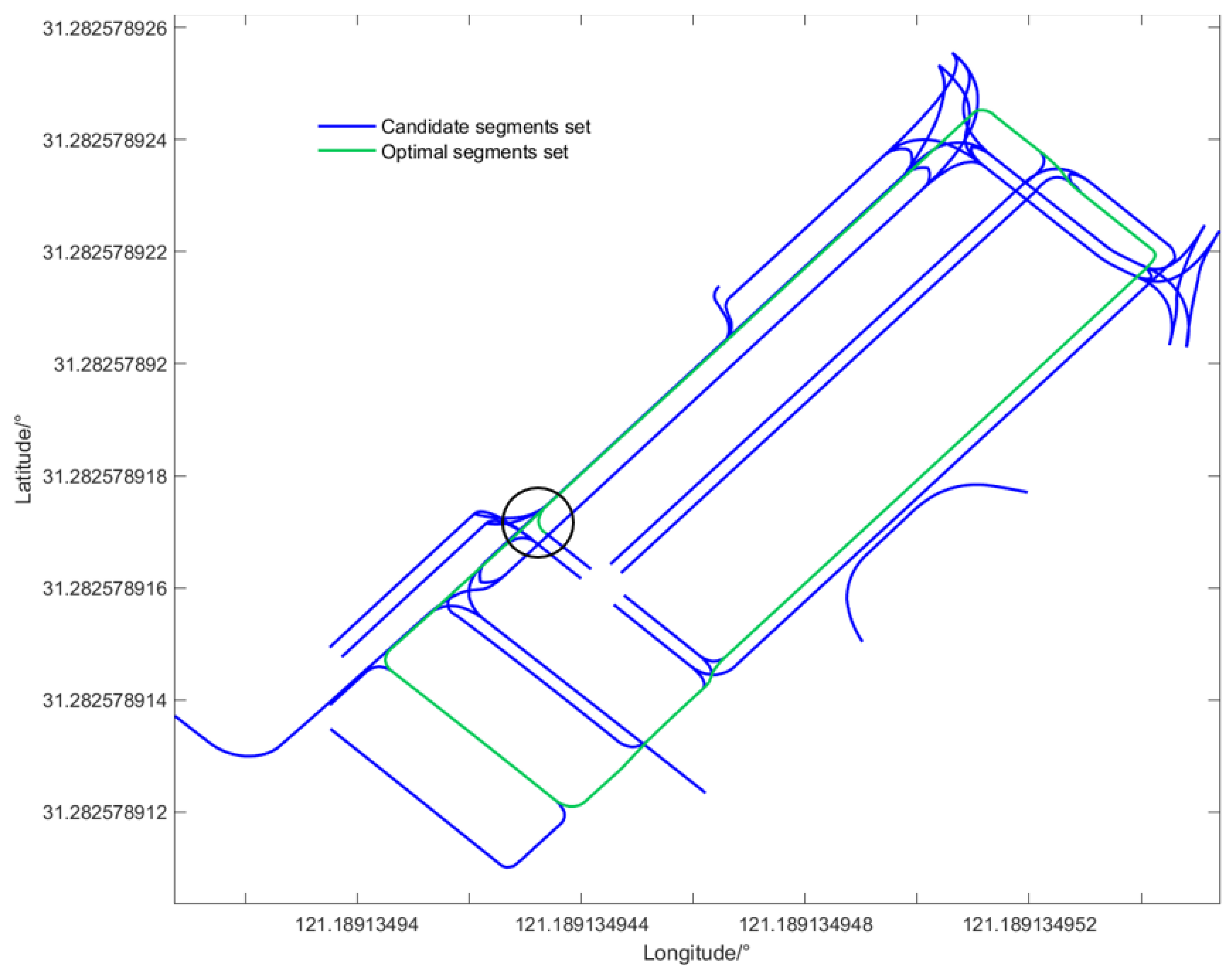
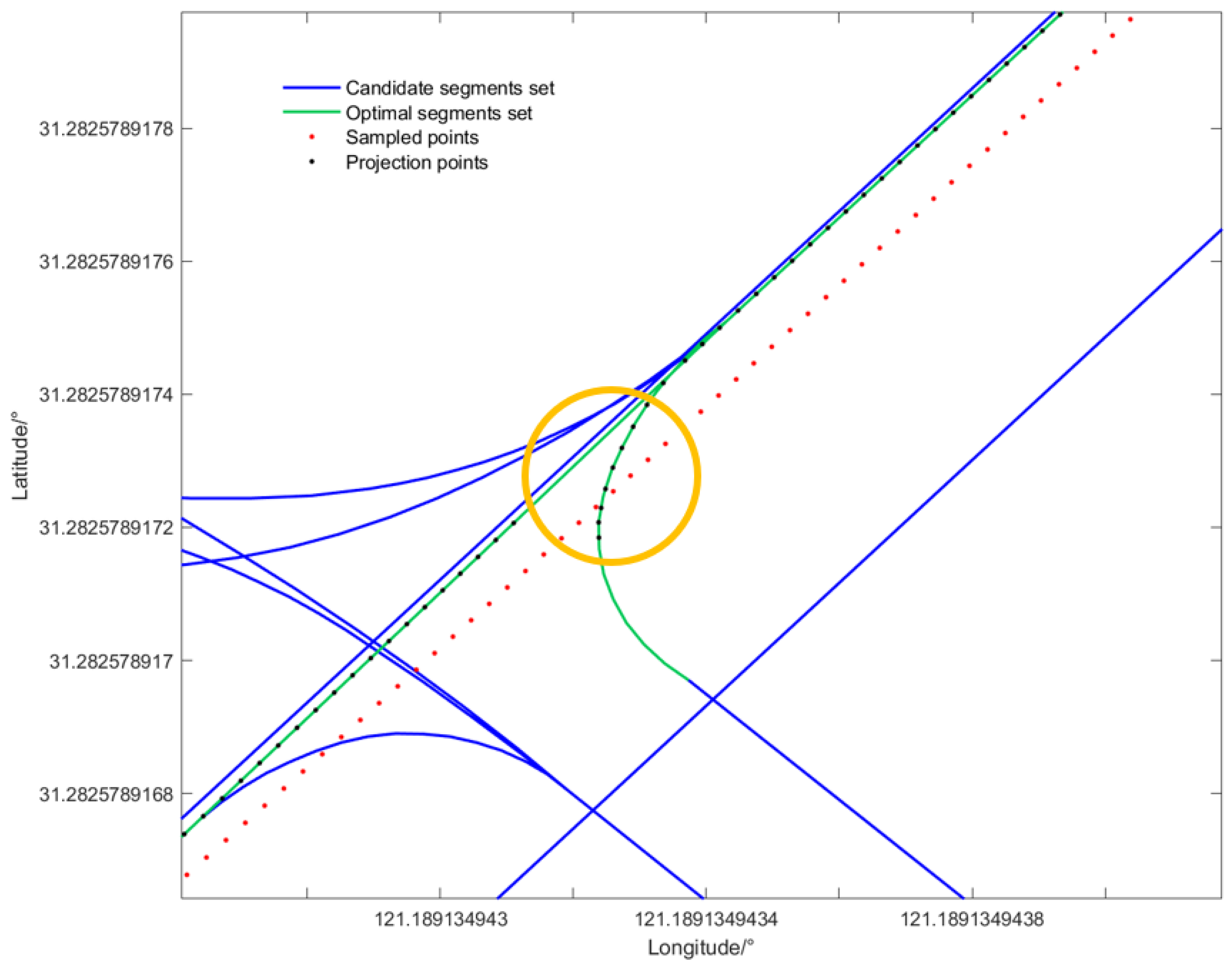
5.1. Selection of Candidate Road Segments
5.2. Initial Distribution Probability
5.3. Transition Probability
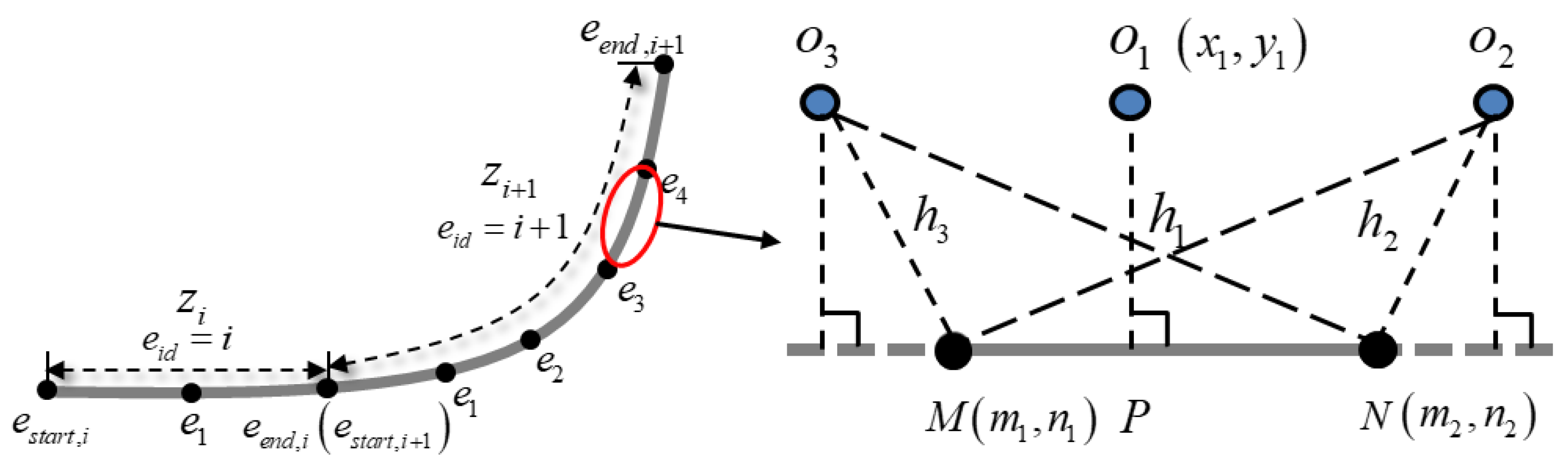
5.4. Observation Probability
6. Optimal Path Selection Based on Viterbi Algorithm
| Algorithm 1: Viterbi Algorithm | |
| Input: Collection of candidate road segments , | |
| Sampled points set | |
| Output: Optimal Segment Sequence | |
| 1: | Let P denote the highest score; |
| 2: | Let Q [ ] denote the set of the optimal segments; |
| 3: | |
| 4: | Set i |
| 5: | for to do |
| 6: | |
| 7: | |
| 8: | Q = Q + ; |
| 9: | end for |
| 10: | for to do |
| 11: | for to do |
| 12: | |
| 13: | |
| 14: | Q = Q + |
| 15: | end for |
| 16: | end for |
| 17: | return |
7. Evaluation Method
8. Experiment and Discussion
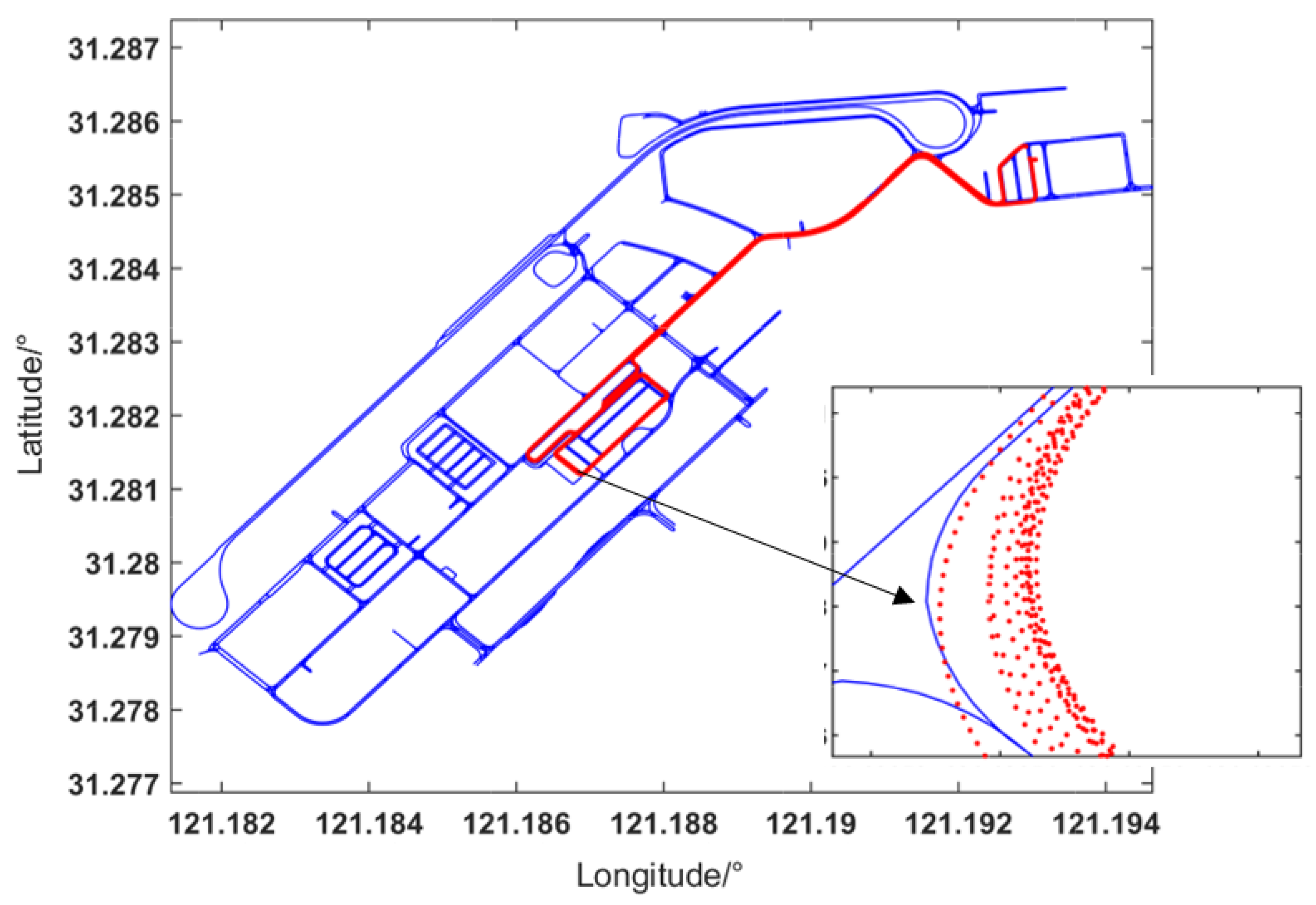
- Case 1:
- The vehicle starts from the northeast corner of the map and drives along the lane line to the southwest corner of the map. The vehicle drives eight laps in the underground garage. The red line in Figure 10 represents the track of the vehicle. A curve is selected in the lower right corner of Figure 10 and enlarged locally for better visualization.
- Case 2:
- The vehicle drives one lap in the underground garage. There are more curves and more complicated road conditions.
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, J.; Kurup, U.; Shah, M. Is It Safe to Drive? An Overview of Factors, Metrics, and Datasets for Driveability Assessment in Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3135–3151. [Google Scholar] [CrossRef]
- Liu, W.; Li, Z.; Sun, S.; Gupta, M.K.; Du, H.; Malekian, R.; Sotelo, M.A.; Li, W. Design a Novel Target to Improve Positioning Accuracy of Autonomous Vehicular Navigation System in GPS Denied Environments. IEEE Trans. Ind. Inform. 2021, 17, 7575–7588. [Google Scholar] [CrossRef]
- Ye, L.; Gao, N.; Yang, Y.; Li, X. A High-Precision and Low-Cost Broadband LEO 3-Satellite Alternate Switching Ranging/INS Integrated Navigation and Positioning Algorithm. Drones 2022, 6, 241. [Google Scholar] [CrossRef]
- Syed, Z.F.; Aggarwal, P.; Niu, X.; El-Sheimy, N. Civilian Vehicle Navigation: Required Alignment of the Inertial Sensors for Acceps Navigation Accuracies. IEEE Trans. Veh. Technol. 2008, 57, 3402–3412. [Google Scholar]
- Zhang, Z.; Niu, X.; Tang, H.; Chen, Q.; Zhang, T. GNSS/INS/ODO/Wheel Angle Integrated Navigation Algorithm for an All-Wheel Steering Robot. Meas. Sci. Technol. 2021, 32, 115122. [Google Scholar] [CrossRef]
- Gu, N.; Xing, F.; You, Z. Visual/Inertial/GNSS Integrated Navigation System under GNSS Spoofing Attack. Remote Sens. 2022, 14, 5975. [Google Scholar] [CrossRef]
- Zhao, H.; Miao, L.; Shao, H. Adaptive Two-Stage Kalman Filter for SINS/Odometer Integrated Navigation Systems. J. Navig. 2017, 70, 242–261. [Google Scholar] [CrossRef]
- Bai, H.; Xue, X. Simulation Research on FOG-SINS/Doppler Radar/Baro-Altimeter Integrated Navigation for Helicopters. In Proceedings of the 2010 Second International Conference on Computer Modeling and Simulation, Sanya, China, 22–24 January 2010; pp. 115–119. [Google Scholar]
- Shan, B.; Qin, Y.; Wang, Y.; Yang, B.; Guo, Z. SINS/Geomagnetic Matching/Barometric Altimeter Integrated Navigation Method for Land Vehicle. In Proceedings of the 2014 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Guilin, China, 5–8 August 2014; pp. 32–35. [Google Scholar]
- Ren, Y.; Wang, L.; Lin, K.; Ma, H.; Ma, M. Improved Iterative Closest Contour Point Matching Navigation Algorithm Based on Geomagnetic Vector. Electronics 2022, 11, 796. [Google Scholar] [CrossRef]
- Shahoud, A.; Shashev, D.; Shidlovskiy, S. Visual Navigation and Path Tracking Using Street Geometry Information for Image Alignment and Servoing. Drones 2022, 6, 107. [Google Scholar] [CrossRef]
- Duo, J.; Zhao, L. A Robust and Efficient Airborne Scene Matching Algorithm for UAV Navigation. In Proceedings of the 2017 IEEE 9th International Conference on Communication Software and Networks (ICCSN), Guangzhou, China, 6–8 May 2017; pp. 1337–1342. [Google Scholar]
- Zhang, T.; Liu, C.; Li, J.; Pang, M.; Wang, M. A New Visual Inertial Simultaneous Localization and Mapping (SLAM) Algorithm Based on Point and Line Features. Drones 2022, 6, 23. [Google Scholar]
- Zhai, C.; Wang, M.; Yang, Y.; Shen, K. Robust Vision-Aided Inertial Navigation System for Protection Against Ego-Motion Uncertainty of Unmanned Ground Vehicle. IEEE Trans. Ind. Electron. 2021, 68, 12462–12471. [Google Scholar] [CrossRef]
- Liu, X.; Sun, X.; Xia, X. LiDAR Point’s Elliptical Error Model and Laser Positioning for Autonomous Vehicles. Meas. Sci. Technol. 2020, 32, 035107. [Google Scholar] [CrossRef]
- Du, B.; Shi, Z.; Wang, H.; Han, L.; Song, J. Multi-Layer Model Aided Inertial Navigation System for Unmanned Ground Vehicles. Meas. Sci. Technol. 2022, 33, 075110. [Google Scholar] [CrossRef]
- Chen, W.; Li, X.; Song, X.; Li, B.; Song, X.; Xu, Q. A Novel Fusion Methodology to Bridge GPS Outages for Land Vehicle Positioning. Meas. Sci. Technol. 2015, 26, 075001. [Google Scholar] [CrossRef]
- Aggarwal, P.; Thomas, D.; Ojeda, L.; Borenstein, J. Map Matching and Heuristic Elimination of Gyro Drift for Personal Navigation Systems in GPS-Denied Conditions. Meas. Sci. Technol. 2011, 22, 025205. [Google Scholar] [CrossRef]
- Zhang, J.; Khodabandeh, A.; Khoshelham, K. Centimeter-Level Positioning by Instantaneous Lidar-Aided GNSS Ambiguity Resolution. Meas. Sci. Technol. 2022, 22, 115020. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Alam, M.M.; Moh, S. Vision-Based Navigation Techniques for Unmanned Aerial Vehicles: Review and Challenges. Drones 2023, 7, 89. [Google Scholar] [CrossRef]
- Antonopoulos, A.; Lagoudakis, M.G.; Partsinevelos, P. A ROS Multi-Tier UAV Localization Module Based on GNSS, Inertial and Visual-Depth Data. Drones 2022, 6, 135. [Google Scholar] [CrossRef]
- Ling, Y.; Chu, X.; Lu, Z.; Wang, L.; Wen, X. PCM: A Positioning Calibration Mechanism for Connected Autonomous Vehicles. IEEE Access 2020, 8, 95046–95056. [Google Scholar] [CrossRef]
- Lei, T.; Xiao, G.; Yin, X. Targeting Lane-Level Map Matching for Smart Vehicles: Construction of High-Definition Road Maps Based on GIS. Appl. Sci. 2023, 13, 862. [Google Scholar] [CrossRef]
- Kassas, Z.Z.M.; Maaref, M.; Morales, J.J.; Khalife, J.J.; Shamei, K. Robust Vehicular Localization and Map Matching in Urban Environments Through IMU, GNSS, and Cellular Signals. IEEE Intell. Transp. Syst. Mag. 2020, 12, 36–52. [Google Scholar] [CrossRef]
- Feng, J.; Li, Y.; Zhao, K.; Xu, Z.; Xia, T.; Zhang, J.; Jin, D. DeepMM: Deep Learning Based Map Matching with Data Augmentation. IEEE Trans. Mob. Comput. 2020, 21, 2372–2384. [Google Scholar] [CrossRef]
- Bernstein, D.; Kornhauser, A. An Introduction to Map Matching for Personal Navigation Assistants; Geometric Distributions; Tech. Rep.; New Jersey Institute of Technology: Newark, NJ, USA, 1998. [Google Scholar]
- White, C.E.; Bernstein, D.; Kornhauser, A.L. Some Map Matching Algorithms for Personal Navigation Assistants. Transp. Res. Part C Emerg. Technol. 2000, 8, 91–108. [Google Scholar]
- Taylor, G.; Blewitt, G.; Steup, D.; Corbett, S.; Car, A. Road Reduction Filtering for GPS-GIS Navigation. Trans. GIS 2001, 5, 193–207. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, T.; Li, Q.; Wu, Z.; Zou, H.; Gao, C. Curvedness Feature Constrained Map Matching for Low-Frequency Probe Vehicle Data. Int. J. Geogr. Inf. Sci. 2016, 30, 660–690. [Google Scholar] [CrossRef]
- Sharma, K.P.; Jain, R. Inscribe the Exigency of Map Matching Performance for Curve Navigation on Road/Highways. In Proceedings of the 2019 Amity International Conference on Artificial Intelligence (AICAI), Dubai, United Arab Emirates, 4–6 February 2019; pp. 850–854. [Google Scholar]
- Fréchet, M.M. Sur Quelques Points Du Calcul Fonctionnel. Rend. Circ. Mat. Palermo 1906, 22, 1–72. [Google Scholar] [CrossRef]
- Bierlaire, M.; Chen, J.; Newman, J. A Probabilistic Map Matching Method for Smartphone GPS Data. Transp. Res. Part C Emerg. Technol. 2013, 26, 78–98. [Google Scholar] [CrossRef]
- Pink, O.; Hummel, B. A Statistical Approach to Map Matching Using Road Network Geometry, Topology and Vehicular Motion Constraints. In Proceedings of the 2008 11th International IEEE Conference on Intelligent Transportation Systems, Beijing, China, 12–15 October 2008; pp. 862–867. [Google Scholar]
- Ochieng, W.; Quddus, M.; Noland, R. Map-Matching in Complex Urban Road Networks. Braz. J. Cartogr. 2003, 55, 1–14. [Google Scholar] [CrossRef]
- Yue, Y.; Zhao, C.; Wen, M.; Wu, Z.; Wang, D. Collaborative Semantic Perception and Relative Localization Based on Map Matching. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 6188–6193. [Google Scholar]
- Quddus, M.A.; Ochieng, W.Y.; Zhao, L.; Noland, R.B. A General Map Matching Algorithm for Transport Telematics Applications. GPS Solut. 2003, 7, 157–167. [Google Scholar] [CrossRef]
- Velaga, N.R.; Quddus, M.A.; Bristow, A.L. Developing an Enhanced Weight-Based Topological Map-Matching Algorithm for Intelligent Transport Systems. Transp. Res. Part C Emerg. Technol. 2009, 17, 672–683. [Google Scholar] [CrossRef]
- Yang, H.; Cheng, S.; Jiang, H.; An, S. An Enhanced Weight-Based Topological Map Matching Algorithm for Intricate Urban Road Network. Procedia Soc. Behav. Sci. 2013, 96, 1670–1678. [Google Scholar] [CrossRef]
- He, M.; Zheng, L.; Cao, W.; Huang, J.; Liu, X.; Liu, W. An Enhanced Weight-Based Real-Time Map Matching Algorithm for Complex Urban Networks. Phys. A Stat. Mech. Its Appl. 2019, 534, 122318. [Google Scholar] [CrossRef]
- Sharath, M.N.; Velaga, N.R.; Quddus, M.A. A Dynamic Two-Dimensional (D2D) Weight-Based Map-Matching Algorithm. Transp. Res. Part C Emerg. Technol. 2019, 98, 409–432. [Google Scholar] [CrossRef]
- Newson, P.; Krumm, J. Hidden Markov Map Matching through Noise and Sparseness. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009; pp. 336–343. [Google Scholar]
- Lou, Y.; Zhang, C.; Zheng, Y.; Xie, X.; Wang, W.; Huang, Y. Map-Matching for Low-Sampling-Rate GPS Trajectories. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009; pp. 352–361. [Google Scholar]
- Hsueh, Y.-L.; Chen, H.-C. Map Matching for Low-Sampling-Rate GPS Trajectories by Exploring Real-Time Moving Directions. Inf. Sci. 2018, 433–434, 55–69. [Google Scholar] [CrossRef]
- Hsueh, Y.-L.; Chen, H.-C.; Huang, W. A Hidden Markov Model-Based Map-Matching Approach for Low-Sampling-Rate GPS Trajectories. In Proceedings of the 2017 IEEE 7th International Symposium on Cloud and Service Computing (SC2), Kanazawa, Japan, 22–25 November 2017; pp. 271–274. [Google Scholar]
- Xie, Y.; Zhou, K.; Miao, F.; Zhang, Q. High-Accuracy Off-Line Map-Matching of Trajectory Network Division Based on Weight Adaptation HMM. IEEE Access 2020, 8, 7256–7266. [Google Scholar] [CrossRef]
- Sadli, R.; Afkir, M.; Hadid, A.; Rivenq, A.; Taleb-Ahmed, A. Map-Matching-Based Localization Using Camera and Low-Cost GPS for Lane-Level Accuracy. Sensors 2022, 22, 2434. [Google Scholar] [CrossRef] [PubMed]

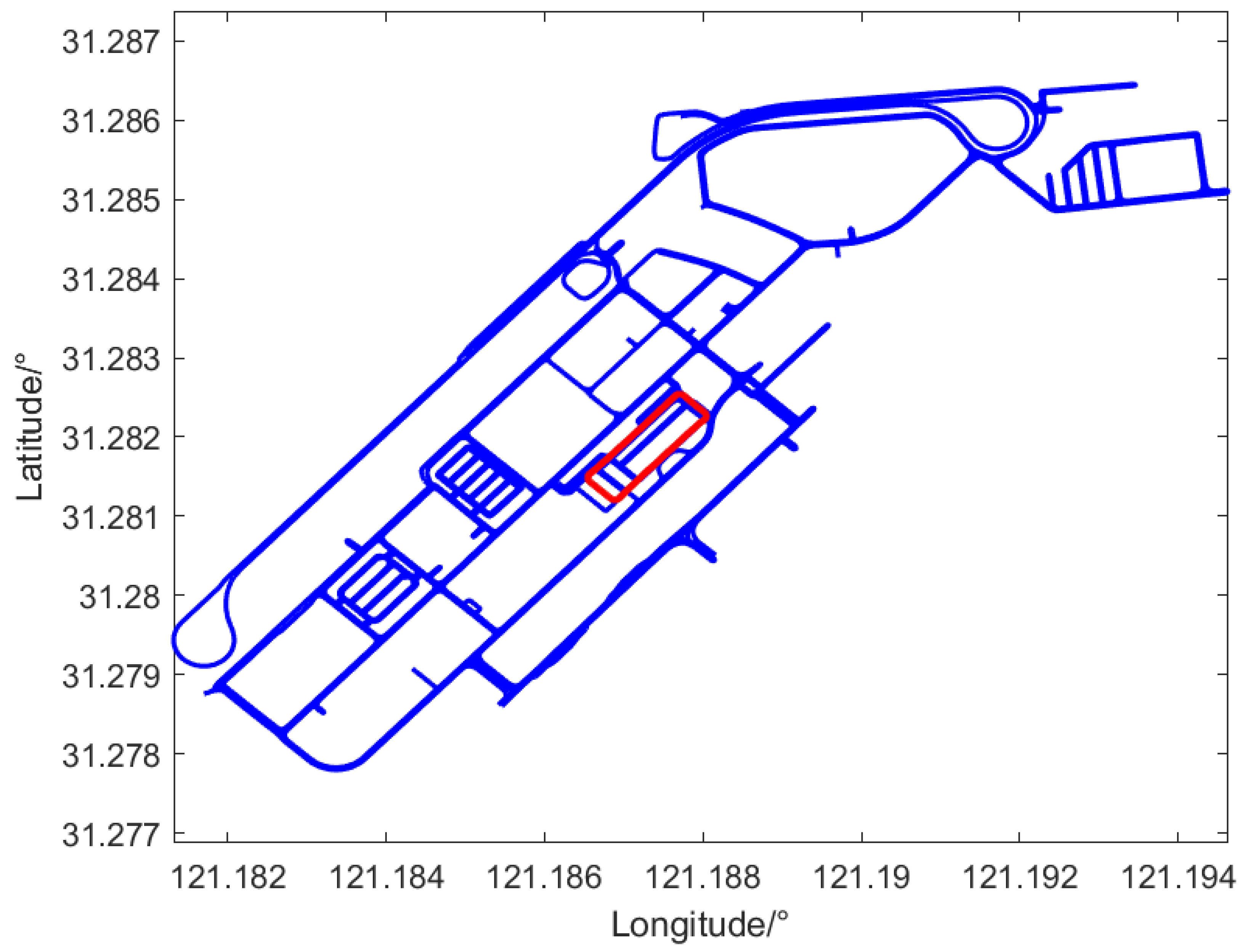
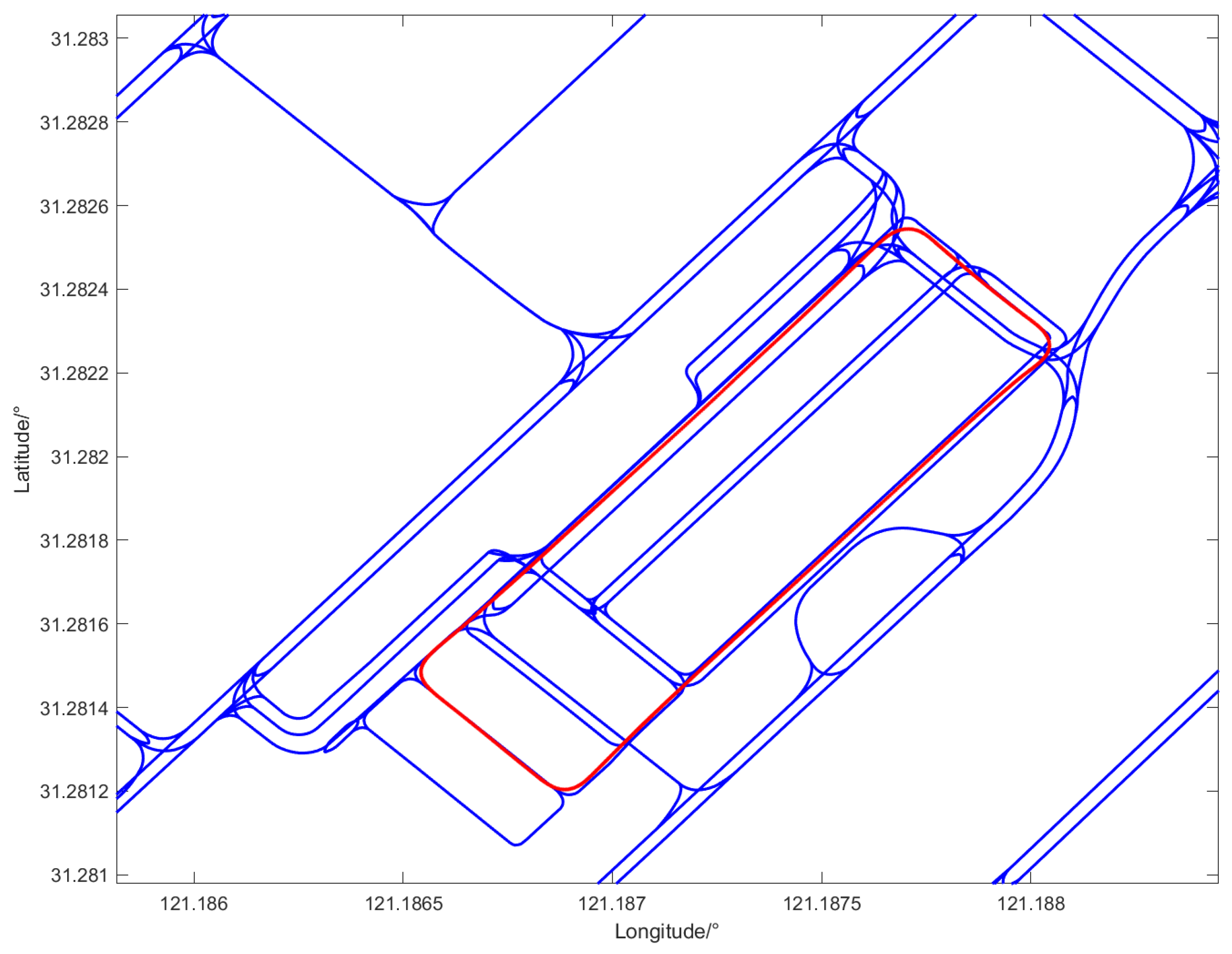


| Method | Typical Work | Advantage | Disadvantage |
|---|---|---|---|
| SINS/OD | [7] | 1. High autonomy; 2. Low cost; | 1. Error accumulation exists; |
| SINS/Altimeter | [8] | 1. Able to suppress divergence of altitude channel; 2. Low cost; | 1. Low accuracy; |
| SINS/GMNS | [9,10] | 1. No accumulated error; 2. Work all-weather; | 1. Vulnerable to interference; 2. Low reliability; |
| SINS + SMNS | [11,12] | 1. Low cost; 2. No accumulated error. | 1. Difficulty in database collection; 2. Vulnerable to weather. |
| Specific Algorithm | Typical Work | Type | Information Source | Positioning Accuracy |
|---|---|---|---|---|
| Line to line | [24] | Geometry-based | GPS | 5.5 m (80%) |
| Enhanced probability statistics | [29] | Probability statistics-based | GPS | —— (85%) |
| Weighted topology matching | [33] | Road topology-based | GPS | 2.82 m (84%) |
| HMM | [38] | Integrated map matching | GPS | 1.3 m (98%) |
| Device | Parameter | Value |
|---|---|---|
| Fiber optic gyroscope | Range | ±400°/s |
| Bias stability | ≤0.1°/h (1 ) | |
| Bias repeatability | ≤0.1°/h (1 ) | |
| Random walk coefficient | ≤0.02°/√h | |
| Scale factor nonlinearity | ≤100 ppm | |
| Scale factor repeatability | ≤100 ppm | |
| Bandwidth | ≥200 Hz | |
| Accelerometer | Range | ±20 g |
| Bias stability | ≤0.2 mg (1 ) | |
| Bias repeatability | ≤0.2 mg (1 ) | |
| Random walk coefficient | ≤100 ppm | |
| Scale factor nonlinearity | ≤100 ppm | |
| Scale factor repeatability | ≥200 Hz |
| Trajectory | Number of Sampled Points | Real Driving Distance (m) | The Radius of the Positioning Circle (m) | Number of Candidate Segments |
|---|---|---|---|---|
| S1 | 1457 | 420 | 5 | 67 |
| S2 | 1368 | 420 | 10 | 78 |
| S3 | 2230 | 550 | 5 | 71 |
| Trajectory | Average Length of Candidate Segments (m) | Average Distance between Adjacent Sampled Points (cm) |
|---|---|---|
| S1 | 27.0 | 30.8 |
| S2 | 30.2 | 49.8 |
| S3 | 27.7 | 26.3 |
| Trajectory | Recall | CMP | PE before Matching (m) | PE after Matching (m) | Time of Running (s) |
|---|---|---|---|---|---|
| S1 | 100% | 100% | 0.59 | 0.12 | 29.38 |
| S2 | 94.4% | 98.57% | 1.03 | 0.24 | 20.18 |
| S3 | 100% | 99.1% | 0.84 | 0.18 | 47.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, M.; Li, H.; Liang, J.; Zhang, C.; Pan, X.; Tian, Y.; Cao, J.; Wang, Y. Lane Level Positioning Method for Unmanned Driving Based on Inertial System and Vector Map Information Fusion Applicable to GNSS Denied Environments. Drones 2023, 7, 239. https://doi.org/10.3390/drones7040239
Dai M, Li H, Liang J, Zhang C, Pan X, Tian Y, Cao J, Wang Y. Lane Level Positioning Method for Unmanned Driving Based on Inertial System and Vector Map Information Fusion Applicable to GNSS Denied Environments. Drones. 2023; 7(4):239. https://doi.org/10.3390/drones7040239
Chicago/Turabian StyleDai, Minpeng, Haoyang Li, Jian Liang, Chunxi Zhang, Xiong Pan, Yizhuo Tian, Jinguo Cao, and Yuxuan Wang. 2023. "Lane Level Positioning Method for Unmanned Driving Based on Inertial System and Vector Map Information Fusion Applicable to GNSS Denied Environments" Drones 7, no. 4: 239. https://doi.org/10.3390/drones7040239
APA StyleDai, M., Li, H., Liang, J., Zhang, C., Pan, X., Tian, Y., Cao, J., & Wang, Y. (2023). Lane Level Positioning Method for Unmanned Driving Based on Inertial System and Vector Map Information Fusion Applicable to GNSS Denied Environments. Drones, 7(4), 239. https://doi.org/10.3390/drones7040239





