Abstract
Future Unmanned Aerial Vehicle (UAV)-assisted wireless communication systems are expected to utilize wide bandwidths available at terahertz (THz) frequencies to enhance system throughput. To compensate for the severe path loss in the THz band, it is essential to have a multitude of antennas in the UAV to generate narrow beams for directional transmission. However, narrow beams severely limit its spatial coverage, which greatly affects the efficiency of large-scale access UAV-assisted THz systems. Moreover, the combination of massive antennas and large bandwidth at THz makes the misalignment of the beams caused by beam squint non-negligible and also high energy consumption. UAV-assisted communication technology can effectively increase spatial coverage and provide reliable LoS communication links. In addition, reducing the number of radio frequency (RF) chains while ensuring the number of transmitted data streams and space division multiplexing capability is also an effective way to reduce energy consumption in the UAV communication. In this paper, a single RF chain uniform planar array (UPA) with true-time-delays (TTDs) is equipped on the UAV to achieve two dimensional (2D) beams and split spatial beams to improve transmission efficiency. We analyze the 2D beam squint of the UPA and design a time-delay phased UPA for UAV-assisted THz communication systems. By introducing TTDs between the single RF chain and phase shifters, the beam squint can be controlled flexibly by introducing the delay between each antenna. When TTDs are arranged in both the horizontal and vertical dimensions, the coverage of the beams becomes more complicated compared to uniform linear arrays (ULA). Simulation results show that the proposed time-delay phased UPA can achieve better performance in both single-beam and multi-beam modes for single user and multi-user scenarios compared with conventional phased UPA, respectively. In addition, we propose frequency division beam multiple access (FDBMA) multi access technology, which achieves more efficient multi access by reusing resources from different frequency beam pairs. Finally, the results also show that the enlargement of the beamwidth through the proposed FDBMA strategy can also increase the performance in multi-user scenarios.
1. Introduction
The main characteristics of the future beyond the fifth generation (B5G) and the sixth generation (6G) wireless communication networks are higher data transmission rates, lower latency, lower energy consumption, and a wider range of application scenarios [1]. Unmanned Aerial Vehicle (UAV)-assisted terahertz (THz) communications are viewed as a promising technology for B5G and the future 6G wireless communication systems. However, although the abundant THz band (0.1∼10 THz) can provide a large bandwidth, the THz signal suffers from severe path loss [2,3]. To compensate for the path loss, large-scale antennas are required to form a highly directional transmission with a large beamforming gain [4,5,6], resulting in high energy consumption, which may hinder the development of UAV-assisted terahertz communication.
In the THz band, benefiting from a small carrier wavelength, a large number of antennas can be implemented with a small form factor. Reducing the number of radio frequency (RF) chains is crucial in order to reduce the huge energy consumption caused by the large number of antennas. Compared to models such as using low-precision ADCs [7,8] and sparse array connection design [9], reducing the number of RF links can effectively reduce system energy consumption while ensuring lower complexity of beam optimization algorithms. Considering the severe limitation of UAV power consumption, we only consider phased arrays with a single RF chain to improve spatial gain. However, phased arrays with single RF chain can only form a full gain beam in one direction throughout the entire space and, more importantly, the beam squint caused by the time delay difference of the transmitted/received signals between different antennas has a huge impact on the wideband communication systems [10,11]. The effect becomes more severe with the increase in the number of antennas and the broadening of the bandwidth [12]. One-dimensional (1D) beam squint of uniform linear array (ULA) was analyzed in [10,13]. To eliminate the impact of 1D beam squint, the authors in [10] divided the entire array into several virtual sub-arrays to generate wider beam. Moreover, a new hardware implementation of the beamformer based on true-time-delay (TTD) was also proposed in [10]. Then, a reconfigurable holographic metasurface was used against the beam squint [14]. Compared with these wideband beamforming methods, introducing the TTD to implement the delay on each subcarrier can achieve the optimal performance of a fully digital array. Benefiting from the TTD-based architecture, a single-shot beam training strategy can be designed to greatly reduce the complexity of the beam training process [15]. Furthermore, the authors in [16] proposed the THzPrism to expand the beam coverage through TTD. Finally, the authors in [17] found that the energy efficiency of the array after introducing TTD is higher compared to traditional architectures, and it can form full gain beams in multiple directions under a single RF chain. Therefore, introducing TTD into UAV-assisted THz communication systems is of great significance. The above work is based on ULA for simplicity. However, in order to ensure high-precision beam pointing and smaller array size in the UAV, it is necessary to integrate the antenna into a two-dimensional (2D) rectangular array. The uniform planar array (UPA) is widely used in UAV-assisted communications due to its higher space efficiency through packing antennas on a 2D grid [18,19,20]. However, the introduction of extra-dimensional antennas brings the 2D beam squint effect, which yields more challenges to the system design.
Furthermore, the aviation capabilities of UAVs enable them to establish temporary communication networks between different locations, providing a wider coverage range for terahertz communication. By flying at high altitudes, UAVs can provide a better signal reception and transmission environment, enhancing the reliability and stability of terahertz communication. Zhao et al. investigated the channel under both Doppler effect and beam squint effect for UAV communications with large antenna array and high frequency band and designed a gridless compressed sensing (GCS) based channel tracking method [12]. Xu et al. studied the problem of unmanned aerial vehicle (UAV) deployment, power allocation, and bandwidth allocation is investigated for a UAV-assisted wireless system operating at terahertz (THz) frequencies [21]. Alali et al. investigated the UAV trajectories in sub-THz band to maximize the secrecy rate of the UAVs communication. To enhance the obtained average secrecy rate, MIMO communication and a cooperative UAV jammer strategy were used in their paper [22].
The existing work utilizes the superior link performance and broader spatial coverage capabilities brought by UAV-assisted communications. However, when facing the THz frequency band with extremely large bandwidth, these advantages can actually constrain the performance of the system. For example, severe beam split effects can cause beam squint in the LoS path. Therefore, it is necessary to seek new arrays that are more suitable for UAV assisted broadband THz communication. In this paper, we still focus on the UAV-assisted wideband THz massive antenna system with the aid of the time-delay phased UPA. Our contributions are as follows:
- Firstly, we analyze the impact of the 2D beam squint effect on the phased UPA and propose a time-delay phased UPA extended from [16], which can be applied in both single-beam large bandwidth communication for single user case and multi-beam large-scale access scenarios for multi-user case.
- Secondly, considering the commonly assumed LoS path in UAV communication, although it can effectively improve gain in traditional ground communication, the presence of beam squint in broadband terahertz communication will seriously affect performance. Therefore, we will apply the time-delay phased UPA studied in unmanned aerial vehicle communication to improve the overall system gain by eliminating or utilizing beam squints, thereby perfectly adapting to UAV communication.
- Thirdly, considering the fact that the beams are more fine-grained in UPA due to the extra vertical dimension, the beam design method of ULA cannot be directly applied to UPA. We further propose a frequency division beam multiple access (FDBMA) strategy to deal with uneven vertical beam distribution. The position of the drone is also variable, making it more suitable for the proposed multi user transmission process.
- Finally, to further enlarge the coverage of the beam in the multi-user case, influence of the beamwidth is also analyzed through antenna dropout.
The rest of the report is organized as follows. The system model and the description of beam squint is presented in Section 2. The proposed architecture and applications in UAV communications are presented in Section 3, while the simulations are then displayed in Section 4. Finally, conclusions are drawn in Section 5.
Notation: is the field of complex numbers. is the complex normal distribution with mean u and variance , is the closed interval between a and b. Lower-case and upper-case boldface letters represent vectors and matrices, respectively, and represents the absolute value operator.
2. System Model and Beam Squint
2.1. System Model
We consider a wideband THz massive antenna system using phased UPA with single RF chain for UAV communications. Orthogonal frequency division multiplexing (OFDM) containing M subcarriers is applied to facilitate wideband transmission where interference between subcarriers can be assumed perfectly eliminated [23]. The system architecture of the conventional wideband phased UPA is shown in Figure 1a. The base station (BS) is equipped with an -antenna UPA and single RF chain, which simultaneously serve K single-antenna users on the downlink and . The UPA contains identical and isotropic vertical antennas with spacing and horizontal antennas with spacing , as shown in Figure 1b. The symbol received at the m-th subcarrier is
where , contains the symbols transmitted on the M subcarriers, denotes the channel at the m-th subcarrier, and is the beamformer that is shared by all the subcarriers due to the fact that phase shifters (PSs) are frequency-independent [24]. Moreover, the constraint must also be satisfied. is the transmission power, and denotes the additive white Gaussian noise (AWGN) at the m-th subcarrier. The AWGN follows the distribution , where represents the noise power.
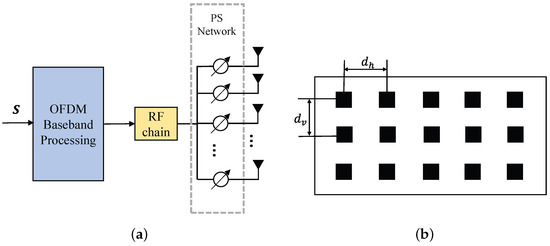
Figure 1.
The conventional phased UPA wideband system. (a) The phased UPA system with OFDM. (b) The structure of the UPA.
For the THz channel, the widely utilized wideband ray-based channel model is adopted [2,10,25]. The channel of the m-th subcarrier frequency where , can be expressed as
where and W are the central frequency and bandwidth, respectively. L denotes the number of resolvable paths, while and are the path gain and path delay of the l-th path, respectively. and represent the spatial horizontal and vertical directions of the transmitter of the l-th path and the m-th subcarrier, respectively. is the array response of the UPA, which can be represented as [19]
where ⊗ is the Kronecker product. Both and are horizontal and vertical array responses, respectively, with
where , and and . Hence, and denote the physical propagation direction angle of departure (AoD) in the horizontal and vertical directions of the l-th path, c is the light speed, and and are the fixed horizontal and vertical antenna spacings, respectively. For simplicity, we do not consider the electromagnetic interaction between deployed antennas.
2.2. 2D Beam Squint Effect of the UPA
In this section, we analyze the 2D beam squint effect of the conventional phased UPA. Differently from [10], where the 1D beam squint in the ULA is analyzed, the beam squint in the UPA containing two dimensions is considered in this work. As mentioned above, the PS is essentially a narrowband device as it can only generate the same phases at different frequencies. In other words, the optimal array gain of the phased UPA is only achievable at a given frequency. Specifically, for the l-th physical propagation direction angle of departure (AoD) with , the phases are usually designed according to the center frequency and the beamformer is denoted as
In this case, at frequency , the array gain is derived as
where and come from and , respectively.
Property 1.
Assuming , , then .
Property 2.
Assuming , , and , then .
Further, contains , and comes from the equation
For a given AoD, when which means that , the array gain . However, when , the array gain . This demonstrates that the spatial directions are frequency-dependent but the beamformer is frequency-independent, which results in misalignment at the frequency , that is the beam squint effect. Moreover, when the bandwidth is further increased in THz communication, the array gain loss will be more severe.
Different from ULA, the beam squint of UPA affects both horizontal and vertical dimensions which results in the 2D beam squint. Figure 2a shows the beam pattern in the line- of-sight (LoS) in the THz channel with parameters GHz, , and .
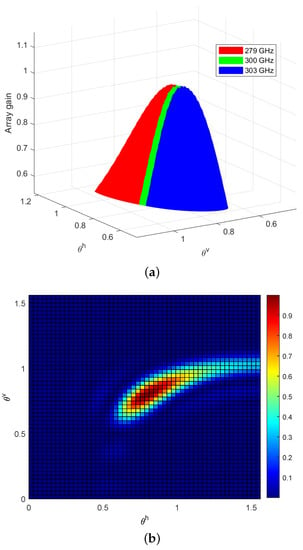
Figure 2.
Beam squint pattern in the LoS THz channel. (a) 3D beam pattern, (b) 2D beam pattern.
We can observe from Figure 2a that the directions are obviously different from at 297 GHz and 303 GHz, which means that the beams other than the beam at the center frequency are suffering from severe misalignment. Figure 2b shows more clearly the difference from the 1D beam squint of the ULA that tends to radiate the entire space [10], the 2D beam squint is distributed in a curve along the horizontal and vertical dimensions at the same time. The reason is that the vertical coverage of UPA is also directional. Although this is usually an advantage for directional transmission, the coverage of UPA in the vertical dimension is worse than that of ULA, which does not allow the 1D model to be used directly in 2D. This is because, compared to full coverage of ULA in the vertical dimension, the coverage of UPA in the vertical dimension is also directional. That is to say, compared with 1D beam squint, 2D beam squint becomes more complicated.
3. The Proposed Architecture and Applications in UAV Communications
The architecture introduced in the paper, due to the fact that only one RF chain is used to transmit data from the UAV to multiple users simultaneously, uses an analog beamforming method. Although the user’s bit stream can be loaded into the same channel through OFDM technology, the transmission performance of the system will be severely degraded due to the fact that analog beamforming can only form full gain in one direction in space. As discussed in Section 2, the 2D beam squint of UPA caused by frequency-independent PSs, makes the narrow beam spreads in a range. By introducing the TTD network into the phased UPA, the frequency-dependent PSs can be realized. In addition, this time-delay phased UPA can work in single-beam or multi-beam modes to meet the needs of different scenarios.
- Eliminate 2D beam squint and increase the array gain at all frequencies to improve the rate of wideband communication (single-beam mode);
- Enhance the 2D beam squint to increase the coverage and improve system accessibility and rate (multi-beam mode).
3.1. Time-Delay Phased UPA
It is impossible to adjust the PSs for each subcarrier in the phased UPA. Therefore, compared with the traditional phased UPA wideband system in Figure 1a, we place a TTD network between the PS network and the RF chain, and obtain the frequency-dependent beam by introducing the delay to each subcarrier. The proposed time-delay phased UPA is shown in Figure 3, and the structure TTD network is shown in Figure 4, where 1D TTD networks [16] are concatenated by inserting TTDs in the horizontal dimension. In addition, the settings of the TTDs are the same in the same dimension. In other words, we only need to control the two parameters of vertical delay and horizontal delay. Next, we elaborate on how the proposed architecture controls the beam squint in the horizontal and vertical dimensions.
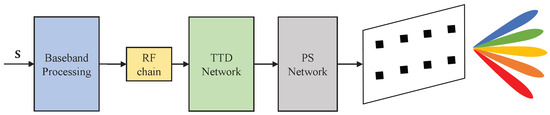
Figure 3.
The proposed time-delay phased UPA architecture.
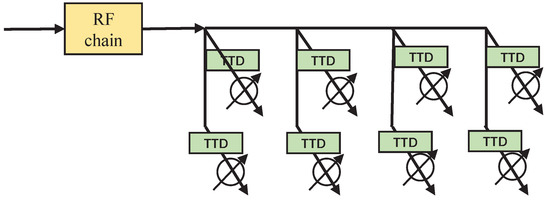
Figure 4.
The structure of the TTD network.
We set the horizontal and vertical delay values to and , respectively. Considering that the time delay should be designed as a periodic form of frequency, then and , where and are real number (to facilitate hardware deployment, they are usually integer), and the PS from the TTD are and . In order to force the phase to belong to , they can be further rewritten as and . The frequency-dependent delay beamformer can be expressed as:
where . By assuming the LoS path for simplicity, the beamformer can be represented as:
Then, the beamformer at can be described as:
where and are the equivalent phase for each frequency, and is the spatial direction of the beam at the center frequency . (e) comes from , and the antenna spacing of in the horizontal and vertical dimensions are both set as .
Property 3.
Assuming , , and , then .
We can find in (10) that due to the addition of the delay beamformer, the system beamformer can design the beam for each frequency sub-carrier. By adjusting the delay coefficients and , the horizontal and vertical frequency-dependent phases of each beam can be separately controlled to achieve the purpose of beam squint control, and the center spatial angle can be controlled by PSs to achieve beam pointing.
It should be noted that although the frequency-dependent phase can be obtained through the TTD network, its time delay is always frequency-independent, which means that the coefficients and are always shared by all beams. Therefore, the beams corresponding to all frequencies adjusted by the TTD network still obey the squint distribution.
3.2. Application Scenarios in UAV Communications
By introducing the TTD, on the one hand, the squint can be eliminated to form a single-beam, thereby increasing the available bandwidth of the access device and realizing large bandwidth communication for the single user case. On the other hand, the proposed architecture can enhance the beam squint to form multi-beam and improve the beam coverage through the TTD network, thereby achieving large-scale access for the multi-user case. As shown in Figure 5, we use this time-delayed phased array in wideband terahertz wireless communication systems assisted by the UAV. Thus, while utilizing the LoS path gain brought by UAV, the severe beam dispersion caused by the LoS path can be overcome.
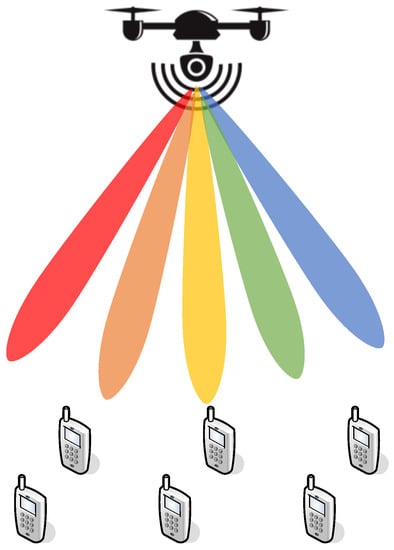
Figure 5.
The UAV-assisted wideband Terahertz wireless communications with time-delay phased UPA.
The high frequency channel between UAVs is dominated by line-of-sight (LOS) path. It may contain a strong LOS component and a few weak non-line-of-sight (NLOS) components, which can be neglected (along with the rician channel). Thus, the UAV channel can be modeled according to Section 2.1, which is similar to [10,21,26,27]. Specifically, we first assume that the drone is at a static fixed altitude to simplify the influence of factors such as Doppler in the model. Secondly, considering that large-scale fading of drones can be suppressed through power control, we have simplified the impact of large-scale fading and focused on studying the gain of drone communication beam strategy on system performance under TTD.
Considering the mobility of UAVs, most of the energy of UAVs is consumed in propulsion, so the energy consumption ratio for communication should be a small portion. The result of integrating large-scale antennas is an increase in communication power consumption, but this is not harmful because the increase in beam gain also increases spectrum utilization and the signal-to-noise ratio of the received signal. Therefore, to evaluate the additional power consumption introduced by additional antennas and the additional system gain (rate, etc.), it brings a trade-off process. The results of [17] indicate that under the same QoS constraints, the system’s power consumption is lower. Therefore, we believe that the feasibility of TTD architecture in practical deployment in UAVs is very high.
3.2.1. Single User Case
In the single user scenario, we assume a single user with large bandwidth requirements on the downlink. It is necessary to adjust the delay parameters to make the beams corresponding to all frequencies point to the same spatial direction. Similarly to [16], the closed-form solution can be obtained in the horizontal and vertical directions, respectively. Based on (10), we can eliminate the beam squint in the horizontal and vertical directions, respectively. Assuming the spatial direction of the beam at the frequency as , we achieve the purpose of beam squint elimination by converging all beams to the spatial direction of the center beam at frequency , that is . The specific delay coefficients can be computed as
In addition, it can be found from (11) that the delay coefficients are only related to the spatial direction of the center frequency . Hence, in the wide bandwidth communication scenario, we first adjust the phases of the beam corresponding to the center frequency , and the delay coefficients can be adjusted to eliminate the array gain loss caused by the beam squint.
3.2.2. Multi-User Case
Phased UPA only transmit single stream but with lower power consumption compared to multiple streams multiple-input and multiple-output (MIMO) with multiple RF chains. The time division multiple access (TDMA) technology is usually employed to transmit data to multiple users in different time slots. In addition, the beam can be split through phase optimization, and multi-user transmission can also be realized using the OFDMA technology.
We propose the FDBMA scheme where each beam depends on frequency separation to fulfill multi-user scenario such as large-scale access in this paper. Contrary to eliminating the beam squint, here we enhance the beam squint such that the beams corresponding to different frequencies are spread. Users in different spatial directions select the best aligned beams for transmission. We assume that the beam coverage angle is in horizontal and in vertical. For convenience, we set the angle of the beam at frequency to be . Then, the beam pattern is shown in Figure 6a. Similar to the nature of the 2D beam squint, the frequency division beams are distributed in a curve at this time. Therefore, UPA has worse coverage compared with ULA, which brings more trouble to beam training and design. To deal with it, we eliminate the beam squint in the vertical dimension and spread the beam in the same horizontal dimension and the beam pattern is presented in Figure 6b. By degrading the vertical dimension, users distributed within vertical 3 dB beam are scheduled together to transmit simultaneously. Moreover, users in different vertical main lobes are scheduled in different time slots.
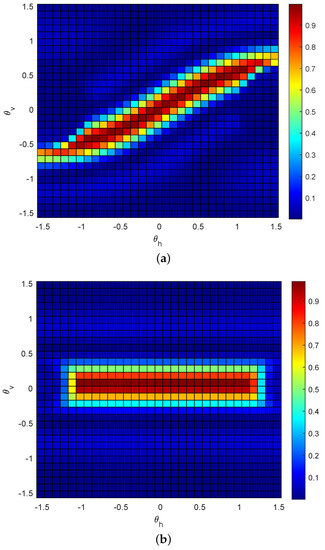
Figure 6.
Beam pattern based on FDBMA. (a) Beam pattern with in horizontal direction and in vertical direction, (b) beam pattern with in horizontal direction and in vertical direction.
Although UPA is mentioned in [17], it is not reasonable to add several dBs directly to ULA under single RF chain assumption. For example, suppose one user is at , and the other two users are at and vertical distribution, then no matter how the beam is vertically and horizontally distributed, the distributed beam cannot cover all users. However, there is no such problem in ULA.
4. Simulation Results
In this section, numerical simulation results are shown to verify the performance of the proposed time-delay phased UPA in both large-bandwidth communication and large-scale access scenarios. The system parameters are , , GHz, GHz, and . The maximum path delay is ns, the subcarrier spacing is 120 KHz, and each resource block (RB) contains 12 subcarriers. Assuming that the UAV is at a fixed altitude, the path gain of the UAV from different users is determined by Equation (2) (here, we only consider the LoS path). We use the Monte Carlo method to generate 20 random samples at each Signal-to-Noise Ratio (SNR) to reflect the comprehensive channel gain of UAV to different users’ path loss and small-scale fading. It should be noted that in this article, is the signal-to-noise ratio on the m-th subcarrier, which can be expressed as dB. When the noise power is set to 1, can be expressed as dB. For simplicity, the Doppler effect caused by the mobility of the UAV is not considered here, and this work adopts the average power allocation strategy. Since the insertion loss can be alleviated by simply introducing extra power amplifiers [10], we ignore the effect of insertion loss here. In addition, despite the introduction of the TTD network, its energy efficiency is still considerable [17].
Figure 7 shows the achievable rate performance comparison between the proposed time-delay phased UPA and other UPA architectures in large-bandwidth communication scenario, including fully digital and phased UPA. The spatial angle of the single user is . The fully digital UPA can implement beamforming on each subcarrier, which can be regarded as the optimal performance. Then, we consider the phased UPA and the optimization method based on the iterative coordinate descent [18] is applied to obtain the beamformer. We can observe from Figure 7 that the proposed time-delay phased UPA outperforms the phased UPA and can achieve the optimal performance of the fully digital UPA. Thus, our proposed time-delay phased UPA can compensate the degradation of array gain incurred by the 2D beam squint.
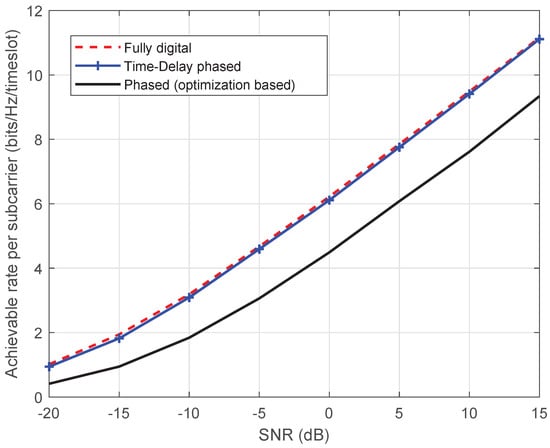
Figure 7.
The achievable rate performance in large-bandwidth communication scenario.
Figure 8 shows the achievable rate performance comparison in large-scale access scenario between the proposed time-delay phased UPA and the phased UPA. In order to transmit data to multiple users, TDMA and wideband beamforming based on iterative coordinate descent [18] can be applied to phased UPA for comparison. In our proposed time-delay phased UPA, narrow beam based FDBMA and wide beam based FDBMA are developed for scenarios of small and large bandwidth, respectively. To simplify the process of user scheduling, we assume that the spatial vertical angle difference of 3 users is (when there are enough users, users with a uniform vertical angle can always be scheduled together), that is, to ensure 3 dB beam coverage in the vertical direction. For the wide beam design, we adopt the antenna dropout strategy and set the number of vertical active antennas as 2.
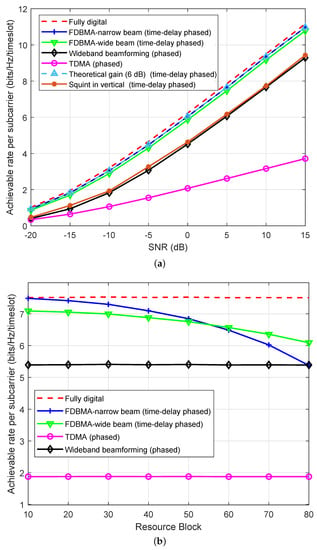
Figure 8.
The achievable rate performance comparison in large-scale access scenario. (a) Achievable rate versus SNR with 3 users each using 80 RBs. (b) Achievable rate versus the number of RBs under SNR = 5 dB and 4 users.
Figure 8a shows that when the number of RBs for each user is 80, the performance of the proposed FDBMA based on time-delay phased UPA is very close to the optimal fully digital architecture and better than the phased UPA. Moreover, although the theoretical gain carried by the additional antenna is fixed, it should be noted that it is unreasonable to directly add 6 dB antenna gain to the performance of the ULA as the performance of the UPA. It can be seen from the last two curves in Figure 8a that if we ignore the squint effect in the vertical direction, its performance is far from that of adding 6 dB directly.
In addition, we can observe from Figure 8b that when the number of RBs further increases, that is, the bandwidth of each user further increases, the performance of the phased UPA hardly changes, while the performance of the proposed FDBMA decreases due to the vertical beam squint. However, the performance of FDBMA based on wide beams declines more slowly, as broadening the beam can reduce the degree of beam squint. Although we design the wide beam by roughly reducing the antennas in vertical direction, we can still find that FDBMA based on narrow beam has no advantage when the number of RBs reaches 80, but it still has a performance improvement under wide beam design. Therefore, how to design the effective wide beam is a key to improving the performance of FDBMA in the large bandwidth scenario. Since the all-digital architecture can perform beam design for each subcarrier of each user, the achievable rate of each subcarrier does not change with the number of RBs. For the phased UPA, since the subcarrier beams are shared, the achievable rate does not vary greatly with different number of RBs.
5. Conclusions
In this paper, we have investigated UAV-assisted wideband wireless communication in THz systems based on UPA. The time-delay phased UPA architecture has been proposed to control the 2D beam squint. The proposed architecture can not only eliminate the beam squint to form a single beam to improve the individual user rate, but also enhance the beam squint for multi-user access based on the proposed FDBMA. In addition, compared with the ULA architecture, the theoretical beam gain of the UPA architecture is higher. However, due to the existence of vertical dispersion, the actual gain is far lower than the theoretical gain. Depending on the proposed time-delayed phased UPA, fast beam training and tracking for UAV communications can be studied in future work. Moreover, when the TTD network adopts the sparse connection architecture, whether the multi-beam mode still has advantages is also of great research value. In order to ensure the feasibility of deployment in practical scenarios and considering the limited power consumption of drones, it is necessary to further analyze the upper limit of the gain caused by TTD insertion loss. Finally, the use of advanced artificial intelligence technology [28] for rapid beam selection and matching is also one of the potential research works in the future.
Author Contributions
Conceptualization, H.H.; Methodology, H.S.; Validation, Q.Z.; Formal analysis, Q.Z. and H.S.; Writing—original draft, H.H.; Writing—review & editing, Q.Z. and H.S.; Supervision, H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Project of Natural Science Foundation of the Higher Education Institutions of Jiangsu Province under Grant 22KJA510002, the Shandong Provincial Natural Science Foundation under Grant ZR2023QF125 and the Project of the Postgraduate Research & Practice Innovation Program of Jiangsu Province under Grant KYCX20-0727.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gui, G.; Liu, M.; Tang, F.; Kato, N.; Adachi, F. 6g: Opening new horizons for integration of comfort, security, and intelligence. IEEE Wirel. Commun. 2020, 27, 126–132. [Google Scholar] [CrossRef]
- Han, C.; Chen, Y. Propagation modeling for wireless communications in the terahertz band. IEEE Commun. Mag. 2018, 56, 96–101. [Google Scholar] [CrossRef]
- Li, Z.; Guan, L.; Li, C.; Radwan, A. A secure intelligent spectrum control strategy for future THz mobile heterogeneous networks. IEEE Commun. Mag. 2018, 56, 116–123. [Google Scholar] [CrossRef]
- Ning, B.; Chen, Z.; Chen, W.; Du, Y.; Fang, J. Terahertz multi-user massive mimo with intelligent reflecting surface: Beam training and hybrid beamforming. IEEE Trans. Veh. Technol. 2021, 70, 1376–1393. [Google Scholar] [CrossRef]
- Raghavan, V.; Subramanian, S.; Cezanne, J.; Sampath, A. Directional beamforming for millimeter-wave MIMO systems. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM)-IEEE Conference, San Diego, CA, USA, 6–10 December 2015; pp. 1–7. [Google Scholar]
- Huang, S.; Zhang, M.; Gao, Y.; Feng, Z. MIMO Radar Aided mmWave Time-Varying Channel Estimation in MU-MIMO V2X Communications. IEEE Trans. Wirel. Commun. 2021, 20, 7581–7594. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Qiao, D.; Zhang, L. Analysis of Indoor THz Communication Systems With Finite-Bit DACs and ADCs. IEEE Trans. Veh. Technol. 2022, 71, 375–390. [Google Scholar] [CrossRef]
- Li, D.; Qiao, D.; Zhang, L. Achievable Rate of Indoor THz Communication Systems with Finite-Bit ADCs. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018; pp. 1–6. [Google Scholar]
- Lin, C.; Li, G.Y.L. Terahertz Communications: An Array-of-Subarrays Solution. IEEE Commun. Mag. 2016, 54, 124–131. [Google Scholar] [CrossRef]
- Gao, F.; Wang, B.; Xing, C.; An, J.; Li, G.Y. Wideband beamforming for hybrid massive MIMO terahertz communications. IEEE J. Sel. Areas Commun. 2021, 39, 1725–1740. [Google Scholar] [CrossRef]
- Wang, B.; Gao, F.; Jin, S.; Lin, H.; Li, G.Y. Spatial and frequency wideband effects in millimeter-wave massive mimo systems. IEEE Trans. Signal Process. 2018, 66, 3393–3406. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, J.; Gao, F.; Jia, W.; Zhang, W. Gridless compressed sensing based channel estimation for UAV wideband communications with beam squint. IEEE Trans. Veh. Technol. 2021, 70, 10265–10277. [Google Scholar] [CrossRef]
- Wan, Q.; Fang, J.; Chen, Z.; Li, H. Hybrid precoding and combining for millimeter wave/sub-thz mimo-ofdm systems with beam squint effects. IEEE Trans. Veh. Technol. 2021, 70, 8314–8319. [Google Scholar] [CrossRef]
- Di, B. Reconfigurable holographic metasurface aided wideband ofdm communications against beam squint. IEEE Trans. Veh. Technol. 2021, 70, 5099–5103. [Google Scholar] [CrossRef]
- Boljanovic, V.; Yan, H.; Ghaderi, E.; Heo, D.; Gupta, S.; Cabric, D. Design of millimeter-wave single-shot beam training for true-time-delay array. In Proceedings of the 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Atlanta, GA, USA, 26–29 May 2020; pp. 1–5. [Google Scholar]
- Zhai, B.; Zhu, Y.; Tang, A.; Wang, X. THzPrism: Frequency-based beam spreading for terahertz communication systems. IEEE Wireless Commun. Lett. 2020, 9, 897–900. [Google Scholar] [CrossRef]
- Zhai, B.; Tang, A.; Peng, C.; Wang, X. Ss-ofdma: Spatial-spread orthogonal frequency division multiple access for terahertz networks. IEEE J. Sel. Areas Commun. 2021, 39, 1678–1692. [Google Scholar] [CrossRef]
- Sohrabi, F.; Yu, W. Hybrid analog and digital beamforming for mmWave OFDM large-scale antenna arrays. IEEE J. Sel. Areas Commun. 2017, 35, 1432–1443. [Google Scholar] [CrossRef]
- Song, J.; Choi, J.; Love, D.J. Common codebook millimeter wave beam design: Designing beams for both sounding and communication with uniform planar arrays. IEEE Trans. Commun. 2017, 65, 1859–1872. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, A.; Xia, X.; Xu, K. Learning the structured sparsity: 3-d massive mimo channel estimation and adaptive spatial interpolation. IEEE Trans. Veh. Technol. 2019, 68, 10663–10678. [Google Scholar] [CrossRef]
- Xu, L.; Chen, M.; Chen, M.; Yang, Z.; Chaccour, C.; Saad, W.; Hong, C.S. Joint location, bandwidth and power optimization for thz-enabled uav communications. IEEE Commun. Lett. 2021, 25, 1984–1988. [Google Scholar] [CrossRef]
- Alali, A.; Rawat, D.B.; Liu, C. Trajectory and power optimization in sub-thz band for uav communications. In Proceedings of the ICC 2022—IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 1–6. [Google Scholar]
- Fan, G.; Sun, J.; Gui, G.; Gacanin, H.; Adebisi, B.; Ohtsuki, T. Fully convolutional neural network-based csi limited feedback for fdd massive mimo systems. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 672–682. [Google Scholar] [CrossRef]
- Ayach, O.E.; Rajagopal, S.; Abu-Surra, S.; Pi, Z.; Heath, R.W. Spatially sparse precoding in millimeter wave MIMO systems. IEEE Trans. Wirel. Commun. 2014, 13, 1499–1513. [Google Scholar] [CrossRef]
- Zhong, W.; Xu, L.; Zhu, Q.; Chen, X.; Zhou, J. MmWave beamforming for UAV communications with unstable beam pointing. China Commun. 2019, 16, 37–46. [Google Scholar] [CrossRef]
- Xia, W.; Semkin, V.; Mezzavilla, M.; Loianno, G.; Rangan, S. Multi-array designs for mmwave and sub-thz communication to uavs. In Proceedings of the 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Atlanta, GA, USA, 26–29 May 2020; pp. 1–5. [Google Scholar]
- Pan, Y.; Wang, K.; Pan, C.; Zhu, H.; Wang, J. Uav-assisted and intelligent reflecting surfaces-supported terahertz communications. IEEE Wirel. Commun. Let. 2021, 10, 1256–1260. [Google Scholar] [CrossRef]
- Huang, H.; Gui, G.; Gacanin, H.; Yuen, C.; Sari, H.; Adachi, F. Deep regularized waveform learning for beam prediction with limited samples in non-cooperative mmwave systems. IEEE Trans. Veh. Technol. 2023, 72, 9614–9619. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).