Dynamic Modeling and Control for Tilt-Rotor UAV Based on 3D Flow Field Transient CFD
Abstract
1. Introduction
- Established the TRUAV unsteady dynamics model of the transition modal based on the transient computational fluid dynamics numerical simulations, and adding the aerodynamic parameters of the tilting angle state change, also considering the influence of different tilting angle slipstream flow regions.
- Conducted the numerical simulations on the rotor thrust, pitch moment of TRUAV, analysis of transition modal’s three-dimensional flow field distribution, and the corresponding conclusions were drawn.
- The TRUAV modal transition simulations are in airborne flight mode without considering ground effects.
2. Dynamics Model and Identification
2.1. Assumptions
- The TRUAV was treated as a rigid body, neglecting the elastic deformation of the fuselage, while the aerodynamic center and the center of mass were consistent;
- The pendulum and flapping motions of the propeller were not considered;
- The mass of the TRUAV and the mass distribution were constant, the cruise speed of the TRUAV was limited, and the atmospheric density was fixed, ignoring the air compression properties.
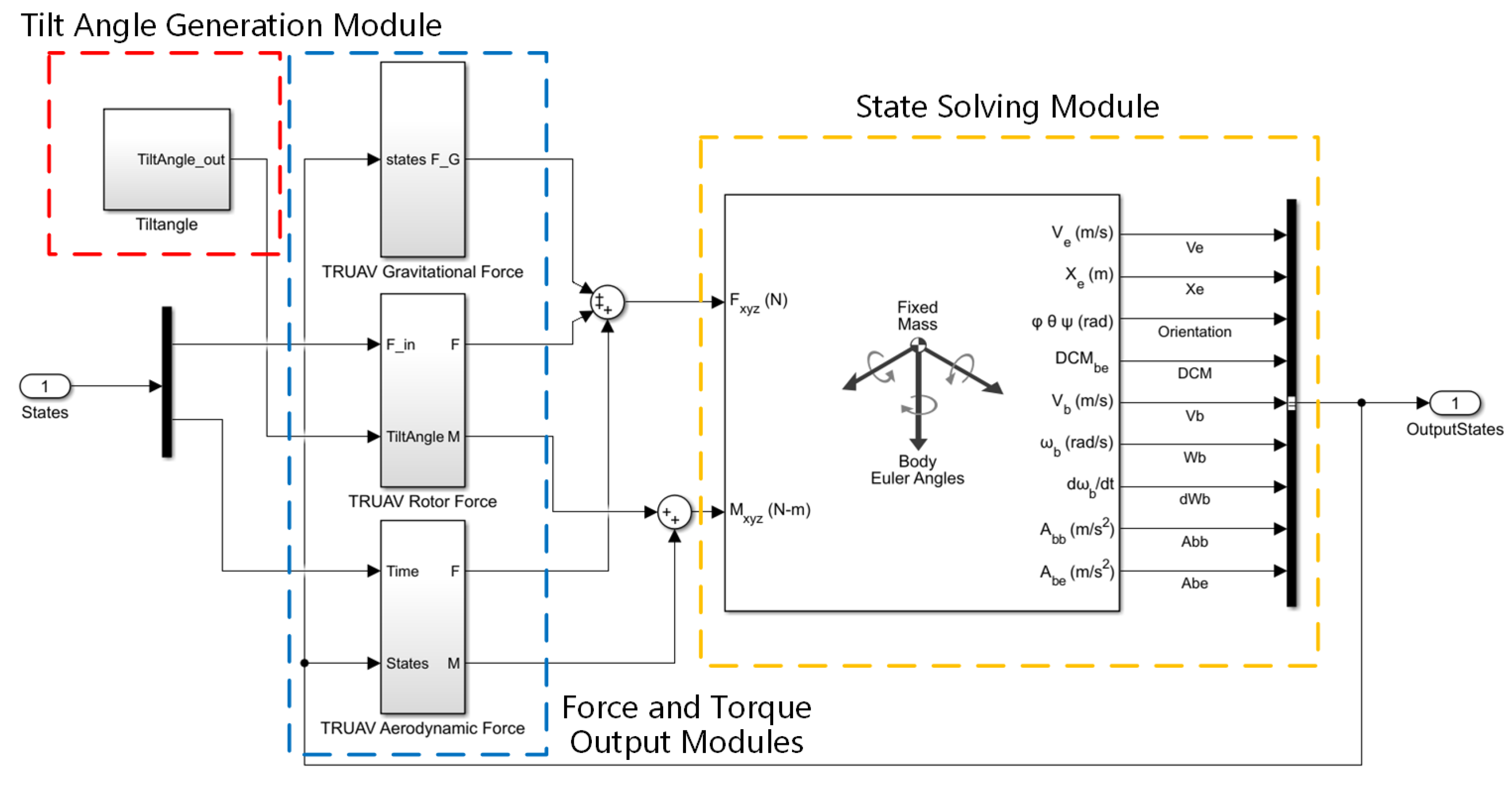
2.2. TRUAV Dynamics Model
3. Methods
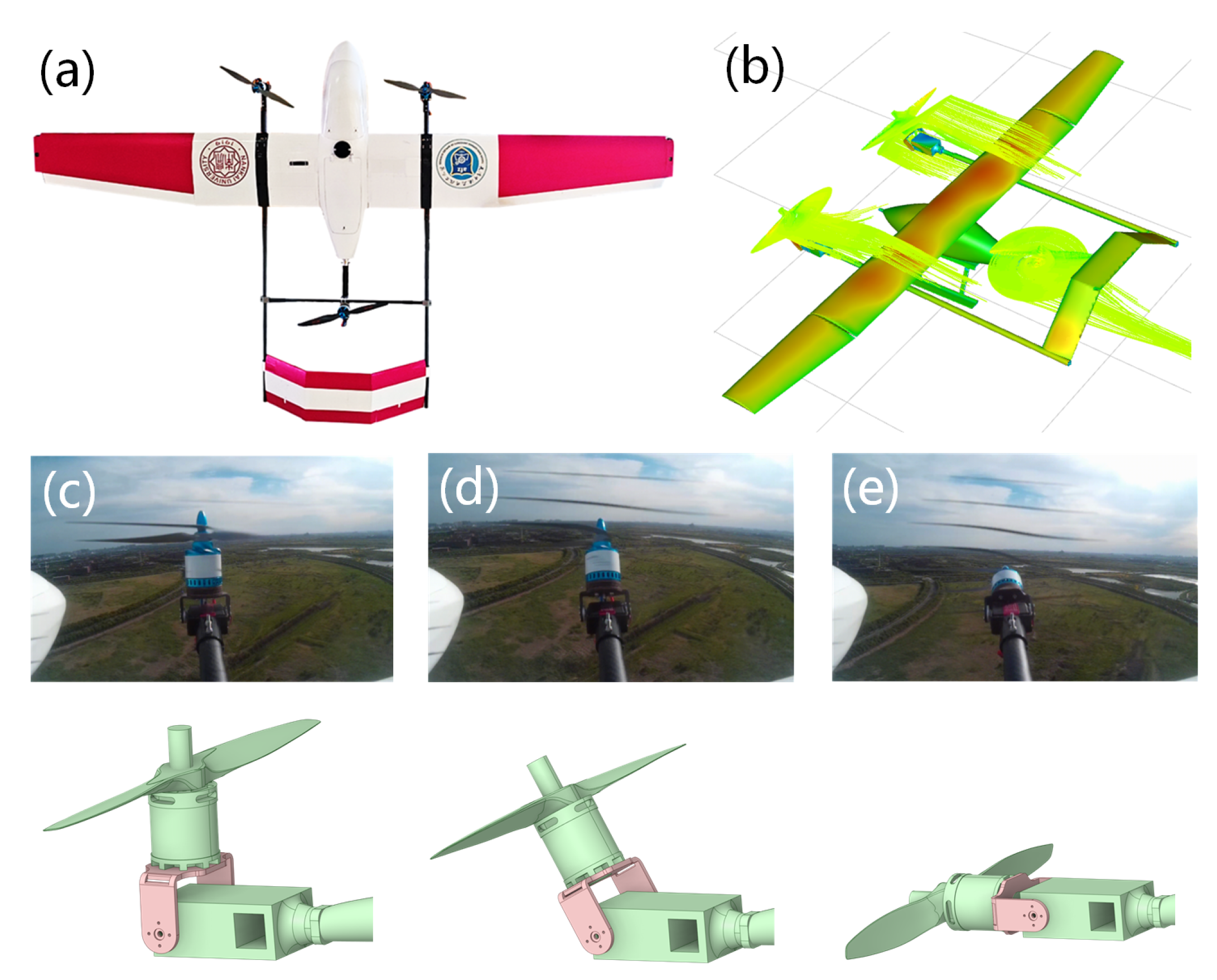
3.1. Mesh System
- The maximum global constrained size of the mesh for TRUAV is set to 0.1 m, the minimum global constrained size is set to 0.002 m and the growth rate is set to 1.2;
- The curvature normal angle is set to 9°, which is used to rationally mesh this complex geometric model of TRUAV, implying the generation of 40 nodes within each geometric circumference;
- To ensure the quality and distribution of the mesh, check the TRUAV mesh for the initial division and repair part of the mesh for smoothness, and the minimum skewness of the TRUAV model is 0.8.
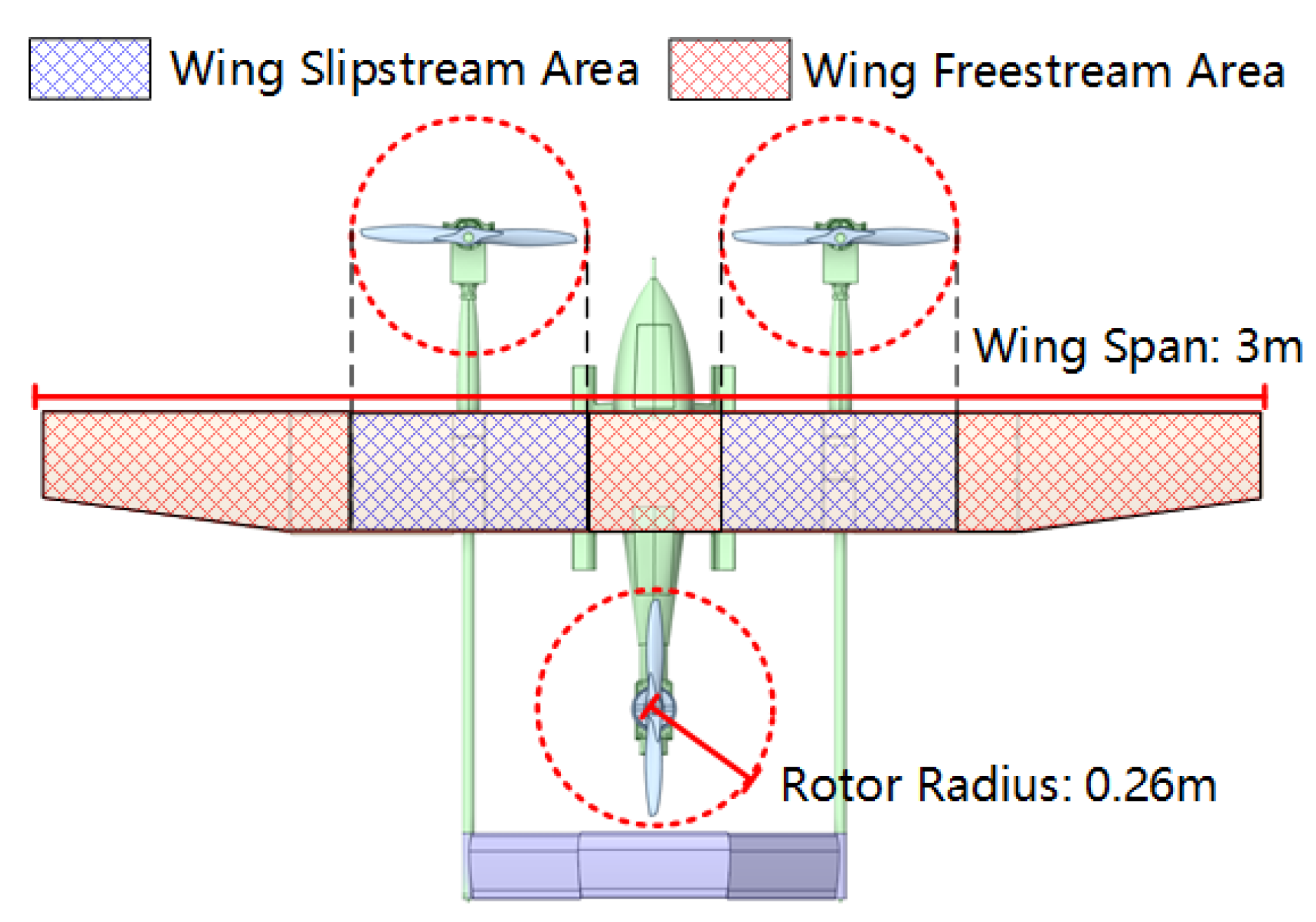
3.2. Boundary Conditions
3.3. Turbulence Model
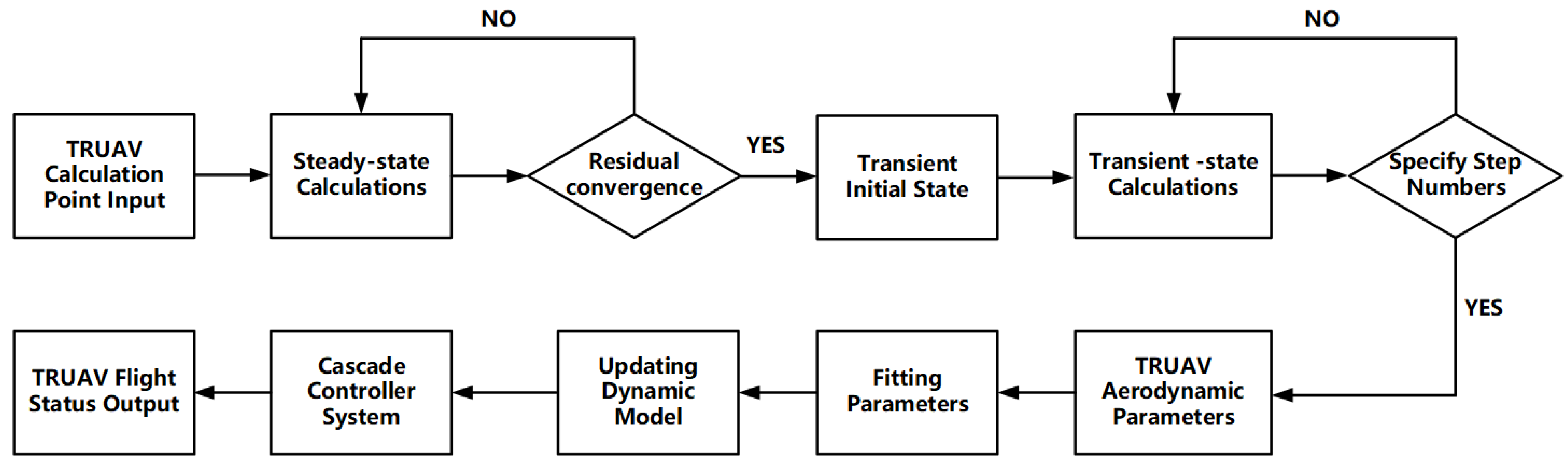
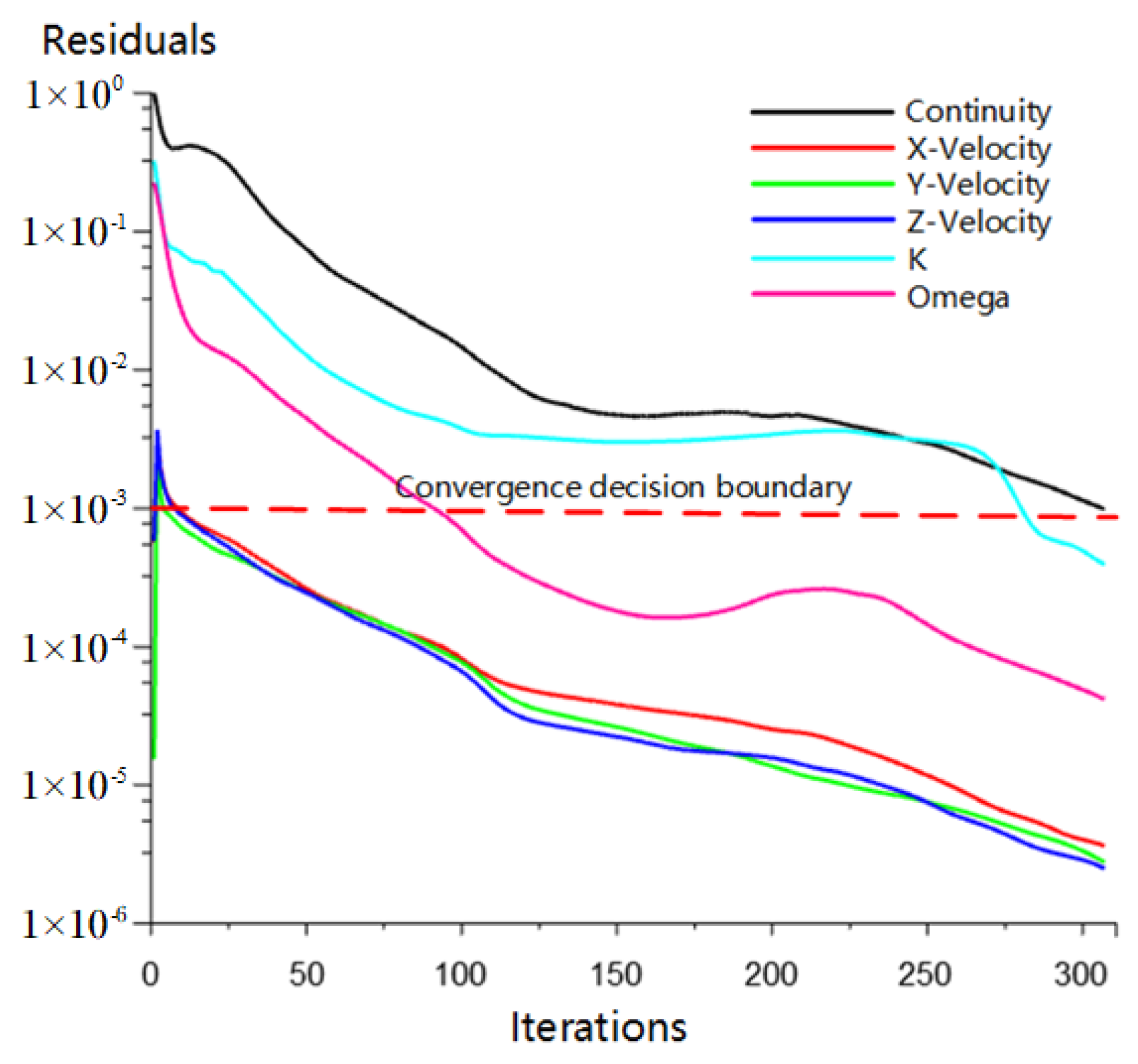
3.4. Termination Conditions
4. Numerical Simulation
Experimental Results Analysis
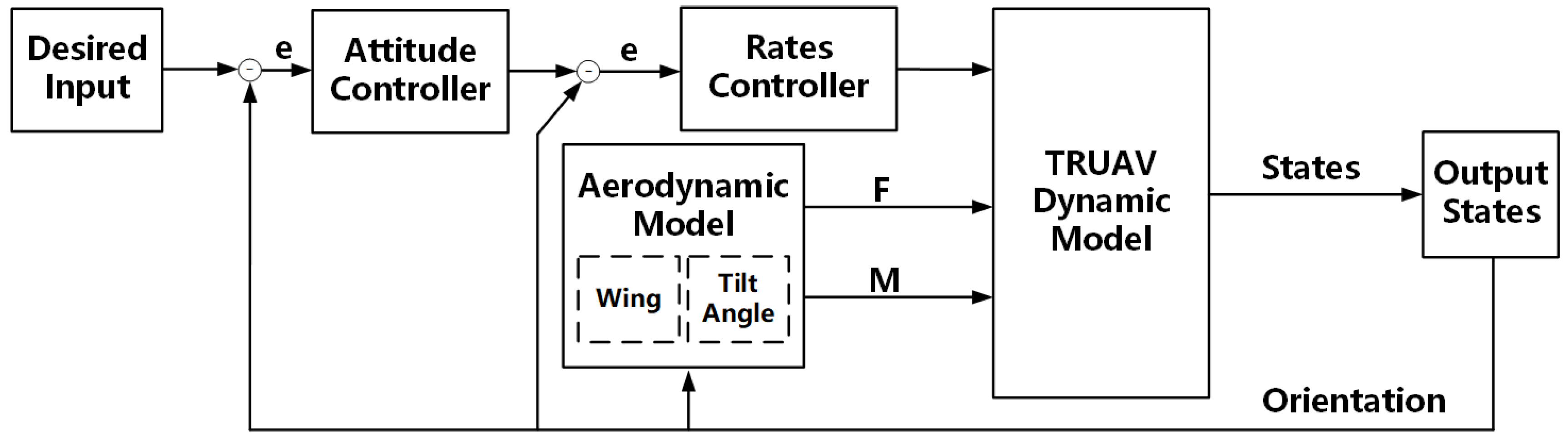
5. Controller Strategy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notations
| world coordinate direction vector | |
| body coordinate direction vector | |
| the angle of rotor tilt | |
| air density | |
| lift force | |
| drag force | |
| pitching moment | |
| lift coefficients | |
| drag coefficients | |
| pitching moment coefficients | |
| thrust coefficient | |
| wing area |
References
- Liu, Z.; Theilliol, D.; Yang, L.; He, Y.; Han, J. Mode transition and fault tolerant control under rotor-tilt axle stuck fault of quad-TRUAV. IFAC-PapersOnLine 2018, 51, 991–997. [Google Scholar] [CrossRef]
- Govdeli, Y.; Muzaffar, S.M.B.; Raj, R.; Elhadidi, B.; Kayacan, E. Unsteady aerodynamic modeling and control of pusher and tilt-rotor quadplane configurations. Aerosp. Sci. Technol. 2019, 94, 105421. [Google Scholar] [CrossRef]
- Yang, H.; Xia, W.; Wang, K.; Hu, S. Aerodynamic performance of a small-scale tilt rotor: Numerical simulation and experiment in steady state. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 0954406220950352. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Yu, H.; Duan, D.; Ding, Z.; Li, J. Trimming analysis method of quad tilt rotor based on aerodynamic interference model. J. Aircr. 2021, 58, 253–265. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, B.; Huang, T. CFD study of an annular-ducted fan lift system for VTOL aircraft. Aerospace 2015, 2, 555–580. [Google Scholar] [CrossRef]
- Wu, Z.; Li, C.; Cao, Y. Numerical simulation of rotor–Wing transient interaction for a tiltrotor in the transition mode. Mathematics 2019, 7, 116. [Google Scholar] [CrossRef]
- Joshi, A.; Tripathi, A.; Ponnalgu, R. Modelling and design of a hybrid aerial vehicle combining vtol capabilities with fixed wing aircraft. In Proceedings of the 2019 6th International Conference on Instrumentation, Control and Automation (ICA), Bandung, Indonesia, 31 July–2 August 2019; pp. 47–51. [Google Scholar]
- Kendoul, F.; Fantoni, I.; Lozano, R. Modeling and control of a small autonomous aircraft having two tilting rotors. IEEE Trans. Robot. 2006, 22, 1297–1302. [Google Scholar] [CrossRef]
- Ferguson, S.W. A Mathematical Model for Real Time Flight Simulation of a Generic Tilt-Rotor Aircraft; NASA CR-166536; NASA: Washington, DC, USA, 1988. [Google Scholar]
- Harendra, P.; Joglekar, M.; Gaffey, T.; Marr, R. V/STOL Tilt Rotor Study. Volume 5: A Mathematical Model for Real Time Flight Simulation of the Bell Model 301 Tilt Rotor Research Aircraft; Technical report; NASA: Washington, DC, USA, 1973. [Google Scholar]
- Barra, F.; Capone, P.; Monstein, R.; Godio, S.; Guglieri, G. Implementation of a comprehensive mathematical model for tilt-rotor real-time flight simulation. In Proceedings of the 45th European Rotorcraft Forum, Warsaw, Poland, 17–20 September 2019; ZHAW Zürcher Hochschule für Angewandte Wissenschaften: Winterthur, Switzerland, 2019. [Google Scholar]
- Chen, C.; Zhang, J.; Zhang, D.; Shen, L. Control and flight test of a tilt-rotor unmanned aerial vehicle. Int. J. Adv. Robot. Syst. 2017, 14, 1729881416678141. [Google Scholar] [CrossRef]
- Flores, G.; Lozano, R. Transition flight control of the quad-tilting rotor convertible MAV. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; pp. 789–794. [Google Scholar]
- Takeuchi, R.; Watanabe, K.; Nagai, I. Development and control of tilt-wings for a tilt-type quadrotor. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 501–506. [Google Scholar]
- Zaide, A.; Raveh, D. Numerical simulation and reduced-order modeling of airfoil gust response. AIAA J. 2006, 44, 1826–1834. [Google Scholar] [CrossRef]
- Funes-Sebastian, D.E.; Ruiz-Calavera, L.P. Numerical simulations of wind tunnel effects on intake flow of a UAV configuration. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; p. 0372. [Google Scholar]
- Prisacariu, V. CFD Analysis of UAV Flying Wing. INCAS Bulletin 2016, 8, 65. [Google Scholar]
- Mazhar, F.; Khan, A.M.; Chaudhry, I.A.; Ahsan, M. On using neural networks in UAV structural design for CFD data fitting and classification. Aerosp. Sci. Technol. 2013, 30, 210–225. [Google Scholar] [CrossRef]
- Lao, C.; Wong, E. Cfd simulation of a wing-in-ground-effect uav. IOP Conf. Ser. Mater. Sci. Eng. 2018, 370, 012006. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- An, K.; Fung, J. An improved SST k- ω model for pollutant dispersion simulations within an isothermal boundary layer. J. Wind. Eng. Ind. Aerodyn. 2018, 179, 369–384. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 54–73. [Google Scholar]
- Huang, H.; He, G.; Yu, L.; Wang, X. Numerical analysis on aerodynamic interference of a novel tilt-rotor uav in transition mode. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 6043–6048. [Google Scholar]
- Houari, A.; Bachir, I.; Mohamed, D.K.; Kara-Mohamed, M. PID vs. LQR controller for tilt rotor airplane. Int. J. Electr. Comput. Eng. (IJECE) 2020, 10, 6309–6318. [Google Scholar] [CrossRef]
- Annamalai, V.K.; Thunaipragasam, S. Design, modeling and simulation of a control surface-less tri-tilt-rotor UAV. Aircr. Eng. Aerosp. Technol. 2021, 94, 541–552. [Google Scholar] [CrossRef]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control. Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Alanezi, M.A.; Haruna, Z.; Sha’aban, Y.A.; Bouchekara, H.R.; Nahas, M.; Shahriar, M.S. Obstacle Avoidance-Based Autonomous Navigation of a Quadrotor System. Drones 2022, 6, 288. [Google Scholar] [CrossRef]
- Sattar, A.; Wang, L.; Hoshu, A.A.; Ansari, S.; Karar, H.E.; Mohamed, A. Automatic Tuning and Turbulence Mitigation for Fixed-Wing UAV with Segmented Control Surfaces. Drones 2022, 6, 302. [Google Scholar] [CrossRef]
- Yi, K.; Liang, X.; He, Y.; Yang, L.; Han, J. Active-model-based control for the quadrotor carrying a changed slung load. Electronics 2019, 8, 461. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, X.; Han, J. Active model-based control for pneumatic artificial muscle. IEEE Trans. Ind. Electron. 2016, 64, 1686–1695. [Google Scholar] [CrossRef]
- Song, D.; Han, J.; Liu, G. Active model-based predictive control and experimental investigation on unmanned helicopters in full flight envelope. IEEE Trans. Control. Syst. Technol. 2012, 21, 1502–1509. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, H.; Wang, X.; Han, J. Active Model-Based Hysteresis Compensation and Tracking Control of Pneumatic Artificial Muscle. Sensors 2022, 22, 364. [Google Scholar] [CrossRef]
- Song, D.; Qi, J.; Han, J.; Liu, G. Active model based predictive control for unmanned helicopter in full flight envelope. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 616–621. [Google Scholar]



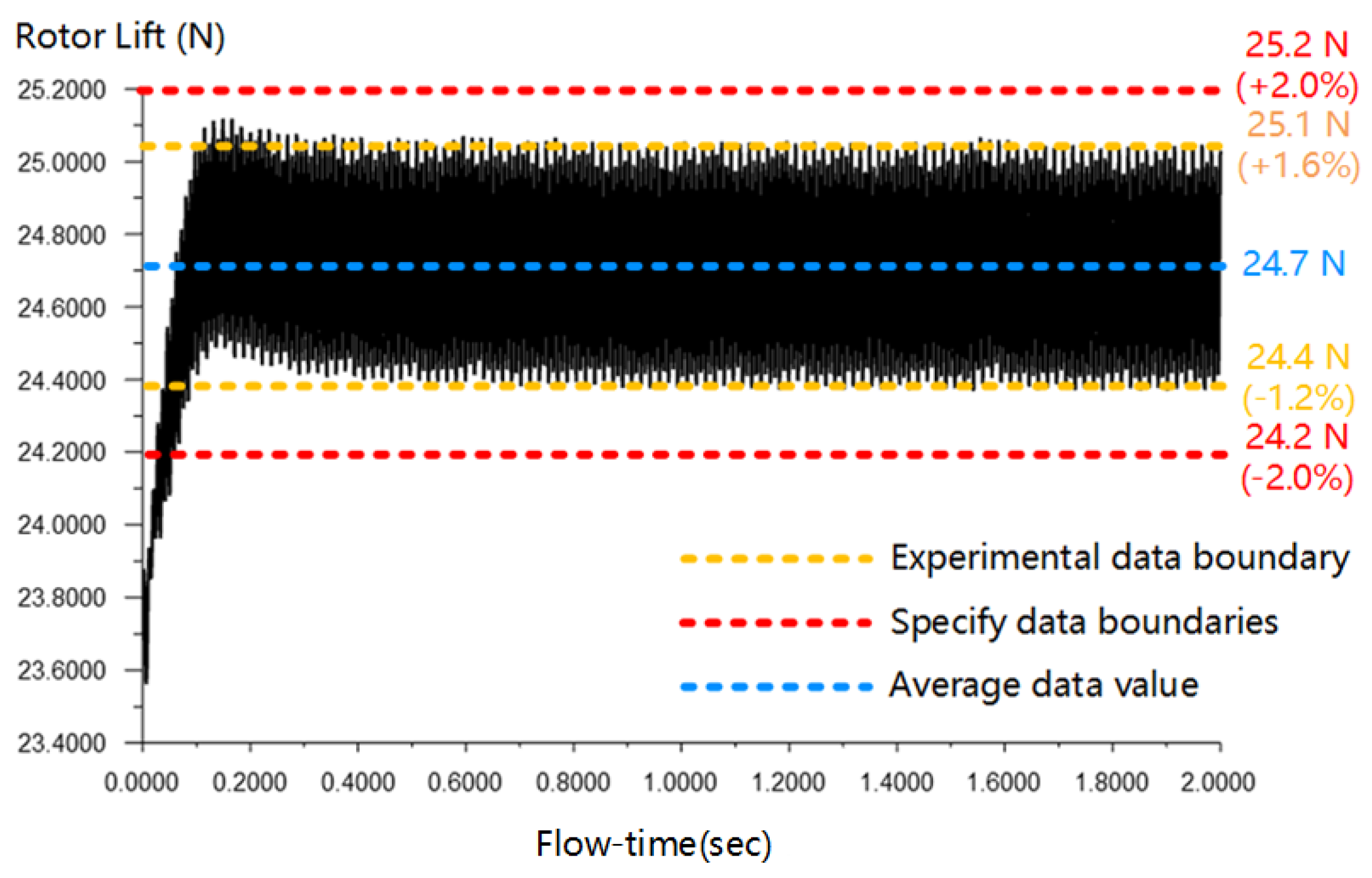
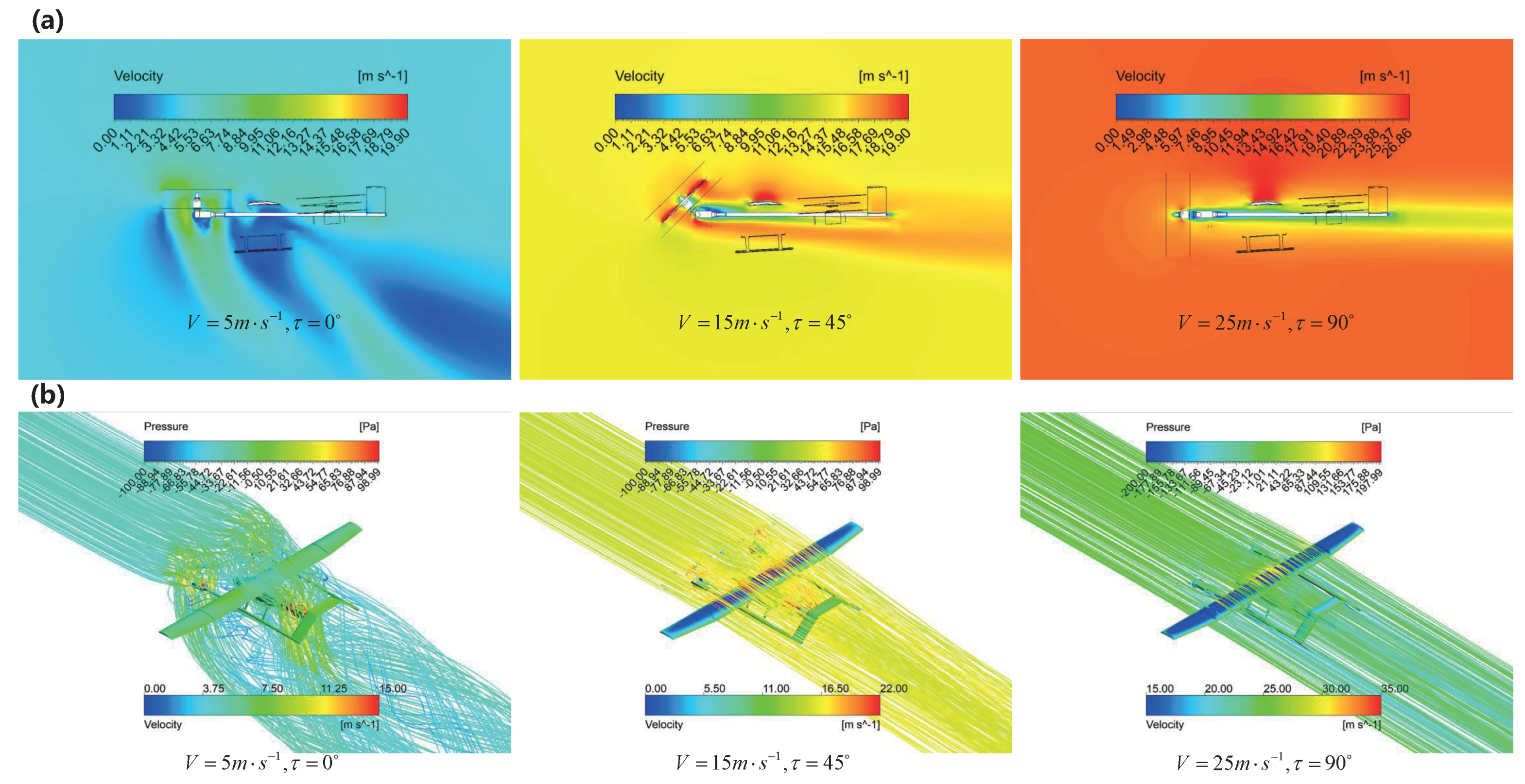

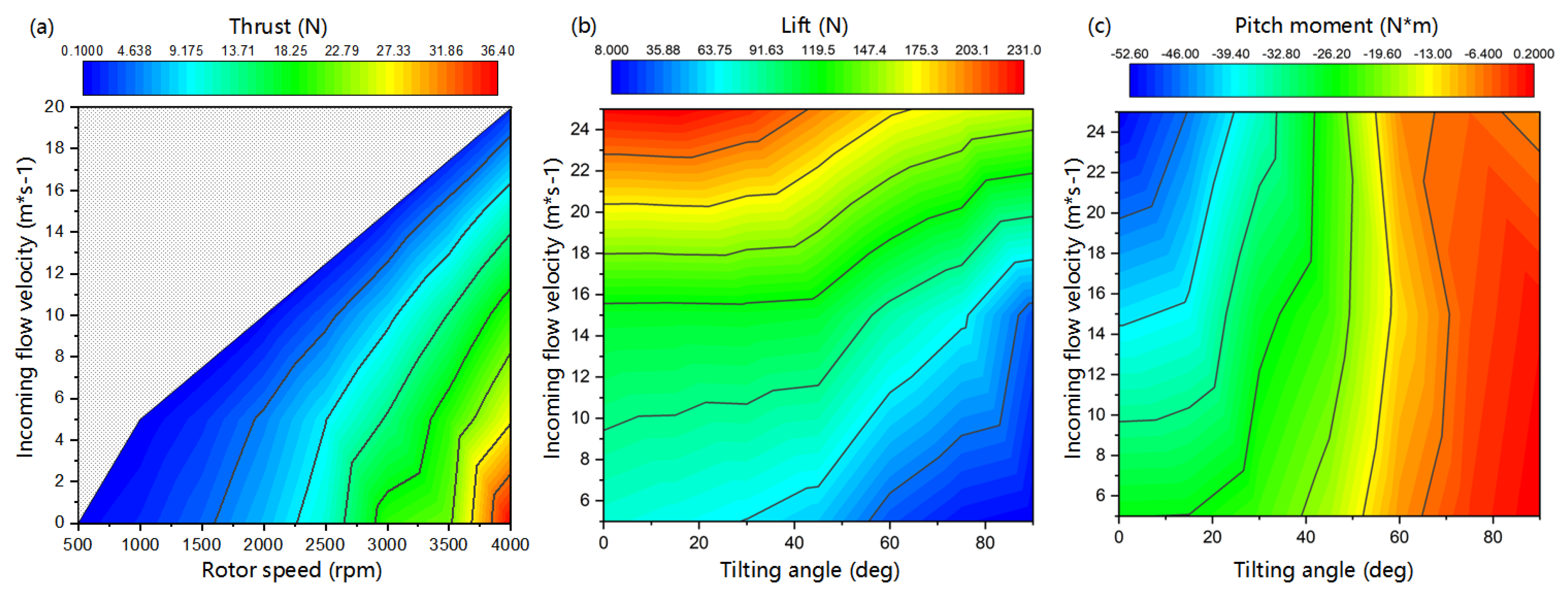
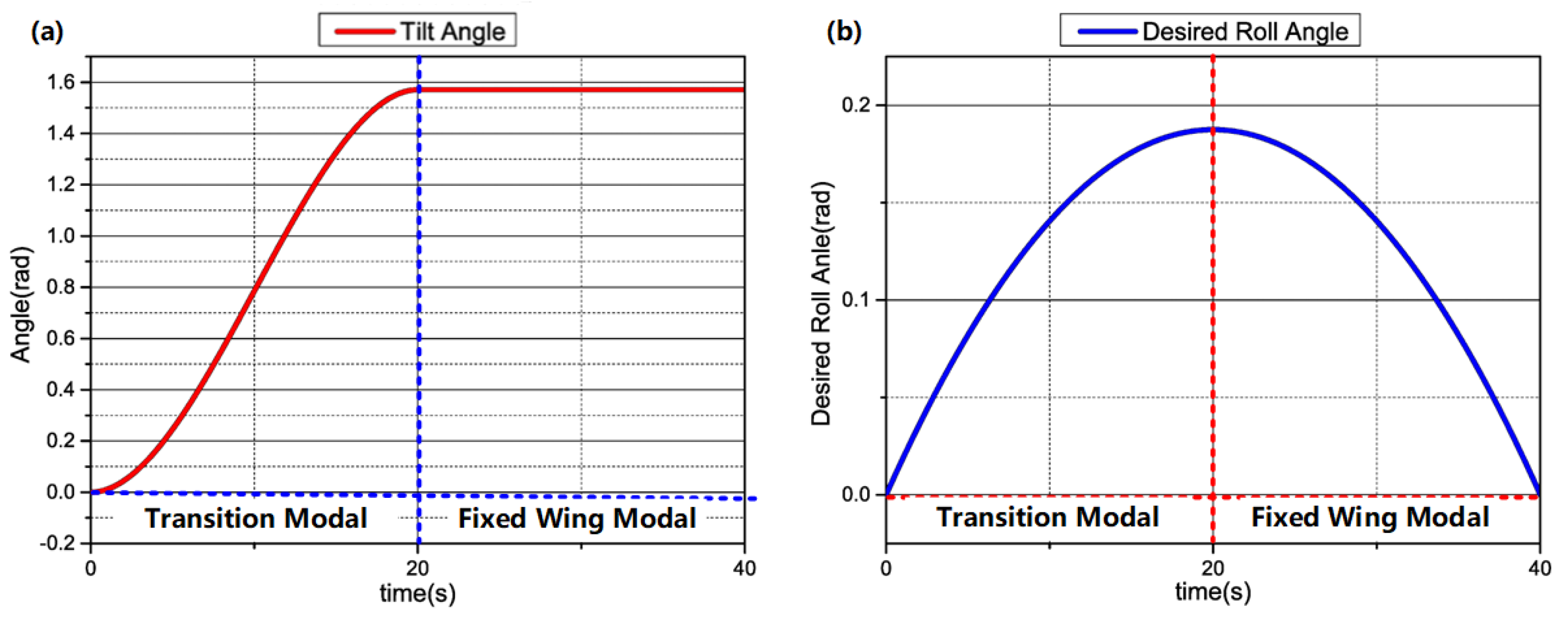
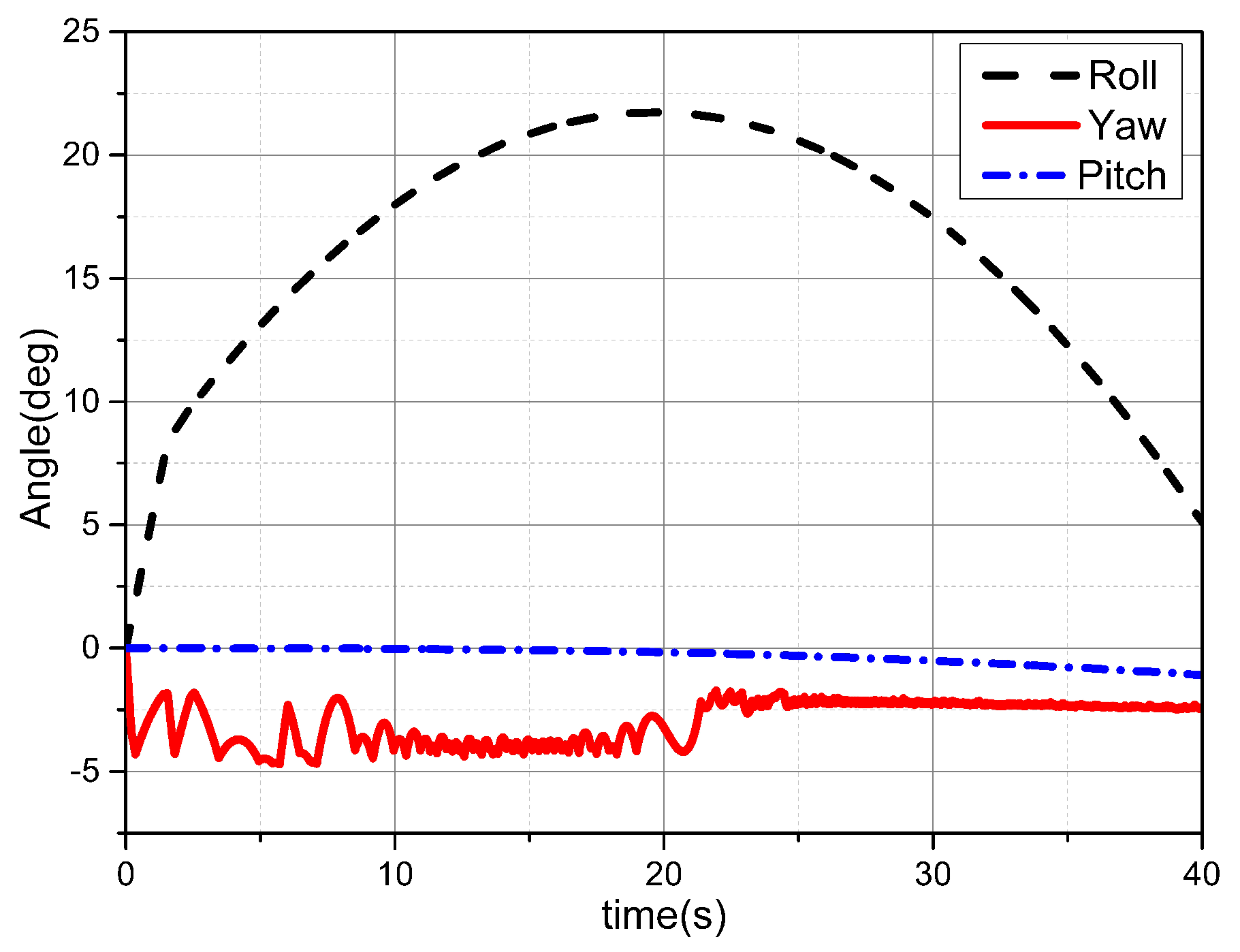
| Tilting Angles (deg) | Forward Flight Speed () | Front Rotor Speed (rpm) | Rear Rotor Speed (rpm) | Time Steps (s) | Number of Time Steps |
|---|---|---|---|---|---|
| 0.0° | 5.0 | 3500 | 3500 | 0.001 | 2000 |
| 7.5° | 8.0 | 3550 | 3500 | 0.001 | 2000 |
| 15.0° | 11.0 | 3600 | 3500 | 0.001 | 2000 |
| 22.5° | 12.0 | 3750 | 3500 | 0.001 | 2000 |
| 30.0° | 13.0 | 3900 | 3500 | 0.001 | 2000 |
| 37.5° | 14.0 | 3950 | 3400 | 0.001 | 2000 |
| 45.0° | 15.0 | 4000 | 3300 | 0.001 | 2000 |
| 52.5° | 17.5 | 3800 | 3750 | 0.001 | 2000 |
| 60.0° | 20.0 | 3600 | 2400 | 0.001 | 2000 |
| 67.5° | 21.5 | 3300 | 2900 | 0.001 | 2000 |
| 75.0° | 23.0 | 3000 | 1400 | 0.001 | 2000 |
| 82.5° | 24.0 | 2700 | 700 | 0.001 | 2000 |
| 90.0° | 25.0 | 2400 | 0 | 0.001 | 2000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Sun, W.; Zhao, C.; Zhang, S.; Han, J. Dynamic Modeling and Control for Tilt-Rotor UAV Based on 3D Flow Field Transient CFD. Drones 2022, 6, 338. https://doi.org/10.3390/drones6110338
Wang H, Sun W, Zhao C, Zhang S, Han J. Dynamic Modeling and Control for Tilt-Rotor UAV Based on 3D Flow Field Transient CFD. Drones. 2022; 6(11):338. https://doi.org/10.3390/drones6110338
Chicago/Turabian StyleWang, Hongpeng, Wenhao Sun, Changli Zhao, Sujie Zhang, and Jianda Han. 2022. "Dynamic Modeling and Control for Tilt-Rotor UAV Based on 3D Flow Field Transient CFD" Drones 6, no. 11: 338. https://doi.org/10.3390/drones6110338
APA StyleWang, H., Sun, W., Zhao, C., Zhang, S., & Han, J. (2022). Dynamic Modeling and Control for Tilt-Rotor UAV Based on 3D Flow Field Transient CFD. Drones, 6(11), 338. https://doi.org/10.3390/drones6110338






