1. Introduction
Low-altitude unmanned aerial vehicles (UAVs), also called drones, have enabled many personal and commercial applications, including aerial photography and sightseeing, parcel delivery, emergency rescue in natural disasters, monitoring and surveillance, and precision farming [
1]. Recently, the interest in this emerging technology is steadily surging as many governments have already facilitated the regulations for UAV usage. As a result, UAV technologies are being developed and deployed at a very rapid pace around the world to offer fruitful business opportunities and new vertical markets [
2]. In particular, UAVs can be employed as aerial communication platforms to enhance wireless connectivity for ground users and Internet of Things (IoT) devices in harsh environments when terrestrial networks are unreachable. Additionally, intelligent UAV platforms can provide important and diverse contributions to the evolution of smart cities by offering cost-efficient services ranging from environmental monitoring to traffic management.
Wireless communication is a key enabling technology for UAVs, and their integration has drawn substantial attention in recent years. In this direction, the third generation partnership project (3GPP) has been active in identifying the requirements, technologies, and protocols for aerial communications to enable networked UAVs in current long-term evolution (LTE) and 5G/B5G networks [
3]. The communications of UAVs fundamentally differ from terrestrial communications in the underlying air-to-ground propagation channel and the inherent size, weight, and power constraints. The 3D mobile UAVs enjoy a higher probability of line-of-sight (LoS) communication than ground users, which can be beneficial for the reliability and power efficiency of UAV communications. Nevertheless, this also implies that UAV communications may easily cause/suffer interference to/from terrestrial networks, which has to be carefully addressed [
4]. The availability of LoS depends not only on the propagation environment but also on the UAVs’ altitude, elevation angle, and movement trajectories, which have to be jointly evaluated for each scenario.
Realizing full-fledged UAVs in the 3D mobile cellular network depends largely on the reliability and efficiency of the communication channels over diverse UAV operating environments and scenarios. Furthermore, these channels are crucial for designing and evaluating UAV communication links for control/non-payload and payload data transmissions across novel UAV operation scenarios, which is one of the significant challenges in this setting. Moreover, the mobility of UAVs and the time-varying topology of the 3D mobile network, along with localization errors and latency, may complicate acquiring a timely and accurate knowledge of channel state information (CSI). Therefore, obtaining accurate channel modeling is paramount for designing robust and efficient beam-forming and beam-tracking algorithms, resource allocation methods, link adaptation approaches, and multiple antenna techniques. While several statistical air-to-ground channel models that trade off between accuracy and mathematical tractability have been proposed in the literature [
5], more practical analysis to bridge this knowledge gap is still needed.
On a parallel avenue, the wireless communication community has paid significant attention to deep learning (DL) techniques owing to their success in various applications, e.g., computer vision, natural language processing, and automatic speech recognition. DL is a neuron-based machine learning approach that can construct deep neural networks (DNNs) with versatile structures based on the application requirements [
6]. Specifically, several works in the open literature have utilized DL methods for channel modeling and CSI acquisition. For instance, a DL-driven channel modeling algorithm is developed in [
7] using a dedicated neural network based on generative adversarial networks designed to learn the channel transition probabilities from receiver observations. Furthermore, in [
8], a DNN-based channel estimation scheme is proposed to jointly design the pilot signals and channel estimator for wideband massive multiple-input multiple-output (MIMO) systems.
To address the limitations of existing systems, researchers have focused on ML and DL methods in recent years. Despite their enormous potential, DL approaches confront significant difficulties that limit their applicability in advanced communication environments. To develop an adequate mapping from features to desired outcomes, deep NNs (DNNs) require enormous datasets, which raises both the computational complexity and the difficulty of the training process. Due to the current state of communication datasets, it is questionable to rely purely on data-based DNNs as black boxes and leave all predictions to model weights. Model-driven DNNs have evolved as a solution to the limitations of model-based and data-based techniques; these DNNs combine the strengths of DNNs in learning and mapping with domain expertise to maximize benefits [
9]. Most model-driven DNN solutions fall into one of two categories: deep unfolded networks, in which DNN layers reproduce rounds of an existing iterative process, or hybrid networks, in which DNNs assist conventional models and boost efficiency. The data scarcity problem has also been eliminated alongside the advancement of DL literature on communication technologies, making room for data-based DL systems [
10]. Nevertheless, the promising enhancements of DL techniques for channel modeling have motivated researchers to investigate utilizing different learning methods and feature extraction approaches in the context of cellular-connected UAV communication systems. To the best of our knowledge, only a few prior relevant research works dealt with UAV channel characterizations using the received signal strength (RSS) in cellular communications [
11,
12,
13,
14]. In [
11], a modeling framework for wave propagation in mobile communications is proposed by combining several learners in an ensemble learning method for RSS modeling. Furthermore, a deep reinforcement learning (DRL) -based model for channel and power assignment is developed in [
10] for UAV-enabled IoT systems, where a single UAV-base station is deployed to collect data from multiple IoT nodes. In [
13], a learning algorithm is used to predict channel characteristics between UAVs and ground users, which provides accurate environmental status information for UAV deployment decisions. Additionally, the authors in [
14] have proposed ensemble methods based on supervised base learning to predict the channel model of UAV using the least squares boosting method, bagging prediction, and support vector machines (SVMs).
In terms of DL methods, Wang et al. [
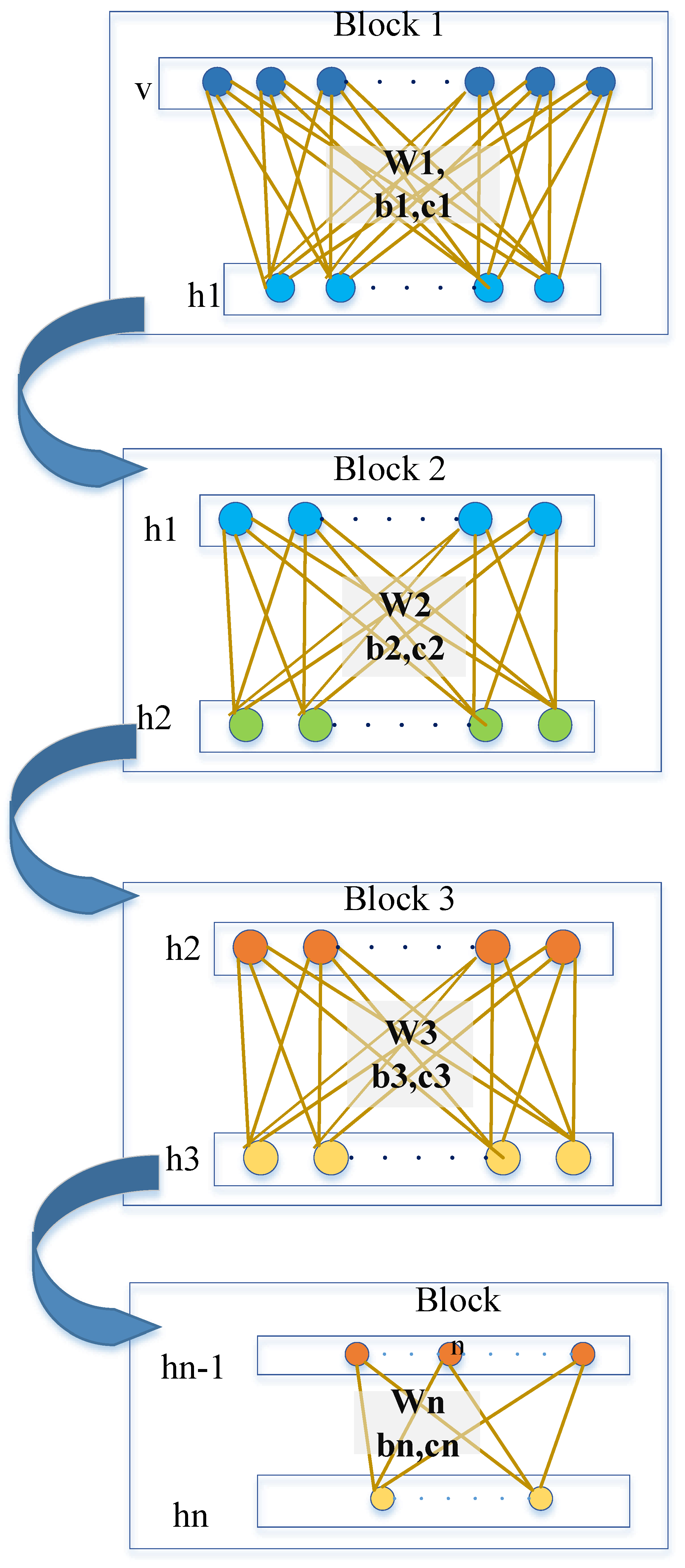
15] have proposed a DL scheme that can fully explore the features of wireless channel data and obtain the optimal weights as fingerprints while incorporating a greedy learning algorithm to reduce computational complexity. Beyond this, the restricted Boltzmann machine (RBM) is a generative stochastic artificial neural network that can learn a probability distribution over a set of inputs in an unsupervised manner. RBM is bipartite, i.e., there are no intra-layer connections, and it consists of a pair of layers that are commonly referred to as the
visible and
hidden units, respectively, as shown in
Figure 1, and they may have a symmetric connection between them. However, RBM has some limitations due to dealing with only binary data, and to circumvent this issue, the Gaussian–Bernoulli restricted Boltzmann machine (GRRBM) [
16] was proposed to process real data where a Gaussian visible node replaced a binary node to initialize DNN for feature extraction and dimension reduction.
The commonality of the works as mentioned earlier [
11,
12,
13,
14,
15] is that they all follow training methods that have high variance and slow diverging behaviors that require a massive volume of training data and extended training time, which is prohibitive in wireless communication systems. This observation has motivated this work to fill this gap in the literature and propose a framework based on GBRBM that incorporates an autoencoder-based deep neural network to estimate the received signal power of UAVs flying in a range of altitudes connected to a cellular network. Moreover, we propose a novel algorithm that employs an adaptive learning rate alongside an enhanced gradient, which speeds up the learning of hidden neurons, contrary to the traditional gradient decent. The main contributions of this work can be summarized as follows:
Apply GBRBM and real measurements to estimate the received signal power at UAV from the cellular network during the flight, where GBRB machines and deep neural network are employed to extract features from the UAV channels as a series set of blocks for channel modeling.
Develop an adaptive learning rate approach and a new enhanced gradient to improve the training performance. Specifically, an autoencoder is used to fine-tune the parameter, while the parameters are trained by using an encoder neural network to model the RSS for the prediction of the ground at different heights.
Verify the effectiveness of the proposed method throughout experimental measurements and comparisons with other benchmark schemes. The numeral results show that the proposed scheme outperforms the conventional autoencoders.
The remainder of this paper is organized as follows.
Section 2 presents the system model. The proposed method is described in
Section 3. Numerical examples and demonstrations of various simulation results are given in
Section 4. Finally, conclusions are drawn in
Section 5.
3. UAV Measurements
In this section, simulation results are provided to evaluate the performance of the proposed CSI prediction scheme for air-ground links in UAV communication systems. For UAV communications, mmWave bands hold a lot of promise to meet the data rate requirements of high-throughput mobile applications. Particularly, by hovering at a preferable place, UAVs can keep line-of-sight (LOS) connection (or at least an acceptable NLOS) link with a desired user. Ray tracing offers a deterministic method of characterizing the mmWave channel under various conditions.
Since studying the behavior of Air-to-Ground channels at mmWave bands using UAVs might be difficult, ray tracing provides a useful alternative. Here, we utilize the Remcom Wireless InSite ray tracing program to simulate the UAV’s real-time movements along a specified trajectory. The simulation parameters were set up as follows: the area’s dimensions are 10 km by 10 km in size as shown in
Table 1. In all situations, the UAVs are flying at a speed of 15 m per second from altitudes of 200 m (resembling a land vehicle); the flight trajectory of the UAV is around 2 km in length. Both the transmitter and receiver employ vertically polarized half-wave dipole antennas. The channel at 28 GHz has a sinusoid to sound the channel at the center of the ferquency. The power level is set at 30 dBm for transmission [
22].
Considering mmWave frequencies of 28 GHz, we present the cumulative distribution functions (CDFs) of the RMS-DS of the multipath channel between the GS transmitter and the UAV in
Figure 5 for four different scenarios. The major reason for this behavior is that at higher UAV altitudes, the UAV moves above tall structures and is able to observe signals that are scattered from a majority of surrounding buildings. In contrast, findings in rural and suburban settings demonstrate that unlike in urban settings, the RMS-DS actually declines as the number of buildings increases. Buildings in rural and suburban areas tend to be smaller and less densely populated than those in cities. These various multipath channel behaviors imply that the environmental variables and UAV height may have a big impact on the channel behavior and consequently the receiver design.
4. Performance Evaluation
In this section, we implement the proposed GBRBM-based DNN in addition to other machine learning algorithms, i.e., backpropagation ANN and SVM. The considered simulation parameters include the GBRBM block, the number of neurons and layers of the network, and the value of the adaptive learning rate and number of the epoch. The total number of training vectors is 710, while the number of test vectors is 177, with 201 unknown variables with 100 iterations.
4.1. GBRBM Blocks
Figure 6 shows the difference error between the measurements and the estimated values by using different numbers of GBRBM-based DNN. Different numbers of GBRBM are considered starting from 2 to 7, while the differences error between the estimated and measured RSS varies from −5 to 15. It can be readily seen that the best results are obtained when six blocks of GBRBM-based DNN in the pre-training stage are used. The performance accuracies are 85.1%, 87.3%, 90.1%, 92.8%, 94.1%, and 93.7%, respectively.
Since a proper epoch number can shorten the training period and the search space of solutions, the best epoch number is important to both the pre-training and training phases. Therefore, the perfect epoch number could be selected based on the value of this reduction function. For example,
Figure 7 presents the difference error versus the number of epochs. Clearly, the difference error is stable when we reached around the 500th epoch. Hence, the epoch number of the pre-training stage is set to 250, and the epoch number of the training stage is set to 500 epochs.
After the GBRBM blocks and epoch number are determined, the neuron number must be set for every layer. The optimization process is quite tedious because the tuning assortment of the neuron number in every layer is arbitrary. Thus, we empirically set the neuron amounts and then run experiments to maximize the neuron amount of the sixth layer depending on the operation of both GBRBM-based DNN. In the pre-training stage, the difference in the RSS value between the estimated measure and the real measure decreases as the epoch number increases and is set to the 250th epoch, as depicted in
Figure 8.
4.2. Adaptive Learning Rate
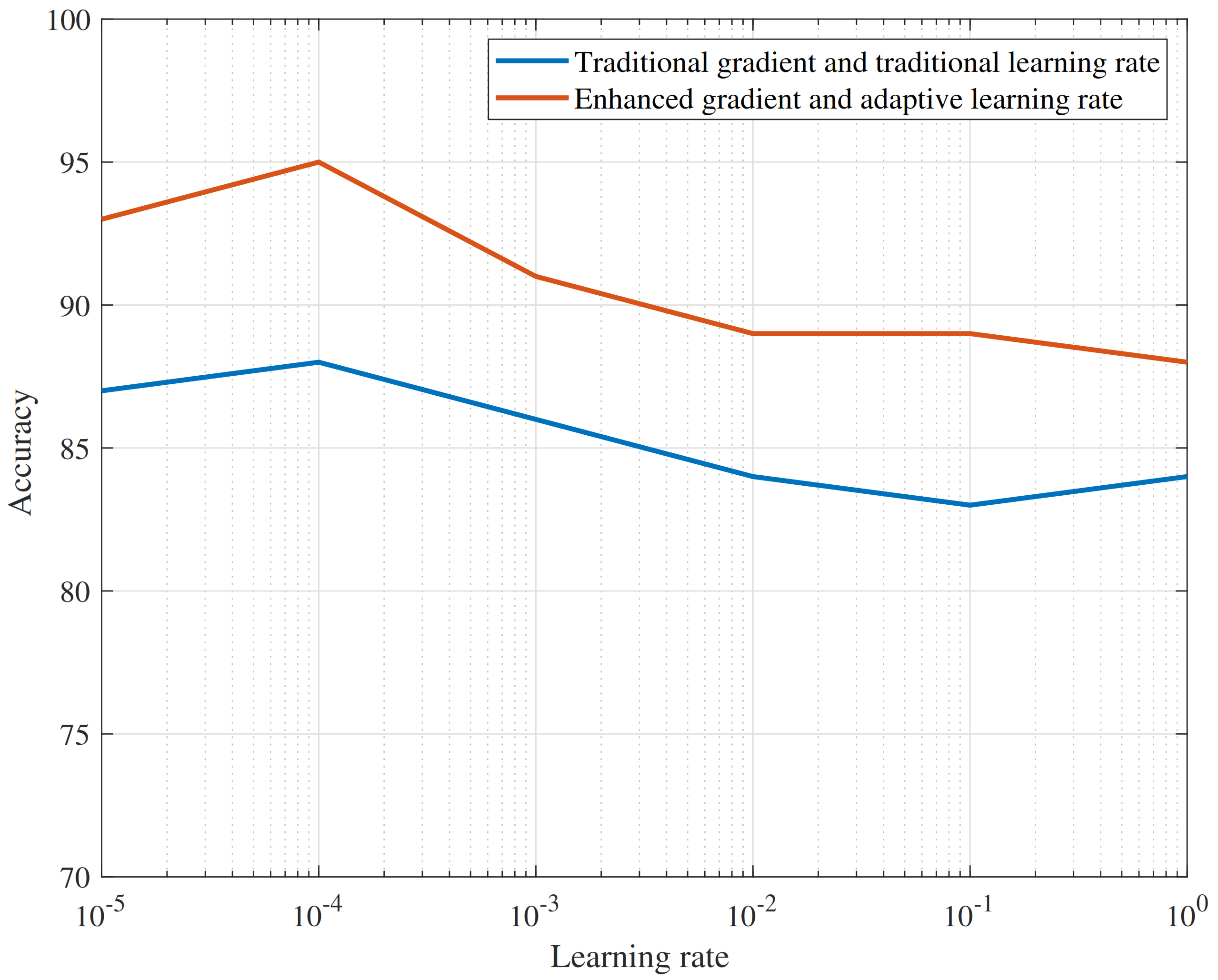
The learning rate is similar to the step size of the gradient descent process. The precision will be greatly affected if it is set too big or too small. In particular, if the learning rate is too small, the training period grows, and a local optimal solution is likely to be trapped. Since there are pre-training and training stages, we must discover an individual optimum learning rate for all of them. We trained the traditional gradient with five learning rates (1, 0.1, 0.01, 0.001, 0.0001) to demonstrate how the learning speed can greatly affect training results. The resulting RBMs have enormous variance determined by the learning rate selection. When the learning rate was large, the result models completely failed, whereas better results were obtained when the learning rate was too low. To test the suggested adaptive learning rate, we trained RBMs of the hidden neurons with the traditional gradient and the same five values (1, 0.1, 0.01, 0.001, 0.0001) to initialize the learning rate. Of this test information, the outcomes are more stable, the variance among the consequent RBMs is smaller than the results obtained with the learning rate regardless of the initial learning rate, and all RBMs were trained efficiently. These results have revealed that the adaptive learning rate performs better, leading to ameliorated results. However, it was slightly better to use a continuous learning rate of 0.001 in both pre-training and training stages.
Figure 7 shows the adaptive learning rate performance during learning. The process found suitable learning rate values when the enhanced gradient was used. Specifically, one will find six GBRBM blocks for the pre-training stages and five network layers to the training in the autoencoder. The neuron numbers for hidden layers of multi-block GBRBM are 64, 56, 48, 32, and 16, respectively. The epoch amounts of the pre-training and coaching phases are set to 250 and 500, respectively. The learning speeds of the two phases are equally set to 0.001, as shown in
Table 2.
The GBRBM-AE parameters were set as training and pre-training algorithms to compare the results for 50 independent trails to obtain the mean, best, and worst values, as shown in
Table 3.
Figure 9 and
Figure 10 depict the best results obtained from the SVM algorithm, and similarly,
Figure 11 and
Figure 12 present the best results of the ANN method. Specifically,
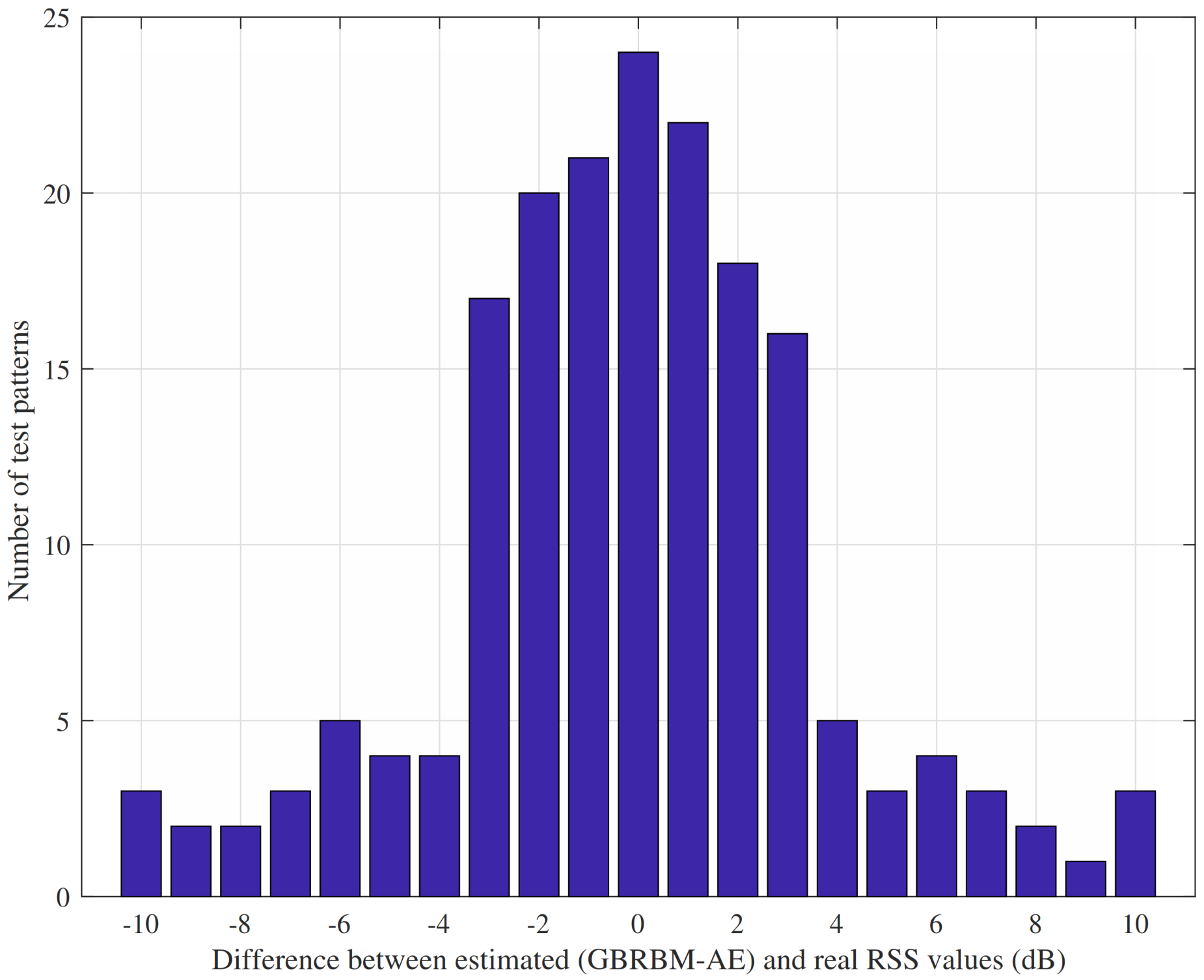
Figure 9 presents the value of the received signal obtained by the best SVM compared to the measurement the UAV took. The red dots represent the measurement values, while the blue line represents the SVM output. Although the SVM predicted value was close to the experimental value, it does not consider adequately near optimum values. Furthermore,
Figure 10 depicts the histogram of the difference between the real and estimated values. Therefore, we may conclude that the SVM is well modeled but insufficient, as it has accentuated large errors.
Table 4 indicates the best results obtained from GBRBM-AE, ANN, and SVM, and the indicators used are the mean absolute error (MAE), mean absolute percent error (MAPE), and the root mean squared error (RMSE).
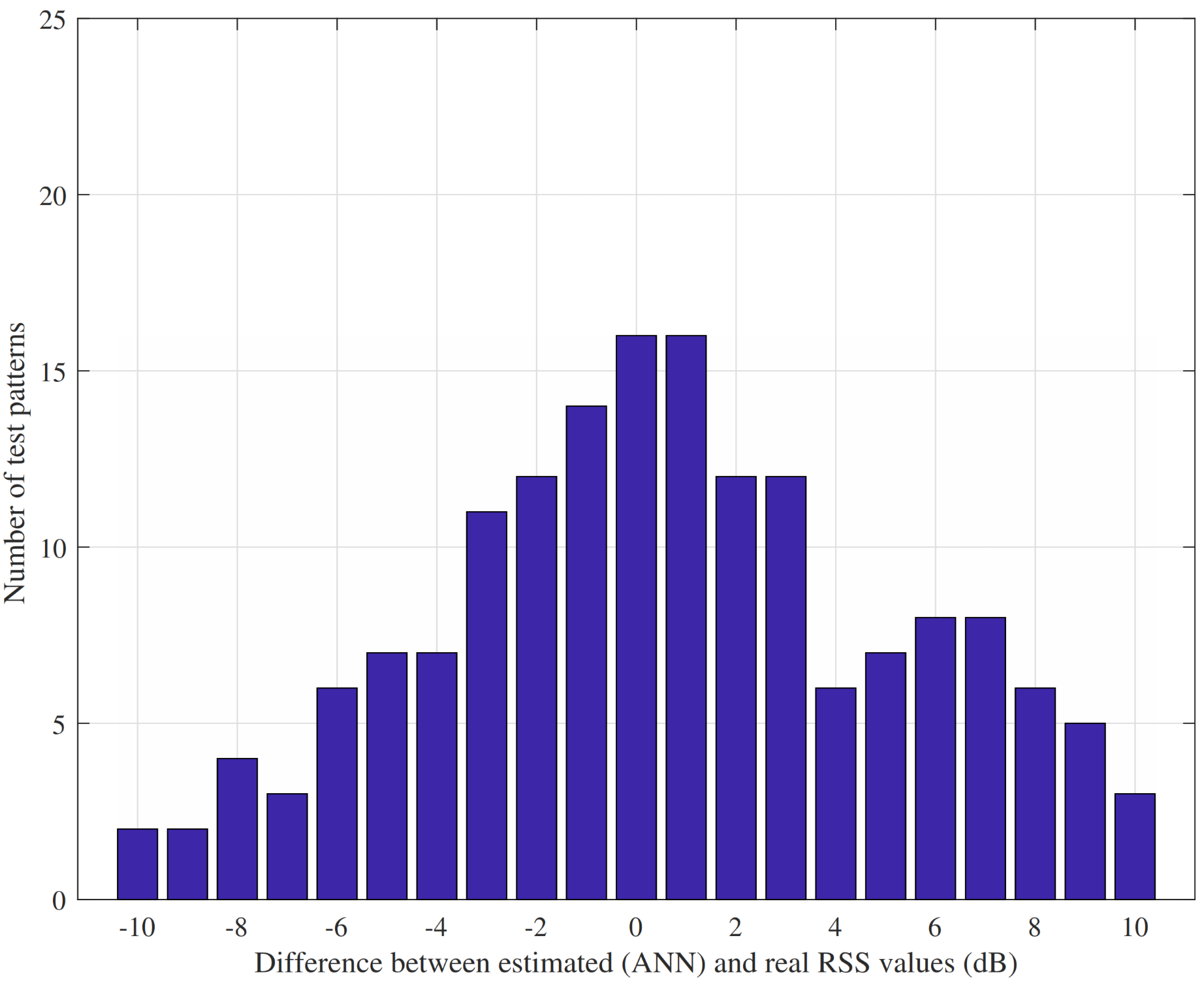
In contrast, the results of ANN show a better performance, as can be seen in
Figure 11 and
Figure 12. ANN performs better than SVM and adequately modeled the received signal power with better prediction accuracy. In addition, the best results were obtained with GBRBM-AE, as presented in
Figure 13 and
Figure 14. Clearly, the values of the GBRBM-AE method are the best results compared to the previously considered algorithms. The green line represents the GBRBM-AE output, while the red dots depict real UAV measurements. In addition, we noticed that the predicted values are adequately close to the measurement values. The accuracy result of the proposed model is shown by the time-complexity analysis, which also shows how long it takes to train and validate the model in
Table 5.