Abstract
The objective of this study was to develop a new rat-tail vibration model for studying finger vibration health effects. Unlike the previous rat-tail models, the vibration strain and stress of the rat tail can be conveniently and reliably quantified and controlled in a biological experiment. This makes it possible to identify and understand the quantitative relationships between these biodynamic responses and vibration health effects.
1. Introduction
The relationships between vibration biodynamic responses (vibration stress, strain, and power absorption density) and vibration biological effects are not sufficiently understood [1], probably because it is difficult to identify their exact relationship using human subjects or existing animal models. Systematically studying this fundamental scientific gap may help resolve major remaining issues outlined in the current ISO 5349-1 [2]: “the vibration exposures required to cause these disorders are not known precisely, neither with respect to vibration magnitude and frequency spectrum nor with respect to daily and cumulative exposure duration.” As the first step is to help conduct systematic studies, the objective of this study was to develop a new rat-tail exposure system and a related analytical method to investigate combined health effects of vibration and contact pressure and to identify their relationships with biodynamic responses.
2. Methods
The proposed new rat-tail exposure system is shown in Figure 1. It is a modification of the existing NIOSH rat-tail model with an addition of a loading device [3]. The loading device is composed of a loading plate, a set of loading springs, and the fixtures for installing the device on the vibration platform.

Figure 1.
A novel rat-tail model: (a) model configuration; and (b) a pictorial view of the model.
The vibration platform can be installed on a shaker or a vibration tool. The loading plate is placed on the middle region (C12–18) of the rat tail that is constrained on the vibration platform. The static force is applied to the tail by loading the plate by compressing the loading springs. The loading plate has a groove with a conical taper, which can conform to the tapering diameter along the tail and secure the tail to the vibration platform.
The rat tail is likely to have a nonlinear force-deformation relationship. However, the dynamic properties of the tail can be locally linearized to reduce the complexity of the system analysis. Hence, the new rat-tail vibration-exposure system under several static forces (FPS) was simulated using a linear analytical model illustrated in Figure 2.
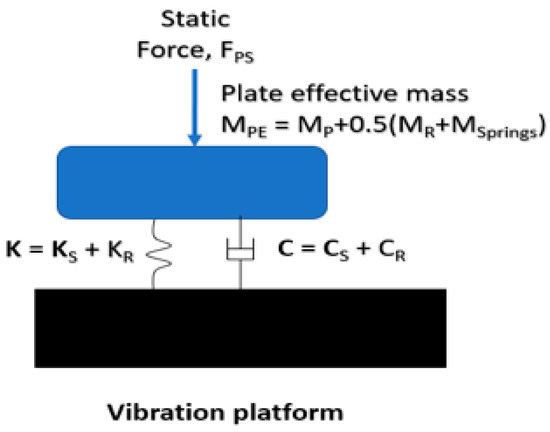
Figure 2.
An analytical model of the new rat-tail vibration exposure.
The effective mass of the loading plate (MPE) includes the loading plate mass (MP), half of the mass of the loaded tail portion (MR), and that of loading springs (MSprings). The total stiffness of the exposure system (K) includes the tail stiffness (KR) and loading spring stiffness (KS). The total damping value includes the tail damping value (CR) and that of the loading system (CS).
Three biomechanical measures, including vibration stress, strain, and power-absorption density (VPAD), were considered for the quantification of the tail-vibration exposure. The average static or dynamic stress/pressure at the tail-plate interface was estimated from
where Lt is the plate length or tail contact length; bt is the average tail contact width; FPD is the complex dynamic force acting on the loaded portion of the tail. FPD was estimated from
where DP and DV are the complex vibration displacements of the loading plate and vibration platform, respectively; VP and VV are their vibration velocities; and Ap is the vibration acceleration of the loading plate.
The stress method assumes that the vibration stress at any point in the loaded portion of the tail (σ) is approximately proportional to the average contact stress. It also assumes that vibration injuries or biological effects are correlated with the stress magnitude and the number of stress cycles. Hence, the vibration exposure dose using the stress method (Γσ) for each frequency (f) was calculated from
where Τ is the time duration (seconds) of the rat-tail vibration exposure; α is termed as stress frequency weighting; is the stress-proportional factor; and Iσ is termed as vibration-stress-dose index, which can be expressed as follows:
where j = ; TP is the transfer function of the loading plate (=AP/AV), where AV is the vibration acceleration of the platform.
The strain is a measure of the material relative deformation. The maximum static strain of the tail subjected to a static force was estimated from the maximum compression deformation (Δ) and the average diameter of the loaded-tail portion (dt):
σMaxi-static ≈ Δ/dt,
The average dynamic strain for a given static force was expressed as follows:
where ht is the deformed height of the loaded tail loaded with a static force, which can be measured in a static test.
Similar to the stress method, the strain method assumes that the distributed strain at any point (ε) is approximately proportional to the average dynamic strain, and the vibration injuries or biological effects are correlated with the strain and the number of strain cycles. Hence, the vibration exposure dose using the strain method (Γε) can be written as follows:
where β is termed as strain frequency weighting; Q is the strain-proportional factor; and Iε is termed as the vibration-strain-dose index, which is expressed as follows:
Similarly, with the model shown in Figure 2, the VPAD method for calculating the dose can be derived as follows:
where ν is the volume of the loaded tail portion (≈ π∙(0.5dt)2∙Lt); P is the VPAD proportional factor; and IVPAD is termed as VPAD dose index:
A spring-calibration test, a damping test, and a rat-tail test were performed in this study to determine the system parameters, evaluate the feasibility of the new rat-tail model, and explore the characteristics of the exposure-dose indexes. The rat-tail test used a dissected tail obtained from a cadaver rat (the tissue collected post-mortem from the rat in a control group of another study).
3. Preliminary Results
As an example, the vibration transmissibility (the magnitude of transfer function) measured with 2.23 N static force is plotted in Figure 3a. The vibration-exposure-dose indexes for the three methods were calculated from the transfer function. While the stress and strain frequency weightings (α and β) cannot be determined in this study, they were assumed to be at unity (or 1.0) in the calculation to identify the fundamental characteristics of the indexes. To directly compare the index spectra, each index spectrum was normalized with respect to its maximum value. The results are plotted in Figure 3b. Their resonant frequencies were marginally higher than the transmissibility-resonant frequency. To explore the influences of the static force on the index spectra, the index spectrum was normalized with respect to the maximum value of the indexes for the same method under three forces (0.46, 1.28, and 2.23 N). The results for stress and strain methods are plotted in Figure 3c,d. The influences on the VPAD method were similar to those on the strain method.
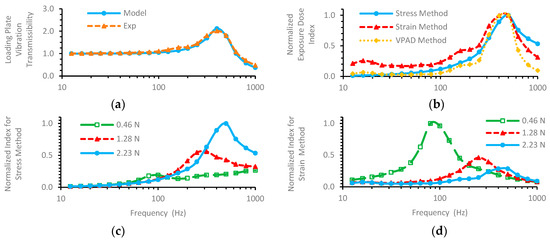
Figure 3.
Preliminary results: (a) Measured and modeled vibration transmissibility spectra; (b) Normalized dose-index spectra of the three methods for 2.23 N static force; (c) Normalized stress-dose index for different static forces; (d) Normalized strain-dose index for different static forces.
4. Discussion and Conclusions
The vibration response of the new rat-tail model worked as expected, as demonstrated by the excellent agreement between the modeling and experimental results (Figure 3). As the tail mass of the loaded portion (about 0.21 g) is much less than that of the loading plate (>20 g), the dynamic force acting on this portion of the tail during a vibration exposure results primarily from the plate acceleration (≈ MPAP). In this way, the biodynamic responses, such as vibration stress and strain of the tail tissues, can be effectively controlled and quantified by measuring and controlling the loading plate acceleration (AP). This makes it convenient and reliable to quantify the tail biodynamic responses required to investigate their relationships with biological effects.
The new methodology opens a window to view the mechanisms of the vibration health effects and their influencing factors. For example, the stress- and strain-dose index formulas (Equations (4) and (8)) suggest that the frequency may affect the vibration injuries or biological effects in two different ways: (I) the frequency determines the stress and strain magnitudes; they reach their peak values at the fundamental resonant frequency under each static force, as shown in Figure 3c,d; and (II) the frequency determines the number of cycles per second. These two different roles may result in different biological effects and/or their different frequency dependencies.
Another unique feature of the new rat-tail model is that the static force applied on the tail can be reliably controlled, which makes it possible to investigate the influences of the combined force and vibration exposures on the biological effects. The results presented in Figure 3 suggest that the static force affected the vibration stress- and strain-exposure doses differently. This is because the rat tail has a nonlinear mechanical behavior. At a low static force, the tissue stiffness is less than that at a higher static force; as a result, the same dynamic force results in a larger strain at the low static force than that at the higher static force. On the other hand, the vibration stress is independent of the deformation, but it depends primarily on the dynamic force itself (Equation (4)). This finding may help identify and understand the static-force influences on the vibration health effects and their frequency dependencies.
Overall, the new rat-tail model provides a new and effective tool for studying human finger vibration health effects.
Author Contributions
Conceptualization, R.G.D. and J.Z.W.; methodology, R.G.D. and C.W.; software, R.G.D. and X.S.X.; validation, J.Z.W., D.E.W. and K.K.; experiments and investigation, all authors; data curation, X.S.X.; writing—original draft preparation, R.G.D.; writing—review and editing, K.K., D.E.W. and S.W.; project administration, K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The experimental data are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dong, R.G.; Wu, J.Z.; Xu, X.S.; Welcome, D.E.; Krajnak, K. A Review of Hand-Arm Vibration Studies Conducted by US NIOSH since 2000. Vibration 2021, 4, 482–528. [Google Scholar] [CrossRef]
- ISO 5349-1; Mechanical Vibration—Measurement and Evaluation of Human Exposure to Hand-Transmitted Vibration—Part 1: General Requirements. International Organization for Standardization: Geneva, Switzerland, 2001.
- Krajnak, K.; Waugh, S.; Miller, G.R.; Johnson, C.; Kashon, M.L. Vascular responses to vibration are frequency dependent. J. Occup. Environ. Med. 2010, 52, 584–594. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).