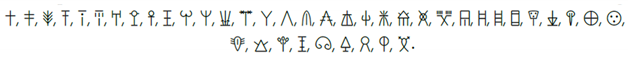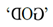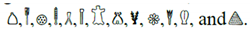Contributions to the 2021 IS4SI Summit from the SIS Conference Symmetry, Structure, and Information ^†

Abstract

This is an outline of the contributions from the Symmetry, Structure, and Information Conference organized by the International Society for the Interdisciplinary Study of Symmetry which was one of the ten conferences of the 2021 Summit of the International Society for the Study of Information held online 12–19 September 2021. Each of the ten conferences contributing to the summit had a 3–6 h block of plenary time with the program (usually invited lectures and panel discussions) intended for all participants of the summit. Outside of the assigned plenary time, conferences had parallel programs of more specialized, technical, or focused presentations. All plenary events and some parallel, internal events of the conferences federated into the summit were recorded. Links to several of these recordings and extended abstracts of all presentations are available at the website of IS4SI. The conference had fifteen presentations (including a plenary invited lecture) and a panel discussion.

1. Introduction

This is an outline of the contributions from the Symmetry, Structure, and Information Conference organized by the International Society for the Interdisciplinary Study of Symmetry which was one of the ten conferences of the 2021 Summit of the International Society for the Study of Information held online 12–19 September 2021. The 13th International Workshop on Natural Computing (IWNC) was one of the ten conferences of the 2021 Summit of the International Society for the Study of Information held online 12–19 September 2021. Each of the ten conferences contributing to the summit had a 3–6 h block of plenary time with the program (usually invited lectures and panel discussions) intended for all participants of the summit. Outside of the assigned plenary time, conferences had parallel programs of more specialized, technical, or focused presentations.

All plenary events and some parallel, internal events of the conferences federated into the summit were recorded and many of these recordings have been edited and published on YouTube. Links to several of these recordings and extended abstracts of all presentations are available at the website of IS4SI: https://summit-2021.is4si.org/ (accessed on 5 March 2022).

This editorial is focused on the Symmetry, Structure, and Information Conference. It presents the subject and content of the conference. The conference had twenty presentations (including the plenary invited lecture) and a panel discussion. The conference was co-chaired by Denes Nagy (President of the International Society for the interdisciplinary Studies of Symmetry, Hungary & Australia), Marcin J. Schroeder (Global Learning Center, IEHE, Tohoku University, Sendai, Japan), and Vea Viana (Faculty of Architecture, The University of Porto, Portugal). The Organizing Committee membership in addition to co-chairs included Jean-Yves Beziau (University of Brazil, Rio de Janeiro), Ferenc FRIEDLER (Széchenyi István University, Győr, Hungary) Ted Goranson (The Australian National University), Ioannis Vandoulakis (Hellenic Open University and FernUniversität in Hagen), and Takashi Yoshino (Department of Mechanical Engineering, Toyo University, Kawagoe, Japan).

2. The Symmetry, Structure, and Information Conference

The conference subject and objectives were explained in its announcement by its co-chairs, Denes Nagy, Marcin J. Schroeder, and Vera Viana, as follows. The task of tracing the presence of the ideas of symmetry, structure, and information in the intellectual history of humanity would be impossible without taking into account every single step of the human mind in the exploration of reality. It is difficult to find any context entirely free from a direct or indirect presence of these ideas, even if they remained hidden under different names or are convoluted or confused with other ideas such as harmony, form, knowledge, etc. They have manifested themselves in human culture from the very beginning without being trivial or obvious, continuously attracting attention of the intellectual giants of the format of Kant who attempted but failed to explain the meaning of symmetry.

Their current conceptualizations, formulated in full generality within the last two centuries are still subject of intense discussions. More recently, their study acquired precise mathematical tools in the group or probability theories, and the development of modern science and technology would not have been possible without the analytic tools of the invariance or its breaking, or of entropy. However, the precision of mathematical formalisms would be blind and incomplete without the ability to gain better insight into the role of these fundamental ideas in obtaining understanding of reality or without knowledge of their mutual relations.

The close relationships between symmetry and structure are well known, although sometimes, not sufficiently appreciated. The most ambitious attempt to bridge science and humanities in the form of philosophical structuralism influenced by Herman Weyl’s book “Symmetry” and widely propagated by Jean Piaget’s book “Structuralism” was its most recognized product. The bridge between science and humanities through symmetry–structure association stimulated multiple studies with an excellent example of the 1982 book with essays by Cyril Stanley Smith.

The relationship between symmetry (or its breaking) and information is probably less known, but it is not less fundamental. After all, Gregory Bateson’s celebrated concept of information as the “difference that makes a difference” had its early appearance in his 1972 paper “A Re-examination of ‘Bateson’s Rule’” on breaking symmetry in the biological context. We are perfectly aware of the interrelations between the ideas of symmetry, structure, and information but we still know very little about them.

The main goal of the 2021 IS4SI Summit is to build bridges between disciplines and to explore the potential of using information as a unifying theme. For this reason, the inquiry of the relations between the ideas of symmetry, structure, and information should have the utmost importance and be worthy of the greatest interest from all participants.

Submissions of extended abstracts of papers intended for a presentation at the conference “Symmetry, Structure, and Information” are invited on all topics related to the interdisciplinary study of symmetry. Naturally, the papers aiming to address the mutual relations between these ideas are in the highest demand and will be given preference. However, papers on subjects focusing mainly on symmetry will also be welcome, since papers on a certain topic may induce associations with other topics in between members of the audience. The intention of the conference, as well of the entire summit is to bring together the widest possible range of perspectives from philosophical or scientific, to visionary and artistic. There will be an opportunity to present original and creative contributions without any restriction by disciplinary divisions or level of advancement of research.

3. Invited Lecture

The Development and Role of Symmetry in Ancient Scripts) by Peter Z. Revesz (Dep. Computer Science and Engineering, University of Nebraska-Lincoln, USA)

Many ancient scripts have an unexpectedly high number of signs that contain a type of symmetry where the left and right sides of the signs are mirrored along a central vertical line. For example, within our English alphabet, which is a late derivative of the Phoenician alphabet, the following letters have this type of symmetry: A, H, I, M, N, O, T, U, V, W, X, and Y. That is, a total of 12/26 = 46.2% of the letters of the English alphabet have this type of symmetry.

Similarly, the ancient Minoan Linear A script, which existed from about 1700 to 1450 BC, contains the following mirrored signs:

In total, 42 signs are about half of the most frequent signs in the Linear A script, which are estimated to be about 90 signs. In this paper, we try to answer the question of “why is there such a high percent of mirrored signs in ancient scripts?”

We believe that the unexpectedly high number of symmetric signs is due to a development of writing that is called boustrophedonic, or literally as ‘the ox goes’ meaning that at the end of a line the next line continues right below the end and goes in the opposite direction. Hence, a left-to-right line is followed by a right-to-left line, which is again followed by a left-to-right line and so on. This is reminiscent of how oxen plow a plot of land. The main problem with boustrophedonic writing is that when we look at a particular line, we do not automatically know which way it should be read, unlike in modern English texts, where every line is read from left to right. As a modern example, suppose we would like to write ‘GOD’ in a row that is to be read from right to left. This looks like an easy task that can be carried out by simply writing: ‘DOG’. The problem is that the reader may not recognize that the row needs to be read from right to left, hence ‘God’ becomes ‘dog’ for the reader. Ancient scribes compensated for this problem by vertically

mirroring any nonsymmetric letter so that the orientation of the words would indicate the direction. Using this concept, instead of ‘DOG’, they would have written: While boustrophedonic writing with mirroring of asymmetric signs is an attractive solution, and it occurs also in the Mycenaean Linear B script and the Indus Valley script, it causes the problem of having to know and correctly write the mirrored versions of the asymmetric signs. Many people make mistakes when writing mirrored letters and can read mirrored letters much slower than ordinary texts. We believe that these factors combined with the observation that only a few frequently occurring asymmetric signs are enough to indicate the writing direction led to the development of symmetric forms for most signs. We test this hypothesis by considering earlier scripts where there are no examples of boustrophedonic writings. For example, the Cretan Hieroglyphic script, a predecessor of the Linear A script, contains significantly fewer symmetric signs, and only the following signs of the Phaistos Disk, which may belong to an even earlier layer of scripts, are symmetric signs:

That is, only 13/45 = 28.9% of the Phaistos Disk signs are symmetric. Hence, on the island of Crete, the percent of scripts signs with symmetry nearly doubled within a few centuries, showing the importance of symmetry in writing.

4. Panel Discussion

The panel discussion on the subject of the conference moderated by Denes Nagy and Marcin J. Schroeder involved panelists Ted Goranson, Eugene Katz, Peter Revesz, Vera Viana, and Takashi Yoshino. The discussion was initiated by the moderators’ introduction.

The theme of this discussion and the conference is Symmetry, Structure, and Information. Each of these three ideas escapes a commonly accepted definition. On the other hand, if you ask a passerby whether he or she understands the words symmetry, structure, and information, the most likely the answer would be “sure”. In a very unlikely case, the answer could be “not at all, but I really would like to understand symmetry” showing that the person knows a lot. Then, invite him or her to attend the Congress on Symmetry in Porto next July.

We can expect a question about the objectives of discussing the triad of symmetry, structure, and information. After all, if we add one more idea of complexity then we have a collection of the most elusive and at the same time most important notions of the philosophical and scientific inquiries. Is it not better to focus on each of them separately and only after we have clear results of such inquiries to attempt synthesis? This is the main question addressed to the panelists and the audience.

This question can be reformulated or complemented by the question concerning the importance, or its lack, of the mutual relationships between the ideas in the leitmotif of the conference. This includes the importance for philosophical, theoretical, or practical reasons.

Finally, we can consider the question about what is missing from the picture which is painted by the title with the three ideas only. What ideas, notions, concepts we should include, or even we should give priority in our inquiries of symmetry?

5. Plenary Talks Presenting Interdependence between Information and Symmetry

Dénes Nagy and Marcin J. Schroeder conducted plenary talks with the objective to present to the community of the IS4SI Summit the interdependence between information and symmetry.

“Symmetry and Information: An odd couple?” by Dénes Nagy.

Symmetry (from the Greek syn + metron, “common measure”), structure (from the Latin structūra, “fitting together, building”), and information (from the Latin īnfōrmātiō, “formation, conception, education”) are scholarly terms that have ancient roots, but gained new meanings in modern science. It is also common that all of these played important roles in interdisciplinary connections, even linking science and art.

The author argues that symmetria–asymmetria could have played a relevant role at the birth of mathematics as an abstract science with a deductive methodology (presenting a partly new hypothesis which unites those ones by Szabó and by Kolmogorov), then we discuss the related, but different modern meaning family of symmetry.

(1)

The structural approach gained special importance in geometric crystallography from the mid-19th century (14 Bravais-lattices), which, using symmetry considerations, led to a major breakthrough in the 1890s by presenting the complete list of all the possible ideal crystal structures, that is the 230 space symmetry groups (Fedorov, Schoenflies, and Barlow). In the early 20th century, the focus on structures in linguistics (Saussure) also inspired the later developments in social sciences, the intensive study of relations and structuralism as a methodology (Lévi-Strauss, Piaget, and others). From the mid-1930s, a group of French mathematicians used a similar path in order to present “new math” (Bourbaki group).

(2)

Theory of communication led to the study of information in a mathematical-statistical context and finally a method for measuring information (Hartley, Shannon, Wiener), which became useful for the emerging computer science in the mid-20th century. Then, information theory was also used for the study of aesthetical questions (Moles, Bense).

Looking back, we may see interesting changes:

-

The original Greek concept of symmetria was related to measurement, but the usual modern understanding of symmetry implies rather a yes/no question: an object or a process is either symmetric or not. We argue that it is important to go back to the roots and to consider symmetry measures. In fact, the concept of dissymmetry (as the lack of some possible elements of symmetry) gained special importance in structural chemistry (Pasteur), theoretical physics (P. Curie), and crystallography (Shubnikov and Koptsik), pointed out to such a direction.

-

The concept information was not originally related to measurement, but the modern mathematical approach introduced measures in bits, with the number of yes/no questions (Hartley, Shannon). On the other hand, the meaning of information was lost in the case of the mathematical-statistical approach. There were important works related to the meaning of information (MacKay, Bar-Hilleland Carnap, Shreider). It would be important to unite these two and modify them according to the new needs. Quantum computing needs a new information theory related not to bit, but to qubit; here we may need symmetry considerations (cf., Bloch sphere representation).

In some sense, the “odd couple” of symmetry (as an ordering principle) and information (knowledge based on measurements) came together for solving the Maxwell’s demon problem. In this thought experiment, which seemingly violates the law of entropy, the demon as the doorman between the two chambers of a closed container filled with gas, introduces a new order by separating the high-speed and the low-speed gas molecules by opening the door always in due time. This method would solve our heating and cooling problem in everyday life. The demon, however, should use information, specifically measuring the speed of molecules for the purpose of his work (Szilard). Thus, it would be a very expensive heating and cooling. Another example where symmetry and information work together: The vertices of some regular and semi-regular polyhedra inscribed into a sphere present the centers of circles in the case of the densest packing of a given number of equal circles on this sphere (Tammes problem), which is important for spherical coding. The term information as symmetry is well-established in economic science. The fact that it may create an imbalance of power in transactions and, in the worst case, market failure led to various studies and actually the Nobel Prize of three economists (Akerlof, Spence, and Stiglitz). The author suspects that some generalized symmetry and information concepts, which are required by the recent developments in science and art, may help each other.

“Antinomies of Symmetry and Information” by Marcin J. Schroeder has been submitted and accepted for the publication in the IS4SI Proceedings and can be found in this volume of the IS4SI Summit Proceedings. The subject of the paper is a resolution of several antinomies present in the independent studies of these concepts which can be resolved through their interdependence.

6. Other Contributions to the Symmetry, Structure, and Information Conference

The following papers (listed in the order of scheduled presentations) were presented at the conference in its part more focused on specialized topics of symmetry. They were not submitted for publication in the proceedings, but their extended abstracts are available on the website of the summit: https://summit-2021.is4si.org/ (accessed on 5 March 2022).

• “Tilings for Conjoined Origami Cranes Using Less Symmetric Quadrilaterals” by Takashi Yoshino.
• “Demonstration of the Conepass to Construct the Golden Angle” by Akio Hizume.
• “Fractal-Like Structures in Indian Temples” Sreeya Ghosh, Paul Sandip and Chanda Bhabatosh.
• “Future Ethnomathematics for A ‘New Bletchley’” by Ted Goranson.
• “Artistic Intuition: How Symmetry, Structure and Information Can Collide in Abstract Painting” by Marina Zagidullina.
• “Inner Angles of Triangles in Parameter Spaces of Probability Distributions” by Takashi Yoshino.
• “Grown Matter Design, Symmetry, Structure, & Information” by Juan Manuel Villa Carrero, Ismael Humberto Garcia Páez and Maria Camila Araque.
• “‘Convenirent…Exactissime’: For Empirical Rigor in the Application of the Concept of (Bilateral) Symmetry” by Michael Selzer.
• “Breaking Symmetry and Information in Design” by Patricia Muñoz.
• “Patterns in Oriental Carpets: Symmetry, Structure, and Knowledge” by Carol Bier.
• “Logical Polygon as A Tool for Philosophical Reasoning: One Question on Introspection” by Oksana Cherkashina.
• “‘The Olympic Flotilla’: Floating-Transportable Array of ‘Mega Events’ Facilities for Rent” by Michael Burt and Yehiel Rosenfeld.
• “Roman Cosmatesco: Symmetry Underfoot” by Eugene A. Katz.
• “Interaction of Symmetry, Structure, and Information in The Oxipo-Model of Learning” by Ferenc Mező and Katalin Mező.
• “Quality of Information and Symmetry” by Miro Brada.
• “Periodic Law in the Context of Cognitive Development” by Dmitry Weise.
• “A Combined Research Platform of Structural Morphology, Dealing with the Ordered 3D Space” by Michael Burt.