Relational Structure of Conceptual Spaces ^†

Abstract

Concepts play an important role in human culture, forming explicit and implicit conceptual spaces. The goal of this paper is to explore the structural organization of information in conceptual spaces.

1. Introduction

Concepts play an important role in human culture as the basic level of our knowledge systems [1]. In essence, all meaningful words are names of concepts. Consequently, dictionaries are collections of concept definitions, while encyclopedias are collections of extended concept descriptions. Thus, it is important to study concepts and their arrangements in the context of knowledge systems.

Concepts are intrinsically related to signs. According to the general understanding, a sign is an object that points to something different than itself, being transcendent to it. At the same time, a concept, or notion, is usually defined as a general idea derived from specific instances, i.e., a concept is a symbolic (usually, linguistic) representation of these instances, and this representation naturally points to these instances. Consequently, a concept is a specific sign.

In terms of their organization, concepts form conceptual spaces, which include relations between and operations with concepts as elements of these spaces [2,3,4]. The goal of this work is to study relations in conceptual spaces.

It is important to understand that the conceptual spaces introduced and explored in [4] are aimed at the study and further development of the structural organization of encyclopedias and encyclopedic dictionaries, while conceptual spaces introduced and studied by other authors are oriented at modeling mental knowledge structures in the mind. The conceptual spaces of the first type are called structural, while the conceptual spaces of the secondtype are called attributive. Here, we continue our studies of structural conceptual spaces with emphasis on the relations of these spaces.

2. Concepts and Their Models

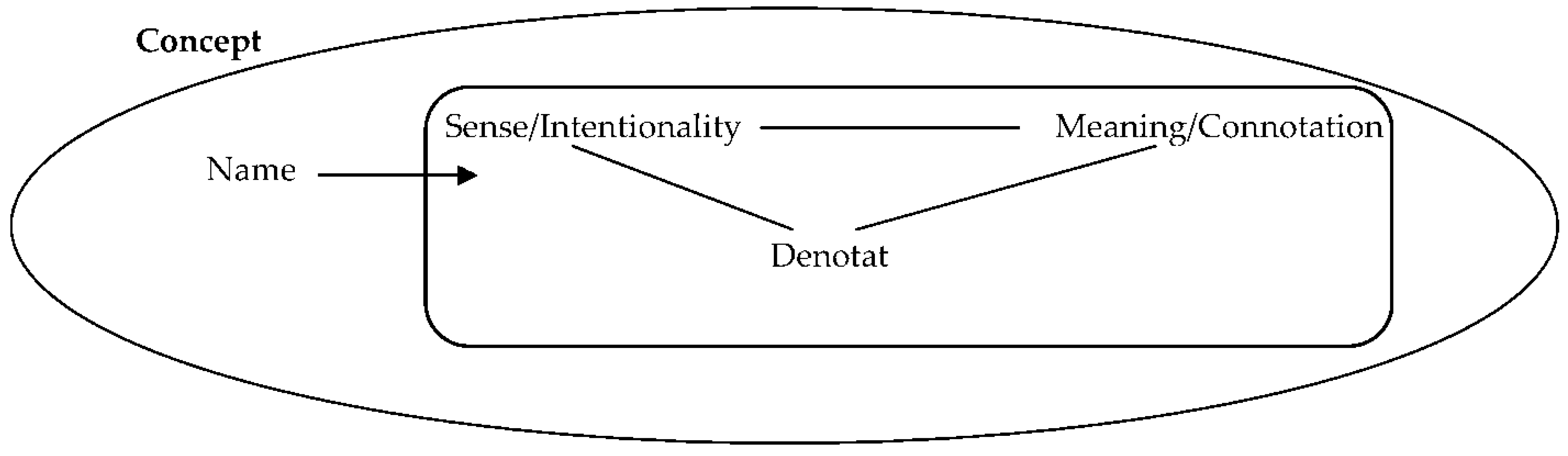
In conceptual spaces, concepts are represented by their models. In our study, we use the most advanced model, which is called the representational model of concept [5]. On its second level, it can be treated as a synthesis of the Russell’s model of concept and Peirce’s model of sign. In the representational model of concept, the name of the concept is connected to the concept representative, which consists of three components: denotat as the collection of all particular exemplifications or instantiations of this concept, meaning or connotation, and sense or intentionality. (cf. Figure 1). We will call this special case of the representational model by the name of the extended Peircean model of a concept.

Meaning represents the semantics of the concept. Sense is associated with the pragmatics of the concept. Denotat is the generalized syntax of the concept. For a symbolic concept, its denotata consists of syntactic relations of this concept.

It is possible to treat other known models of concepts as specifications of the representational model of the concept [6,7].

Thus, the theory of concepts in general and the extended Peircean model of a concept, in particular, bring us to the notion of the generalized syntax of the concept, which consists not only of names (words) of objects that constitute the denotat, but also include the physical and mental objects from the denotat and relations between all kinds of these objects. While the conventional syntax is defined as the arrangement of words (names) in a sentence, the generalized syntax is defined as the arrangement of symbolic (e.g., words as names), mental and physical objects in the denotat of a concept.

Using properties of concepts, which form intermediate relations in conceptual spaces, it is possible to differentiate all concepts in a conceptual space into three groups—general, individual and impossible concepts—which are defined in the following ways:

• A general concept has many instantiations;
• An individual concept has only one instantiation;
• An impossible concept does not have instantiations.

Note that the membership of a concept in one of these groups is contextual, i.e., it depends on the context. For instance, the name of a person can be an individual concept in one group where there are no other people with this name, and a general concept in another group where there are several people with this name.

The concept cat is general.The concept of the Earth is individual. The concept “a ball larger than the Sun and smaller than the Earth” is impossible.

According to the type of the denotat, general concepts can be:

• Set concepts, in which the denotat is a set;
• Class concepts, in which the denotat is a class;
• Ensemble concepts, in which the denotat is an ensemble.

In contrast to general sets and classes, elements in an ensemble are related to one another.

Note that each classification or typology of a concept determines intermediate relations in the conceptual space.

According to the exactness of the denotat, general concepts can be:

• Strict concepts, in which the denotat is a set;
• Fuzzy concepts, in which the denotat is a fuzzy set;
• Blurry concepts, in which the membership in the denotat is not clearly defined.

3. Categorization of Conceptual Spaces

Existential stratification induces three basic types of conceptual spaces:

• Mental conceptual spaces consist of mental concepts and relations between them;
• Symbolic conceptual spaces consist of symbolic concepts and relations between them being physical representations of ideal conceptual structures;
• Substantial conceptual spaces include physical components of concepts in addition to symbolic conceptual representations.

Mental conceptual spaces are in the heads of people and are studied by psychologists and educators.

Encyclopedia is an example of a symbolic conceptual space.

If the concept tree belongs to asubstantial conceptual space, then this space also includes some number of trees.

Here, we study symbolic conceptual spaces with the goal to explicate the structural organization of information in conceptual spaces.

4. Relations in Conceptual Spaces

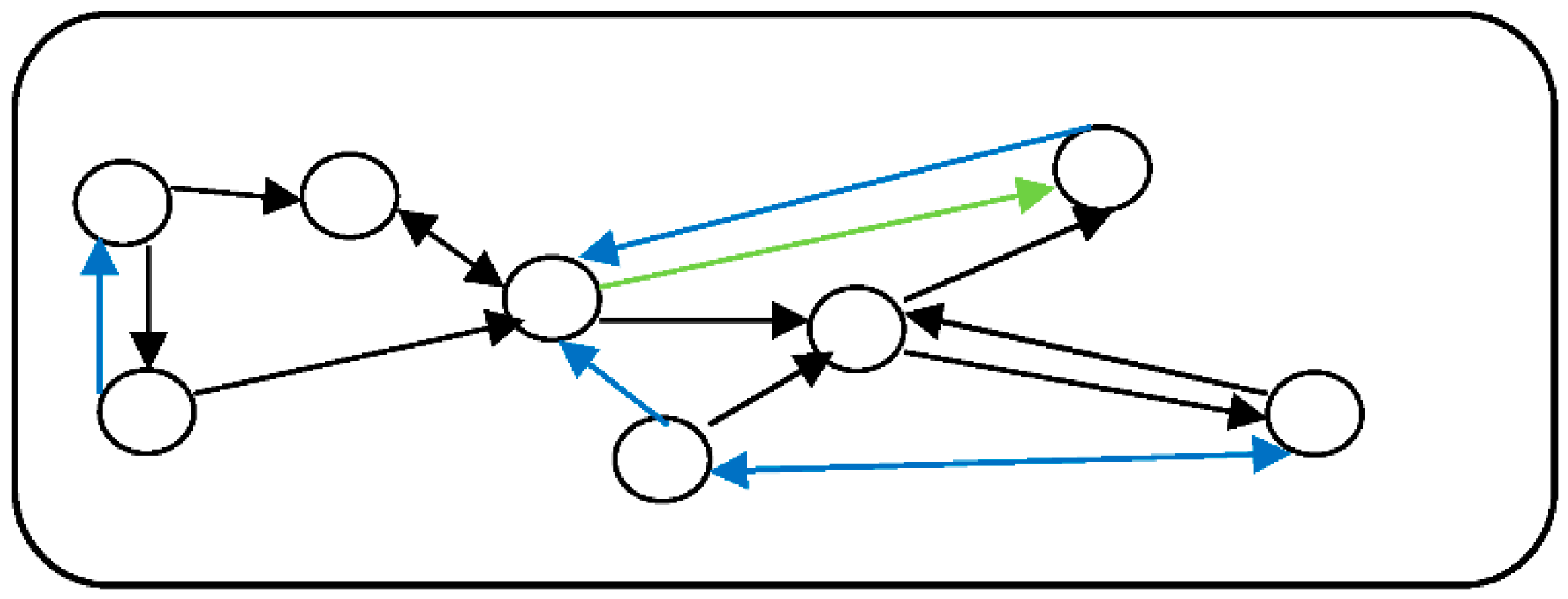
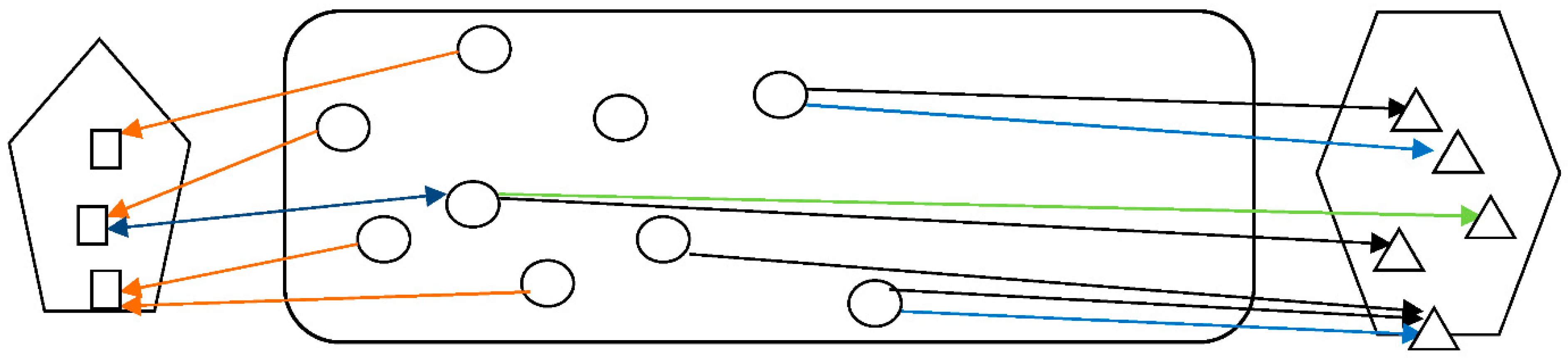
Studying conceptual spaces, we consider relations of two types: inner and intermediate relations [6]. On the first level of the space structure, inner relations of a conceptual space are relations between elements of this space (cf. Figure 2), while intermediate relations of a conceptual space are relations between elements of this space and some other objects (see Figure 3). Examples of intermediate relations are abstract properties of concepts. Examples of inner relations are relations“to be more (less) general” or “to be more (less) abstract.”

Conceptual relations can be divided into three groups:

• Semantic relations explicate the meaning of the concept;
• Pragmatic relations display the intentionality of the concept;
• Syntactic relations form the (symbolic) denotat of the concept.

Let us consider some basic inner relations in conceptual spaces.

A concept C is more abstract than a concept D if the properties that define the concept C form a part of the properties that define the concept D.

For instance, the concept tree is more abstract than the concept pine. The concept number is more abstract than the concept natural number. The concept feeling is more abstract than the concept love.

Proposition 1.

The relation “to be more abstract” is transitive.

A concept C is more general than a concept D if the denotat of the concept D is a subset of the denotat of the concept C.

For instance, the concept real number is more general than the concept whole number.

Proposition 2.

The relation “to be more general” is transitive.

Often, but not always, more general concepts are also more abstract. For instance, the concept tree is more abstract and more general than the concept pine. At the same time, the concept real number is more general than the concept whole number, but it is not more abstract than the concept whole number. Both concepts are situated on the same level of abstraction. In a similar way, the concept feeling is more abstract than the concept love, but it is not more general than the concept love.

5. Conclusions

Explicating and exploring the relational structure of conceptual spaces, here we formally described and studied only the most popular relations between concepts. Derivation of a more complete picture of conceptual spaces is the goal of further studies.

Another important direction of the research in this area is the study of existing operators and the creation of new operators in structural conceptual spaces forming, in such a way, conceptual algebras.