Development of Control Circuit for Inductive Levitation Micro-Actuators †
Abstract
:1. Introduction
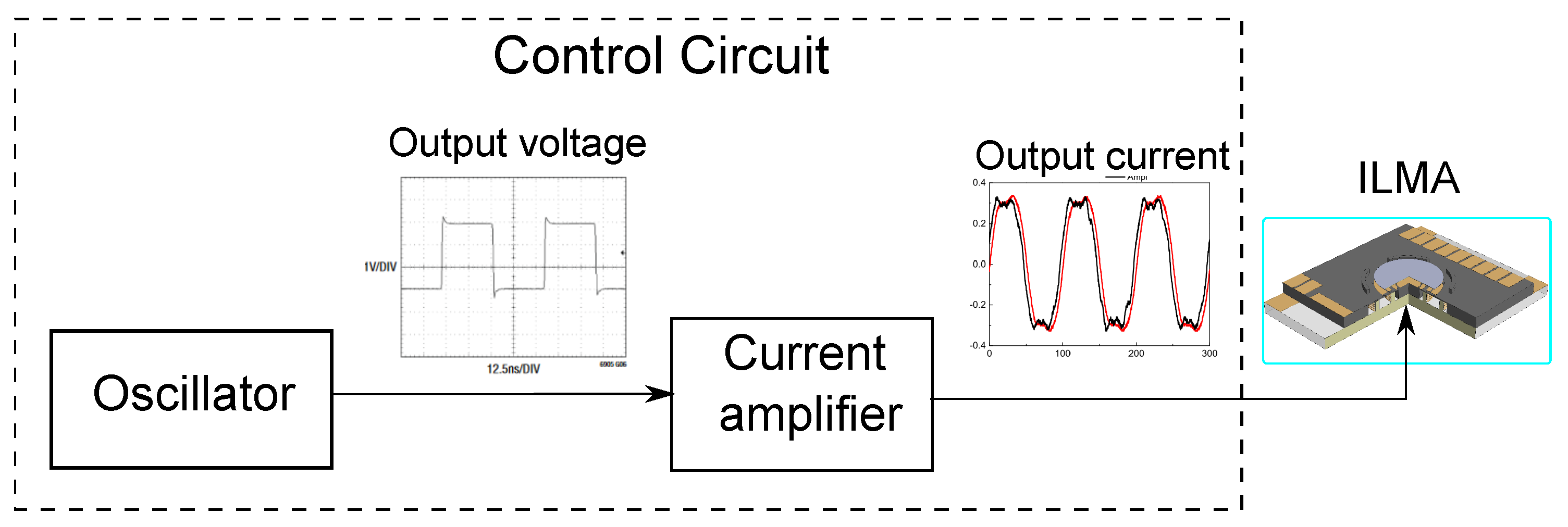
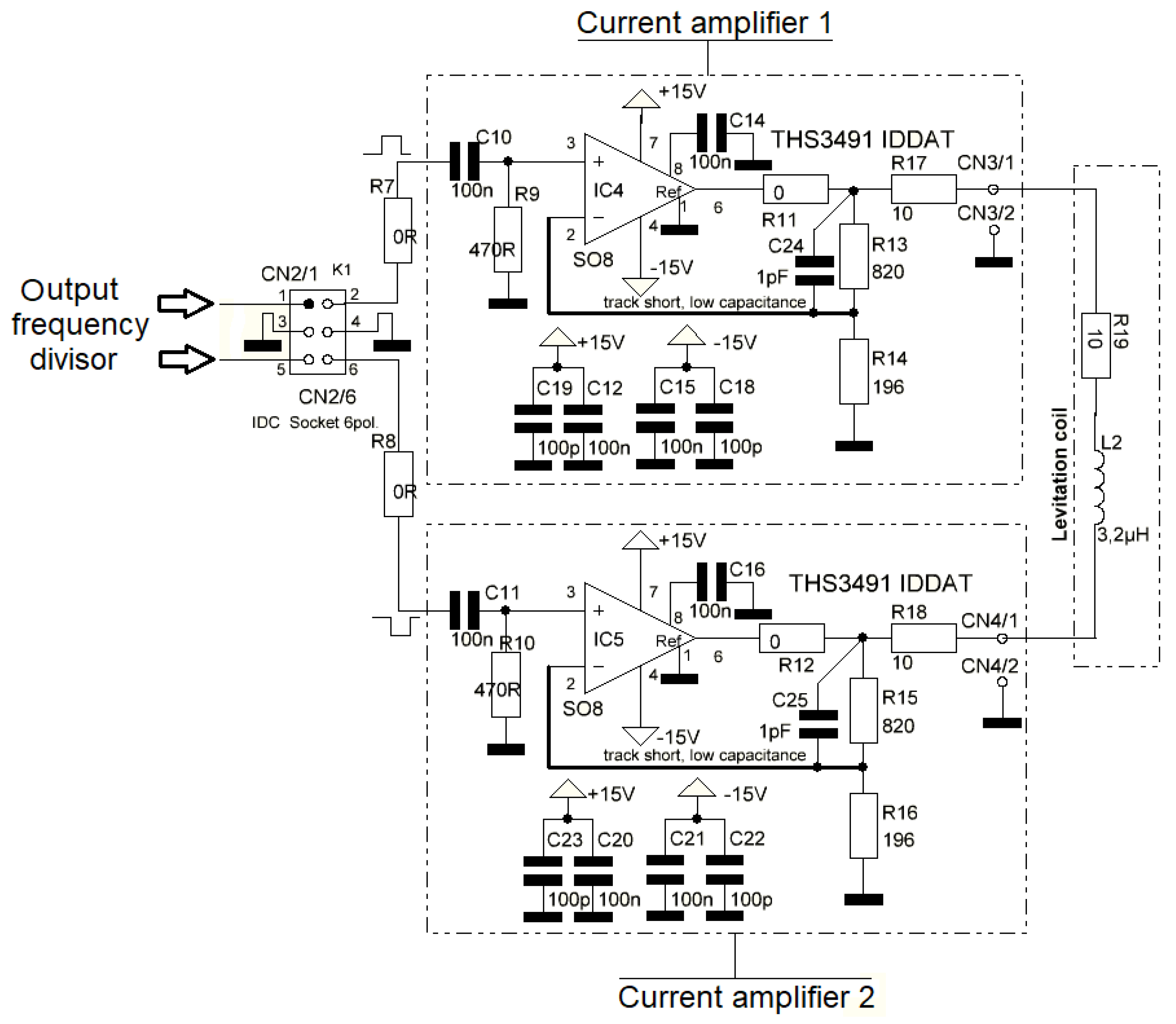
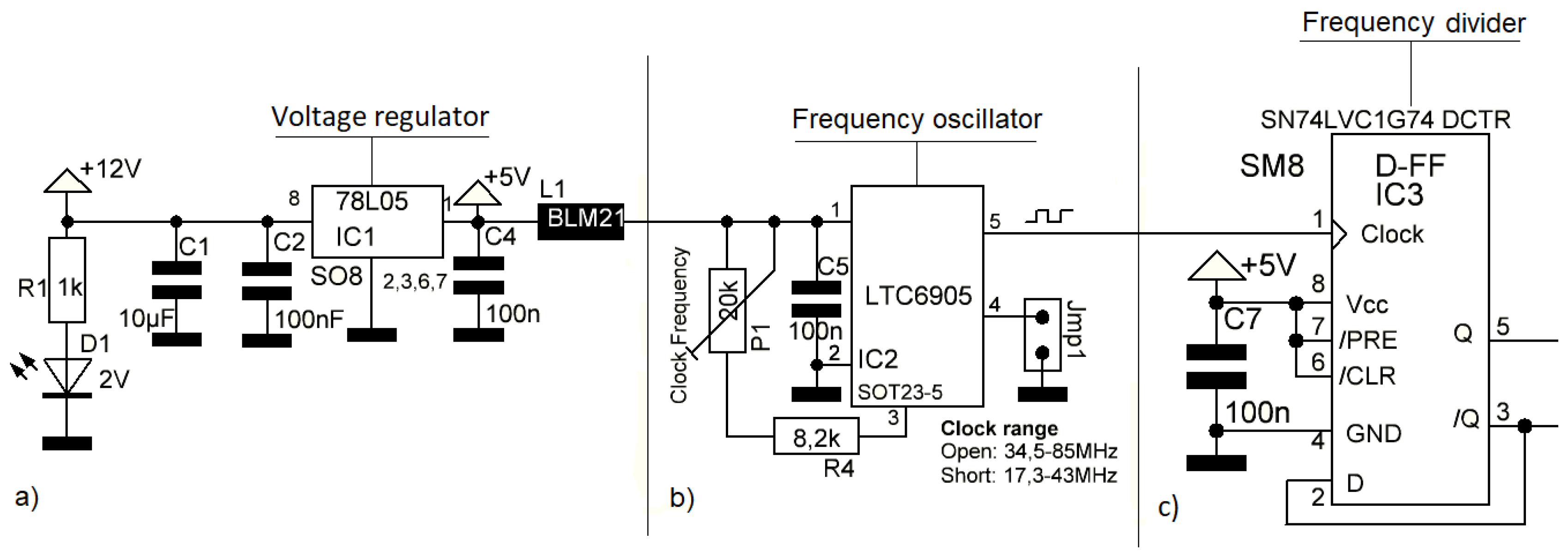
2. Development of Control Circuit
- High frequency output voltage suppler from 0 to 40 Vpp;
- High frequency current (maximum peak to peak) from 0 to 400 mA;
- Rectangular waveform of the current;
- Frequency operation range from 8.4 to 40 MHz.
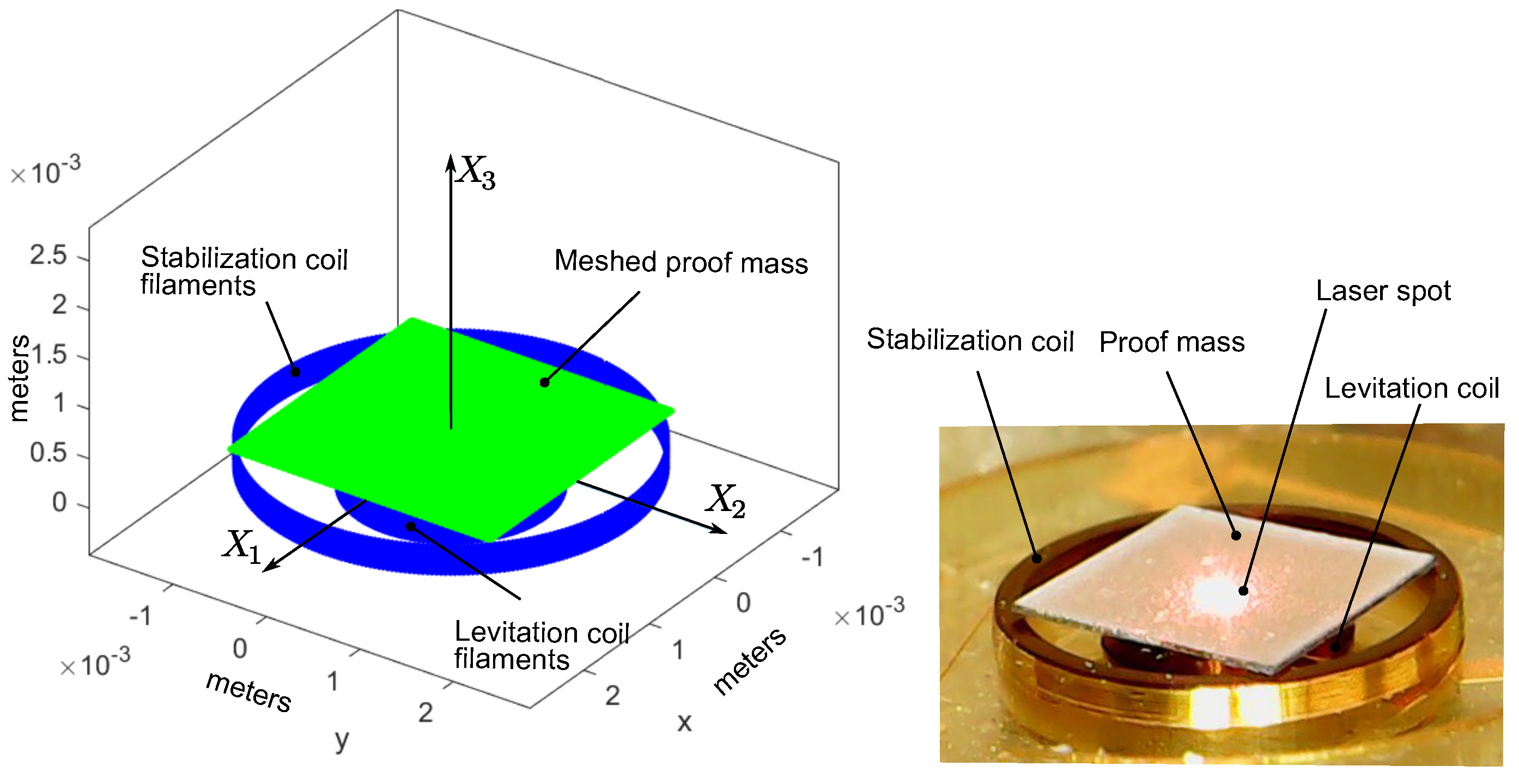
2.1. Experimental Setup
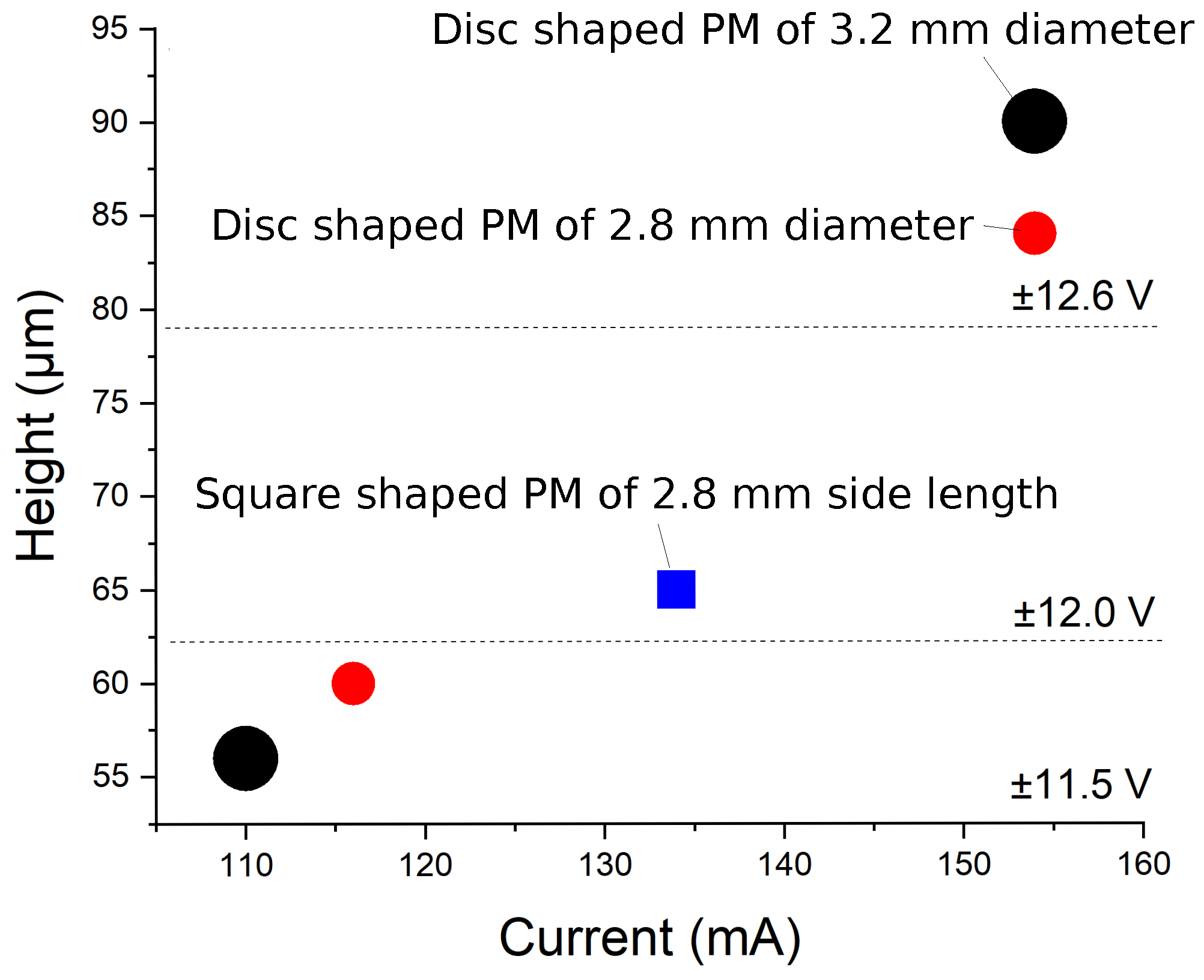
3. Simulation
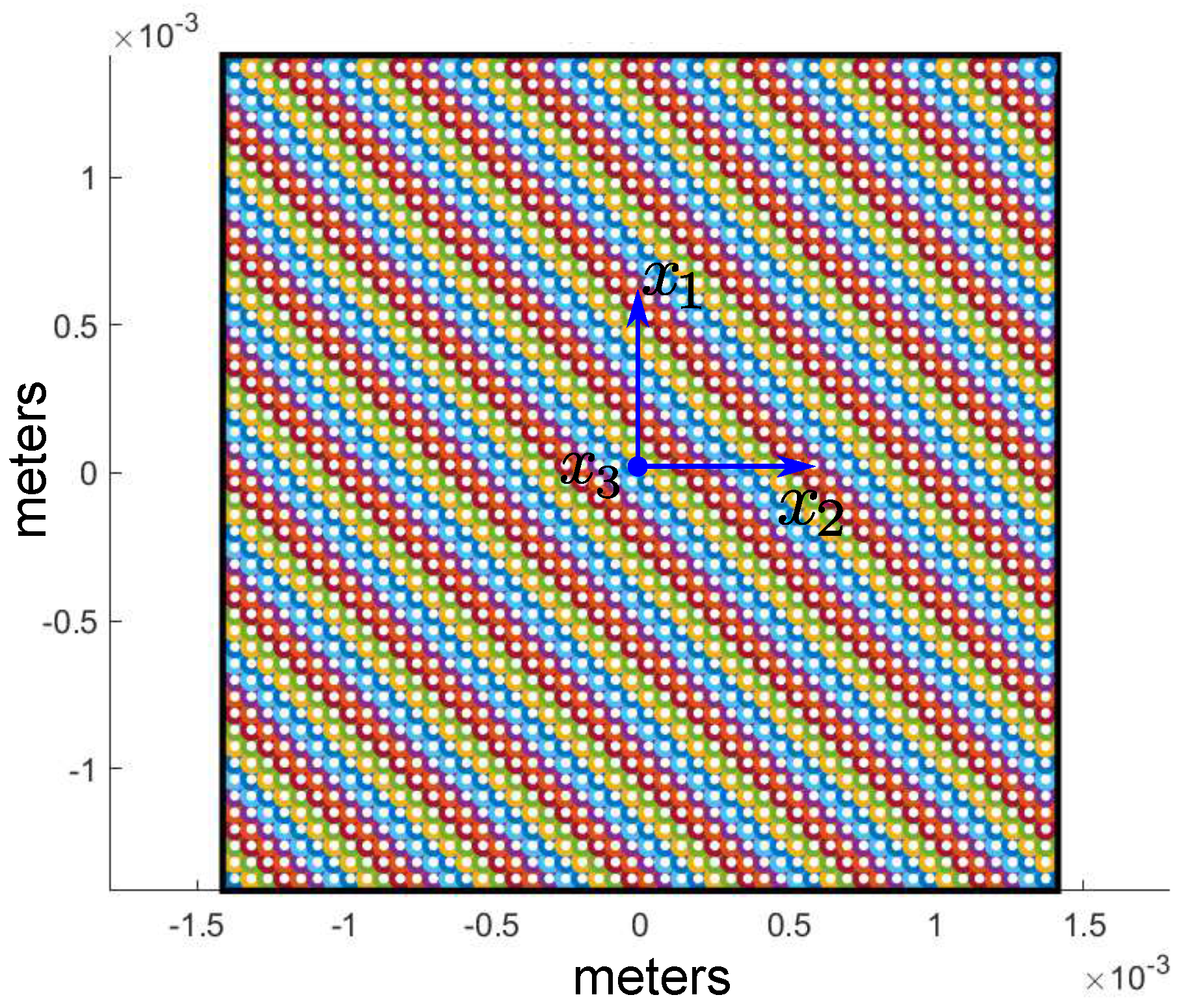
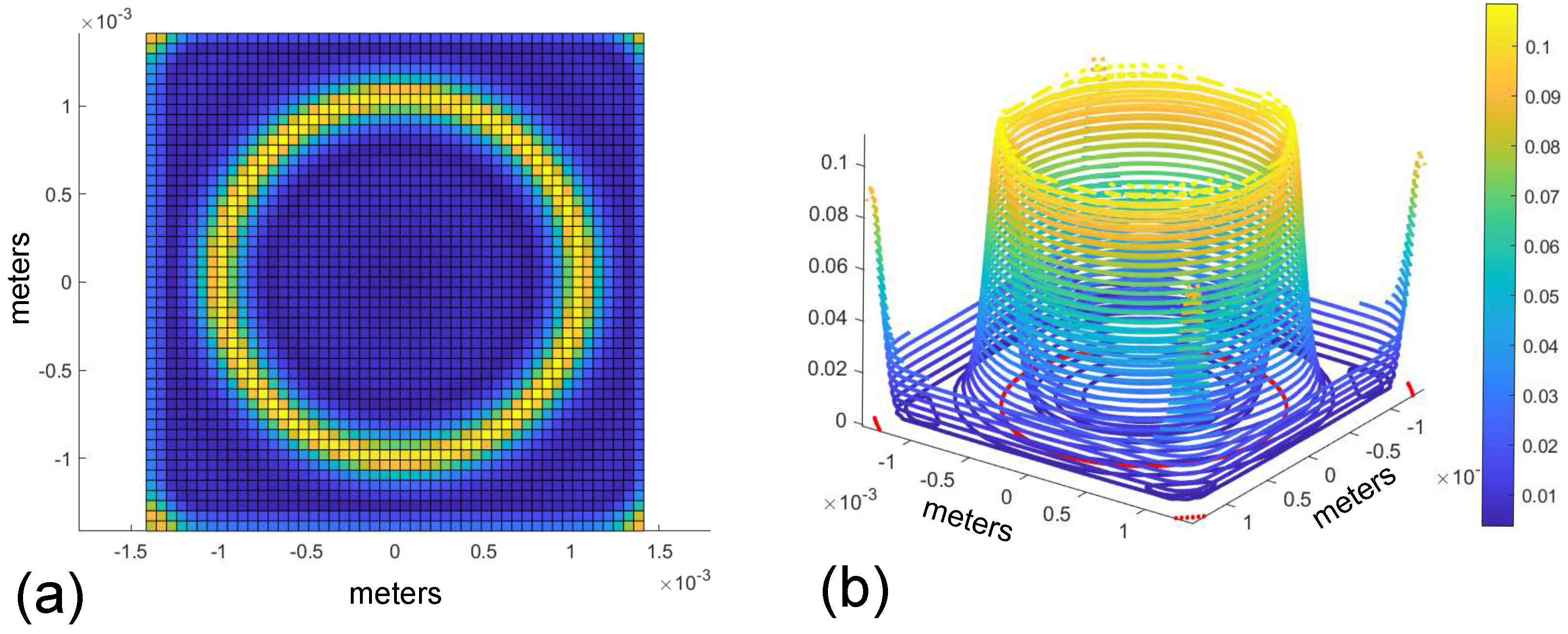
3.1. Simulation of Induced Eddy Current within the Proof Mass
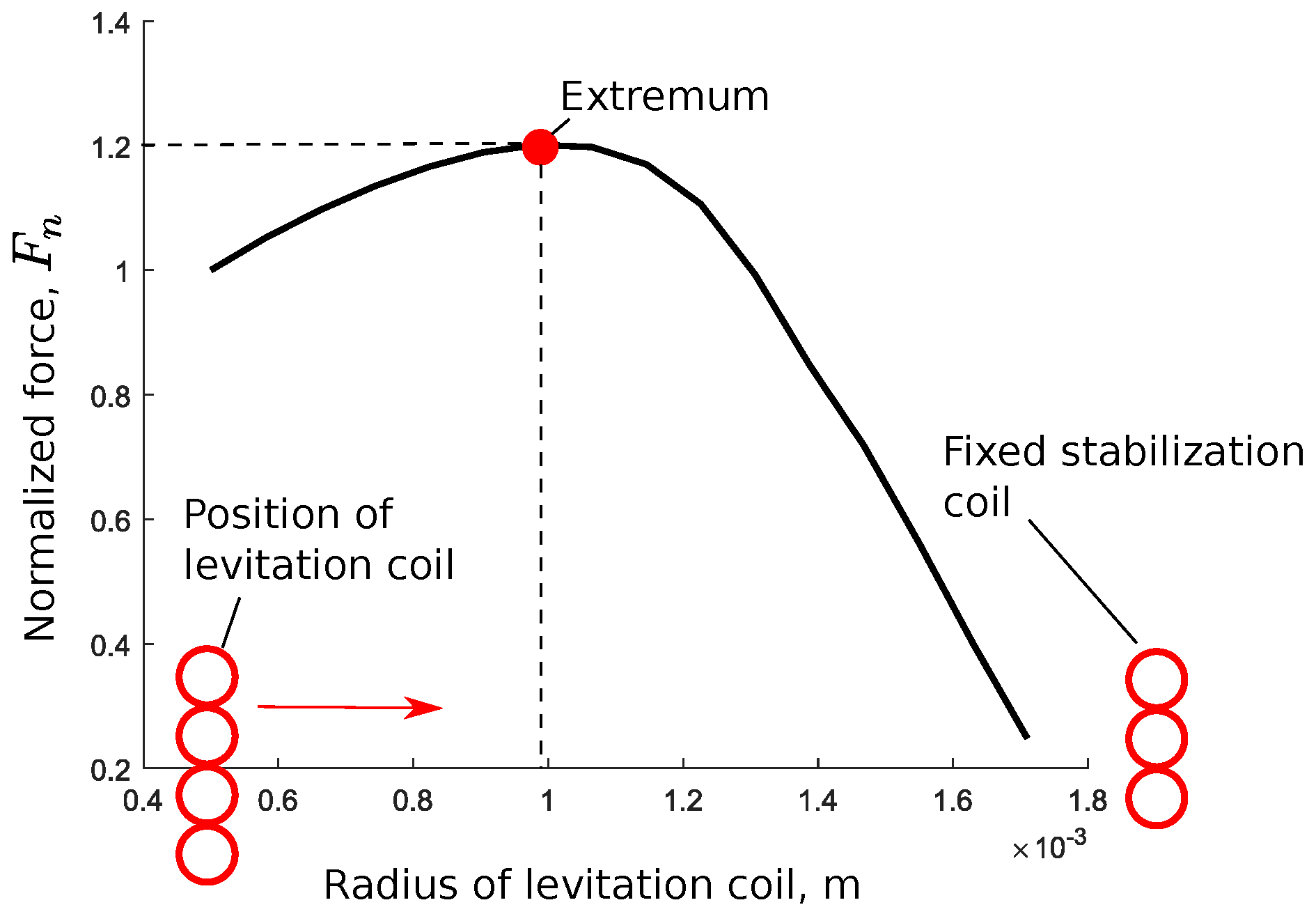
3.2. Levitation Force
4. Conclusions
5. Materials
- Voltage regulator, chip 78L05 IC1 (National Semiconductors, Danbury, CT, USA) [28];
- Frequency oscillator, chip LTC6905 (Linear Technology, Milpitas, CA, USA) [29];
- Frequency divider, chip D-FF-IC3 (Texas Instruments, Dalas, TX, USA) [30];
- High-power output current feedback amplifier THS3491 (Texas Instruments, Dalas, TX, USA) [31].
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ILMA | Inductive Levitation Micro-Actuator |
| PM | Proof Mass |
| MLMA | Magnetic Levitation Micro-Actuator |
| ELMA | Electric Levitation Micro-Actuator |
References
- Jin, J.; Yih, T.C.; Higuchi, T.; Jeon, J.U. Direct electrostatic levitation and propulsion of silicon wafer. IEEE Trans. Ind. Appl. 1998, 34, 975–984. [Google Scholar] [CrossRef]
- Murakoshi, T.; Endo, Y.; Fukatsu, K.; Nakamura, S.; Esashi, M. Electrostatically levitated ring-shaped rotational gyro/accelerometer. Jpn. J. Appl. Phys. 2003, 42, 2468–2472. [Google Scholar] [CrossRef]
- Han, F.T.; Liu, Y.F.; Wang, L.; Ma, G.Y. Micromachined electrostatically suspended gyroscope with a spinning ring-shaped rotor. J. Micromech. Microeng. 2012, 22, 105032. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Asadollahbaik, A.; Kampmann, R.; Korvink, J.G. Levitating Micro-Actuators: A Review. Actuators 2018, 7, 17. [Google Scholar] [CrossRef]
- Coombs, T.A.; Samad, I.; Ruiz-Alonso, D.; Tadinada, K. Superconducting micro-bearings. IEEE Trans. Appl. Supercond. 2005, 15, 2312–2315. [Google Scholar] [CrossRef]
- Lu, Z.; Poletkin, K.; den Hartogh, B.; Wallrabe, U.; Badilita, V. 3D micro-machined inductive contactless suspension: Testing and modeling. Sens. Actuators Phys. 2014, 220, 134–143. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Lu, Z.; Moazenzadeh, A.; Mariappan, S.G.; Korvink, J.G.; Wallrabe, U.; Badilita, V. Polymer Magnetic Composite Core Boosts Performance of Three-Dimensional Micromachined Inductive Contactless Suspension. IEEE Magn. Lett. 2016, 7, 1–3. [Google Scholar] [CrossRef]
- Shearwood, C.; Williams, C.B.; Mellor, P.H.; Chang, K.Y.; Woodhead, J. Electro-magnetically levitated micro-discs. In Proceedings of the IEE Colloquium on Microengineering Applications in Optoelectronics, London, UK, 7–27 February 1996; pp. 6/1–6/3. [Google Scholar] [CrossRef]
- Xiao, Q.; Wang, Y.; Dricot, S.; Kraft, M. Design and experiment of an electromagnetic levitation system for a micro mirror. Microsyst. Technol. 2019, 25, 3119–3128. [Google Scholar] [CrossRef]
- Shearwood, C.; Ho, K.Y.; Williams, C.B.; Gong, H. Development of a levitated micromotor for application as a gyroscope. Sens. Actuators A Phys. 2000, 83, 85–92. [Google Scholar] [CrossRef]
- Su, Y.; Xiao, Z.; Ye, Z.; Takahata, K. Micromachined Graphite Rotor Based on Diamagnetic Levitation. IEEE Electron. Device Lett. 2015, 36, 393–395. [Google Scholar] [CrossRef]
- Garmire, D.; Choo, H.; Kant, R.; Govindjee, S.; Sequin, C.; Muller, R.; Demmel, J. Diamagnetically levitated MEMS accelerometers. In Proceedings of the TRANSDUCERS 2007—2007 International Solid-State Sensors, Actuators and Microsystems Conference 2007, Lyon, France, 10–14 June 2007; pp. 1203–1206. [Google Scholar]
- Dieppedale, C.; Desloges, B.; Rostaing, H.; Delamare, J.; Cugat, O.; Meunier-Carus, J. Magnetic bistable micro-actuator with integrated permanent magnets. Proc. IEEE Sens. 2004, 1, 493–496. [Google Scholar]
- Abadie, J.; Piat, E.; Oster, S.; Boukallel, M. Modeling and experimentation of a passive low frequency nanoforce sensor based on diamagnetic levitation. Sens. Actuators A Phys. 2012, 173, 227–237. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Lu, Z.; Wallrabe, U.; Korvink, J.G.; Badilita, V. A qualitative technique to study stability and dynamics of micro-machined inductive contactless suspensions. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 528–531. [Google Scholar] [CrossRef]
- Sari, I.; Kraft, M. A MEMS Linear Accelerator for Levitated Micro-objects. Sens. Actuators A Phys. 2015, 222, 15–23. [Google Scholar] [CrossRef]
- Poletkin, K.; Lu, Z.; Wallrabe, U.; Badilita, V. A New Hybrid Micromachined Contactless Suspension With Linear and Angular Positioning and Adjustable Dynamics. J. Microelectromech. Syst. 2015, 24, 1248–1250. [Google Scholar] [CrossRef]
- Xu, Y.; Cui, Q.; Kan, R.; Bleuler, H.; Zhou, J. Realization of a Diamagnetically Levitating Rotor Driven by Electrostatic Field. IEEE/ASME Trans. Mechatron. 2017, 22, 2387–2391. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, J.; Bleuler, H.; Kan, R. Passive diamagnetic contactless suspension rotor with electrostatic glass motor. Micro Nano Lett. 2019, 14, 1056–1059. [Google Scholar] [CrossRef]
- Chen, X.; Keskekler, A.; Alijani, F.; Steeneken, P.G. Rigid body dynamics of diamagnetically levitating graphite resonators. Appl. Phys. Lett. 2020, 116, 243505. [Google Scholar] [CrossRef]
- Kratt, K.; Badilita, V.; Burger, T.; Korvink, J.; Wallrabe, U. A fully MEMS-compatible process for 3D high aspect ratio micro coils obtained with an automatic wire bonder. J. Micromech. Microeng. 2010, 20, 015021. [Google Scholar] [CrossRef]
- Lu, Z.; Poletkin, K.; Wallrabe, U.; Badilita, V. Performance Characterization of Micromachined Inductive Suspensions Based on 3D Wire-Bonded Microcoils. Micromachines 2014, 5, 1469–1484. [Google Scholar] [CrossRef]
- Poletkin, K.; Lu, Z.; Wallrabe, U.; Korvink, J.; Badilita, V. Stable dynamics of micro-machined inductive contactless suspensions. Int. J. Mech. Sci. 2017, 131–132, 753–766. [Google Scholar] [CrossRef]
- Poletkin, K. Static Pull-in Behavior of Hybrid Levitation Micro-Actuators: Simulation, Modelling and Experimental Study. arXiv 2020, arXiv:2001.09428. [Google Scholar]
- Poletkin, K.V. Levitation Micro-Systems: Applications to Sensors and Actuators, 1st ed.Springer: Berlin/Heidelberg, Germany; p. 145. [CrossRef]
- Poletkin, K.V.; Korvink, J.G. Efficient calculation of the mutual inductance of arbitrarily oriented circular filaments via a generalisation of the Kalantarov-Zeitlin method. J. Magn. Magn. Mater. 2019, 483, 10–20. [Google Scholar] [CrossRef]
- Lu, Z.; Jia, F.; Korvink, J.; Wallrabe, U.; Badilita, V. Design optimization of an electromagnetic microlevitation System based on copper wirebonded coils. In Proceedings of the 2012 Power MEMS, Atlanta, GA, USA, 2–5 December 2012; pp. 363–366. [Google Scholar]
- National Semiconductors. Data Sheet: LM78LXX Series3-Terminal Positive Regulators. Available online: http://users.ece.utexas.edu/~valvano/Datasheets/LM78L05.pdf (accessed on 9 October 2020).
- Linear Technologies. Data Sheet: LTC6905—17 MHz to 170 MHz Resistor Set SOT-23 Oscillator. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/6905fd.pdf (accessed on 9 October 2020).
- Texas Instruments. Data Sheet: D-FFIC3—SN74LVC1G74 Single Positive-Edge-Triggered D-Type Flip-Flop with Clear and Preset. Available online: https://www.ti.com/lit/ds/symlink/sn74lvc1g74.pdf (accessed on 9 October 2020).
- Texas Instruments. Data Sheet: THS3491—900-MHz, 500-mA High-Power Output Current Feedback Amplifier. Available online: https://www.ti.com/lit/ds/symlink/ths3491.pdf (accessed on 9 October 2020).


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlnieska, V.; Voigt, A.; Wadhwa, S.; Korvink, J.; Kohl, M.; Poletkin, K. Development of Control Circuit for Inductive Levitation Micro-Actuators. Proceedings 2020, 64, 39. https://doi.org/10.3390/IeCAT2020-08479
Vlnieska V, Voigt A, Wadhwa S, Korvink J, Kohl M, Poletkin K. Development of Control Circuit for Inductive Levitation Micro-Actuators. Proceedings. 2020; 64(1):39. https://doi.org/10.3390/IeCAT2020-08479
Chicago/Turabian StyleVlnieska, Vitor, Achim Voigt, Sagar Wadhwa, Jan Korvink, Manfred Kohl, and Kirill Poletkin. 2020. "Development of Control Circuit for Inductive Levitation Micro-Actuators" Proceedings 64, no. 1: 39. https://doi.org/10.3390/IeCAT2020-08479
APA StyleVlnieska, V., Voigt, A., Wadhwa, S., Korvink, J., Kohl, M., & Poletkin, K. (2020). Development of Control Circuit for Inductive Levitation Micro-Actuators. Proceedings, 64(1), 39. https://doi.org/10.3390/IeCAT2020-08479






