Abstract
Surface-enhanced Raman scattering (SERS) nanoprobes have shown tremendous potential in in vivo imaging. The development of single oligomer resolution in the SERS promotes experiments on DNA and protein identification using SERS as a nanobiosensor. As Raman scanners rely on a multiple spectrum acquisition, the faster imaging in real-time is required. SERS weak signal requires averaging of the acquired spectra that erases information on conformation and interaction. To build spectral libraries, the simulation of measurement conditions and conformational variations for the nucleotides relative to enhancer nanostructures would be desirable. In the molecular dynamic (MD) model of a sensing system, we simulate vibrational spectra of the cytosine nucleotide in FF2/FF3 potential in the dynamic interaction with the Au20 nanoparticles (NP) (EAM potential). Fourier transfer of the density of states (DOS) was performed to obtain the spectra of bonds in reaction coordinates for nucleotides at a resolution 20 to 40 cm−1. The Au20 was optimized by ab initio DFT GGA and relaxed by MD. The optimal localization of nucleotide vs. NP was defined and spectral modes of both components vs. interaction studied. Bond-dependent spectral maps of nucleotide and NP have shown response to interaction. The marker frequencies of the Au20—nucleotide interaction have been evaluated.
1. Introduction
Sensing and analysis of DNA sequences and epigenetic structure modifications in the human genome are essential for the understanding of the mechanism of gene expression in cells and the development of diseases. Efforts to detect and map DNA sequences and modifications with 2D materials such as graphene and hexagonal BN had been made and utilized a number of methods: Nanopore-based ionic and transverse current, bonding to complimentary molecules in nanopores and STM. Development of the surface-enhanced and tip-enhanced Raman spectroscopy (SERS and TERS) [1,2,3,4,5] with nanoscale resolution [6,7,8,9] applicable to single biomolecule [10,11] analysis as well as stimulated Raman scattering and ultrafast two-dimensional infrared (2D-IR) spectroscopy of small organic molecules [11,12,13,14] opens a way to identify molecular structures in a label-free way and investigate mechanisms of interaction with the environment in biomolecules. Attention to DNA molecules in the manifold of applications, from sequencing, epigenetic studies, disease relation, etc., to nano-biostructures, makes identification of nucleotides and bases in a variety of states highly desirable in the non-contact label-free way of nanophotonic vibrational spectroscopy. SERS is a promising method for nucleic acid and protein detection. In terms of its abundant fingerprint information, anti-interference with water, and extraordinarily high sensitivity, SERS holds many attractive advantages over other techniques.
Another path to the identification of small organic molecules, such as nucleotides, can employ interaction with a nanopore in a 2D solid film, especially graphene [15,16,17,18,19,20,21,22,23], though experiments and calculations with hexagonal BN were also carried out [24,25,26,27]. The detection of the DNA/RNA mononucleotides [28,29,30] and nucleobases [31] with SERS techniques has been done as well. Despite many advantages and simplicity of the 2D nanopore sequencing, a few issues [16] remain to be resolved, including controlling the DNA translocation rate, suppressing stochastic nucleobase motions, and determining the signal overlap between different nucleobases. The graphene-based nanopores suffer from significant signal noises due to graphene hydrophobicity and trapping of DNA bases during translocation [32]. Study of the influence of the interaction force between the nucleobases and graphene nanopore on translocating molecules helps to find a solution to some of the mentioned issues.
Surface-enhanced Raman scattering (SERS) using plasmonic metal nanoparticles has been applied to characterize complex biological samples, ranging from biomacromolecules such as nucleic acids and proteins to living eukaryotic and prokaryotic cells in whole animals for several decades now. The sensitivity of the SERS signal with respect to interactions at the surface of the plasmonic nanoparticles makes it specifically useful for studies of molecular contacts of nanoparticles in biological systems
In order to design and simulate the system that would let single molecule selection and detection of its state by high-resolution SERS methods, we try to predict direction and possible range of spectral changes in the interacting molecule–SERS enhancer systems. The placement or growth of the small Au nanoparticle at the edge of the graphene nanopore is considered. Plasmonic enhancement by the Au NP will make the vibrational signal measurable while graphene nanopores would allow for control localization and transient conformation of passing DNA nucleotide, strand fragment, or protein. Interaction at the Van der Waals interaction distances with both components, graphene and metal NP, has high probability to change the vibrational spectral maps of the passing molecules. The vibrational mode changes in nucleotides with respect to interaction with graphene were shown in molecular dynamic (MD) simulation to be present at short distances in our previous calculations. At present, the estimation of influence of the small Au nanoparticle on the vibrational spectral modes of the cytosine nucleotide is attempted to be clarified in MD calculations as a model of nucleotide–Au NP interaction. If the spectral modes of both components of interaction are studied relative to localization and molecule conformation, changes in nucleotide spectra due to interaction conditions can be mapped into a kind of library. We do the initial steps by clarifying the possibility of such mapping. Bond-dependent spectra of nucleotide and NP are tested on their response to interactions to reveal the marker frequencies of the Au20–nucleotide interaction.
2. Model and Methods
The present study considers the MD approach to the identification of nucleotides in interactions with the nanopore environment for vibrational spectroscopy. The nucleotide vibrational frequencies we obtained have been attributed to stretching, bending, or ring-breathing modes. By comparison of nucleobase spectra with the ones of nucleotides, the presence of the 2′-deoxyribose in the nucleotides can be separated into spectral mapping and mode relaxation. The vibrational density of states is calculated in the transient regime during passing time through the graphene nanopore for each atom of the molecule to resolve the difference in the structure of nucleotides. In dynamics, the vibrational spectra are being evaluated from MD propagation velocities computed in the anharmonic interaction potential, in graphene, and the molecule, with the LJ potential between them. Fourier transfer I(f) of the velocity autocorrelation function G(τ) is as follows:
where is the duration of correlation, is the velocity of the atom at time , and is the velocity of the atom during correlation time. According to the Wiener–Khinchin theorem, defines the vibrational density of states (DOS) of the system. The potential used for DNA nucleotides is MM2/MM3 force field potential [33]. We investigate the transient interaction with graphene modelled by REBO potential [34] and the molecule-graphene interaction for C-X (X = H, O, C, N) by the LJ potential [33]. The interaction causes a shift in some frequencies of vibrations of the nucleotide DOSes. The vibrational spectra in MD exhibit shifts and intensity changes due to interaction with the environment that causes intramolecular vibrational mode dynamics.
The calculation setup is presented in Figure 1. The graphene sheet with the 1.5 nm in diameter pore at its center is shown in two projections, at the top and front view, with a location of the nucleotide molecule relative to the pore plane and center. The graphene sheet is oriented in the x-y-plane, the edges along the y-axis are fixed, and the edges along the x-axis are free. The nucleotide can move with a given fixed velocity of the center of mass (vc.o.m.) in the positive z-direction that reproduces the motion of DNA fragments through the pores [35,36] in a driving constant electric field in experimental setups. The vc.o.m. is optimized to enhance the interaction force between the nucleotide and edge of graphene pore and reduce rotation of the nucleotide in the translocation as much as possible. All atoms of the system except fixed ones are thermally relaxed to the temperatures Tgraphene = 300 K and Tnucleotide = 30 °C, as in Figure 1, before sampling. In the translocation process, the single-layer graphene sheet interacts with nucleotides in graphene nanopore. Graphene affects the interaction field of the passing molecule close to the pore edge. The graphene-molecule C-X (X = H, O, N, C) potential is considered as a VdW one to avoid bond creation and nucleotide attachment to the pore.
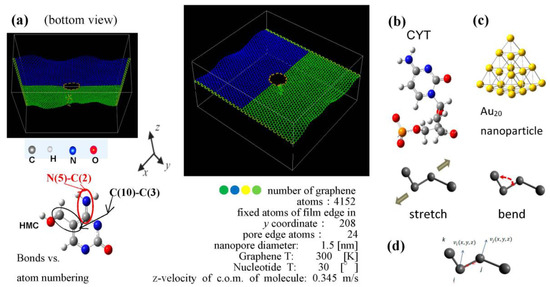
Figure 1.
(a) The structure and initial position of cytosine nucleotide relative to the graphene pore. The spatial orientation of the nucleotide’s cyclic plane is at 30° to the z-x plane. Atoms are shown: C in grey, N in blue, O in red, and H in light grey. (b) Initial configuration of cytosine (right), Hydroxymethylcytosine (HMC) base is shown on the left as an example of corresponding atom numbering for bonds in molecular dynamic (MD) calculations. (c) Optimized by DFT GGA calculations Au20 nanoparticle. (d) Reaction coordinates for stretching and bending in velocity correlation calculation use the projections along the bonds.
The relative size and weight of the nucleotides as compared with nucleobases reduce rotational motion inside the pore [37,38,39,40] that is further controlled by translocation velocity. For the given graphene-nucleotide setup, evaluation of the vibrational spectral maps of the DNA nucleotides cytosine, thymine, adenine, and guanine has been initially done in reactive coordinates by accumulating spectra of individual atom of bonds obtained by autocorrelation functions of Equation (1). It was confirmed that the nucleotides–graphene pore interaction does not generate recognizable changes in the spectral map of graphene pore in our system. However, the conformation of the molecules responds to the interaction flexibly, exhibiting spectral changes. The center of mass (c.o.m.) of nucleotides was adjusted relative to the center of the pore along the y-axis to maximize force at the pore edge. The orientation of the cyclic planes of each type of nucleotide was selected to have the same tilt angle for comparison of spectra for variety of nucleotides interactions. An initial position of the nucleotides was chosen to be outside the interaction region in the z-direction with the tilt of the nucleobase plane taken to be 30 degrees relative to z-x-plane. The single-layer graphene was thermally equilibrated at room temperature prior to sampling. The present simulation is done in the absence of hydration in the system and hydrophobicity of graphene; therefore, the electrostatic interactions term is not included. For correlation evaluation of nucleotide spectra, the interaction time with graphene is taken at the interaction interval of the passing time through the pore. The high-resolution spectral calculations were carried out at the step size of = 0.05 fs and = 32768 steps of correlation delay for the shown states of nucleotides; in the present calculations, cytosine was used to test the system. To attribute obtained frequencies to a particular type of vibrations, such as stretching, bending, or torsion, the autocorrelation function of Equation (1) was calculated over the reaction coordinates that were taken by the projection of velocities on the bond vector, and the respective angle between these vectors as can be seen in Figure 1d. The single frequency obtained in such coordinates can be pinpointed as a corresponding to the atom of the vibrating molecule as well as to the type of vibrational mode can be pinpointed as a corresponding to the particular bond or angle. The ring-breathing modes can be identified by the same frequency present in the spectra of all bonds forming the ring. However, a low-level noise from the nearest bonds the bond studied is also present due to the way of correlation calculation. Therefore, only relatively high intensity spectral modes will be considered for evaluation.
The stability of the obtained frequencies relative to the trajectory randomization has also been tested for cytosine molecule. The 10% to 15% randomization in the initial position and velocity distributions of the cytosine nucleotide at five different calculations have shown a preliminary absence of the changes in spectra above a few percent for stretching of the X-Y (X, Y = C, N, O) bonds. Our calculation system does not include solution molecules yet.
To create calculation model that would be close to an experimental set up in a SERS type of measurement we decided to introduce a metal nanoparticle in the nucleotide-graphene of Figure 1c. The Au20 nanoparticle was pyramid-shaped and optimized in ab initio DFT GGA (density functional theory with generalized gradient approximation) calculations with the b3pw91 basis set. The size and shape of the NP was taken to be a stable configuration [41]. The obtained configuration was further relaxed by the MD calculation with the EAM potential [42] and free boundary conditions during 3000 steps with = 0.1 fs at T = 300 K to get stable nanoparticle samples that can be used separately or on the top of the graphene sheet. The potential parameters for LJ interaction with nucleotide and graphene were defined using the Lorentz–Berthelot mixing rule and based on the LJ parameters (Au − Au) = 0.039 kcal/mol, (Au − Au) = 2.9 Å [43]. The mixing is done using Van der Waals parameters of the MM2/MM3 force field potential for nucleotides. For the interaction with graphene, mixing uses the sp3 C atom parameters from the force field potential, the same values that have been applied for the nucleotide-graphene Van der Waals parameters.
The study of vibrational spectra of the nucleotides in the dynamic interaction with the metallic nanoparticles (NP) [44,45] located close to graphene nanopore can combine translocation localization and nucleotide interaction enhancement or modification due to (1) the graphene LJ interaction and (2) the Au LJ interaction. For the initial interaction of the Au20 nanoparticle with cytosine nucleotide, the Au20 NP was localized close to the cytosine initial position as it is shown in Figure 2. As the first step, both NP and cytosine had zero c.o.m. velocity. Initial orientation and distance of NP relative to nucleotide has been initially controlled to estimate vibrational spectra of both interacting part of the system.
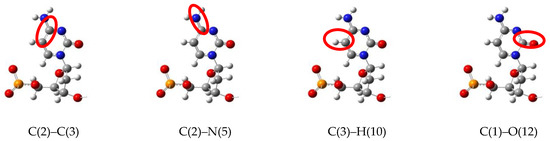
Figure 2.
Bonds in cytosine nucleotide (cytidine) for which vibrational spectra are shown below.
3. Results
The influence of interaction in the nucleotide–metal nanoparticle system is numerically modelled in MD system. Validation of the model has been done twofold: First, to obtain spectral resolution sufficient to register changes due to the LJ interaction; and secondly, to evaluate the corresponding variations in the vibrational spectra of nucleotide-nanoparticle system.
3.1. Resolution of Nucleotide Spectra
First, we have evaluated the variations in the nucleotide–graphene system at translocation. Examined spectral variations due to interaction force in the nucleobase–graphene nanopore system have pointed to the influence of the conformation on the nucleotide spectral maps [46,47]. The transient vibrational frequencies of all passing nucleotides were calculated at the same initial incident angle and shift distance from pore edge. To separate decay in the calculated data from the proper spectrum, we have extracted decay component out of calculated spectral data. Calculation of transient autocorrelation function includes relatively short interaction time during which the correlation data are accumulated. As a result of the transience of the correlation signal, the exponential function of time decay is converted by the Fourier transfer into a decaying spectral map. In order to separate decay components from the spectra itself, we propose the two-parametric exponential fitting, as follows:
The introduced exponential function was fitted by parameters either to the function’s low-frequency region (head) or high-frequency (tail) region. The exponential decay component was then subtracted from the calculated spectra. The low-frequency fitting produced better-resolved spectra above 5 THz compared with the high-frequency fitting. All calculated spectra of nucleotides that are discussed were obtained in the low-frequency fitting. The initial spectral resolution of Fourier transform that was tested was 40 cm−1.
In contrast with quantum DFT calculations of IR and Raman spectra, transient MD calculations are sensitive to the duration of correlation time and relative interaction of the structures studied. Therefore, obtained spectra should be compared with the other available calculations and experimental data. The spectral maps of nucleotides that we calculated were highly sensitive to interactions in the system. Since all nucleotide spectral maps were calculated in identical conditions of nanopore translocation, the obtained transient frequencies could be used as reference values to distinguish nucleotides from each other. Comparison with results of 2D-IR experiments and DFT calculations [48] shows a 50–80 cm−1 discrepancy between corresponding stretching C-C, C-N frequencies calculated in the MD model at 40 cm−1 resolution. The SERS data on the breathing mode [31] of nucleotides with the full width at the half maximum of the peak wavenumber being 13 and 20 cm−1 show the presence of the mode in the 660–800 cm−1 interval for nucleotides. Our single bond spectra in Appendix A exhibit presence of the bending type of mode in the above interval, different for each nucleotide; however, our resolution in the case is limited by 40 cm−1. For guanine, we obtain a bending peak at 655 cm−1 as compared to the measured [31] peak at 661 cm−1; thymine exhibits calculated 860 cm−1 peak vs. measured 795 cm−1. All measurements are held in the aqueous solution with nucleotides in proximity to the gold nanoslits or nanoparticles for enhancement of the signal. To improve our model, the resolution has been improved and the metal nanoparticle has been introduced.
The employed spectral resolution in our MD calculations has been sufficient/enough to register structural dependence of the molecular spectral map on the bond-to-bond basis. However, the 2000 cm−1 upper limit excludes the C-H and N-H bonds from the calculated frequency region. With increased resolution of IR and SERS/TERS SM spectroscopy [31,49], ab initio MD (AIMD) calculations of the chemical bonding effect in SERS [50,51,52], the information on vibrational mode variations due to interaction with environment, which could be hydration changes or Van der Waals interaction with graphene pore, should be available in MD calculations as well. The approximation of MM2/MM3 potential used for nucleotides cannot allow the estimation of dipole moment and polarizability changes with the environment that are calculated in DFT and AIMD spectra. However, transient dynamics sample a sufficient number of states that constitute several periods of vibrations. The coupled anharmonic bonding is also present in used MD potentials. To extend the spectral range up to 4000 cm−1, we considered sampling resolution in real space over interaction potential by decreasing of ∆t and in reciprocal space by extending the number of time steps [53].
The time step of 0.05 fs and 32,768 steps has given the resolution of vibrational modes at ∆f = 20 cm−1 and up to 4000 cm−1. The ∆f = 20 cm−1 spectral resolution is comparable to the 15 cm−1 half-width of Lorentzian function that is used to broaden Raman spectral lines in DFT calculation [45]. As compared with the typical sampling timescale of the SERS and TERS techniques being a few microseconds, the typical time scale of the plasmon excitation of the metal enhancer system relates to the scale of 100 fs and the coupling between the electronic and vibrational degrees of freedom is on the time scale of 0.1–0.5 ps. Therefore, interaction and conformation-dependent single molecule measurements and calculations should concentrate on the time scale of few vibrational periods that we presently cover with a 1.64 ps time interval. Experimentally, nanophotonic probing of the acoustic phonon propagation has been achieved now at the ps timescale [52]. Only the highest peaks in the spectrum are considered as modes in our case. In spectral calculations, the increase in the spectral range resolution simultaneously causes a noise connected to the time step reduction as a consequence of Fourier transfer. The source of the noise is twofold at short time step: (1) The velocity projection on the bond vectors starts to resolve traces of vibrations related to nearest bonds connected by the atom and (2) the FFT procedure in spectra calculations can produce the low intensity side lobes of the signal peaks that are not smoothed out with window functions in order not to lose spectral information on essential modes.
3.2. Interaction between Metal Clusters and Nucleotides
In order to confirm effect of the LJ interaction on the vibration spectra of in the nucleotide–Au20 nanoparticle system, the Au20 NP was placed into an already-tested graphene–nucleotide system close to initial nucleotide position as shown in Figure 3a. Cytosine nucleotide’s vibrational spectra have been estimated for its base bonds circled in Figure 2 in red. To exclude the interaction with the graphene sheet at initial stage, the distance from the graphene was out of range of the LJ interaction. The initial orientation of the NP relative to cytosine nucleotide at the 4 Å distance between the tip of NP and atoms of nucleotide was selected to keep LJ interaction at a relatively weak level. Figure 4 compares vibrational spectra of the bonds C(2)–C(3), C(2)–N(5), C(3)–H(10), C(1)–O(12) in the absence and presence of Au20 NP. Explicit changes in modes due to interaction are shown with vertical arrows ↓ in each case.
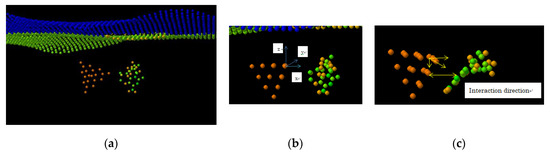
Figure 3.
(a) System of Au20 nanoparticle and cytosine nucleotide vs. graphene sheet in initial Au20 NP orientation where interaction is localized primarily within the tip atom of the Au20 pyramid; (b) rotated NP with the upper plane of the pyramid parallel to the graphene (x,y) plane and interaction with the edge atoms of the Au20 pyramid enhanced; (c) interaction direction of nucleotide with NP changes during nucleotide conformation and alignment at the vibration time. Calculations have been first carried out with the initial vcom = 0 in x,y,z directions for cytosine and NP.
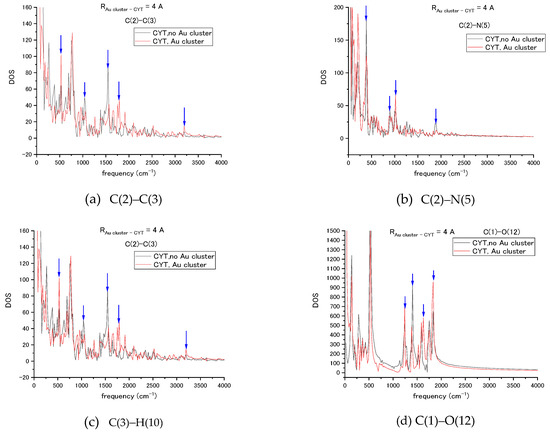
Figure 4.
Vibrational spectra of the cytosine bonds (a) C(2)–C(3), (b) C(2)–N(5), (c) C(3)–H(10), and (d) C(1)–O(12) in the absence and presence of interaction with the Au20 NP. Changes in spectra such as mode shifts and large amplitude changes are marked by vertical arrows.
In the C(2)–C(3) case, there are changes in bending and twisting at 500–1000 [cm−1] frequency range. On the interval 1300–2000 [cm−1], the stretch mode is blue shifted due to interaction with NP, so it is attributed to the breathing mode of the nucleotide base. In the C(2)–N(5) bond, the changes in modes related to bending and twisting can be also seen, the amplitude of breathing mode is very weak, and the C-N stretching mode has no shift but only an increase in amplitude. The C(3)–H(10) bond has changes in C-H bending and stretching modes at the 1000–2000 [cm−1] interval. For the C(1)–O(12) bond, the largest changes are in breathing and its stretching modes at the 1300–2000 [cm−1] range. Interaction with the nanoparticle modifies transient vibrational frequencies of cytosine at ps interval in our MD simulation.
For the Au20 NP, the vibrational spectra were also estimated for individual atoms in Cartesian coordinates. Figure 5 exhibits the spectra of the tip atoms in the pyramid in the absence of interaction in x, y, and z coordinates with the basic 188 cm−1 cluster mode for all tip atoms that can be a mode characterising the whole Au20 nanoparticle. Comparing results in Figure 5, it can be seen that the closer to the nucleotide, the stronger the influence. In addition, it can be seen that there is an even greater effect between 4190 and 4196. Obtained spectra relate to a single orientation of the NP vs. nucleotide. Change in NP orientation would lead to variation in LJ interaction strength and subsequent changes in vibration spectrum.
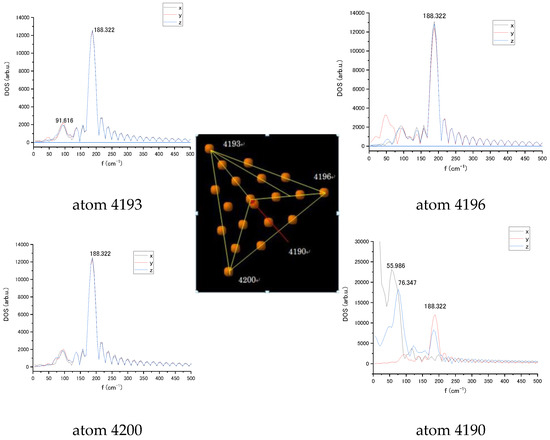
Figure 5.
Vibrational spectra of the tip atoms of Au20 nanoparticle numbered 4190, 4193, 4196, and 4200 in x, y, and z coordinates without interaction with the cytosine.
The Au NP has then been rotated as seen in Figure 3b,c. The upper plane of the pyramid was moved to be in the (x,y) plane and z-axis rotation placed the 4 atoms of edge of the pyramid into the LJ interaction proximity to the nucleotide. Figure 3c shows the animation snapshot after rotation, and Figure 6 shows the spectral change in 4196 atom’s modes after rotation. The vibrational spectra of the interacting with cytosine single atom (4196) of Au20 nanoparticle contrast with the spectra of rotated NP with edge interaction (Figure 6a,b). A strong amplitude enhancement is seen for the frequencies 76 and 81 cm−1 in y and z direction as a result of the change in the LJ interaction. The interaction with the nucleotide causes a slight movement of the NP, which can be reflected in the appearance of the low-frequency modes. For relatively large spherically shaped Au nanoparticles, a typical Raman band over the range of 300–900 cm−1 was observed experimentally.
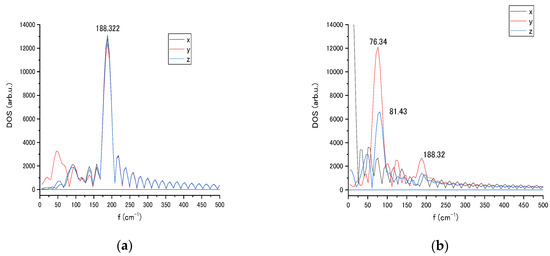
Figure 6.
Vibrational spectra of the interacting tip atom (4196) of Au20 nanoparticle in x, y, and z coordinates at initial (a) and rotated (b) orientation relative to cytosine localization.
4. Discussion
In perspective of existing experimental studies of single-molecule SERS of DNA and proteins [54,55], researchers gradually develop methods to characterize single biological molecule with Raman spectra at the time scale of interaction with environment and other molecules and structures. The simulation methods can create spectral libraries for vibrations of molecular species vs. different types of interaction to specify the type and strength of interaction. The findings presented in the current research prove the applicability of MD simulation for transient vibrational spectra of biomolecular building blocks such as nucleotides or amino acids. The obtained vibrational spectra are sensitive enough to reflect even weak Van der Waals interactions in the few component systems studied. Testing of the current method for protein fragments and conformations is considered.
Author Contributions
Conceptualization, methodology, software development, validation, supervision T.Z.; data curation, M.Y. and S.I.; writing—original draft preparation, review, and editing, T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
T.Z. gratefully acknowledges the technical assistance in the nucleotide calculations and preparation of the results of Appendix A done by H. Mizuguchi and T. Kitani. All calculations were performed at Applied Mechano-Informatics Laboratory in Toyama University.
Conflicts of Interest
The authors declare no conflict of interest.
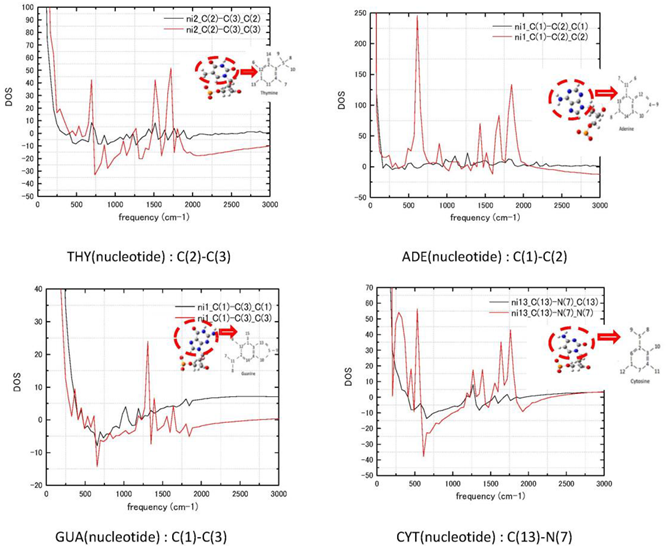
Appendix A
Stretching spectra of adenine, guanine, thymine C(1)–C(2)–C(3) bonds for atoms in hexagonal ring of the base, C(13)–N(7) stretching frequencies of cytosine in the base -to- 2′-deoxyribose bond, see numbering in the inserted scheme of each base. Red and black colours mark i-j bond from i and j side. Atoms at the side of the bond are written after the bond: X-Y X.
References
- Stöckle, R.M.; Suh, Y.D.; Deckert, V.; Zenobi, R. Nanoscale chemical analysis by tip-enhanced Raman spectroscopy. Chem. Phys. Lett. 2000, 318, 131–136. [Google Scholar] [CrossRef]
- Hayazawa, N.; Inouye, Y.; Sekkat, Z.; Kawata, S. Metallized tip amplification of near-field Raman scattering. Opt. Commun. 2000, 183, 333–336. [Google Scholar] [CrossRef]
- Anderson, M.S. Locally enhanced Raman spectroscopy with an atomic force microscope. Appl. Phys. Lett. 2000, 76, 3130–3132. [Google Scholar] [CrossRef]
- Knoll, B.; Keilmann, F. Near-field probing of vibrational absorption for chemical microscopy. Nature 1999, 399, 134–137. [Google Scholar] [CrossRef]
- Taubner, T.; Keilmann, F.; Hillenbrand, R. Nanomechanical Resonance Tuning and Phase Effects in Optical Near-Field Interaction. Nano Lett. 2004, 4, 1669–1672. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhan, L.; Hou, C.; Wang, Z. Nanostructured Metal-Enhanced Raman Spectroscopy for DNA Base Detection. IEEE Photonics J. 2012, 4, 1333–1339. [Google Scholar]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef]
- Saha, K.; Agasti, S.S.; Li, C.K.X.N.; Rotello, V.M. Gold Nanoparticles in Chemical and Biological Sensing. Chem. Rev. 2012, 112, 2739–2779. [Google Scholar] [CrossRef]
- Guerrini, L.; Krpetic, Z.; van Lierop, D.; Alvarez-Puebla, R.A.; Graham, D. Direct surface-enhanced Raman scattering analysis of DNA duplexes. Angew. Chem. Int. Ed. 2015, 54, 1144–1148. [Google Scholar] [CrossRef]
- Kneipp, K.; Wang, Y.; Kneipp, H.; Perelman, L.T.; Itzkan, I.; Dasari, R.R.; Field, M.S. Single Molecule Detection Using Surface-Enhanced Raman Scattering (SERS). Phys. Rev. Lett. 1997, 78, 1667–1670. [Google Scholar] [CrossRef]
- Greve, C.; Elsaesser, T.J. Ultrafast Two-Dimensional Infrared Spectroscopy of Guanine–Cytosine Base Pairs in DNA Oligomers. Phys. Chem. B 2013, 117, 14009–14017. [Google Scholar] [CrossRef] [PubMed]
- Hamm, P.; Zanni, M. Concepts and Methods of 2D Infrared Spectroscopy; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Peng, C.S.; Jones, K.C.; Tokmakoff, A.J. Anharmonic Vibrational Modes of Nucleic Acid Bases Revealed by 2D IR Spectroscopy. Am. Chem. Soc. 2011, 133, 15650–15660. [Google Scholar] [CrossRef] [PubMed]
- Sanstead, P.J.; Stevenson, P.; Tokmakof, A.J. Sequence-Dependent Mechanism of DNA Oligonucleotide Dehybridization Resolved through Infrared Spectroscopy. Am. Chem. Soc. 2016, 138, 11792–11801. [Google Scholar] [CrossRef]
- Li, J.; Gershow, M.; Golovchenko, J.A. DNA molecules and configurations in a solid-state nanopore microscope. Nat. Mater. 2003, 2, 611–615. [Google Scholar] [CrossRef] [PubMed]
- Yang, N.; Jiang, X. Nanocarbons for DNA sequencing: A review. Carbon 2017, 115, 293–311. [Google Scholar] [CrossRef]
- Franc, L.T.C.; Carrilho, E.; Kist, T.B.L.Q. A review of DNA sequencing techniques. Rev. Biophys. 2002, 35, 169–200. [Google Scholar] [CrossRef] [PubMed]
- Thompson, J.F.; Milos, P.M. The properties and applications of single-molecule DNA sequencing. Genome Biol. 2011, 12, 217. [Google Scholar]
- Izrailev, S.; Stepaniants, S.; Isralewitz, B.; Kosztin, D.; Lu, H.; Molnar, F.; Wriggers, W.; Schulten, K. Steered Molecular Dynamics. In Computational Molecular Dynamics: Challenges, Methods, Ideas; Springer: Berlin/Heidelberg, Germany, 1999; pp. 39–65. [Google Scholar]
- Shankla, M.; Aksimentiev, A. Conformational transitions and stop-and-go nanopore transport of single-stranded DNA on charged graphene. Nat. Commun. 2014, 5, 5171. [Google Scholar] [CrossRef]
- Liang, L.; Shen, J.-W.; Zhang, Z.; Wang, Q. DNA sequencing by two-dimensional materials: As theoretical modeling meets experiments. Biosens. Bioelectron. 2017, 89, 280–292. [Google Scholar] [CrossRef]
- Zhang, Z.; Shen, J.-W.; Wang, H.; Wang, Q.; Zhang, J.; Liang, L.; Ågren, H.; Tu, Y.J. Effects of Graphene Nanopore Geometry on DNA Sequencing. Phys. Chem. Lett. 2014, 5, 1602–1607. [Google Scholar] [CrossRef]
- Liang, L.; Zhang, Z.; Shen, J.; Zhe, K.; Wang, Q.; Wu, T.; Ågren, H.; Tu, Y. Theoretical studies on the dynamics of DNA fragment translocation through multilayer graphene nanopores. RSC Adv. 2014, 4, 50494–50502. [Google Scholar] [CrossRef]
- Zhou, Z.; Hu, Y.; Wang, H.; Xu, Z.; Wang, W.; Bai, X.; Shan, X.; Lu, X. DNA Translocation through Hydrophilic Nanopore in Hexagonal Boron Nitride. Sci. Rep. 2013, 3, 3287. [Google Scholar] [CrossRef] [PubMed]
- de Souza, F.A.L.; Amorim, R.G.; Scopel, W.L.; Scheicher, R.H. Electrical detection of nucleotides via nanopores in a hybrid graphene/h-BN sheet. Nanoscale 2017, 9, 2207–2212. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, X. DNA Sequencing by Hexagonal Boron Nitride Nanopore: A Computational Study. Nanomaterials 2016, 6, 111. [Google Scholar] [CrossRef]
- Gilbert, S.M.; Dunn, G.; Azizi, A.; Pham, T.; Shevitski, B.; Dimitrov, E.; Liu, S.; Aloni, S.; Zettl, A. Fabrication of Subnanometer-Precision Nanopores in Hexagonal Boron Nitride. Sci. Rep. 2017, 7, 15096. [Google Scholar] [CrossRef]
- Lee, D.; Lee, S.; Seong, G.H.; Choo, J.; Lee, E.K.; Gweon, D.-G.; Lee, S.A. Quantitative analysis of methyl parathion pesticides in a polydimethylsiloxane microfluidic channel using confocal surface-enhanced Raman spectroscopy. Appl. Spectroscopy 2006, 60, 373–377. [Google Scholar] [CrossRef]
- Bell, S.E.J.; Sirimuthu, N.M.S.J. Surface-Enhanced Raman Spectroscopy (SERS) for Sub-Micromolar Detection of DNA/RNA Mononucleotides. Am. Chem. Soc. 2006, 128, 15580–15581. [Google Scholar] [CrossRef]
- Madzharova, F.; Heiner, Z.; Gühlke, M.; Kneipp, J.J. Surface-Enhanced Hyper-Raman Spectra of Adenine, Guanine, Cytosine, Thymine, and Uracil. Phys. Chem. C 2016, 120, 15415–15423. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Kerman, S.; Neutens, P.; Willems, K.; Cornelissen, S.; Lagae, L.; Stakenborg, T.; van Dorpe, P. High spatial resolution nanoslit SERS for single-molecule nucleobase sensing. Nat. Commun. 2018, 9, 1733. [Google Scholar] [CrossRef]
- Merchant, C.A.; Healy, K.; Wanunu, M.; Ray, V.; Peterman, N.; Bartel, J.; Fischbein, M.D.; Venta, K.; Luo, Z.; Johnson, A.T.C.; et al. DNA Translocation through Graphene Nanopores. Nano Lett. 2010, 10, 2915–2921. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Baryly, C.T.; Gould, I.R.; Merz, K.M., Jr.; Ferguson, F.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Zayak, A.T.; Hu, Y.S.; Choo, H.; Bokor, J.; Cabrini, S.; Schuck, P.J.; Neaton, J.B. Chemical Raman Enhancement of Organic Adsorbates on Metal Surfaces. Phys. Rev. Lett. 2011, 106, 083003. [Google Scholar] [CrossRef] [PubMed]
- Akahori, R.; Hag, T.; Hatano, T.; Yanagi, I.; Ohura, T.; Hamamura, H.; Iwasaki, T.; Yokoi, T.; Anazawa, T. Slowing single-stranded DNA translocation through a solid-state nanopore by decreasing the nanopore diameter. Nanotechnology 2014, 25, 275501. [Google Scholar] [CrossRef] [PubMed]
- Mirsaidov, U.; Comer, J.; Dimitrov, V.; Aksimentiev, A.; Timp, G. Slowing the translocation of double-stranded DNA using a nanopore smaller than the double helix. Nanotechnology 2010, 21, 395501. [Google Scholar] [CrossRef]
- El-Khoury, P.Z.; Hu, D.; Hess, W.P. Junction Plasmon-Induced Molecular Reorientation. J. Phys. Chem. Lett. 2013, 4, 3435–3439. [Google Scholar] [CrossRef]
- El-Khoury, W.P.; Hess, W.P. Raman scattering from 1,3-propanedithiol at a hot spot: Theory meets experiment. Chem. Phys. Lett. 2013, 581, 57–63. [Google Scholar] [CrossRef]
- El-Khoury, P.Z.; Ueltschi, T.W.; Mifflin, A.L.; Hu, D.; Hess, W.P. Frequency-Resolved Nanoscale Chemical Imaging of 4,4′-Dimercaptostilbene on Silver. J. Phys. Chem. C 2014, 118, 27525–27530. [Google Scholar] [CrossRef]
- El-Khoury, P.Z.; Johnson, G.E.; Novikova, I.V.; Gong, Y.; Joly, A.G.; Evans, J.E.; Zamkov, M.; Laskin, J.; Hess, W.P. Enhanced Raman scattering from aromatic dithiols electrosprayed into plasmonic nanojunctions. Faraday Discuss. 2015, 184, 339–357. [Google Scholar] [CrossRef]
- Wang, J.; Wang, G.; Zhao, J. Structures and electronic properties of Cu20, Ag20, and Au20 clusters with density functional method. Chem. Phys. Lett. 2003, 380, 716–720. [Google Scholar] [CrossRef]
- Olsson, P.A.T. Transverse resonant properties of strained gold nanowires. J. Appl. Phys. 2010, 108, 34318. [Google Scholar] [CrossRef]
- Qing, P.; Leng, Y.; Zhao, X.; Cummings, P.T. Molecular simulations of stretching gold nanowires in solvents. Nanotechnology 2007, 18, 424007. [Google Scholar]
- Muntean, C.M.; Bratu, I.; Leopold, N.; Morari, C.; Buimaga-Iarincaa, L.; Purcaru, M.A.P. Subpicosecond surface dynamics in genomic DNA from in vitro-grown plant species: A SERS assessment. Phys. Chem. Chem. Phys. 2015, 17, 21323–21330. [Google Scholar] [CrossRef] [PubMed]
- Latorre, F.; Kupfer, S.; Bocklitz, T.; Kinzel, D.; Trautmann, S.; Grafe, S.; Deckert, V. Spatial resolution of tip-enhanced Raman spectroscopy–DFT assessment of the chemical effect. Nanoscale 2016, 8, 10229–10239. [Google Scholar] [CrossRef] [PubMed]
- Keyser, U.F.; Koeleman, B.N.; Dorp, S.V.; Krapf, D.; Smeets, R.M.M.; Lemay, S.G.; Dekker, N.H.; Dekker, C. Direct force measurements on DNA in a solid-state nanopore. Nat. Phys. 2006, 2, 473–477. [Google Scholar] [CrossRef]
- Takeuchi, K.; Zolotoukhina, T. Individual DNA base identification at the transport through graphene nanopore. In Proceedings of the ASME 11th International Conference on Nanochannels, Microchannels, and Minichannels, ICNMM2013, Sapporo, Japan, 16–19 June 2013. [Google Scholar]
- Fornaro, T.; Biczysko, M.; Monti, S.; Barone, V. Dispersion corrected DFT approaches for anharmonic vibrational frequency calculations: Nucleobases and their dimers. Phys. Chem. Chem. Phys. 2014, 16, 10112–10128. [Google Scholar] [CrossRef]
- Guchhait, B.; Liu, Y.; Siebert, T.; Elsaessera, T. Ultrafast vibrational dynamics of the DNA backbone at different hydration levels mapped by two-dimensional infrared spectroscopy. Struct. Dyn. 2016, 3, 043202. [Google Scholar] [CrossRef]
- Fisher, S.A.; Apra, E.; Govind, N.; Hess, W.P.; El-Khoury, P.Z. Nonequilibrium Chemical Effects in Single-Molecule SERS Revealed by Ab Initio Molecular Dynamics Simulations. J. Phys. Chem. A 2017, 121, 1344–1350. [Google Scholar] [CrossRef]
- Fisher, S.A.; Ueltschi, T.W.; El-Khoury, P.Z.; Miffin, A.L.; Hess, W.P.; Wang, H.-F.; Cramer, C.J.; Govind, N. Infrared and Raman Spectroscopy from Ab Initio Molecular Dynamics and Static Normal Mode Analysis: The C–H Region of DMSO as a Case Study. J. Phys. Chem. B 2016, 120, 1429–1436. [Google Scholar] [CrossRef]
- Mante, P.-A.; Belliard, L.; Perrin, B. Acoustic phonons in nanowires probed by ultrafast pump-probe spectroscopy. Nanophotonics 2018, 7, 1759–1780. [Google Scholar] [CrossRef]
- Zolotoukhina, T.; Nitta, T.; Takeuchi, S.; Wakamatsu, D. Vibrational spectra of methylated forms of cytosine and adenine in the graphene nanopore and for regions of hydrogen binding. In Proceedings of the 19th International Conference on the Science and Application of Nanotubes and Low-Dimensional Materials (NT18), Beijing, China, 15–20 July 2018. [Google Scholar]
- Giannozzi, P.; Baroni, S. Nicola Bonini4, Matteo Calandra5, Roberto Car6, Carlo Cavazzoni7,8, Davide Ceresoli4, Guido L Chiarotti9, Matteo Cococcioni10, Ismaila Dabo QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Almehmadi, L.M.; Curley, S.M.; Tokranova, N.A.; Tenenbaum, S.A.; Lednev, I.K. Surface Enhanced Raman Spectroscopy for Single Molecule Protein Detection. Sci. Rep. 2019, 9, 12356. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).